Correction: Michler et al. Review and Assessment of the Effect of Hydrogen Gas Pressure on the Embrittlement of Steels in Gaseous Hydrogen Environment. Metals 2021, 11, 637
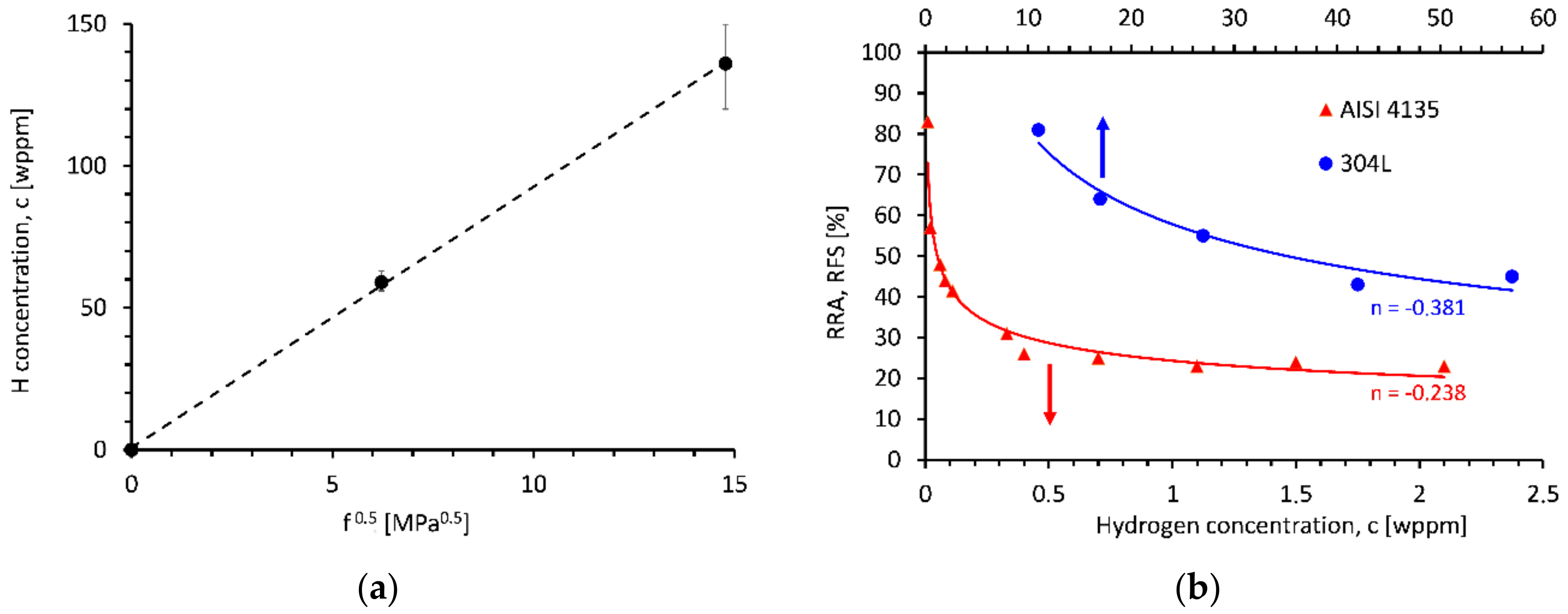
- The exponent was found to be smaller than 0.4. Since theoretical assumptions predict n = 0.5 for a fully undistorted hydrogen reaction chain, the reviewed data are interpreted in a way that hydrogen-dislocation interactions are the rate-limiting step controlling hydrogen effects in steels.
Conflicts of Interest
Reference
- Michler, T.; Wackermann, K.; Schweizer, F. Review and Assessment of the Effect of Hydrogen Gas Pressure on the Embrittlement of Steels in Gaseous Hydrogen Environment. Metals 2021, 11, 637. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michler, T.; Wackermann, K.; Schweizer, F. Correction: Michler et al. Review and Assessment of the Effect of Hydrogen Gas Pressure on the Embrittlement of Steels in Gaseous Hydrogen Environment. Metals 2021, 11, 637. Metals 2021, 11, 1158. https://doi.org/10.3390/met11081158
Michler T, Wackermann K, Schweizer F. Correction: Michler et al. Review and Assessment of the Effect of Hydrogen Gas Pressure on the Embrittlement of Steels in Gaseous Hydrogen Environment. Metals 2021, 11, 637. Metals. 2021; 11(8):1158. https://doi.org/10.3390/met11081158
Chicago/Turabian StyleMichler, Thorsten, Ken Wackermann, and Frank Schweizer. 2021. "Correction: Michler et al. Review and Assessment of the Effect of Hydrogen Gas Pressure on the Embrittlement of Steels in Gaseous Hydrogen Environment. Metals 2021, 11, 637" Metals 11, no. 8: 1158. https://doi.org/10.3390/met11081158
APA StyleMichler, T., Wackermann, K., & Schweizer, F. (2021). Correction: Michler et al. Review and Assessment of the Effect of Hydrogen Gas Pressure on the Embrittlement of Steels in Gaseous Hydrogen Environment. Metals 2021, 11, 637. Metals, 11(8), 1158. https://doi.org/10.3390/met11081158





