A New Approach to Calculate the Velocity of Interdendritic Fluid Flow during Solidification Using Etched Surface Height of Actual Metal Ingot
Abstract
1. Introduction
2. Etched Surface Height Measurement
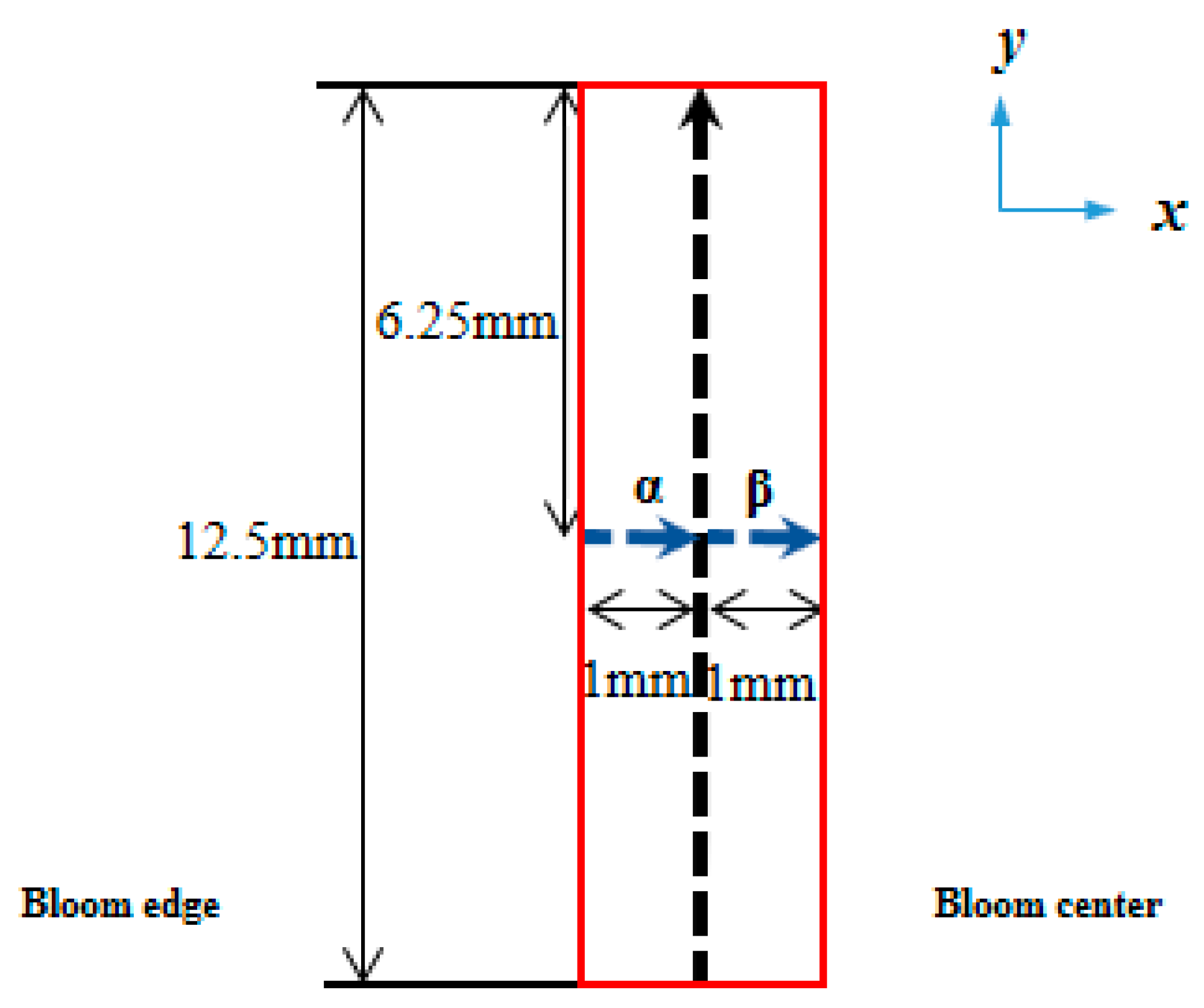
2.1. Sample Preparation
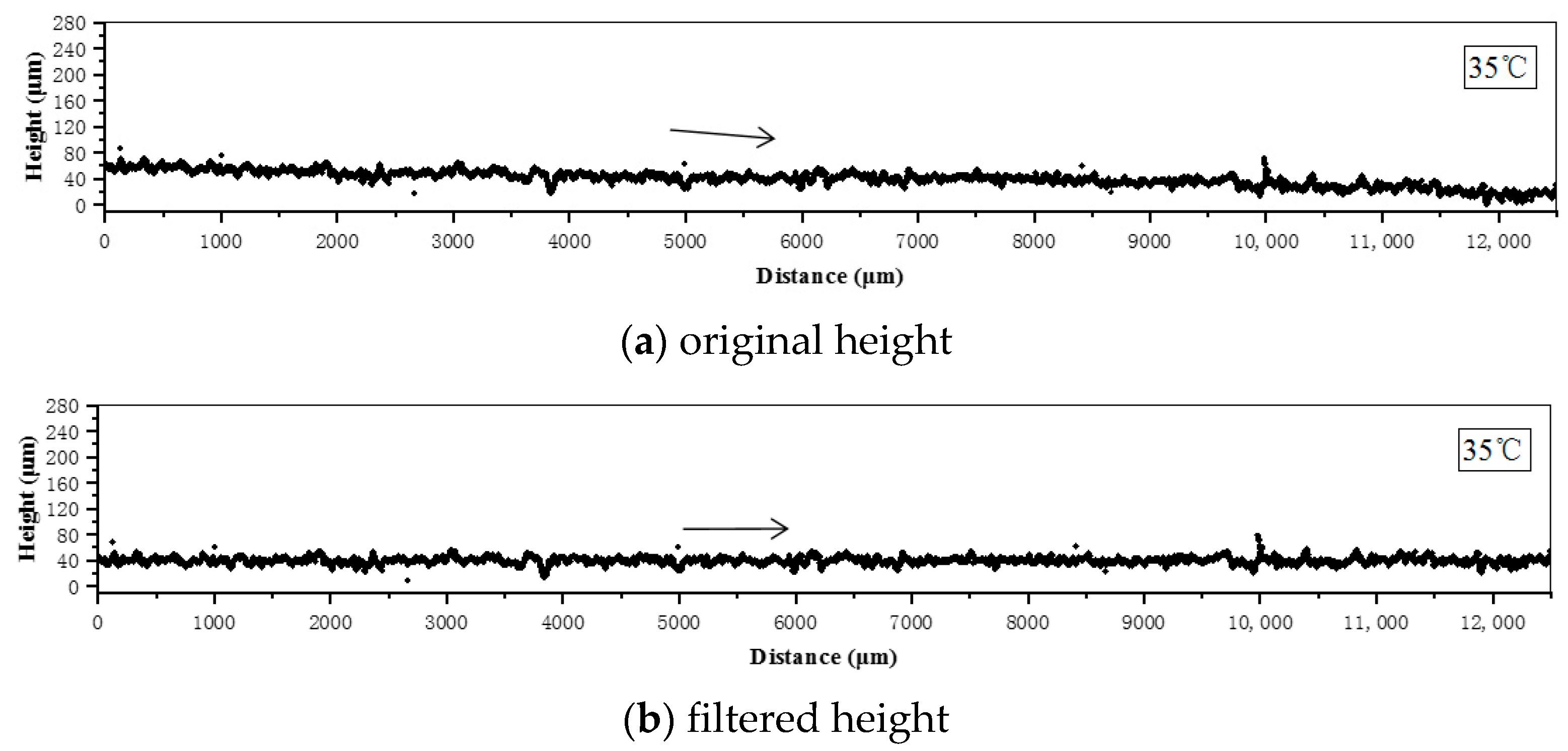
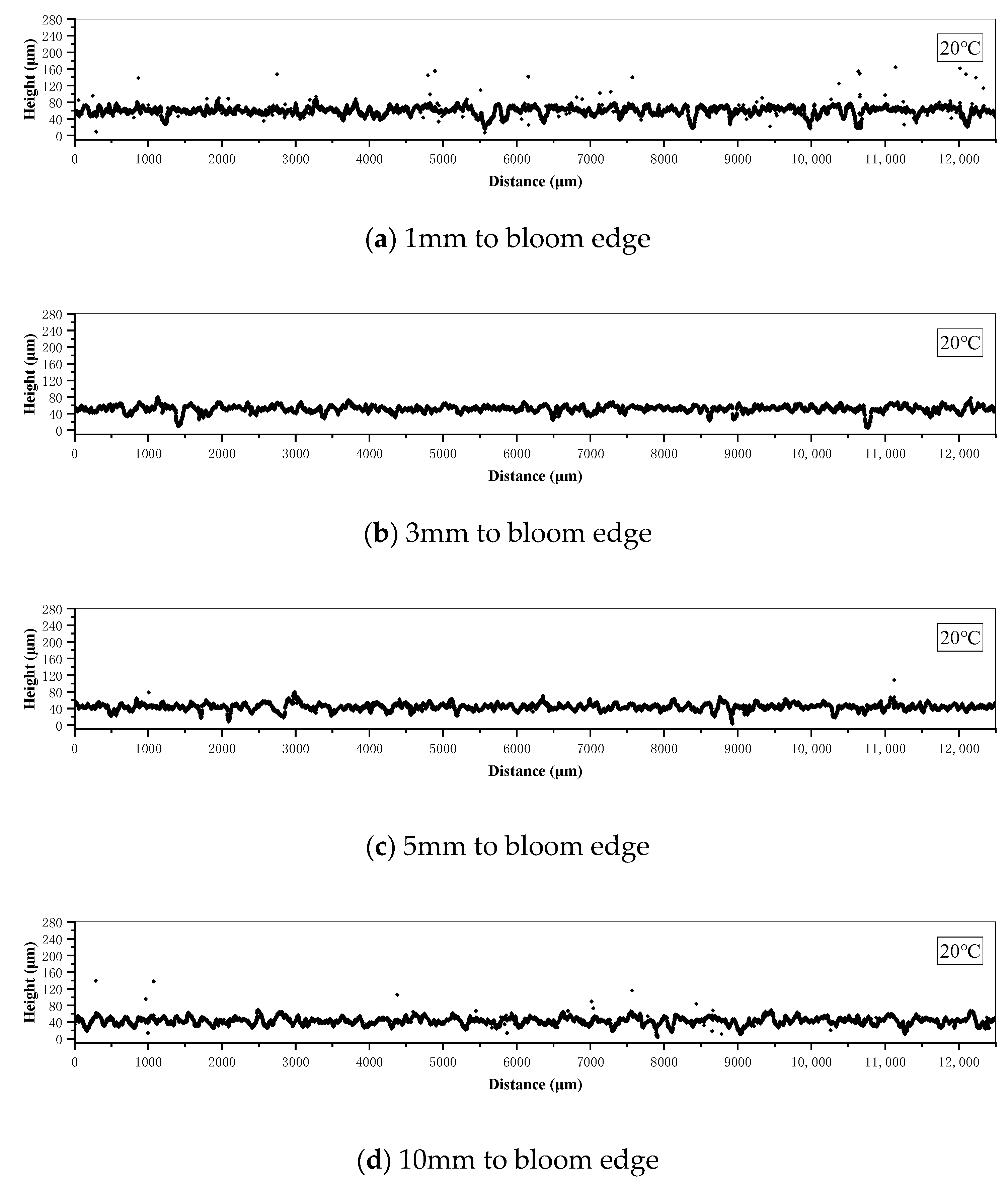
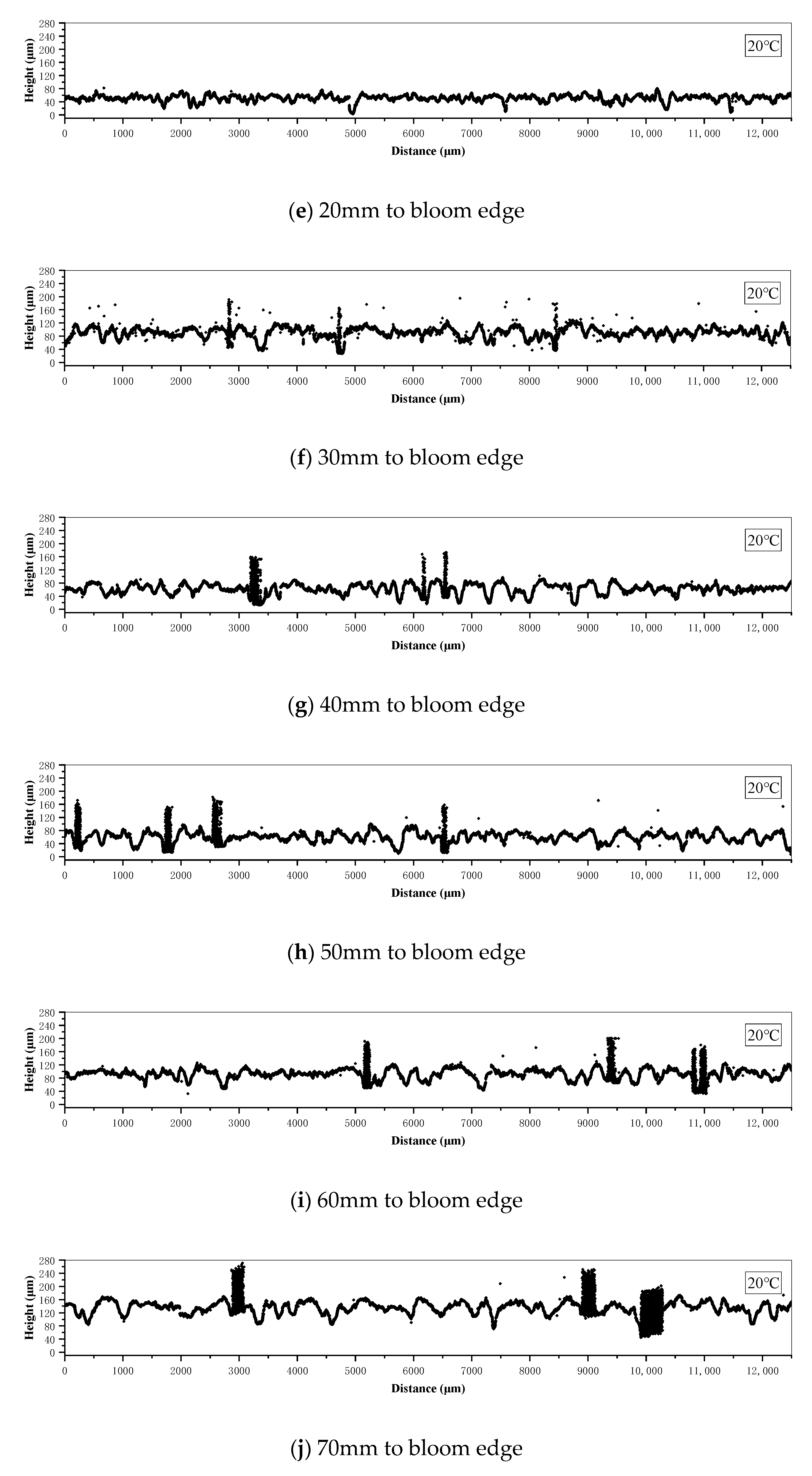
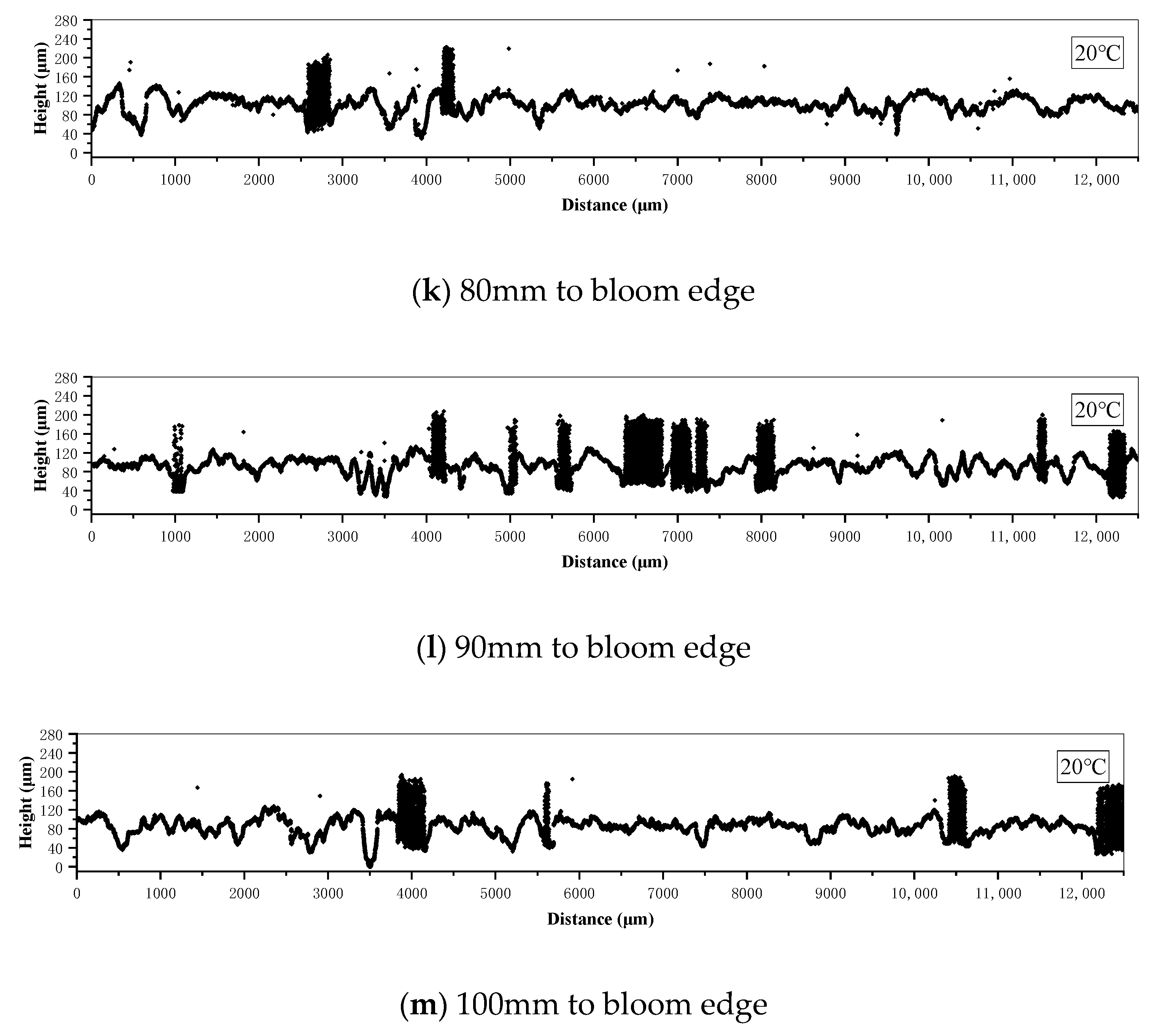
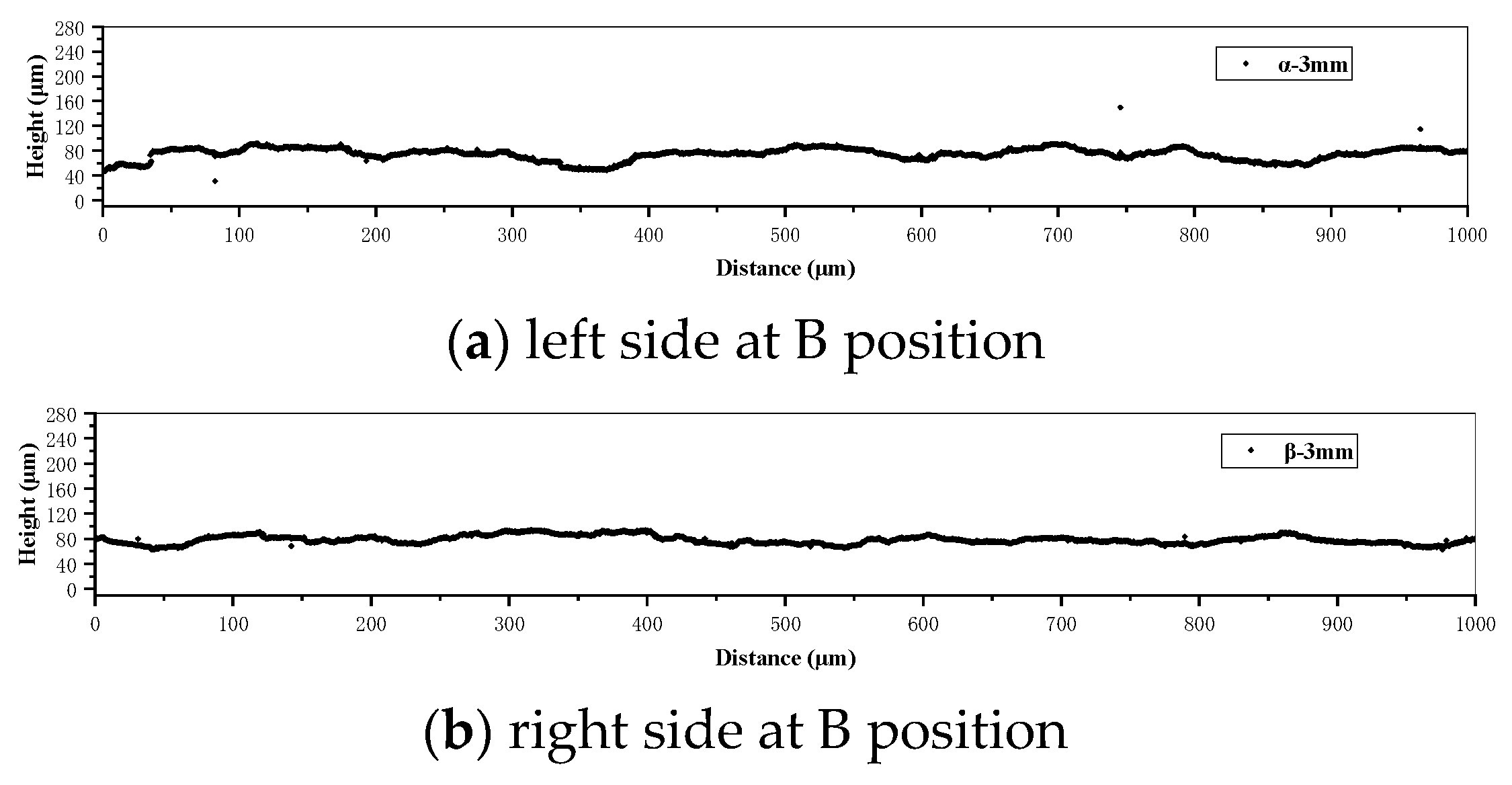
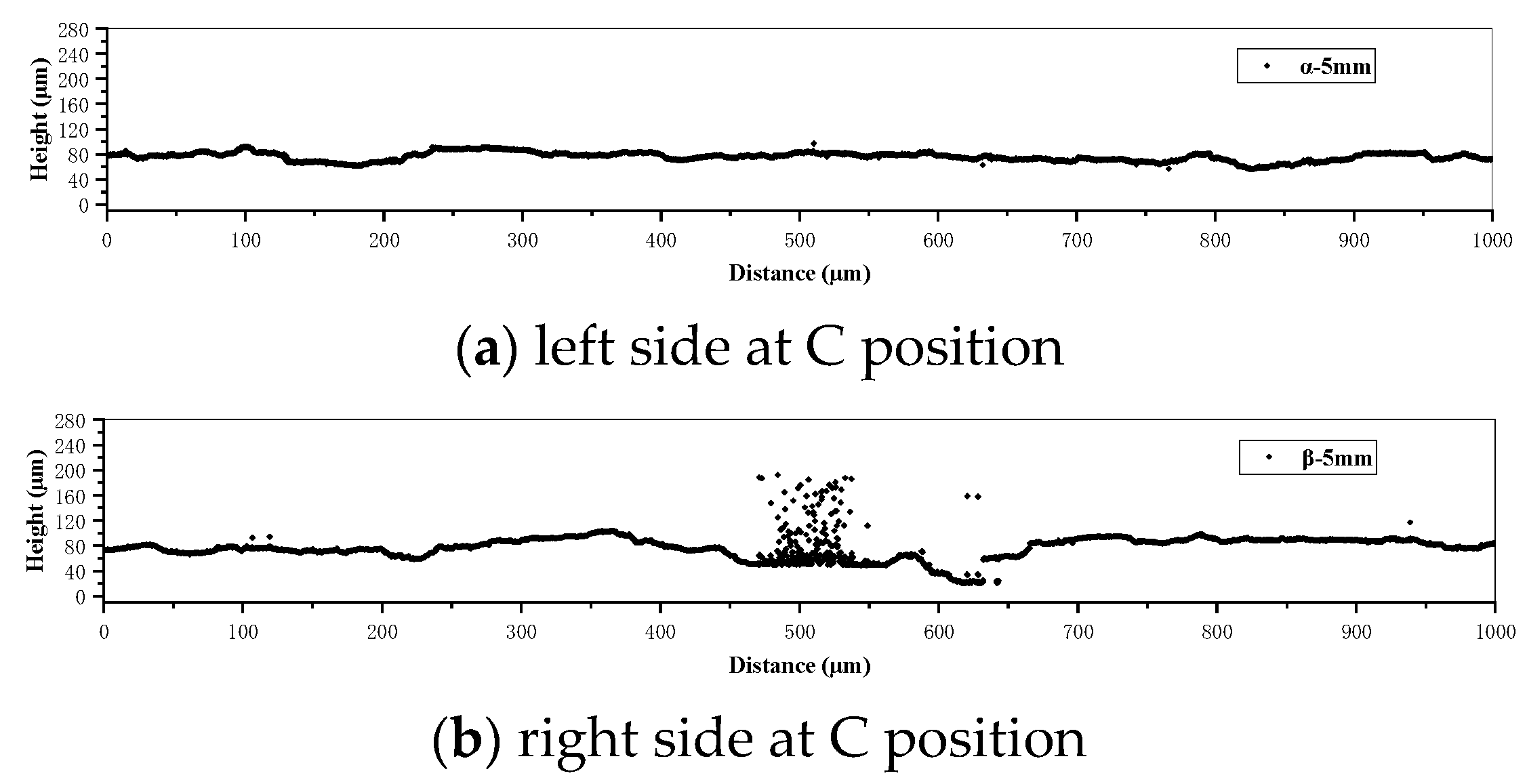
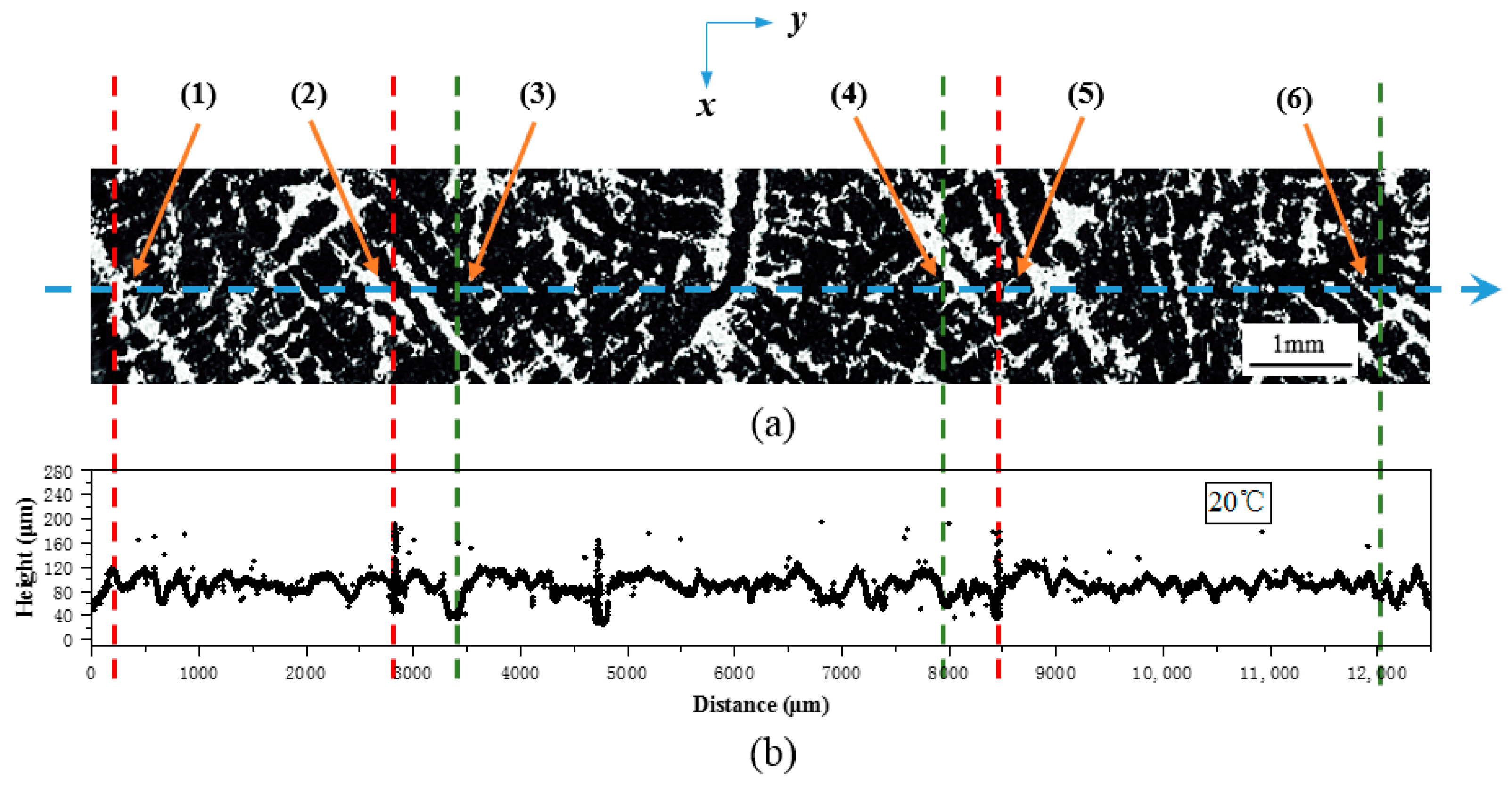
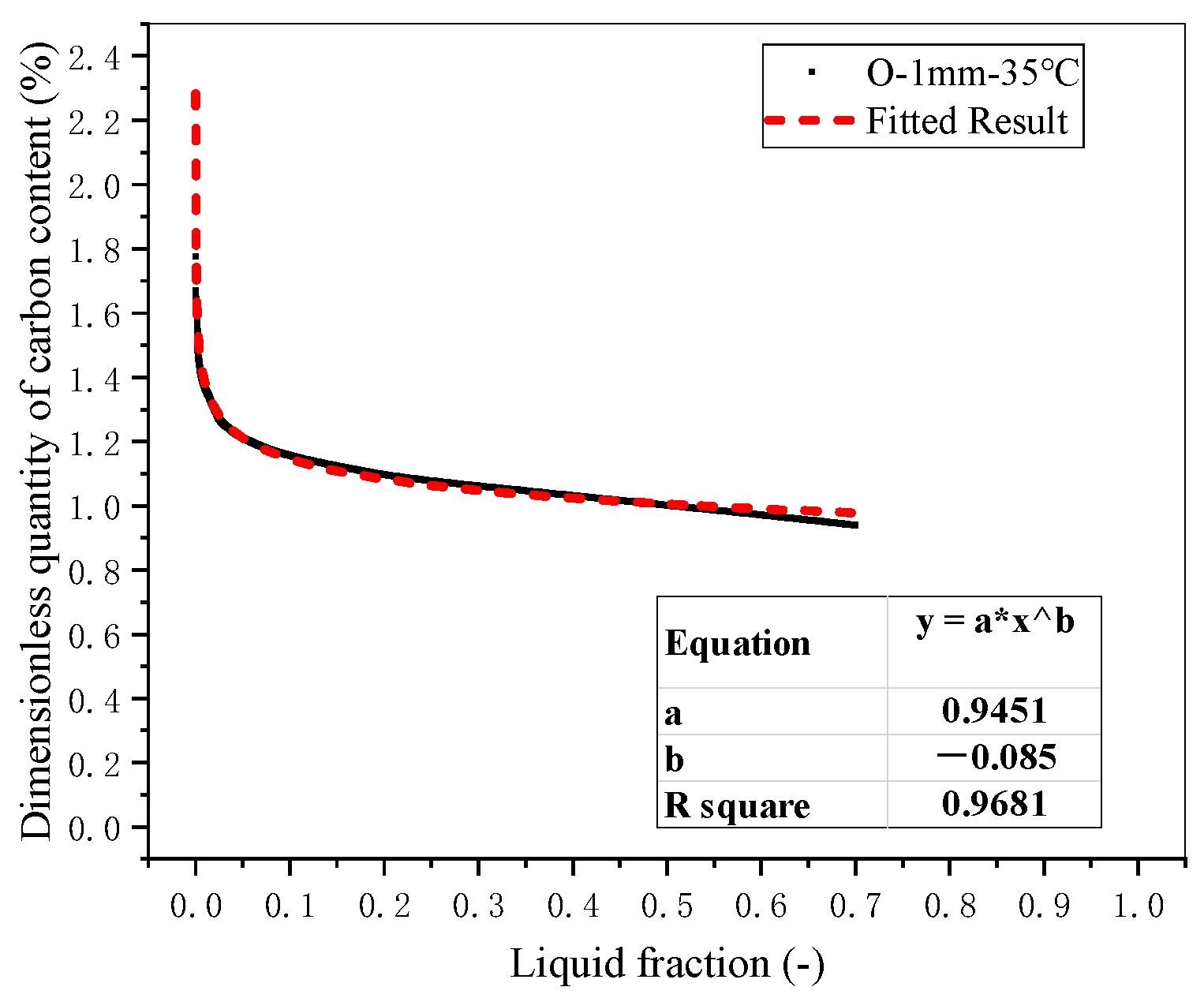
2.2. Etched Surface Height
3. Model Description
4. Results and Discussion
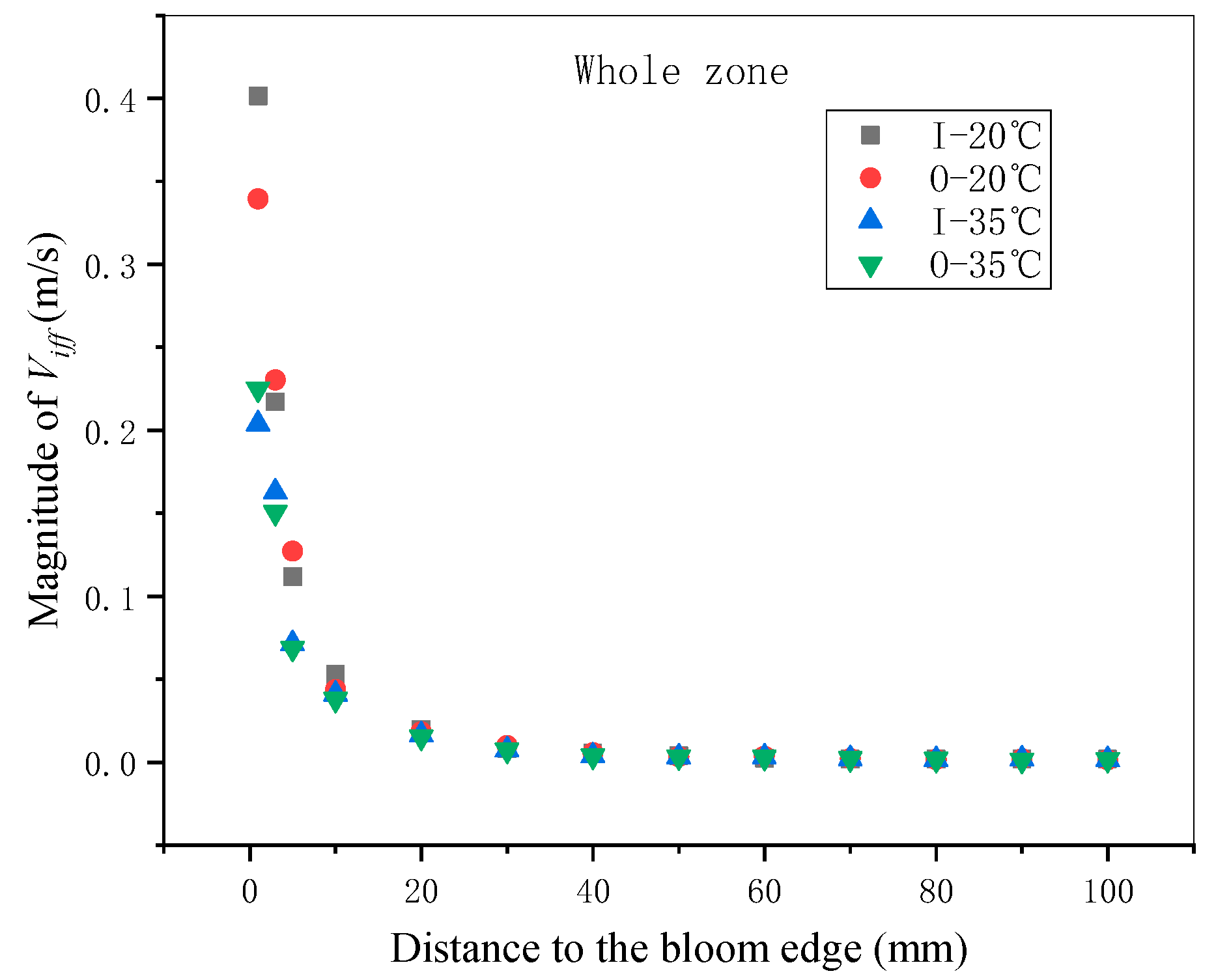
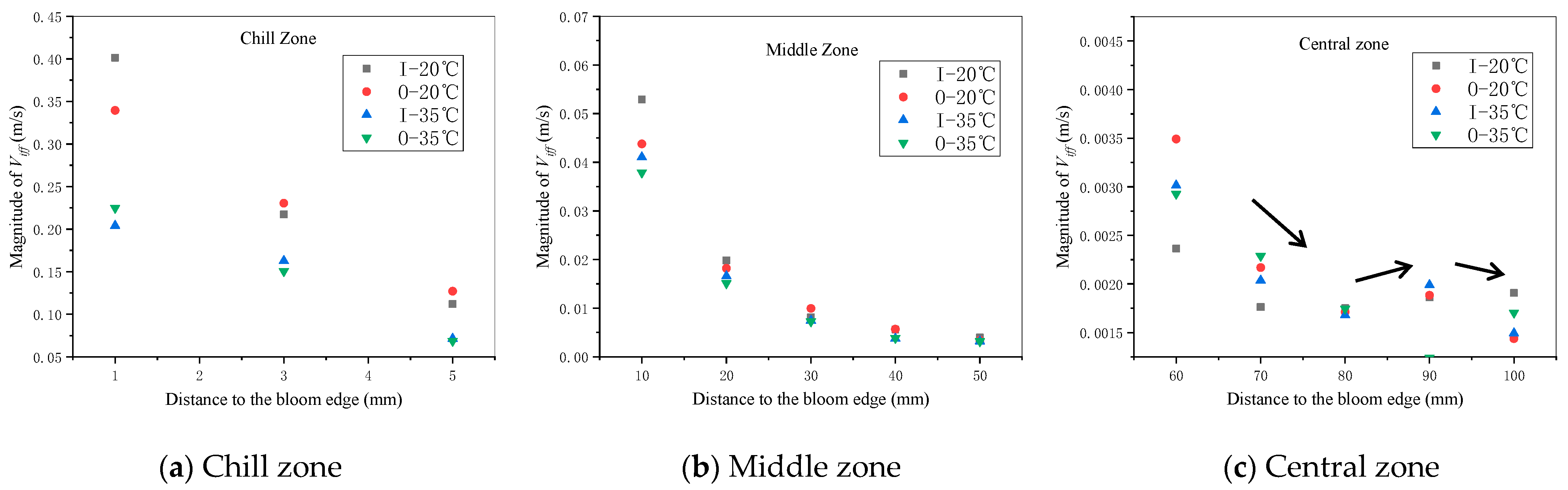
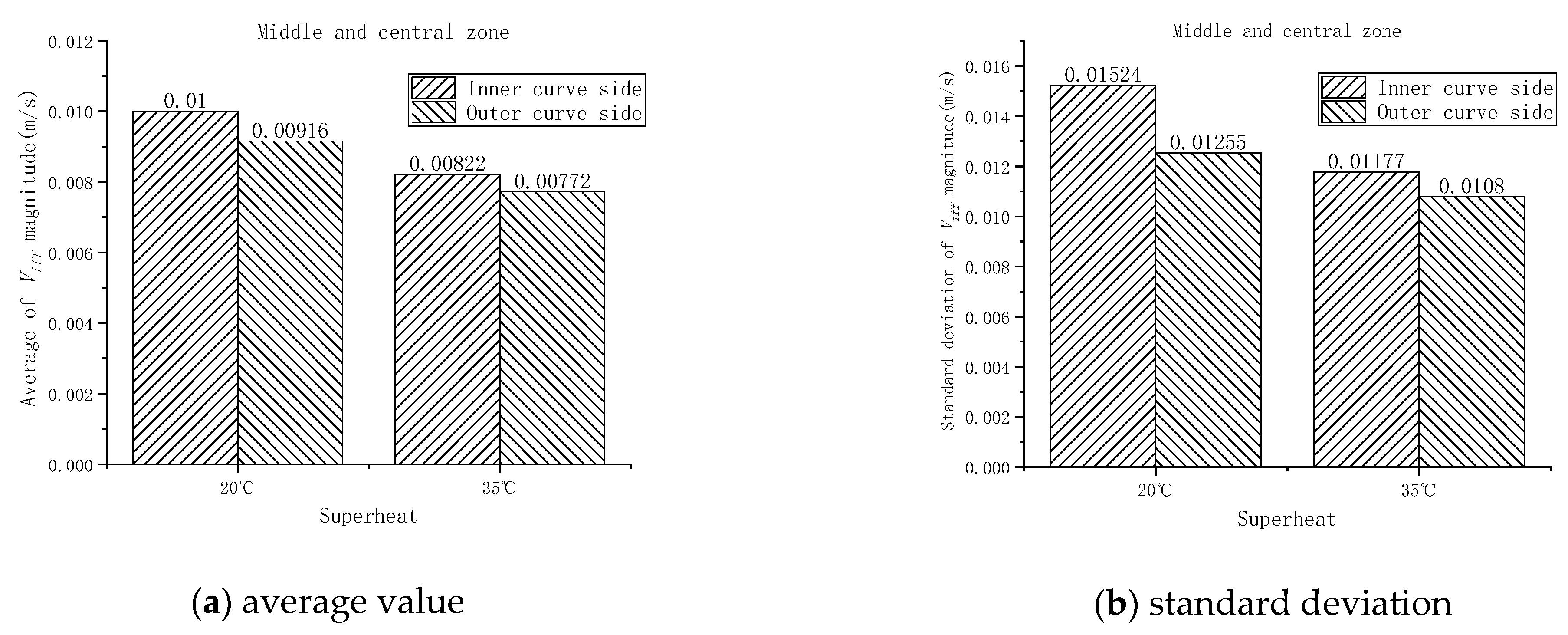
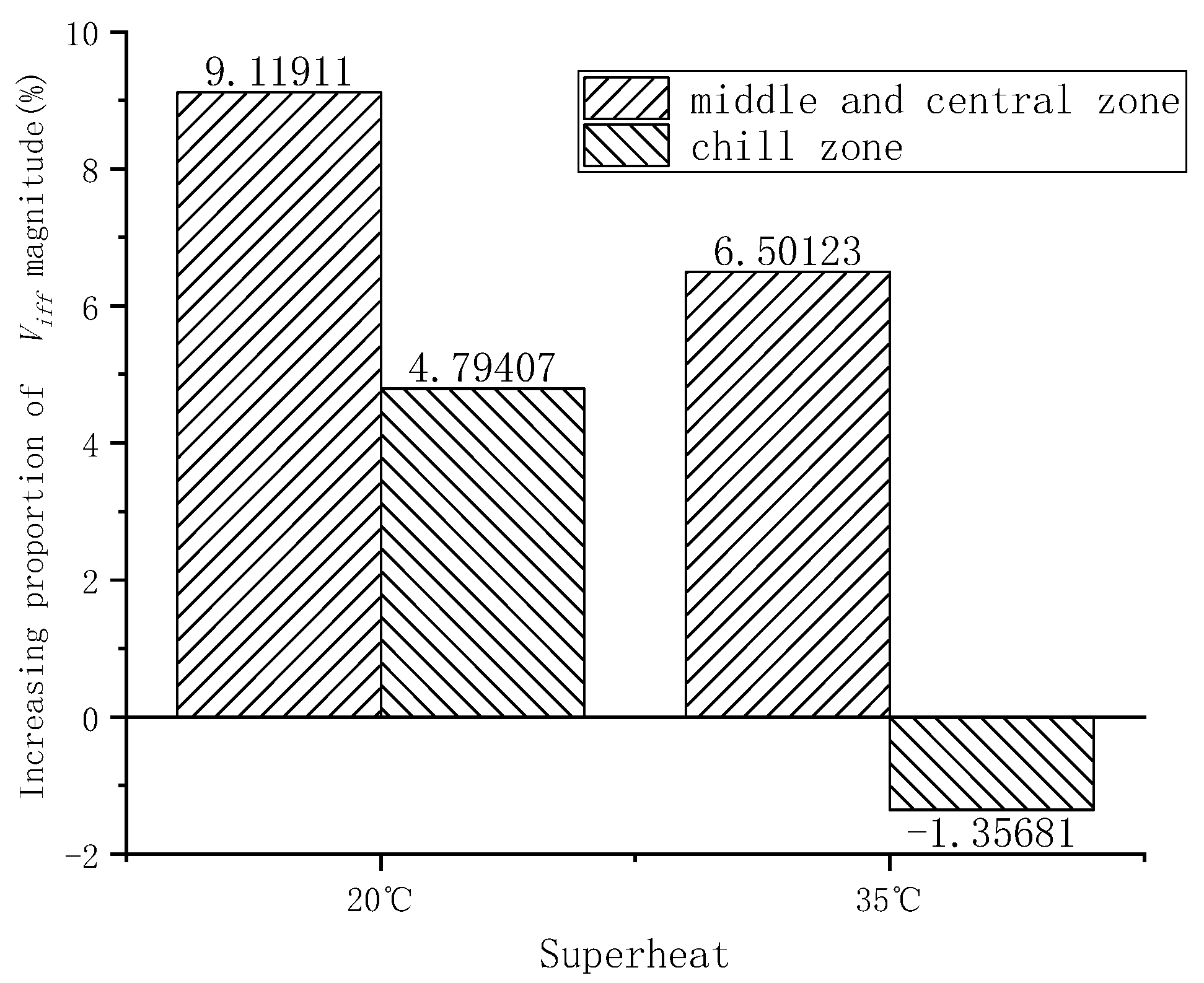
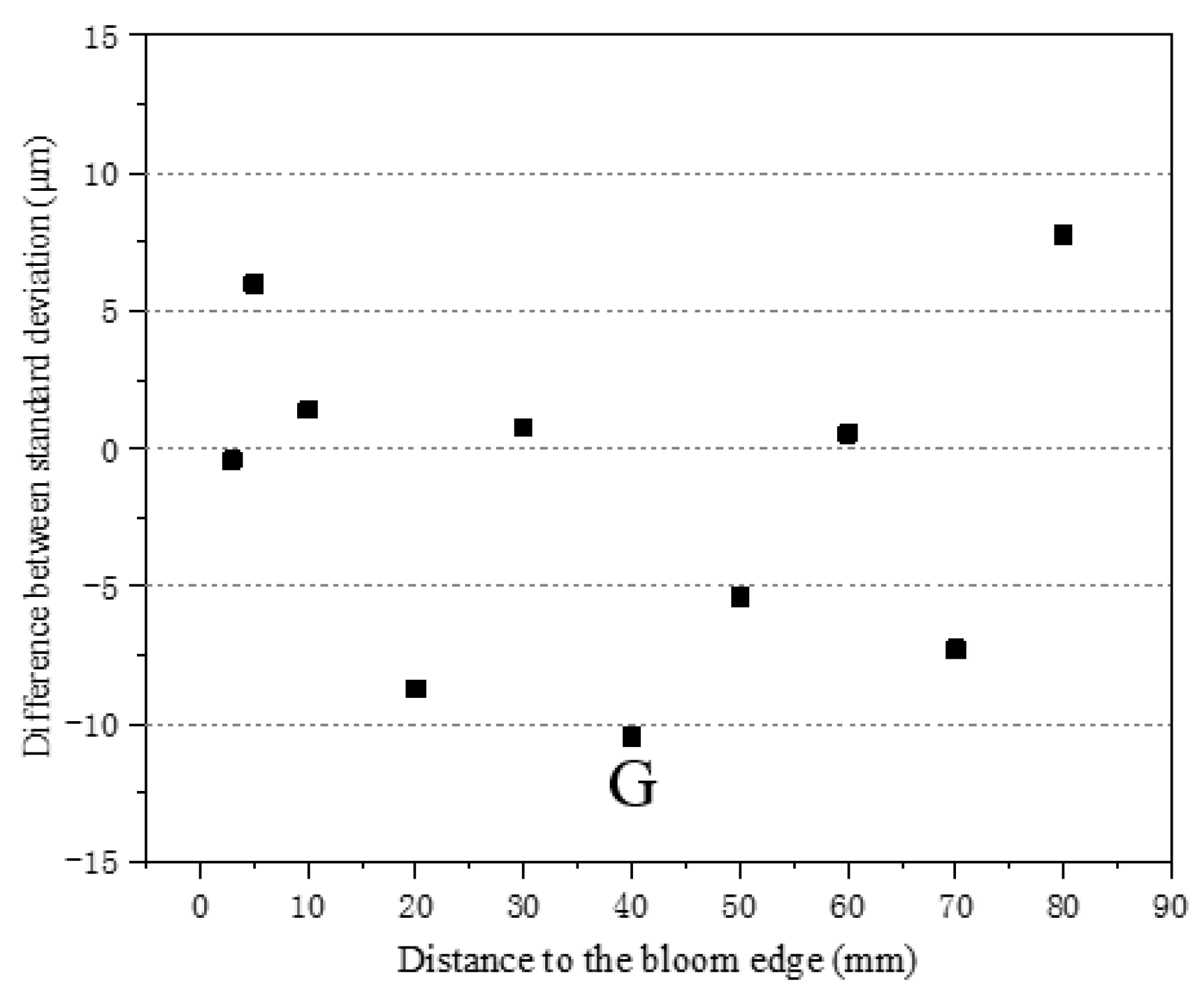
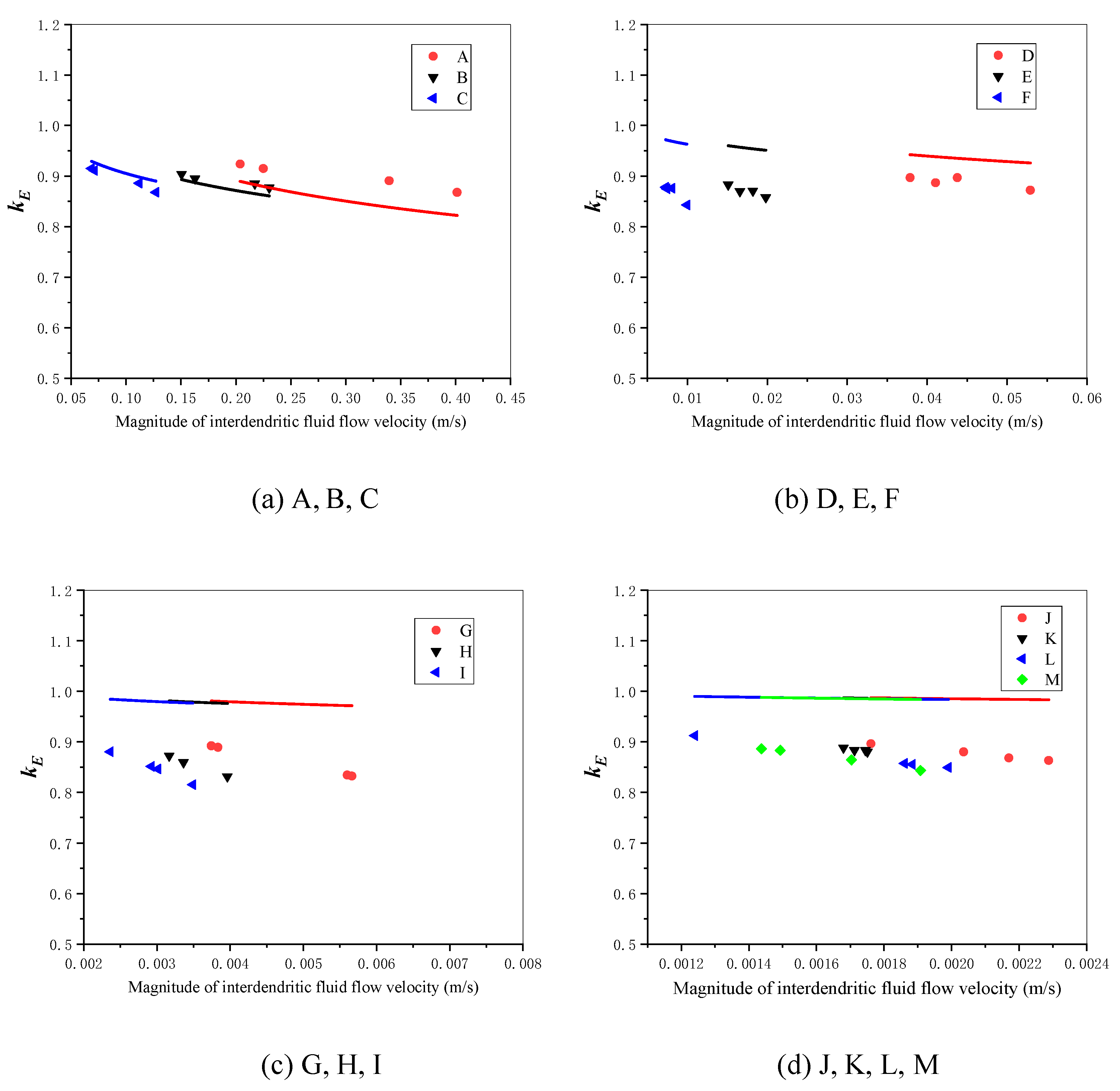
4.1. Magnitude of Interdendritic Fluid Flow Velocity
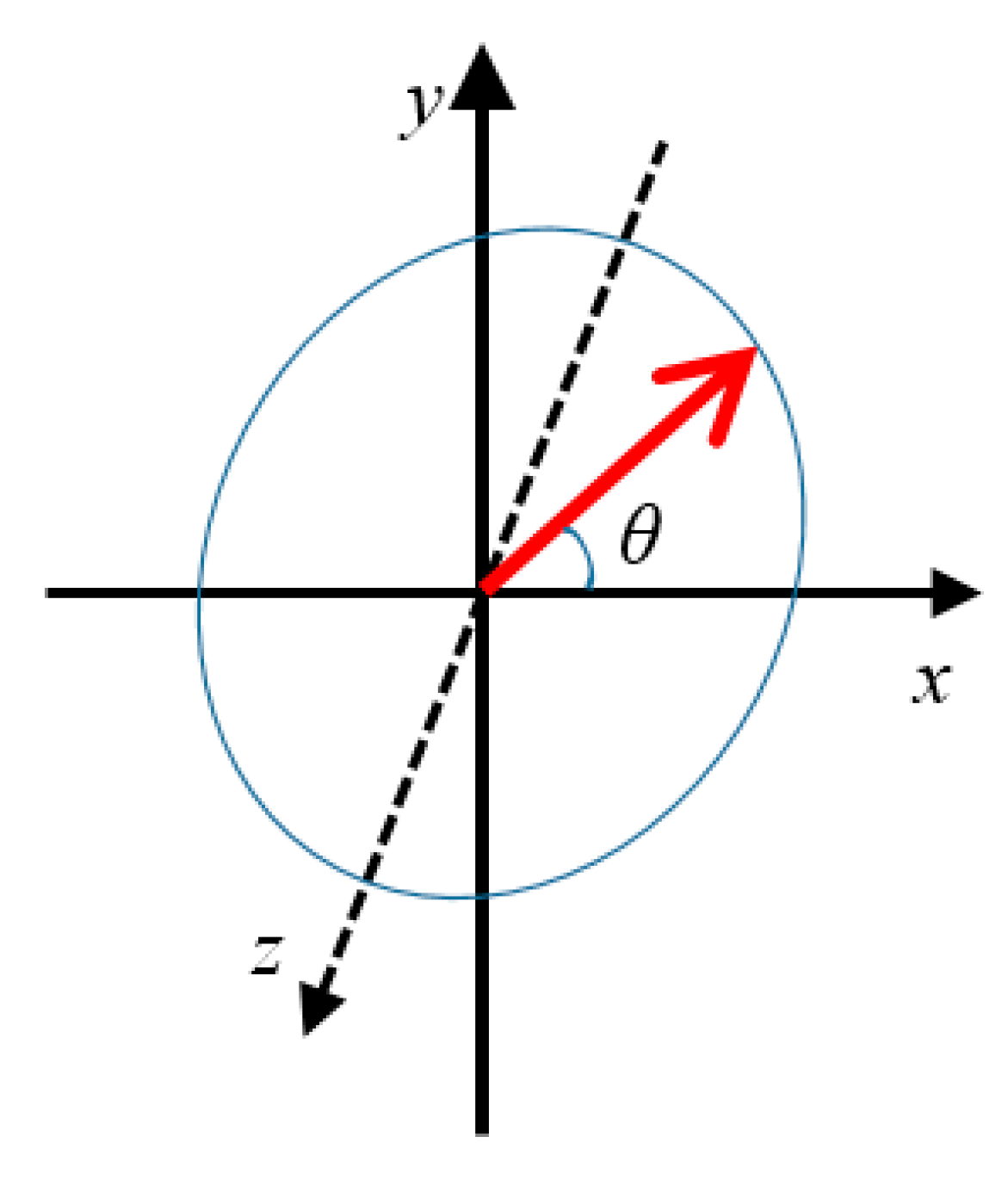
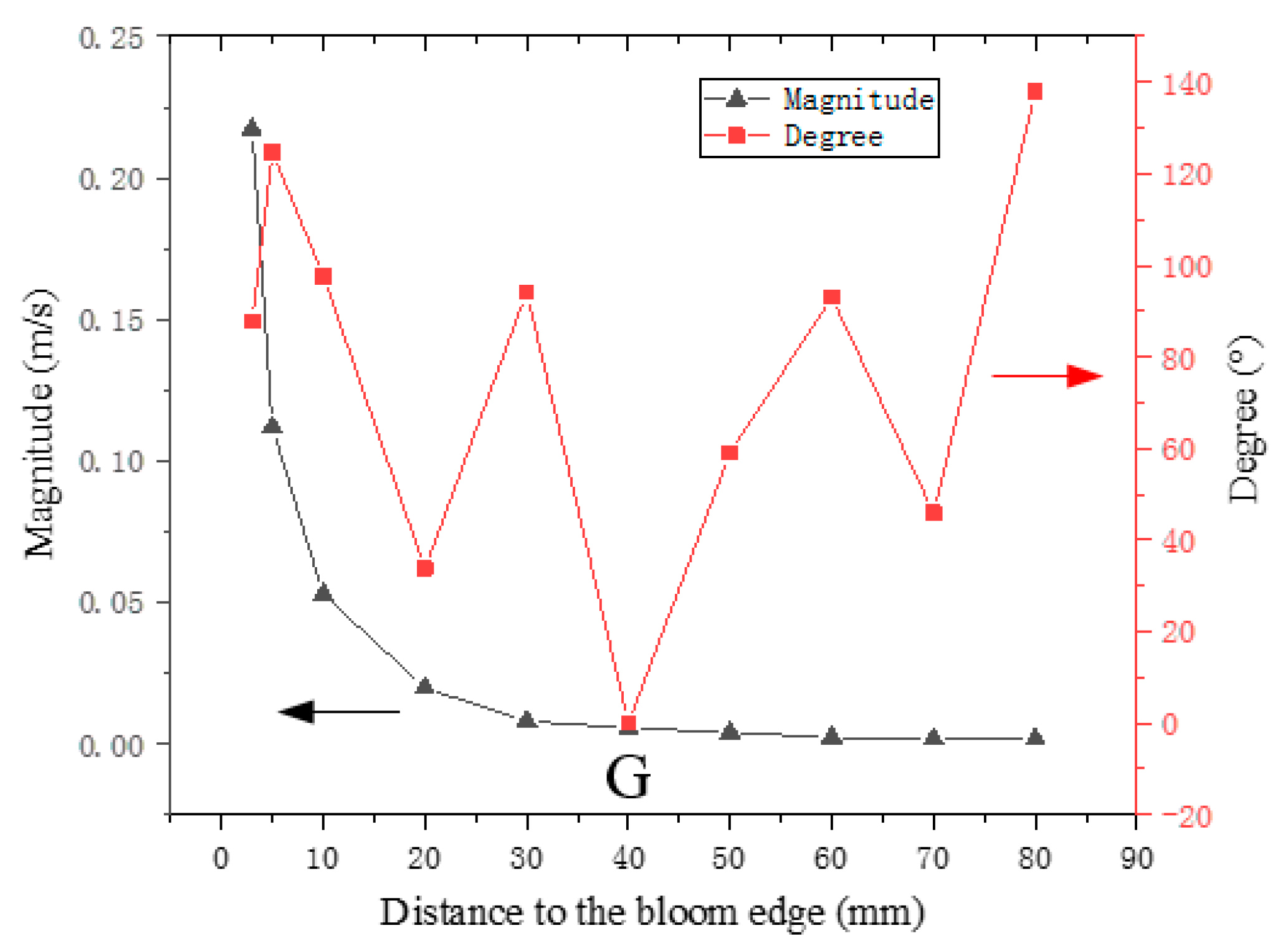
4.2. Direction of Interdendritic Fluid Flow Velocity
5. Model Verification Discussion and Further Work
6. Conclusions
- We have put forward a full model that can calculate the magnitude and direction of interdendritic fluid flow during solidifying at different positions by measuring the corresponding etched surface heights of casting metal bloom.
- Calculated results show that the velocity magnitude decreases from continuous casting bloom margin toward the center as a whole, and it decreases in the central zone first, then shows an increasing trend, and decreases again finally, which is in correspondence with segregation morphology. Besides the chilled zone, the velocity magnitude of the interdendritic fluid flow in the inner curve side is higher than that in the outer curve side. The velocity magnitude and related fluctuation is higher under 20 °C. Moreover, it is indicated that the fluctuation extent of SDAS is more relevant with interdendritic fluid flow, although the SDAS magnitude is mainly determined by the cooling rate.
- Meanwhile, on the basis of the magnitude and direction of velocity, there is a positive correlation between segregation area ratio and the effective ratio between interdendritic flow velocity and growth velocity, especially in equiaxed grain zones.
- On the whole, the model is demonstrated as a useful approach for determining the velocity of interdendritic fluid flow. The velocity distribution and associated defects formation in two or three-dimensional multiscale space can be better understand based on this model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kerr, R.; Woods, A.W.; Worster, M.; Huppert, H.E. Disequilibrium and macrosegregation during solidification of a binary melt. Nature 1989, 340, 357–362. [Google Scholar] [CrossRef]
- Pickering, E.J. Macrosegregation in Steel Ingots: The Applicability of Modelling and Characterisation Techniques. ISIJ Int. 2013, 53, 935–949. [Google Scholar] [CrossRef]
- Combeau, H.; Založnik, M.; Hans, S.; Richy, P.E. Prediction of Macrosegregation in Steel Ingots: Influence of the Motion and the Morphology of Equiaxed Grains. Met. Mater. Trans. A 2009, 40, 289–304. [Google Scholar] [CrossRef]
- Li, D.; Chen, X.; Fu, P.; Ma, X.; Liu, H.; Chen, Y.; Cao, Y.; Luan, Y.; Li, Y. Inclusion flotation-driven channel segregation in solidifying steels. Nat. Commun. 2014, 5, 5572. [Google Scholar] [CrossRef]
- Flemings, M.C.; Nero, G.E. Macrosegregation: Part 1. Trans. Metall. Soc. AIME 1967, 239, 1449–1461. [Google Scholar]
- Flemings, M.C. Our Understanding of Macrosegregation. Past and Present. ISIJ Int. 2000, 40, 833–841. [Google Scholar] [CrossRef]
- Beckermann, C. Modelling of macrosegregation: Applications and future needs. Int. Mater. Rev. 2002, 47, 243–261. [Google Scholar] [CrossRef]
- Poirier, D.; Ocansey, P. Permeability for flow of liquid through equiaxial mushy zones. Mater. Sci. Eng. A 1993, 171, 231–240. [Google Scholar] [CrossRef]
- Brown, S.; Spittle, J.; Jarvis, D.; Walden-Bevan, R. Numerical determination of liquid flow permeabilities for equiaxed dendritic structures. Acta Mater. 2002, 50, 1559–1569. [Google Scholar] [CrossRef]
- Bernard, D.; Nielsen, Ø.; Salvo, P.L. Cloetens, Permeability assessment by 3D interdendritic flow simulations on microto-mography mappings of Al–Cu alloys. Mater. Sci. Eng. A 2005, 392, 112–120. [Google Scholar] [CrossRef]
- Santos, R.; Melo, M. Permeability of interdendritic channels. Mater. Sci. Eng. A 2005, 391, 151–158. [Google Scholar] [CrossRef]
- Khajeh, E.; Maijer, D.M. Physical and numerical characterization of the near-eutectic permeability of aluminum–copper alloys. Acta Mater. 2010, 58, 6334–6344. [Google Scholar] [CrossRef]
- Mitraa, S.; Mansori, M.; Castro, A.; Costin, M. Study of the evolution of transport properties induced by additive processing sand mold using X-ray computed tomography. J. Mater. Process. Technol. 2020, 277, 116495. [Google Scholar] [CrossRef]
- Takaki, T.; Sakane, S.; Ohno, M.; Shibuta, Y.; Aoki, T. Permeability prediction for flow normal to columnar solidification struc-tures by large scale simulations of phase field and lattice Boltzmann methods. Acta Mater. 2019, 164, 237–249. [Google Scholar] [CrossRef]
- Koshikawa, T.; Bellet, M.; Gandin, C.-A.; Yamamura, H.; Bobadilla, M. Experimental study and two-phase numerical modeling of macrosegregation induced by solid deformation during punch pressing of solidifying steel ingots. Acta Mater. 2017, 124, 513–527. [Google Scholar] [CrossRef]
- Pakanati, A.; Tveito, K.O.; M’Hamdi, M.; Combeau, H.; Založnik, M. Application of an Equiaxed Grain Growth and Transport Model to Study Macrosegregation in a DC Casting Experiment. Met. Mater. Trans. A 2019, 50, 1773–1786. [Google Scholar] [CrossRef]
- Sengupta, J.; Leung, J.; Leung, J. Bridging the gap: MXRF technique rapidly maps centerline segregation. Iron Steel Technol. 2017, 7, 66–74. [Google Scholar]
- Tsuchinaga, M.; Abe, S. The Pickling Process of Hot Rolled Ferritic Stainless Steel in Sulfuric Acid and Nitric Acid Solution. Tetsu-to-Hagane 2006, 92, 10–15. [Google Scholar] [CrossRef][Green Version]
- Preßlinger, H.; Ilie, S.; Reisinger, P.; Schiefermüller, A.; Pissenberger, A.; Parteder, E.; Bernhard, C. Methods for Assessment of Slab Centre Segregation as a Tool to Control Slab Continuous Casting with Soft Reduction. ISIJ Int. 2006, 46, 1845–1851. [Google Scholar] [CrossRef]
- Hou, Z.; Guo, D.; Cao, J.; Chang, Y. A method based on the centroid of segregation points: A Voronoi polygon application to solidification of alloys. J. Alloys Compd. 2018, 762, 508–519. [Google Scholar] [CrossRef]
- Abraham, S.; Cottrel, J.; Raines, J.; Wang, Y.; Bodnar, R.; Wilder, S.; Thomas, J.; Peters, J. Development of an Image Analysis Technique for Quantitative Evaluation of Centerline Segregation in As-Cast Products. Iron Steel Technol. 2017, 8, 148–157. [Google Scholar]
- Kazakov, A.; Kiselev, D.; Pakhomova, O. Microstructural Quantification for Pipeline Steel Structure-Property Relationships. CIS Iron Steel Rev. 2012, 1, 4–12. [Google Scholar]
- Hou, Z.; Guo, Z.; Guo, D.; Cao, J. A new method for carbon content distribution based on grayscale image of casting blank macrostructure in carbon steel. J. Iron Steel Res. 2019, 31, 620–627. [Google Scholar]
- Thomas, T.R. Rough Surfaces, 2nd ed.; Imperial College Press: London, UK, 1999. [Google Scholar]
- Howell, D.; Behrends, B. A review of surface roughness in antifouling coatings illustrating the importance of cutoff length. Biofouling 2006, 22, 401–410. [Google Scholar] [CrossRef]
- Bowe, T.F.; Brody, H.D.; Flemings, M.C. Measurement of solute redistribution in dendritic solidification. Trans. Metall. Soc. AIME 1966, 236, 624–634. [Google Scholar]
- Burton, J.A.; Prim, R.C.; Slichter, W.P. The Distribution of Solute in Crystals Grown from the Melt. Part I. Theoretical. J. Chem. Phys. 1953, 21, 1987–1991. [Google Scholar] [CrossRef]
- Schaffnit, P.; Stallybrass, C.; Konrad, J.; Stein, F.; Weinberg, M. A Scheil–Gulliver model dedicated to the solidification of steel. Calphad 2015, 48, 184–188. [Google Scholar] [CrossRef]
- Dong, H.; Lee, P. Simulation of the columnar-to-equiaxed transition in directionally solidified Al–Cu alloys. Acta Mater. 2005, 53, 659–668. [Google Scholar] [CrossRef]
- Ryan, T.P. Modern Regression Theory, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Trivedi, R.; Kurz, W. Dendritic Growth. Int. Mater. Rev. 1994, 39, 49–74. [Google Scholar] [CrossRef]
- Byron, R.; Bird, W.E.; Stewart, E.N. Lightfoot, Transport Phenomena, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
- Choudhary, S.K.; Ganguly, S. Morphology and Segregation in Continuously Cast High Carbon Steel Billets. ISIJ Int. 2007, 47, 1759–1766. [Google Scholar] [CrossRef]
- Hou, Z.; Jiang, F.; Cheng, G. Solidification Structure and Compactness Degree of Central Equiaxed Grain Zone in Continuous Casting Billet Using Cellular Automaton-Finite Element Method. ISIJ Int. 2012, 52, 1301–1309. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary Layer Theory, 9th ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Kurz, W.; Fisher, D.J. Fundamentals of Solidification, 4th ed.; Trans Tech Publications Ltd.: Zurich, Switzerland, 1998. [Google Scholar]
- Isobe, K. Formation Mechanisms of Several Kinds of Segregation on Continuous Casting of Bloom. Tetsu-to-Hagane 2012, 98, 405–414. [Google Scholar] [CrossRef][Green Version]
- Natsume, Y.; Takahashi, D.; Kawashima, K.; Tanigawa, E.; Ohsasa, K. Evaluation of Permeability for Columnar Dendritic Structures by Three-dimensional Numerical Flow Analysis. ISIJ Int. 2014, 54, 366–373. [Google Scholar] [CrossRef][Green Version]
- Hou, Z.; Cao, J.; Chang, Y.; Wang, W.; Chen, H. Morphology Characteristics of Carbon Segregation in Die Steel Billet by ESR Based on Fractal Dimension. Acta Metall. Sin. 2017, 53, 769–777. [Google Scholar]
- Takahashi, T.; Ichikawa, K.; Kudou, M.; Shimahara, K. The Effect of Fluid Flow on the Macrosegregation in Steel Ingot. Tetsu-to-Hagane 1975, 61, 2198–2213. [Google Scholar] [CrossRef]
- Miyazawa, K.; Schwerdtfeger, K. Macrosegregation in continuously cast steel slabs: Preliminary theoretical investigation on the effect of steady state bulging. Archiv für das Eisenhüttenwesen 1981, 52, 415–422. [Google Scholar] [CrossRef]
- Huang, J.T.; He, J.C. Numerical simulation of steel solidification and electromagnetic brake in the billet mold. Acta Metall. Sin. 2001, 37, 281–286. [Google Scholar]
- Kajatani, T.; Drezet, J.-M.; Rappaz, M. Numerical simulation of deformation-induced segregation in continuous casting of steel. Met. Mater. Trans. A 2001, 32, 1479–1491. [Google Scholar] [CrossRef]











| Sample | Superheat, °C | Casting Speed, m/min | Specific Water Ratio, L/kg |
|---|---|---|---|
| 1# | 20 | 1.1 | 0.38 |
| 2# | 35 | 1.1 | 0.38 |
| Distance to Bloom Edge, mm | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 0.8903 | −0.132 | 0.9713 | 0.868 | 0.2125 | 0.0960 | 1.03 |
| 3 | 0.9089 | −0.115 | 0.9849 | 0.885 | 0.1661 | 0.1276 | 1.03 |
| 5 | 0.9224 | −0.114 | 0.9695 | 0.886 | 0.1197 | 0.1775 | 1.04 |
| 10 | 0.9158 | −0.128 | 0.9338 | 0.872 | 0.0782 | 0.2631 | 1.05 |
| 20 | 0.8841 | −0.142 | 0.9772 | 0.858 | 0.0457 | 0.4371 | 1.03 |
| 30 | 0.9055 | −0.124 | 0.9634 | 0.876 | 0.0310 | 0.6707 | 1.03 |
| 40 | 0.8784 | −0.166 | 0.9158 | 0.834 | 0.0227 | 0.8413 | 1.05 |
| 50 | 0.8824 | −0.169 | 0.9072 | 0.831 | 0.0189 | 1.0027 | 1.06 |
| 60 | 0.9105 | −0.120 | 0.9429 | 0.880 | 0.0170 | 1.2317 | 1.03 |
| 70 | 0.9243 | −0.104 | 0.9496 | 0.896 | 0.0156 | 1.3922 | 1.03 |
| 80 | 0.9154 | −0.120 | 0.9548 | 0.880 | 0.0146 | 1.4312 | 1.04 |
| 90 | 0.9069 | −0.143 | 0.9189 | 0.857 | 0.0140 | 1.4277 | 1.06 |
| 100 | 0.8835 | −0.157 | 0.9558 | 0.843 | 0.0136 | 1.4298 | 1.05 |
| Distance to Bloom Edge, mm | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 0.9226 | −0.109 | 0.9396 | 0.891 | 0.2125 | 0.1011 | 1.04 |
| 3 | 0.9107 | −0.123 | 0.9526 | 0.877 | 0.1661 | 0.1253 | 1.04 |
| 5 | 0.934 | −0.132 | 0.9738 | 0.868 | 0.1197 | 0.1705 | 1.08 |
| 10 | 0.9295 | −0.103 | 0.9777 | 0.897 | 0.0782 | 0.2788 | 1.04 |
| 20 | 0.8968 | −0.129 | 0.9872 | 0.871 | 0.0457 | 0.4492 | 1.03 |
| 30 | 0.8845 | −0.157 | 0.9548 | 0.843 | 0.0310 | 0.6264 | 1.05 |
| 40 | 0.8764 | −0.168 | 0.9116 | 0.832 | 0.0227 | 0.8381 | 1.05 |
| 50 | 0.9027 | −0.141 | 0.9112 | 0.859 | 0.0189 | 1.0594 | 1.05 |
| 60 | 0.8711 | −0.185 | 0.9004 | 0.815 | 0.0170 | 1.0819 | 1.07 |
| 70 | 0.9027 | −0.132 | 0.9279 | 0.868 | 0.0156 | 1.3058 | 1.04 |
| 80 | 0.9341 | −0.117 | 0.8953 | 0.883 | 0.0146 | 1.4410 | 1.06 |
| 90 | 0.9126 | −0.145 | 0.8871 | 0.855 | 0.0140 | 1.4219 | 1.07 |
| 100 | 0.9257 | −0.114 | 0.906 | 0.886 | 0.0136 | 1.5661 | 1.04 |
| Distance to Bloom Edge, mm | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 0.9336 | −0.076 | 0.9615 | 0.924 | 0.1928 | 0.1218 | 1.01 |
| 3 | 0.9188 | −0.105 | 0.9859 | 0.895 | 0.1496 | 0.1451 | 1.03 |
| 5 | 0.9283 | −0.089 | 0.9439 | 0.911 | 0.1064 | 0.2125 | 1.02 |
| 10 | 0.9161 | −0.113 | 0.9702 | 0.887 | 0.0728 | 0.2926 | 1.03 |
| 20 | 0.8988 | −0.130 | 0.9793 | 0.870 | 0.0435 | 0.4712 | 1.03 |
| 30 | 0.9029 | −0.125 | 0.9706 | 0.875 | 0.0296 | 0.6991 | 1.03 |
| 40 | 0.9179 | −0.108 | 0.9771 | 0.892 | 0.0224 | 0.9613 | 1.03 |
| 50 | 0.8972 | −0.128 | 0.9558 | 0.872 | 0.0191 | 1.0751 | 1.03 |
| 60 | 0.8834 | −0.154 | 0.9062 | 0.846 | 0.0172 | 1.1343 | 1.04 |
| 70 | 0.8944 | −0.120 | 0.9143 | 0.880 | 0.0158 | 1.3273 | 1.02 |
| 80 | 0.9042 | −0.112 | 0.9840 | 0.888 | 0.0148 | 1.4442 | 1.02 |
| 90 | 0.8897 | −0.151 | 0.9554 | 0.849 | 0.0141 | 1.3918 | 1.05 |
| 100 | 0.9239 | −0.117 | 0.9517 | 0.883 | 0.0137 | 1.5435 | 1.05 |
| Distance to Bloom Edge, mm | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 0.9451 | −0.085 | 0.9681 | 0.915 | 0.1928 | 0.1186 | 1.03 |
| 3 | 0.9232 | −0.096 | 0.9809 | 0.904 | 0.1496 | 0.1484 | 1.02 |
| 5 | 0.9387 | −0.085 | 0.9631 | 0.915 | 0.1064 | 0.2149 | 1.03 |
| 10 | 0.9162 | −0.103 | 0.9811 | 0.897 | 0.0728 | 0.2997 | 1.02 |
| 20 | 0.9119 | −0.117 | 0.9832 | 0.883 | 0.0435 | 0.4850 | 1.03 |
| 30 | 0.9040 | −0.122 | 0.9706 | 0.878 | 0.0296 | 0.7037 | 1.03 |
| 40 | 0.9182 | −0.111 | 0.9713 | 0.889 | 0.0224 | 0.9545 | 1.03 |
| 50 | 0.9002 | −0.128 | 0.972 | 0.872 | 0.0191 | 1.0751 | 1.03 |
| 60 | 0.8807 | −0.149 | 0.9639 | 0.851 | 0.0172 | 1.1456 | 1.03 |
| 70 | 0.9171 | −0.137 | 0.9316 | 0.863 | 0.0158 | 1.2791 | 1.06 |
| 80 | 0.9148 | −0.117 | 0.9545 | 0.883 | 0.0148 | 1.4275 | 1.04 |
| 90 | 0.9337 | −0.088 | 0.9864 | 0.912 | 0.0141 | 1.6087 | 1.02 |
| 100 | 0.8952 | −0.136 | 0.9415 | 0.864 | 0.0137 | 1.4805 | 1.04 |
| Distance to Bloom Edge, mm | ||||
|---|---|---|---|---|
| 20 °C | 35 °C | |||
| Inner Curve Side | Outer Curve Side | Inner Curve Side | Outer Curve Side | |
| 1 | 0.40143 | 0.33952 | 0.20392 | 0.22494 |
| 3 | 0.21726 | 0.23041 | 0.16279 | 0.15060 |
| 5 | 0.11190 | 0.12724 | 0.07137 | 0.06856 |
| 10 | 0.05290 | 0.04377 | 0.04105 | 0.03787 |
| 20 | 0.01981 | 0.01819 | 0.01658 | 0.01511 |
| 30 | 0.00806 | 0.00994 | 0.00744 | 0.00728 |
| 40 | 0.00560 | 0.00566 | 0.00374 | 0.00383 |
| 50 | 0.00396 | 0.00336 | 0.00317 | 0.00317 |
| 60 | 0.00236 | 0.00349 | 0.00301 | 0.00293 |
| 70 | 0.00176 | 0.00217 | 0.00204 | 0.00229 |
| 80 | 0.00175 | 0.00171 | 0.00168 | 0.00175 |
| 90 | 0.00186 | 0.00188 | 0.00199 | 0.00124 |
| 100 | 0.00191 | 0.00144 | 0.00149 | 0.00170 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, Z.; Peng, Z.; Liu, Q.; Guo, Z.; Dong, H. A New Approach to Calculate the Velocity of Interdendritic Fluid Flow during Solidification Using Etched Surface Height of Actual Metal Ingot. Metals 2021, 11, 927. https://doi.org/10.3390/met11060927
Hou Z, Peng Z, Liu Q, Guo Z, Dong H. A New Approach to Calculate the Velocity of Interdendritic Fluid Flow during Solidification Using Etched Surface Height of Actual Metal Ingot. Metals. 2021; 11(6):927. https://doi.org/10.3390/met11060927
Chicago/Turabian StyleHou, Zibing, Zhiqiang Peng, Qian Liu, Zhongao Guo, and Hongbiao Dong. 2021. "A New Approach to Calculate the Velocity of Interdendritic Fluid Flow during Solidification Using Etched Surface Height of Actual Metal Ingot" Metals 11, no. 6: 927. https://doi.org/10.3390/met11060927
APA StyleHou, Z., Peng, Z., Liu, Q., Guo, Z., & Dong, H. (2021). A New Approach to Calculate the Velocity of Interdendritic Fluid Flow during Solidification Using Etched Surface Height of Actual Metal Ingot. Metals, 11(6), 927. https://doi.org/10.3390/met11060927







