Strength of Superelastic NiTi Velcro-Like Fasteners

Abstract

Velcro hook-and-loop fasteners invented more than 70 years ago are examples of the mechanism inspired by the tiny hooks found on the surface of burs of a plant commonly known as burdock. Several years ago, a novel Velcro-like fastener made of two arrays of hook-shaped thin NiTi wires was developed. Unique features of such fasteners, such as high thermally-tunable strength, fair force–stroke reproducibility, forceless contact or silent release, all derive from the superelasticity of the NiTi micro-wires. Recently, it was noticed that the presented fastener design allowed for a prediction of the number of active hooks. In this continuing study, the tension strength of the fastener was simulated as a function of hook density. Based on statistics, the model showed non-linear dependency of the number of interlocked hooks, N, on the hook density, m (N = round (0.21 m + 0.0035 m² − 6.6)), for the simple hook pairs and the given hook geometry. The dependence of detachment force on stroke was simulated based on the Gaussian distribution of unhooking of individual hook connections along the stroke. The strength of the studied NiTi hook fasteners depended on hook density approximately linearly. The highest strength per cm² reached at room temperature was 10.5 Ncm⁻² for a density of m = 240 hooks/cm².

1. Introduction

Various concepts of Velcro-like fasteners have been suggested so far [1,2,3]. The idea of employing NiTi shape memory alloys (SMA) for producing Velcro-like fasteners is not new. Temperature controlled NiTi hook array engagement based on the two-way shape memory effect (TWSME) [4,5,6] is studied in Refs. [7,8]. An exhaustive analysis of superelastic NiTi hook array fasteners, including their manufacture and thermomechanical properties, is presented by the current authors in Refs. [8,9]. Unlike the NiTi hook arrays in Refs. [7,8], the hook arrays reported on by the current authors’ [9,10] work are based on the superelastic effect (SE) of SMAs. The superelasticity of NiTi alloy refers to the ability of the alloy to recover from deformations beyond the elasticity as large as about 8% upon unloading at a constant temperature in the range between A_f and M_d (A_f is the austenite finish temperature whereas M_d > A_f is the temperature at which it is no longer possible to stress-induce martensite and achieve superelasticity). Superelasticity is related to the reversible phase transformation occurring in NiTi and other SMAs [4], whereas the TWSME (the effect employed in hooks in [7,8]) relates to the repeatable shape change upon temperature cycling. The TWSME is not an inherent property of SMAs, but can only be obtained through a certain thermo-mechanical treatment.

When using Velcro-like NiTi SE fasteners, one has to be careful when approaching the temperature range close to M_d during the fastener detachment because of a detrimental possibility of reaching the yield stress of martensite (the phase with the crystallographic symmetry lower than that of austenite) at a local level. The advantage of the high temperature environment for NiTi SE fasteners is the high detachment force. The drawback of detachments in such an environment is the occurrence of irreversible plastic deformation in NiTi hooks at high temperatures close to M_d. The temperature environment also influences the number of cycles until failure [11].

The strength of the NiTi Velcro-like fastener depends, among other factors, on the number of interlocked hooks prior to the detachment of the two hook arrays. Knowing this dependence would allow one to optimize the hook array density and the hook’s shape in order to activate an optimum and stable number of hook pair connections during the attachment. The arrays cannot be too dense in order to allow a forceless contact and not to waste the material. Hence, it is of interest to find a way to determine the number of interlocked hooks and their variation in dependence on the hook geometry and the hook distribution in the array.

Several published studies analyze the strength of a single hook occurring in plants, insects or Velcro-like fasteners using non-linear mechanics, taking geometric and material properties, including friction, into account [12,13,14,15]. However, the results of the mentioned studies cannot be simply applied to NiTi hooks because of the strong thermo-mechanical nonlinearity of NiTi SMAs. In one of our preceding papers, the mechanical response of a single NiTi hook at a given temperature during the unhooking process was simulated using a finite element method specially proposed for shape memory wires [9]. Other published studies simulate strength (in shear, tension, or combined shear and tension loading) of Velcro-like fasteners with the involvement of all active connections in the fasteners using frictional dynamics [16] and the cohesive zone model [17]. When thinking of strength modeling of Velcro-like fasteners, it is worth mentioning that, unlike conventional Velcro fasteners consisting of hooks and loops, the superelastic NiTi fasteners presently studied allow for prediction of the active hooks and types of hooks’ connections (e.g., 1 + 1, 2 + 1, etc.) during the fastener’s attachment on the condition that the hooks’ coordinates in the frame firmly connected to the substrate are known before the fastener attachment.

In the present study, the focus is on modeling the hook array engagement in order to statistically estimate the number of interlocked (active) hooks based on the hook’s distribution in the array and hook’s geometry using Monte Carlo simulations (simulations that rely on repeated random sampling to obtain numerical results). The force-stroke curve associated with the hook array unhooking process is simulated based on knowing the number of interlocked hooks and the force–stroke curve of a single hook pair at a given temperature.

2. Materials and Methods

2.1. NiTi Wires and Their Properties

The as-drawn NiTi wire labeled as NiTi#1 by the provider, (Ni 56.0 wt. %, C 330 ppm, O₂ 280 ppm, H₂ 25 ppm and Ti balance) with a diameter 100 µm used in this study was purchased from Fort Wayne Metals in hard condition. Annealing at 450 °C for 30 min. resulted in the following transformation temperatures [18]: (A→R)_s = 32 °C, (A→R)_f = 8 °C, (R→M)_s is below −60 °C, (R→M)_f is below −60 °C, (M→R)_s = −8 °C, (M→R)_f = 16 °C, (R→A)_s = 20 °C and (R→A)_f = 43 °C, where A, R, M, s and f stands for austenite, R-phase, martensite, start and finish, respectively. The abovementioned annealing was applied as a part of shape setting of the NiTi hooks.

Figure 1 shows the tensile stress-strain curve of the NiTi wire annealed at 450 °C for 30 min, quenched and loaded in tension at room temperature (20 °C). The small unrecovered strain formed in the initial loading cycle is predominantly due to the re-orientation of the R-phase variants. The other characteristics of the annealed wire are summarized in

Table 1. Material parameters for the NiTi wire used in the present study (annealed at 450 °C for 30 min).

Material Parameter’s Name/Unit	Material Parameter’s Value
Transformation yield stress of austenite at room temperature (MPa)	553
Maximum recoverable transformation strain in tension (%)	5.2
Ultimate tensile strength (MPa)	1665
Yield stress (MPa)	1476
Strain at failure (%)	14.2
Superelastic stress hysteresis (MPa)	340

Generally, the Poisson ratio of NiTi SMAs is about 0.3 [4].

.

2.2. NiTi Velcro-Type Samples

The manufacture of NiTi Velcro-type samples consists of (i) the shape setting of NiTi wires (with a diameter of 100 µm) into the shape of hooks during annealing at 450 °C for 30 min and (ii) the alignment of NiTi hooks in an array. The alignment procedure is described in Ref. [9]. In summary, liquid resin was mixed with a hardener in the ratio indicated in the instructions. The resin was then poured into a container with standing aligned NiTi hooks so that the resin level did not reach the hook heads. After waiting 24 h, a solid resin substrate with NiTi hooks was obtained. Hooks were firmly connected to the substrate and could not rotate in the substrate.

The hooks were perpendicular to the substrate and fixed in the substrate over a square lattice with a constant lattice parameter. For each sample, the array area formed a square 20 mm × 20 mm. All the hooks in the array were approximately identical, having the same height above the substrate. The hook heads did not follow any preferred direction when projected onto the plane of the substrate, but their turning angle was random. Each fastener consisted of two identical parts—arrays of NiTi hooks embedded in a non-flexible matrix (Figure 2).

Table 2. NiTi hook samples.

Sample (A Single Array of Hooks)	NiTi Hook Density [hook/cm2]	Number of Hooks in Sample
A	30	121
B	110	441
C	240	961

summarizes the basic characteristics of three fasteners used for the present experiments. The fasteners differ from one another by the hook density. At room temperature, NiTi hooks in the fastener samples consist of a mixture of the R-phase and austenite. The amount of the R-phase prior to detachment does not affect strength of the NiTi fasteners.

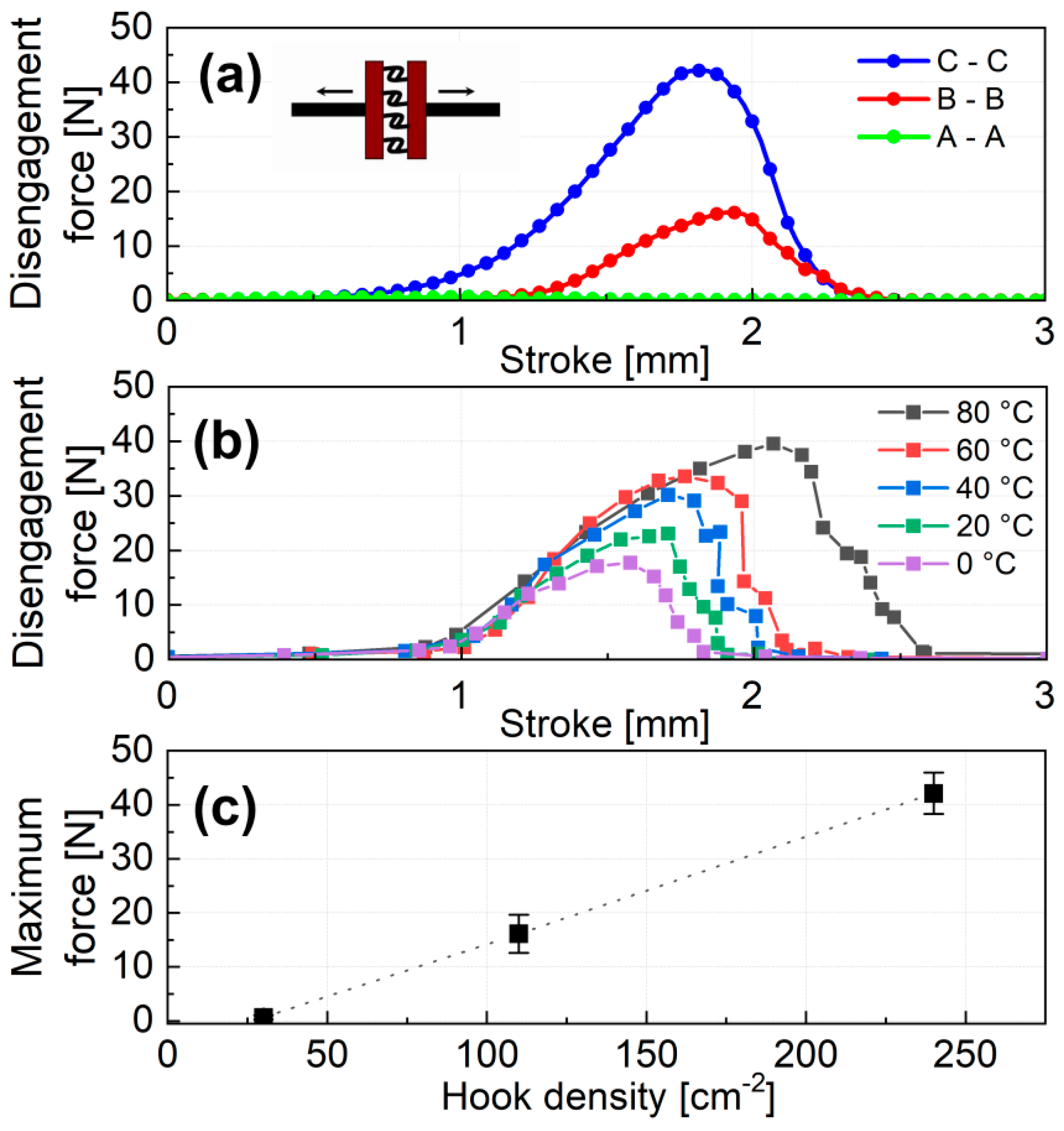
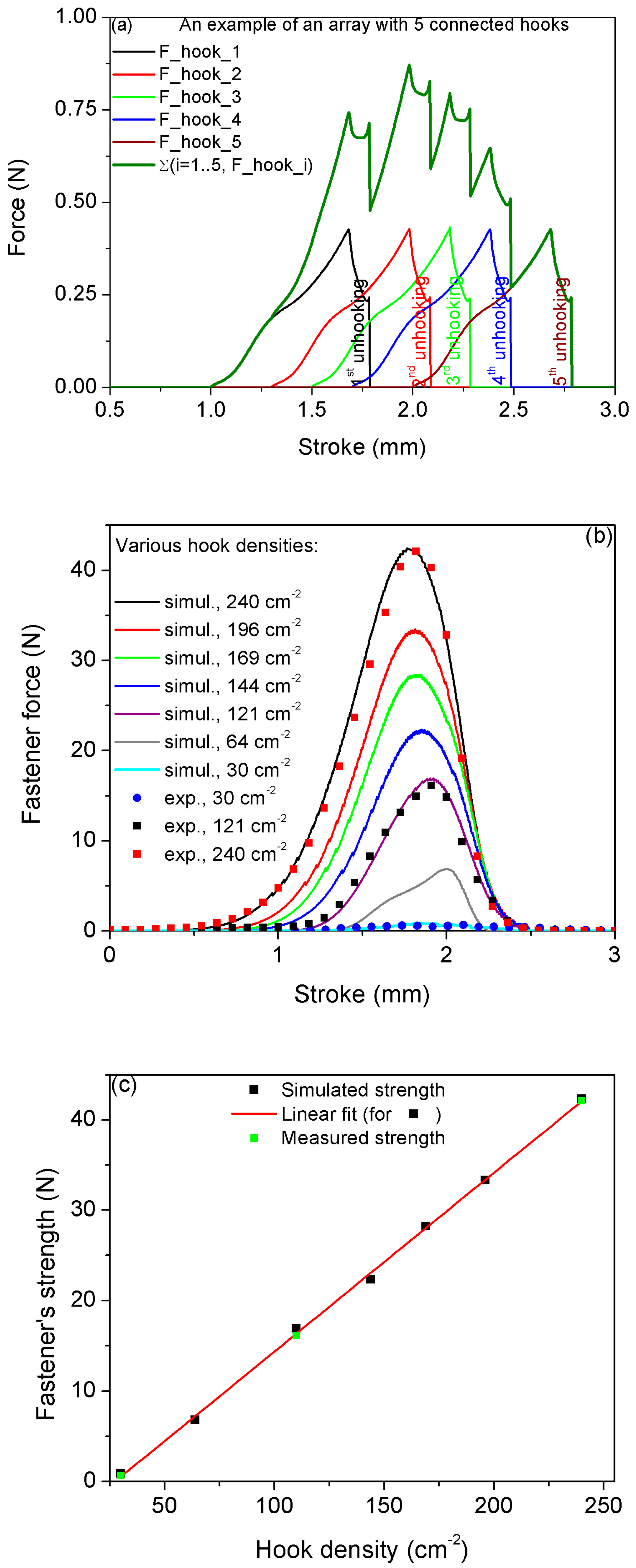
2.3. Force Measurement

Tensile tests performed on single wires and NiTi fasteners were carried out using a tensile tester Walter + Bai (500 N load cell) (Walter + Bai AG, Löhningen, Switzerland) equipped with a Peltier thermal chamber to control the temperature of test samples. This tester was screw-driven (stroke resolution about 1 μm) and a fully computerized device with the possibility of setting PID parameters.

Finally, tensile tests performed on a single NiTi hook pair were carried out using a deformation rig with a size of ~50 cm × ~10 cm × ~10 cm, specially designed for the testing of thermomechanical properties of thin NiTi wires in tension. Principally, the rig consisted of a stepping motor, a 10 N load cell, a position sensor and a Peltier thermal chamber.

Figure 3a shows the dependences of the pulling force versus stroke of NiTi hook fasteners with three different hook densities at room temperature. With increasing stroke, the pulling force increases up to a maximum, beyond which it slowly decreases down to zero in a different way from just two interlocked NiTi hooks which detach more abruptly. Obviously, the force-stroke curves in Figure 3a are related to multiple detachment events taking place in a coordinated manner. Most importantly, it is found that the maximum detachment force (i.e., strength) strongly depends on a hooks’ density and temperature (Figure 3a,b). For comparison, the maximum pulling force per cm² for the conventional Velcro fastener made of polyester is 4 Ncm⁻² [7]. Figure 3a implies the maximum force per cm² for sample C-C, having a value of 10.5 Ncm⁻² (Figure 3c), well exceeds that of the conventional Velcro fastener. The detachment force can still be greatly tuned using temperature regulation (for instance, temperature regulation in the form of resistive heating embedded in the resin substrate).

The reason for the increase in the maximum force with increasing density is the increasing number of interconnected hooks. Hence, assuming the hook material properties and shape were known, it was necessary to predict the number of interconnected hooks as a function of hook density.

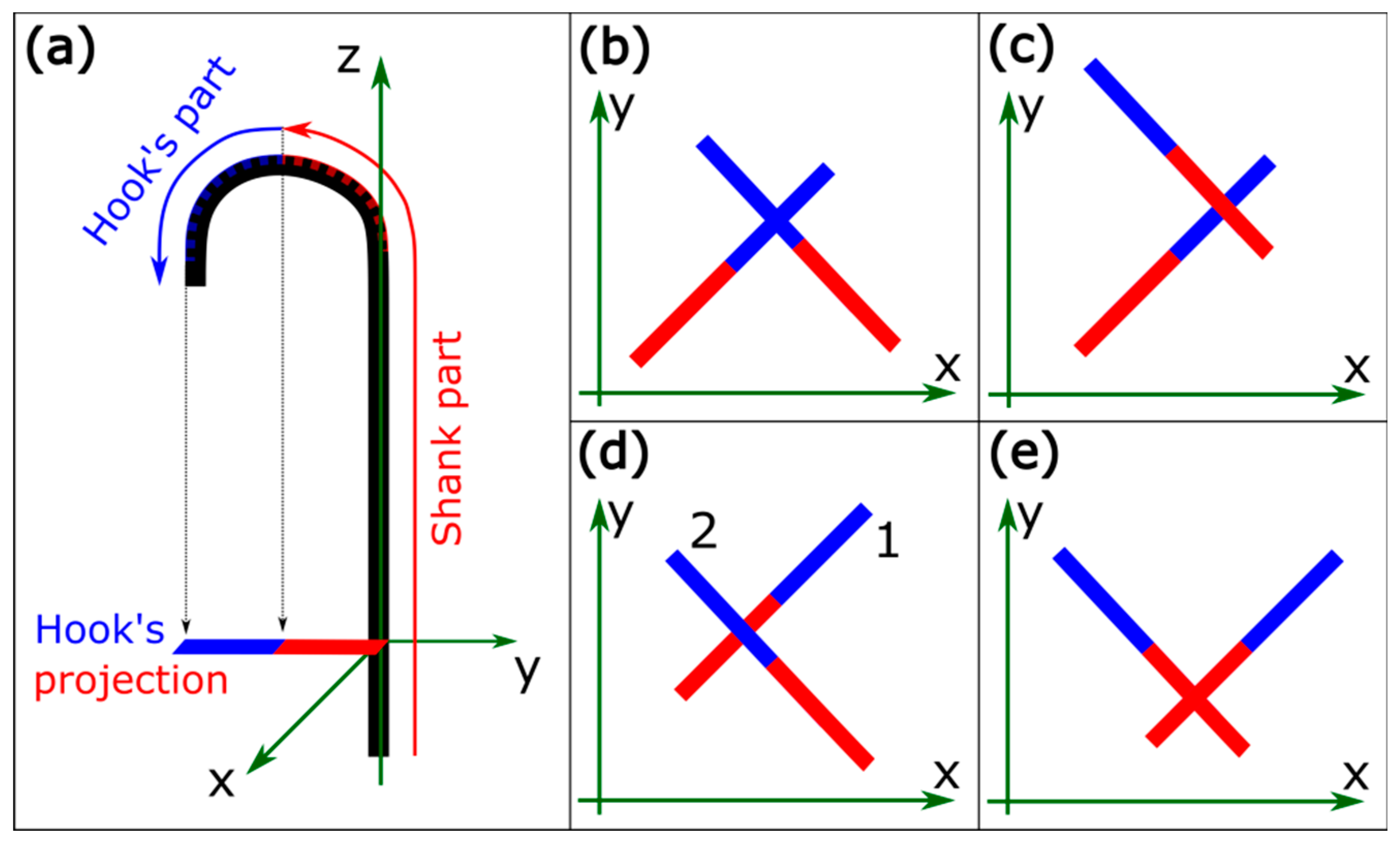
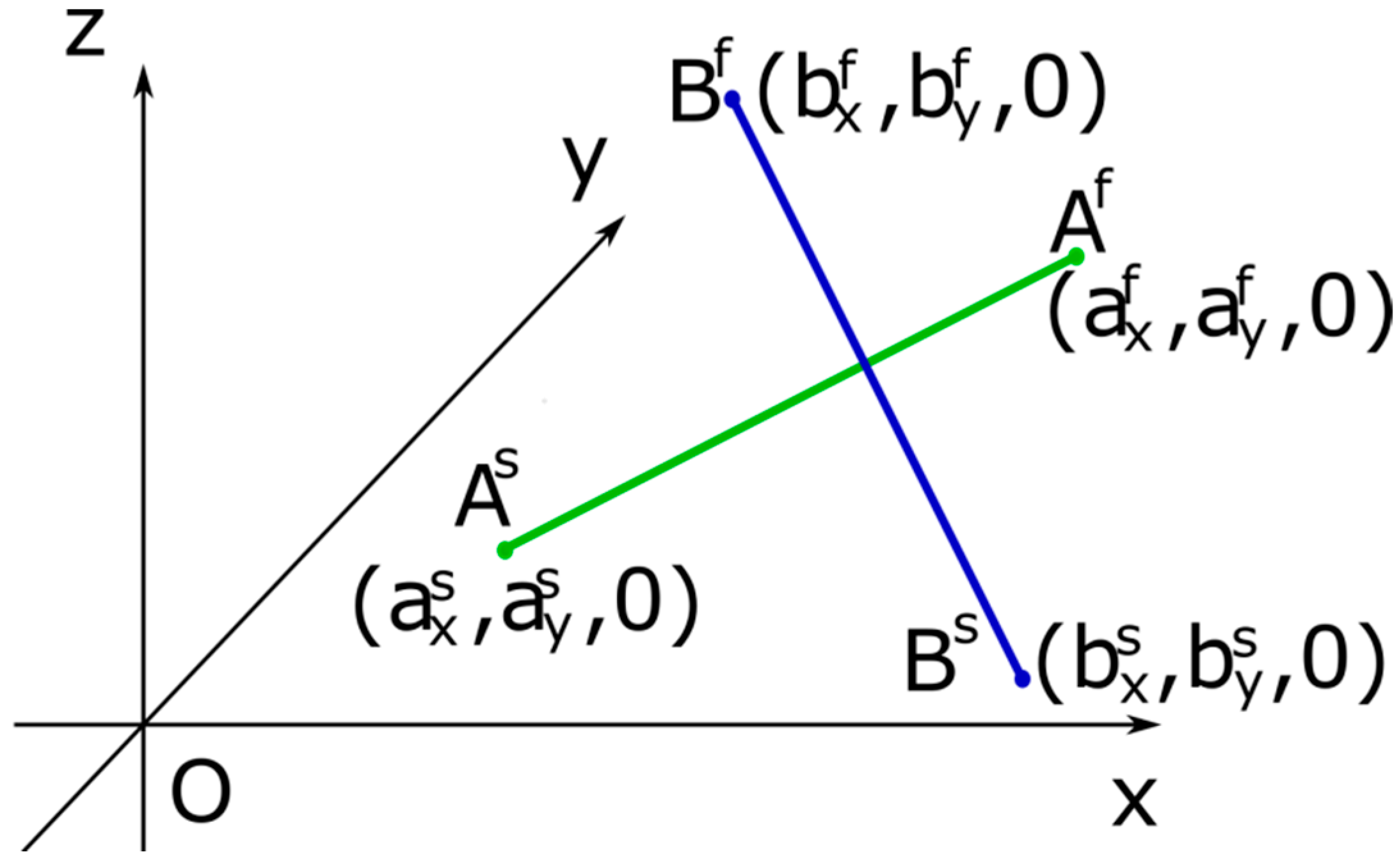
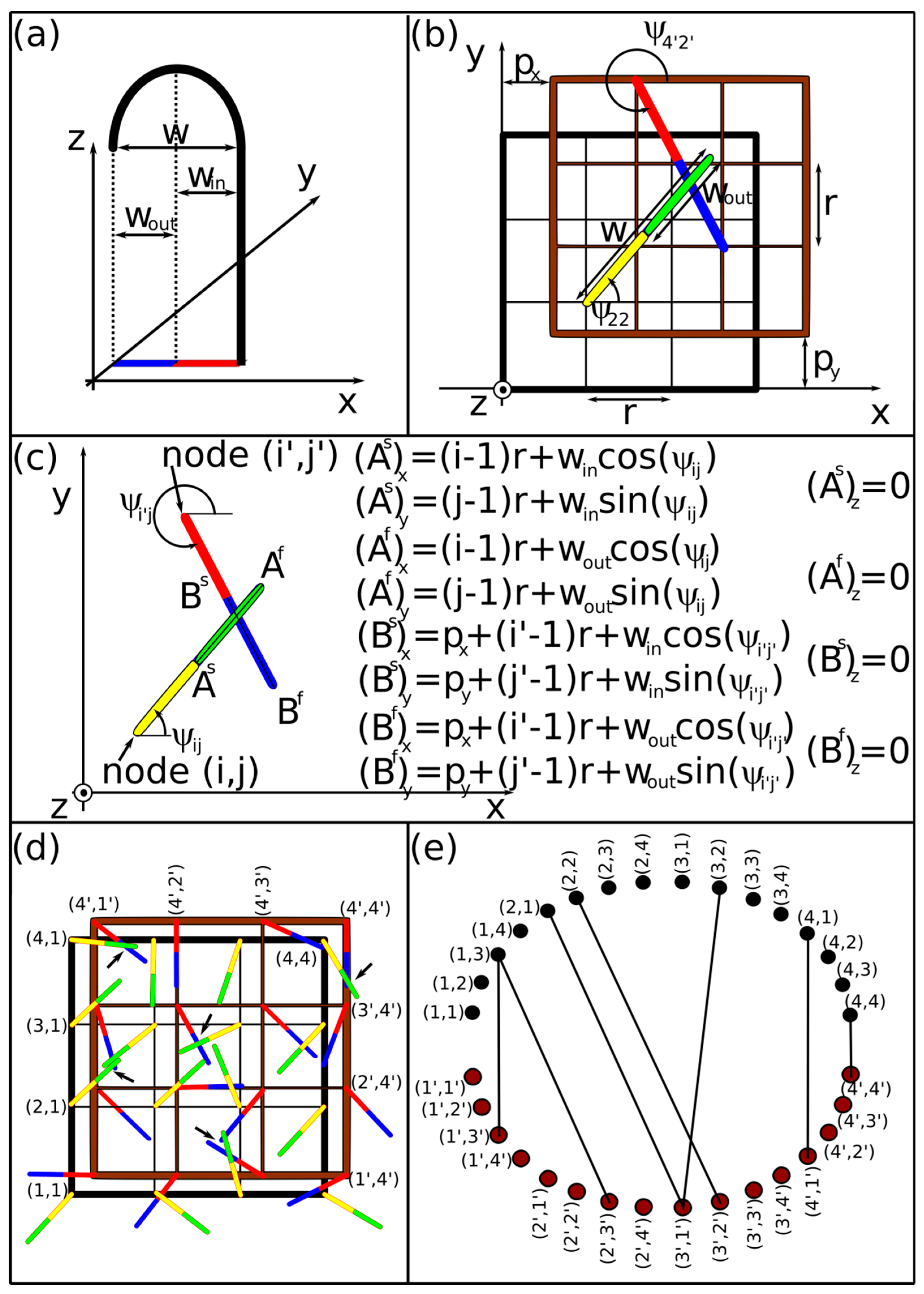
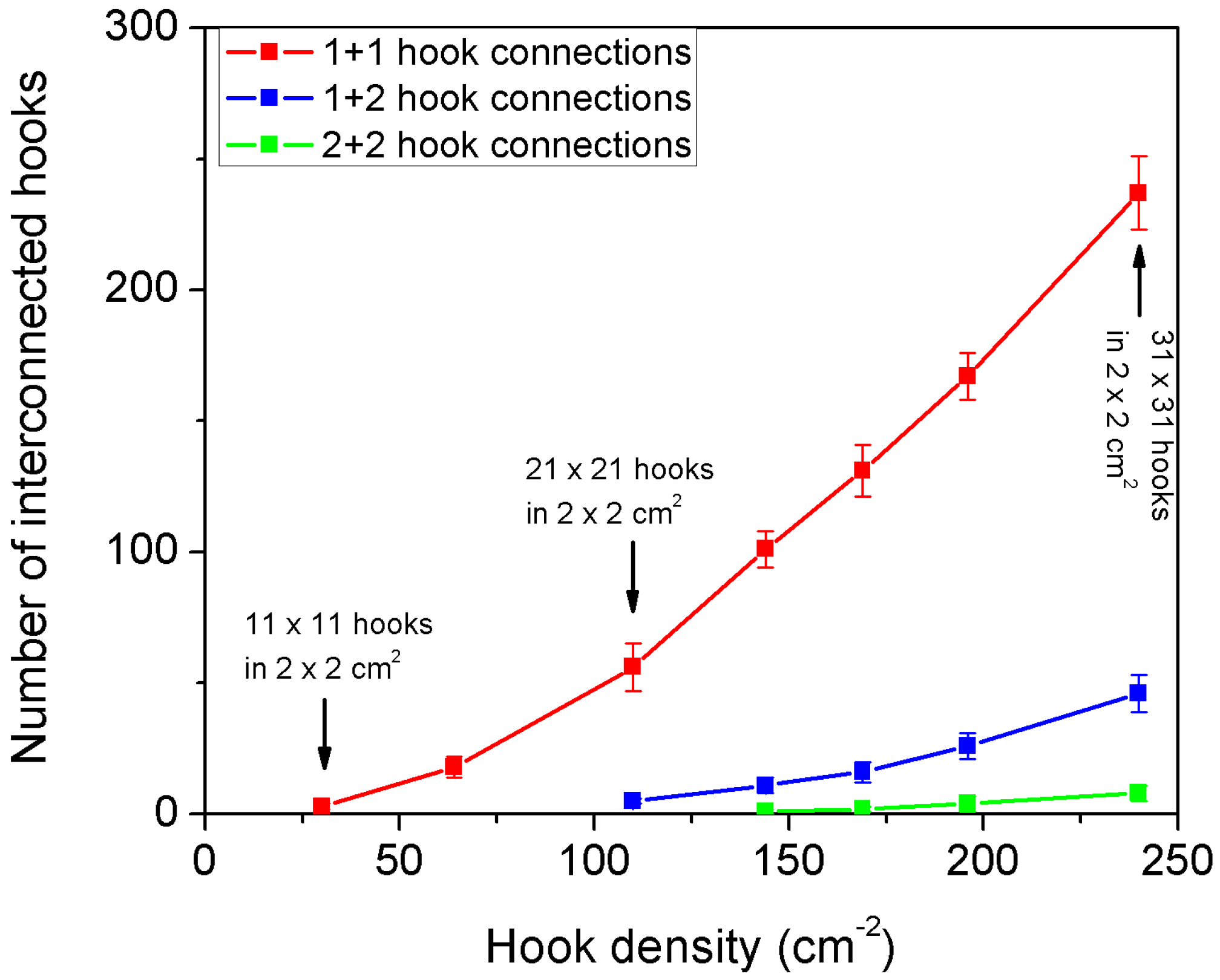
2.4. Method to Estimate the Number of Interlocked Hooks

The process of hook interlocking depends on the way two hook arrays approach each other. Therefore, it is necessary to standardize this process. It is reasonable to adopt the conditions that hold during the detachment force measurement reported on in part 2.3. These conditions are:

(i)

During approaching and the fastener engagement, the substrate planes remain parallel. So do the arrays’ edges (no mutual rotation of the arrays).

(ii)

When drawing the two fastener’s parts closer to each other, no lateral movements are made.

The studied fasteners allow for prediction of the interlocked hooks and types of hooks’ connections before the fastener’s attachment on the condition that the hooks’ coordinates, in respect to one of the two substrates, are known. The model works with the axial projection of individual hooks onto the substrate plane (plane xy).

Figure 4 explains on which conditions two NiTi hooks become interlocked. When considering the descending (denoted as hook’s part in Figure 4a) and ascending (denoted as Shank’s part in Figure 4a) parts and their projections (blue and red, respectively, in Figure 4), only case (b) (Figure 4b) demonstrated how the descending projections intersect each other, which guarantees the interlocking of the two NiTi hooks. It was found empirically that cases (c)–(e), representing two NiTi hooks axially pushed against each other, resulted in no interlocking.

It is helpful to express, mathematically, the necessary and sufficient conditions on which any two segments (in plane xy) A^sA^f (green color in Figure 5) and B^sB^f (blue color in Figure 5) intersect with each other. A Cartesian coordinate system is introduced, as shown in Figure 5.

The conditions for intersecting segments A^sA^f and B^sB^f (Figure 5) are as follows:

d ≡ ((b^s − b^f) × (a^f − a^s))_z ≠ 0,

(1)

0 < ((b^s − a^s) × (b^f − b^s))_z/d < 1,

(2)

0 < ((b^s − a^s) × (a^f − a^s))_z/d < 1,

(3)

where a^s, a^f, b^s, b^f are the position vectors of points A^s, A^f, B^s, B^f, respectively, ()_z means the z-component of a vector and “×” is the cross product.

Figure 6 shows examples of the projections for two NiTi hook 4 × 4 arrays with certain hook density and a small mutual lateral displacement. In this example, the model parameters are introduced. In addition, the parameters and their values are summarized in

Table 3. Model parameters.

Parameter’s Name/Unit	Value Used in the Model	Way of Obtaining the Value
Hook’s head width, w (mm)	1	Measured
win (mm), (Figure 6)	0.5	Measured
wout (mm), (Figure 6)	0.5	Measured
r (mm), (Figure 6)	2; 1; 2/3	Measured
Hook densities (cm−2)	30; 110; 240	Measured
Hook’s head orientation, ψij, ψi’j’.	Random, 0–2 π	Generated randomly in the Monte-Carlo model
Lateral shifts, px, py (mm), (Figure 6)	Random, (px)2 + (py)2 ≤ 1	The limit value (1) was estimated to comply with the force-stroke measurements

. In the model, the hooks are inserted to either substrate in nodes (i, j) (array 1) and (i’, j’) (array 2). The rotation angles of the hook’s heads, ψ_ij, ψ_i’j’ and the small lateral displacement p = (p_x, p_y, 0) (see Figure 6b) are set randomly. Interlocked hooks in Figure 6c,d are the hook pairs that are represented by the mutually intersected blue and green segments (pointed out by arrows). Figure 6e shows an undirected graph with nodes (i, j) and (i’, j’) and several edges that correspond to the interconnected hooks. The reason for introducing the corresponding graphs is to allow the utilization of certain algorithms. More specifically, the depth first search (DFS) algorithm [19] is useful for finding all connected components in a graph. A connected component in an undirected graph is defined as a maximal connected subgraph in which each pair of nodes is connected with each other via a path, e.g., in Figure 6e, nodes (2, 1), (3′, 1′) and (3, 2) form a connected component of the graph. For higher hook densities and large parameter w_out, the associated graph can contain large, connected components not easily findable without the DFS algorithm. Generally, the purpose of the DFS algorithm is, as traveling through graph’s paths, to mark each node as visited while avoiding cycles.

The proposed model involves the following steps:

• Choosing hook density related to parameter r and working with fixed parameters w_in, and w_out.
• Generating random values of hook’s head angles, ψ_ij, ψ_i’j’ and small lateral shifts, p_x, p_y.
• Calculating the coordinates of points A^s_ij, A^f_ij, B^s_i’j’ and B^f_i’j’ according to the equations in Figure 6c.
• Finding all hook connections between array 1 and array 2 according to Equations (1)–(3) and forming the equivalent undirected graph.
• Finding all connected components (using the DFS algorithm), their types and their numbers (e.g., fifty 1 + 1 connections, ten 1 + 2 connections, two 3 + 1 connections, etc., where the term “m + n connections” means that m hooks from array 1 are interconnected with n hooks from array 2.)
• Repeating steps 2–5 at least ten times.
• Calculating the mean value and standard deviation for each type of connection.

The source code of the model was written in C# programming language [20] using built-in classes Math and Random.

3. Results and Discussion

Figure 7 shows the diagram of the unhooking force of a single hook pair versus stroke for various temperatures. The maximum unhooking force increases with increasing temperature. A similar force increase with increasing temperature was already seen in Figure 3b for NiTi hook arrays. This property is a consequence of the Clausius-Clapeyron law for phase changes. The force-stroke curve for 20 °C was used to simulate strength of the studied NiTi fasteners at room temperature. The curve can be fitted with polynomials as follows:

$$P_{20}\left(x\right)=P_a\left(\mathrm{x}\right)S\left(\mathrm{x}\right)S\left(0.682- \mathrm{x}\right)+P_b\left(\mathrm{x}\right)S\left(\mathrm{x} -0.682\right)S\left(0.785- \mathrm{x}\right)$$

(4)

$$P_a\left(x\right)={\displaystyle \sum }_{i=0}^9{a}_i{x}^i$$

(5)

$$P_b\left(x\right)={\displaystyle \sum }_{i=0}^4{b}_i{x}^i$$

(6)

where P₂₀, x, a_i and b_j are the fitting function, stroke and the coefficients of polynomials P_a and P_b, respectively. Values of coefficients a_i and b_j are summarized in

Table 4. Coefficients of polynomials P_a and P_b.

Coefficients of Pa	Coefficients of Pa	Coefficients of Pb
a0 = 0.00208	a5 = −2594.50272	b0 = 2426.0141
a1 = 0.37693	a6 = 8558.6707	b1 = −13,158.46915
a2 = −3.10433	a7 = −14,225.90391	b2 = 26,774.58836
a3 = 13.82738	a8 = 11,915.33198	b3 = −24,217.58423
a4 = 302.65256	a9 = −4012.15607	b4 = 8214.6907

. S(x) is the step function, S(x) = 0 for x < 0 and S(x) = 1 for x ≥ 0.

Figure 8 is the main output of the model described in the preceding part and it shows the dependence of the mean number and type of interlocked hooks as a function of hook density. The mean number and standard deviation for each set of simulations were calculated based on from ten to fifteen repeated individual simulations. The number of 1 + 1 connections, N, increases non-linearly with the hook density, m, according to the following relation: N = round (0.21m + 0.0035m² − 6.6). In addition, as hook density increases, groups of interlocked hooks larger than 1 + 1 connections appear.

Parameters w_in and w_out are related to the shape of the NiTi hooks. It was confirmed that an increase in w_in at the expense of w_out in the simulations resulted in a decrease in the number of interlocked hooks.

The maximum unhooking force for the 1 + 2 hook connection is not different from that of the 1 + 1 connection, whereas the maximum unhooking force of the 2 + 2 connection is double of that of the 1 + 1 connection. Based on these counts, the mean equivalent number of 1 + 1 connections is obtained (see

Table 5. Mean number of interlocked hooks for samples A-A, B-B and C-C and the mean equivalent number of 1 + 1 connections. SD means standard deviation.

Sample	Number of Hook Connections of Various Types at Hook Array Engagement as an Output of the Developed Method (Part 2.4) Mean ± SD			The Mean Equivalent Number of 1 + 1 Connections
	1 + 1 Connections	1 + 2 Connections	2 + 2 Connections
A-A	3 ± 1	0	0	3
B-B	56 ± 9	5 ± 1	0	61
C-C	237 ± 14	46 ± 7	8 ± 3	299

).

The detachment force of the developed superelastic NiTi fasteners was simulated as a sum of the individual force-stroke curves associated with the active 1 + 1 connections (Figure 9a). However, the active hooks in the fasteners do not unhook all at the same moment since the hooks are not exactly the same height and, during pulling, some connected hook pairs may be slightly diverted from the axial (pulling) direction. Therefore, the individual unhooking events take place gradually along the changing distance between the two NiTi hook array substrates (Figure 9a). It is assumed that the unhooking events are distributed along the stroke length according to the Gaussian distribution given by Equation (7). Parameter µ, which serves as a left-right shift of f(x), can be approximately identified as the stroke associated with the maximum detachment force of the fastener. Parameter σ, which relates to the width of the bell-like part of f(x), is connected to the stroke interval of non-zero detachment force. The number of unhooking events during one detachment is given by the mean equivalent number of 1 + 1 connections (see Table 5). According to the Gaussian distribution, 68.2% {99.6%} of unhooking events takes place in the stroke interval from µ − σ to µ + σ (according to Equation (8)) {from µ − 3σ to µ + 3σ}, respectively. Using inverse error function, erf⁻¹, it is not difficult to calculate the corresponding stroke interval (around µ) for arbitrarily chosen fractions of unhooking events taking place in the interval. For instance, if the number of unhooking events is five, the corresponding stroke values are listed in Equation (9).

$$f\left(x\right)=\frac{1}{\mathsf{\sigma }\sqrt{2\mathsf{\pi }}}{e}^{-\frac{{\left(x-\mu \right)}^2}{2{\mathsf{\sigma }}^2}}$$

(7)

$$\underset{\mu -\mathsf{\sigma }}{\overset{\mu +\mathsf{\sigma }}{{\displaystyle \int }}}f\left(x\right)dx=\mathrm{erf}\left(\frac{1}{\sqrt{2}}\right)=0.6826$$

(8)

$$\mu , \mu \pm \mathsf{\sigma }\sqrt{2}·er{f}^{-1}\left(\frac{3}{5}\right), \mu \pm \mathsf{\sigma }\sqrt{2}·er{f}^{-1}\left(\frac{4}{5}\right)$$

(9)

Figure 9b,c shows the diagram of both the measured and simulated fastener force versus stroke for various hook densities (b) and the fastener’s strength as a function of hook density (c). Fasteners with densities of 240 cm⁻², 110 cm⁻² and 30 cm⁻² are samples C-C, B-B and A-A, respectively. Samples with the other densities were not produced, since the fabrication of NiTi Velcro-like fasteners was time-consuming. The diagram of the simulated fastener’s strength versus hook density indicates that strength of the studied NiTi hook fasteners depends on hook density approximately linearly. The presented simulations can be also used for the modeling of NiTi fastener’s strength as a function of the number of attachment–detachment cycles if the fatigue properties of a plain NiTi hook are known. Fatigue properties of a single NiTi hook and NiTi Velcro-like fasteners will be a subject of future work.

4. Conclusions

The strength of the developed superelastic NiTi fastener was investigated at various temperatures experimentally and by using simulations (only room temperature results were shown in the case of simulations). The maximum axial detachment force strongly increased with increasing temperature due to the superelasticity of NiTi or with increasing hook density due to increasing number of interlocked hooks. The number of interlocked hooks was well predictable based on repeated random sampling to obtain a mean number of interlocked hooks in either array of a certain hook density. The force–stroke curve associated with the hook array detachment was simulated based on knowing the number of the interlocked hooks and the force-stroke curve of a single hook pair at room temperature. The simulated strength of the studied NiTi hook fasteners depended on hook density approximately linearly.