Effect of Scanning Strategy in the L-PBF Process of 18Ni300 Maraging Steel
Abstract
1. Introduction
1.1. Effect of Energy Input in L-PBF Processing
1.2. The Shortcomings of Andrew Number as a Sufficient Measure for Process Control
2. Experimental
2.1. Materials
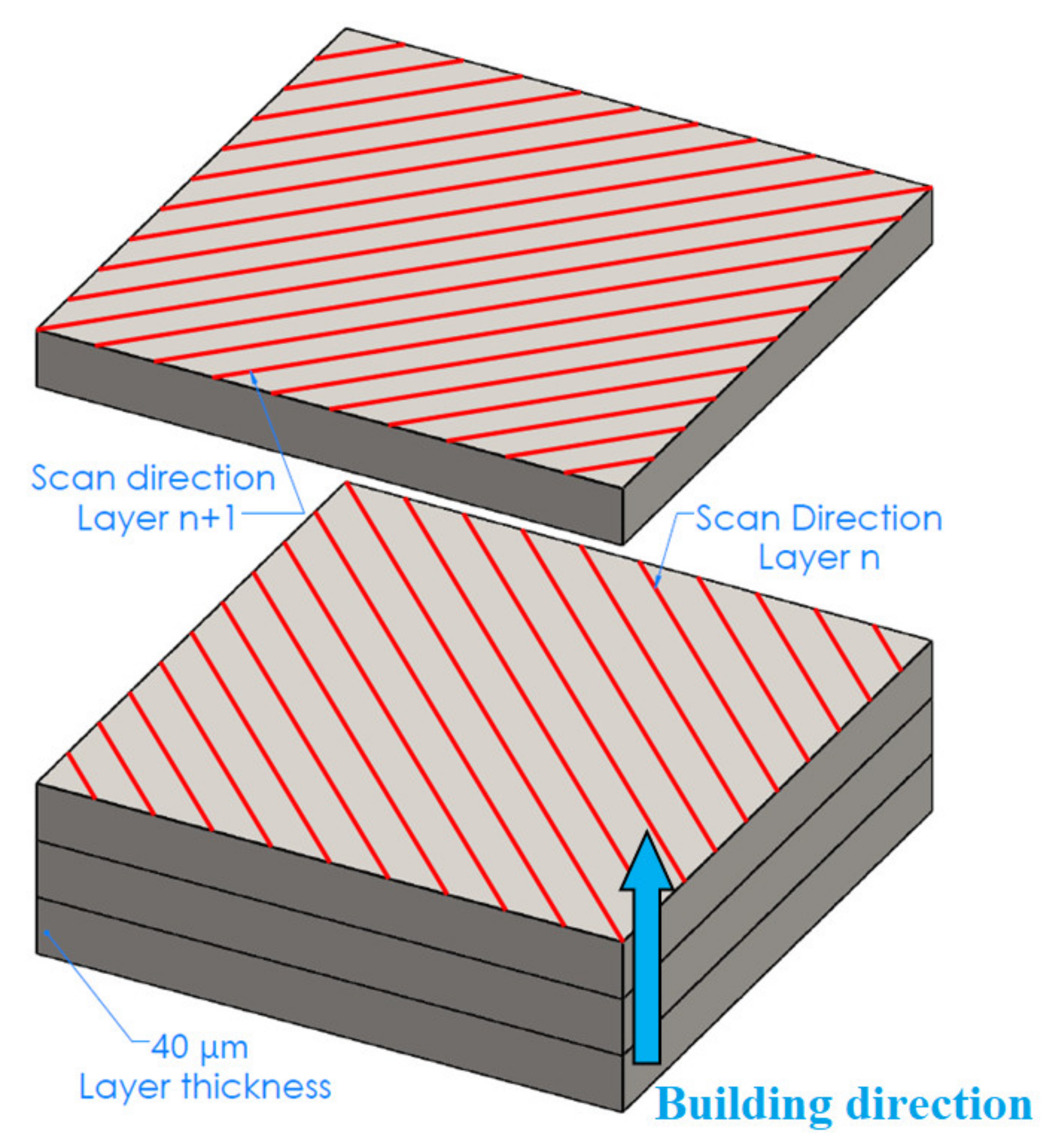
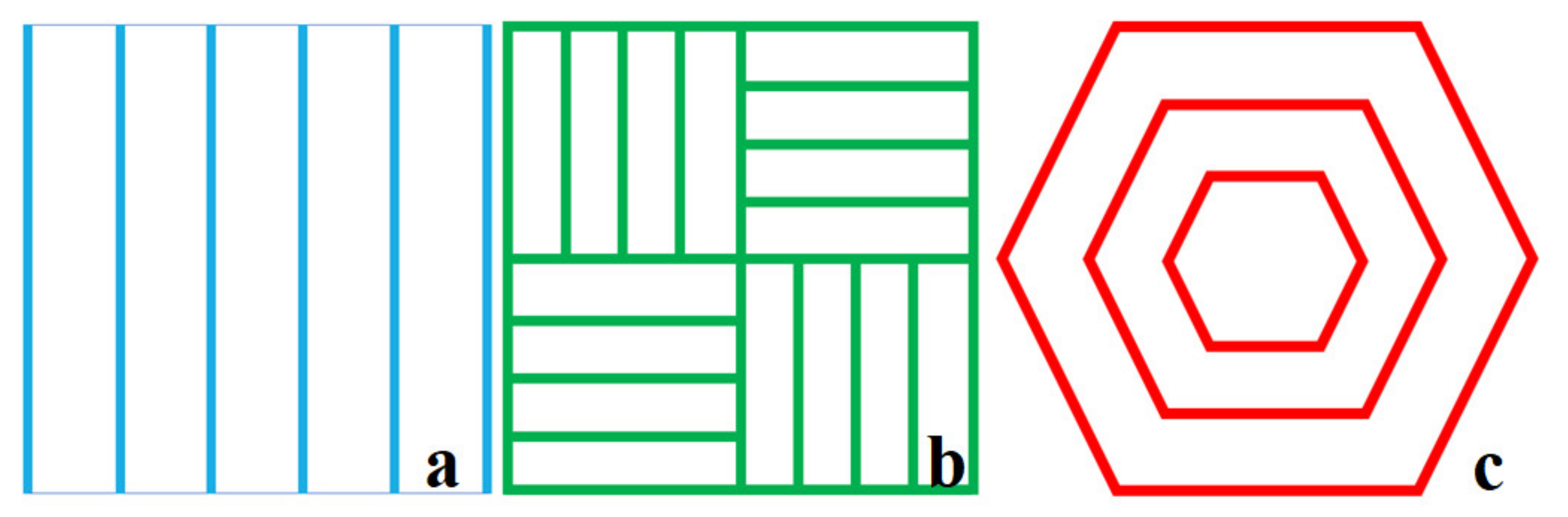
2.2. Process Planning and Variation
2.3. Characterization
2.3.1. Sample Dimension
2.3.2. Average Surface Roughness Ra
2.3.3. Density
2.3.4. Microscopy
2.3.5. Nano Hardness
3. Results
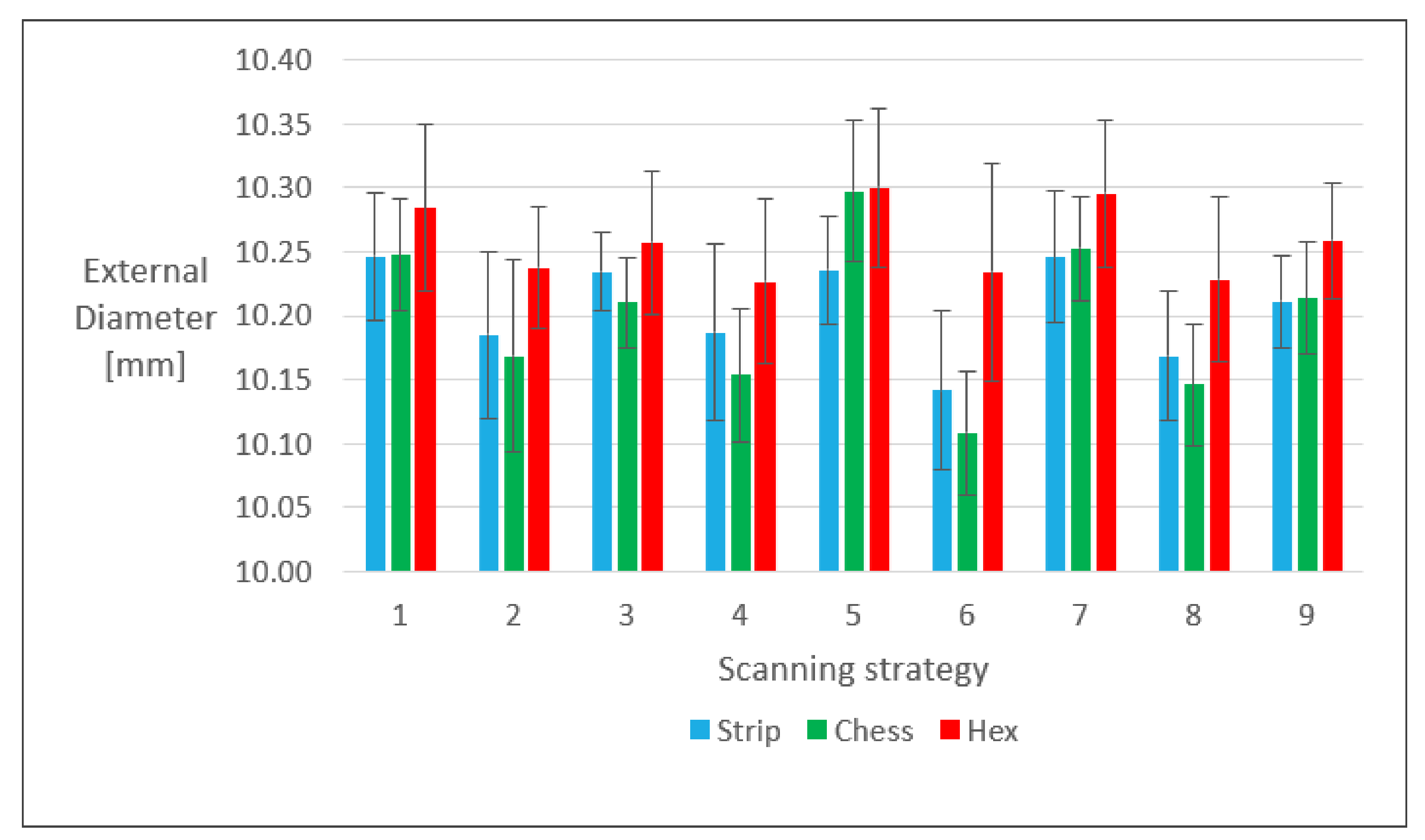
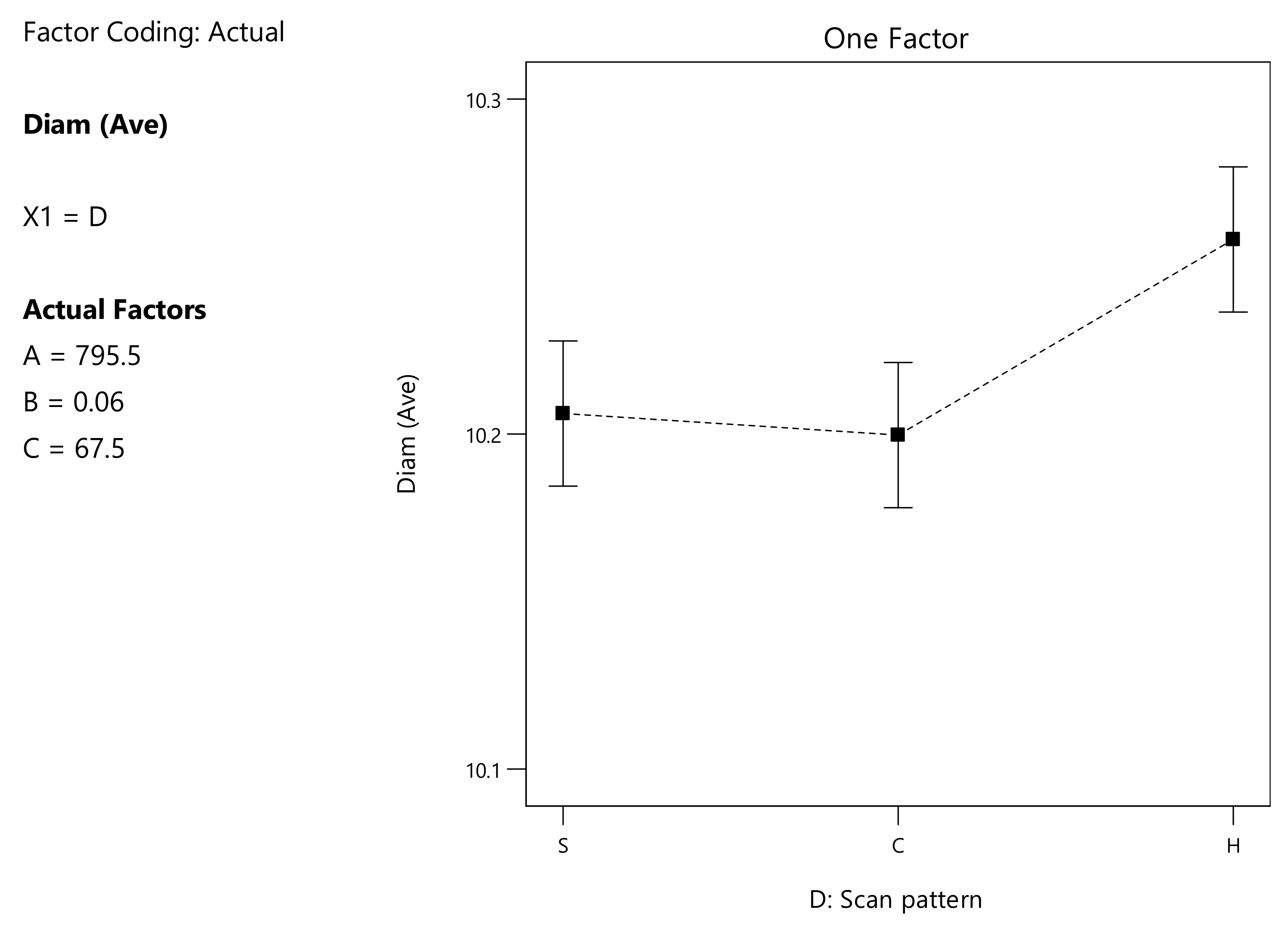
3.1. External Diameter
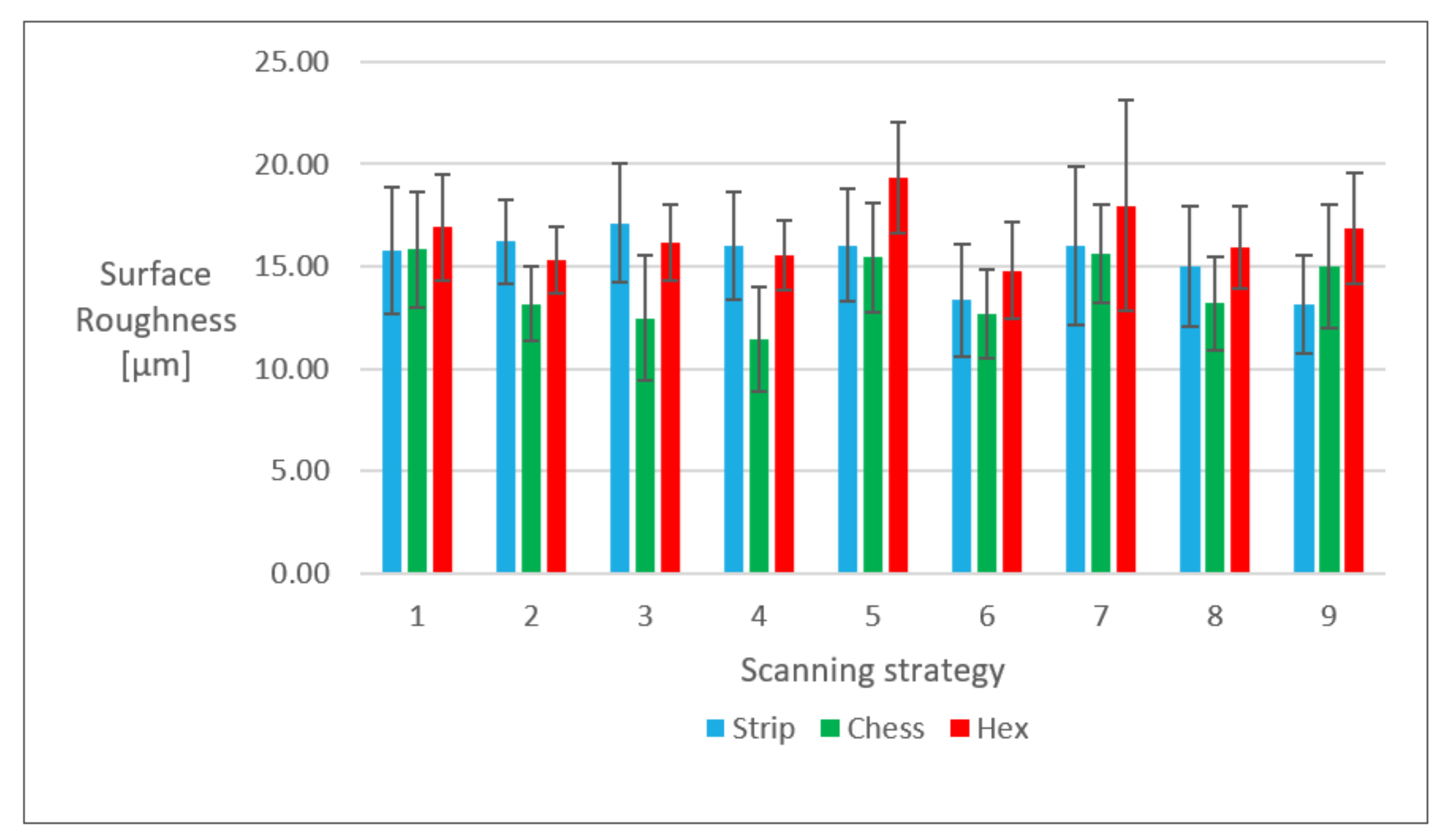
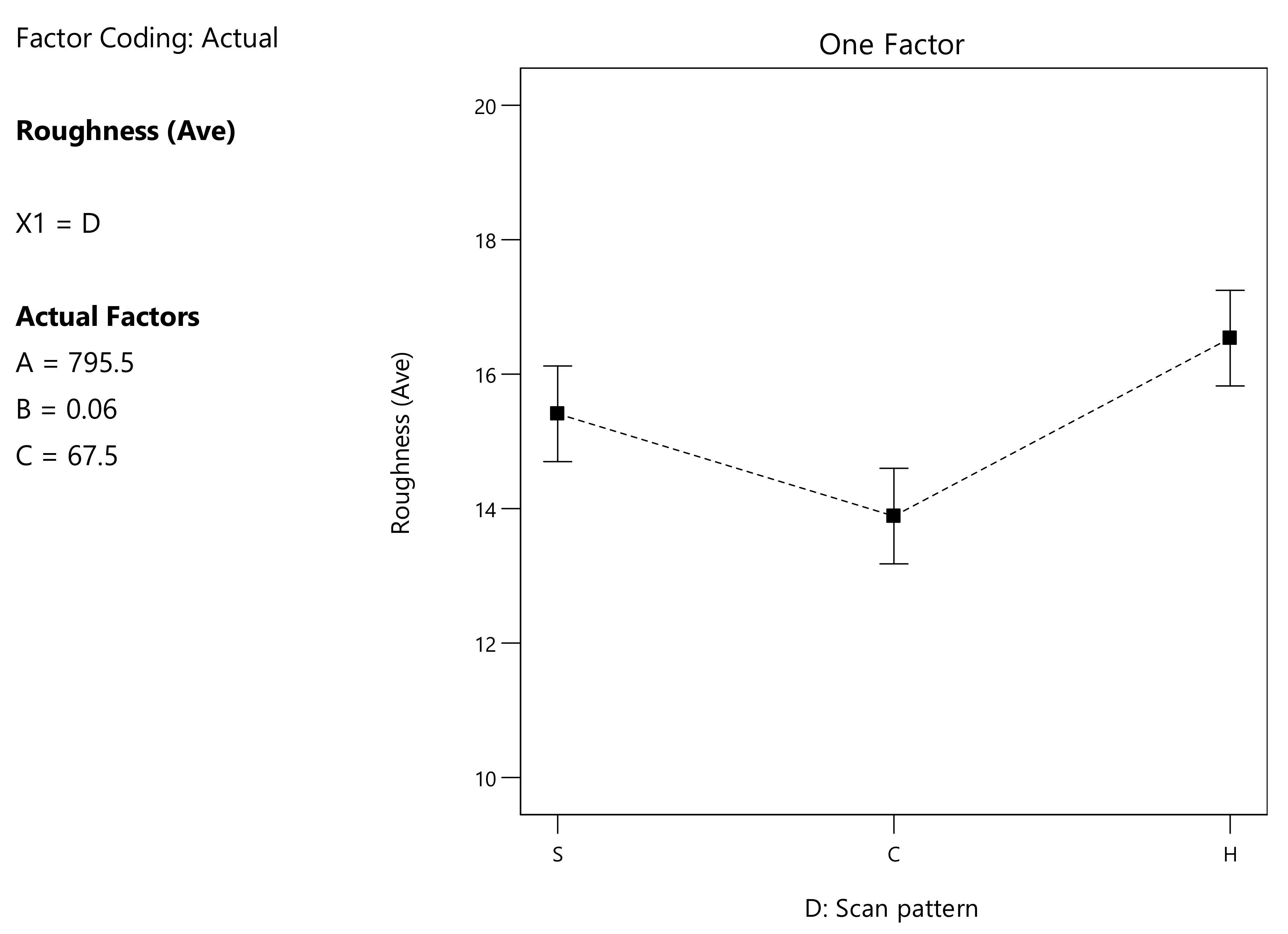
3.2. Average Surface Roughness Ra
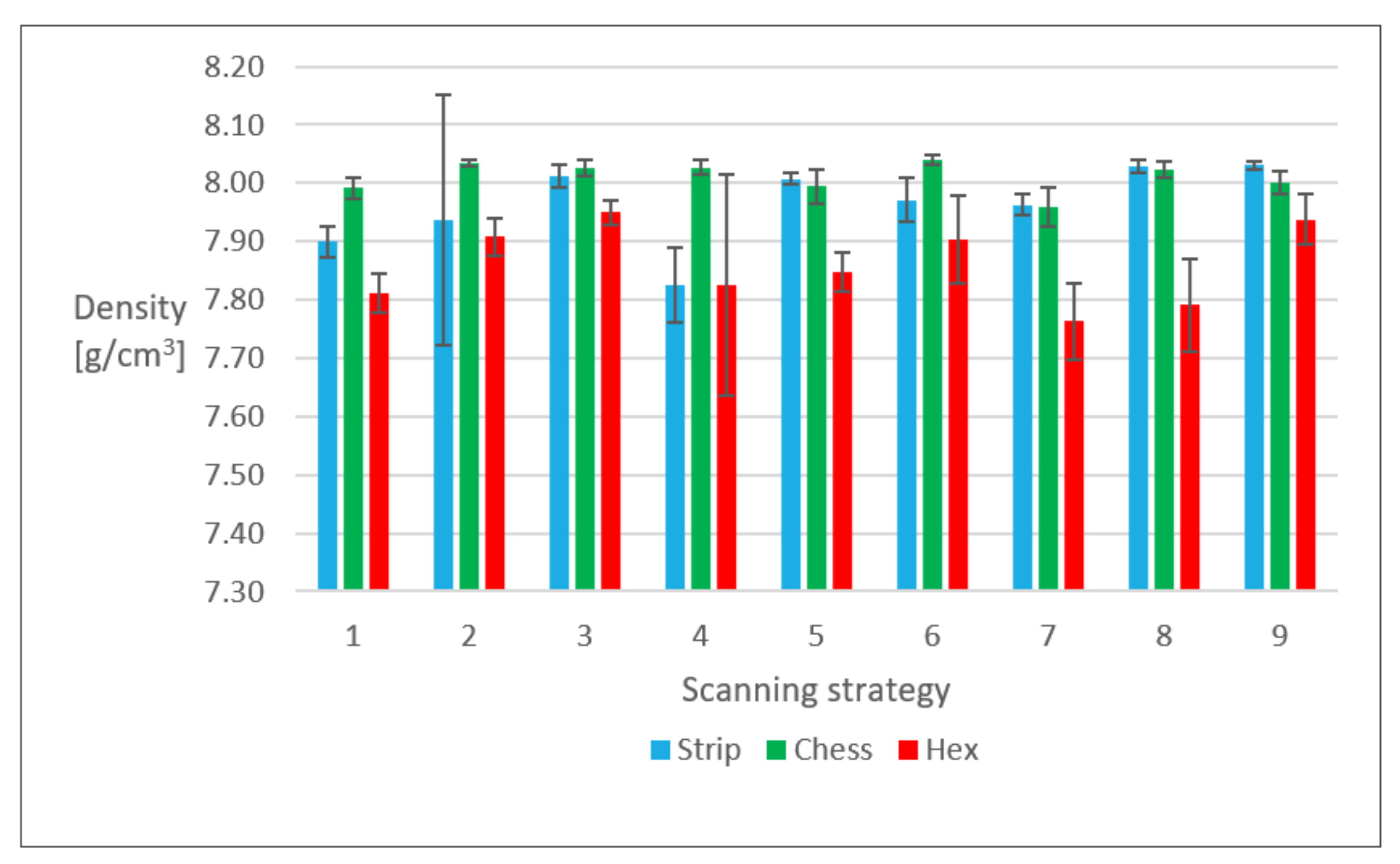
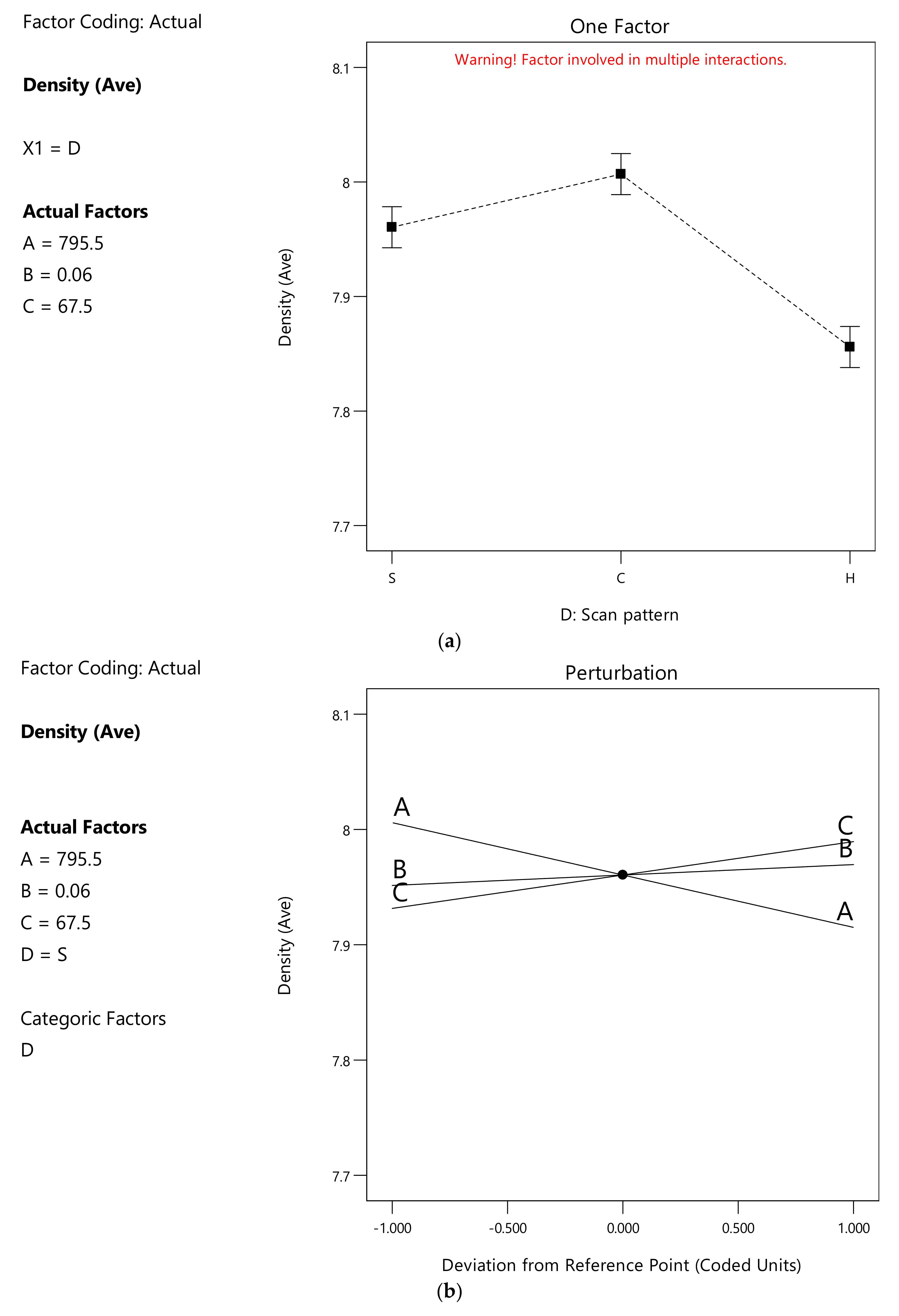
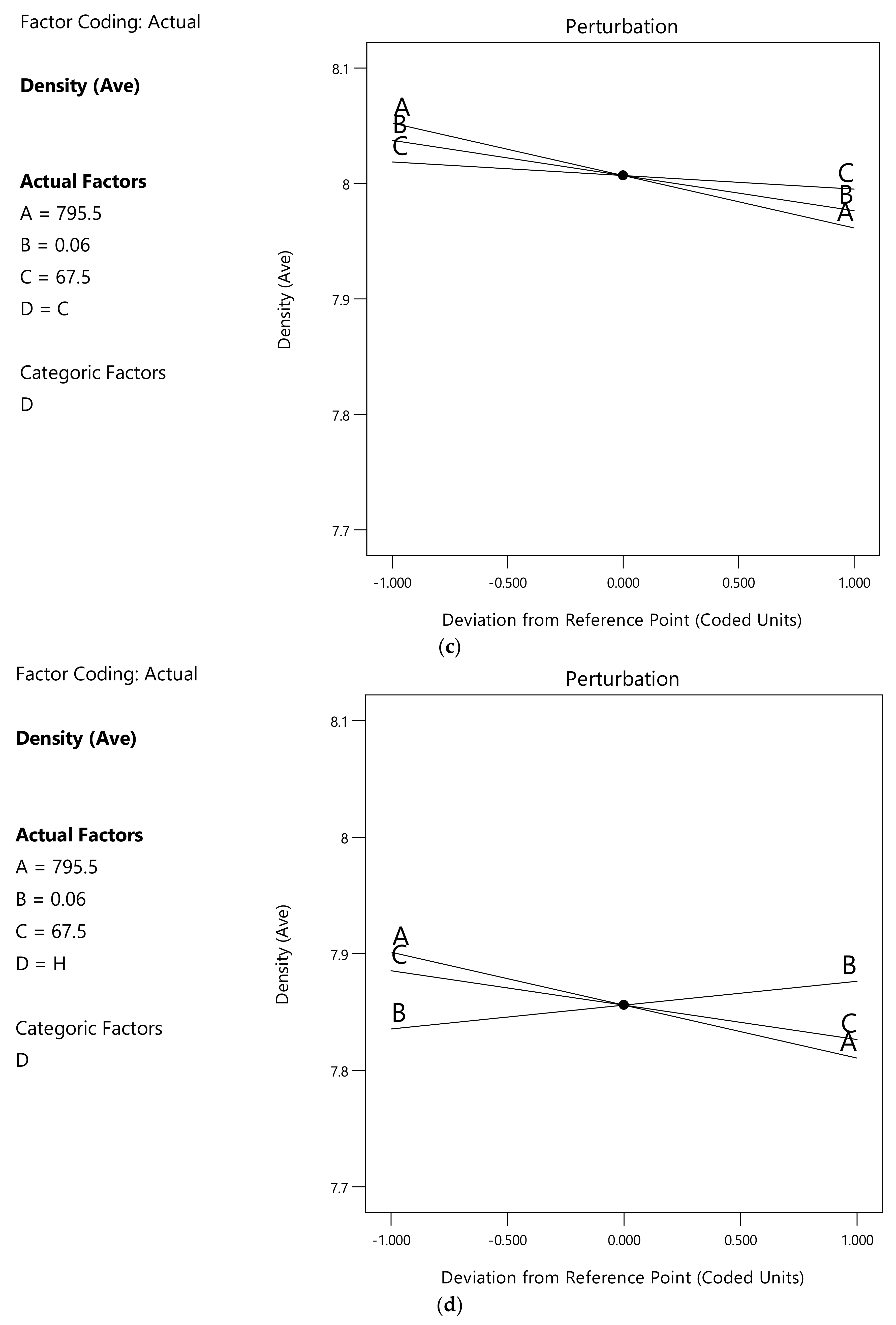
3.3. Density
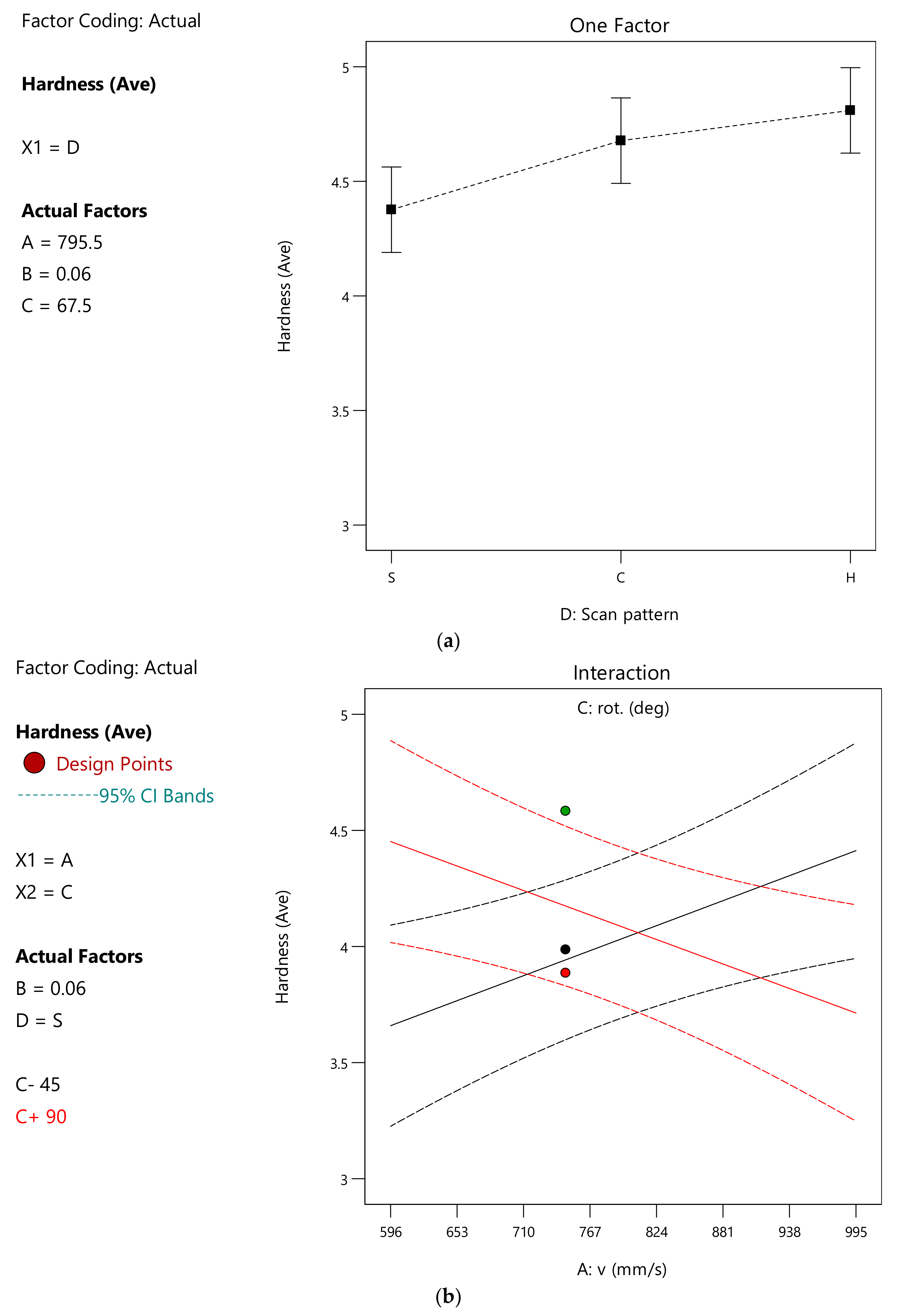
3.4. Nano-Hardness
4. Discussion
4.1. External Diameter
4.2. Average Surface Roughness Ra
4.3. Density
4.4. Nano-Hardness
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Details of the ANOVA Analysis
Appendix A.1. ANOVA Analysis of the External Diameter
| (a) ANOVA for Reduced Linear model Response 1: Diam (Ave). | ||||||
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Comment |
| Model | 0.0185 | 2 | 0.0092 | 4.65 | 0.0197 | significant |
| D-Scan pattern | 0.0185 | 2 | 0.0092 | 4.65 | 0.0197 | significant |
| Residual | 0.0476 | 24 | 0.002 | - | - | - |
| Cor Total | 0.0661 | 26 | - | - | - | - |
| (b) ANOVA Quality measures for Reduced Linear model Response 1: Diam (Ave). | ||||||
| Entity | Value | Entity | Value | |||
| Std. Dev. | 0.0445 | R2 | 0.2793 | |||
| Mean | 10.22 | Adjusted R2 | 0.2192 | |||
| C.V.% | 0.4358 | Predicted R2 | 0.0878 | |||
| - | - | Adeq Precision | 3.9327 | |||
- -
- SP is 1 for the stripes pattern, otherwise it is equal to 0.
- -
- CP is 1 for the chessboard pattern, otherwise it is equal to 0.
- -
- HP is 1 for the hexagonal scanning strategy, otherwise it is 0.
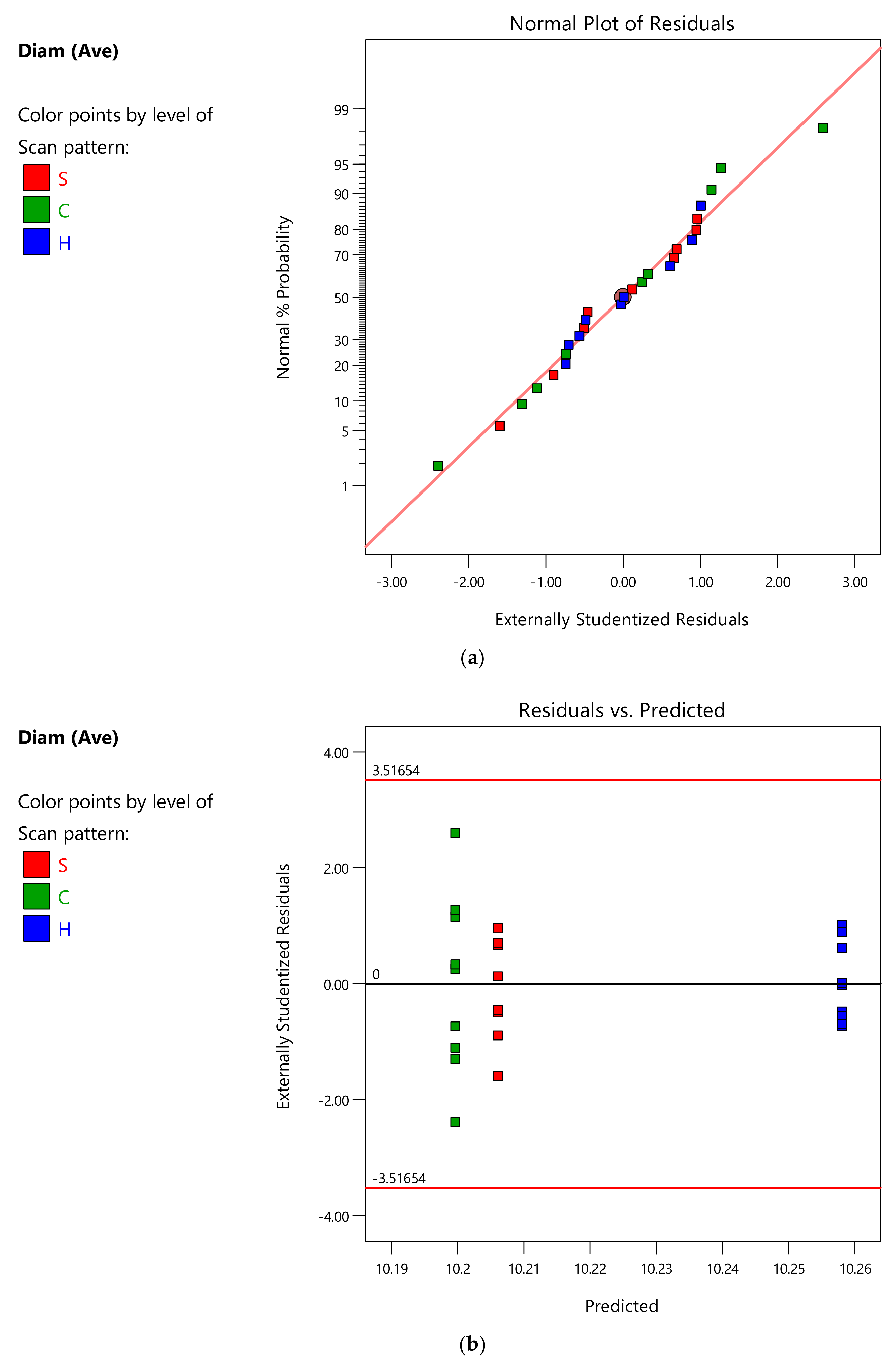
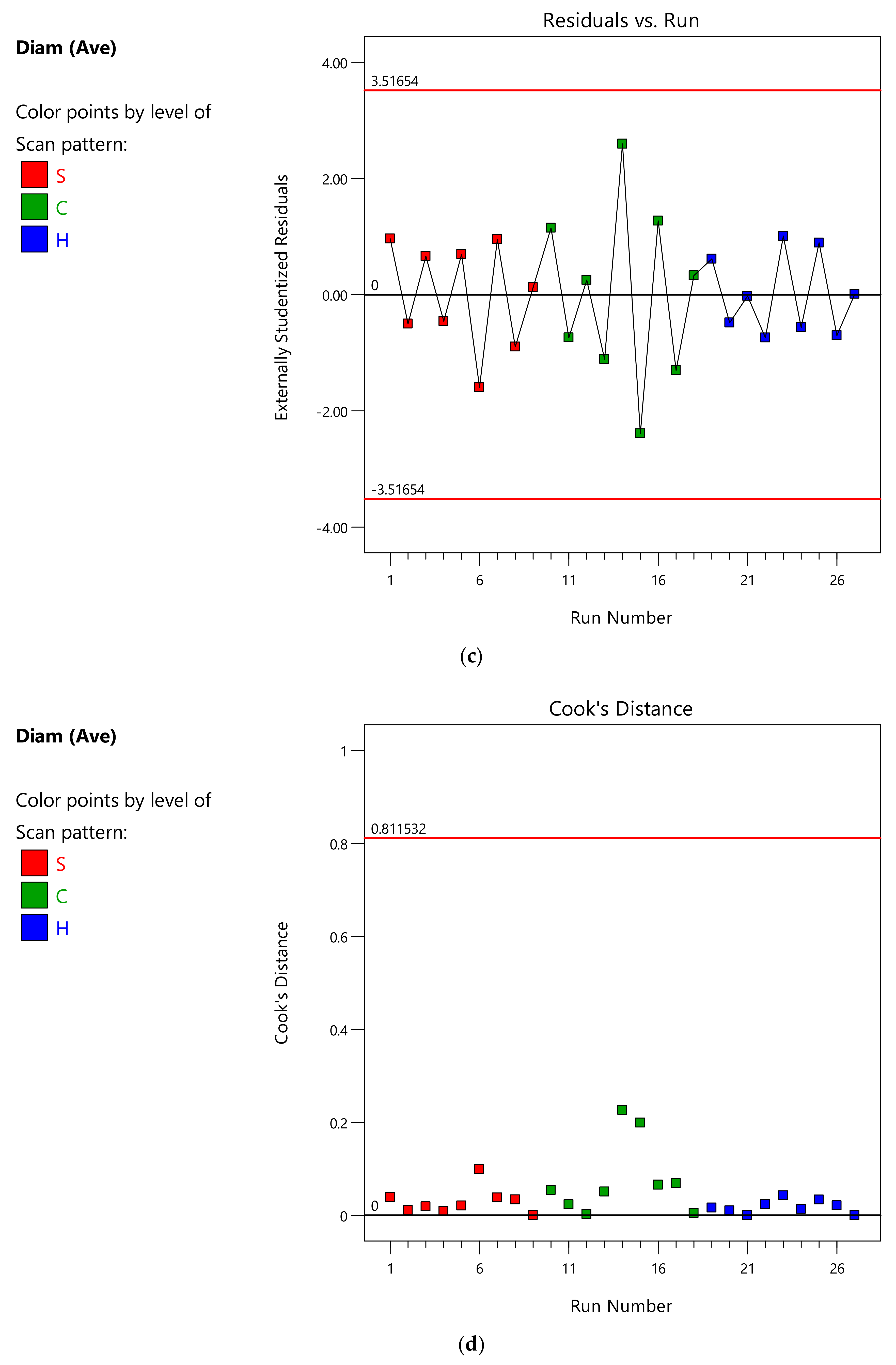
Appendix A.2. ANOVA Analysis of the Average Surface Roughness Ra
| (a) ANOVA for Reduced Linear model Response 1: Average surface roughness Ra. | ||||||
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Comment |
| Model | 31.78 | 2 | 15.89 | 7.44 | 0.0031 | significant |
| D-Scan pattern | 31.78 | 2 | 15.89 | 7.44 | 0.0031 | significant |
| Residual | 51.26 | 24 | 2.14 | - | - | - |
| Cor Total | 83.03 | 26 | - | - | - | - |
| (b) ANOVA Quality measures for Reduced Linear model Response 1: Average surface roughness Ra. | ||||||
| Entity | Value | Entity | Value | |||
| Std. Dev. | 1.46 | R2 | 0.3827 | |||
| Mean | 15.28 | Adjusted R2 | 0.3312 | |||
| C.V.% | 9.56 | Predicted R2 | 0.2187 | |||
| - | - | Adeq Precision | 5.4346 | |||
- -
- SP is 1 for the stripes pattern, otherwise it is equal to 0.
- -
- CP is 1 for the chessboard pattern, otherwise it is equal to 0.
- -
- HP is 1 for the hexagonal scanning strategy, otherwise it is 0.
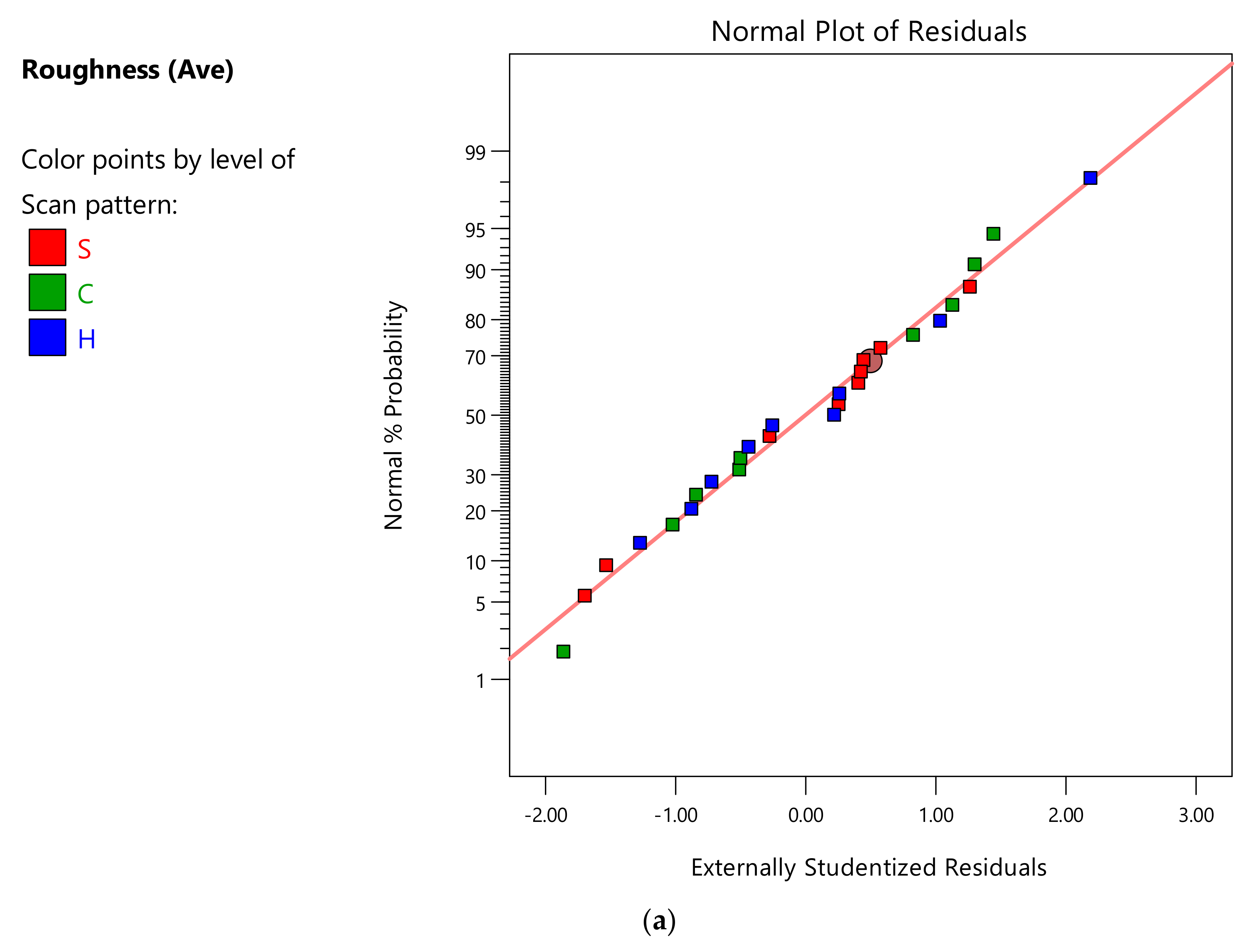
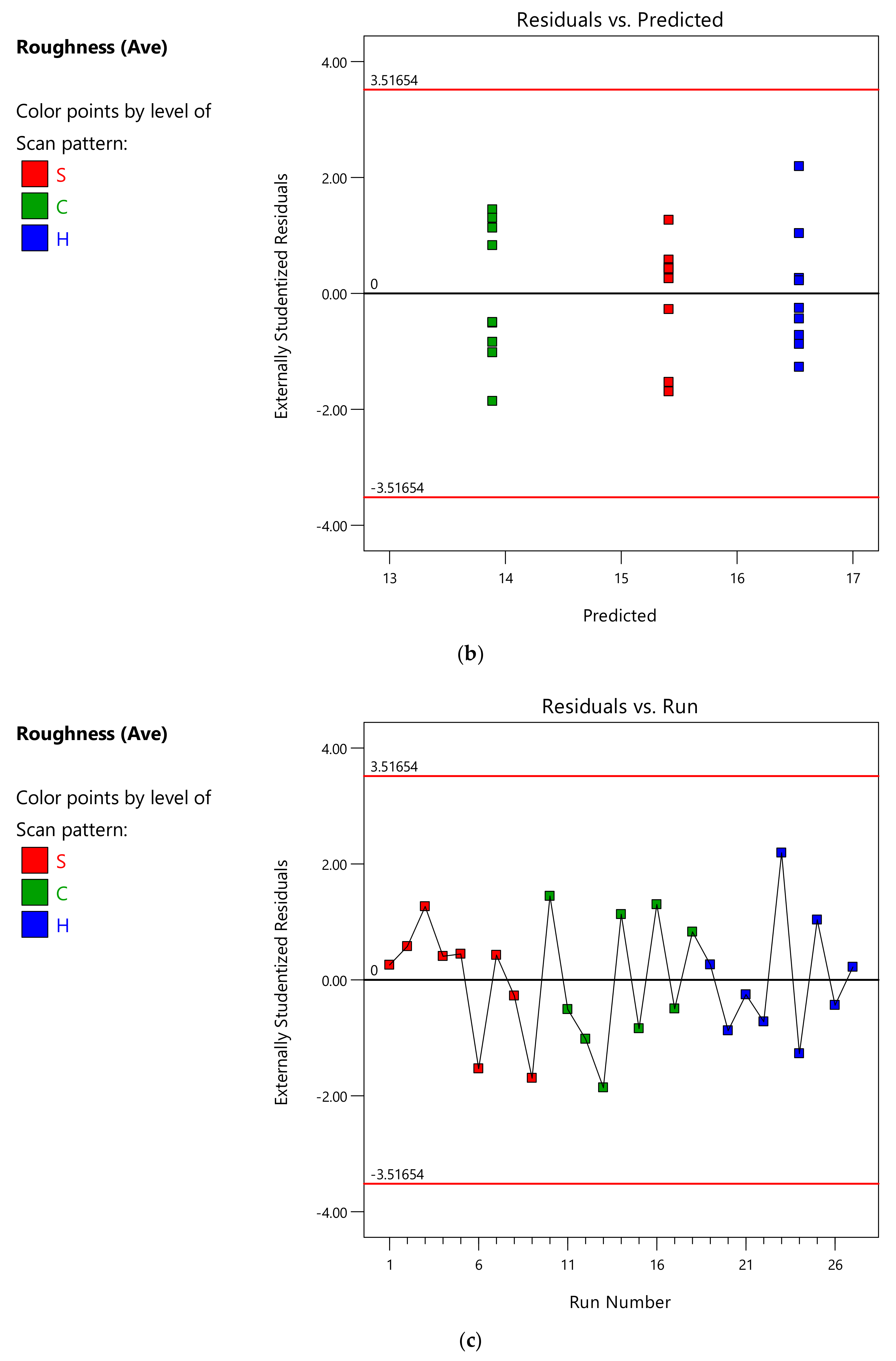
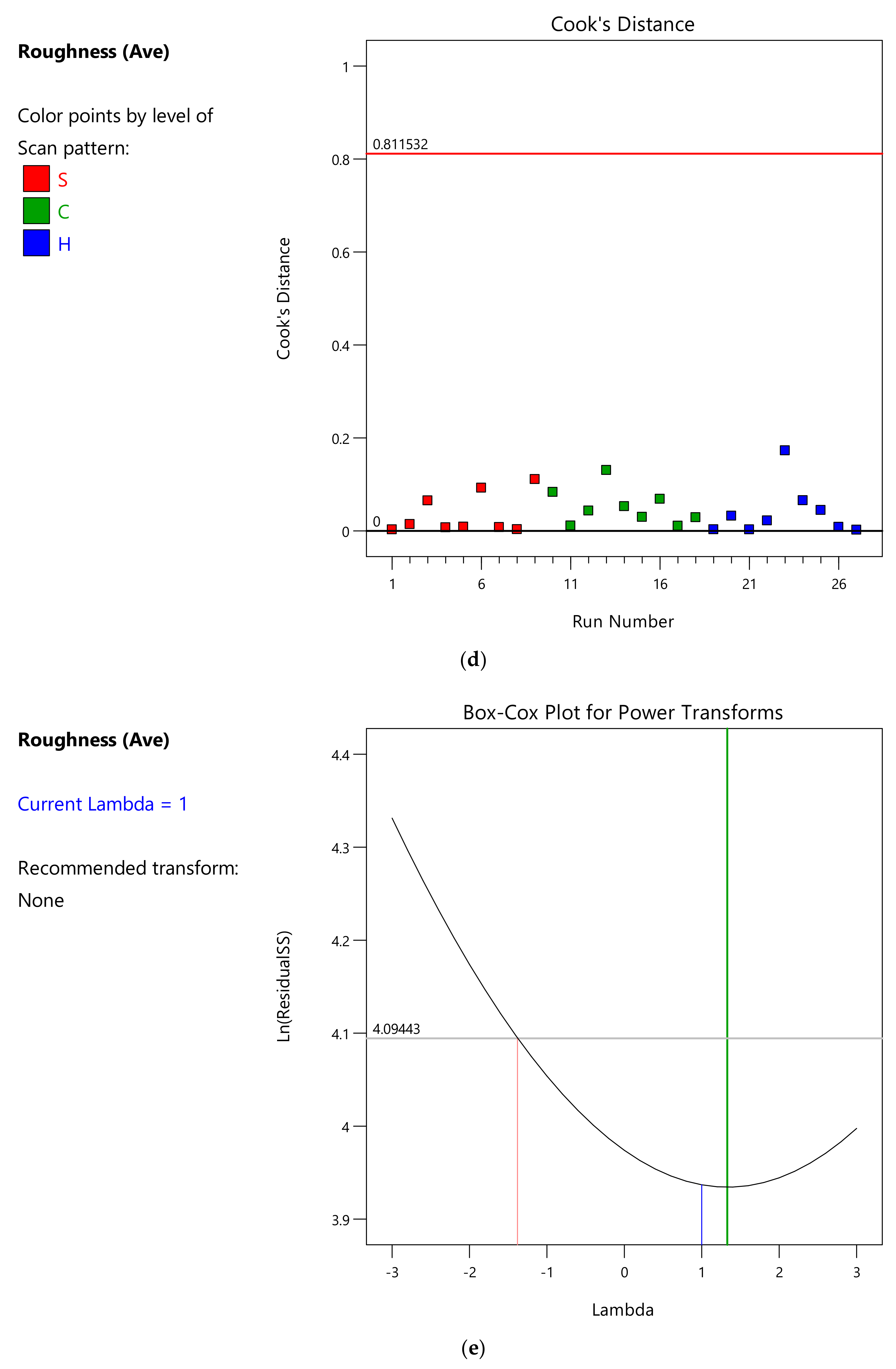
Appendix A.3. ANOVA Analysis of the Density
| (a) ANOVA for Reduced Linear model Response 1: Density. | ||||||
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Comment |
| Model | 0.1642 | 9 | 0.0182 | 14.06 | 3.12 × 10−6 | Significant |
| A-v | 0.0008 | 1 | 0.0008 | 0.593 | 0.4518 | Hierarchy |
| B-h | 3.74 × 10−8 | 1 | 3.74 × 10−8 | 0 | 0.9958 | Hierarchy |
| C-rot. | 0.0003 | 1 | 0.0003 | 0.2337 | 0.635 | Hierarchy |
| D-Scan pattern | 0.1074 | 2 | 0.0537 | 41.35 | 2.95 × 10−7 | Significant |
| BD | 0.0086 | 2 | 0.0043 | 3.3 | 0.0614 | Not insignificant |
| CD | 0.0108 | 2 | 0.0054 | 4.16 | 0.0339 | Significant |
| Residual | 0.0221 | 17 | 0.0013 | - | - | - |
| Cor Total | 0.1863 | 26 | - | - | - | - |
| (b) ANOVA Quality measures for Reduced Linear model Response 1: Density. | ||||||
| Entity | Value | Entity | Value | |||
| Std. Dev. | 0.036 | R2 | 0.8815 | |||
| Mean | 7.94 | Adjusted R2 | 0.8188 | |||
| C.V.% | 0.4535 | Predicted R2 | 0.72 | |||
| - | - | Adeq Precision | 12.9156 | |||
- -
- SP is 1 for the stripes pattern, otherwise it is equal to 0.
- -
- CP is 1 for the chessboard pattern, otherwise it is equal to 0.
- -
- HP is 1 for the hexagonal scanning strategy, otherwise it is 0.
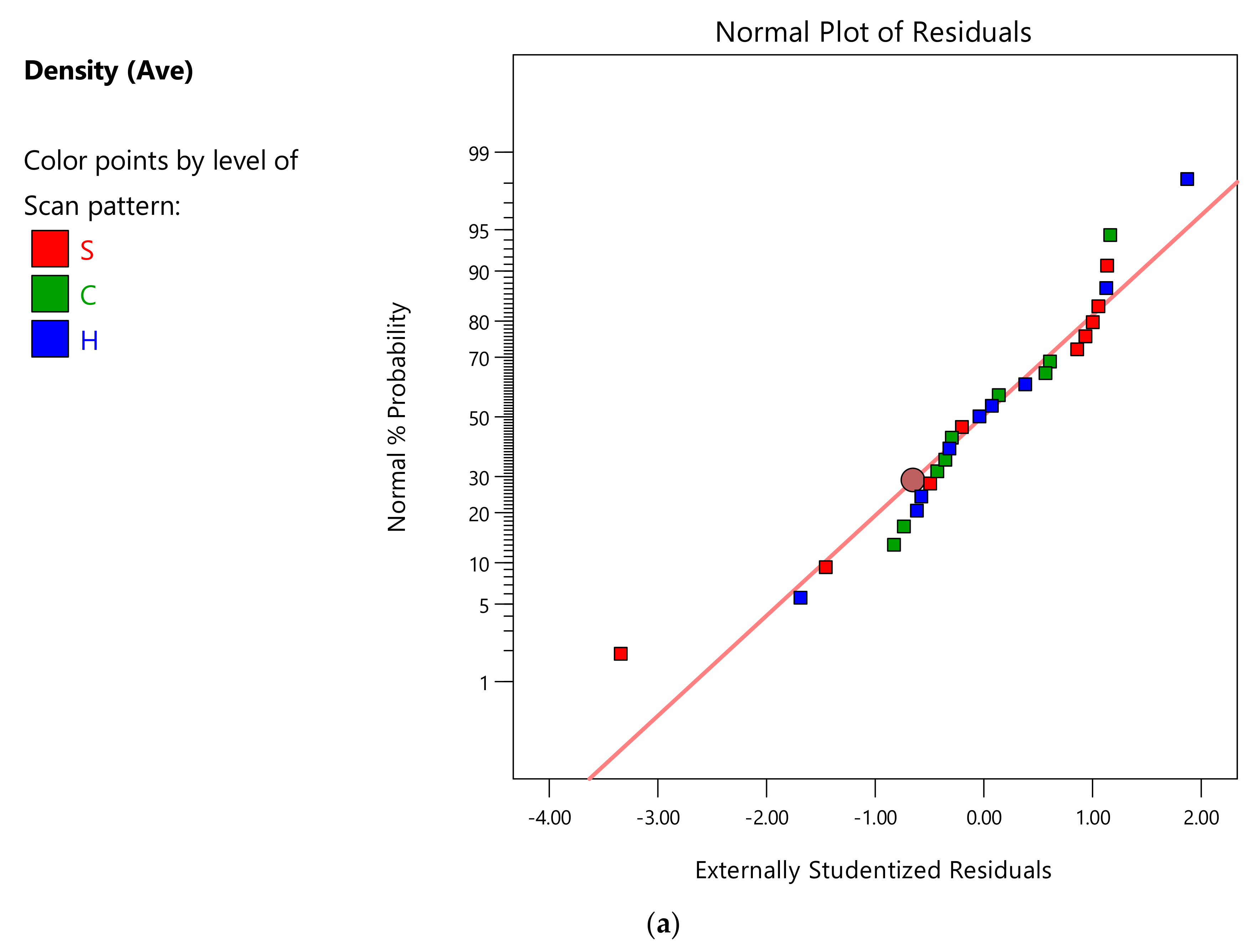
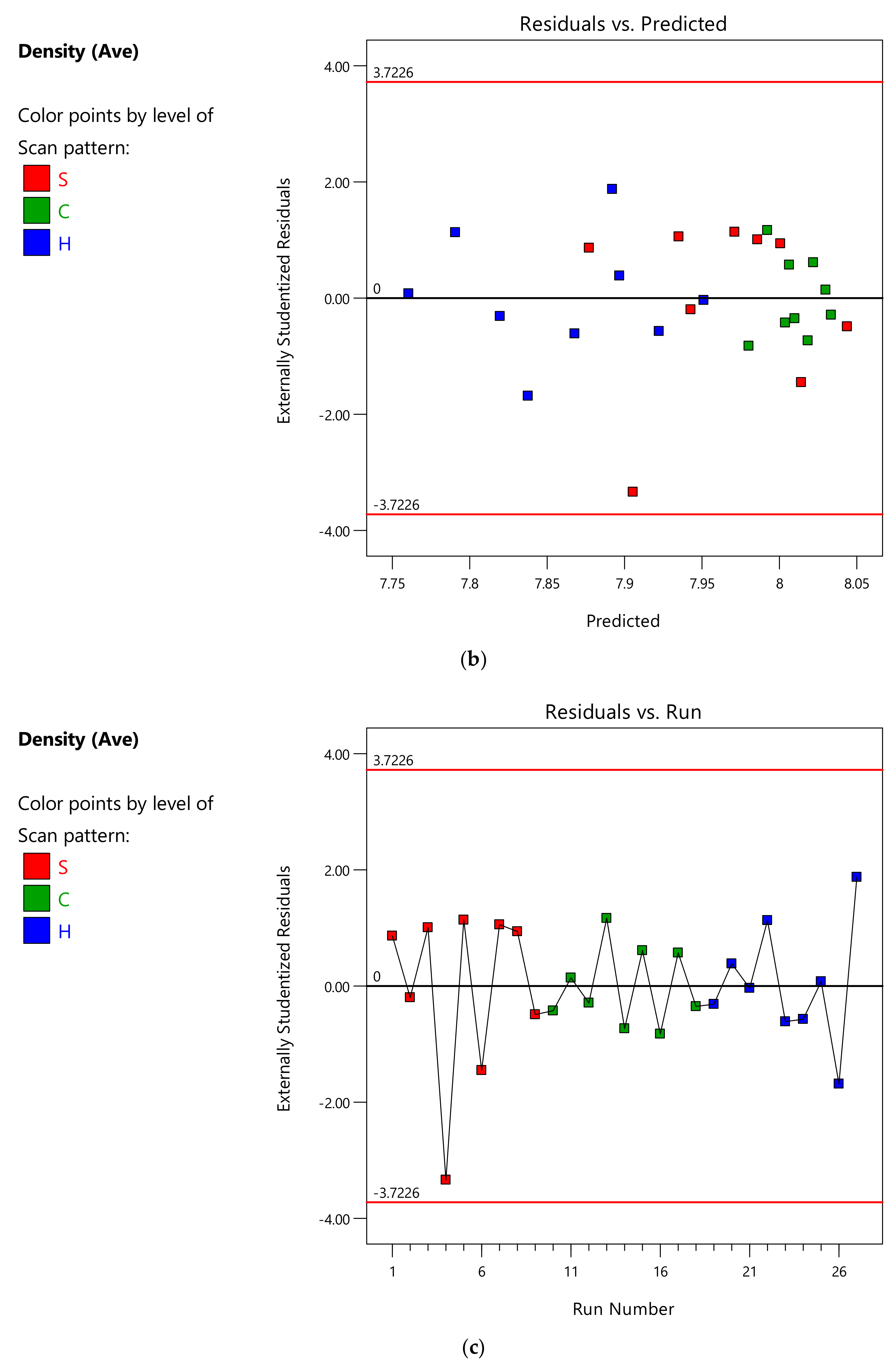
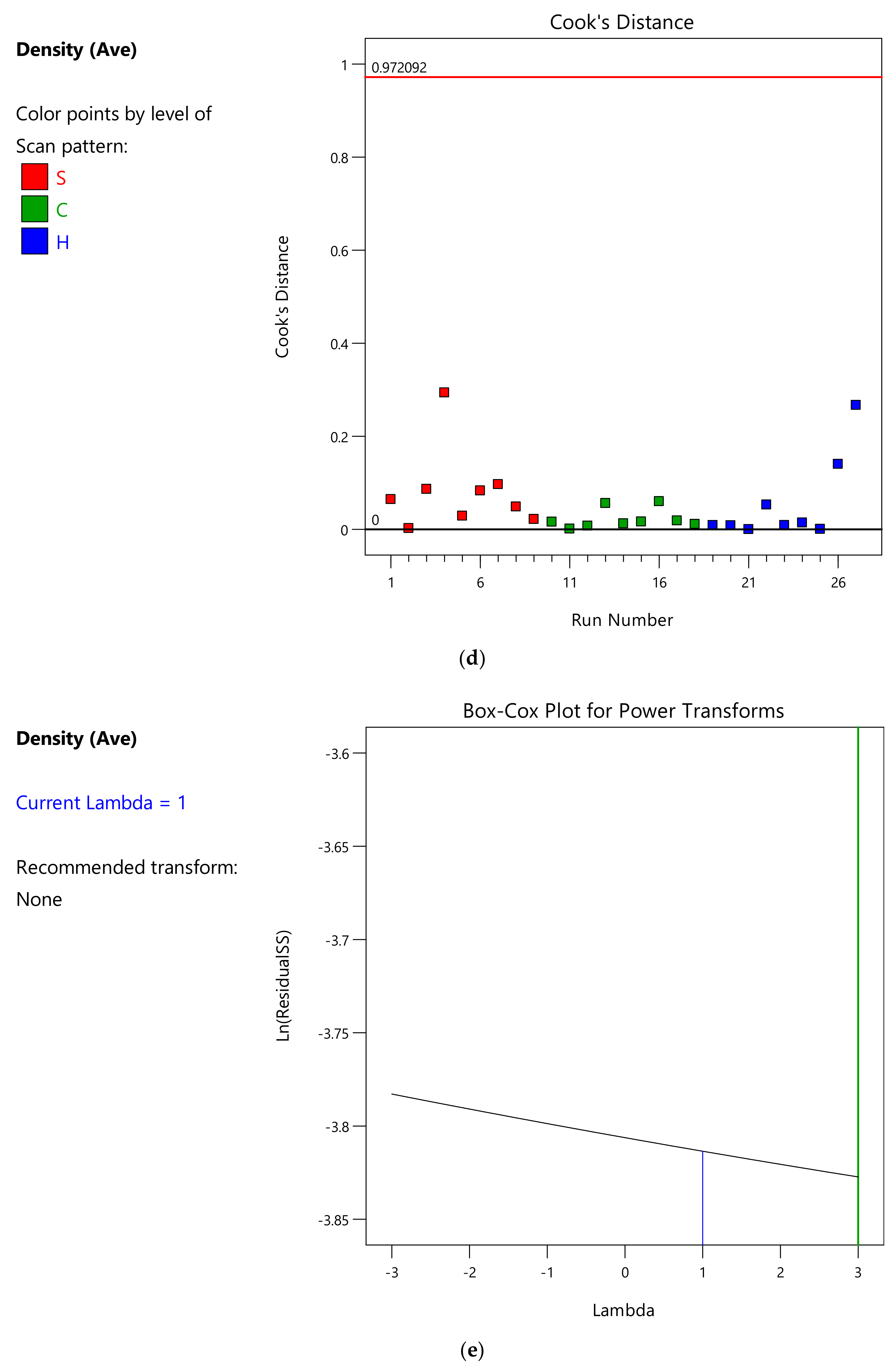
Appendix A.4. ANOVA Analysis of the Nano-Hardness
| (a) ANOVA for Reduced Linear model Response 1: Nano-hardness. | ||||||
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Comment |
| Model | 3.23 | 6 | 0.5391 | 3.75 | 0.0116 | Significant |
| A-v | 0.0008 | 1 | 0.0008 | 0.0055 | 0.9414 | Hierarchy |
| C-rot. | 0.048 | 1 | 0.048 | 0.3332 | 0.5702 | Hierarchy |
| D-Scan pattern | 0.8881 | 2 | 0.4441 | 3.09 | 0.068 | Not insignificant |
| AC | 1.7 | 1 | 1.7 | 11.78 | 0.0026 | significant |
| C2 | 0.6021 | 1 | 0.6021 | 4.18 | 0.0542 | Not insignificant |
| Residual | 2.88 | 20 | 0.1439 | - | - | - |
| Cor Total | 6.11 | 26 | - | - | - | - |
| (b) ANOVA Quality measures for Reduced Linear model Response 1: Nano-hardness. | ||||||
| Entity | Value | Entity. | Value | |||
| Std. Dev. | 0.3794 | R2 | 0.5291 | |||
| Mean | 4.41 | Adjusted R2 | 0.3878 | |||
| C.V.% | 8.6 | Predicted R2 | 0.067 | |||
| - | - | Adeq Precision | 6.3327 | |||
- -
- SP is 1 for the stripes pattern, otherwise it is equal to 0.
- -
- CP is 1 for the chessboard pattern, otherwise it is equal to 0.
- -
- HP is 1 for the hexagonal scanning strategy, otherwise it is 0.
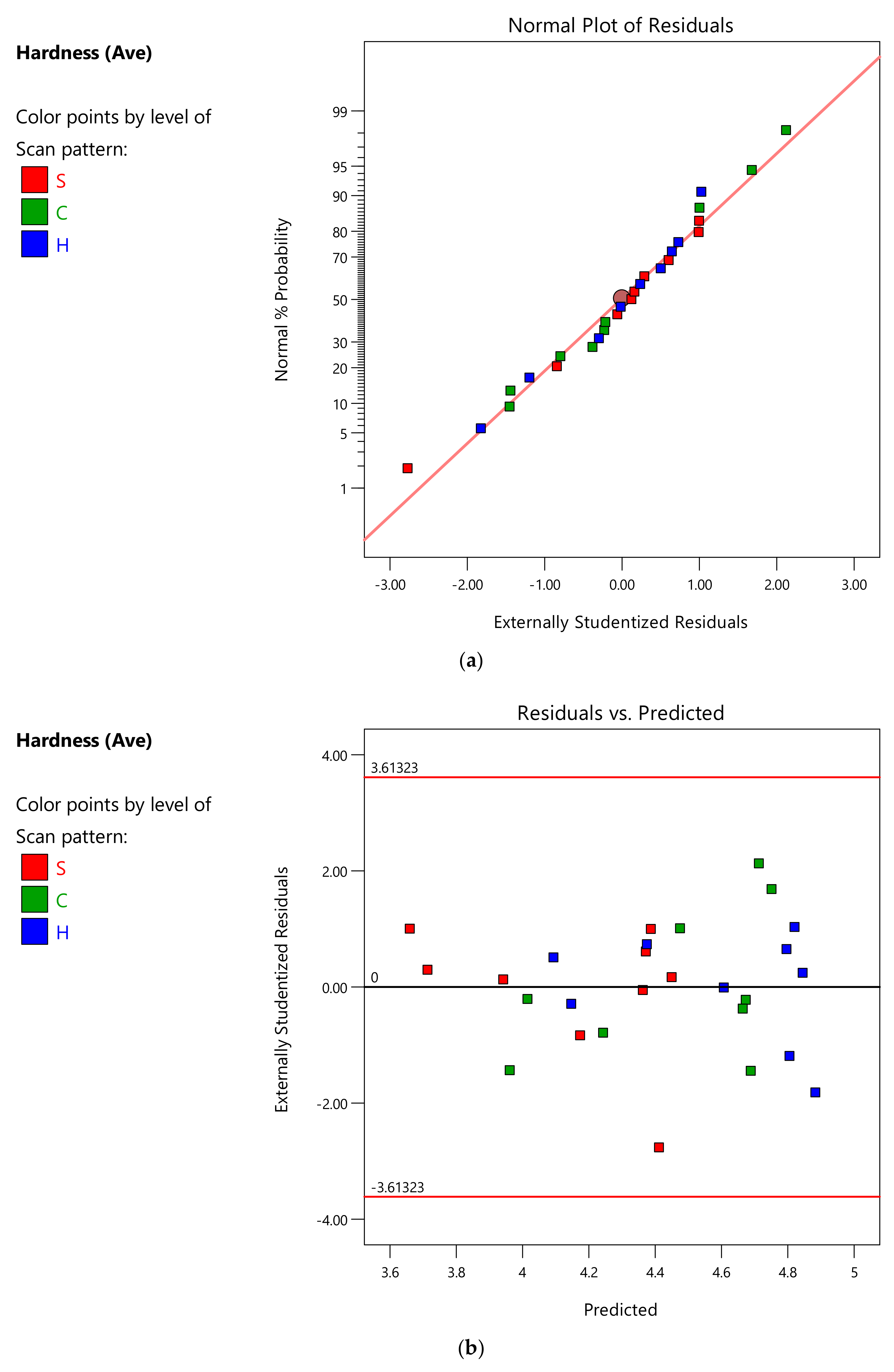
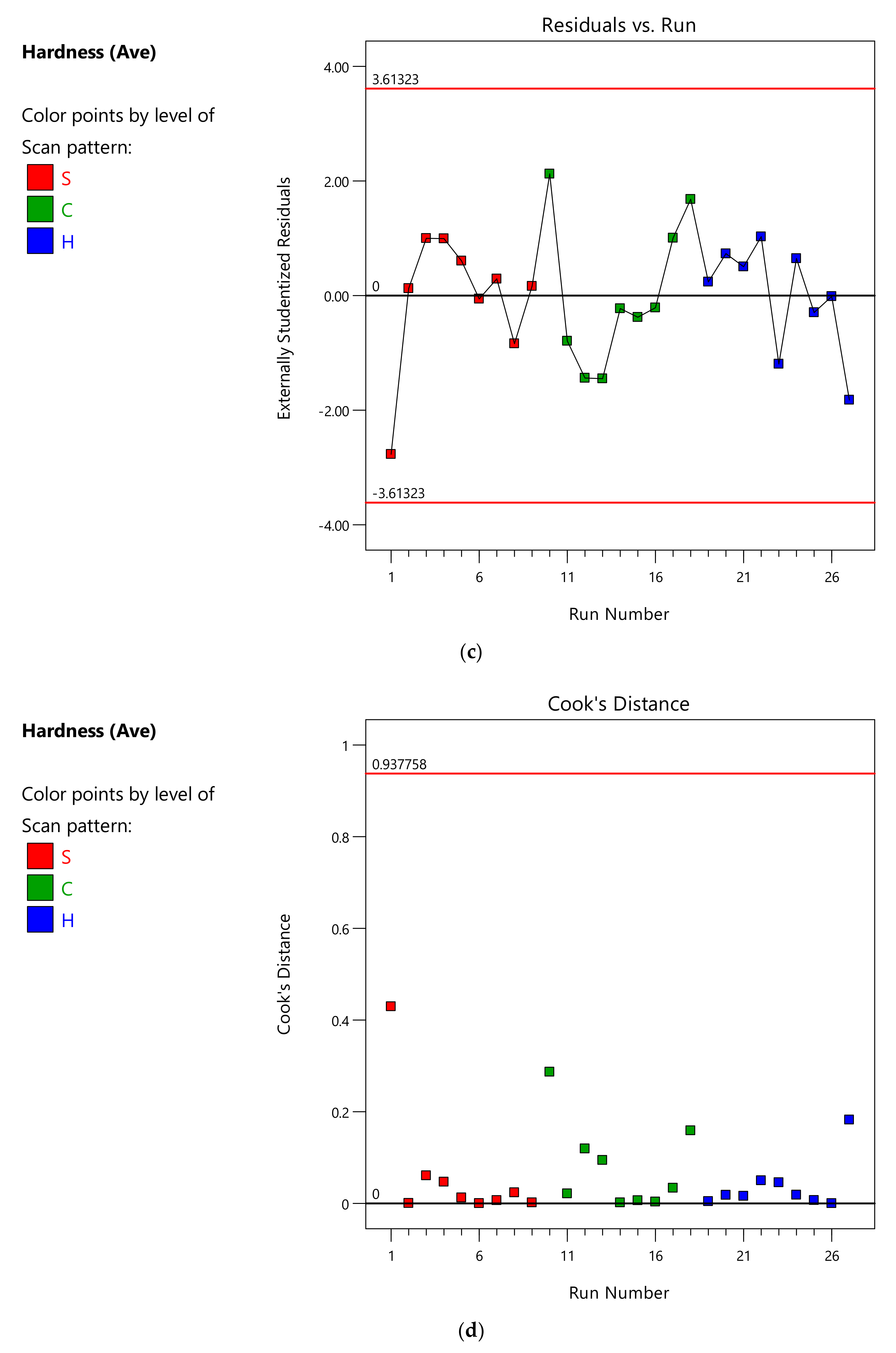
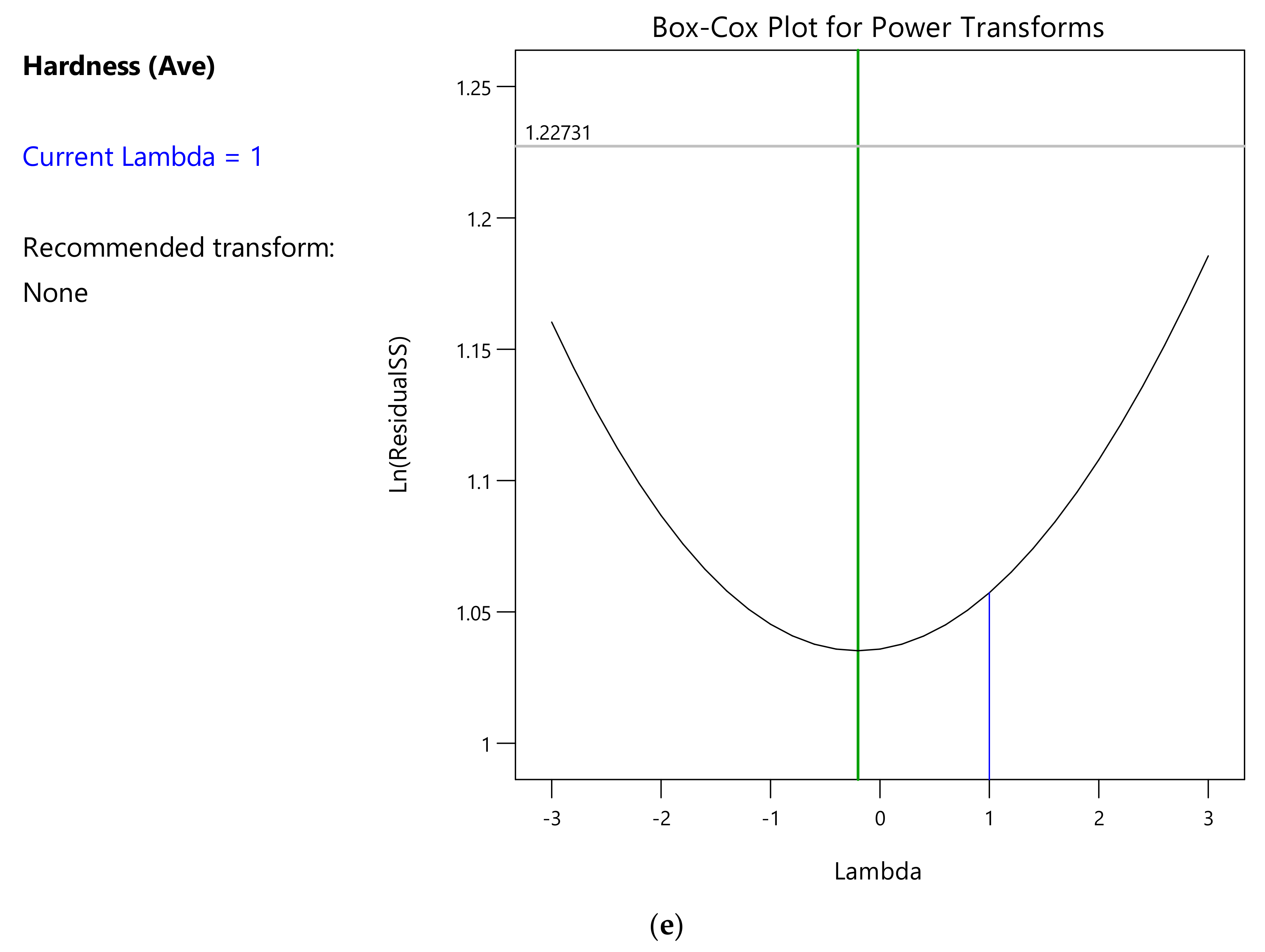
References
- Li, R.; Shi, Y.; Wang, L.; Liu, J.; Wang, Z. The Key Metallurgical Features of Selective Laser Melting of Stainless Steel Powder for Building Metallic Part. Powder Metall. Met. Ceram. 2011, 50, 141–150. [Google Scholar] [CrossRef]
- Cacace, S.; Semeraro, Q. About Fluence and Process Parameters on Maraging Steel Processed by Selective Laser Melting: Do They Convey the Same Information? Int. J. Precis. Eng. Manuf. 2018, 19, 1873–1884. [Google Scholar] [CrossRef]
- Wang, L.; Wei, Q.S.; Shi, Y.S.; Liu, J.H.; He, W.T. Experimental Investigation into the Single-Track of Selective Laser Melting of IN625. Adv. Mater. Res. 2011, 233–235, 2844–2848. [Google Scholar] [CrossRef]
- Campanelli, S.L.; Casalino, G.; Contuzzi, N.; Angelastro, A.; Ludovico, A.D. Analysis of the Molten/Solidified Zone in Selective Laser Melted Parts. In Proceedings of the SPIE, High-Power Laser Materials Processing: Lasers, Beam Delivery, Diagnostics, and Applications III, San Francisco, CA, USA, 20 February 2014; Volume 8963. [Google Scholar]
- Casalino, G.; Campanelli, S.L.; Contuzzi, N.; Ludovico, A.D. Experimental Investigation and Statistical Optimisation of the Selective Laser Melting Process of a Maraging Steel. Opt. Laser Technol. 2015, 65, 151–158. [Google Scholar] [CrossRef]
- Bai, Y.; Yang, Y.; Wang, D.; Zhang, M. Influence Mechanism of Parameters Process and Mechanical Properties Evolution Mechanism of Maraging Steel 300 by Selective Laser Melting. Mater. Sci. Eng. A 2017, 703, 116–123. [Google Scholar] [CrossRef]
- Goodridge, R.; Ziegelmeier, S. Powder bed fusion of polymers. In Laser Additive Manufacturing; Brandt, M., Ed.; Woodhead Publishing: Sawston, UK, 2017; pp. 181–204. ISBN 9780081004333. [Google Scholar]
- Nozar, M.; Zetková, I.; Hronek, O. Searching for Favourable Powder Bed Fusion Settings in Sintering of Maraging Steel MS1. In Annals of DAAAM and Proceedings of the International DAAAM Symposium; DAAAM International: Vienna, Austria, 2018; Volume 29, pp. 777–785. ISSN 1726-9679. ISBN 978-3-902734-20-4. [Google Scholar]
- Scipioni Bertoli, U.; Wolfer, A.J.; Matthews, M.J.; Delplanque, J.P.R.; Schoenung, J.M. On the Limitations of Volumetric Energy Density as a Design Parameter for Selective Laser Melting. Mater. Des. 2017, 113, 331–340. [Google Scholar] [CrossRef]
- Ciurana, J.; Hernandez, L.; Delgado, J. Energy Density Analysis on Single Tracks Formed by Selective Laser Melting with CoCrMo Powder Material. Int. J. Adv. Manuf. Technol. 2013, 68, 1103–1110. [Google Scholar] [CrossRef]
- De Souza, A.F.; Al-Rubaie, K.S.; Marques, S.; Zluhan, B.; Santos, E.C. Effect of Laser Speed, Layer Thickness, and Part Position on the Mechanical Properties of Maraging 300 Parts Manufactured by Selective Laser Melting. Mater. Sci. Eng. A 2019, 767, 138425. [Google Scholar] [CrossRef]
- Suzuki, A.; Nishida, R.; Takata, N.; Kobashi, M.; Kato, M. Design of Laser Parameters for Selectively Laser Melted Maraging Steel Based on Deposited Energy Density. Addit. Manuf. 2019, 28, 160–168. [Google Scholar] [CrossRef]
- Delcuse, L.; Bahi, S.; Gunputh, U.; Rusinek, A.; Wood, P.; Miguelez, M.H. Effect of Powder Bed Fusion Laser Melting Process Parameters, Build Orientation and Strut Thickness on Porosity, Accuracy and Tensile Properties of an Auxetic Structure in IN718 Alloy. Addit. Manuf. 2020, 36, 101339. [Google Scholar] [CrossRef]
- Kempen, K.; Yasa, E.; Thijs, L.; Kruth, J.P.; Van Humbeeck, J. Microstructure and Mechanical Properties of Selective Laser Melted 18Ni-300 Steel. Phys. Procedia 2011, 12, 255–263. [Google Scholar] [CrossRef]
- Campanelli, S.L.; Contuzzi, N.; Ludovico, A.D. Manufacturing of 18 Ni Marage 300 Steel Samples by Selective Laser Melting. Adv. Mater. Res. 2010, 83–86, 850–857. [Google Scholar] [CrossRef]
- Leuders, S.; Vollmer, M.; Brenne, F.; Tröster, T.; Niendorf, T. Fatigue Strength Prediction for Titanium Alloy TiAl6V4 Manufactured by Selective Laser Melting. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2015, 46, 3816–3823. [Google Scholar] [CrossRef]
- Gusarov, A.V.; Kruth, J.P. Modelling of Radiation Transfer in Metallic Powders at Laser Treatment. Int. J. Heat Mass Transf. 2005, 48, 3423–3434. [Google Scholar] [CrossRef]
- Van de Hulst, H.C. Light Scattering by Small Particles. Q. J. R. Meteorol. Soc. 1958, 84, 198–199. [Google Scholar] [CrossRef]
- He, K.; Zhao, X. 3D Thermal Finite Element Analysis of the SLM 316L Parts with Microstructural Correlations. Complexity 2018, 2018. [Google Scholar] [CrossRef]
- Kruth, J.P.; Froyen, L.; van Vaerenbergh, J.; Mercelis, P.; Rombouts, M.; Lauwers, B. Selective Laser Melting of Iron-Based Powder. J. Mater. Process. Technol. 2004, 149, 616–622. [Google Scholar] [CrossRef]
- Trevisan, F.; Calignano, F.; Lorusso, M.; Pakkanen, J.; Aversa, A.; Ambrosio, E.P.; Lombardi, M.; Fino, P.; Manfredi, D. On the Selective Laser Melting (SLM) of the AlSi10Mg Alloy: Process, Microstructure, and Mechanical Properties. Materials 2017, 10, 76. [Google Scholar] [CrossRef]
- Thijs, L.; Verhaeghe, F.; Craeghs, T.; van Humbeeck, J.; Kruth, J.P. A Study of the Microstructural Evolution during Selective Laser Melting of Ti-6Al-4V. Acta Mater. 2010, 58, 3303–3312. [Google Scholar] [CrossRef]
- Zaeh, M.F.; Branner, G. Investigations on Residual Stresses and Deformations in Selective Laser Melting. Prod. Eng. 2010, 4, 35–45. [Google Scholar] [CrossRef]
- Nadammal, N.; Cabeza, S.; Mishurova, T.; Thiede, T.; Kromm, A.; Seyfert, C.; Farahbod, L.; Haberland, C.; Schneider, J.A.; Portella, P.D.; et al. Effect of Hatch Length on the Development of Microstructure, Texture and Residual Stresses in Selective Laser Melted Superalloy Inconel 718. Mater. Des. 2017, 134, 139–150. [Google Scholar] [CrossRef]
- Tolochko, N.K.; Mozzharov, S.E.; Yadroitsev, I.A.; Laoui, T.; Froyen, L.; Titov, V.I.; Ignatiev, M.B. Balling Processes during Selective Laser Treatment of Powders. Rapid Prototyp. J. 2004, 10, 78–87. [Google Scholar] [CrossRef]
- Jhabvala, J.; Boillat, E.; Antignac, T.; Glardon, R. On the Effect of Scanning Strategies in the Selective Laser Melting Process. Virtual Phys. Prototyp. 2010, 5, 99–109. [Google Scholar] [CrossRef]
- Salman, O.O.; Brenne, F.; Niendorf, T.; Eckert, J.; Prashanth, K.G.; He, T.; Scudino, S. Impact of the Scanning Strategy on the Mechanical Behavior of 316L Steel Synthesized by Selective Laser Melting. J. Manuf. Process. 2019, 45, 255–261. [Google Scholar] [CrossRef]
- Biffi, C.A.; Fiocchi, J.; Ferrario, E.; Fornaci, A.; Riccio, M.; Romeo, M.; Tuissi, A. Effects of the Scanning Strategy on the Microstructure and Mechanical Properties of a TiAl6V4 Alloy Produced by Electron Beam Additive Manufacturing. Int. J. Adv. Manuf. Technol. 2020, 107, 4913–4924. [Google Scholar] [CrossRef]
- Yasa, E.; Kruth, J.P. Microstructural Investigation of Selective Laser Melting 316L Stainless Steel Parts Exposed to Laser Re-Melting. Procedia Eng. 2011, 19, 389–395. [Google Scholar] [CrossRef]
- Yasa, E.; Deckers, J.; Kruth, J.P. The Investigation of the Influence of Laser Re-Melting on Density, Surface Quality and Microstructure of Selective Laser Melting Parts. Rapid Prototyp. J. 2011, 17, 312–327. [Google Scholar] [CrossRef]
- Huang, S.; Yeong, W.Y. Laser Re-Scanning Strategy in Selective Laser Melting for Part Quality Enhancement: A Review. In Proceedings of the 3rd International Conference on Progress in Additive Manufacturing (Pro-AM), Nanyang Executive Centre, Singapore, 14–17 May 2018; pp. 413–419. [Google Scholar] [CrossRef]
- Xie, J.W.; Fox, P.; O’Neill, W.; Sutcliffe, C.J. Effect of Direct Laser Re-Melting Processing Parameters and Scanning Strategies on the Densification of Tool Steels. J. Mater. Process. Technol. 2005, 170, 516–523. [Google Scholar] [CrossRef]
- Tian, Y.; Tomus, D.; Rometsch, P.; Wu, X. Influences of Processing Parameters on Surface Roughness of Hastelloy X Produced by Selective Laser Melting. Addit. Manuf. 2017, 13, 103–112. [Google Scholar] [CrossRef]
- Beevers, E.; Brandão, A.D.; Gumpinger, J.; Gschweitl, M.; Seyfert, C.; Hofbauer, P.; Rohr, T.; Ghidini, T. Fatigue Properties and Material Characteristics of Additively Manufactured AlSi10Mg—Effect of the Contour Parameter on the Microstructure, Density, Residual Stress, Roughness and Mechanical Properties. Int. J. Fatigue 2018, 117, 148–162. [Google Scholar] [CrossRef]
- Parry, L.A.; Ashcroft, I.A.; Wildman, R.D. Geometrical Effects on Residual Stress in Selective Laser Melting. Addit. Manuf. 2019, 25, 166–175. [Google Scholar] [CrossRef]
- Mutua, J.; Nakata, S.; Onda, T.; Chen, Z.C. Optimization of Selective Laser Melting Parameters and Influence of Post Heat Treatment on Microstructure and Mechanical Properties of Maraging Steel. Mater. Des. 2018, 139, 486–497. [Google Scholar] [CrossRef]
- Bhardwaj, T.; Shukla, M. Effect of Laser Scanning Strategies on Texture, Physical and Mechanical Properties of Laser Sintered Maraging Steel. Mater. Sci. Eng. A 2018, 734, 102–109. [Google Scholar] [CrossRef]
- Parry, L.; Ashcroft, I.A.; Wildman, R.D. Understanding the Effect of Laser Scan Strategy on Residual Stress in Selective Laser Melting through Thermo-Mechanical Simulation. Addit. Manuf. 2016, 12, 1–15. [Google Scholar] [CrossRef]
- Guo, M.; Ye, Y.; Jiang, X.; Wang, L. Microstructure, Mechanical Properties and Residual Stress of Selective Laser Melted AlSi10Mg. J. Mater. Eng. Perform. 2019, 28, 6753–6760. [Google Scholar] [CrossRef]
- Wang, L.; Jiang, X.; Zhu, Y.; Ding, Z.; Zhu, X.; Sun, J.; Yan, B. Investigation of Performance and Residual Stress Generation of AlSi10Mg Processed by Selective Laser Melting. Adv. Mater. Sci. Eng. 2018, 2018, 7814039. [Google Scholar] [CrossRef]
- Dimitrov, D.; Becker, T.H.; Yadroitsev, I.; Booysen, G. On the impact of different system strategies on the material performance of selective laser melting- manufactured ti6al4v components. S. Afr. J. Ind. Eng. 2016, 27, 184–191. [Google Scholar] [CrossRef]
- Lu, Y.; Wu, S.; Gan, Y.; Huang, T.; Yang, C.; Junjie, L.; Lin, J. Study on the Microstructure, Mechanical Property and Residual Stress of SLM Inconel-718 Alloy Manufactured by Differing Island Scanning Strategy. Opt. Laser Technol. 2015, 75, 197–206. [Google Scholar] [CrossRef]
- Promoppatum, P.; Yao, S.C. Influence of Scanning Length and Energy Input on Residual Stress Reduction in Metal Additive Manufacturing: Numerical and Experimental Studies. J. Manuf. Process. 2020, 49, 247–259. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y.; Wang, D. A Study on the Residual Stress during Selective Laser Melting (SLM) of Metallic Powder. Int. J. Adv. Manuf. Technol. 2016, 87, 647–656. [Google Scholar] [CrossRef]
- Yan, X.; Pang, J.; Jing, Y. Ultrasonic Measurement of Stress in SLM 316L Stainless Steel Forming Parts Manufactured Using Different Scanning Strategies. Materials 2019, 12, 2719. [Google Scholar] [CrossRef] [PubMed]
- Demir, A.G.; Previtali, B. Investigation of Remelting and Preheating in SLM of 18Ni300 Maraging Steel as Corrective and Preventive Measures for Porosity Reduction. Int. J. Adv. Manuf. Technol. 2017, 93, 2697–2709. [Google Scholar] [CrossRef]
- Catchpole-Smith, S.; Aboulkhair, N.; Parry, L.; Tuck, C.; Ashcroft, I.A.; Clare, A. Fractal Scan Strategies for Selective Laser Melting of ‘Unweldable’ Nickel Superalloys. Addit. Manuf. 2017, 15, 113–122. [Google Scholar] [CrossRef]
- Zou, S.; Xiao, H.; Ye, F.; Li, Z.; Tang, W.; Zhu, F.; Chen, C.; Zhu, C. Numerical Analysis of the Effect of the Scan Strategy on the Residual Stress in the Multi-Laser Selective Laser Melting. Results Phys. 2020, 16, 103005. [Google Scholar] [CrossRef]
- AlMangour, B.; Grzesiak, D.; Yang, J.M. Scanning Strategies for Texture and Anisotropy Tailoring during Selective Laser Melting of TiC/316L Stainless Steel Nanocomposites. J. Alloys Compd. 2017, 728, 424–435. [Google Scholar] [CrossRef]
- Nandwana, P.; Lee, Y. Influence of Scan Strategy on Porosity and Microstructure of Ti-6Al-4V Fabricated by Electron Beam Powder Bed Fusion. Mater. Today Commun. 2020, 24, 100962. [Google Scholar] [CrossRef]
- Aboulkhair, N.T.; Everitt, N.M.; Ashcroft, I.; Tuck, C. Reducing Porosity in AlSi10Mg Parts Processed by Selective Laser Melting. Addit. Manuf. 2014, 1, 77–86. [Google Scholar] [CrossRef]
- Lee, Y.S.; Kirka, M.M.; Ferguson, J.; Paquit, V.C. Correlations of Cracking with Scan Strategy and Build Geometry in Electron Beam Powder Bed Additive Manufacturing. Addit. Manuf. 2020, 32, 101031. [Google Scholar] [CrossRef]
- Klingbeil, N.W.; Beuth, J.L.; Chin, R.K.; Amon, C.H. Residual Stress-Induced Warping in Direct Metal Solid Freeform Fabrication. Int. J. Mech. Sci. 2002, 44, 57–77. [Google Scholar] [CrossRef]
- Conde, F.F.; Escobar, J.D.; Oliveira, J.P.; Jardini, A.L.; Bose Filho, W.W.; Avila, J.A. Austenite Reversion Kinetics and Stability during Tempering of an Additively Manufactured Maraging 300 Steel. Addit. Manuf. 2019, 29, 100804. [Google Scholar] [CrossRef]




| Ni. | Co | Mo | Ti | Al | C | Mn | N | O | P | S | Si |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 17.0–19.0 | 8.5–10.0 | 4.50–5.20 | 0.50–1.00 | 0.05–0.15 | <0.03 | <0.15 | <0.02 | <0.035 | <0.010 | <0.010 | <0.10 |
| 18.5 | 9 | 4.84 | 0.64 | 0.07 | <0.01 | 0.03 | 0 | 0.034 | 0.005 | 0.002 | <0.01 |
| Entity, (Unit) | Value |
|---|---|
| Energy density, E (J/mm3) | 89 |
| Laser power, P (W) | 160 |
| Layer thickness, t (mm) | 0.04 |
| Scan speed, v (mm/s) | variable |
| Hatch spacing, h (mm) | variable |
| Inter-layer rotation, angle (°) | variable |
| Stripes | Chessboard | Hexagonal | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| set | v (mm/s) | h (mm) | Angle (°) | set | v (mm/s) | h (mm) | Angle (°) | set | v (mm/s) | h (mm) | Angle (°) |
| Strip1 | 995 | 0.045 | 45 | Chess1 | 995 | 0.045 | 45 | Hex1 | 995 | 0.045 | 45 |
| Strip2 | 746 | 0.060 | 45 | Chess2 | 746 | 0.060 | 45 | Hex2 | 746 | 0.060 | 45 |
| Strip3 | 597 | 0.075 | 45 | Chess3 | 597 | 0.075 | 45 | Hex3 | 597 | 0.075 | 45 |
| Strip4 | 995 | 0.045 | 67 | Chess4 | 995 | 0.045 | 67 | Hex4 | 995 | 0.045 | 67 |
| Strip5 | 746 | 0.060 | 67 | Chess5 | 746 | 0.060 | 67 | Hex5 | 746 | 0.060 | 67 |
| Strip6 | 597 | 0.075 | 67 | Chess6 | 597 | 0.075 | 67 | Hex6 | 597 | 0.075 | 67 |
| Strip7 | 995 | 0.045 | 90 | Chess7 | 995 | 0.045 | 90 | Hex7 | 995 | 0.045 | 90 |
| Strip8 | 746 | 0.060 | 90 | Chess8 | 746 | 0.060 | 90 | Hex8 | 746 | 0.060 | 90 |
| Strip9 | 597 | 0.075 | 90 | Chess9 | 597 | 0.075 | 90 | Hex9 | 597 | 0.075 | 90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rivalta, F.; Ceschini, L.; Jarfors, A.E.W.; Stolt, R. Effect of Scanning Strategy in the L-PBF Process of 18Ni300 Maraging Steel. Metals 2021, 11, 826. https://doi.org/10.3390/met11050826
Rivalta F, Ceschini L, Jarfors AEW, Stolt R. Effect of Scanning Strategy in the L-PBF Process of 18Ni300 Maraging Steel. Metals. 2021; 11(5):826. https://doi.org/10.3390/met11050826
Chicago/Turabian StyleRivalta, Francesco, Lorella Ceschini, Anders E. W. Jarfors, and Roland Stolt. 2021. "Effect of Scanning Strategy in the L-PBF Process of 18Ni300 Maraging Steel" Metals 11, no. 5: 826. https://doi.org/10.3390/met11050826
APA StyleRivalta, F., Ceschini, L., Jarfors, A. E. W., & Stolt, R. (2021). Effect of Scanning Strategy in the L-PBF Process of 18Ni300 Maraging Steel. Metals, 11(5), 826. https://doi.org/10.3390/met11050826







