Robust Additive Manufacturing Performance through a Control Oriented Digital Twin
Abstract
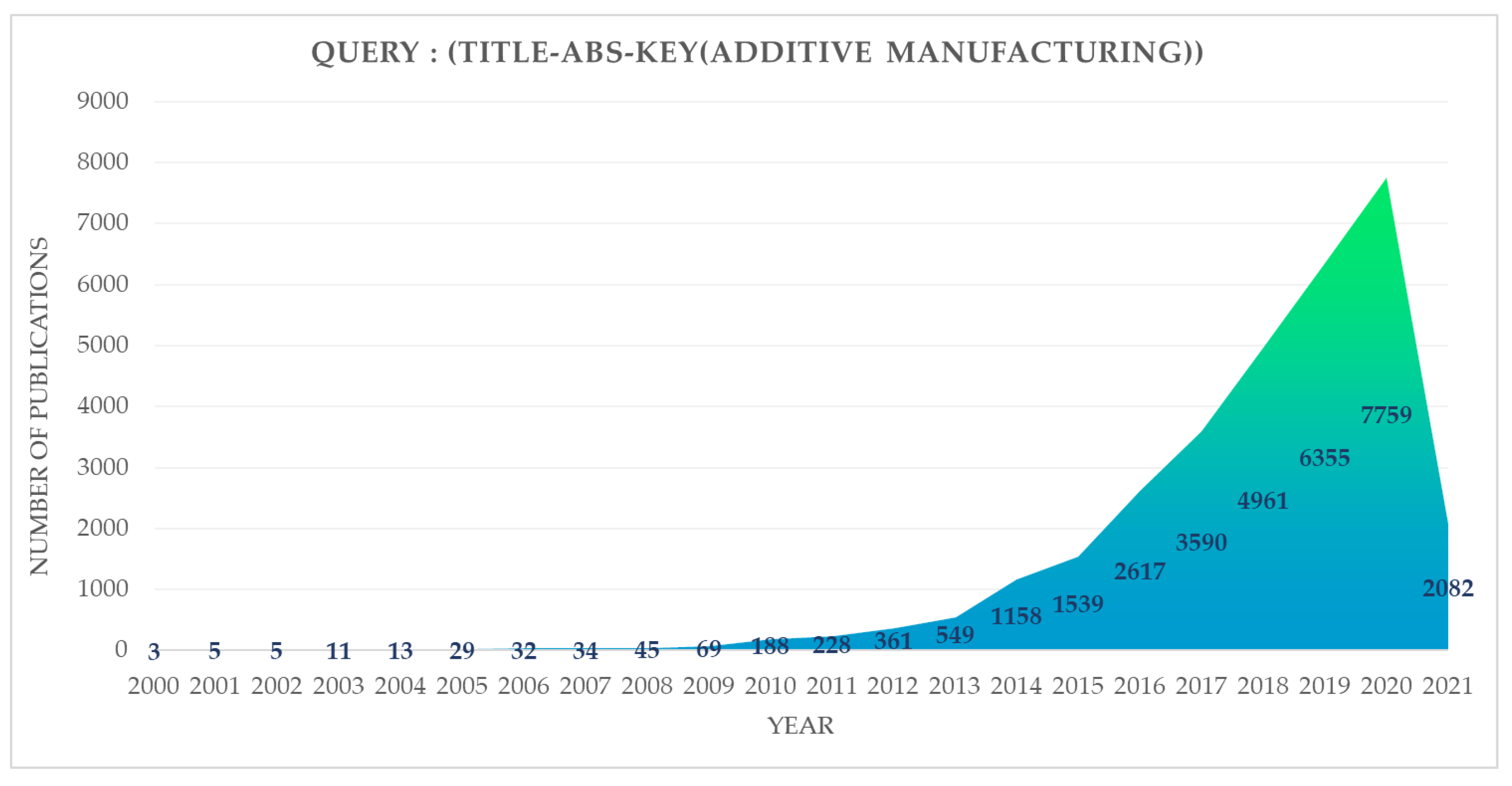
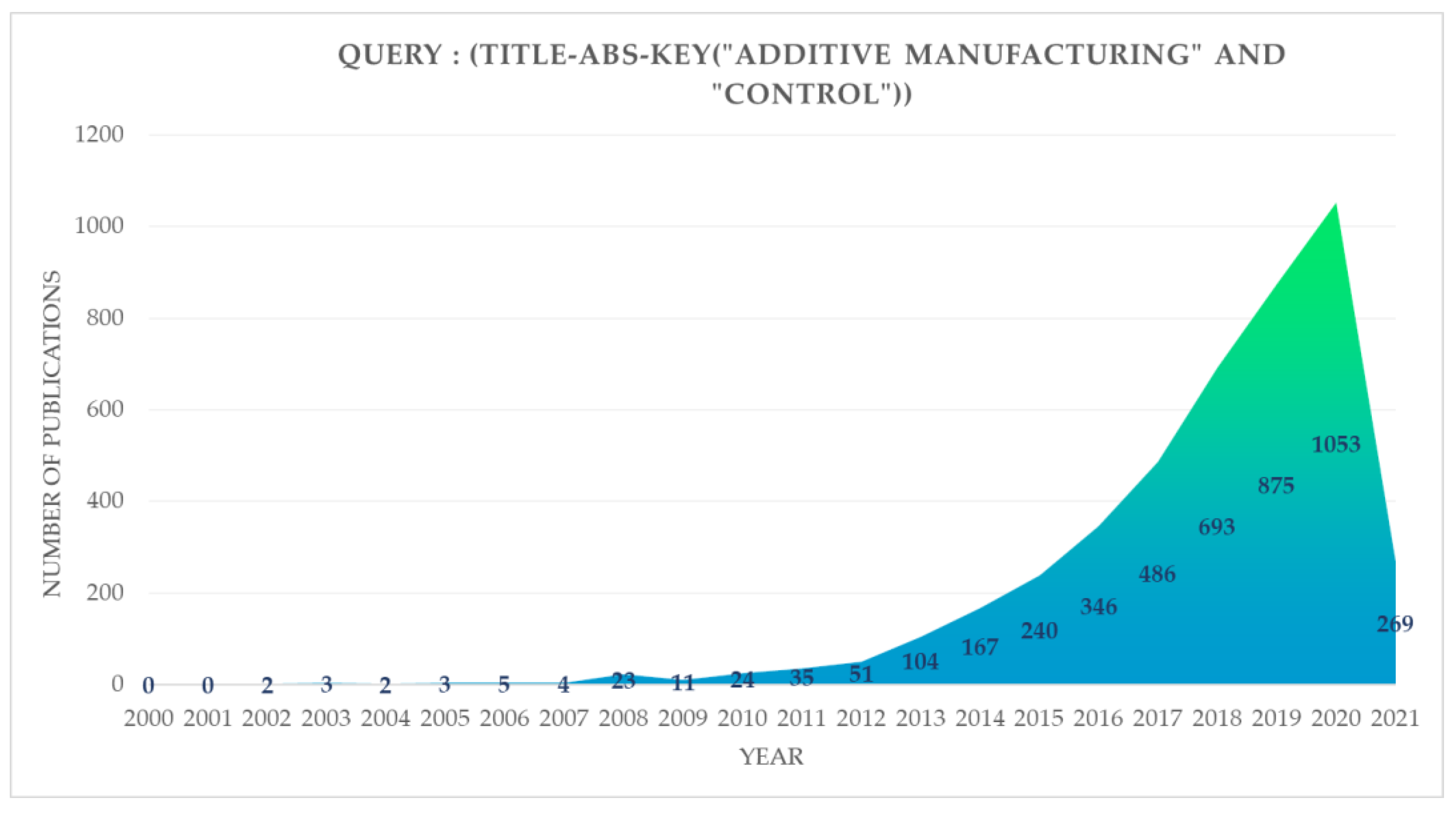
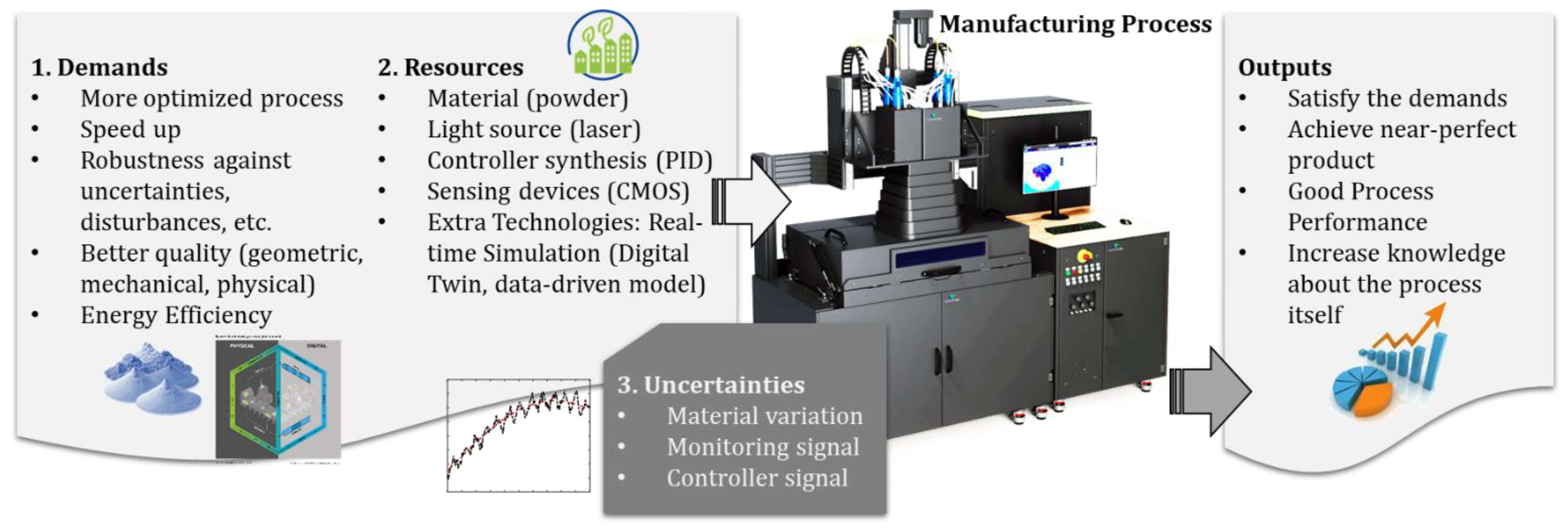
1. Introduction
State of the Art on Manufacturing Processes Monitoring and Control
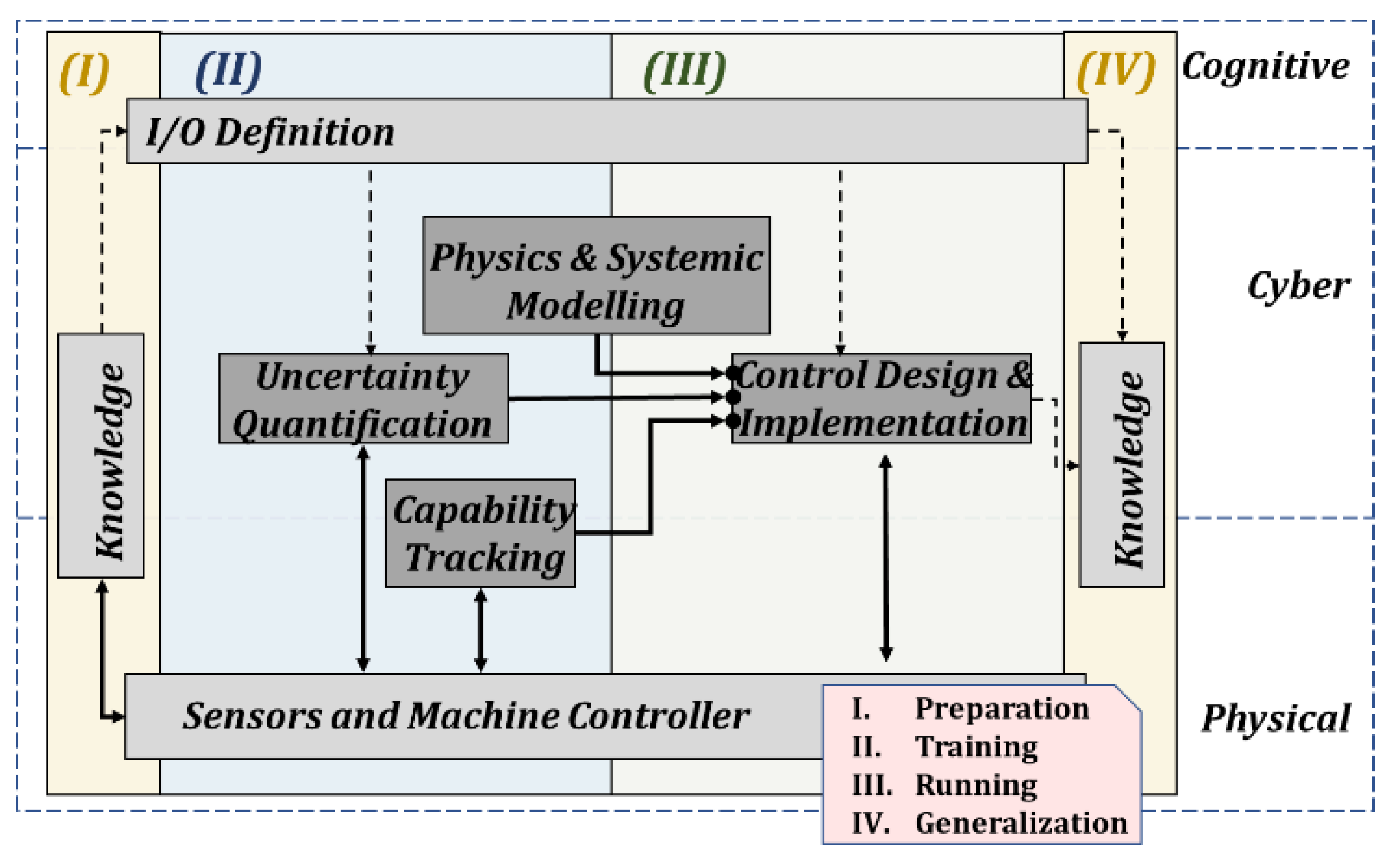
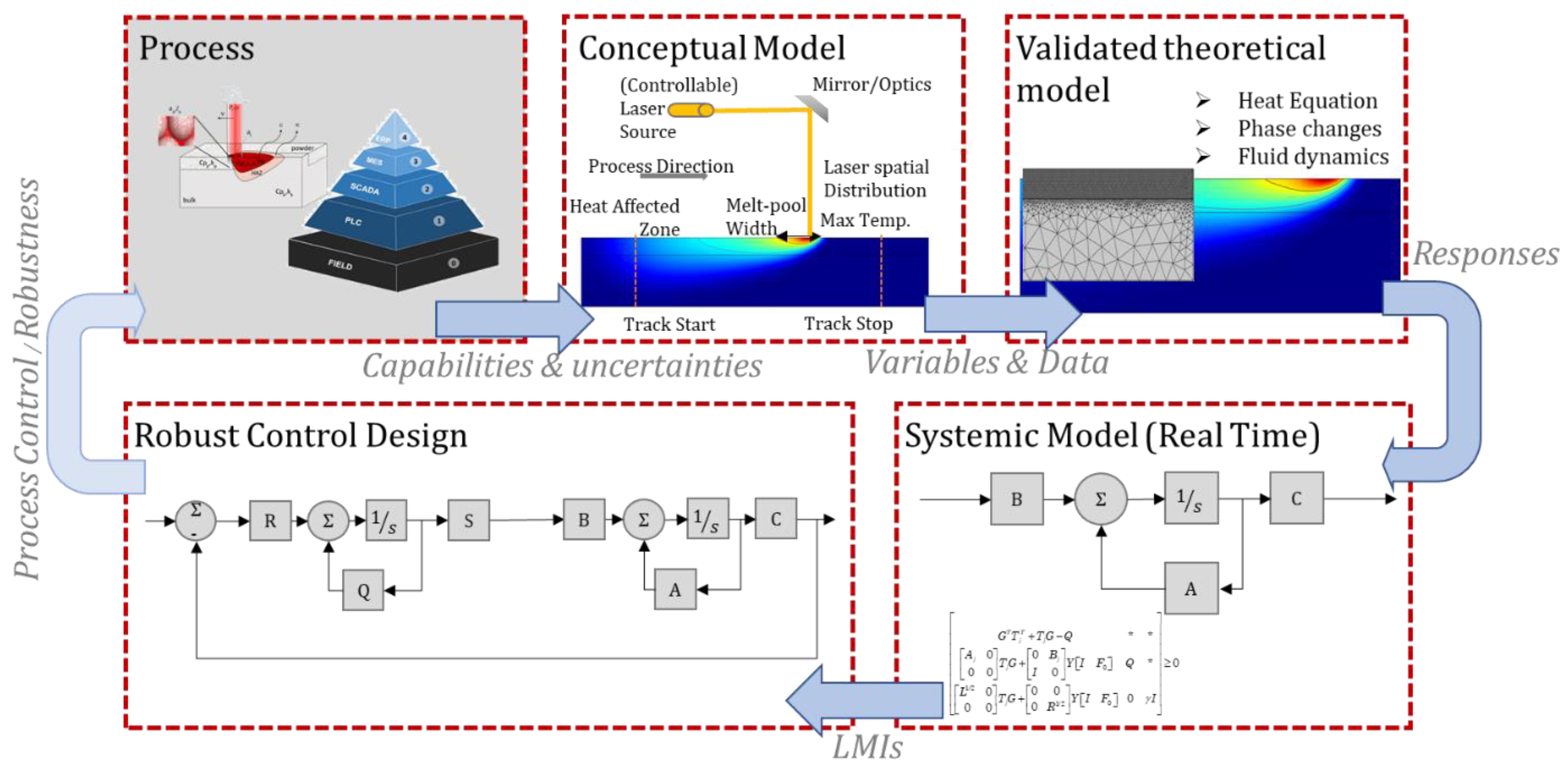
2. Approach
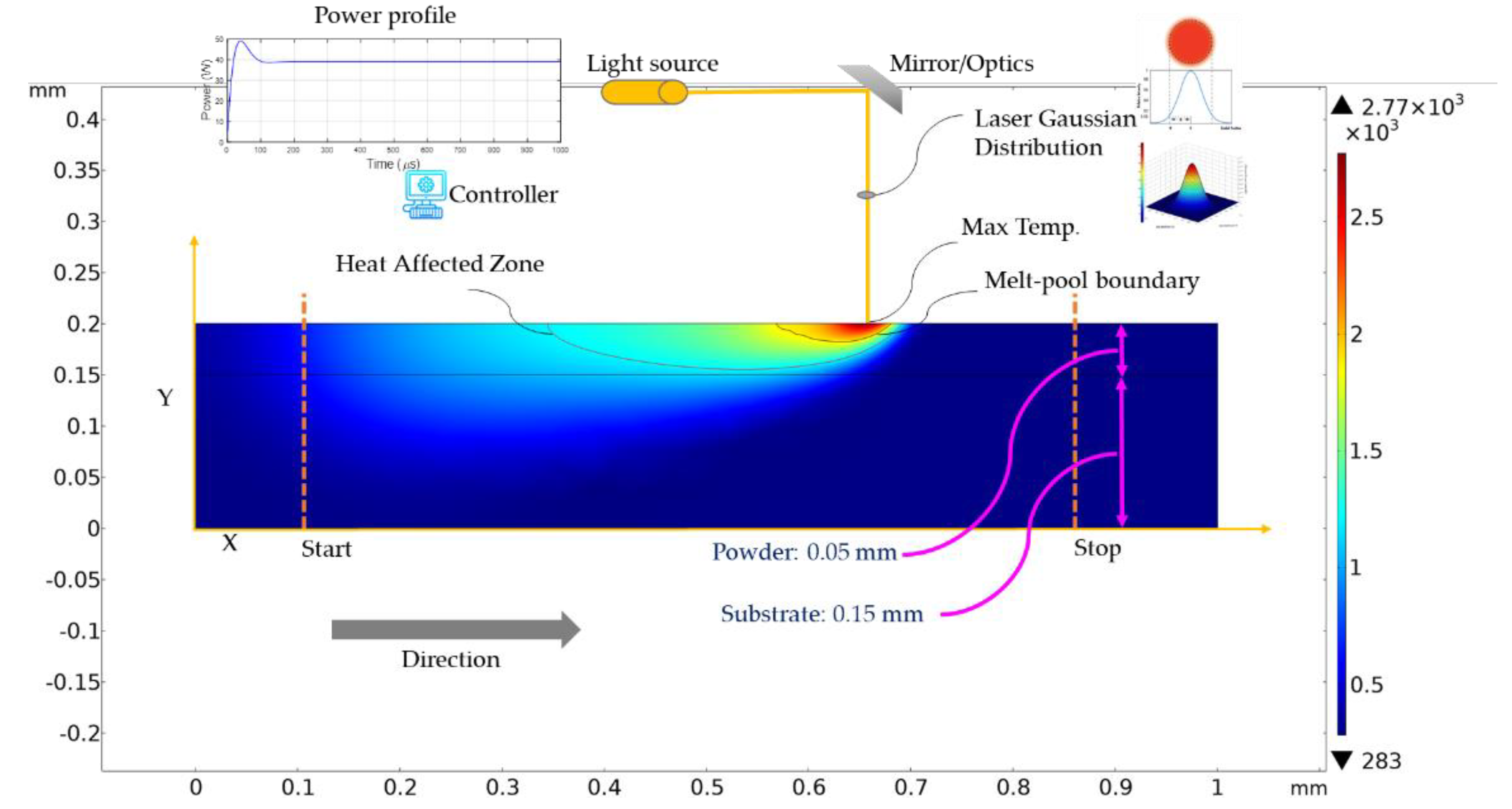
2.1. Simulation
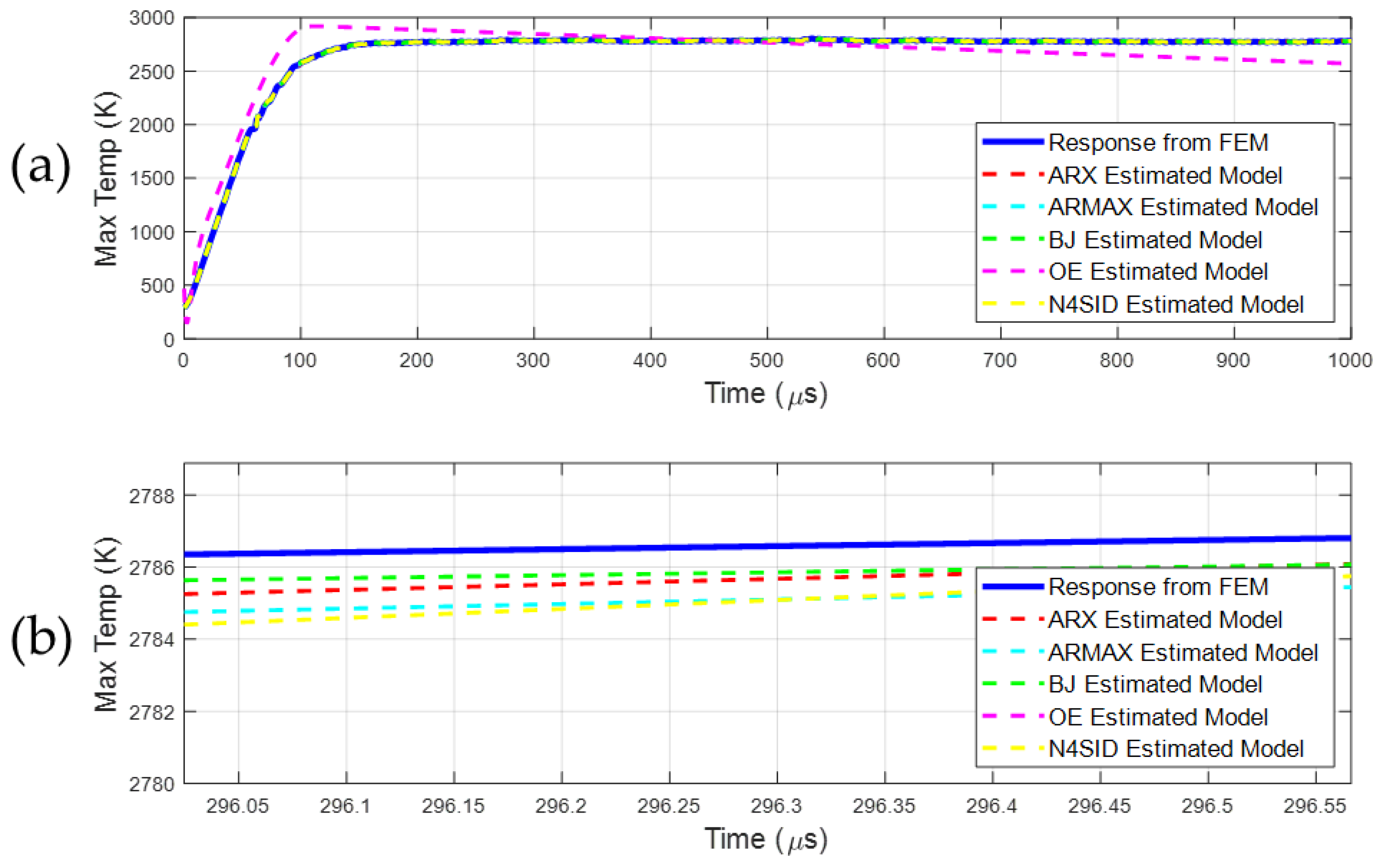
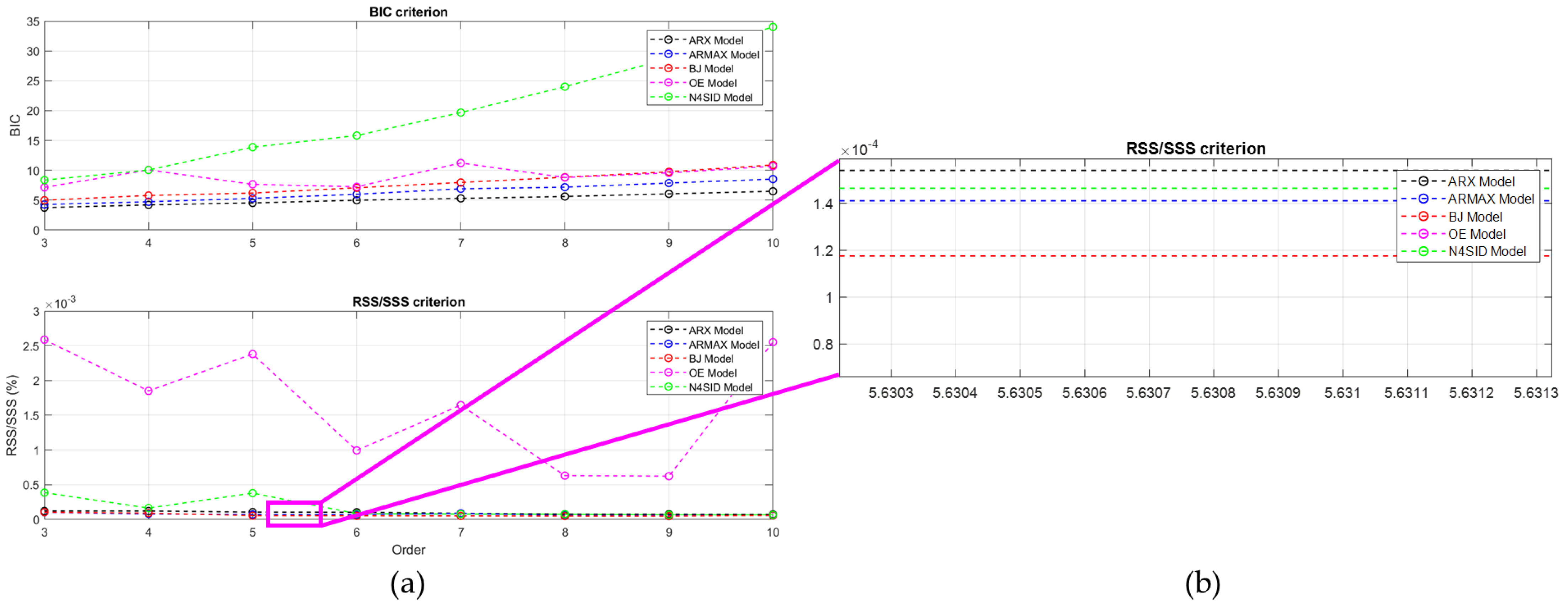
2.2. Dynamic System Identification of Simulation
2.3. Process Control of Laser-Based Manufacturing Processes
2.4. Uncertainty Manipulation through Robustness
- Disturbances existence;
- Noise existence;
- Uncertainties existence;
- Delays existence.
- H-Infinity Optimal Dynamic Output Feedback Control;
- H-2 Optimal Dynamic Output Feedback Control;
- Observed-based controller (H-Infinity state-feedback gain and observer; gain ) in the form as described by Apkarian and Noll [55];
- Robust MPC with polytopic uncertainties.
3. Case Study: Robust Digital Twin for LPBF
3.1. Heat Transfer of the Model
3.2. Boundary and Initial Conditions
3.3. Upper Free Side
3.4. Left and Right Side
3.5. Lower Side
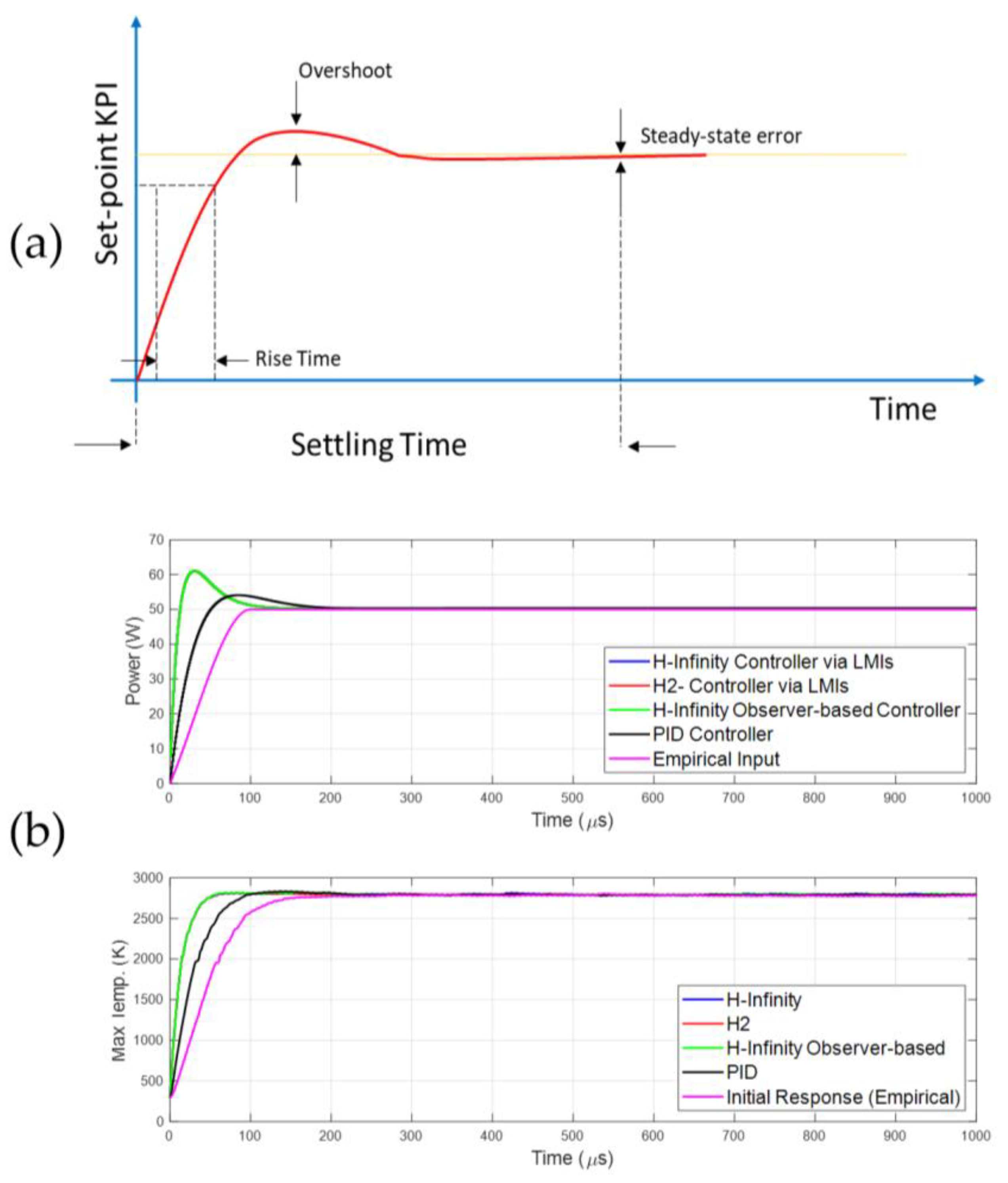
3.6. Systemic Modelling and Design of Controllers
4. Results and Discussion
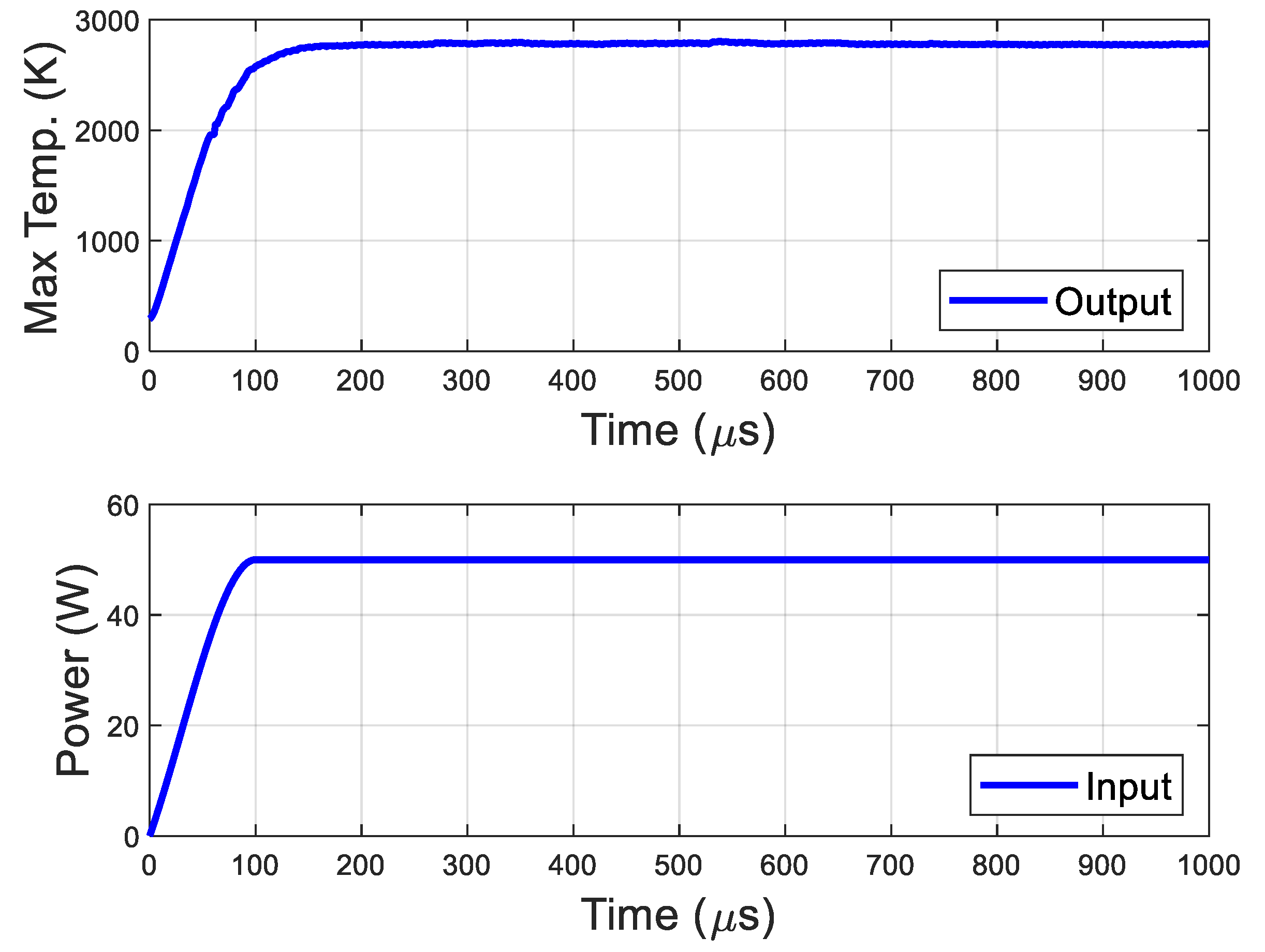
4.1. System Representation
4.2. Performance of the Initial Digital Twin
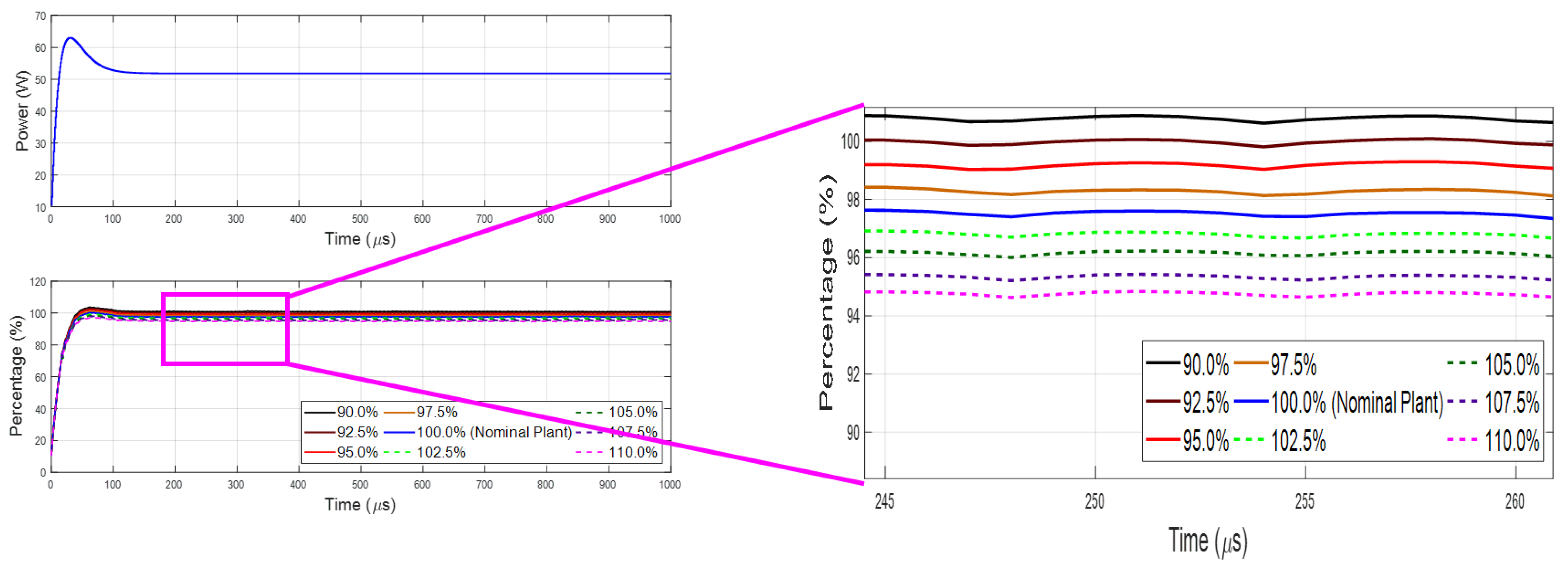
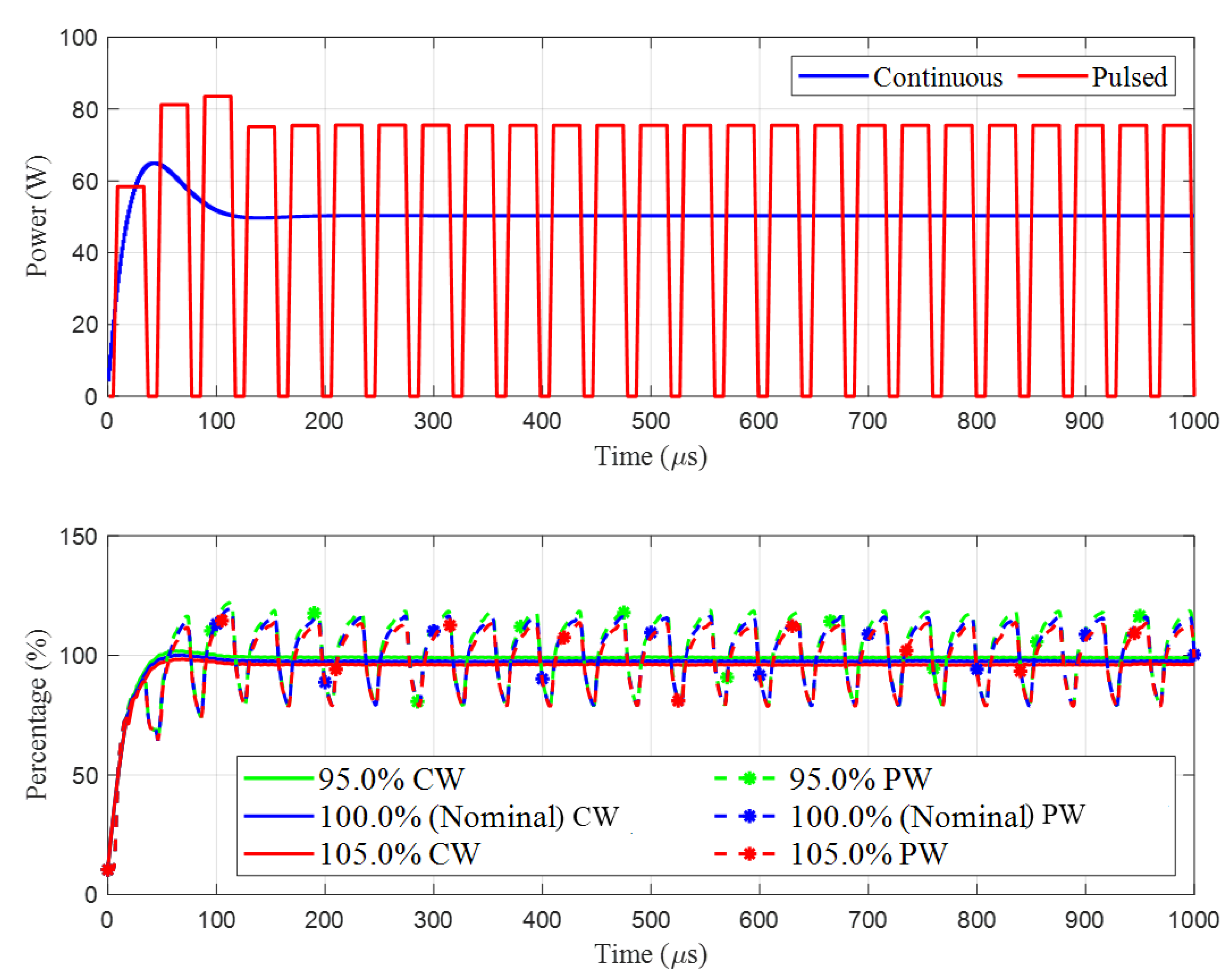
4.3. Robustness of the LPBF DT
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Acronym | Definition |
| AM | Additive Manufacturing |
| ARX | AutoRegressive with eXogenous (parametric system identification method) |
| CCD | Charge-coupled device |
| CMOS | Complementary metal–oxide–semiconductor |
| DOF | Dynamic Output Feedback controller |
| DT | Digital Twin |
| FEM | Finite Element Method |
| H2 | Optimal H2 Controller |
| H∞ | Optimal H∞ Controller |
| KPI | Key Performance Indicator |
| LMI | Linear Matrix Inequality |
| LPBF | Laser-based Powder Bed Fusion |
| PID | Proportional-Integral-Differential controller |
| RMPC | Robust Model Predictive Control |
| SISO | Single-Input-Single-Output control system |
Appendix A
| Property | Unit | Nomenclature | Value |
|---|---|---|---|
| Liquidus Temperature | K | Tl | 1923.0 |
| Solidus Temperature | K | Ts | 1877.0 |
| Evaporation Temperature | K | Tv | 3533.0 |
| Solid Specific Heat | J/kgK | Cs | |
| Liquidus Specific Heat | J/kgK | Cl | 831.0 |
| Thermal Conductivity | W/mK | K | |
| Solid Density | kg/m3 | ρs | 4420-0.154 (T-298 K) |
| Liquidus Density | kg/m3 | ρl | 3920-0.68 (T-1923 K) |
| Latent heat of fusion | J/kg | Lm | 2.86 × 105 |
| Radiation emissivity | – | ε | 0.154 + 1.838 × 10-4(T-300 K) |
| Absorption | – | α | 0.3 |
| Ambient Temperature | K | T0 | 293.15 |
| Ambient Pressure | Pa | P0 | 1.0 × 105 |
| Convective coefficient | W/m2K | H | 10.0 |
References
- Chryssolouris, G. Laser Machining: Theory and Practice; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1991; ISBN 1475740840. [Google Scholar]
- Hagqvist, P.; Heralić, A.; Christiansson, A.K.; Lennartson, B. Resistance based iterative learning control of additive manufacturing with wire. Mechatronics 2015, 31, 116–123. [Google Scholar] [CrossRef]
- Papacharalampopoulos, A.; Michail, C.; Stavropoulos, P. Manufacturing Process Control through a digital twin: Encoding Issues. In Proceedings of the TESConf 2020—9th International Conference on Through-life Engineering Services, Bedford, UK, 3–4 November 2020. [Google Scholar]
- Lopez, F.; Witherell, P.; Lane, B. Identifying Uncertainty in Laser Powder Bed Fusion Additive Manufacturing Models. J. Mech. Des. 2016, 138, 119. [Google Scholar] [CrossRef]
- Apostolos, F.; Alexios, P.; Georgios, P.; Panagiotis, S.; George, C. Energy Efficiency of Manufacturing Processes: A Critical Review. Procedia CIRP 2013, 7, 628–633. [Google Scholar] [CrossRef]
- Stavropoulos, P.; Chantzis, D.; Doukas, C.; Papacharalampopoulos, A.; Chryssolouris, G. Monitoring and Control of Manufacturing Processes: A Review. Procedia CIRP 2013, 8, 421–425. [Google Scholar] [CrossRef]
- Papacharalampopoulos, A.; Stavropoulos, P.; Stavridis, J. Adaptive Control of Thermal Processes: Laser Welding and Additive Manufacturing Paradigms. Procedia CIRP 2018, 67, 233–237. [Google Scholar] [CrossRef]
- Sammons, P.M.; Bristow, D.A.; Landers, R.G. A Model Predictive Repetitive Process Control Formulation for Additive Manufacturing Processes. In Proceedings of the ASME 2015 Dynamic Systems and Control Conference, Columbus, OH, USA, 28–30 October 2015; Volume 2, p. V002T32A003. [Google Scholar]
- Cao, X.; Ayalew, B. Robust multivariable predictive control for laser-aided powder deposition processes. J. Frankl. Inst. 2019, 356, 2505–2529. [Google Scholar] [CrossRef]
- Ladani, L. Additive Manufacturing of Metals: Materials, Processes, Tests, and Standards; DEStech Publications, Incorporated: Lancaster, PA, USA, 2020; ISBN 9781605956008. [Google Scholar]
- Andreotta, R.; Ladani, L.; Brindley, W. Finite element simulation of laser additive melting and solidification of Inconel 718 with experimentally tested thermal properties. Finite Elem. Anal. Des. 2017, 135, 36–43. [Google Scholar] [CrossRef]
- Romano, J.; Ladani, L.; Sadowski, M. Thermal Modeling of Laser Based Additive Manufacturing Processes within Common Materials. Procedia Manuf. 2015, 1, 238–250. [Google Scholar] [CrossRef]
- Gaikwad, A.; Yavari, R.; Montazeri, M.; Cole, K.; Bian, L.; Rao, P. Toward the Digital Twin of Additive Manufacturing—Integrating Thermal Simulations, Sensing, and Analytics to Detect Process Faults. IISE Trans. 2019, 1–22. [Google Scholar] [CrossRef]
- Lewis, F.L.; Vrabie, D.L.; Syrmos, V.L. Optimal Control, 3rd ed.; Wiley: Hoboken, NJ, USA, 2012; ISBN 9780470633496. [Google Scholar]
- Lavretsky, E.; Wise, K.A. Robust and Adaptive Control; Springer: London, UK, 2013; ISBN 978-1-4471-4395-6. [Google Scholar]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994; ISBN 1611970776. [Google Scholar]
- Graham, E.; Mehrpouya, M.; Nagamune, R.; Park, S.S. Robust prediction of chatter stability in micro milling comparing edge theorem and LMI. CIRP J. Manuf. Sci. Technol. 2014, 7, 29–39. [Google Scholar] [CrossRef]
- Boukas, E.K. Manufacturing Systems: LMI Approach. IEEE Trans. Autom. Contr. 2006, 51, 1014–1018. [Google Scholar] [CrossRef]
- Gibson, B.T.; Bandari, Y.K.; Richardson, B.S.; Henry, W.C.; Vetland, E.J.; Sundermann, T.W.; Love, L.J. Melt pool size control through multiple closed-loop modalities in laser-wire directed energy deposition of Ti-6Al-4V. Addit. Manuf. 2020, 32, 100993. [Google Scholar] [CrossRef]
- Tatipala, S.; Wall, J.; Johansson, C.; Larsson, T. A Hybrid Data-Based and Model-Based Approach to Process Monitoring and Control in Sheet Metal Forming. Processes 2020, 8, 89. [Google Scholar] [CrossRef]
- Kwon, O.; Kim, H.G.; Ham, M.J.; Kim, W.; Kim, G.-H.; Cho, J.-H.; Kim, N.I.; Kim, K. A deep neural network for classification of melt-pool images in metal additive manufacturing. J. Intell. Manuf. 2020, 31, 375–386. [Google Scholar] [CrossRef]
- Stavropoulos, P.; Papacharalampopoulos, A.; Stavridis, J.; Sampatakakis, K. A three-stage quality diagnosis platform for laser-based manufacturing processes. Int. J. Adv. Manuf. Technol. 2020, 69, 245. [Google Scholar] [CrossRef]
- Granado, E.; Colmenares, W.; Bernussou, J.; Garcia, G. LMI BASED MPC. IFAC Proc. Vol. 2002, 35, 177–182. [Google Scholar] [CrossRef]
- Thombre, M.; Mdoe, Z.; Jäschke, J. Data-Driven Robust Optimal Operation of Thermal Energy Storage in Industrial Clusters. Processes 2020, 8, 194. [Google Scholar] [CrossRef]
- López-Estrada, F.-R.; Rotondo, D.; Valencia-Palomo, G. A Review of Convex Approaches for Control, Observation and Safety of Linear Parameter Varying and Takagi-Sugeno Systems. Processes 2019, 7, 814. [Google Scholar] [CrossRef]
- Tabernero, I.; Calleja, A.; Lamikiz, A.; López de Lacalle, L.N. Optimal Parameters for 5-axis Laser Cladding. Procedia Eng. 2013, 63, 45–52. [Google Scholar] [CrossRef]
- Hofman, J.T.; Pathiraj, B.; van Dijk, J.; de Lange, D.F.; Meijer, J. A camera based feedback control strategy for the laser cladding process. J. Mater. Process. Technol. 2012, 212, 2455–2462. [Google Scholar] [CrossRef]
- Calleja, A.; Tabernero, I.; Ealo, J.A.; Campa, F.J.; Lamikiz, A.; de Lacalle, L.N.L. Feed rate calculation algorithm for the homogeneous material deposition of blisk blades by 5-axis laser cladding. Int. J. Adv. Manuf. Technol. 2014, 74, 1219–1228. [Google Scholar] [CrossRef]
- Renken, V.; Lübbert, L.; Blom, H.; von Freyberg, A.; Fischer, A. Model assisted closed-loop control strategy for selective laser melting. Procedia CIRP 2018, 74, 659–663. [Google Scholar] [CrossRef]
- Shi, T.; Lu, B.; Shen, T.; Zhang, R.; Shi, S.; Fu, G. Closed-loop control of variable width deposition in laser metal deposition. Int. J. Adv. Manuf. Technol. 2018, 97, 4167–4178. [Google Scholar] [CrossRef]
- Rodriguez-Araujo, J.; Rodriguez-Andina, J.J.; Farina, J.; Vidal, F.; Mato, J.L.; Montealegre, M.A. Industrial Laser Cladding Systems: FPGA-Based Adaptive Control. IEEE Ind. Electron. Mag. 2012, 6, 35–46. [Google Scholar] [CrossRef]
- Xiong, J.; Zhu, B.; Chen, H.; Zheng, S. Peak elimination of cross structures in wire and arc additive manufacturing using closed-loop control. J. Manuf. Process. 2020, 58, 368–376. [Google Scholar] [CrossRef]
- Craeghs, T.; Bechmann, F.; Berumen, S.; Kruth, J.-P. Feedback control of Layerwise Laser Melting using optical sensors. Phys. Procedia 2010, 5, 505–514. [Google Scholar] [CrossRef]
- Xia, C.; Pan, Z.; Zhang, S.; Polden, J.; Wang, L.; Li, H.; Xu, Y.; Chen, S. Model predictive control of layer width in wire arc additive manufacturing. J. Manuf. Process. 2020, 58, 179–186. [Google Scholar] [CrossRef]
- Song, L.; Mazumder, J. Feedback Control of Melt Pool Temperature During Laser Cladding Process. IEEE Trans. Contr. Syst. Technol. 2011, 19, 1349–1356. [Google Scholar] [CrossRef]
- LIU, Y.; Wang, L.; Brandt, M. Model predictive control of laser metal deposition. Int. J. Adv. Manuf. Technol. 2019, 105, 1055–1067. [Google Scholar] [CrossRef]
- Song, L.; Bagavath-Singh, V.; Dutta, B.; Mazumder, J. Control of melt pool temperature and deposition height during direct metal deposition process. Int. J. Adv. Manuf. Technol. 2012, 58, 247–256. [Google Scholar] [CrossRef]
- Baillieul, J.; Samad, T. Encyclopedia of Systems and Control; Springer: London, UK, 2015; ISBN 978-1-4471-5057-2. [Google Scholar]
- Apel, M.; Boussinot, G.; Döring, M.; Schmidt, M. Eutectic solidification in Al-Ni for L-PBF conditions: A phase-field simulation study. Procedia CIRP 2020, 94, 64–68. [Google Scholar] [CrossRef]
- Ertay, D.S.; Vlasea, M.; Erkorkmaz, K. Thermomechanical and geometry model for directed energy deposition with 2D/3D toolpaths. Addit. Manuf. 2020, 35, 101294. [Google Scholar] [CrossRef]
- Foteinopoulos, P.; Papacharalampopoulos, A.; Angelopoulos, K.; Stavropoulos, P. Development of a simulation approach for laser powder bed fusion based on scanning strategy selection. Int. J. Adv. Manuf. Technol. 2020, 108, 3085–3100. [Google Scholar] [CrossRef]
- Leitz, K.H.; Redlingshöfer, B.; Reg, Y.; Otto, A.; Schmidt, M. Metal Ablation with Short and Ultrashort Laser Pulses. Phys. Procedia 2011, 12, 230–238. [Google Scholar] [CrossRef]
- Rankouhi, B.; Agrawal, A.K.; Pfefferkorn, F.E.; Thoma, D.J. A dimensionless number for predicting universal processing parameter boundaries in metal powder bed additive manufacturing. Manuf. Lett. 2021, 27, 13–17. [Google Scholar] [CrossRef]
- MATLAB®. R2018a Documentation; Mathworks Inc.: Natick, MA, USA, 2018. [Google Scholar]
- Stark, R.; Fresemann, C.; Lindow, K. Development and operation of Digital Twins for technical systems and services. CIRP Ann. 2019, 68, 129–132. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, M.; Liu, Y.; Nee, A.Y.C. Digital twin driven prognostics and health management for complex equipment. CIRP Ann. 2018, 67, 169–172. [Google Scholar] [CrossRef]
- Papacharalampopoulos, A.; Stavropoulos, P. Towards a Digital Twin for Thermal Processes: Control-centric approach. Procedia CIRP 2019, 86, 110–115. [Google Scholar] [CrossRef]
- Noll, R.; Fricke-Begemann, C.; Connemann, S.; Meinhardt, C.; Sturm, V. LIBS analyses for industrial applications–an overview of developments from 2014 to 2018. J. Anal. Spectrom. 2018, 33, 945–956. [Google Scholar] [CrossRef]
- Cook, P.S.; Murphy, A.B. Simulation of melt pool behaviour during additive manufacturing: Underlying physics and progress. Addit. Manuf. 2020, 31, 100909. [Google Scholar] [CrossRef]
- Calignano, F.; Cattano, G.; Manfredi, D. Manufacturing of thin wall structures in AlSi10Mg alloy by laser powder bed fusion through process parameters. J. Mater. Process. Technol. 2018, 255, 773–783. [Google Scholar] [CrossRef]
- El Ghaoui, L.; Niculescu, S.-l. Advances in Linear Matrix Inequality Methods in Control; SIAM, University City Science Center: Philadelphia, PA, USA, 2000; ISBN 0898714389. [Google Scholar]
- Caverly, R.J.; Forbes, J.R. LMI Properties and Applications in Systems, Stability, and Control Theory. arXiv 2019, arXiv:1903.08599. [Google Scholar]
- de Oliveira, M.C.; Geromel, J.C.; Bernussou, J. Extended H 2 and H norm characterizations and controller parametrizations for discrete-time systems. Int. J. Control 2002, 75, 666–679. [Google Scholar] [CrossRef]
- Hu, J.; Ding, B. Dynamic output feedback robust MPC with convex optimisation for system with polytopic uncertainty. Int. J. Syst. Sci. 2019, 50, 739–748. [Google Scholar] [CrossRef]
- Apkarian, P.; Noll, D. The H Control Problem Is Solved; Appriou, A., Ed.; Aerospace Lab: Palaiseau, France, 2017. [Google Scholar]
- Greitemeier, D.; Dalle Donne, C.; Schoberth, A.; Jürgens, M.; Eufinger, J.; Melz, T. Uncertainty of Additive Manufactured Ti-6Al-4V: Chemistry, Microstructure and Mechanical Properties. AMM 2015, 807, 169–180. [Google Scholar] [CrossRef]
- Hu, Z.; Mahadevan, S. Uncertainty quantification and management in additive manufacturing: Current status, needs, and opportunities. Int. J. Adv. Manuf. Technol. 2017, 93, 2855–2874. [Google Scholar] [CrossRef]
- Srivastava, S.; Garg, R.K.; Sharma, V.S.; Alba-Baena, N.G.; Sachdeva, A.; Chand, R.; Singh, S. Multi-physics continuum modelling approaches for metal powder additive manufacturing: A review. Rapid Prototyp. J. 2020, 26, 737–764. [Google Scholar] [CrossRef]
- Ansari, M.J.; Nguyen, D.-S.; Park, H.S. Investigation of SLM Process in Terms of Temperature Distribution and Melting Pool Size: Modeling and Experimental Approaches. Materials 2019, 12, 1272. [Google Scholar] [CrossRef] [PubMed]
- Ahsan, F.; Ladani, L. Temperature Profile, Bead Geometry, and Elemental Evaporation in Laser Powder Bed Fusion Additive Manufacturing Process. JOM 2020, 72, 429–439. [Google Scholar] [CrossRef]
- Foteinopoulos, P.; Papacharalampopoulos, A.; Stavropoulos, P. On thermal modeling of Additive Manufacturing processes. CIRP J. Manuf. Sci. Technol. 2018, 20, 66–83. [Google Scholar] [CrossRef]
- Zhang, T.; Li, H.; Liu, S.; Shen, S.; Xie, H.; Shi, W.; Zhang, G.; Shen, B.; Chen, L.; Xiao, B.; et al. Evolution of molten pool during selective laser melting of Ti–6Al–4V. J. Phys. D Appl. Phys. 2019, 52, 55302. [Google Scholar] [CrossRef]
- Vlasea, M.L.; Lane, B.; Lopez, F.; Mekhontsev, S.; Donmez, A. Development of powder bed fusion additive manufacturing test bed for enhanced real-time process control. In Proceedings of the International Solid Freeform Fabrication Symposium, Austin, TX, USA, 10–12 August 2015. [Google Scholar]
- Yang, R.; Lu, L.; Xie, L. Robust H2 and H∞ control of discrete-time systems with polytopic uncertainties via dynamic output feedback. Int. J. Control 2005, 78, 1285–1294. [Google Scholar] [CrossRef]
- Paudel, B.; Thompson, S. Localized Effect of Overhangs on Heat Transfer during Laser Powder Bed Fusion Additive Manufacturing. In Proceedings of the 30th Annual InternationalSolid Freeform Fabrication Symposium—An Additive Manufacturing Conference, Austin, TX, USA, 12–14 August 2019. [Google Scholar]
- Bayat, M.; Mohanty, S.; Hattel, J.H. A systematic investigation of the effects of process parameters on heat and fluid flow and metallurgical conditions during laser-based powder bed fusion of Ti6Al4V alloy. Int. J. Heat Mass Transf. 2019, 139, 213–230. [Google Scholar] [CrossRef]
- VanAntwerp, J.G.; Braatz, R.D. A tutorial on linear and bilinear matrix inequalities. J. Process. Control 2000, 10, 363–385. [Google Scholar] [CrossRef]
- Lane, B.; Mekhontsev, S.; Grantham, S.; Vlasea, M.; Whiting, J.; Yeung, H.; Fox, J.; Zarobila, C.; Neira, J.; McGlauflin, M. Design, Developments, and Results from the NIST Additive Manufacturing Metrology Testbed (AMMT). In Proceedings of the Solid Freeform Fabrication Symposium, Austin, TX, USA, 8–10 August 2016. [Google Scholar]
- Younes, D.; Yuegang, T.; Xin, C.; Alghannam, E.; Altazah, A. Design of Control System for 3D Printer Based on DSP and FPGA. J. Autom. Control Eng. 2017, 6, 40–46. [Google Scholar] [CrossRef]
- Mills, K.C. Recommended Values of Thermophysical Properties for Selected Commercial Alloys; Woodhead Publishing: Cambridge, UK, 2002; ISBN 1855735695. [Google Scholar]


| Process Parameters | Units | Nomenclature | Value |
|---|---|---|---|
| Laser beam radius | μm | Ro | 50 |
| Laser power | W | Po | 50 |
| Laser speed | mm/s | V | 750 |
| Laser power peak | μs | Δton | 100 |
| Laser power duration | μs | Δt | 1000 |
| Reference | Controller | Settling Time (μs) | Rise Time (μs) | Overshoot (%) | Comparison to Settling Time (%) | Comparison to Rise Time (%) |
|---|---|---|---|---|---|---|
| Current work | Initial | 140 | 82.1 | 0.9 | – | – |
| H-Infinity | 45.2 | 29.4 | 1.1 | 67.7% | 64.2% | |
| H2 | 45.3 | 29.5 | 1.4 | 67.6% | 64.1% | |
| Observer-based H-Infinity | 45.1 | 29.4 | 0.9 | 67.8% | 64.2% | |
| PID | 86.7 | 55.6 | 1.5 | 38.1% | 32.3% | |
| [65] | Constant parameters | ~250.0 | ~125.0 | – | – | – |
| [66] at the case of 200 W, 800 mm/s | ~150.0 | ~75.0 | – | – | – |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stavropoulos, P.; Papacharalampopoulos, A.; Michail, C.K.; Chryssolouris, G. Robust Additive Manufacturing Performance through a Control Oriented Digital Twin. Metals 2021, 11, 708. https://doi.org/10.3390/met11050708
Stavropoulos P, Papacharalampopoulos A, Michail CK, Chryssolouris G. Robust Additive Manufacturing Performance through a Control Oriented Digital Twin. Metals. 2021; 11(5):708. https://doi.org/10.3390/met11050708
Chicago/Turabian StyleStavropoulos, Panagiotis, Alexios Papacharalampopoulos, Christos K. Michail, and George Chryssolouris. 2021. "Robust Additive Manufacturing Performance through a Control Oriented Digital Twin" Metals 11, no. 5: 708. https://doi.org/10.3390/met11050708
APA StyleStavropoulos, P., Papacharalampopoulos, A., Michail, C. K., & Chryssolouris, G. (2021). Robust Additive Manufacturing Performance through a Control Oriented Digital Twin. Metals, 11(5), 708. https://doi.org/10.3390/met11050708








