Numerical Study on the Plastic Forming of Doubly Curved Surfaces of Aluminum Foam Sandwich Panel Using 3D Voronoi Model
Abstract
1. Introduction
2. Geometric Model and Numerical Model
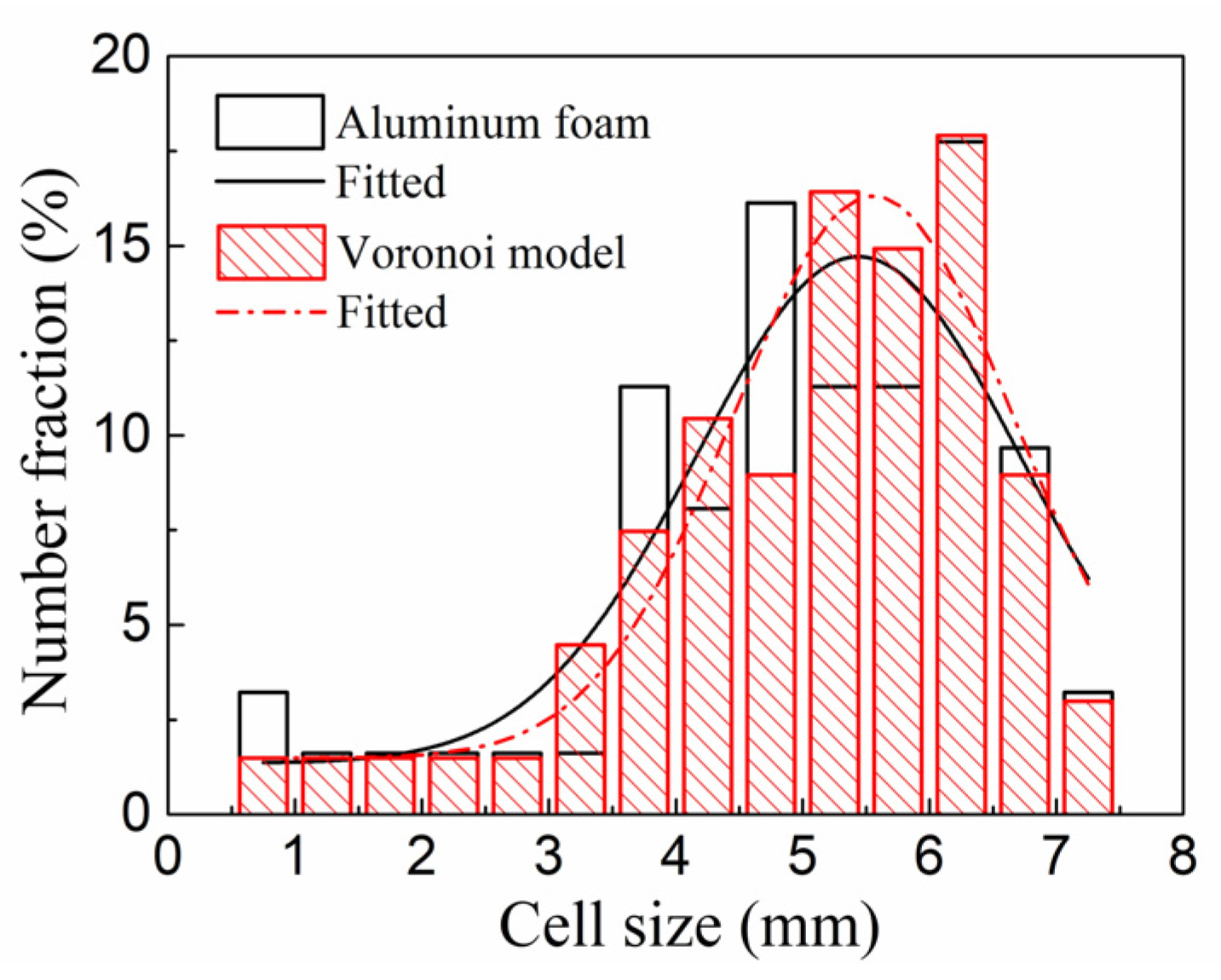
2.1. Voronoi Foam Geometric Model
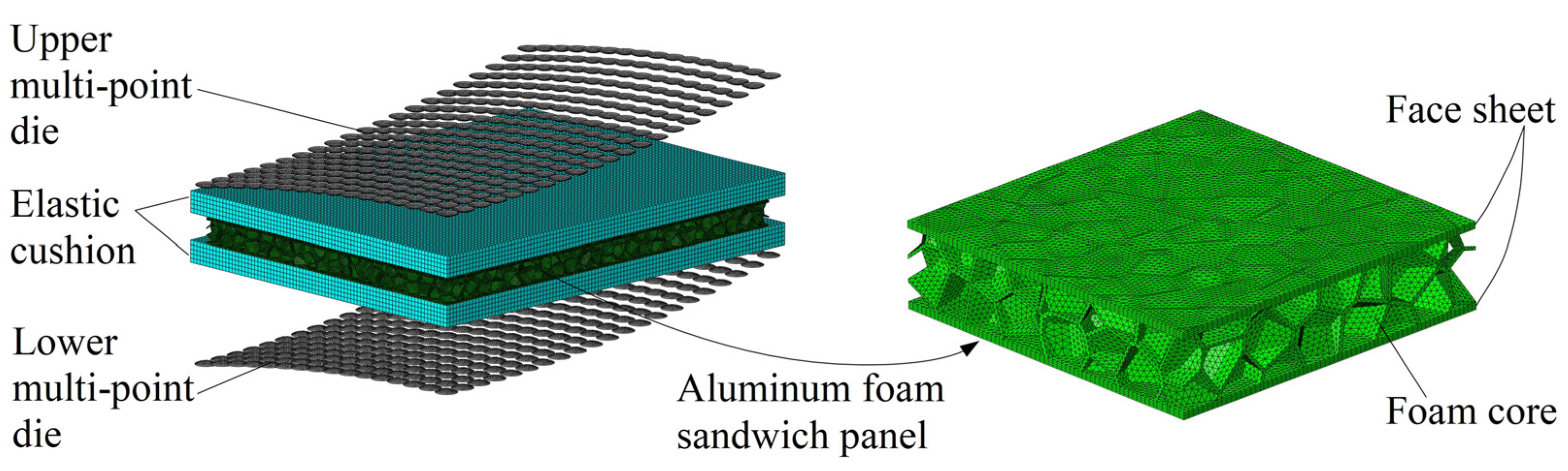
2.2. FE Model for the Numerical Simulation of MPF Process
3. Numerical Results Analysis
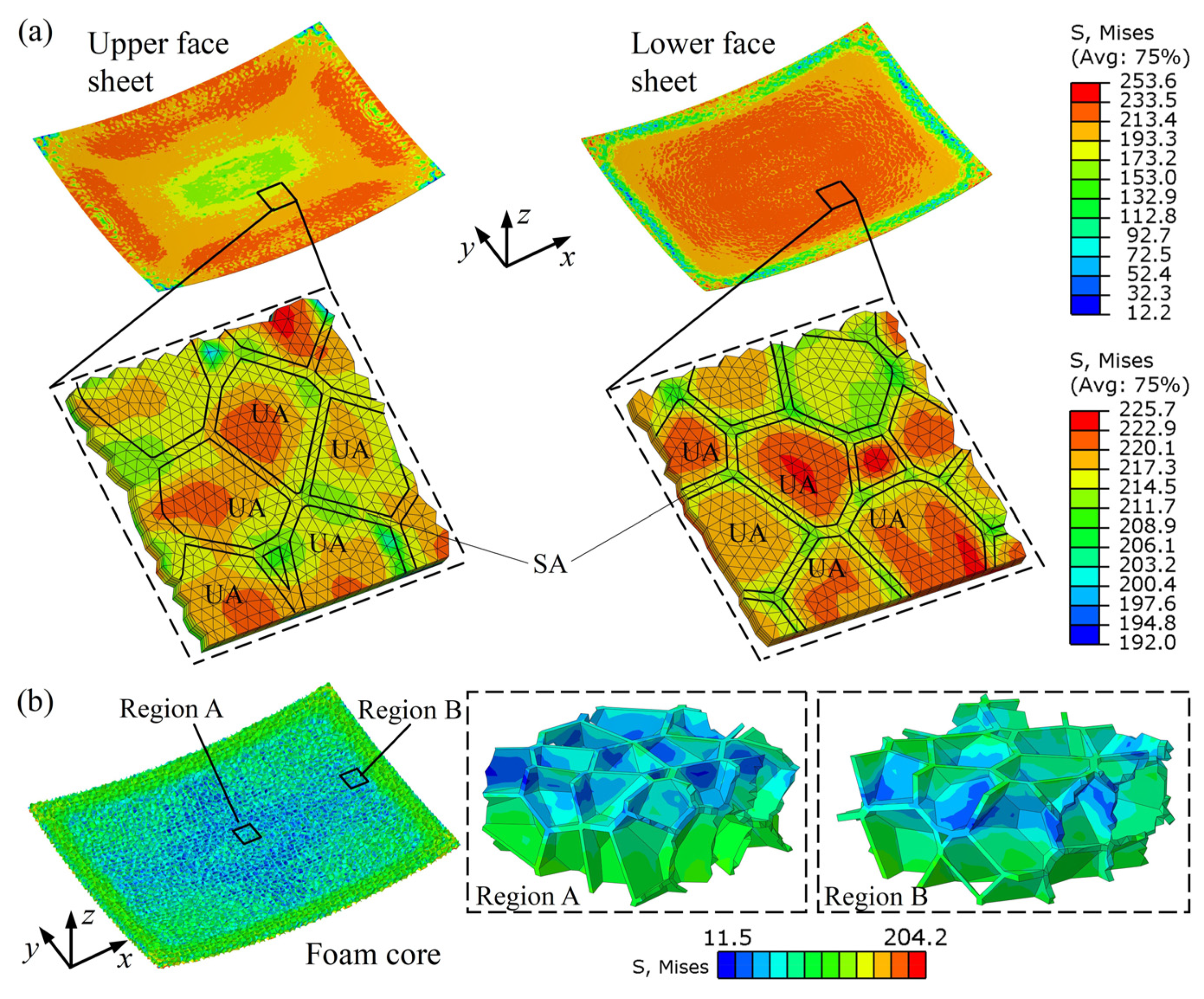
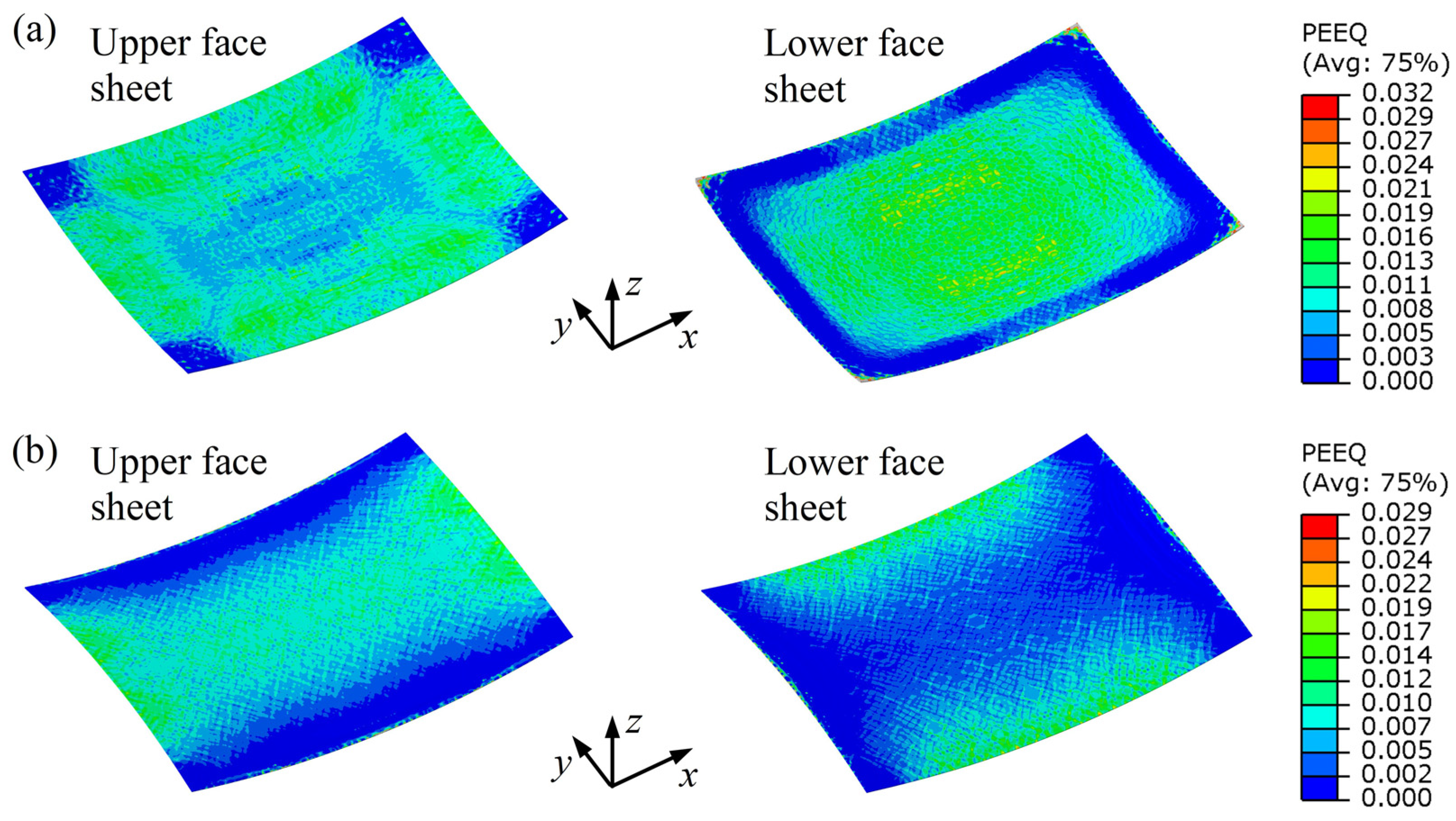
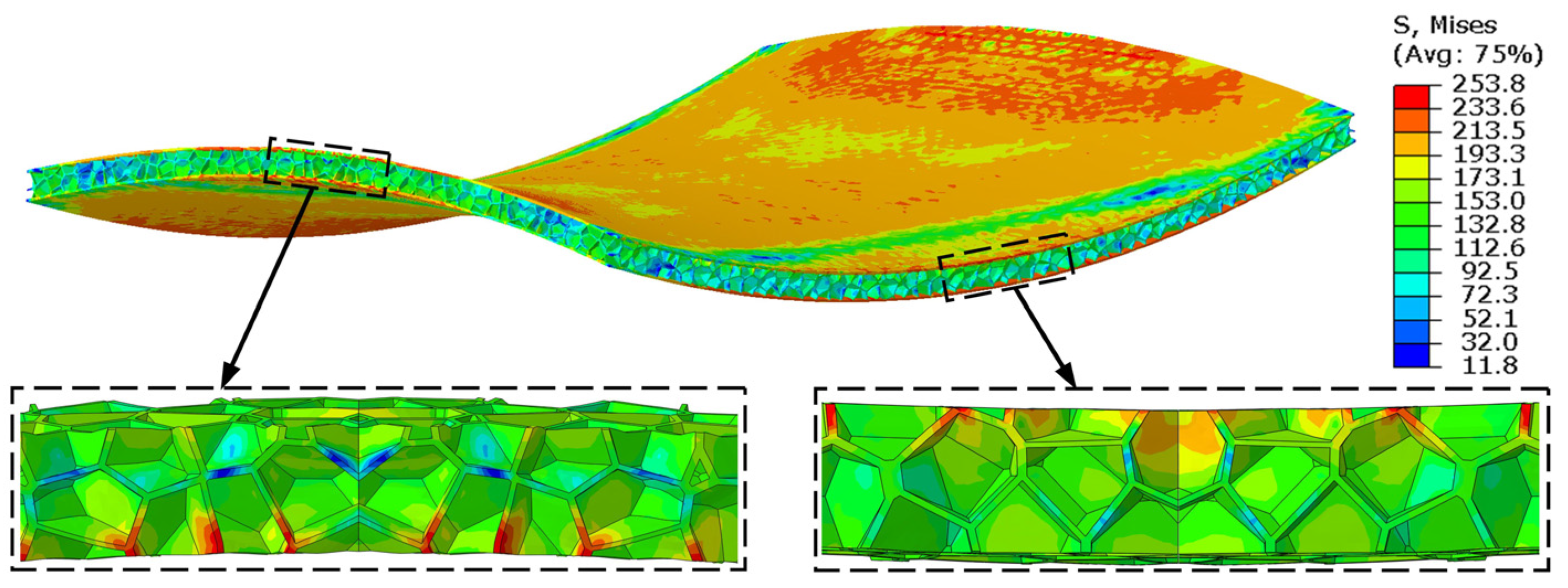
3.1. Deformation Characteristics of Voronoi AFSP
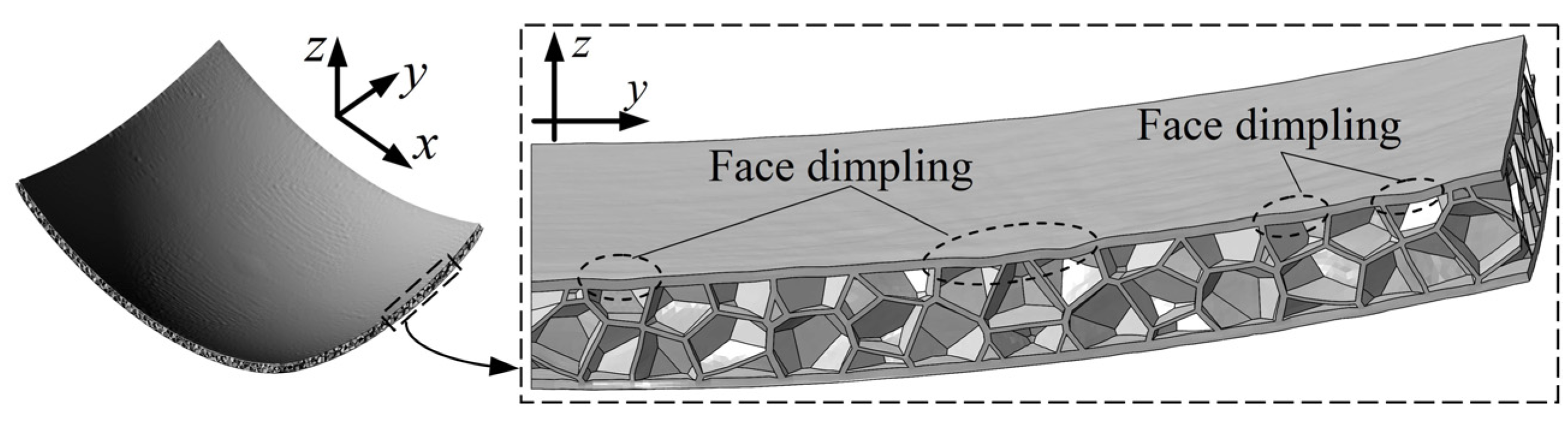
3.2. Forming Defects of Voronoi AFSP
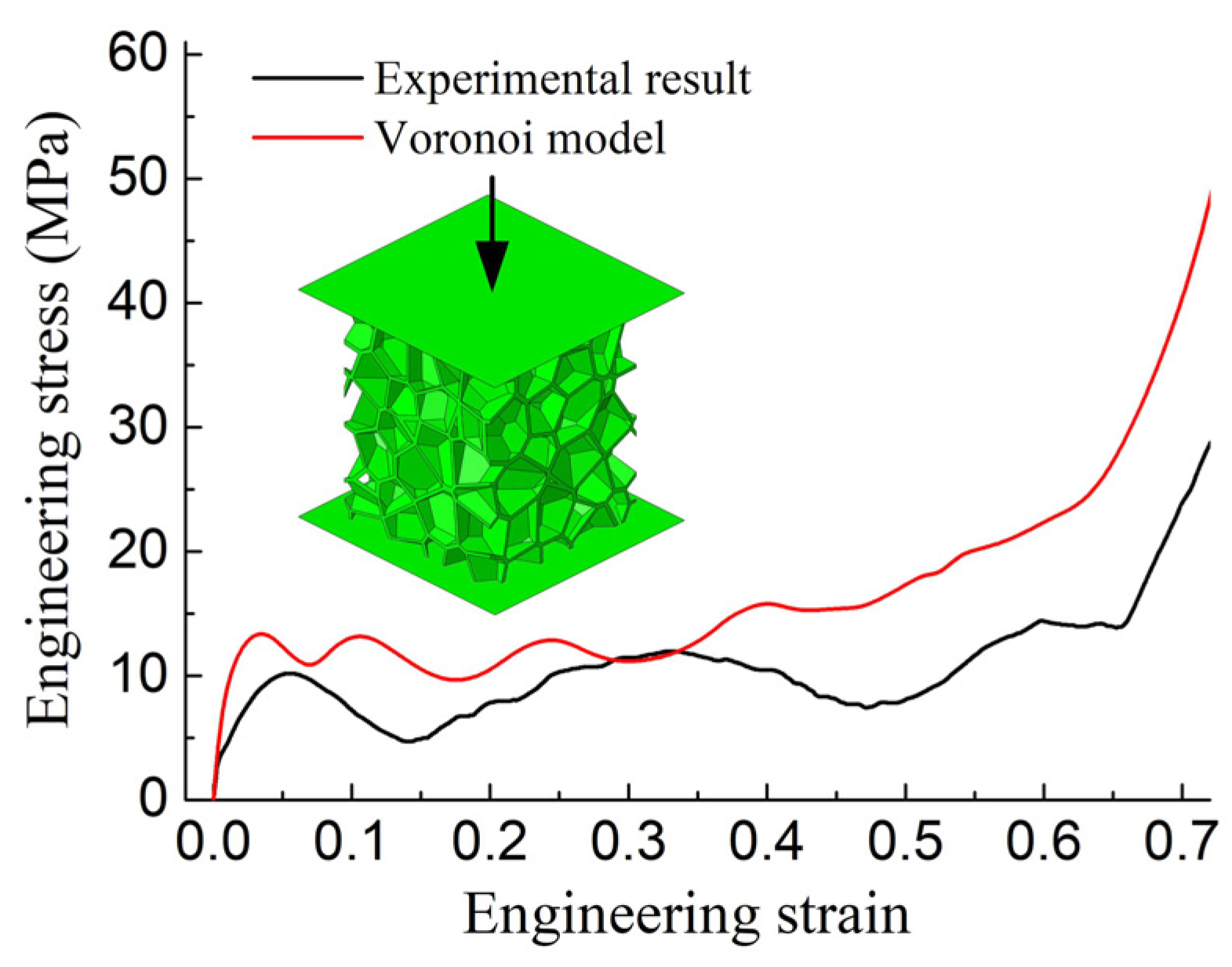
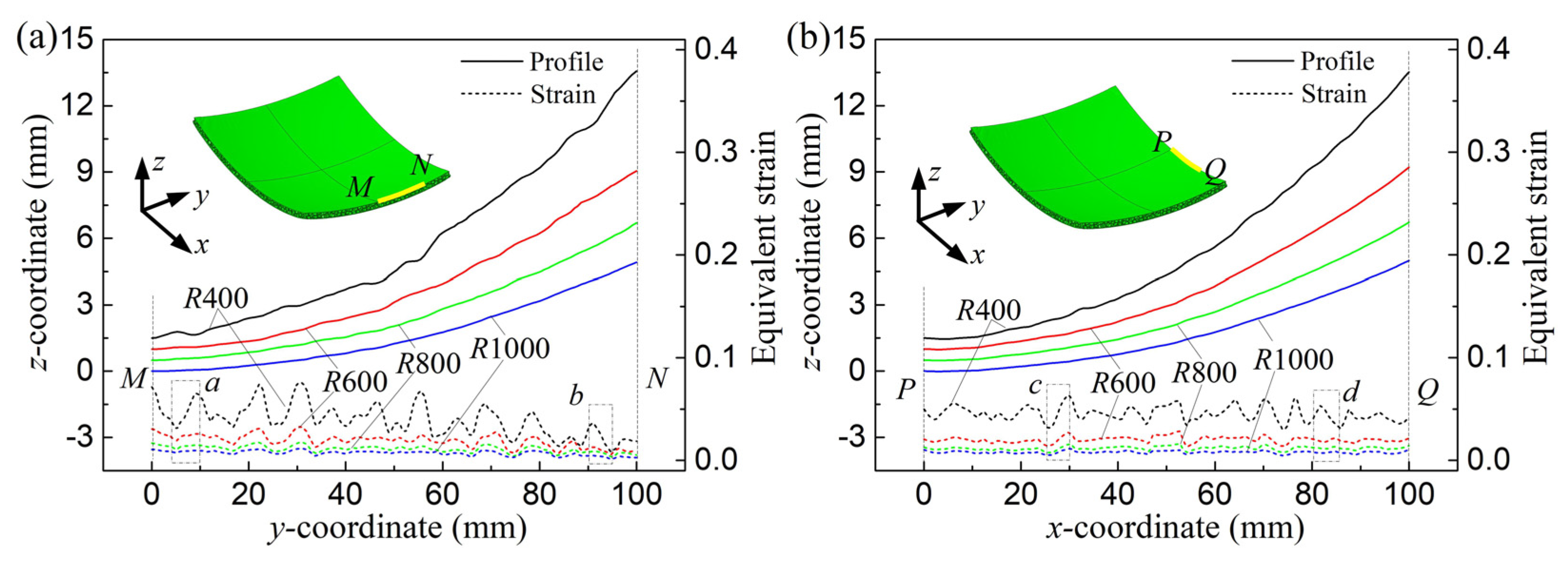
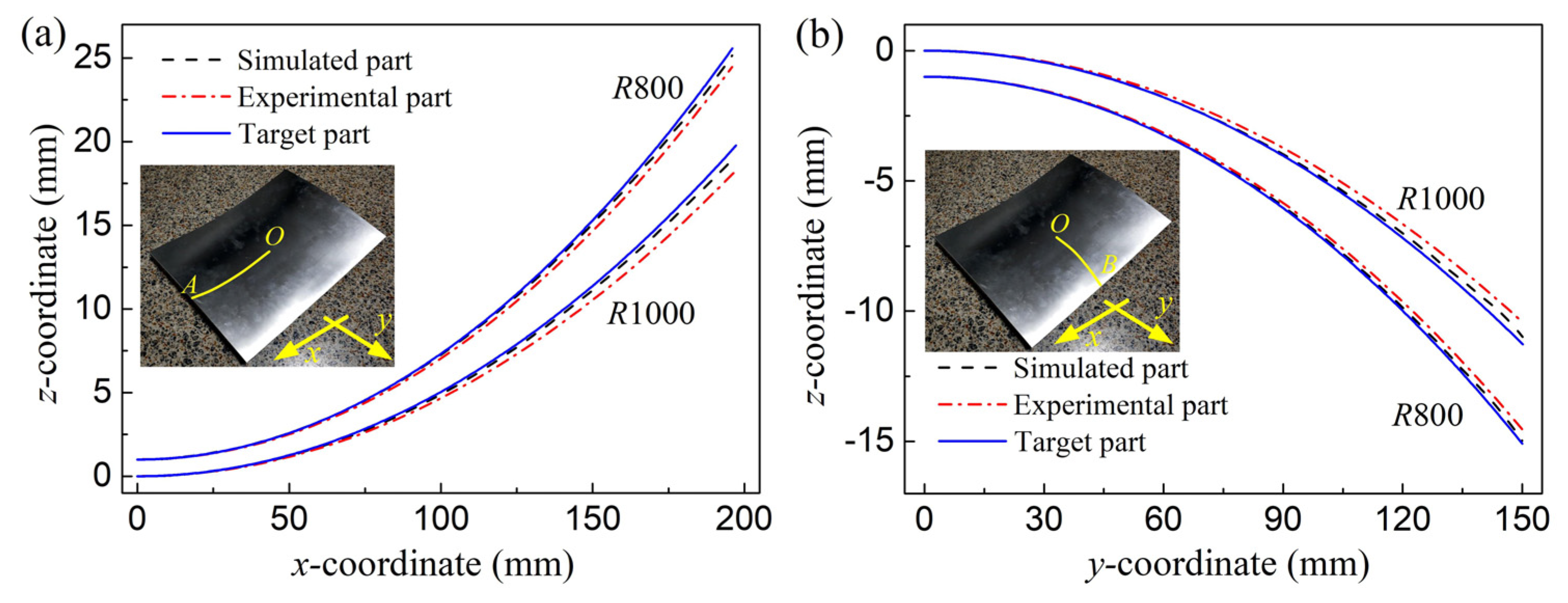
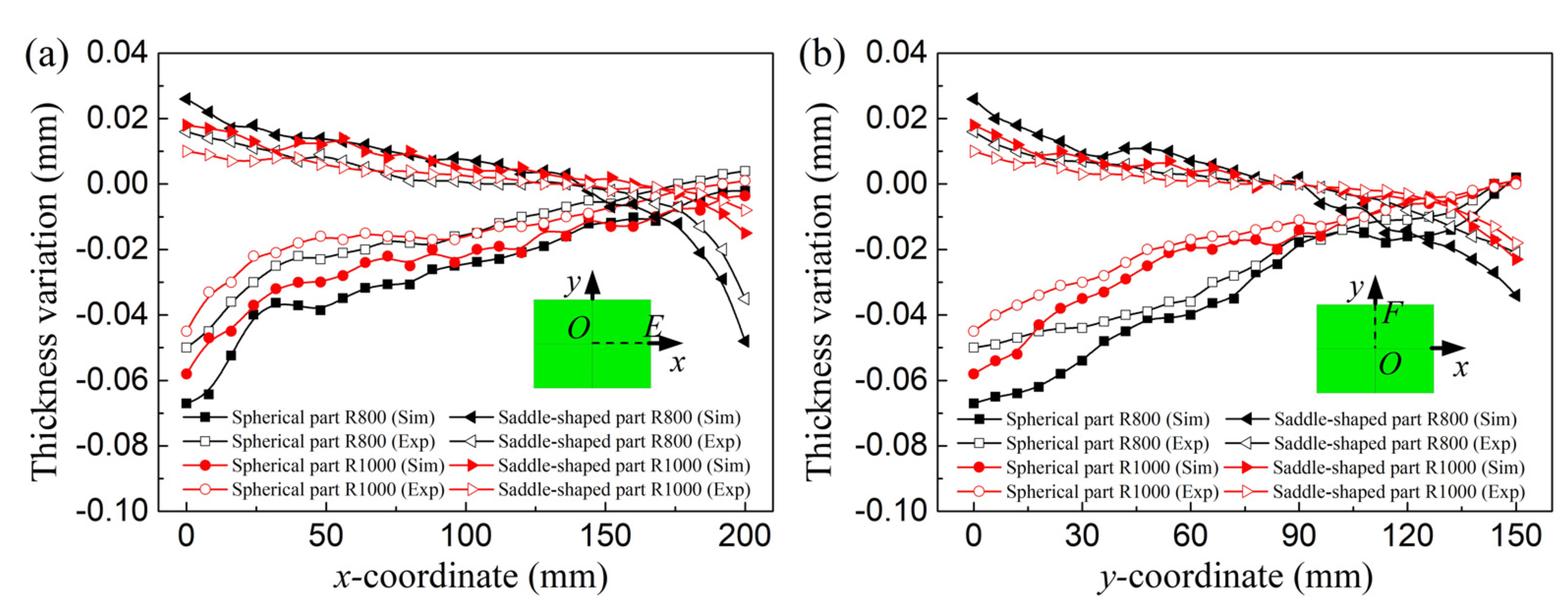
4. Experimental Validation
4.1. Multi-Point Forming Experiment
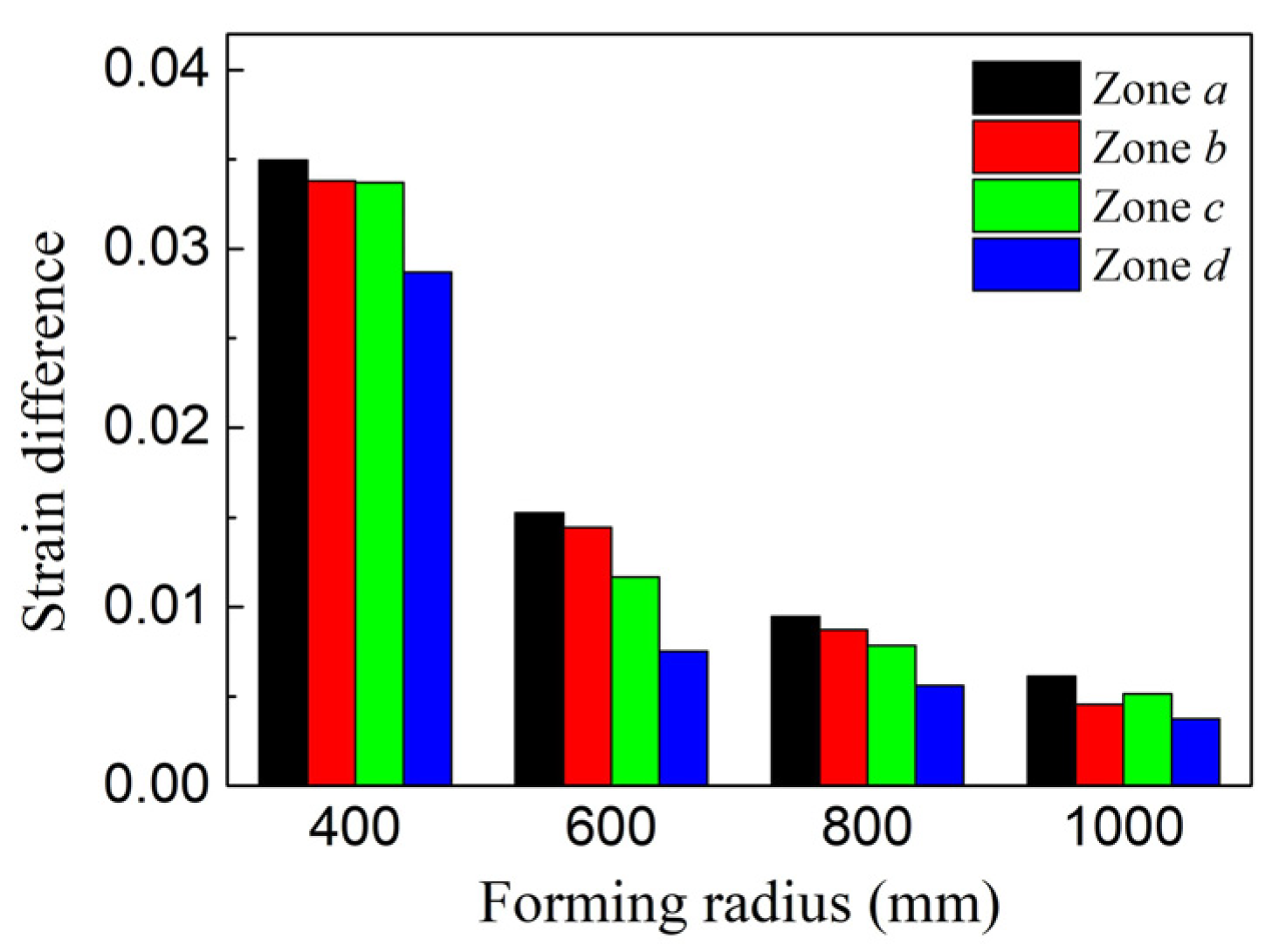
4.2. Experimental Results and Analyses
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Banhart, J.; Seeliger, H.-W. Aluminium Foam Sandwich Panels: Manufacture, Metallurgy and Applications. Adv. Eng. Mater. 2008, 10, 793–802. [Google Scholar] [CrossRef]
- Crupi, V.; Epasto, G.; Guglielmino, E. Comparison of aluminium sandwiches for lightweight ship structures: Honeycomb vs. foam. Mar. Struct. 2013, 30, 74–96. [Google Scholar] [CrossRef]
- Schwingel, D.; Seeliger, HW.; Vecchionacci, C.; Alwes, D.; Dittrich, J. Aluminium foam sandwich structures for space applications. Acta Astronaut. 2007, 61, 326–330. [Google Scholar] [CrossRef]
- García-Moreno, F. Commercial Applications of Metal Foams: Their Properties and Production. Materials 2016, 9, 85. [Google Scholar] [CrossRef] [PubMed]
- Cai, Z.-Y.; Liang, X.-B.; Chen, Q.-M.; Zhang, X. Numerical and experimental investigations on the formability of three-dimensional aluminum alloy sandwich panels with egg-box-like cores. Int. J. Adv. Manuf. Technol. 2018, 99, 387–397. [Google Scholar] [CrossRef]
- Cai, Z.-Y.; Zhang, X.; Liang, X.-B. Multi-point forming of sandwich panels with egg-box-like cores and failure behaviors in forming process: Analytical models, numerical and experimental investigations. Mater. Des. 2018, 160, 1029–1041. [Google Scholar] [CrossRef]
- Liang, X.-B.; Cai, Z.-Y.; Zhang, X.; Gao, J.-X. Plastic forming of the doubly curved surfaces of sandwich plates with bi-directionally trapezoidal cores of different sizes. Thin-Walled Struct. 2020, 146, 106188. [Google Scholar] [CrossRef]
- Zhang, X.; Cai, Z.-Y.; Liang, X.-B.; Gao, J.-X. Numerical investigation on the plastic forming of aluminum foam sandwich panel based on three-dimensional mesoscopic and macroscopic models. Int. J. Adv. Manuf. Technol. 2020, 109, 1431–1445. [Google Scholar] [CrossRef]
- Kabir, K.; Vodenitcharova, T.; Hoffman, M. Response of aluminium foam-cored sandwich panels to bending load. Compos. Part B Eng. 2014, 64, 24–32. [Google Scholar] [CrossRef]
- Crupi, V.; Montanini, R. Aluminium foam sandwiches collapse modes under static and dynamic three-point bending. Int. J. Impact Eng. 2007, 34, 509–521. [Google Scholar] [CrossRef]
- Hanssen, A.; Girard, Y.; Olovsson, L.; Berstad, T.; Langseth, M. A numerical model for bird strike of aluminium foam-based sandwich panels. Int. J. Impact Eng. 2006, 32, 1127–1144. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, Z.H.; Yu, T.L.; Xin, D.B. Mechanical properties and energy absorption capabilities of aluminum foam sandwich structure subjected to low-velocity impact. Constr. Build. Mater. 2021, 273, 121996. [Google Scholar] [CrossRef]
- Jing, L.; Liu, K.; Su, X.; Guo, X. Experimental and numerical study of square sandwich panels with layered-gradient foam cores to air-blast loading. Thin-Walled Struct. 2021, 161, 107445. [Google Scholar] [CrossRef]
- Hou, W.; Zhu, F.; Lu, G.; Fang, D.-N. Ballistic impact experiments of metallic sandwich panels with aluminium foam core. Int. J. Impact Eng. 2010, 37, 1045–1055. [Google Scholar] [CrossRef]
- Jackson, K.; Allwood, J.; Landert, M. Incremental forming of sandwich panels. J. Mater. Process. Technol. 2008, 204, 290–303. [Google Scholar] [CrossRef]
- Seong, D.; Jung, C.; Yang, D.; Kim, J.; Chung, W.; Lee, M. Bendable metallic sandwich plates with a sheared dimple core. Scr. Mater. 2010, 63, 81–84. [Google Scholar] [CrossRef]
- Weiss, M.; Abeyrathna, B.; Pereira, M. Roll formability of aluminium foam sandwich panels. Int. J. Adv. Manuf. Technol. 2018, 97, 953–965. [Google Scholar] [CrossRef]
- Nayyeri, M.J.; Mirbagheri, S.M.H.; Fatmehsari, D.H. Numerical evaluation of the stacking effect of spheres on the mechanics of tailor-made aluminum foams. Compos. Struct. 2017, 159, 316–326. [Google Scholar] [CrossRef]
- Nammi, S.; Myler, P.; Edwards, G. Finite element analysis of closed-cell aluminium foam under quasi-static loading. Mater. Des. 2010, 31, 712–722. [Google Scholar] [CrossRef]
- Dou, R.; Qiu, S.; Ju, Y.; Hu, Y. Simulation of compression behavior and strain-rate effect for aluminum foam sandwich panels. Comput. Mater. Sci. 2016, 112, 205–209. [Google Scholar] [CrossRef]
- Vengatachalam, B.; Poh, L.H.; Liu, Z.S.; Qin, Q.H.; Swaddiwudhipong, S. Three dimensional modelling of closed-cell aluminium foams with predictive macroscopic behaviour. Mech. Mater. 2019, 136, 103067. [Google Scholar] [CrossRef]
- Contorno, D.; Filice, L.; Fratini, L.; Micari, F. Forming of aluminum foam sandwich panels: Numerical simulations and experimental tests. J. Mater. Process. Technol. 2006, 177, 364–367. [Google Scholar] [CrossRef]
- Nassar, H.; Albakri, M.; Pan, H.; Khraisheh, M. On the gas pressure forming of aluminium foam sandwich panels: Experiments and numerical simulations. CIRP Ann. 2012, 61, 243–246. [Google Scholar] [CrossRef]
- Bucher, T.; Cardenas, S.; Verma, R.; Li, W.; Yao, Y.L. Laser Forming of Sandwich Panels With Metal Foam Cores. J. Manuf. Sci. Eng. 2018, 140, 111015. [Google Scholar] [CrossRef]
- Li, M.; Cai, Z.; Sui, Z.; Yan, Q. Multi-point forming technology for sheet metal. J. Mater. Process. Technol. 2002, 129, 333–338. [Google Scholar] [CrossRef]
- Cai, Z.-Y.; Wang, S.-H.; Xu, X.-D.; Li, M.-Z. Numerical simulation for the multi-point stretch forming process of sheet metal. J. Mater. Process. Technol. 2009, 209, 396–407. [Google Scholar] [CrossRef]
- Gan, Y.; Chen, C.; Shen, Y. Three-dimensional modeling of the mechanical property of linearly elastic open cell foams. Int. J. Solids Struct. 2005, 42, 6628–6642. [Google Scholar] [CrossRef]
- Sun, G.; Wang, E.; Zhao, T.; Zheng, G.; Li, Q. Inverse identification of cell-wall material properties of closed-cell aluminum foams based upon Vickers nano-indentation tests. Int. J. Mech. Sci. 2020, 176, 105524. [Google Scholar] [CrossRef]
- Zhang, Q.; Dean, T.; Wang, Z. Numerical simulation of deformation in multi-point sandwich forming. Int. J. Mach. Tools Manuf. 2006, 46, 699–707. [Google Scholar] [CrossRef]









| Density (g/cm3) | Young’s Modulus (MPa) | Yield Stress (MPa) | Poisson’s Ratio | |
|---|---|---|---|---|
| Face sheet | 2.71 | 70,300 | 193 | 0.33 |
| Core cell wall | 2.7 | 63,000 | 63 | 0.33 |
| Radius (mm) | Along OA | Along OB | |||
|---|---|---|---|---|---|
| Sim | Exp | Sim | Exp | ||
| Spherical part | 800 | 0.023 | 0.209 | 0.017 | 0.081 |
| 1000 | 0.043 | 0.339 | 0.032 | 0.124 | |
| Saddle-shaped part | 800 | 0.033 | 0.240 | 0.028 | 0.087 |
| 1000 | 0.050 | 0.440 | 0.040 | 0.162 | |
| Radius (mm) | Along OE | Along OF | |||
|---|---|---|---|---|---|
| Sim | Exp | Sim | Exp | ||
| Spherical part | 800 | 0.026 | 0.016 | 0.033 | 0.026 |
| 1000 | 0.022 | 0.015 | 0.022 | 0.017 | |
| Saddle-shaped part | 800 | 0.013 | 0.007 | 0.013 | 0.007 |
| 1000 | 0.008 | 0.004 | 0.007 | 0.004 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Chen, Q.; Gao, J.; Wang, M.; Zhang, Y.; Cai, Z. Numerical Study on the Plastic Forming of Doubly Curved Surfaces of Aluminum Foam Sandwich Panel Using 3D Voronoi Model. Metals 2021, 11, 675. https://doi.org/10.3390/met11050675
Zhang X, Chen Q, Gao J, Wang M, Zhang Y, Cai Z. Numerical Study on the Plastic Forming of Doubly Curved Surfaces of Aluminum Foam Sandwich Panel Using 3D Voronoi Model. Metals. 2021; 11(5):675. https://doi.org/10.3390/met11050675
Chicago/Turabian StyleZhang, Xi, Qingmin Chen, Jiaxin Gao, Mingwei Wang, Ya Zhang, and Zhongyi Cai. 2021. "Numerical Study on the Plastic Forming of Doubly Curved Surfaces of Aluminum Foam Sandwich Panel Using 3D Voronoi Model" Metals 11, no. 5: 675. https://doi.org/10.3390/met11050675
APA StyleZhang, X., Chen, Q., Gao, J., Wang, M., Zhang, Y., & Cai, Z. (2021). Numerical Study on the Plastic Forming of Doubly Curved Surfaces of Aluminum Foam Sandwich Panel Using 3D Voronoi Model. Metals, 11(5), 675. https://doi.org/10.3390/met11050675





