A Review of Bubble Dynamics in Liquid Metals
Abstract
1. Introduction
2. Measurement Methods
2.1. Theoretical Investigations
2.2. Experimental Measurements
2.3. Direct Numerical Simulation
3. Bubble Formation Mechanisms
3.1. Bubble Generation at Single Nozzles
| Ref. | Year | Method | Nozzle [cm] | Flowrate [cm3/s] | Fluid | Result |
|---|---|---|---|---|---|---|
| Sano & Mori [15] | 1976 | Pres Pul | dno: 0.22–0.82 dni: 0.1–0.3 | 0.0167–70 | Hg/Ag | Correlations from water can be used in case the O.D. instead of the I.D is used (non-wettability) |
| Andreini et al. [17] | 1977 | Ac | dni: 0.015–0.1 | Cu/Pb/Sn | Bubble size depend on We and Fr, not on Re. Water model correlations cannot be used | |
| Irons & Guthrie [18] | 1978 | Ac | dno: 0.64–5.1, dni: 0.16–0.64 | 0.5–1000 | Fe | Use of O.D because of non-wettability, BSD becomes independent of fluid properties at higher flow rates |
| Mori et al. [46] | 1979 | Pres. Pul | dno: 0.32–0.68 dni: 0.12–0.33 | 0.1–36 | Fe | Empirical Equation (7) for various liquids. At high flow rates, BSD becomes independent of the fluid |
| Sano & Mori [42] | 1980 | Res | dno: 0.4–1.0 dni: 0.2–0.6 | 50–1330 | Hg | Good agreement with water model correlation, BSD is independent of fluid properties, empirical correlation Equation (9) |
| Mori et al. [20] | 1982 | Res | dni: 0.1–0.4 | 0.05–4500 | Hg | Good agreement with Equation (6) at higher flow rates |
| Xie et al. [47] | 1992 | Res | dni: 0.2–0.5 | 100–1200 | Woods | BSD follows log-normal distribution, BSD becomes independent of nozzle, BSD is result of breakup |
| Tsuchiya et al. [16] | 1993 | Pres Pul | dno: 0.2–0.64 dni: 0.1–0.4 | 0.5–10 | H20/Hg CH3OH Li17Pb83 | Fitting parameters of Equation (7) depend on nozzle orientation and fluid properties |
| Iguchi et al. [21] | 1995 | Res | dno: 0.6 dni: 0.1 | 50–100 | Fe | Larger bubbles than predicted by Equation (7) |
| Iguchi et al. [26] | 1995 | X-ray | dno: 0.13–0.45 dni: 0.09–0.19 | 20–413 | Fe | At high flow rates, BSD depend on I.D, not O.D. BSD depends on fluid and gas properties |
| Iguchi et al. [50] | 1997 | Res | dni = 0.005 | 60 | Woods | Confirmed Equation (10) |
| Gnyloskurenko & Nakamura [48] | 2003 | X-ray | dno: 0.2–1 dni: 0.1–0.4 | 0.43–12 | Al | Non-wettability of the nozzle increases bubble size |
3.2. Bubble Generation from Porous Plugs
3.3. Bubble Generation from Slot Plugs
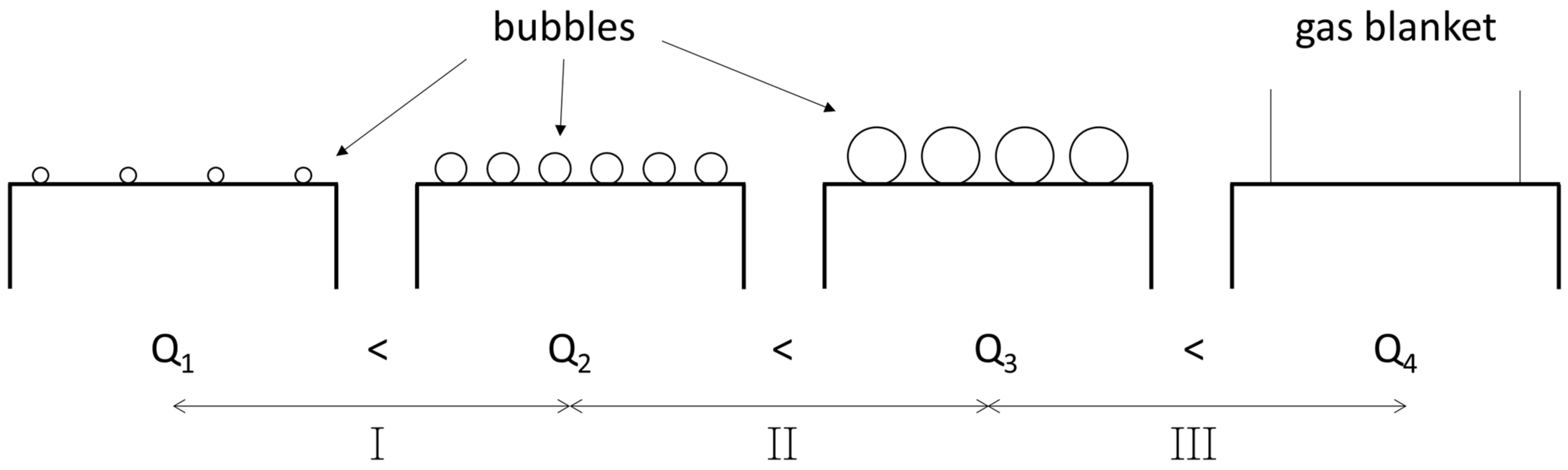
3.4. Bubble Size in a Steel Casting Ladle
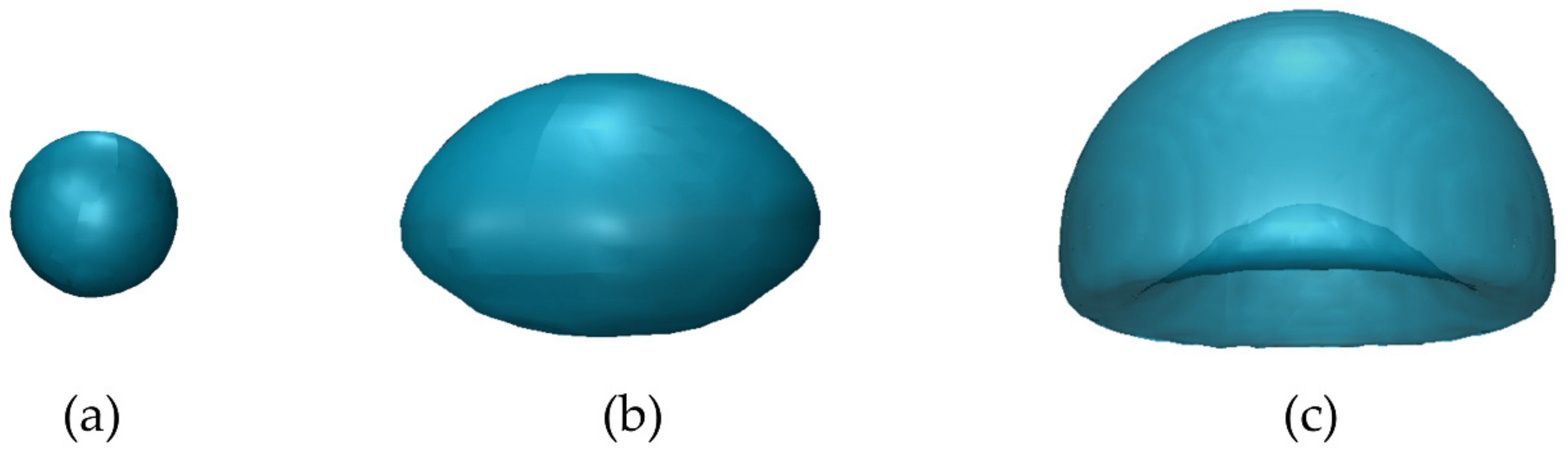
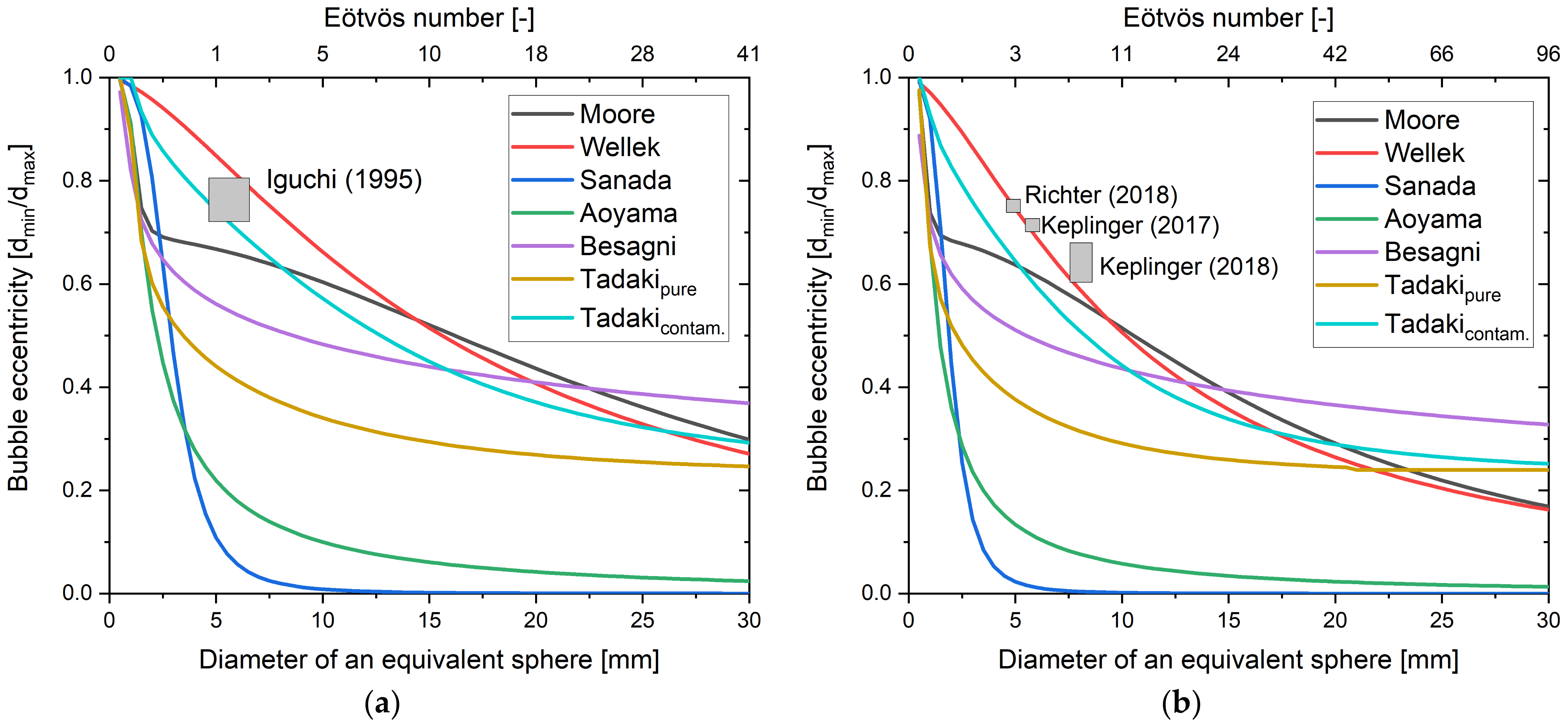
4. Bubble Deformation
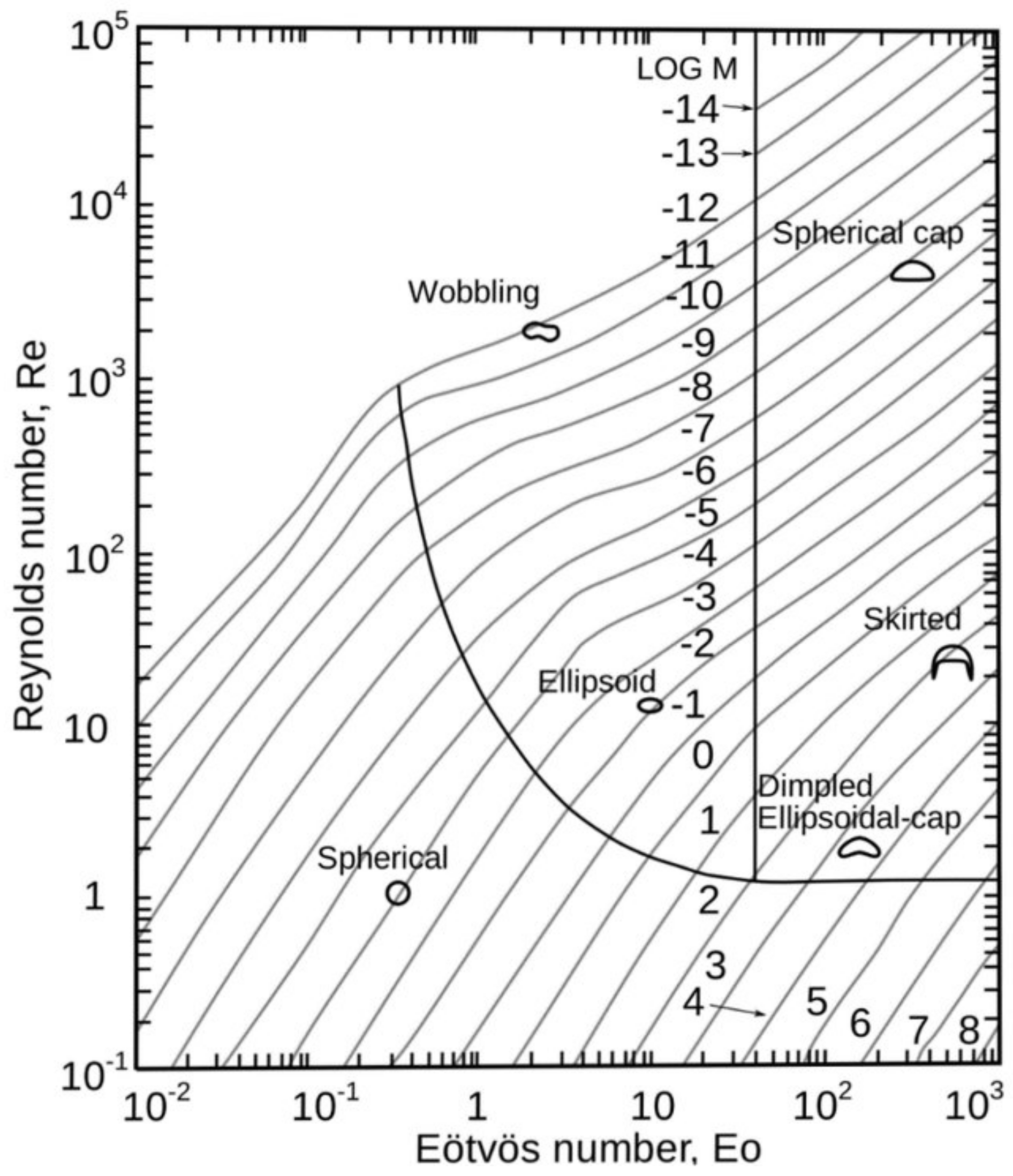
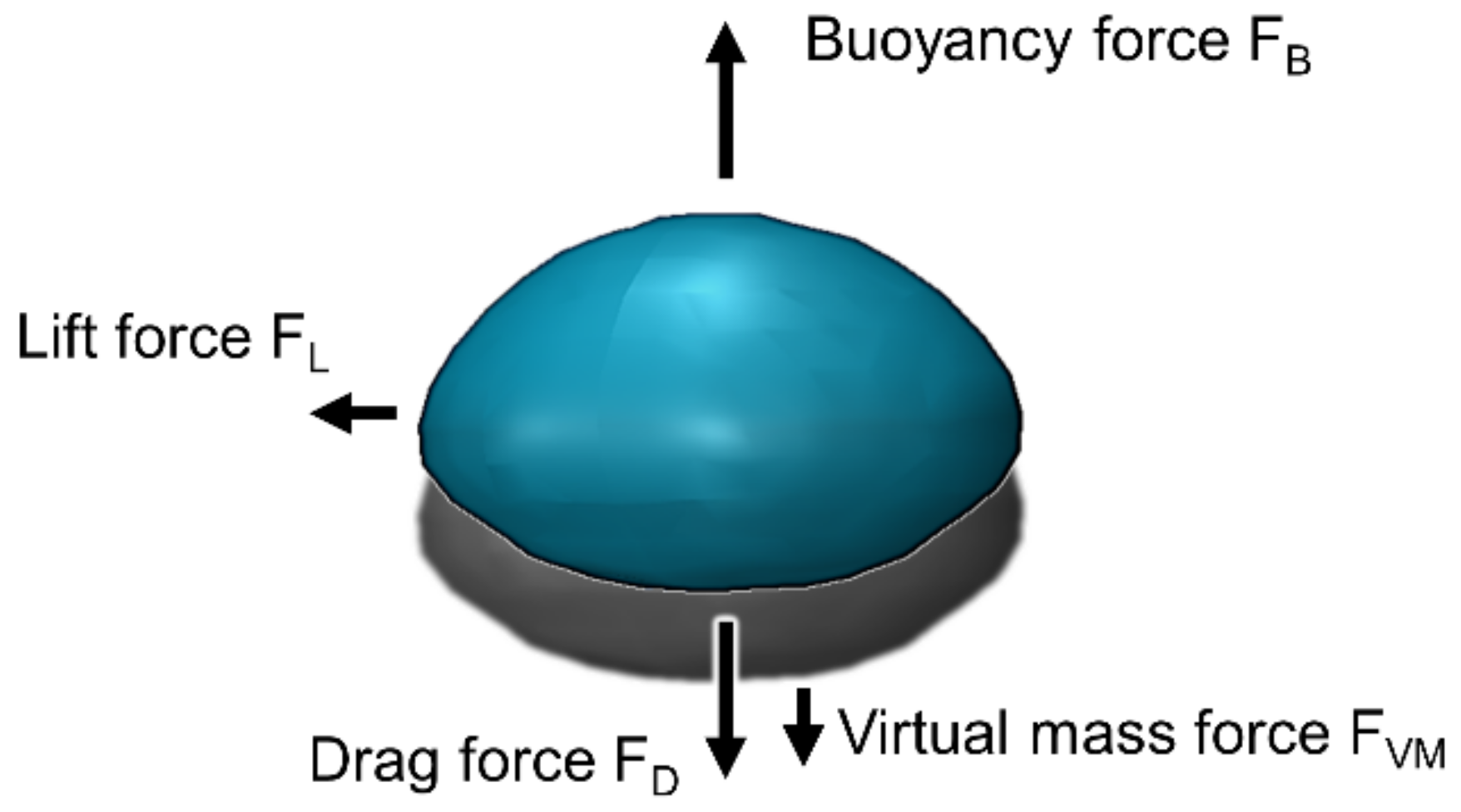
5. Interfacial Force Closure
5.1. Drag Force
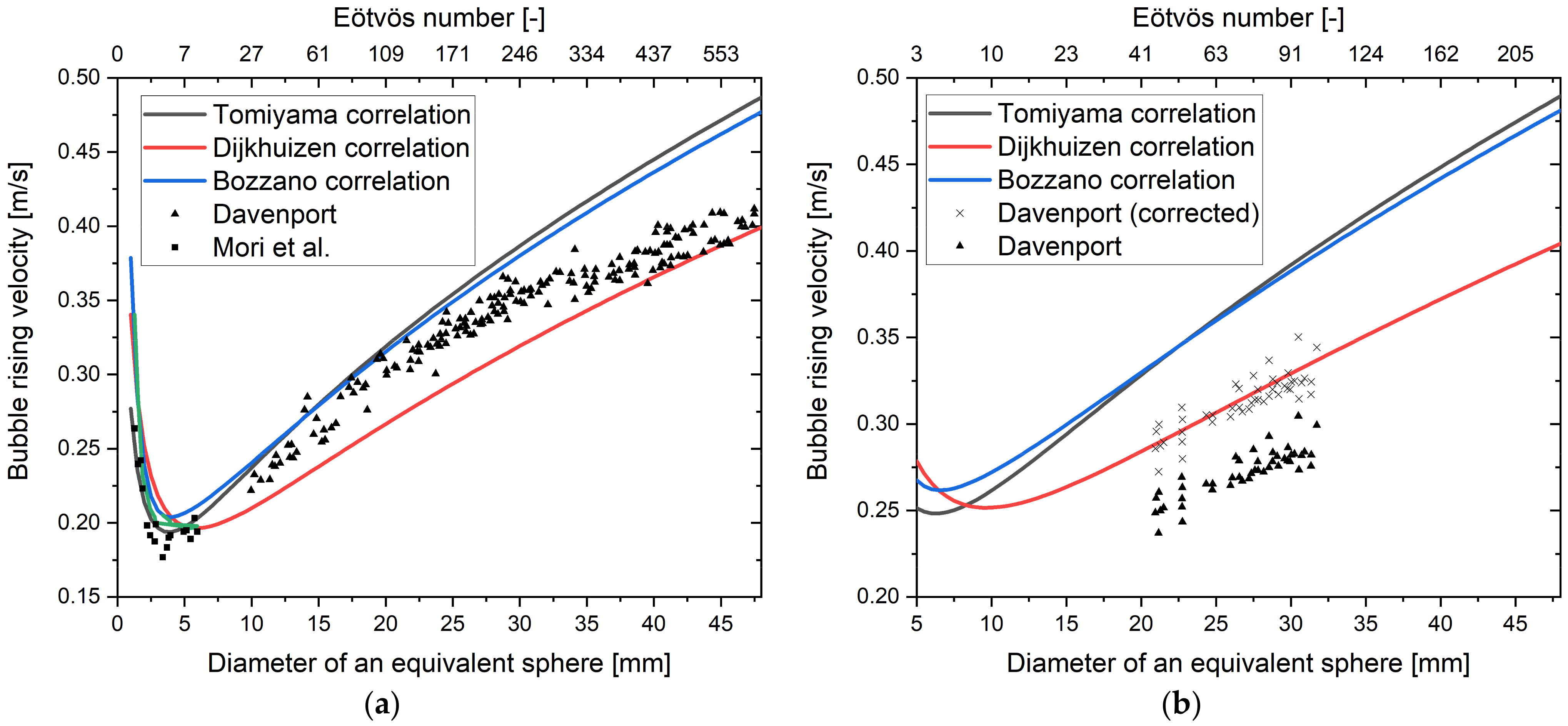
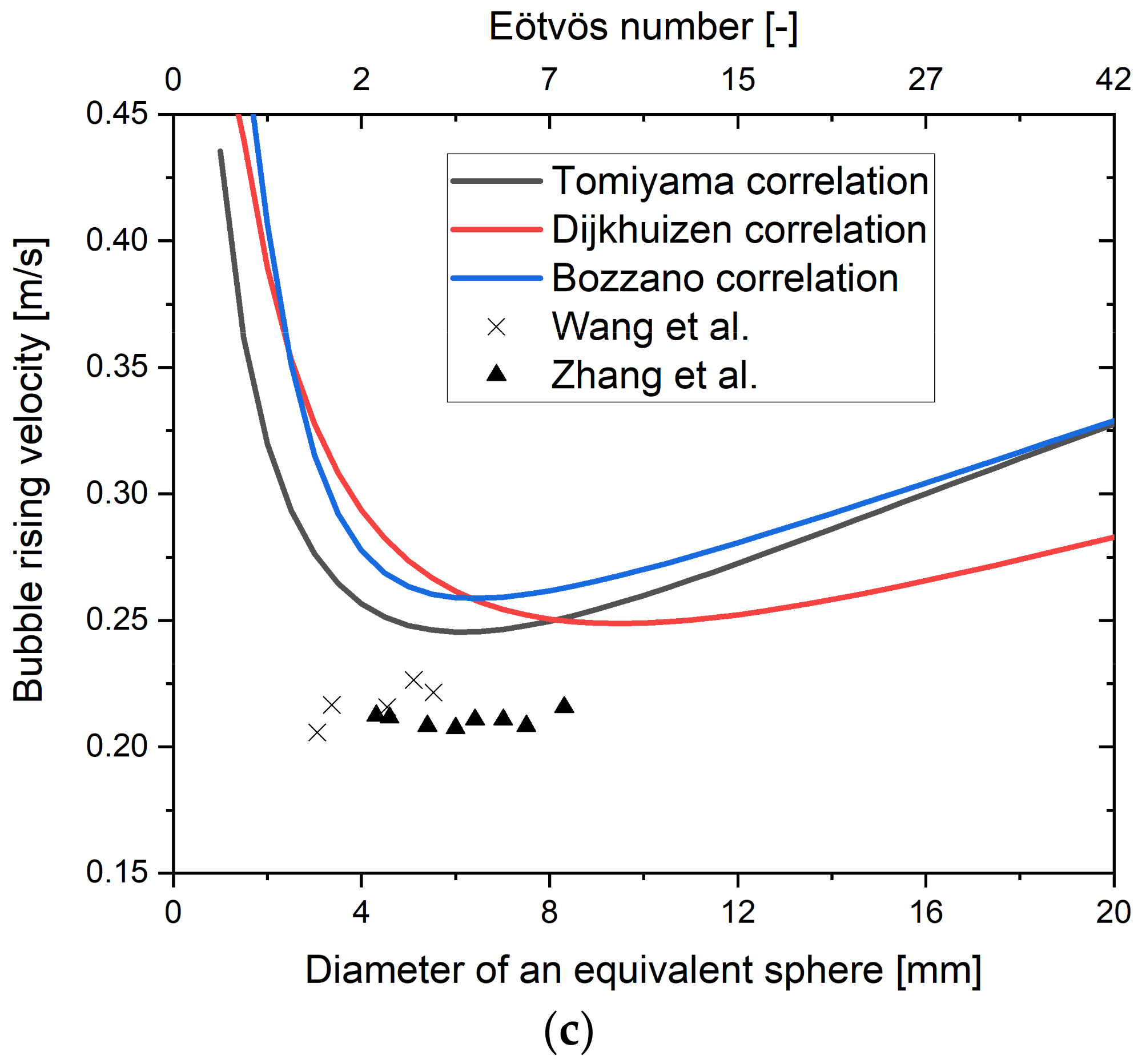
5.1.1. Influence of Contaminants
5.1.2. Influence of Surrounding Bubbles
5.2. Lift Force
Influence of Contamination
5.3. Virtual Mass Force
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol | Description |
| cD | Drag coefficient |
| c1–4 | Fitting parameter |
| cL | Lift coefficient |
| cVM | Virtual mass coefficient |
| c∞ | Far-field concentration of contaminants, mol/m3 |
| db | Arithmetic mean equivalent bubble diameter, m |
| db,32 | Bubble Sauter mean diameter, m |
| deq | Equivalent bubble diameter, m |
| dmax | Length of bubble major axis, m |
| dmin | Length of bubble minor axis, m |
| dni | Orifice inner diameter, m |
| dno | Orifice outer diameter, m |
| dpo | Pore diameter |
| E | Bubble eccentricity |
| Eo | Eötvös number |
| Eod | Modified Eötvös number |
| Fr | Froude number |
| Fi | Force i on bubble, N |
| FD | Drag force, N |
| FL | Lift force, N |
| FVM | Virtual mass force, N |
| f | Friction factor in Bozzano drag model |
| g | Gravity, 9.81 m/s2 |
| H0 | Distance between nozzle and the mathematical origin of the nozzle, m |
| HFill | Filling height, m |
| K | Empirical constant in Mersmann correlation |
| k | Adsorption rate, m3/mol∙s |
| Lc | Characteristic length, m |
| Mo | Morton number |
| m | Fitting parameter |
| mB | Bubble mass, kg |
| n | Number of activated orifices |
| Qg | Gas flow rate in m3/s |
| Qmin | Minimum gas flow rate at which an orifice gets activated, m3/s |
| Rg | Universal gas constant, 8.3145 J/mol∙K |
| Re | Reynolds number |
| ror | Orifice radius, m |
| Sr | Dimensionless shear rate |
| Sbr | Breakup rate |
| Sc | Coalescence rate |
| T | Temperature, K |
| Ta | Tadaki number |
| uc | Characteristic velocity, m/s |
| usg | Superficial gas velocity |
| ub | Bubble velocity, m/s |
| ul | Liquid velocity, m/s |
| Vb | Bubble volume, m3 |
| We | Weber number |
| wsl | Slot width, m |
| ŷ | Fitting parameter |
| z | Height, m |
| α | Global void fraction |
| αi | Fitting parameter |
| αloc | Local void fraction |
| β | Desorption rate, mol/m3 |
| Γ | Contaminant concentration, mol/m2 |
| ε | Porosity of a porous plate |
| θ | Fitting parameter |
| κ | Permeability of a porous plug |
| λsl | Distance between active bubble formation sites on slot nozzles, m |
| μg | Gas viscosity, Ns/m2 |
| μl | Liquid viscosity, Ns/m2 |
| ρb | Bubble density, kg/m3 |
| ρl | Liquid density, kg/m3 |
| σ | Surface tension, N/m |
| φ | Shape factor |
| ω | Shear rate, 1/s |
References
- Deckwer, W.-D.; Field, R.W. Bubble Column Reactors; Wiley: New York, NY, USA, 1992; Volume 200. [Google Scholar]
- Prosperetti, A. Bubbles. Phys. Fluids 2004, 16, 1852–1865. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F.; Ziegenhein, T. Two-phase bubble columns: A comprehensive review. ChemEngineering 2018, 2, 13. [Google Scholar] [CrossRef]
- Veldhuis, C.; Biesheuvel, A.; Van Wijngaarden, L. Shape oscillations on bubbles rising in clean and in tap water. Phys. Fluids 2008, 20, 040705. [Google Scholar] [CrossRef]
- Sanada, T.; Sugihara, K.; Shirota, M.; Watanabe, M. Motion and drag of a single bubble in super-purified water. Fluid Dynam. Res. 2008, 40, 534. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, Y. Development of a robust image processing technique for bubbly flow measurement in a narrow rectangular channel. Int. J. Multiph. Flow 2016, 84, 217–228. [Google Scholar] [CrossRef]
- Bröder, D.; Sommerfeld, M. Planar shadow image velocimetry for the analysis of the hydrodynamics in bubbly flows. Meas. Sci. Technol. 2007, 18, 2513. [Google Scholar] [CrossRef]
- Ferreira, A.; Pereira, G.; Teixeira, J.; Rocha, F. Statistical tool combined with image analysis to characterize hydrodynamics and mass transfer in a bubble column. Chem. Eng. J. 2012, 180, 216–228. [Google Scholar] [CrossRef]
- Karn, A.; Ellis, C.; Arndt, R.; Hong, J. An integrative image measurement technique for dense bubbly flows with a wide size distribution. Chem. Eng. Sci. 2015, 122, 240–249. [Google Scholar] [CrossRef]
- Lau, Y.; Sujatha, K.T.; Gaeini, M.; Deen, N.; Kuipers, J. Experimental study of the bubble size distribution in a pseudo-2D bubble column. Chem. Eng. Sci. 2013, 98, 203–211. [Google Scholar] [CrossRef]
- Poletaev, I.; Pervunin, K.; Tokarev, M. Artificial neural network for bubbles pattern recognition on the images. J. Phys. Conf. Ser. 2016, 754, 072002. [Google Scholar] [CrossRef]
- Haas, T.; Schubert, C.; Eickhoff, M.; Pfeifer, H. BubCNN: Bubble detection using Faster RCNN and shape regression network. Chem. Eng. Sci. 2020. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, Y. 3D bubble reconstruction using multiple cameras and space carving method. Meas. Sci. Technol. 2018, 29, 075206. [Google Scholar] [CrossRef]
- Haas, T.; Suarez, A.L.; Eickhoff, M.; Pfeifer, H. Toward a Strong-Sense Validation Benchmark Database for Numerical Ladle Flow Models. Metal. Mater. Trans. B 2021, 52, 199–222. [Google Scholar] [CrossRef]
- Sano, M.; Mori, K. Bubble formation from single nozzles in liquid metals. Trans. Jpn. Instit. Metals 1976, 17, 344–352. [Google Scholar] [CrossRef]
- Tsuchiya, K.; Aida, M.; Fujii, Y.; Okamoto, M. Bubble formation from a single nozzle in moderator liquids and liquid metal for tritium breeding. J. Nucl. Mater. 1993, 207, 123–129. [Google Scholar] [CrossRef]
- Andreini, R.; Foster, J.; Callen, R. Characterization of gas bubbles injected into molten metals under laminar flow conditions. Metal. Trans. B 1977, 8, 625–631. [Google Scholar] [CrossRef]
- Irons, G.; Guthrie, R. Bubble formation at nozzles in pig iron. Metal. Trans. B 1978, 9, 101–110. [Google Scholar] [CrossRef]
- Davenport, W.G. Bubbles in Liquids Including Liquid Metals; The Royal School of Mines: London, UK, 1964. [Google Scholar]
- Mori, K.; Ozawa, Y.; Sano, M. Characterization of gas jet behavior at a submerged orifice in liquid metal. Trans. Iron Steel Inst. Jpn. 1982, 22, 377–384. [Google Scholar] [CrossRef]
- Iguchi, M.; Kawabata, H.; Nakajima, K.; Morita, Z.-I. Measurement of bubble characteristics in a molten iron bath at 1600 °C using an electroresistivity probe. Metal. Mater. Trans. B 1995, 26, 67–74. [Google Scholar] [CrossRef]
- Keplinger, O.; Shevchenko, N.; Eckert, S. Visualization of bubble coalescence in bubble chains rising in a liquid metal. Int. J. Multiph. Flow 2018, 105, 159–169. [Google Scholar] [CrossRef]
- Iguchi, M.; Nakatani, T.; Tokunaga, H. The shape of bubbles rising near the nozzle exit in molten metal baths. Metal. Mater. Trans. B 1997, 28, 417–423. [Google Scholar] [CrossRef]
- Iguchi, M.; Nakatani, T.; Kawabata, H. Development of a multineedle electroresistivity probe for measuring bubble characteristics in molten metal baths. Metal. Mater. Trans. B 1997, 28, 409–416. [Google Scholar] [CrossRef]
- Davis, K.G.; Irons, G.A.; Guthrie, R.I.L. X-ray cinematographic observations of gas injection into liquid metals. Metal. Mater. Trans. B 1978, 9, 721–722. [Google Scholar] [CrossRef]
- Iguchi, M.; Chihara, T.; Takanashi, N.; Ogawa, Y.; Tokumitsu, N.; Morita, Z.-I. X-ray fluoroscopic observation of bubble characteristics in a molten iron bath. ISIJ Int. 1995, 35, 1354–1361. [Google Scholar] [CrossRef]
- Keplinger, O.; Shevchenko, N.; Eckert, S. Validation of X-ray radiography for characterization of gas bubbles in liquid metals. IOP Conf. Ser. Mater. Sci. Eng. 2017, 228, 012009. [Google Scholar] [CrossRef]
- Mishima, K.; Hibiki, T.; Saito, Y.; Nishihara, H.; Tobita, Y.; Konishi, K.; Matsubayashi, M. Visualization and measurement of gas–liquid metal two-phase flow with large density difference using thermal neutrons as microscopic probes. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectromet. Detect. Assoc. Equip. 1999, 424, 229–234. [Google Scholar] [CrossRef]
- Sarma, M.; Ščepanskis, M.; Jakovičs, A.; Thomsen, K.; Nikoluškins, R.; Vontobel, P.; Beinerts, T.; Bojarevičs, A.; Platacis, E. Neutron radiography visualization of solid particles in stirring liquid metal. Phys. Proc. 2015, 69, 457–463. [Google Scholar] [CrossRef][Green Version]
- Baake, E.; Fehling, T.; Musaeva, D.; Steinberg, T. Neutron radiography for visualization of liquid metal processes: Bubbly flow for CO2 free production of Hydrogen and solidification processes in EM field. IOP Conf. Ser. Mater. Sci. Eng. 2017, 228, 12026. [Google Scholar] [CrossRef]
- Richter, T.; Keplinger, O.; Strumpf, E.; Wondrak, T.; Eckert, K.; Eckert, S.; Odenbach, S. Measurements of the Diameter of Rising Gas Bubbles by Means of the Ultrasound Transit Time Technique. Magnetohydrodynamics (0024-998X) 2017, 53, 383–392. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, S.; Meng, X.; Ni, M. UDV measurements of single bubble rising in a liquid metal Galinstan with a transverse magnetic field. Int. J. Multiph. Flow 2017, 94, 201–208. [Google Scholar] [CrossRef]
- Gundrum, T.; Büttner, P.; Dekdouk, B.; Peyton, A.; Wondrak, T.; Galindo, V.; Eckert, S. Contactless inductive bubble detection in a liquid metal flow. Sensors 2016, 16, 63. [Google Scholar] [CrossRef]
- Karcher, C.; Lyu, Z.; Boeck, T.; Tran, N.; Lüdtke, U. Experimental and numerical investigation on particle-induced liquid metal flow using Lorentz force velocimetry. IOP Conf. Ser. Mater. Sci. Eng. 2018, 424, 1. [Google Scholar] [CrossRef]
- Zhang, L.; Taniguchi, S. Fundamentals of inclusion removal from liquid steel by bubble flotation. Int. Mater. Rev. 2000, 45, 59–82. [Google Scholar] [CrossRef]
- Stapurewicz, T.; Themelis, N.J. Mixing and mass transfer phenomena in bottom-injected gas–liquid reactors. Can. Metal. Quart. 1987, 26, 123–128. [Google Scholar] [CrossRef]
- Owusu, K.B.; Haas, T.; Gajjar, P.; Eickhoff, M.; Kowitwarangkul, P.; Pfeifer, H. Interaction of Injector Design, Bubble Size, Flow Structure, and Turbulence in Ladle Metallurgy. Steel Res. Int. 2019, 90, 1800346. [Google Scholar] [CrossRef]
- Haas, T.; Schubert, C.; Eickhoff, M.; Pfeifer, H. Numerical modeling of the ladle flow by a LES-based Eulerian-Lagrange approach: A systematic survey. Metal. Mater. Trans. B 2021, 52, 903–921. [Google Scholar] [CrossRef]
- Kraume, M.; Zehner, P. Modellierung der Fluiddynamik in Blasensäulen. Chemieingenieurtechnik 1989, 61, 332–333. [Google Scholar] [CrossRef]
- Kulkarni, A.A.; Joshi, J.B. Bubble formation and bubble rise velocity in gas− liquid systems: A review. Ind. Eng. Chem. Res. 2005, 44, 5873–5931. [Google Scholar] [CrossRef]
- Leibson, I.; Holcomb, E.G.; Cacoso, A.G.; Jacmic, J.J. Rate of flow and mechanics of bubble formation from single submerged orifices. I. Rate of flow studies. AIChE J. 1956, 2, 296–300. [Google Scholar] [CrossRef]
- Sano, M.; Mori, K. Size of bubbles in energetic gas injection into liquid metal. Trans. Iron Steel Inst. Jpn. 1980, 20, 675–681. [Google Scholar] [CrossRef]
- Tate, T. On the magnitude of a drop of liquid formed under different circumstances. Lond. Edinb. Dublin Philos. Magaz. J. Sci. 1864, 27, 176–180. [Google Scholar] [CrossRef]
- Davidson, L.; Amick, E.H., Jr. Formation of gas bubbles at horizontal orifices. AIChE J. 1956, 2, 337–342. [Google Scholar] [CrossRef]
- Mersmann, A. Druckverlust und Schaumhöhen von gasdurchströmten Flüssigkeitsschichten auf Siebböden. VDI ForschHft B 1962, 28, 144. [Google Scholar]
- Mori, K.; Sano, M.; Sato, T. Size of bubbles formed at single nozzle immersed in molten iron. Trans. Iron Steel Inst. Jpn. 1979, 19, 553–558. [Google Scholar] [CrossRef]
- Xie, Y.; Orsten, S.; Oeters, F. Behaviour of bubbles at gas blowing into liquid Wood’s metal. ISIJ Int. 1992, 32, 66–75. [Google Scholar] [CrossRef]
- Gnyloskurenko, S.V.; Nakamura, T. Wettability effect on bubble formation at nozzles in liquid aluminum. Mater. Trans. 2003, 44, 2298–2302. [Google Scholar] [CrossRef]
- Zhang, L.; Taniguchi, S.; Matsumoto, K. Water model study on inclusion removal from liquid steel by bubble flotation under turbulent conditions. Ironmak. Steelmak. 2002, 29, 326–336. [Google Scholar] [CrossRef]
- Iguchi, M.; Tokunaga, H.; Tatemichi, H. Bubble and liquid flow characteristics in a wood’s metal bath stirred by bottom helium gas injection. Metal. Mater. Trans. B 1997, 28, 1053–1061. [Google Scholar] [CrossRef]
- Castillejos, A.; Brimacombe, J. Physical characteristics of gas jets injected vertically upward into liquid metal. Metal. Trans. B 1989, 20, 595–601. [Google Scholar] [CrossRef]
- Houghton, G.; McLean, A.; Ritchie, P. Mechanism of formation of gas bubble-beds. Chem. Eng. Sci. 1957, 7, 40–50. [Google Scholar] [CrossRef]
- Loimer, T.; Machu, G.; Schaflinger, U. Inviscid bubble formation on porous plates and sieve plates. Chem. Eng. Sci. 2004, 59, 809–818. [Google Scholar] [CrossRef]
- Mirsandi, H.; Baltussen, M.; Peters, E.; van Odyck, D.; van Oord, J.; van der Plas, D.; Kuipers, J. Numerical simulations of bubble formation in liquid metal. Int. J. Multiph. Flow 2020, 131, 103363. [Google Scholar] [CrossRef]
- Wang, Z.; Mukai, K.; Izu, D. Influence of wettability on the behavior of argon bubbles and fluid flow inside the nozzle and mold. ISIJ Int. 1999, 39, 154–163. [Google Scholar] [CrossRef]
- Koide, K.; Kato, S.; Tanaka, Y.; Kubota, H. Bubbles generated from porous plate. J. Chem. Eng. Jpn. 1968, 1, 51–56. [Google Scholar] [CrossRef]
- Baxter, R.; Wraith, A. Transitions in the bubble formation mode of a submerged porous disc. Chem. Eng. Sci. 1970, 25, 1244–1247. [Google Scholar] [CrossRef]
- Anagbo, P.; Brimacombe, J. Plume characteristics and liquid circulation in gas injection through a porous plug. Metal. Trans. B 1990, 21, 637–648. [Google Scholar] [CrossRef]
- Goyal, P.; Themelis, N.; Zanchuk, W.A. Gaseous refining of anode copper. JOM 1982, 34, 22–28. [Google Scholar] [CrossRef]
- Iguchi, M.; Kaji, M.; Morita, Z.-I. Effects of pore diameter, bath surface pressure, and nozzle diameter on the bubble formation from a porous nozzle. Metal. Mater. Trans. B 1998, 29, 1209–1218. [Google Scholar] [CrossRef]
- Kazakis, N.; Papadopoulos, I.; Mouza, A. Bubble columns with fine pore sparger operating in the pseudo-homogeneous regime: Gas hold up prediction and a criterion for the transition to the heterogeneous regime. Chem. Eng. Sci. 2007, 62, 3092–3103. [Google Scholar] [CrossRef]
- Mohagheghian, S.; Ghajar, A.J.; Elbing, B. Effect of operation regime on bubble size and void fraction in a bubble column with porous sparger. Authorea Prepr. 2020. [Google Scholar] [CrossRef]
- Lucas, D.; Ziegenhein, T. Influence of the bubble size distribution on the bubble column flow regime. Int. J. Multiph. Flow 2019, 120, 103092. [Google Scholar] [CrossRef]
- Koide, K.; Hayashi, T.; Noro, M.; Takemura, Y.; Kawamata, N.; Kubota, H. Bubbles generated from porous plate in pure liquid and in aqueous solutions of inorganic electrolytes. J. Chem. Eng. Jpn. 1972, 5, 236–242. [Google Scholar] [CrossRef][Green Version]
- Miyahara, T.; Tanaka, A. Size of bubbles generated from porous plates. J. Chem. Eng. Jpn. 1997, 30, 353–355. [Google Scholar] [CrossRef]
- Li, R.-Q.; Harris, R. Bubble formation from a very narrow slot. Can. Metal. Quart. 1993, 32, 31–37. [Google Scholar] [CrossRef]
- Li, R.-Q.; Wraith, A.; Harris, R. Gas dispersion phenomena at a narrow slot submerged in a liquid. Chem. Eng. Sci. 1994, 49, 531–540. [Google Scholar] [CrossRef]
- Wraith, A.; Li, R.-Q.; Harris, R. Gas bubble volume at a narrow slot nozzle in a liquid. Chem. Eng. Sci. 1995, 50, 1057–1058. [Google Scholar] [CrossRef]
- Harris, R.; Ng, K.; Wraith, A. Spargers for controlled bubble size by means of the multiple slot disperser (MSD). Chem. Eng. Sci. 2005, 60, 3111–3115. [Google Scholar] [CrossRef]
- Okumura, K.; Harrist, R.; Sanot, M. Bubble formation from nonwetted slot nozzles. Can. Metal. Quart. 1998, 37, 49–56. [Google Scholar] [CrossRef]
- Okumura, K.; Komarov, S.V.; Sano, M. Gas injection from slot nozzles with various shapes in water. ISIJ Int. 2000, 40, 544–548. [Google Scholar] [CrossRef]
- Trummer, B.; Fellner, W.; Viertauer, A.; Kneis, L.; Hackl, G. A Water Modelling Comparison of Hybrid Plug, Slot Plug and Porous Plug Designs. RHI Worldwide 2016, 1, 35. [Google Scholar]
- Polli, M.; Di Stanislao, M.; Bagatin, R.; Bakr, E.A.; Masi, M. Bubble size distribution in the sparger region of bubble columns. Chem. Eng. Sci. 2002, 57, 197–205. [Google Scholar] [CrossRef]
- Liao, Y.; Lucas, D. A literature review of theoretical models for drop and bubble breakup in turbulent dispersions. Chem. Eng. Sci. 2009, 64, 3389–3406. [Google Scholar] [CrossRef]
- Keplinger, O.; Shevchenko, N.; Eckert, S. Experimental investigation of bubble breakup in bubble chains rising in a liquid metal. Int. J. Multiph. Flow 2019, 116, 39–50. [Google Scholar] [CrossRef]
- Liao, Y.; Lucas, D. A literature review on mechanisms and models for the coalescence process of fluid particles. Chem. Eng. Sci. 2010, 65, 2851–2864. [Google Scholar] [CrossRef]
- Sahai, Y.; Guthrie, R. Hydrodynamics of gas stirred melts: Part I. Gas/liquid coupling. Metal. Trans. B 1982, 13, 193–202. [Google Scholar] [CrossRef]
- Moore, D. The velocity of rise of distorted gas bubbles in a liquid of small viscosity. J. Fluid Mech. 1965, 23, 749–766. [Google Scholar] [CrossRef]
- Bozzano, G.; Dente, M. Shape and terminal velocity of single bubble motion: A novel approach. Comp. Chem. Eng. 2001, 25, 571–576. [Google Scholar] [CrossRef]
- Liang-Shih, F.; Tsuchiya, K. Bubble Wake Dynamics in Liquids and Liquid-Solid Suspensions; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Wellek, R.; Agrawal, A.; Skelland, A. Shape of liquid drops moving in liquid media. AIChE J. 1966, 12, 854–862. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Courier Corporation: Chelmsford, MA, USA, 2005. [Google Scholar]
- Aoyama, S.; Hayashi, K.; Hosokawa, S.; Tomiyama, A. Shapes of single bubbles in infinite stagnant liquids contaminated with surfactant. Exp. Therm. Fluid Sci. 2018, 96, 460–469. [Google Scholar] [CrossRef]
- Besagni, G.; Deen, N.G. Aspect ratio of bubbles in different liquid media: A novel correlation. Chem. Eng. Sci. 2020, 215, 115383. [Google Scholar] [CrossRef]
- Tomiyama, A.; Tamai, H.; Zun, I.; Hosokawa, S. Transverse migration of single bubbles in simple shear flows. Chem. Eng. Sci. 2002, 57, 1849–1858. [Google Scholar] [CrossRef]
- Vakhrushev, I.; Efremov, G. Interpolation formula for computing the velocities of single gas bubbles in liquids. Chem. Technol. Fuels Oils 1970, 6, 376–379. [Google Scholar] [CrossRef]
- Aoyama, S.; Hayashi, K.; Hosokawa, S.; Tomiyama, A. Shapes of ellipsoidal bubbles in infinite stagnant liquids. Int. J. Multiph. Flow 2016, 79, 23–30. [Google Scholar] [CrossRef]
- Ziegenhein, T.; Lucas, D. Observations on bubble shapes in bubble columns under different flow conditions. Exp. Therm. Fluid Sci. 2017, 85, 248–256. [Google Scholar] [CrossRef]
- Dijkhuizen, W.; Roghair, I.; Annaland, M.V.S.; Kuipers, J. DNS of gas bubbles behaviour using an improved 3D front tracking model—Drag force on isolated bubbles and comparison with experiments. Chem. Eng. Sci. 2010, 65, 1415–1426. [Google Scholar] [CrossRef]
- Xu, Y.; Ersson, M.; Jönsson, P. Numerical simulation of single argon bubble rising in molten metal under a laminar flow. Steel Res. Int. 2015, 86, 1289–1297. [Google Scholar] [CrossRef]
- Wang, G.; Zhou, H.; Tian, Q.; Ai, X.; Zhang, L. The Motion of Single Bubble and Interactions between Two Bubbles in Liquid Steel. ISIJ Int. 2017. [Google Scholar] [CrossRef]
- Magnaudet, J.; Eames, I. The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 2000, 32, 659–708. [Google Scholar] [CrossRef]
- Mei, R.; Klausner, J.F. Unsteady force on a spherical bubble at finite Reynolds number with small fluctuations in the free-stream velocity. Phys. Fluids A Fluid Dynam. 1992, 4, 63–70. [Google Scholar] [CrossRef]
- Pang, M.J.; Wei, J.J. Analysis of drag and lift coefficient expressions of bubbly flow system for low to medium Reynolds number. Nucl. Eng. Design 2011, 241, 2204–2213. [Google Scholar] [CrossRef]
- Tomiyama, A.; Kataoka, I.; Zun, I.; Sakuguchi, T. Drag Coefficients of Single Bubbles under Normal and Micro Gravity Conditions. JSME Int. J. Ser. B Fluids Therm. Eng. 1998, 41, 472–479. [Google Scholar] [CrossRef]
- Frank, T.; Shi, J.; Burns, A. Validation of Eulerian multiphase flow models for nuclear safety applications. In Proceedings of the 3rd International Symposium on Two-Phase Flow Modelling and Experimentation, Pisa, Italy, 22–24 September 2014. [Google Scholar]
- Peebles, F.; Garber, H. Studies on the Motion of Gas Bubbles in Liquids. Chem. Eng. Progress 1953, 49, 88–97. [Google Scholar]
- Mori, Y.; Hijikata, K.; Kuriyama, I. Experimental study of bubble motion in mercury with and without a magnetic field. J. Heat Transfer 1977, 99, 404–410. [Google Scholar] [CrossRef]
- Zhang, C.; Eckert, S.; Gerbeth, G. Experimental study of single bubble motion in a liquid metal column exposed to a DC magnetic field. Int. J. Multiph. Flow 2005, 31, 824–842. [Google Scholar] [CrossRef]
- Takagi, S.; Matsumoto, Y. Surfactant effects on bubble motion and bubbly flows. Annu. Rev. Fluid Mech. 2011, 43, 615–636. [Google Scholar] [CrossRef]
- Tasoglu, S.; Demirci, U.; Muradoglu, M. The effect of soluble surfactant on the transient motion of a buoyancy-driven bubble. Phys. Fluids 2008, 20, 040805. [Google Scholar] [CrossRef]
- Cuenot, B.; Magnaudet, J.; Spennato, B. The effects of slightly soluble surfactants on the flow around a spherical bubble. J. Fluid Mech. 1997, 339, 25–53. [Google Scholar] [CrossRef]
- Zhang, Y.; Finch, J. A note on single bubble motion in surfactant solutions. J. Fluid Mech. 2001, 429, 63. [Google Scholar] [CrossRef]
- Takagi, S.; Ogasawara, T.; Matsumoto, Y. The effects of surfactant on the multiscale structure of bubbly flows. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2008, 366, 2117–2129. [Google Scholar] [CrossRef]
- Fukuta, M.; Takagi, S.; Matsumoto, Y. Numerical study on the shear-induced lift force acting on a spherical bubble in aqueous surfactant solutions. Phys. Fluids 2008, 20, 040704. [Google Scholar] [CrossRef]
- Simonnet, M.; Gentric, C.; Olmos, E.; Midoux, N. Experimental determination of the drag coefficient in a swarm of bubbles. Chem. Eng. Sci. 2007, 62, 858–866. [Google Scholar] [CrossRef]
- Richardson, J.; Zaki, W. The sedimentation of a suspension of uniform spheres under conditions of viscous flow. Chem. Eng. Sci. 1954, 3, 65–73. [Google Scholar] [CrossRef]
- Lockett, M.J.; Kirkpatrick, R.D. Ideal bubbly flow and actual flow in bubble columns. Trans. Inst. Chem. Eng. 1975, 53, 267–273. [Google Scholar]
- Garnier, C.; Lance, M.; Marié, J. Measurement of local flow characteristics in buoyancy-driven bubbly flow at high void fraction. Exp. Therm. Fluid Sci. 2002, 26, 811–815. [Google Scholar] [CrossRef]
- Guet, S.; Ooms, G.; Oliemans, R.; Mudde, R. Bubble size effect on low liquid input drift–flux parameters. Chem. Eng. Sci. 2004, 59, 3315–3329. [Google Scholar] [CrossRef]
- Roghair, I.; Lau, Y.; Deen, N.; Slagter, H.; Baltussen, M.; Annaland, M.V.S.; Kuipers, J. On the drag force of bubbles in bubble swarms at intermediate and high Reynolds numbers. Chem. Eng. Sci. 2011, 66, 3204–3211. [Google Scholar] [CrossRef]
- Grienberger, J.; Hofmann, H. Investigations and modelling of bubble columns. Chem. Eng. Sci. 1992, 47, 2215–2220. [Google Scholar] [CrossRef]
- Simonnet, M.; Gentric, C.; Olmos, E.; Midoux, N. CFD simulation of the flow field in a bubble column reactor: Importance of the drag force formulation to describe regime transitions. Chem. Eng. Proces. Process Intensif. 2008, 47, 1726–1737. [Google Scholar] [CrossRef]
- Lau, Y.; Roghair, I.; Deen, N.; van Sint Annaland, M.; Kuipers, J. Numerical investigation of the drag closure for bubbles in bubble swarms. Chem. Eng. Sci. 2011, 66, 3309–3316. [Google Scholar] [CrossRef]
- Zun, I. The transverse migration of bubbles influenced by walls in vertical bubbly flow. Int. J. Multiph. Flow 1980, 6, 583–588. [Google Scholar] [CrossRef]
- Saffman, P. The lift on a small sphere in a slow shear flow. J. Fluid Mech. 1965, 22, 385–400. [Google Scholar] [CrossRef]
- McLaughlin, J.B. Inertial migration of a small sphere in linear shear flows. J. Fluid Mech. 1991, 224, 261–274. [Google Scholar] [CrossRef]
- Legendre, D.; Magnaudet, J. A note on the lift force on a spherical bubble or drop in a low-Reynolds-number shear flow. Phys. Fluids 1997, 9, 3572–3574. [Google Scholar] [CrossRef]
- Mei, R.; Klausner, J. Shear lift force on spherical bubbles. Int. J. Heat Fluid Flow 1994, 15, 62–65. [Google Scholar] [CrossRef]
- Auton, T. The lift force on a spherical body in a rotational flow. J. Fluid Mech. 1987, 183, 199–218. [Google Scholar] [CrossRef]
- Legendre, D.; Magnaudet, J. The lift force on a spherical bubble in a viscous linear shear flow. J. Fluid Mech. 1998, 368, 81–126. [Google Scholar] [CrossRef]
- Lance, M.; De Bertodano, M.L. Phase distribution phenomena and wall effects in bubbly two-phase flows. Multiph. Sci. Technol. 1994, 8. [Google Scholar] [CrossRef]
- Liu, T. Bubble size and entrance length effects on void development in a vertical channel. Int. J. Multiph. Flow 1993, 19, 99–113. [Google Scholar] [CrossRef]
- Hibiki, T.; Ishii, M. Lift force in bubbly flow systems. Chem. Eng. Sci. 2007, 62, 6457–6474. [Google Scholar] [CrossRef]
- Serizawa, A.; Kataoka, I. Dispersed flow-I. Multiph. Sci. Technol. 1994, 8. [Google Scholar] [CrossRef]
- Tomiyama, A.; Zun, I.; Sou, A.; Sakaguchi, T. Numerical analysis of bubble motion with the VOF method. Nucl. Eng. Design 1993, 141, 69–82. [Google Scholar] [CrossRef]
- Brücker, C. Structure and dynamics of the wake of bubbles and its relevance for bubble interaction. Phys. Fluids 1999, 11, 1781–1996. [Google Scholar] [CrossRef]
- Adoua, R.; Legendre, D.; Magnaudet, J. Reversal of the lift force on an oblate bubble in a weakly viscous linear shear flow. J. Fluid Mech. 2009, 628, 23–41. [Google Scholar] [CrossRef]
- Aoyama, S.; Hayashi, K.; Hosokawa, S.; Lucas, D.; Tomiyama, A. Lift force acting on single bubbles in linear shear flows. Int. J. Multiph. Flow 2017, 96, 113–122. [Google Scholar] [CrossRef]
- Dhotre, M.; Deen, N.; Niceno, B.; Khan, Z.; Joshi, J. Large Eddy simulation for dispersed bubbly flows. Int. J. Chem. Eng. 2013. [Google Scholar] [CrossRef]
- Bothe, D.; Schmidtke, M.; Warnecke, H.J. VOF-simulation of the lift force for single bubbles in a simple shear flow. Chem. Eng. Technol. Ind. Chem. Plant Equipm. Process Eng. Biotechnol. 2006, 29, 1048–1053. [Google Scholar] [CrossRef]
- Dijkhuizen, W.; van Sint Annaland, M.; Kuipers, J. Numerical and experimental investigation of the lift force on single bubbles. Chem. Eng. Sci. 2010, 65, 1274–1287. [Google Scholar] [CrossRef]
- Ziegenhein, T.; Tomiyama, A.; Lucas, D. A new measuring concept to determine the lift force for distorted bubbles in low Morton number system: Results for air/water. Int. J. Multiph. Flow 2018, 108, 11–24. [Google Scholar] [CrossRef]
- Ma, T.; Santarelli, C.; Ziegenhein, T.; Lucas, D.; Fröhlich, J. Direct numerical simulation–based Reynolds-averaged closure for bubble-induced turbulence. Phys. Rev. Fluids 2017, 2, 034301. [Google Scholar] [CrossRef]
- Ogasawara, T. Surfactant effect on bubble migration toward the wall in upward bubbly flow. Prog. Multiphase Flow Res. 2006, 1, 9–16. [Google Scholar] [CrossRef][Green Version]
- Hayashi, K.; Tomiyama, A. Effects of surfactant on lift coefficients of bubbles in linear shear flows. Int. J. Multiph. Flow 2018, 99, 86–93. [Google Scholar] [CrossRef]
- Rastello, M.; Marié, J.-L.; Lance, M. Clean versus contaminated bubbles in a solid-body rotating flow. J. Fluid Mech. 2017, 831, 592–617. [Google Scholar] [CrossRef]
- Hessenkemper, H.; Ziegenhein, T.; Lucas, D. Contamination effects on the lift force of ellipsoidal air bubbles rising in saline water solutions. Chem. Eng. J. 2019. [Google Scholar] [CrossRef]
- Dhotre, M.T.; Niceno, B.; Smith, B.L.; Simiano, M. Large-eddy simulation (LES) of the large scale bubble plume. Chem. Eng. Sci. 2009, 64, 2692–2704. [Google Scholar] [CrossRef]
- Auton, T.; Hunt, J.; Prud’Homme, M. The force exerted on a body in inviscid unsteady non-uniform rotational flow. J. Fluid Mech. 1988, 197, 241–257. [Google Scholar] [CrossRef]
- Ishii, M.; Mishima, K. Two-fluid model and hydrodynamic constitutive relations. Nucl. Eng. Design 1984, 82, 107–126. [Google Scholar] [CrossRef]
- Paladino, E.E.; Maliska, C.R. Virtual mass in accelerated bubbly flows. In Proceedings of the 4th European Thermal Sciences, National Exhibition Centre, Birmingham, UK, 29–31 March 2004. [Google Scholar]
- Niemann, J.; Laurien, E. The Virtual Mass of Gas-Bubbles in a Liquid at High Void Fractions. In Proceedings of the Abstract submitted to: ERCOFTAC Conference on Particle-Laden Flows, Kappel, Switzerland, 3–5 June 2000. [Google Scholar]
- Koebe, M. Numerische Simulation Aufsteigender Blasen Mit und Ohne Stoffaustausch Mittels der Volume of Fluid (VOF) Methode; University of Paderborn: Paderborn, Germany, 2004. [Google Scholar]


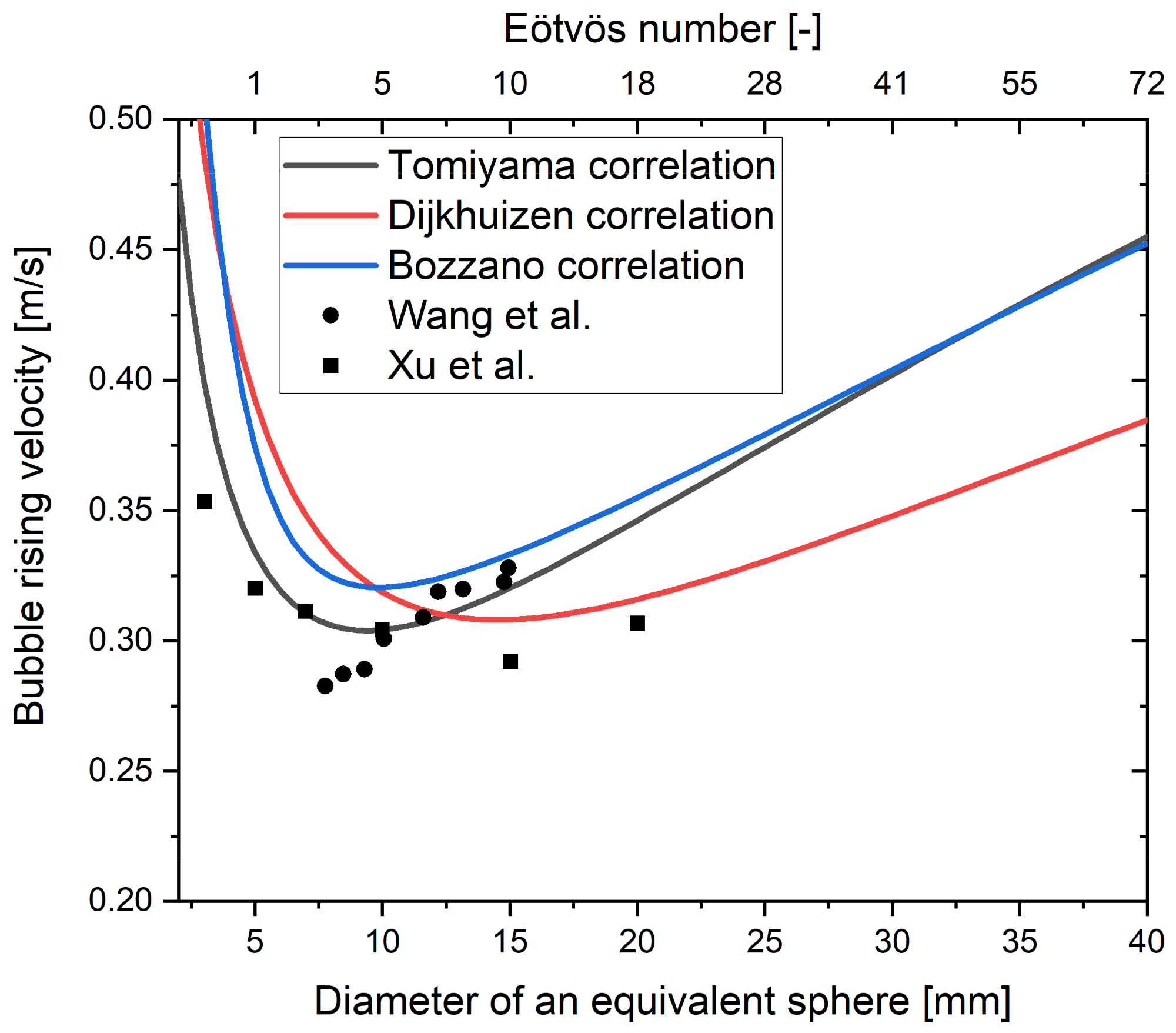
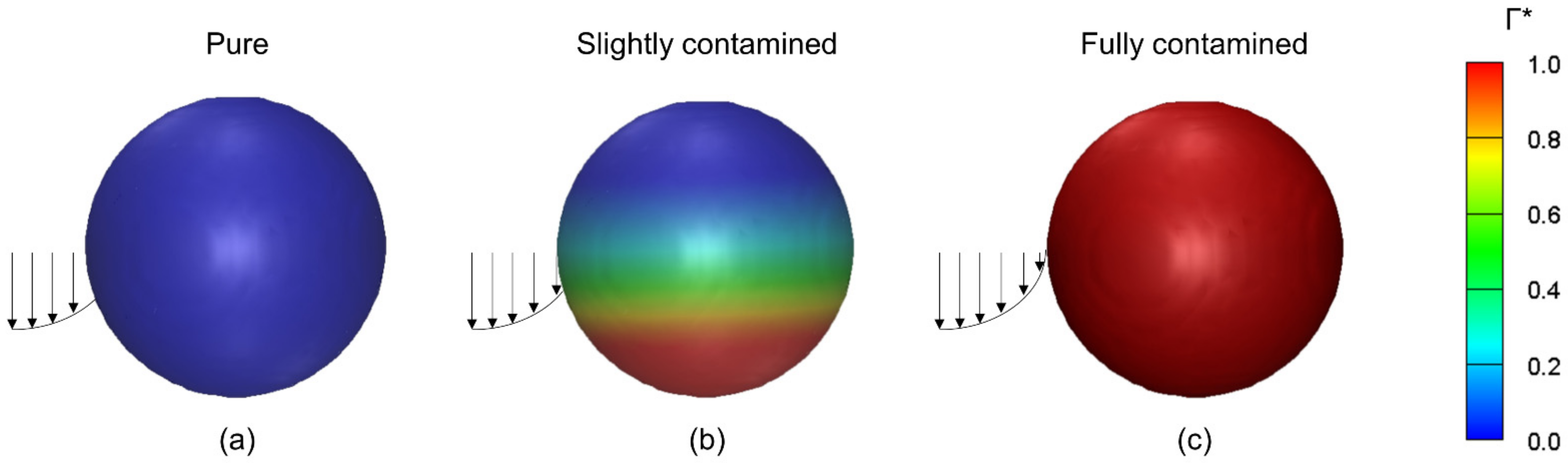
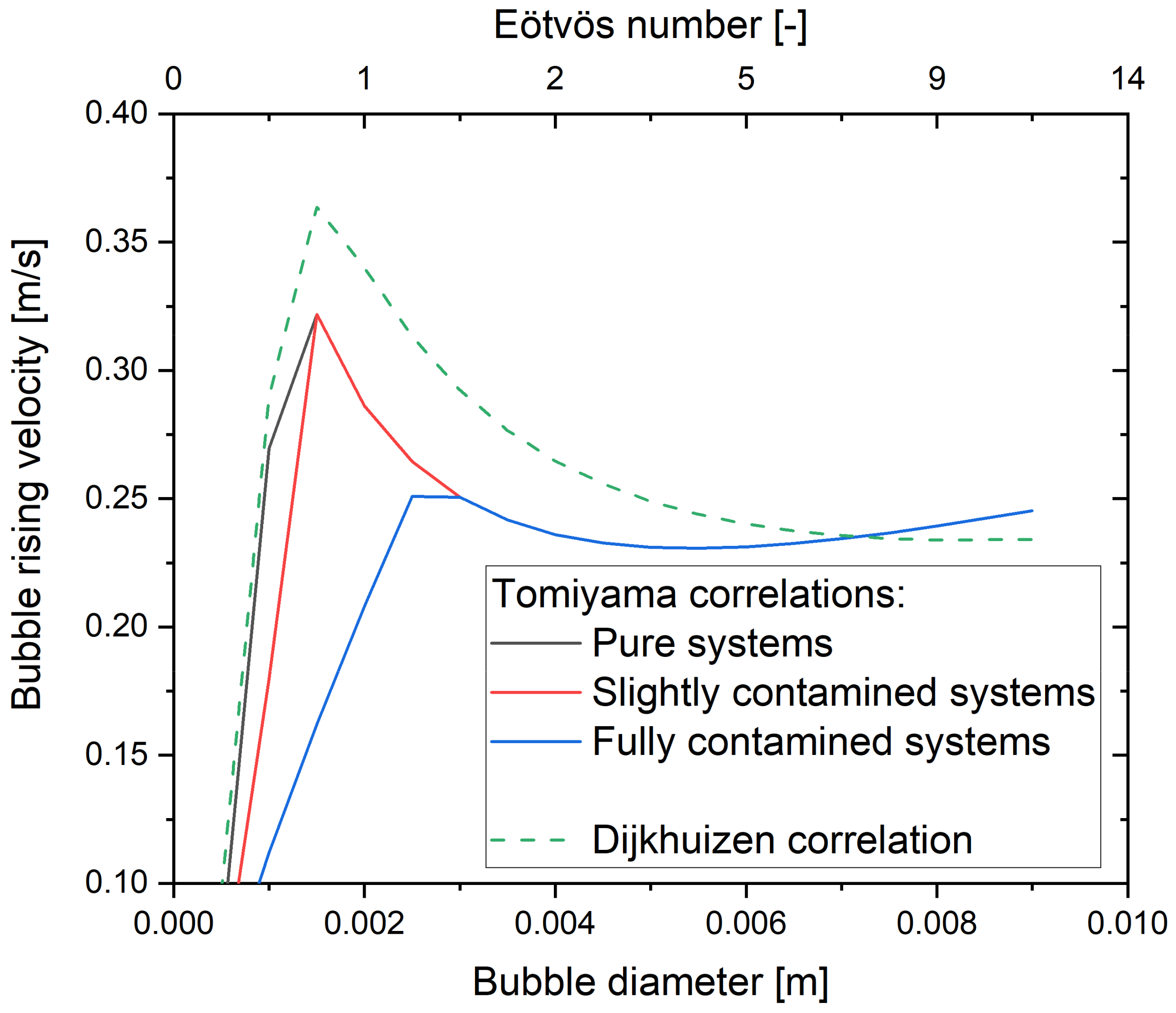
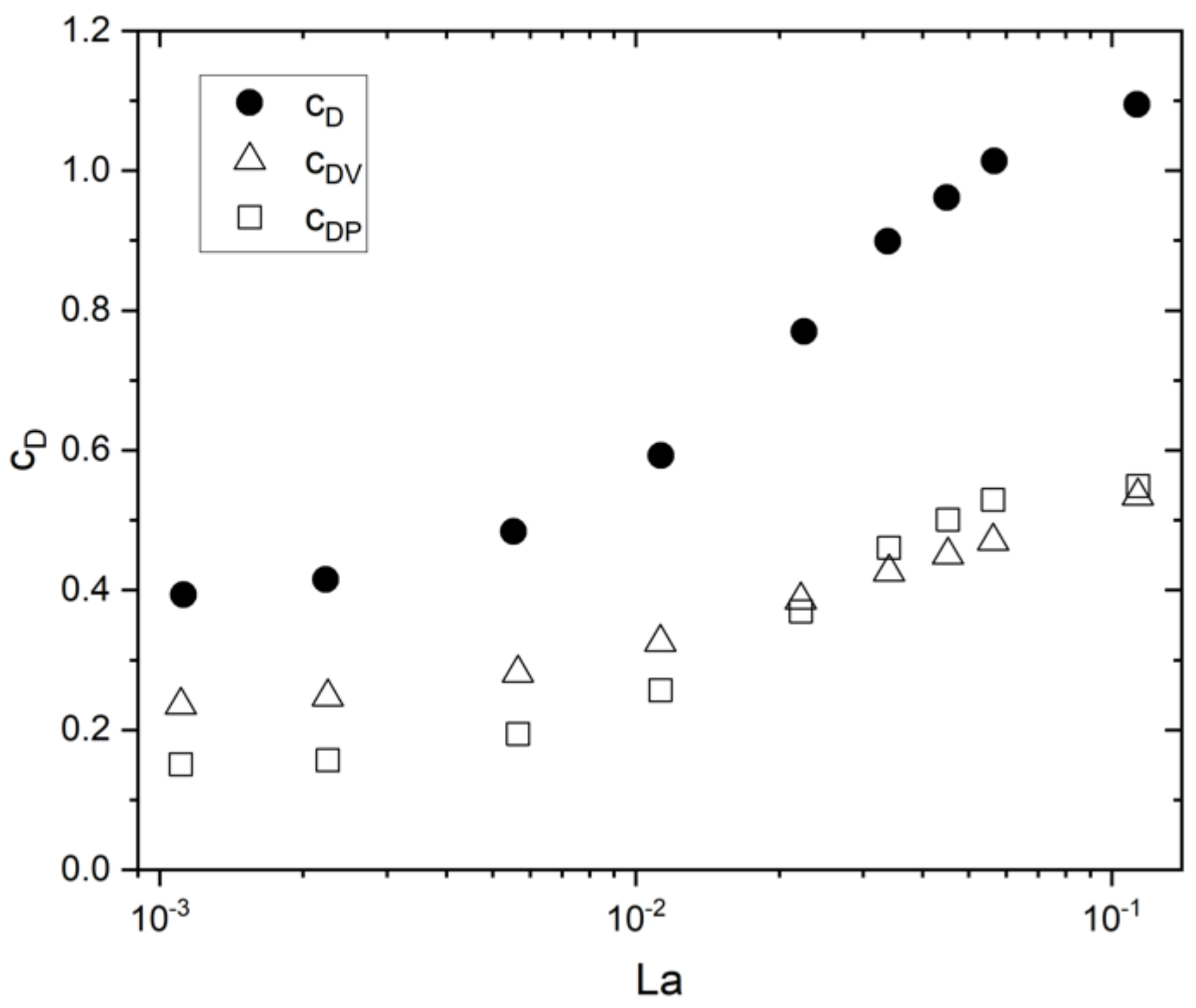
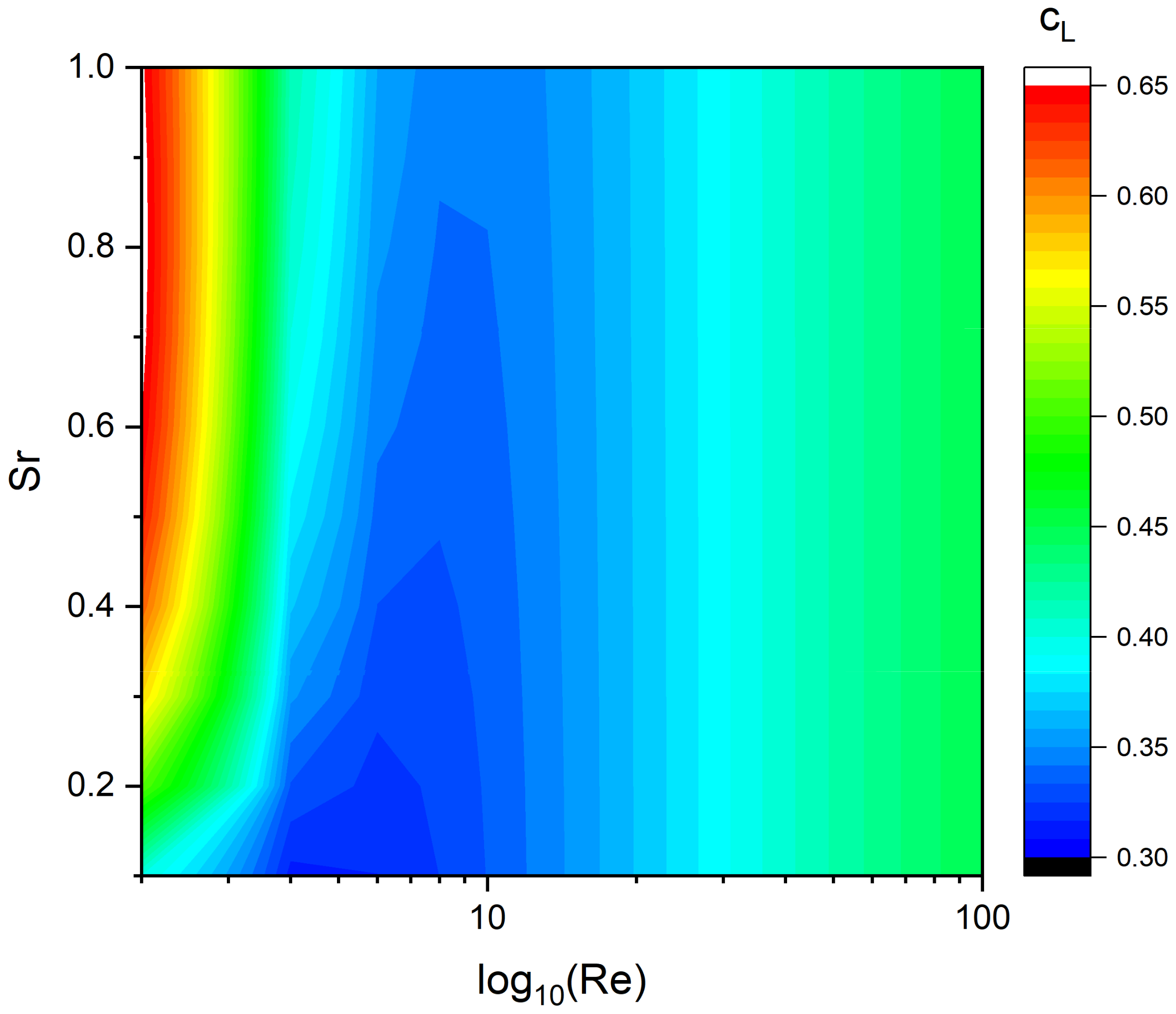
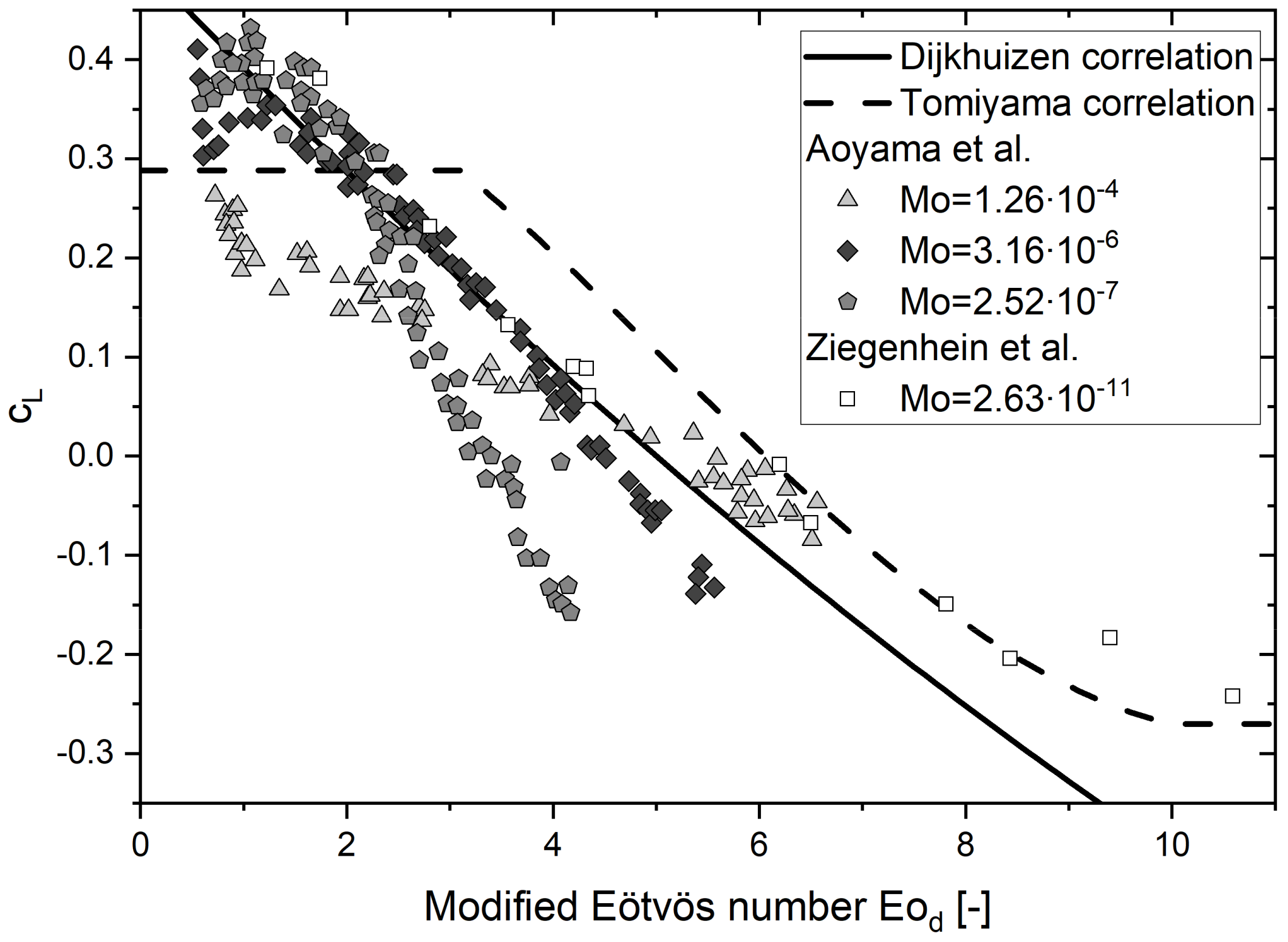
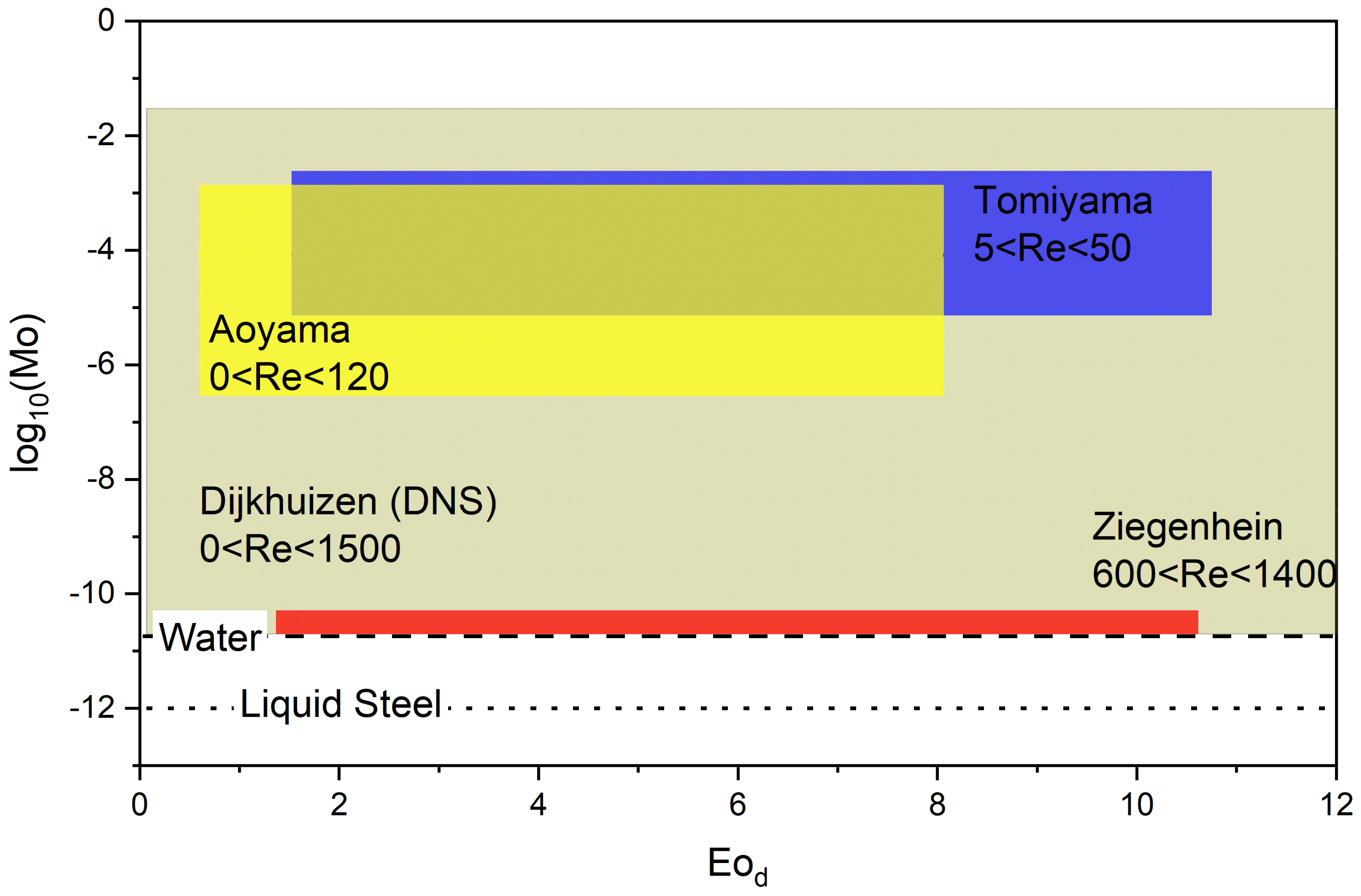
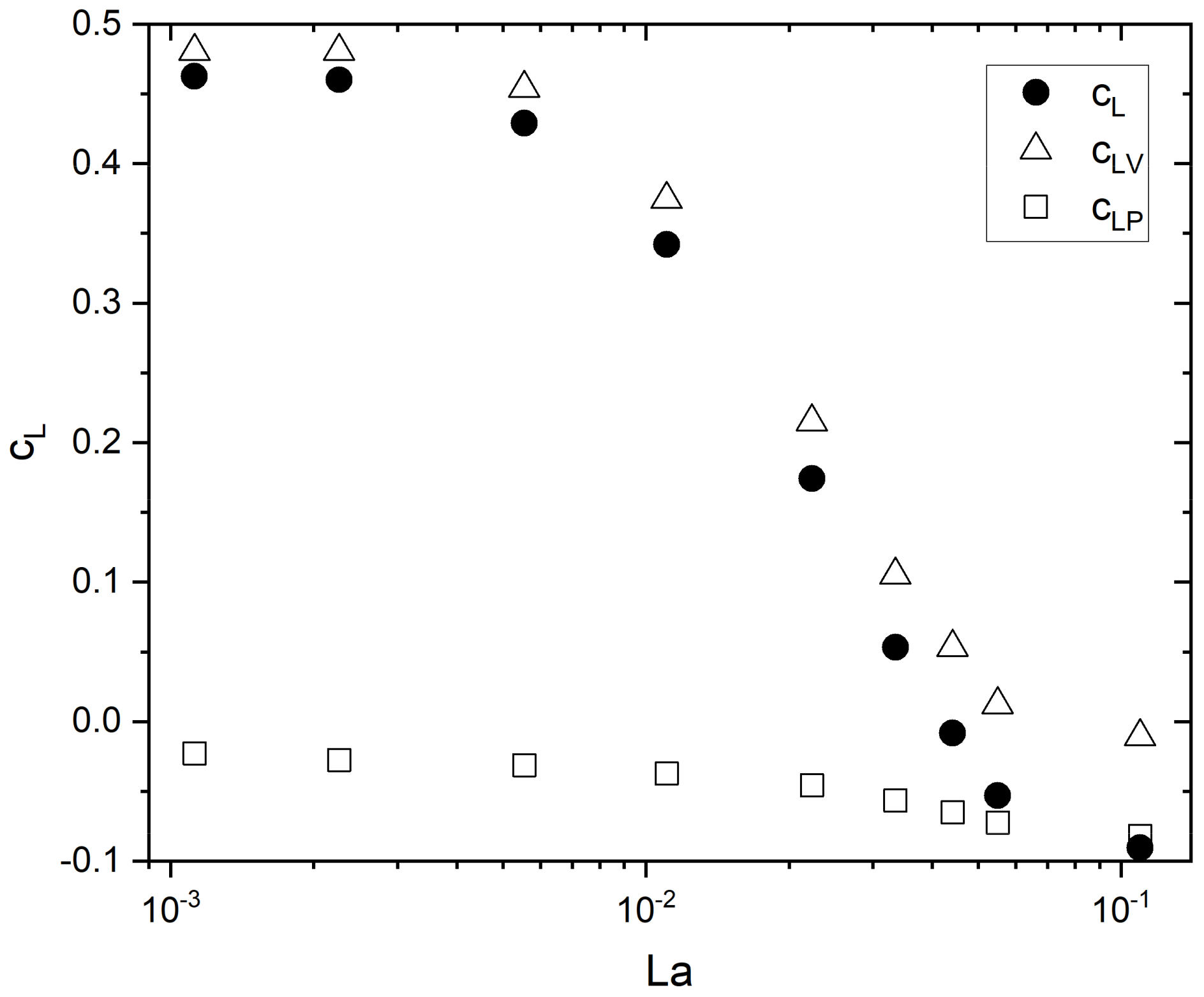
| System | Ref. | Equation | db,ladle |
|---|---|---|---|
| Analytical | [39] | 8.5 mm | |
| Single Nozzles | [47] | 15.8 mm | |
| [15] | 31.2 mm | ||
| [42] | 96.8 mm | ||
| Porous Plugs (heterogenous regime) | [64] | 13.5 mm | |
| [62] | 0.65 mm | ||
| Slot plug | [71] | 13.2 mm |
| System | m | (h/b)cap | Ta1 | Ta2 | c1 | c2 | c3 | c4 |
|---|---|---|---|---|---|---|---|---|
| 3Dcontaminated | 3 | 0.24 | 1 | 40 | 0.81 | 0.2 | 2.0 | 0.8 |
| 3Dpure | 3 | 0.24 | 0.3 | 20 | 0.81 | 0.2 | 1.8 | 0.4 |
| Fluid | Density [kg/m3] | Viscosity [Ns/m2] | Surface Tension [N/m] | log10 (Mo) |
|---|---|---|---|---|
| GaInSn | 6330 | 0.00234 | 0.585 | −12.6 |
| Steel | 6900 | 0.00506 | 1.5 | −12.6 |
| Mercury | 13,550 | 0.00155 | 0.487 | −13.4 |
| Silver | 9510 | 0.00389 | 0.92 | −12.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haas, T.; Schubert, C.; Eickhoff, M.; Pfeifer, H. A Review of Bubble Dynamics in Liquid Metals. Metals 2021, 11, 664. https://doi.org/10.3390/met11040664
Haas T, Schubert C, Eickhoff M, Pfeifer H. A Review of Bubble Dynamics in Liquid Metals. Metals. 2021; 11(4):664. https://doi.org/10.3390/met11040664
Chicago/Turabian StyleHaas, Tim, Christian Schubert, Moritz Eickhoff, and Herbert Pfeifer. 2021. "A Review of Bubble Dynamics in Liquid Metals" Metals 11, no. 4: 664. https://doi.org/10.3390/met11040664
APA StyleHaas, T., Schubert, C., Eickhoff, M., & Pfeifer, H. (2021). A Review of Bubble Dynamics in Liquid Metals. Metals, 11(4), 664. https://doi.org/10.3390/met11040664







