Abstract
The need for predicting pipeline service life and improving risk assessment relating to corrosion hazards requires establishing a correlation between the corrosion rate (CR) of pipeline steel and its coating condition, cathodic protection (CP) levels and surrounding soil conditions. This paper presents a systematic study of the CR of bare and coated—with and without a dent or holiday defect—X60 pipeline steel in simulated field environments. Three CP scenarios, i.e., no, optimized, and over-protection, were studied to cover a wide range of possible CP conditions that pipeline steel may encounter in the field. Two types of salt solutions (sodium chloride or sodium sulfate) with a variation of temperatures (10 °C, 40 °C, 65 °C) and pH values (2, 7, 12) were investigated to simulate different levels of soil corrosivity. A mathematical model was developed to reveal the impact of various parameters and their interactions on the CR of X60 steel. The coating condition was the most important factor. The individual effects of other factors including temperature, pH, salt composition and CP were not shown to be significant. Instead, the interactions between temperature and salt composition, and particularly the interaction between pH and CP appeared more important in determining the overall CR.
1. Introduction
Metal loss, especially external corrosion, accounted for a large percent (30.9%) of all pipeline incidents in Canada from 2010 to 2014 [1]. While pipeline metal loss predictions are important, they remain challenging due to the complexities inherent in the pipeline/soil system. For buried oil and gas steel pipelines, cathodic protection (CP) and protective coatings are used to mitigate external corrosion. However, when an adequate balance between the condition of the coating and the CP level cannot be established, external corrosion usually occurs, exposing the steel surface at coating holidays or under disbonded sections [2]. The rate of external metal loss is mainly controlled by the soil environment that the steel surface is in contact with. For this reason, soil corrosivity, which is determined by many physicochemical parameters such as soil resistivity, pH, temperature, and sulphate and chloride concentrations, is a crucial factor in evaluating the pipeline’s external corrosion process and the significance of the hazard. The correlation of external corrosion with the condition of the pipeline coating and applied CP levels, as well as the soil corrosivity is key to predicting the pipeline steel CR in the field.
Table 1 lists some representative corrosion studies on steels (X52, X60, X65, X70 and X80) that have been widely used for underground pipelines. As expected, an intact coating together with a CP application provides good protection of pipe steel (X52) for corrosion (CR ), whereas the existence of a holiday in the coating contributes to an increased corrosion risk at pH 8.2 at room temperature (RT), even though the CR is still negligible due to CP protection [3]. For bare X52 without CP protection in a similar electrolyte environment, CR increases to 0.023 mm/y [4]. Differences in microstructure (percentage of pearlite and ferrite phases) in various pipe steels, e.g., X60, X65 and X70, leads to a difference in the corrosion products formed, which can affect the corrosion processes and the CRs. X65 steel, which has the highest percentage of pearlite phase, shows the highest CR among the three steels [5]. For a given pipe grade, the literature is not consistent with respect to the relationship between corrosion resistance and soil pH. Two review papers published lately gave two different opinions. One considered pH as one of the most important factors influencing the corrosion of buried pipes when looking at the effects of the solution chemistry in short-term (months) laboratory experiments [6], while the other, by analyzing long-term (years) field corrosion data of buried pipes, argued that even though an extremely low pH may be an indication of corrosion, there is no direct relationship between pH and CR since many other factors contribute to CR [7]. These differing opinions imply the existence of complex interactions between pH and other factors, which is one of the aspects queried in the present study. CP is very effective in lowering the CR. For example, when studying the CR of bare X70 in a clay–sand soil (pH 4.8~5.6), it was found that CR decreased from around 0.2 mm/y to about 0.03 mm/y after applying CP for two days [8]. In addition to the effect of the pH and CP, temperature also plays an important role. In a study of X60 steel, the corrosion current density increased by nearly three times when the temperature increased from 20 °C to 60 °C [9]. It is also worth mentioning that the long-term corrosion behavior of pipe steel would differ from that observed in relatively short-term tests due to the formation of semi-protective corrosion products over time. One corrosion study of X80 steel compared its CR at 38 weeks and that after five years; CR decreased from 0.0902 mm/y to 0.0226 mm/y after five years buried in the soil. The corrosion products formed at 24 weeks consisted of two loose layers (the outer corrosion product was a mixture of FeO(OH) and FeCO3, and the inner product was composed mainly of FeCO3), while those formed after five years had only a single denser layer that was composed of FeOOH, 𝛾-Fe2O3, FeCO3, and a small amount of Fe3O4.

Table 1.
CR of different pipe steels with and without a coating.
The primary mathematical models used for predicting pipeline CR have been reviewed in [11]. A linear CR model characterized by a power function, as shown in Equation (1), is widely used to describe the CR represented by the loss of wall thickness [12].
where is the loss of wall thickness; is the time of exposure; are constants that depend on localized physicochemical conditions as well as the presence and effectiveness of any corrosion protection measures. For pitting corrosion, a non-linear CR Equation (2), a modified form of Equation (1), was proposed to correlate the maximum pit depth () with the exposure time () [13].
where is the pit initiation time, relies primarily on soil pH, redox potential, soil resistivity and dissolved ion concentration; and is depended primarily on pipe coating, pipe-to-soil potential, soil bulk density, and water content. There were regression equations developed for revealing the effects of different environmental variables (such as the temperature, relative humidity, time of wetness, and NaCl concentration, etc.) as well as their significance on the atmospheric CR of carbon steels [14,15]. For buried pipelines in a soil environment, using field data or experimental data, mathematical models were established for either general or localized corrosion [16,17,18] that considered many parameters, but these have limitations in demonstrating the significance of the parameters as well as the interactions between them. This information, however, is essential in identifying the location of the most significant corrosion threat and is therefore critical in pipeline integrity management. Moreover, the influence(s) of CP levels and the pipeline coating condition on the CR are not often included or well-explored. This is likely due to the difficulty and cost of obtaining a corrosion dataset that accounts for a large variability of soil and pipe parameters along pipeline sections in the field; or due to the significant number of experiments required to elucidate the influence of so many variables in a lab setting. As reflected in Table 1, the literature corrosion data are mostly for bare steel samples, with very few studies focusing on coated samples with or without a defect. This is because the techniques for detecting the CR (such as polarization tests) for bare steels are more established and widely accepted, and the CR of coated samples is very low and quite often negligible when CP is applied. However, as coating defects including holidays, dents, gouges, etc. are unavoidably formed during pipe manufacturing, transportation and construction processes, corrosion at and/or under the coating defects will take place. Increased corrosion may also occur in these defect areas when CP is inadequate, e.g., due to an interruption, over-protection, or under-protection of CP.
Elucidating the correlation between the corrosion of pipe steel and its coating conditions, CP levels and the surrounding soil conditions are obviously critical for service life prediction and risk assessment. Such information is nevertheless lacking in the literature, which motivates the present work. Here, a statistical and mathematical method, i.e., via the response surface method (RSM), was adopted to design multi-variable corrosion experiments. This method has been proved to be effective in conducting corrosion research with statistical analysis [19]. Furthermore, given the advantages of selecting and generating a diverse and representative set of tests, experimental design methods including RSM allow for evaluating the relative significance of all factors and their interactions with a reduced number of experiments [20,21,22]. By using this method, the influence of major factors including solution corrosivity, CP levels, and coating scenarios on the external CR of bare and fusion-bonded epoxy (FBE)-coated X60 pipeline steels (CSA Z245.1 Cat. 2) were studied. A wide range of soil pH (2 to 12) and temperature (10 to 65 °C) together with two common types of soil salts as well as various levels of CP and different coating scenarios were considered, aiming to provide improved extrapolation of laboratory testing conditions to field environments, which has often been identified as a limitation of mathematical models developed from simulated conditions in a laboratory [23]. The mathematical model generated in this study is for predicting the average CR of pipe steel, which gives insight into the significance of each individual factor as well as their interactions. This research provides data and knowledge to facilitate pipeline risk assessment. For instance, with the input of coating, CP and soil conditions, pipeline segments with the highest CR/risk may be identified, in part by using the mathematical model developed here.
2. Materials and Methods
2.1. Experimental Design
The RSM using an I-optimal design from Design Expert was used to plan the experiments. The independent variables selected in this study include:
- The solution corrosivity factor, related to solution temperature, solution pH, and salt composition;
- The treatment factor, related to the absence or presence of various levels of CP;
- The pipe steel condition factor, related to the coated (different coating scenarios) or non-coated (i.e., bare steel) condition.
Table 2 describes each independent variable. The temperature and solution pH are two numerical variables, having a range from 10 °C to 65 °C and pH 2 to 12, respectively. The salt composition refers to either using NaCl or Na2SO4 solution in the test and is a categorical variable. The CP and coating are the two other categorical variables since they are not continuous numeric but discrete factors. A total of 42 experiments were generated using a quadratic model, which are listed in Table 3. The testing period was set to four-weeks (28 days). The CRs were collected by conducting the experiments in a random order of run numbers. A mathematical model was established, and is discussed below, to describe the relationship of CR with all of the factors that were studied. Six more tests (X1-X6 in Table 3), including applying an under-protection CP potential of −0.4 V vs. Ag/AgCl as well as a temperature that was periodically on and off (to model stoppage in the pipe flow), were conducted to consider more possible field conditions and to support model validation.

Table 2.
Independent parameters studied (either numerical or categorical type).

Table 3.
Levels and description of variables in actual form.
2.2. Expriemental Procedure
2.2.1. Weight Loss Tests and Electrochemical Tests for Bare Steel
Weight loss tests based on ASTM G31 [24] were performed to obtain the CR of the bare steel samples. All the bare steels were ground with 1200 grit emery paper and washed using deionized water. A jacketed glass cell connected to a water bath was used to conduct the tests at different experimental temperatures. In each test solution, three samples (each with an exposed area of 1.5 cm2) were simultaneously immersed and tested for four weeks to obtain an average CR (Figure 1a). One exception was for run #35, in which the CR was so high that four-week testing led to complete dissolution of the sample. Therefore, a four-day test was applied to obtain its CR. For samples with CP, a power supply was used to provide a constant negative current to the samples. During the tests, CP was checked/adjusted daily or every other day to ensure it was ±50 mV around its set values (0.4 V, 0.8 V, or 1.6 V vs. Ag/AgCl reference electrode (+0.199 V vs. NHE)). This is because the changes in steel surface composition/morphology and/or the electrolyte resistance during the tests can alter the applied potential to the sample. A graphite rod was used as an anode.
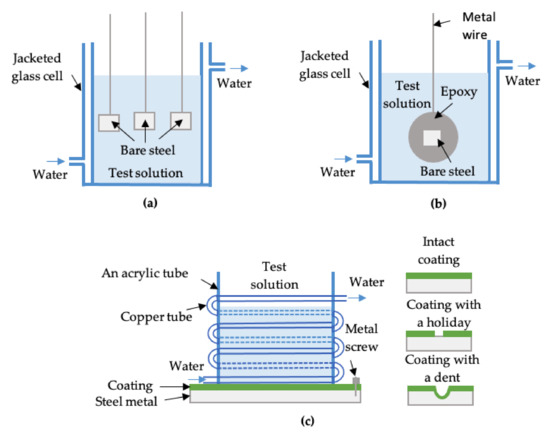
Figure 1.
A schematic of (a) 1.5 cm2 bare electrodes for weight loss tests; (b) a 1 cm2 bare electrode for electrochemical tests (EIS); and (c) a coated X60 panel sample for corrosion immersion and electrochemical tests.
Another group of immersion tests with electrochemical impedance spectroscopy (EIS) was carried out separately from the weight loss tests and was carried out on bare samples with a 1 cm2 surface area that were mounted in epoxy (Figure 1b). EIS was performed periodically by applying an AC ± 10 mV peak-to-peak signal in the frequency range of 100 kHz to 100 mHz. A three-electrode setup was used, i.e., the bare steel as the working electrode, a graphite rod as the counter electrode, and a double junction Ag/AgCl reference electrode. A constant potential was applied during the EIS tests. For samples without CP protection, this constant potential was the open circuit potential. For samples with CP, the constant potential was the applied CP potential. All electrochemical experiments were carried out using a potentiostat (VersaSTAT 3, Princeton Applied Research). It should be noted that samples tested at CP potentials were disconnected from the power supply during the EIS tests, but the potentiostat then served as the power source.
For both the weight loss and immersion/electrochemical tests, the base solution was 0.01 M NaCl or 0.01 M Na2SO4, with its pH initially adjusted by either 0.03~0.3 M HClO4 or 0.1~1 M NaOH solution. pH 2, 7, and 12 were studied to cover a wide spectrum of pH conditions that pipeline steel might encounter in the field. For example, in some areas, such as in the Rocky Mountains in British Columbia, pipelines are sited near acid-generating rocks (e.g., pyrite or other sulfides), where the pH can be as low as 2; pH 7 is the most representative of pipeline soil; in other areas, such as salt lakes in north-west China, highly saline soil is deemed as a risk to the pipeline integrity [25]. For bare samples as well as coated samples with a holiday, CP application results in proton consumption through hydrogen evolution in acidic electrolytes while hydroxyl ions are continually produced through water electrolysis in neutral and alkaline electrolytes. Both reactions lead to an increase of pH. For some of the bare steel samples tested, solution acidification was observed during the immersion tests, leading to a decrease of pH. In order to maintain the initial pH, it was adjusted either manually or by a pH controller. In this way, the electrolyte pH was adjusted around its initial value (0.7/0.4 to pH 2; 0.7/2 to pH 7 and 0.5/2 to pH 12).
2.2.2. Electrochemical Tests for Coated Steel
For FBE coated X60 steel panel samples (10 cm × 10 cm), the coating surface was wiped with alcohol and then deionized water to remove any grease and dirt. An acrylic tube was attached on the cleaned coating surface to contain the solution for conducting electrochemical tests. The coated samples were in three different conditions, i.e., intact coating, coating with a holiday (6 mm in diameter), or coating with an indent (about 1.2 mm in depth). Figure 1c shows a schematic of coated (panel) samples undergoing immersion and electrochemical tests. A coiled copper tube attached on the outside of the acrylic tube was connected to a water bath for testing of coated samples at 10 °C. Hot plates were used for coated samples with experiments running at temperatures of 40 °C and 65 °C. Rubber stoppers were used as lids on the top of the electrochemical cells to minimize water evaporation at high temperatures. The base solution preparation and pH adjustment was carried out in the same way as that used for the bare samples.
The corrosion behavior of coated X60 was monitored and studied using electrochemical noise measurement (ENM) and EIS. ENM with a single cell arrangement as introduced in [26] was applied to assess the corrosion resistance. During the tests, a two-electrode setup was used, which was comprised of the working electrode (coated pipe steel panel sample) and a double junction Ag/AgCl reference electrode serving as both the reference and counter electrode. The electrochemical noise potential (ENP) was measured by recording the sample potential against the reference electrode under the open circuit condition. The noise resistance was calculated in accordance with Ohm’s law by Equation (3), where and are the standard deviations of potential and current fluctuations.
The current density was estimated by using Equation (4), the Stern–Geary coefficient , for most cases, was assumed to be 0.026 V for active and 0.052 V for passive corrosion of galvanized rebar in concrete [27]. For the coated samples, was taken as 0.052 V. The CR was then calculated by Equation (5) and was taken as an average value of that measured at the start, middle and last day of the four-week testing. is the atomic weight, is the electrons transferred, is the Faraday constant, and is the density. It should be noted that since is the resistance of the coating instead of the steel substrate directly, the calculated reflects the corrosion resistance of the coated samples, but may not accurately represent the true CR. Thus, these measurements should be considered qualitative and indicative rather than absolute.
EIS was also carried out on the coated panel samples, similar to that for bare steel samples (i.e., measured either at open circuit potential or CP potential that is consistent with the immersion testing conditions), except that the frequency range was from 100 kHz to 10 mHz. During the immersion tests, water uptake occurs in the coatings due to the presence of hydrophilic hydroxyl groups [28] and was estimated from the capacitance of the coating using Equation (6) proposed by Brasher and Kingsburry [29].
is the volume fraction of water in the coating, is the capacitance of the coating after immersion time t and is obtained from impedance measurements at 10 kHz, and is the dry coating capacitance, which is generally obtained by extrapolating t to zero.
3. Results
A mathematical model was established using the CR data obtained from either the weight loss tests for bare steel samples or ENM tests for coated steel panel samples. An ANOVA analysis was applied to check the significance and accuracy of the model developed, as well as to reveal the relative significance of each individual factor and the interactions between them.
3.1. Statistical Model Based on the CR Data
The CRs of both bare and coated samples are summarized in Table 3. Due to the wide range of CR (10−8 to 102 mm/y), a power transformation of CR was applied. By using a modified quadratic model, a general mathematical equation was fitted to the data and is presented in Equation (7). As listed in Table 4, the value of coefficients , , and in the equation depends on the coating condition, salt type, and CP levels, respectively. Applying this equation, CR can be estimated for any pH from 2 to 12.
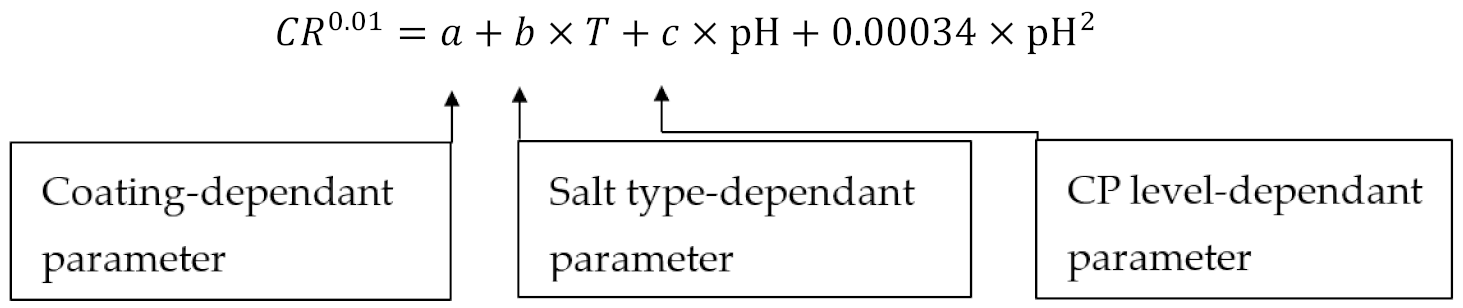


Table 4.
The coefficients in the established mathematical equation.
It should be noted that in this model, the time effect cannot be reflected since all the CR data were obtained after a constant testing time, i.e., 28 days, with one exception for run #35, which was explained in Section 2.2.1. For bare samples and coated samples with a defect, discrepancy in the CR between short-term (months) and long-term (years) tests should be expected as a result of, e.g., changes in corrosion products. Furthermore, the present model has limitations in that it predicts the CR at only one salt concentration of 0.01 M and through a limited temperature range from 10 °C to 65 °C.
3.2. ANOVA Analysis
The corresponding ANOVA for this model is shown in Table 5. The model F-value of 9.27 implies the model is significant. There is only a 0.01% chance that an F-value this large could occur due to noise. p-values less than 0.05 indicate that model terms are significant. The square of the correlation coefficient, R2, and adjusted R2 are 0.7933 and 0.7078, respectively, which are high compared to those reported from quadratic regression equations developed for modelling the atmospheric corrosion of carbon steels [14]. The model explains 79.33% of the dependent variables. In addition, the adequate precision, which means the signal to noise ratio is 11.414 (>4 is desirable), indicates an adequate signal. In this case, only E-coating is considered as a significant model term. This result is not surprising as E-coating is expected to be the most critical and determinant factor. The two endpoints of the broad CR range presented in Table 3, i.e., 1.81 × 10−8 and 30.87 mm/y, correspond to a sample with an intact coating versus bare steel. When statistically evaluating other factors along with the E-coating factor, the calculated p-values of factors other than the E-coating do not meet the 0.05 rule of thumb. On the other hand, from the p-values, the relative significance of individual factors as well as their interactions can be indicated. From Table 5, other than the E-coating, the A-Temp, with a p-value of 0.08, is the most influencing factor, followed by the D-CP (p-value of 0.15). There are two principles for choosing these model items: (1) all five individual factors were included in the model, as they all play roles in CR determination; (2) model items in the quadratic model were reduced to ensure that the generated model is significant and the lack of fit is not significant, and there is a good correlation between the CR predicted by the model and obtained by the experiments. The final model interaction terms include:

Table 5.
ANOVA test for modified quadratic model.
- AC—interaction between temperature and salt composition
- BD—interaction between pH and CP
- B2—a quadratic term of pH, which models/predicts the curvature on a response surface.
The adequacy of the regression model was checked using the normal probability plot of the studentized residual to confirm the normal error distribution (Figure 2a), and the studentized residuals versus predicted values to check for constant variance (Figure 2b). Figure 3 shows the predicted response values versus the actual response values for designed runs 1–42 (displayed in black dots). Using the mathematical model established from the results of these 42 runs, the predicted CR values of extra test points (X1–X6) were plotted as orange dots, which present a consistent trend with the model.
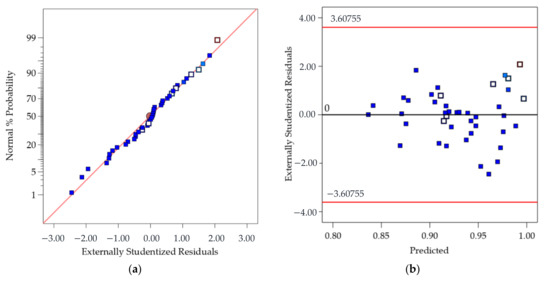
Figure 2.
(a) Normal probability plot of the studentized residuals to check for normality of residuals (the approximately linear plot allows to assume that the error/residual terms are normally distributed, and the estimates/predicted values are unbiased or on average correct); and (b) Studentized residuals versus predicted values to check for constant variation (a random distribution should be expected and so the model predicts values higher and lower than the actual with equal probability).
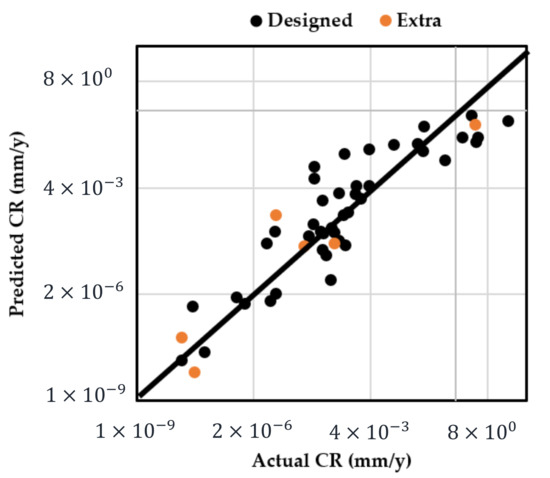
Figure 3.
Predicted CR using the established mathematical model vs. actual measured CR (designed points: runs 1–42; extra test points: runs X1–X6 in Table 3).
4. Discussion
This section focuses on discussing the model developed above from two aspects, i.e., model explanation and model application. The former relates the model analysis to the experimental data and highlights some important experimental findings. The latter points out typical field conditions in which the model can be applied and gives prediction on the external CRs.
4.1. Model Explanation with Experimental Data and Results
As seen in the above ANOVA analysis, in addition to each individual factor, the interaction between the temperature and salt composition (AC) and between the pH and CP (BD), as well as the squared pH (B2) were identified as the influencing quadratic terms. This can be well-explained via an analysis of the experimental data. As revealed in the following discussion, the AC interaction affects the solution conductivity, the BD interaction determines the cathodic reaction process and influences the overall CR, and B2 reflects the higher CRs observed at the two endpoints of the pH range studied, i.e., pH 12 and pH 2, when compared to that tested at pH 7. In order to provide an intuitive overview of CR obtained at various conditions, CR data presented in Table 3 are plotted as CR maps for bare (Figure 4) and coated (Figure 5) X60 samples, respectively.
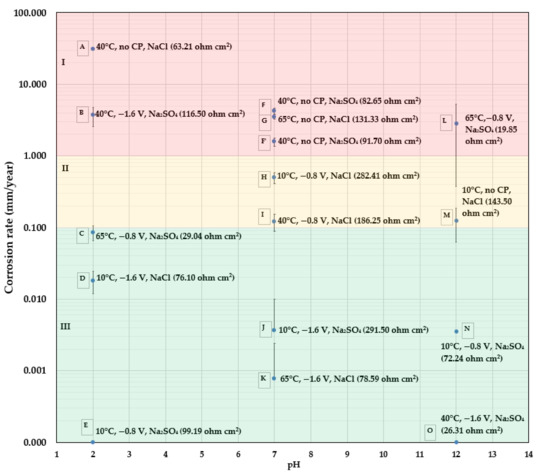
Figure 4.
CR map of bare X60, small electrode samples, under different test conditions using the weight loss data (the data in the bracket is the electrolyte resistance estimated from EIS tests).
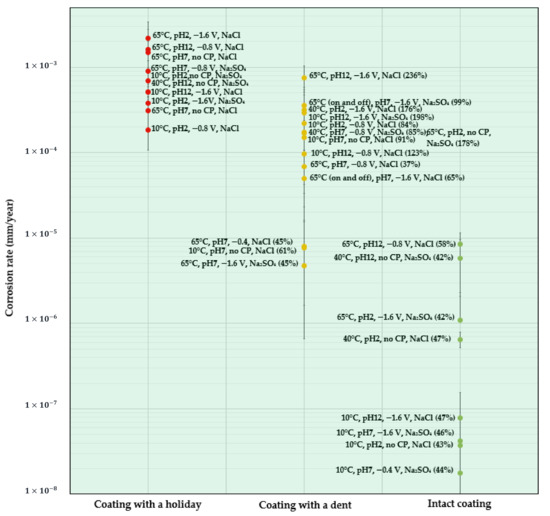
Figure 5.
CR map of coated X60 steel under different test conditions (the data in brackets is the volume of water absorbed by the coating after the 28-day test).
In Figure 4, the CR of bare metals is presented as a function of pH. Besides each tested point shown in blue, the testing temperature, CP value, type of salt and the electrolyte resistance are presented in parentheses. This CR mapping is divided into three regions: region I, in red, where the CR is above 1 mm/y; region II, in yellow, where the CR is from 0.1 mm/y to 1 mm/y; and region III, in green, where the CR is below 0.1 mm/y; 0.1 mm/y is considered the maximum allowable CR for carbon steel heat exchanger tubes for cooling water in the oil and petroleum industries [30]. The maximum allowable CR for a pipeline could be lower, depending on the thickness of the pipe as well as its design life.
- At pH 7, that which is most representative of “normal” pipeline soil, it is interesting to observe that the CR data fell into the three regions based on the level of CP. All three samples (F, G, and F’) without CP protection appeared in region I (CR > 1 mm/y); two samples (H and I) having a CP of , were located in region II (1 mm/y > CR > 0.1 mm/y); and the other two samples (J and K) were in region III with a negligible CR due to a CP of It is reiterated here that these CRs are based on mass loss.
- At pH 2, the highest CR (30.87 mm/y) is found in sample A, which was tested without CP, and at a temperature of 40 °C. At the same temperature of 40 °C (sample B), with a high CP of , there is still an unacceptably high CR of 3.69 mm/y. Comparing to sample B: (1) sample C, which has a higher testing temperature of 65 °C, a higher solution conductivity, but a lower CP level of , shows a much lower CR of 0.09 mm/y; and (2); sample D, which has the same CP of but has a lower temperature of 10 °C, also shows an acceptable CR of 0.02 mm/y. One indication from the result is that the presence of both a high CP of and a temperature higher than 10 °C in acidic solutions led to the high CR observed in sample B. A high CP of , i.e., an overprotection, results in a large amount of hydrogen produced from the acidic solution and from the cathodic reaction (). CP that is more negative than vs. Cu/CuSO4 ( can cause problems including hydrogen-induced cracking (HIC), hydrogen embrittlement (HE), and stress corrosion cracking (SCC) [31]. Though it is normally acknowledged that hydrogen-related attack does not cause significant material loss—rather, it makes the material more susceptible to mechanical failure [32]—there seems to be a correlation between the large amount of hydrogen produced at a high temperature and the observed high CR based on the tested results. The reasons for this are not yet clear and need more detailed research.
- At pH 12, without CP protection, sample M has a CR of 0.124 mm/y at a low temperature of 10 °C. However, the highest CR of 2.86 mm/y was measured for sample L, which had a CP of and a high temperature of 65 °C. The test solution also had the lowest electrolyte resistance/highest electrolyte conductivity. When the testing temperature was 10 °C, at the same CP level of , the CR of sample N was reduced (0.004 mm/y). An increase of the CP level to also appeared to be very effective at depressing the CR to a negligible value, as seen for sample O, for which the testing temperature was 40 °C. The comparison among sample L, N, and O implies that in a hot alkaline environment, a moderate CP level of is not sufficient to protect steel from corrosion. Furthermore, if considering coated samples with a holiday (exposed steel substrate area), it is well-known that an application of CP causes an alkaline environment at the coating/substrate interface, leading to a loss of adhesion at the interface and causing cathodic disbondment. The high pH environment is supposed to protect the exposed substrate from corrosion. However, based on the present result on bare steel samples, if the coated sample is tested at a high temperature of 65 °C with a CP of , both the exposed holiday area and the substrate underneath the disbonded coating may still experience corrosion. This is exactly what was found in holiday samples, as discussed in Figure 5.
Figure 5 shows a CR map for all the coated samples. Since the type of coating defect influences the CR the most, the CR of the coated samples is presented as a function of the coating scenarios. As can be seen, the coated samples all had acceptable CRs for the studied conditions and so the background map color is green.
- Coatings with a holiday: due to the exposed metal surface, which is similar to the bare steel samples, holiday samples show relatively high CRs. The top three samples shown in Figure 5 are those tested at a high temperature of 65 °C and at pH 2, pH 7, and pH 12. The one tested at pH 2 showing the highest CR is accompanied with a high CP of , followed by that tested at pH 12 with a CP of , and then the one tested at pH 7 with no CP. It can be found that these three conditions are predicted to result in the highest CR at each pH condition for bare metal samples. In other words, the CR results for holiday samples are consistent with that observed for bare steel samples, which further supports the proposal of two quadratic items in the mathematical model, i.e., temperature–salt type and pH–CP interactions.
- Coatings with a dent: most of the studied samples with a dent (yellow circles) are in the region where 5 × 10−5 < CR < 1 × 10−3 mm/y, having comparable CRs to the holiday samples, indicating a similar corrosion resistance of the coating with these two kinds of defect. No particular trend in CR can be found in the dented samples with respect to temperature, pH, or CP. On the other hand, if looking at the volume of water () being absorbed in the coating (the data in the parentheses), it is found that, in general, when is higher than 65%, the CR is above 1 × 10−5 mm/y; when is below 65%, the CR is less than 1 × 10−5 mm/y. It is also interesting to observe that dented samples immersed in solutions with pH 7 show a relatively low water uptake (61% on average), while higher water absorption was observed in samples tested at pH 12 (186% on average) and pH 2 (146% on average). Compared to neutral solutions, a highly alkaline environment was reported to promote the absorption of moisture in FBE coatings, and with the presence of defects, the penetration of aggressive ions can be facilitated, contributing to increased CR [33]. The present work supports this statement and further shows that an acidic environment also can accelerate the process of water absorption in FBE coatings with the presence of defects.
- Intact coatings: due to a good protection from the coating, the CRs for all the intact coating samples (green circles) are extremely low and less than 1 × 10−5 mm/y. for these samples are all below 65%. Among all the factors, the temperature seems to be the most critical, which is consistent with the ANOVA analysis. Negligible CRs on the order of 10−8 were found for the four samples tested at 10 °C. Increasing the temperature accelerates the CR by one to two orders of magnitude.
4.2. Model Application/Prediction
Since coatings and CP are commonly applied for in-service pipelines to protect them from corrosion, a prediction of the combined effect of coating and CP using this model is of primary interest. In Figure 6, CR as a function of both coating and CP at different pH conditions is shown.
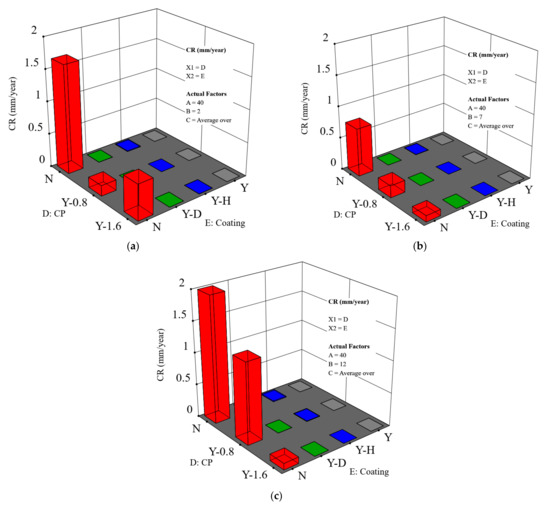
Figure 6.
CR as a function of both applied CP level and coating scenarios: (a) pH = 2; (b) pH = 7; and (c) pH = 12. The temperature is 40 °C and the salt composition effect was averaged for that of sodium chloride and sodium sulfate (A is the temperature, B is the pH, C is the salt composition, D is the CP level and shows as abscissa X1, and E is the coating scenario and shows as abscissa X2).
- The effect of coating
As expected, CR decreases in the order: holiday sample > dented sample > intact coating. It is noteworthy that the CR of dented and holiday samples are in a similar order of magnitude (Figure 7 shows more details on this).
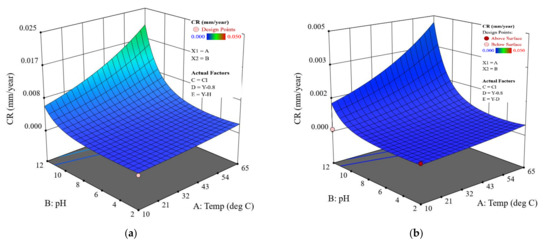
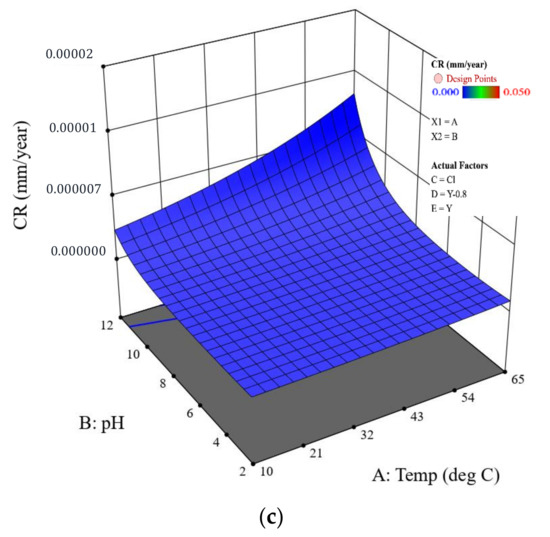
Figure 7.
CR predicted by the model for the coated samples with different scenarios: (a) coating with a holiday, (b) coating with a dent, and (c) intact coating. The CP is fixed at , and the salt is sodium chloride.
- The effect of CP
It is shown that the effect of the CP depends on the pH level. This is primarily relevant for the bare steel samples. In Figure 6a, when the pH is 2, a higher/more negative CP level of does not provide extra protection, but instead leads to a higher CR as compared to a CP level of This is evidenced by comparing sample B and sample C, shown in Figure 4. Hydrogen damage could be a reason, which indeed requires more in-depth study. At pH 7 and pH 12, the major cathodic reaction is oxygen reduction. An increased CP level results in an improved corrosion protection. For example, at pH 7 (Figure 6b), a CP of brings down the CR to an acceptable level, i.e., less than 0.1 mm/y. At pH 12, an increased temperature requires an enhanced CP level to ensure corrosion protection. Especially when the temperature is higher than 40 °C, a CP level of is needed to maintain an acceptable CR (Figure 6c). For bare steels with an application of CP, the model predicted value is higher overall than the measured value.
Considering coated pipelines that are protected by a CP of −0.8 V (i.e., widely adopted in the field), based on the coating scenarios, the established mathematical model offers a prediction of their CRs as a function of the temperature and pH in a given salt composition environment. Figure 7 shows the details. It is obvious that all the coated samples protected at −0.8 V exhibit the same surface response pattern; i.e., at a given temperature, the highest CR appears at pH 12, as evidenced by the poorest resistance of FBE coating to moisture and ion absorption in an alkaline environment. At pH 12, the CR increases more rapidly with increased temperature, resulting in the highest CR being located at 65 °C. The CR range for the dented samples is similar to that of the holiday samples, which is consistent with the experimental results (Figure 5). The model result further implies that these two types of coating defect should be treated with the same level of attention. It should also be noted that CR predicted by the model for both the holiday and dented samples protected at −0.8 V is higher than what is observed. For example, the highest CR for the holiday sample in Figure 7a is predicted to be ~0.02 mm/y at 65 °C, pH 12, while the actual measured value is 0.0002 mm/y, two orders of magnitude lower. For samples with an intact coating, the predicted highest value is close to the measured value, i.e., 0.000011 vs. 0.000009 mm/y. For pipelines operated at a low temperature of 10 °C, both the experimental and model results show acceptable/negligible CR over a wide range of pH conditions. For the eight coated samples tested at pH 7, i.e., the most relevant pH in the field, the difference between the predicted and measured CR is shown in Figure 8. For the one intact coating sample and two holiday samples, the predicted CR values were in the same order of magnitude with the measured CR values; i.e., the model provides a very good prediction. For the coating samples with a dent, the difference between the predicted and measured CR was within one order of magnitude (approximately within a factor of 8.4) for the three tested samples, which is not significant considering the CR range for these dented samples was from 0.0001 to 0.00001 mm/y. Further, the model provides a relatively conservative CR prediction for coating samples with a dent.
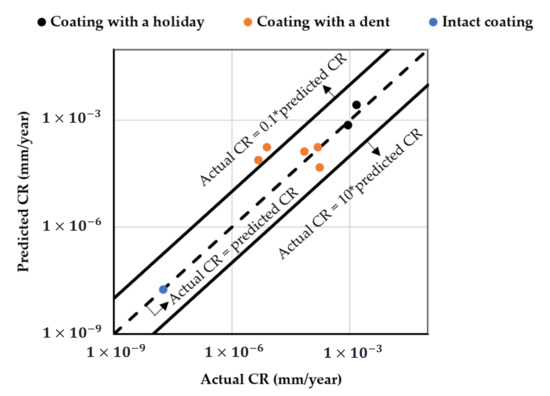
Figure 8.
Predicted CR vs. Actual CR for coated samples tested at pH 7.
As shown in the experimental design, the salt concentration was fixed at 0.01 M, which is a commonly used value to simulate the soil environment [34]. However, the salt concentration could be influenced by many factors such as the use of salt brine deicer in the winter, which can lead to an increased CR of pipeline steels with degraded coatings [35]. One limitation of the developed model is that it does not provide CR prediction of buried pipelines in soil environments with varied salt concentrations. Furthermore, since all the CR results were based on 4-week tests, this model has limitations in predicting long-term corrosion behavior. As shown by the experimental results, the interactions between the temperature and salt composition, as well as that between pH and CP, appeared important in determining the overall CR; further experiments designed for emphasizing these two interactions are expected to better train the established model.
5. Conclusions
The RSM using an I-optimal design was used to study and model the influence of five factors (temperature, pH, salt composition, CP, and coating scenarios) as well as their complicated interactions on the CR of both bare and coated pipeline steel samples. A mathematical equation was established to predict the CR under different conditions. The selection of a wide range of testing temperatures and pH levels provides improved extrapolation from laboratory tests to field conditions. Moreover, the incorporation of various levels of CP as well as the consideration of different types of coating defects including dent and holiday enabled the model developed herein to offer informative predictions for relevant field conditions. This model accurately reflects the CR trend for coated samples with different damage scenarios: holiday sample CR > dented sample CR > intact coating CR. The differences between the measured and predicted CR values depend on the testing conditions. For coated samples tested at pH 7, i.e., the most relevant cases in the field, the predicted CR values for the holiday samples and intact coating samples were within a factor of 0.9 to 1.8 times the measured CR values, i.e., the model provides a very good prediction. For coating samples with a dent, the predicted CR values were largely within an order of magnitude of the measured values. A statistical analysis of the results shows that the condition of the coating is the most important factor, which is as expected. The individual effect of other factors including the temperature, pH, salt composition, and CP were not shown to be significant. Instead, the interaction between temperature and salt composition that affects the solution conductivity, as well as the interaction between pH and CP that determines the cathodic reaction processes, appeared to be more important for determining the overall CR.
Author Contributions
Conceptualization, M.X. and E.A.; methodology, M.X.; software, M.X.; validation, M.X. and H.L.; investigation, M.X., H.L. and Y.L.; writing—original draft preparation, M.X.; writing—review and editing, E.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by MITACS with the British Columbia Oil and Gas Research and Innovation Society as the partner organization. The grant number is IT13626.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is available in the article.
Acknowledgments
The authors acknowledge Fortis BC for providing all the samples used in this research. The technical support from our departmental machine shop for preparing the holiday samples and that from Scott Nesbitt and Roger Bennett in our department for making the dented samples is also greatly appreciated. The authors wish to thank Stat-Ease for providing the trial version of Design-Expert 12.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Canadian Energy Pipeline Association (CEPA). 2015 Pipeline Industry Performance Report; Canadian Energy Pipeline Association: Calgary, AB, Canada, 2015. [Google Scholar]
- Kowalski, A.R.; Sánchez, A.N. Soil Corrosivity in Buried Onshore Pipelines: A Bayesian Network Approach. In Proceedings of the CORROSION 2016 NACE International, Vancouver, BC, Canada, 6–10 March 2016. [Google Scholar]
- Li, X.; Castaneda, H. Influence of Soil Parameters on Coating Damage Evolution of X52 Pipeline Steel under Cathodic Protection Conditions. In Proceedings of the CORROSION 2014, San Antonio, TX, USA, 9–13 March 2014; NACE International: Houston, TX, USA, 2014. [Google Scholar]
- De Cunha Lins, V.F.; Magalhães Ferreira, M.L.; Saliba, P.A. Corrosion Resistance of API X52 Carbon Steel in Soil Environment. J. Mater. Res. Technol. 2012, 1, 161–166. [Google Scholar] [CrossRef]
- Quej-Ake, L.M.; Contreras, A.; Liu, H.B.; Alamilla, J.L.; Sosa, E. Assessment on external corrosion rates for API pipeline steels exposed to acidic sand-clay soil. Anti-Corros. Methods Mater. 2018, 65, 281–291. [Google Scholar] [CrossRef]
- Cole, I.S.; Marney, D. The science of pipe corrosion: A review of the literature on the corrosion of ferrous metals in soils. Corros. Sci. 2012, 56, 5–16. [Google Scholar] [CrossRef]
- Wasim, M.; Shoaib, S.; Mubarak, N.M.; Inamuddin; Asiri, A.M. Factors influencing corrosion of metal pipes in soils. Environ. Chem. Lett. 2018, 16, 861–879. [Google Scholar] [CrossRef]
- Barbalat, M.; Lanarde, L.; Caron, D.; Meyer, M.; Vittonato, J.; Castillon, F.; Fontaine, S.; Refait, P. Electrochemical study of the corrosion rate of carbon steel in soil: Evolution with time and determination of residual corrosion rates under cathodic protection. Corros. Sci. 2012, 55, 246–253. [Google Scholar] [CrossRef]
- Benmoussa, A.; Hadjel, M.; Traisnel, M. Corrosion behavior of API 5L X-60 pipeline steel exposed to near-neutral pH soil simulating solution. Mater. Corros. 2006, 57, 771–777. [Google Scholar] [CrossRef]
- Wang, S.; Liu, D.; Du, N.; Zhao, Q.; Xiao, J. Analysis of the Long-Term Corrosion Behavior of X80 Pipeline Steel in Acidic Red Soil Using Electrical Resistance Test Technique. Adv. Mater. Sci. Eng. 2015, 2015, 931761. [Google Scholar] [CrossRef]
- Vanaei, H.R.; Eslami, A.; Egbewande, A. A review on pipeline corrosion, in-line inspection (ILI), and corrosion growth rate models. Int. J. Press. Vessel. Pip. 2017, 149, 43–54. [Google Scholar] [CrossRef]
- Ahammed, M.; Melchers, R.E. Reliability of Underground Pipelines Subject to Corrosion. J. Transp. Eng. 1994, 120, 989–1002. [Google Scholar] [CrossRef]
- Velázquez, J.C.; Caleyo, F.; Valor, A.; Hallen, J.M. Predictive model for pitting corrosion in buried oil and gas pipelines. Corrosion 2009, 65, 332–342. [Google Scholar] [CrossRef]
- Chico, B.; de la Fuente, D.; Díaz, I.; Simancas, J.; Morcillo, M. Annual Atmospheric Corrosion of Carbon Steel Worldwide. An Integration of ISOCORRAG, ICP/UNECE and MICAT Databases. Materials 2017, 10, 601. [Google Scholar] [CrossRef] [PubMed]
- Simillion, H.; Dolgikh, O.; Terryn, H.; Deconinck, J. Atmospheric corrosion modeling. Corros. Rev. 2014, 32, 73–100. [Google Scholar] [CrossRef]
- Wang, X.; Wang, H.; Tang, F.; Castaneda, H.; Liang, R. Statistical analysis of spatial distribution of external corrosion defects in buried pipelines using a multivariate Poisson-lognormal model. Struct. Infrastruct. Eng. 2020. [Google Scholar] [CrossRef]
- He, B.; Han, P.; Hou, L.; Zhang, D.; Bai, X. Understanding the effect of soil particle size on corrosion behavior of natural gas pipeline via modelling and corrosion micromorphology. Eng. Fail. Anal. 2017, 80, 325–340. [Google Scholar] [CrossRef]
- Gadala, I.M.; Abdel Wahab, M.; Alfantazi, A. Numerical simulations of soil physicochemistry and aeration influences on the external corrosion and cathodic protection design of buried pipeline steels. Mater. Des. 2016, 97, 287–299. [Google Scholar] [CrossRef]
- Kosari, A.; Davoodi, A.; Moayed, M.H.; Gheshlaghi, R. The response surface method as an experimental design technique to explore and model the performance of corrosion inhibitors. Corrosion 2015, 71, 819–827. [Google Scholar] [CrossRef]
- Tansel, B.; Pascual, B. Factorial evaluation of operational variables of a DAF process to improve PHC removal efficiency. Desalination 2004, 169, 1–10. [Google Scholar] [CrossRef]
- Bursali, N.; Ertunc, S.; Akay, B. Process improvement approach to the saponification reaction by using statistical experimental design. Chem. Eng. Process. Process. Intensif. 2006, 45, 980–989. [Google Scholar] [CrossRef]
- Mahdi, K.; Gheshlaghi, R.; Zahedi, G.; Lohi, A. Characterization and modeling of a crude oil desalting plant by a statistically designed approach. J. Pet. Sci. Eng. 2008, 61, 116–123. [Google Scholar] [CrossRef]
- Arriba-Rodríguez, L.-d.; Rodríguez-Montequín, V.; Villanueva-Balsera, J.; Ortega-Fernández, F. Design of Predictive Models to Estimate Corrosion in Buried Steel Structures. Sustainability 2020, 12, 9879. [Google Scholar] [CrossRef]
- ASTM International. Standard Practice for Laboratory Immersion Corrosion Testing of Metals; ASTM G31-72; ASTM International: West Conshohocken, PA, USA, 2004. [Google Scholar]
- Du, C.W.; Li, X.G.; Liang, P.; Liu, Z.Y.; Jia, G.F.; Cheng, Y.F. Effects of Microstructure on Corrosion of X70 Pipe Steel in an Alkaline Soil. J. Mater. Eng. Perform. 2009, 18, 216–220. [Google Scholar] [CrossRef]
- Jamali, S.S.; Mills, D.J.; Sykes, J.M. Measuring electrochemical noise of a single working electrode for assessing corrosion resistance of polymer coated metals. Prog. Org. Coat. 2014, 77, 733–741. [Google Scholar] [CrossRef]
- González, J.A.; Andrade, C. Effect of Carbonation, Chlorides and Relative Ambient Humidity on the Corrosion of Galvanized Rebars Embedded in Concrete. Br. Corros. J. 1982, 17, 21–28. [Google Scholar] [CrossRef]
- Saliba, P.A.; Mansur, A.A.; Santos, D.B.; Mansur, H.S. Fusion-bonded epoxy composite coatings on chemically functionalized API steel surfaces for potential deep-water petroleum exploration. Appl. Adhes. Sci. 2015, 3, 22. [Google Scholar] [CrossRef]
- Brasher, D.M.; Kingsbury, A.H. Electrical measurements in the study of immersed paint coatings on metal. I. Comparison between capacitance and gravimetric methods of estimating water-uptake. J. Appl. Chem. 1954, 4, 62–72. [Google Scholar] [CrossRef]
- Groysman, A. Corrosion for Everybody; Springer: New York, NY, USA; Dordrecht, The Netherlands, 2010. [Google Scholar]
- Leeds, J.M. Interaction between coatings and CP deserves basic review. Pipe Line Gas. Ind. 1995, 78, 21. [Google Scholar]
- Song, F. Corrosion of Coated Pipelines with Cathodic Protection. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2002. [Google Scholar]
- Singh, D.D.N.; Ghosh, R. Unexpected deterioration of fusion-bonded epoxy-coated rebars embedded in chloride-contaminated concrete environments. Corrosion 2005, 61, 815–829. [Google Scholar] [CrossRef]
- Nakhaie, D.; Ferdowsi, B.A.S. Soil and Pitting Corrosion of Hot-Dip Galvanized Steel: Experimental and Mathematical Modeling. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2010. [Google Scholar]
- Sajid, H.U.; Kiran, R.; Qi, X.; Bajwa, D.S.; Battocchi, D. Employing corn derived products to reduce the corrosivity of pavement deicing materials. Constr. Build. Mater. 2020, 263, 120662. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).