Stretch Forming Behavior and Constitutive Equation of a Modified 5083 Alloy with High Mg Content at Elevated Temperatures
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Mechanical Properties
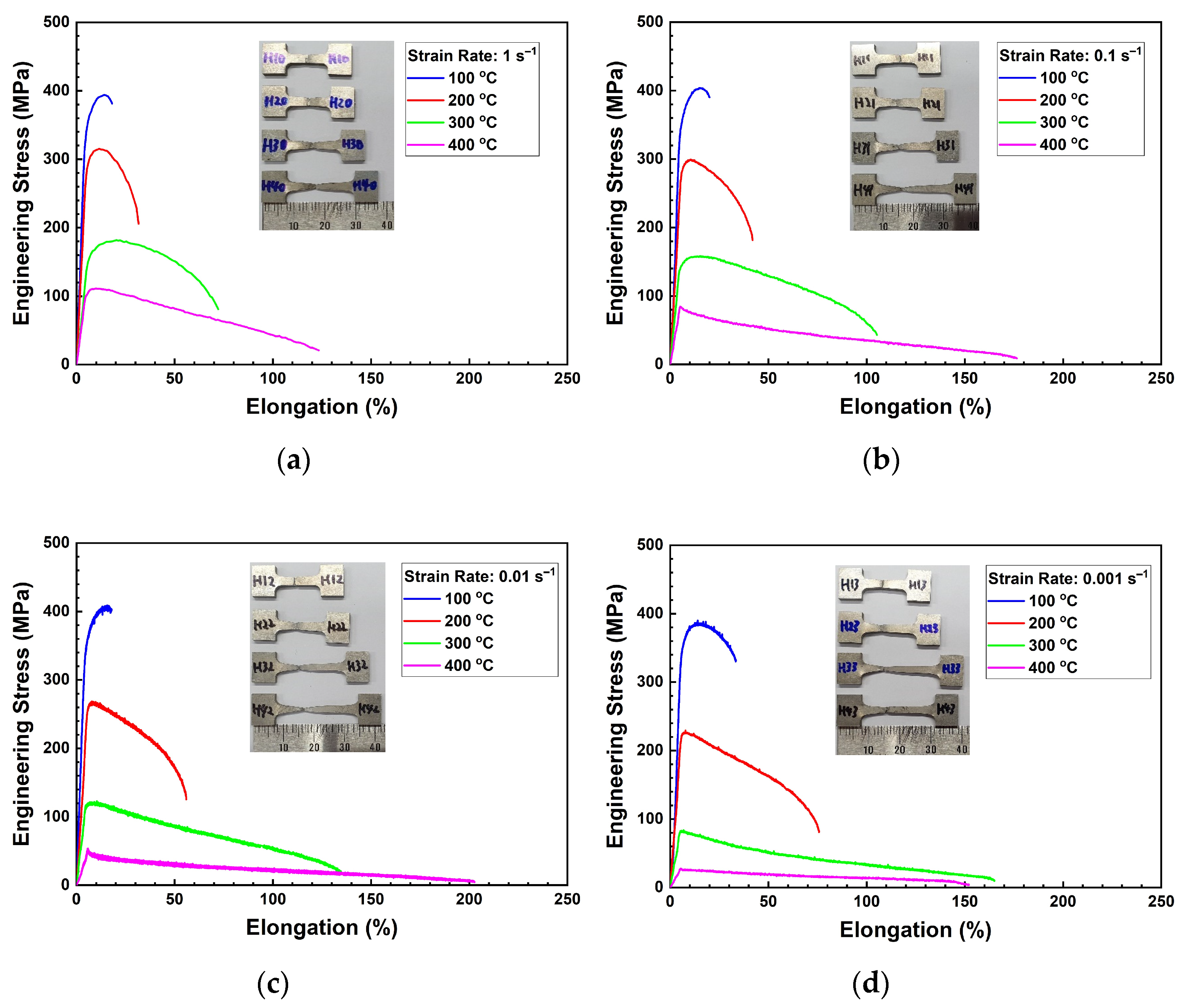
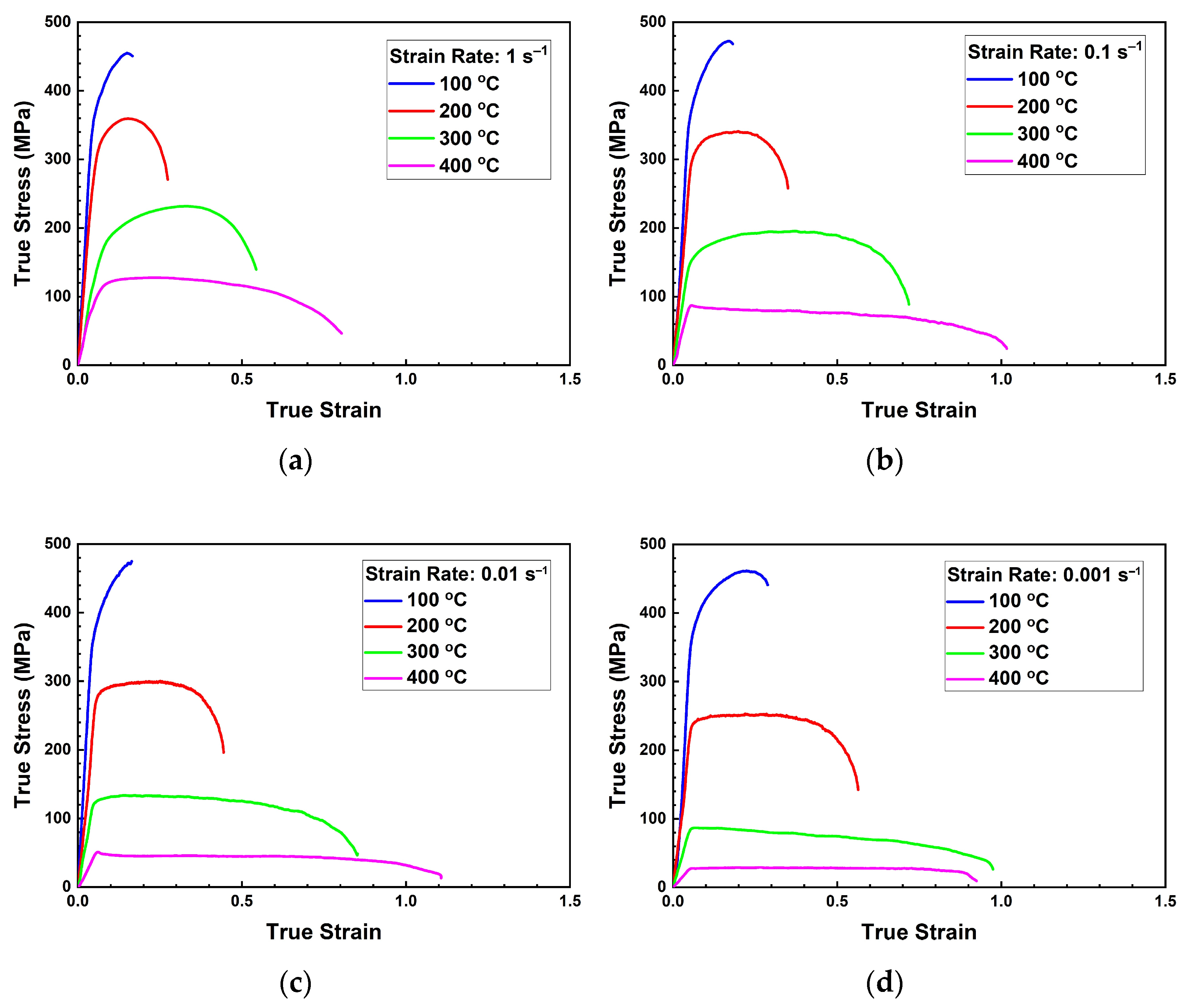
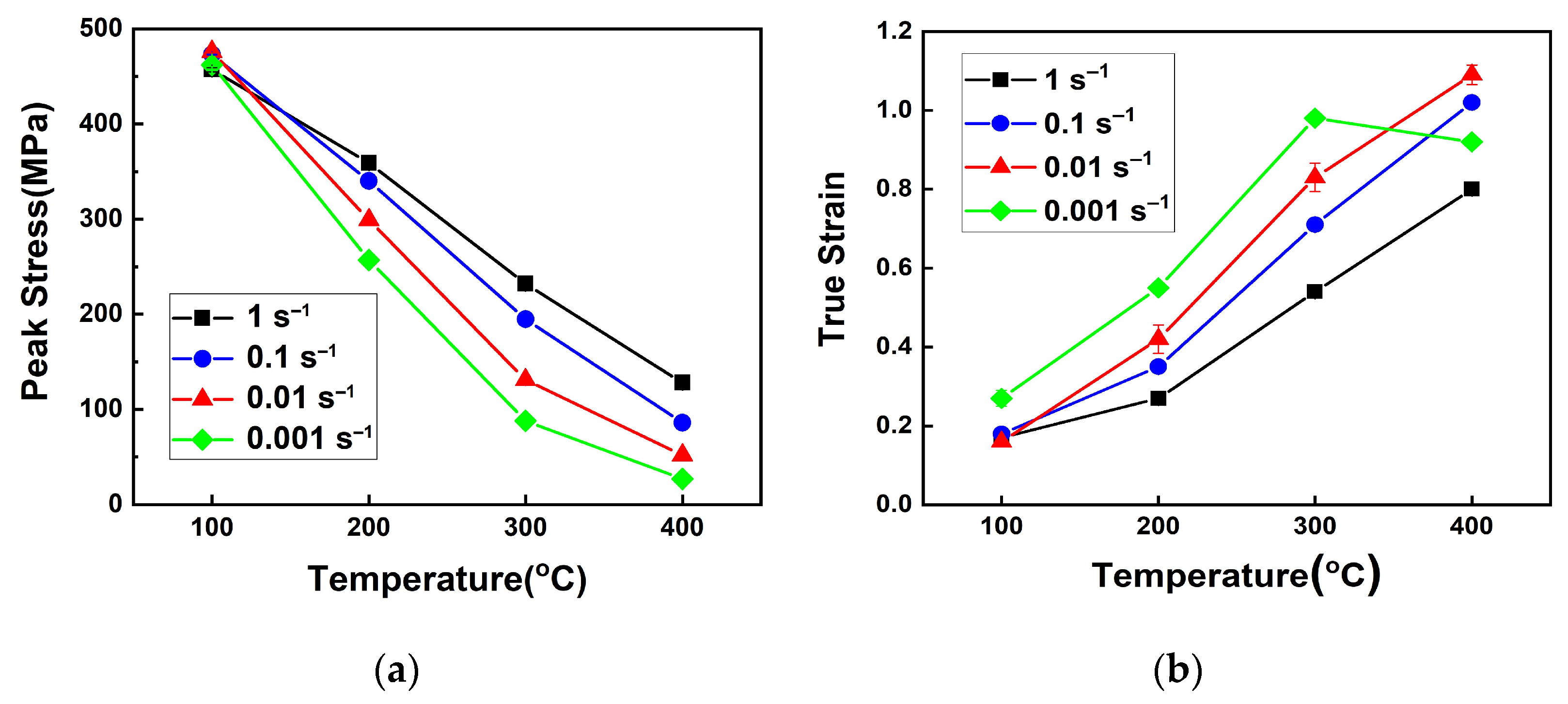
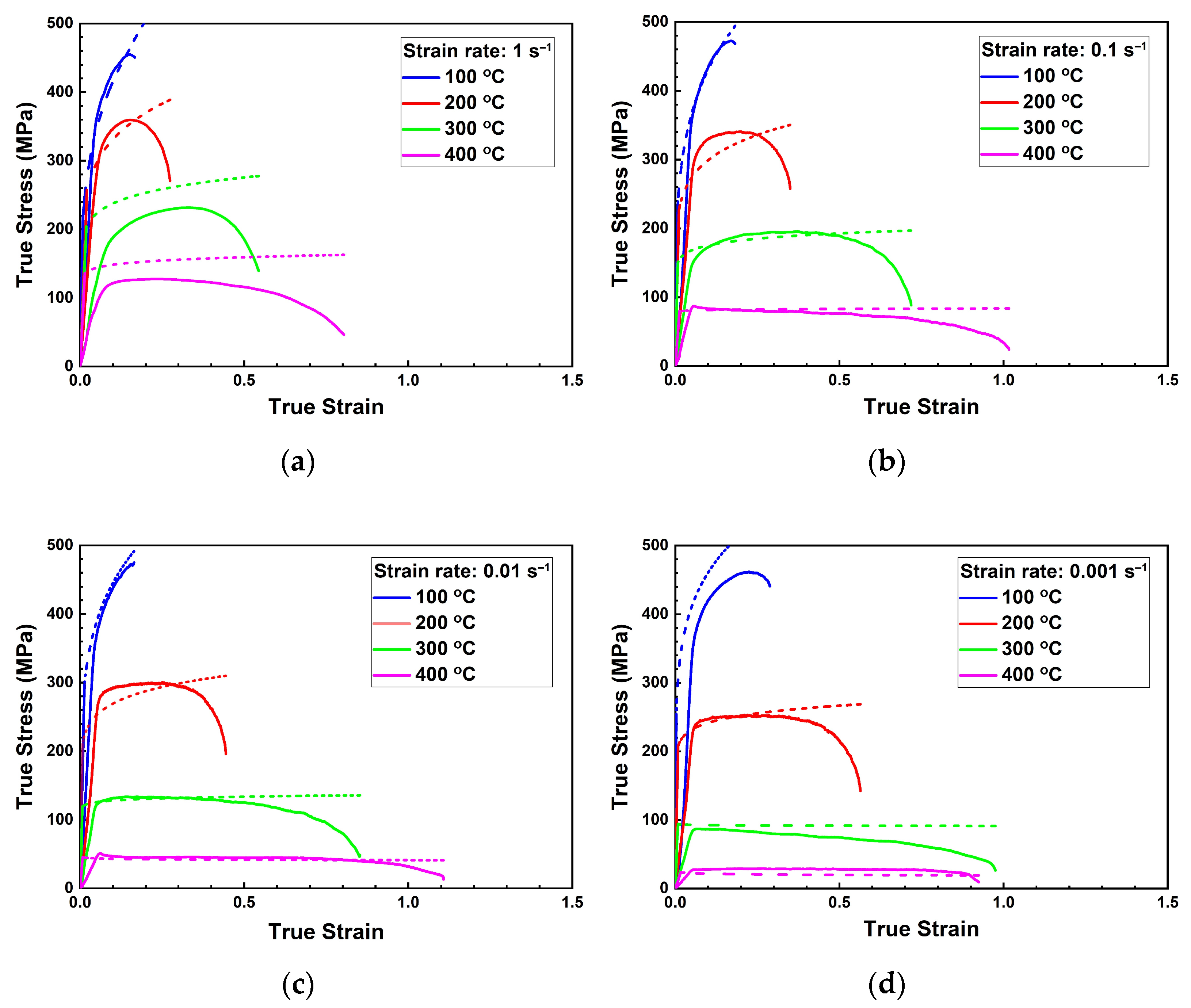
3.1.1. Stress–Strain Curves of the 5083M Alloy in Tension Mode
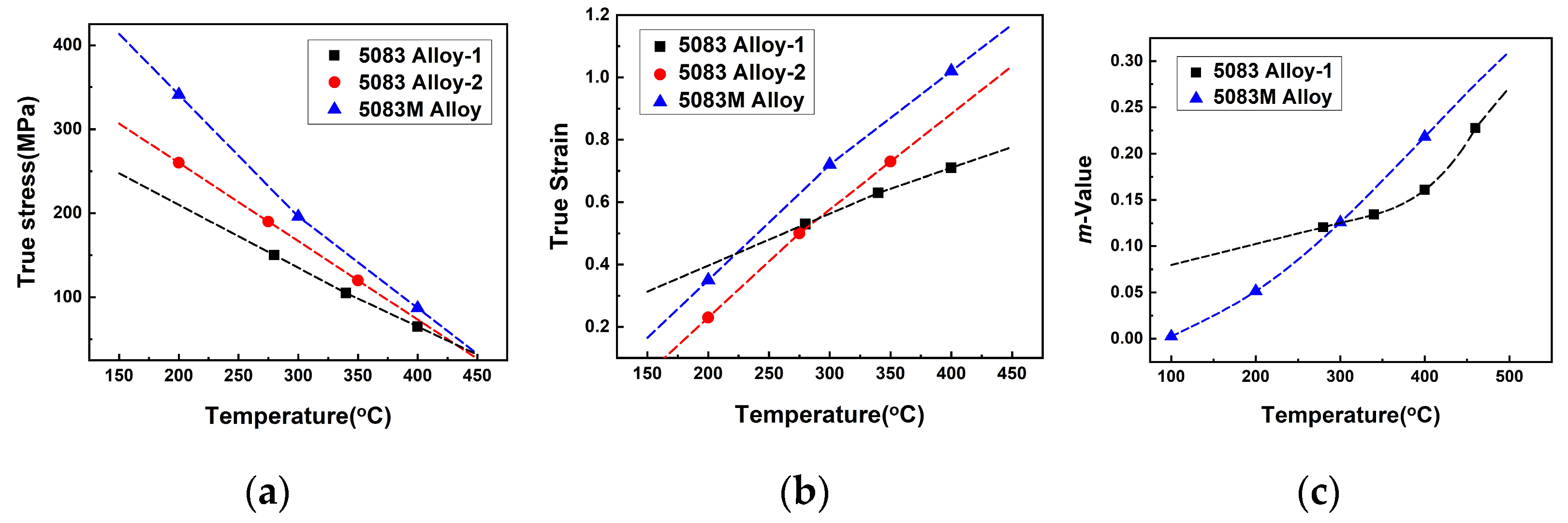
3.1.2. Comparison with the Commercial 5083 Alloy
3.2. Metallurgical Evolution
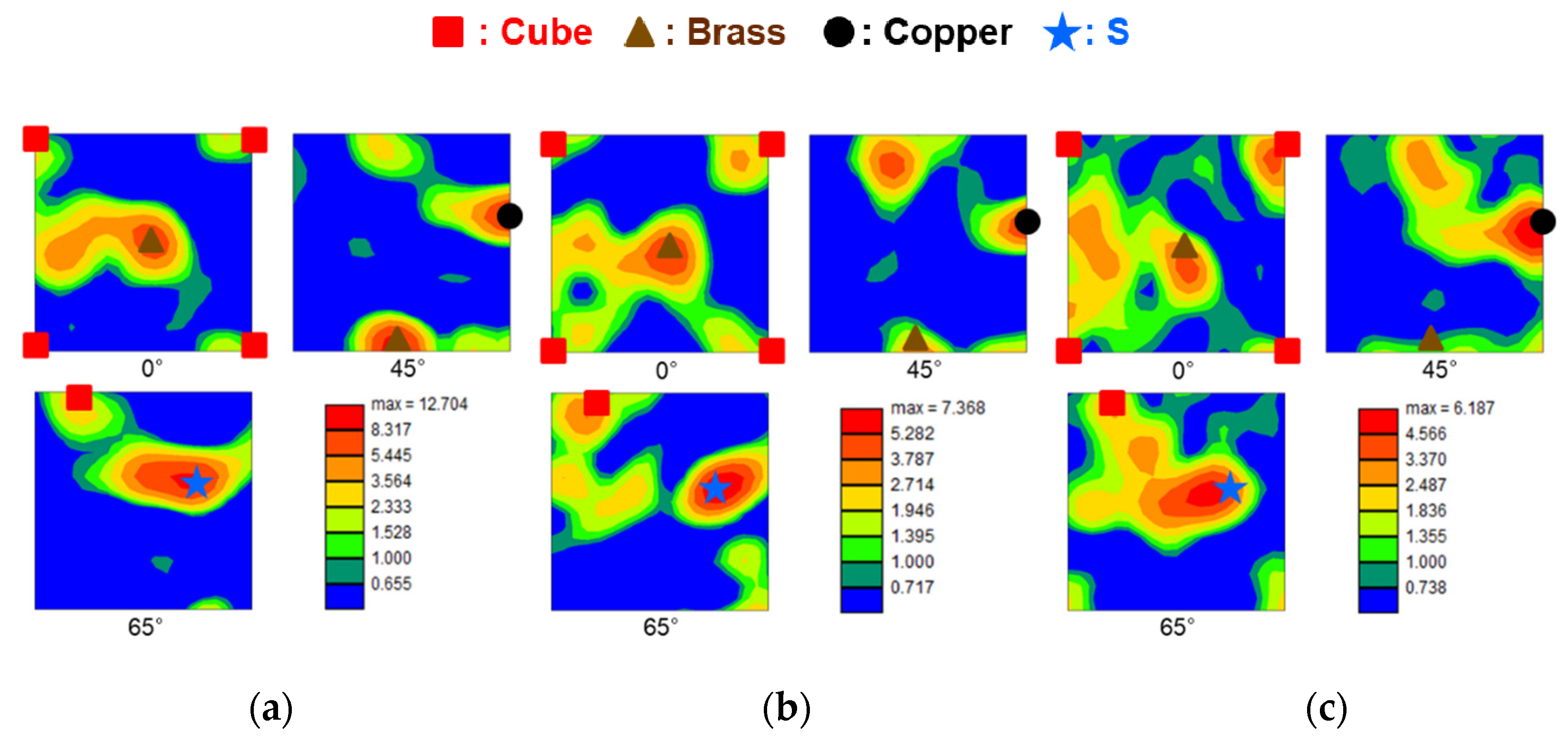
3.2.1. Microstructure of the 5083M Alloy
3.2.2. Cavities
3.3. Constitutive Equation
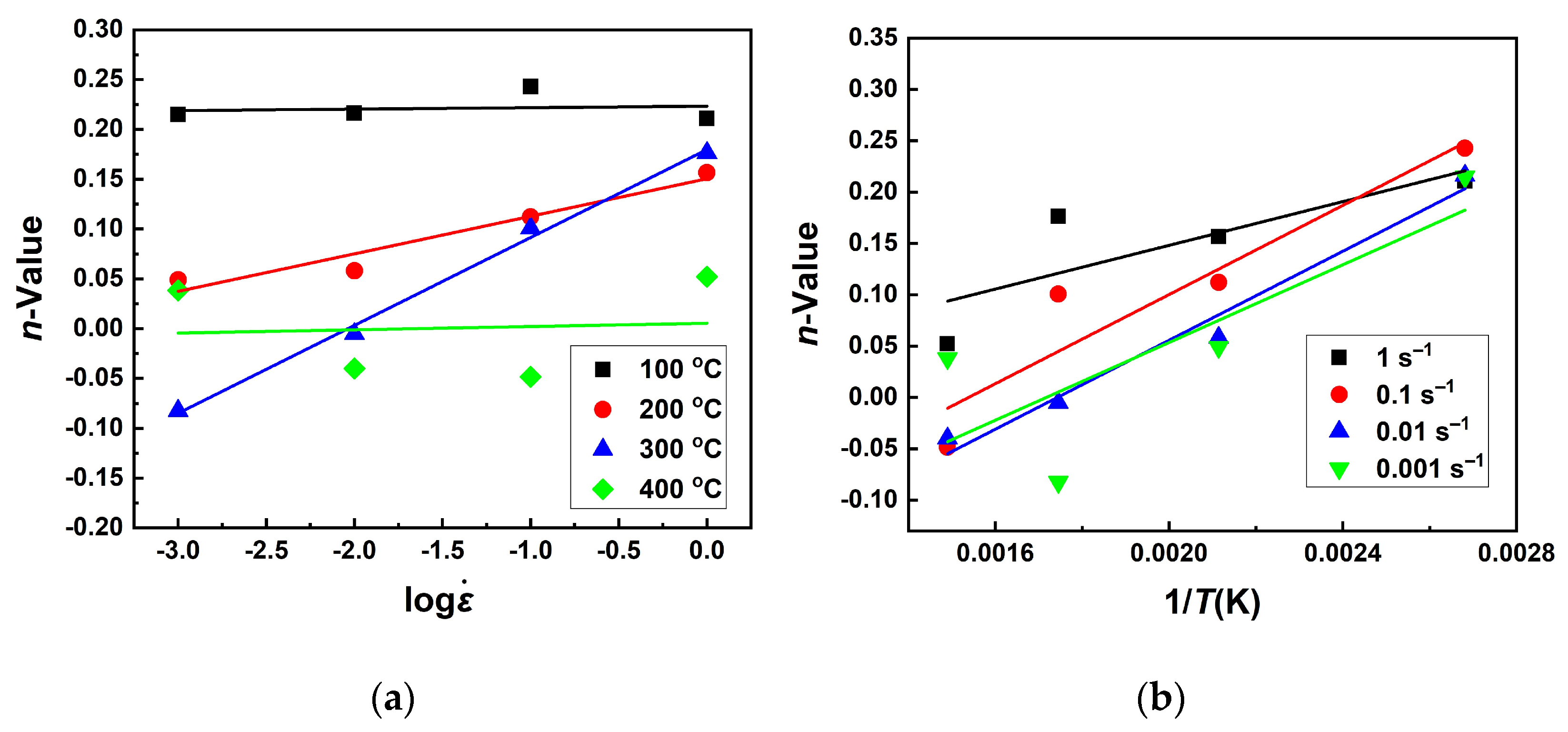
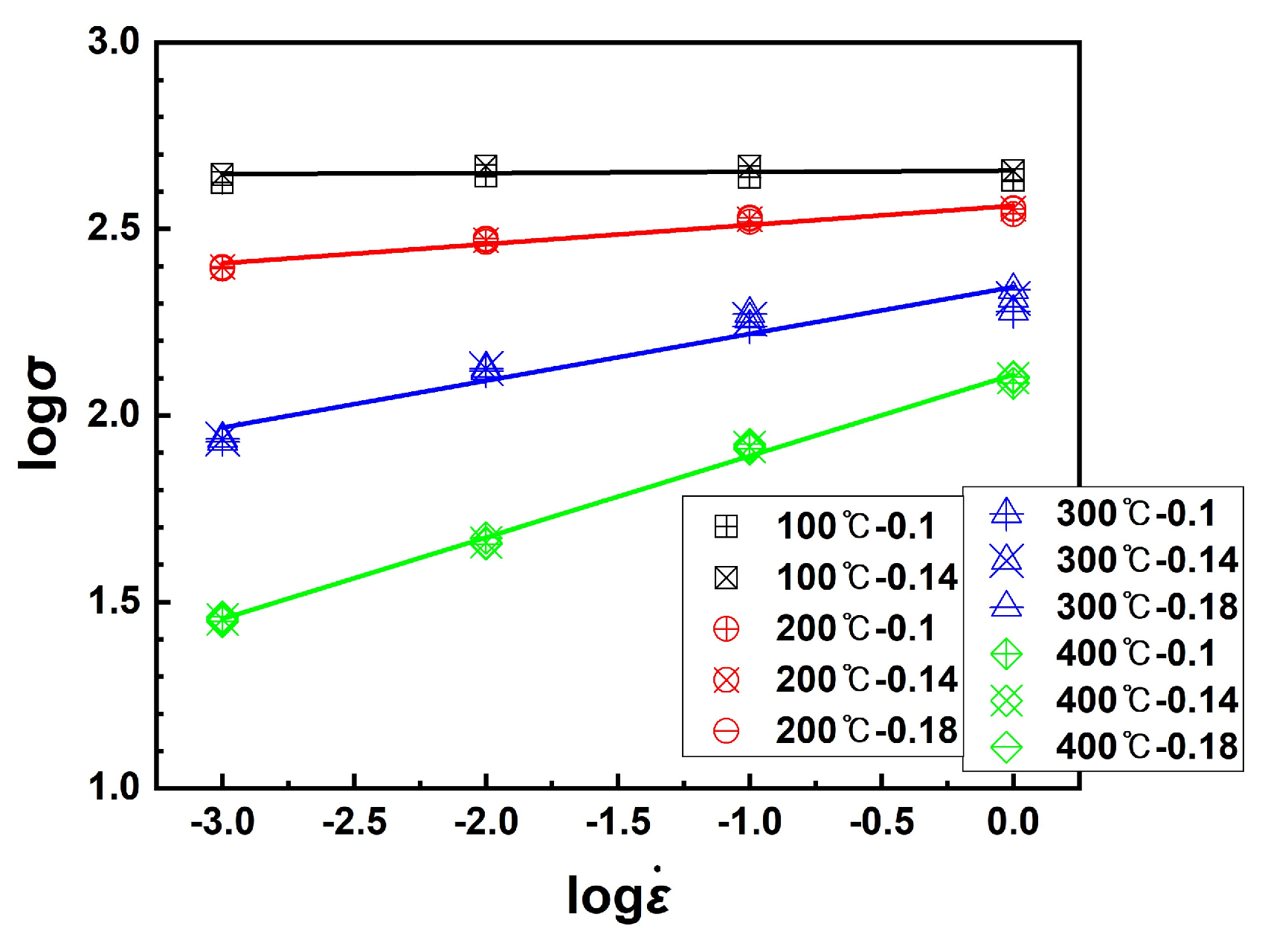
3.3.1. n-Value
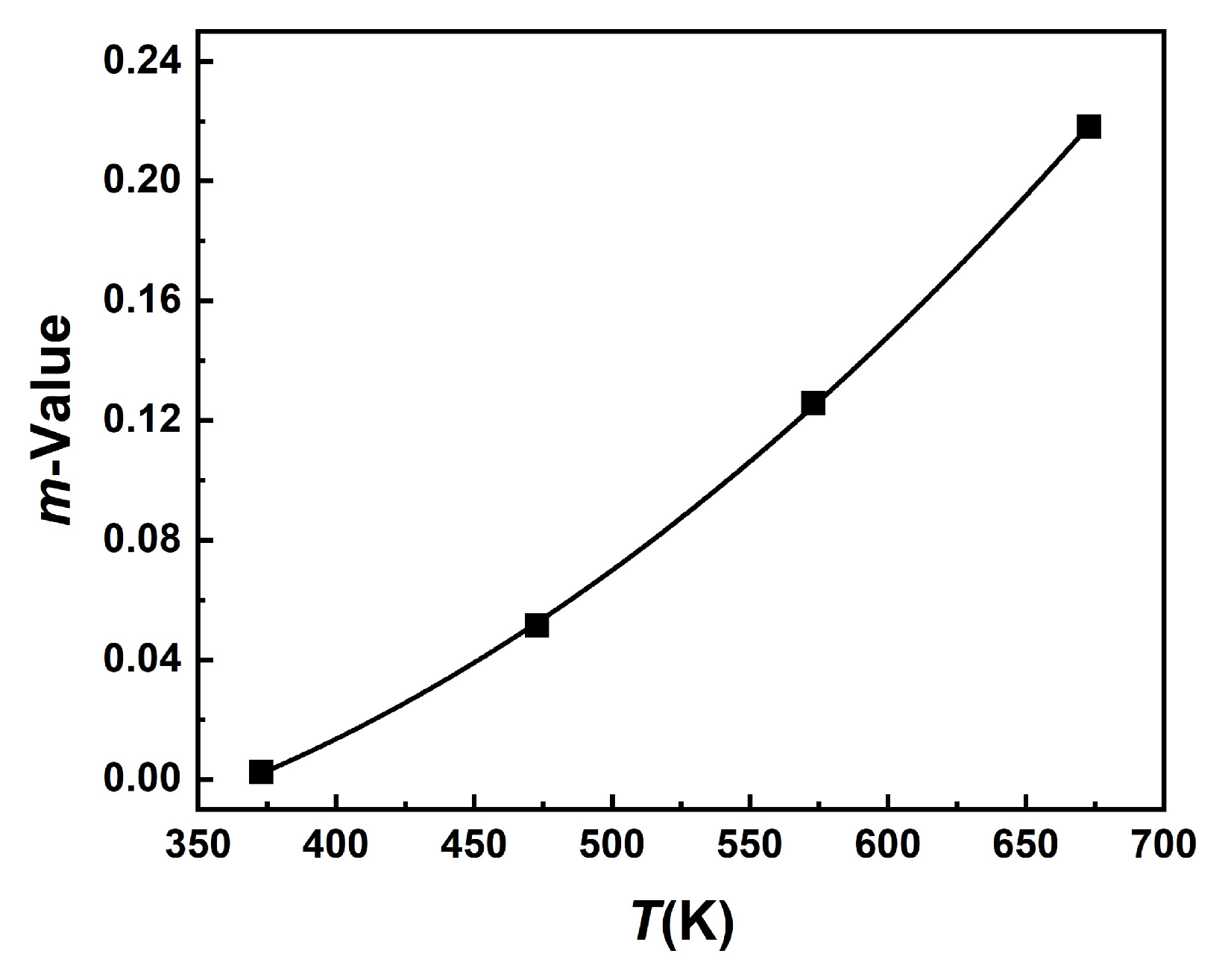
3.3.2. m-Value
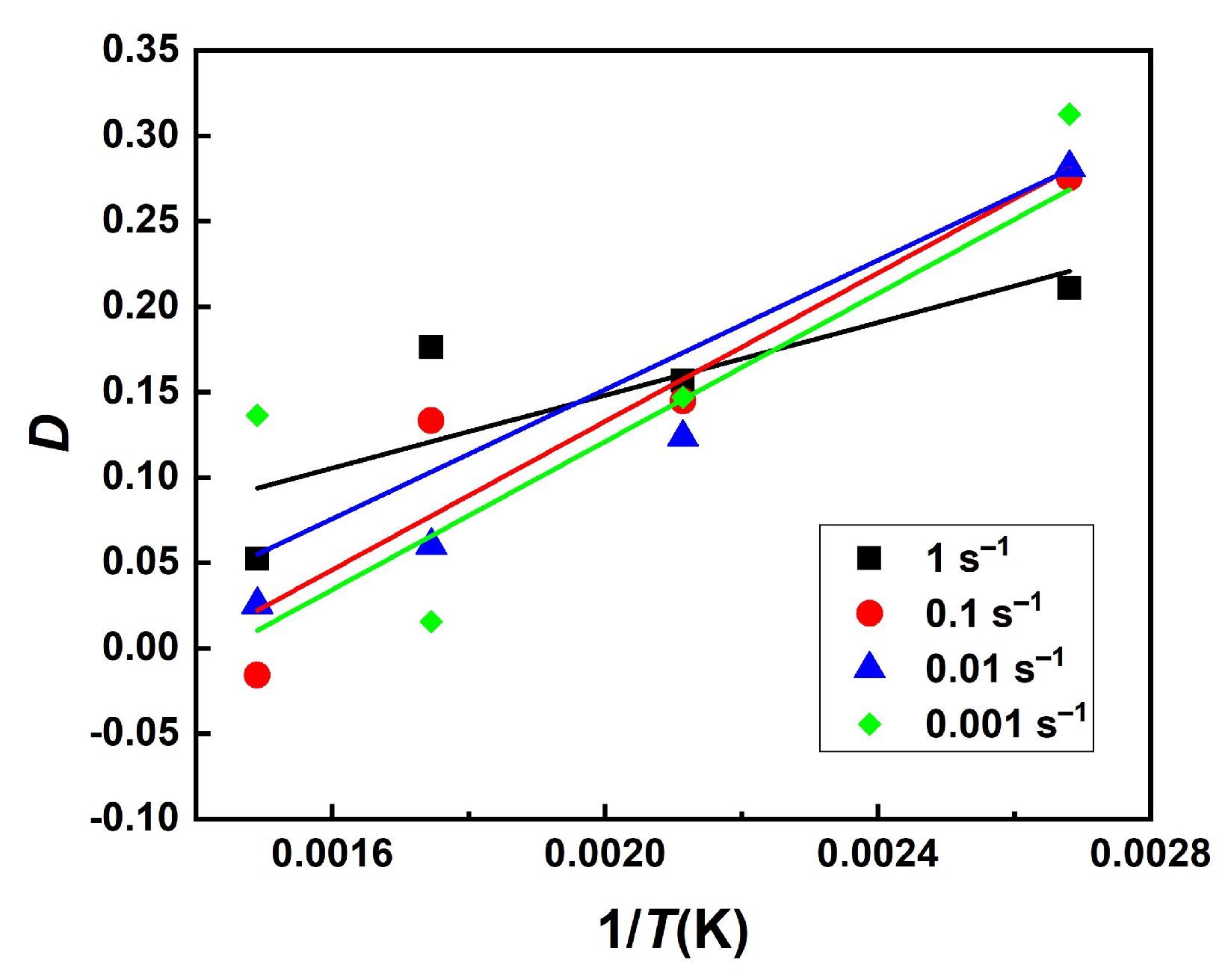
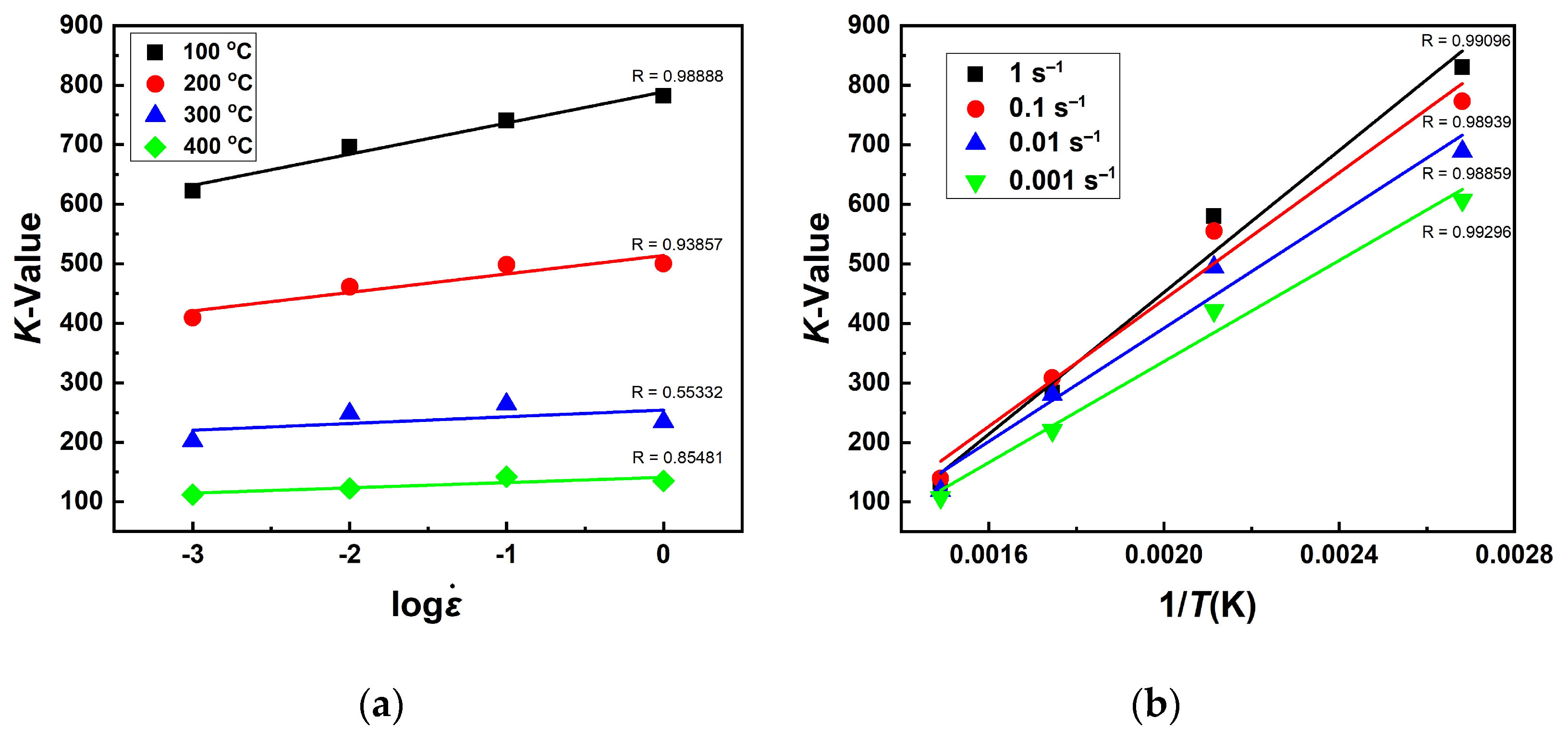
3.3.3. K-Value
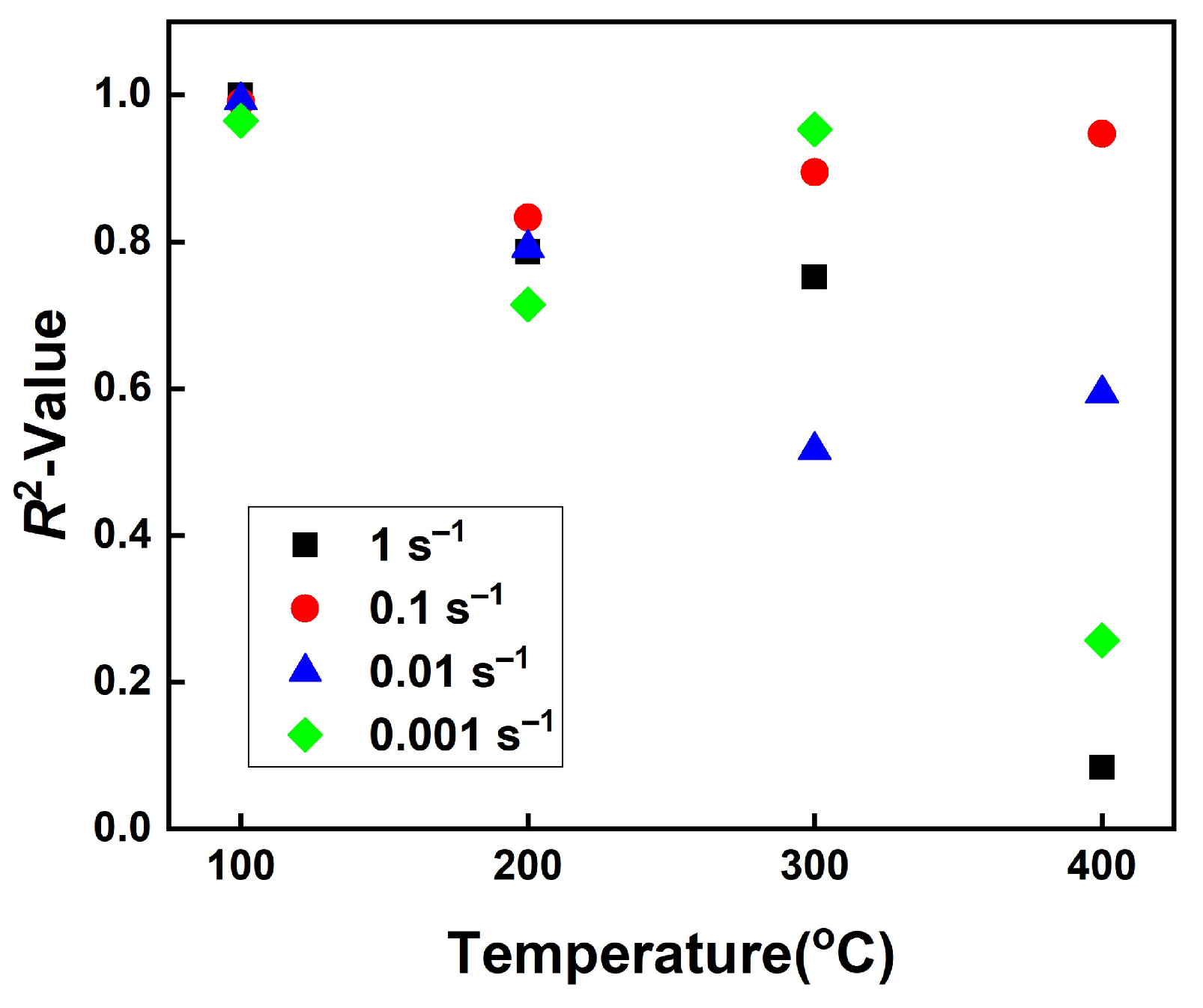
3.3.4. Validation of the Constitutive Equation
4. Conclusions
- The 5083M alloy showed a tendency of decreasing peak stress and increasing true strain with increasing temperature and decreasing strain rate. Compared with the commercial 5083 alloy, the 5083M alloy had higher strength and ductility at elevated temperatures. The strain rate sensitivity exponent of the 5083M alloy was also higher, so it is predicted to have better formability.
- In the 5083M alloy, dynamic recrystallization occurred under the deformation temperature condition of 300 °C or higher, and dynamic restoration occurred by dynamic recovery (DRV) at temperatures below that. At the lowest strain rate condition among the 300 °C conditions, it was observed that the fine equiaxed grains were uniformly distributed, and that the deformation texture remained regardless of the fully recrystallized microstructure.
- After the stretch forming at 400 °C and 0.001 s−1 condition, cavities with complex shapes were observed at grain boundaries and grain triple junctions. These cavities were formed by grain boundary sliding which operates as deformation mechanism under the high temperature and low strain rate conditions. As a result, the formation of the cavities resulted in a decrease in ductility under the 400 °C and 0.001 s−1 condition.
- From the results of stretch forming conducted under various process conditions, a constitutive equation for predicting the deformation behavior of the 5083M alloy was derived. The calculated curves were in good agreement with the measured curves in low temperature and high strain rate conditions. However, due to the limitation of the Field–Backofen equation, the strain hardening region was predicted well, but the softening region was not. Future work needs to be done for predicting the softening region using the modified Fields–Backofen equation containing softening parameters.
- The superior mechanical properties of the 5083M alloy over the commercial 5083 alloy may provide more effective weight reduction in the automotive industry. In addition, the better ductility will make it possible to apply the 5083M alloy to more complex shaped parts such as inner panels of moving modules (e.g., door, hood, trunk lid, etc.).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bariani, P.F.; Bruschi, S.; Ghiotti, A.; Michieletto, F. Hot Stamping of AA5083 Aluminium Alloy Sheets. CIRP Ann. 2013, 62, 251–254. [Google Scholar] [CrossRef]
- Kabirian, F.; Khan, A.S.; Pandey, A. Negative to Positive Strain Rate Sensitivity in 5xxx Series Aluminum Alloys: Experiment and Constitutive Modeling. Int. J. Plast. 2014, 55, 232–246. [Google Scholar] [CrossRef]
- Nam, T.-H.; Kim, S.-H.; Kim, J.-G.; Kim, S.-K. Corrosion Resistance of Extruded Mg–3Al–1Zn Alloy Manufactured by Adding CaO for the Replacement of the Protective Gases. Mater. Corros. 2014, 65, 577–581. [Google Scholar] [CrossRef]
- Jung, I.-H.; Lee, J.K.; Kim, S.K. Mg-Ca Alloys Produced by Reduction of CaO: Understanding of ECO-Mg Alloy Production. Met. Mater. Trans. B 2017, 48, 1073–1078. [Google Scholar] [CrossRef]
- Lee, T.W.; Park, H.W.; Lim, H.; Kim, S.K.; Lim, S.H. Microstructural Characterization of Oxide Layers in CaO Added AZ31 Mg Alloy. J. Alloys Compd. 2017, 714, 397–408. [Google Scholar] [CrossRef]
- Schulthess, T.C.; Turchi, P.E.A.; Gonis, A.; Nieh, T.-G. Systematic Study of Stacking Fault Energies of Random Al-Based Alloys. Acta Mater. 1998, 46, 2215–2221. [Google Scholar] [CrossRef]
- Rohatgi, A.; Vecchio, K.S.; Gray, G.T. The Influence of Stacking Fault Energy on the Mechanical Behavior of Cu and Cu-Al Alloys: Deformation Twinning, Work Hardening, and Dynamic Recovery. Met. Mat. Trans. A 2001, 32, 135–145. [Google Scholar] [CrossRef]
- Lee, B.-H.; Kim, S.-H.; Park, J.-H.; Kim, H.-W.; Lee, J.-C. Role of Mg in Simultaneously Improving the Strength and Ductility of Al–Mg Alloys. Mater. Sci. Eng. A 2016, 657, 115–122. [Google Scholar] [CrossRef]
- Huang, K.; Logé, R.E. A Review of Dynamic Recrystallization Phenomena in Metallic Materials. Mater. Des. 2016. [Google Scholar] [CrossRef]
- Maeno, T.; Mori, K.; Yachi, R. Hot Stamping of High-Strength Aluminium Alloy Aircraft Parts Using Quick Heating. CIRP Ann. 2017, 66, 269–272. [Google Scholar] [CrossRef]
- Neugebauer, R.; Altan, T.; Geiger, M.; Kleiner, M.; Sterzing, A. Sheet Metal Forming at Elevated Temperatures. CIRP Ann. 2006, 55, 793–816. [Google Scholar] [CrossRef]
- Li, D.; Ghosh, A. Tensile Deformation Behavior of Aluminum Alloys at Warm Forming Temperatures. Mater. Sci. Eng. A 2003, 352, 279–286. [Google Scholar] [CrossRef]
- Toros, S.; Ozturk, F. Modeling Uniaxial, Temperature and Strain Rate Dependent Behavior of Al–Mg Alloys. Comput. Mater. Sci. 2010, 49, 333–339. [Google Scholar] [CrossRef]
- Hua, L.; Meng, F.; Song, Y.; Liu, J.; Qin, X.; Suo, L. A Constitutive Model of 6111-T4 Aluminum Alloy Sheet Based on the Warm Tensile Test. J. Mater. Eng. Perform. 2014, 23, 1107–1113. [Google Scholar] [CrossRef]
- Wang, H.; Luo, Y.; Friedman, P.; Chen, M.; Gao, L. Warm Forming Behavior of High Strength Aluminum Alloy AA7075. Trans. Nonferrous Met. Soc. China 2012, 22, 1–7. [Google Scholar] [CrossRef]
- Li, D.; Ghosh, A.K. Biaxial Warm Forming Behavior of Aluminum Sheet Alloys. J. Mater. Process. Technol. 2004, 145, 281–293. [Google Scholar] [CrossRef]
- Geng, P.; Qin, G.; Zhou, J.; Zou, Z. Hot Deformation Behavior and Constitutive Model of GH4169 Superalloy for Linear Friction Welding Process. J. Manuf. Process. 2018, 32, 469–481. [Google Scholar] [CrossRef]
- Ha, S.-H.; Yoon, Y.-O.; Kim, B.-H.; Lim, H.-K.; Lee, T.-W.; Lim, S.-H.; Kim, S.K. Oxide Scale Behavior and Surface Protection of Al–Mg Alloys Containing a Trace of Ca. Inter. Met. 2019, 13, 121–129. [Google Scholar] [CrossRef]
- Kim, B.-H.; Ha, S.-H.; Yoon, Y.-O.; Lim, H.-K.; Kim, S.K.; Kim, D.-H. Effect of Ca Addition on Selective Oxidation of Al3Mg2 Phase in Al-5 mass% Mg Alloy. Mater. Lett. 2018, 228, 108–111. [Google Scholar] [CrossRef]
- Humphreys, F.J.; Hatherly, M. Recrystallization and Related Annealing Phenomena, 1st ed.; Pergamon: Oxford, UK; Tarrytown, NY, USA, 1995; ISBN 978-0-08-041884-1. [Google Scholar]
- Dai, Q.; Deng, Y.; Jiang, H.; Tang, J.; Chen, J. Hot Tensile Deformation Behaviors and a Phenomenological AA5083 Aluminum Alloy Fracture Damage Model. Mater. Sci. Eng. A 2019, 766, 138325. [Google Scholar] [CrossRef]
- Darras, B.M.; Abed, F.H.; Abdul-Latif, A.; Pervaiz, S. Experimental Investigation of Deformation in 5083 Marine-Grade Aluminum Alloy at Elevated Temperatures. J. Mater. Eng. Perform. 2015, 24, 1663–1668. [Google Scholar] [CrossRef]
- Chan, K.C.; Tong, G.Q. Strain Rate Sensitivity of a High-Strain-Rate Superplastic Al6061r20SiC W Composite under Uniaxial and Equibiaxial Tension. Scr. Mater. 2001, 7. [Google Scholar] [CrossRef]
- Ozturk, F.; Pekel, H.; Halkaci, H.S. The Effect of Strain-Rate Sensitivity on Formability of AA 5754-O at Cold and Warm Temperatures. J. Mater. Eng. Perform. 2011, 20, 77–81. [Google Scholar] [CrossRef]
- Huang, K. Towards the Modelling of Recrystallization Phenomena in Multi-Pass Conditions: Application to 304L Steel. HAL 2012. [Google Scholar] [CrossRef]
- Xiao, W.; Wang, B.; Wu, Y.; Yang, X. Constitutive Modeling of Flow Behavior and Microstructure Evolution of AA7075 in Hot Tensile Deformation. Mater. Sci. Eng. A 2018, 712, 704–713. [Google Scholar] [CrossRef]
- Sidor, J.J.; Petrov, R.H.; Kestens, L.A.I. Modeling the Crystallographic Texture Changes in Aluminum Alloys during Recrystallization. Acta Mater. 2011, 59, 5735–5748. [Google Scholar] [CrossRef]
- Mishin, O.V.; Godfrey, A.; Juul Jensen, D.; Hansen, N. Recovery and Recrystallization in Commercial Purity Aluminum Cold Rolled to an Ultrahigh Strain. Acta Mater. 2013, 61, 5354–5364. [Google Scholar] [CrossRef]
- Raj, R.; Ashby, M.F. Intergranular Fracture at Elevated Temperature. Acta Metall. 1975, 23, 653–666. [Google Scholar] [CrossRef]
- Du, N.; Bower, A.F.; Krajewski, P.E. Numerical Simulations of Void Growth in Aluminum Alloy AA5083 during Elevated Temperature Deformation. Mater. Sci. Eng. A 2010, 527, 4837–4846. [Google Scholar] [CrossRef]
- Langdon, T.G. A Unified Approach to Grain Boundary Sliding in Creep and Superplasticity. Acta Metall. Mater. 1994, 42, 2437–2443. [Google Scholar] [CrossRef]
- McNelley, T.R.; Oh-Ishi, K.; Zhilyaev, A.P.; Swaminathan, S.; Krajewski, P.E.; Taleff, E.M. Characteristics of the Transition from Grain-Boundary Sliding to Solute Drag Creep in Superplastic AA5083. Met. Mat. Trans. A 2008, 39, 50–64. [Google Scholar] [CrossRef]
- Boydon, J.F. Study of Cavitation and Failure Mechanisms of a Superplastic 5083 Aluminum Alloy; Naval Postgraduate School: Monterey, CA, USA, 2003. [Google Scholar]
- Cheng, Y.Q.; Zhang, H.; Chen, Z.H.; Xian, K.F. Flow Stress Equation of AZ31 Magnesium Alloy Sheet during Warm Tensile Deformation. J. Mater. Process. Technol. 2008, 208, 29–34. [Google Scholar] [CrossRef]
- Tsao, L.C.; Wu, H.Y.; Leong, J.C.; Fang, C.J. Flow Stress Behavior of Commercial Pure Titanium Sheet during Warm Tensile Deformation. Mater. Des. 2012, 34, 179–184. [Google Scholar] [CrossRef]
- Ling, C.P.; McCormick, P.G. Constitutive modelling of strain rate sensitivity. In Advances in Engineering Plasticity and Its Applications; Lee, W.B., Ed.; Elsevier: Oxford, UK, 1993; pp. 217–222. ISBN 978-0-444-89991-0. [Google Scholar]
- Guo, Z.; Saunders, N.; Schillé, J.P.; Miodownik, A.P. Modelling high temperature flow stress curves of titanium alloys. In Proceedings of the MRS International Materials Research Conference, Chongqing, China, 9–12 June 2008. [Google Scholar]
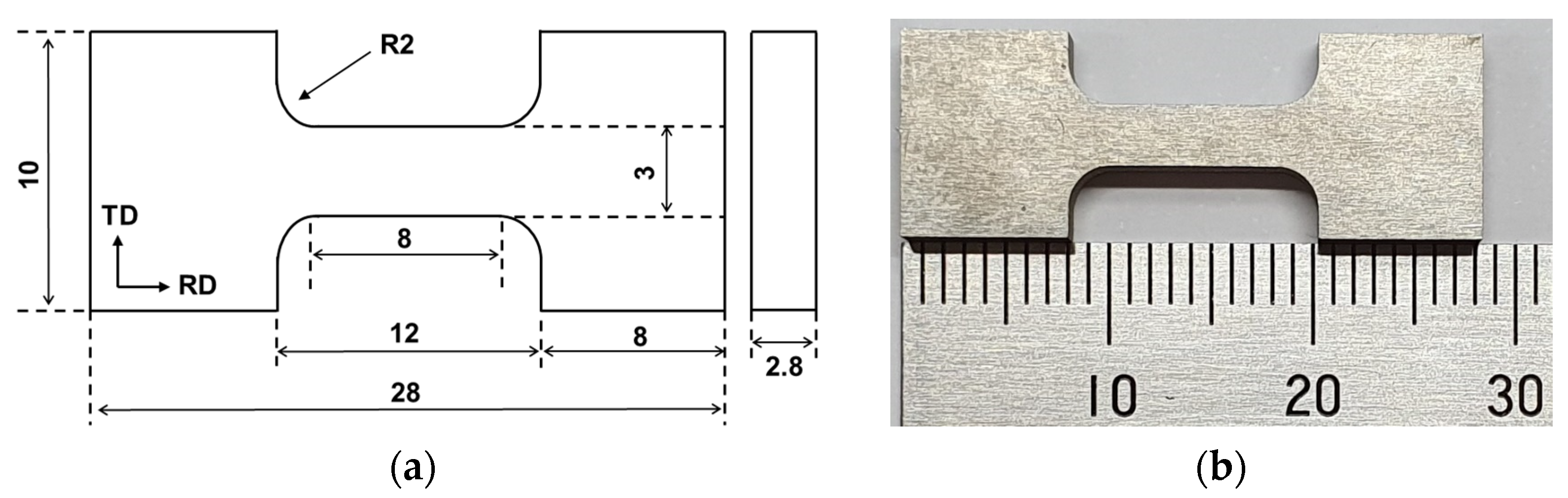







| Alloy | Si | Fe | Mg | Ti | Al |
|---|---|---|---|---|---|
| 5083M alloy | 0.1 | 0.2 | 6.0 | 0.01 | Bal. |
| Commercial 5083 alloy | 0.4–0.7 | 0.4 | 4.0–4.9 | 0.15 | Bal. |
| Temperature (°C) | A |
|---|---|
| 100 | 0.00146 |
| 200 | 0.03768 |
| 300 | 0.08190 |
| 400 | 0.00328 |
| Strain Rate (s–1) | B | C |
|---|---|---|
| 1 | 106.53624 | −0.06496 |
| 0.1 | 217.12627 | −0.30150 |
| 0.01 | 189.16917 | −0.22690 |
| 0.001 | 216.72551 | −0.31252 |
| Temperature (°C) | m-Value |
|---|---|
| 100 | 0.00239 |
| 200 | 0.05147 |
| 300 | 0.12580 |
| 400 | 0.21823 |
| Temperature (°C) | A |
|---|---|
| 100 | 52.35672 |
| 200 | 31.06404 |
| 300 | 11.31608 |
| 400 | 8.82928 |
| Strain Rate (s–1) | B | C |
|---|---|---|
| 1 | 559,474.49203 | −710.28342 |
| 0.1 | 510,270.09992 | −587.19311 |
| 0.01 | 486,071.28817 | −541.91309 |
| 0.001 | 438,505.99469 | −466.32879 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.-Y.; Lee, D.-B.; Choi, K.-H.; Kim, N.-S.; Ha, S.-H.; Kim, B.-H.; Yoon, Y.-O.; Lim, H.-K.; Kim, S.K.; Kim, Y.-J. Stretch Forming Behavior and Constitutive Equation of a Modified 5083 Alloy with High Mg Content at Elevated Temperatures. Metals 2021, 11, 410. https://doi.org/10.3390/met11030410
Yang S-Y, Lee D-B, Choi K-H, Kim N-S, Ha S-H, Kim B-H, Yoon Y-O, Lim H-K, Kim SK, Kim Y-J. Stretch Forming Behavior and Constitutive Equation of a Modified 5083 Alloy with High Mg Content at Elevated Temperatures. Metals. 2021; 11(3):410. https://doi.org/10.3390/met11030410
Chicago/Turabian StyleYang, Seung-Yoon, Da-Bin Lee, Kweon-Hoon Choi, Nam-Seok Kim, Seong-Ho Ha, Bong-Hwan Kim, Young-Ok Yoon, Hyun-Kyu Lim, Shae K. Kim, and Young-Jig Kim. 2021. "Stretch Forming Behavior and Constitutive Equation of a Modified 5083 Alloy with High Mg Content at Elevated Temperatures" Metals 11, no. 3: 410. https://doi.org/10.3390/met11030410
APA StyleYang, S.-Y., Lee, D.-B., Choi, K.-H., Kim, N.-S., Ha, S.-H., Kim, B.-H., Yoon, Y.-O., Lim, H.-K., Kim, S. K., & Kim, Y.-J. (2021). Stretch Forming Behavior and Constitutive Equation of a Modified 5083 Alloy with High Mg Content at Elevated Temperatures. Metals, 11(3), 410. https://doi.org/10.3390/met11030410









