Dislocation Loop Generation Differences between Thin Films and Bulk in EFDA Pure Iron under Self-Ion Irradiation at 20 MeV
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Material
2.2. Irradiation
2.3. Sample Characterisation
3. Results
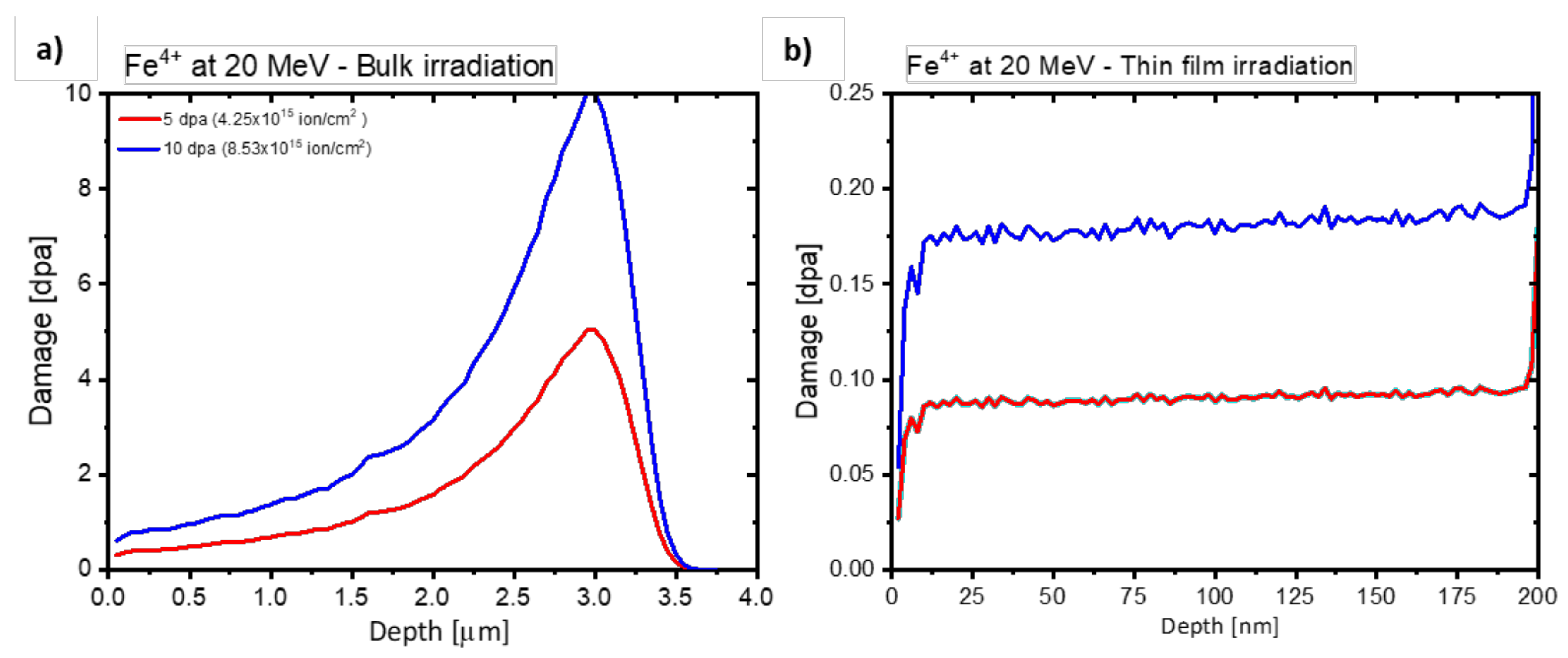
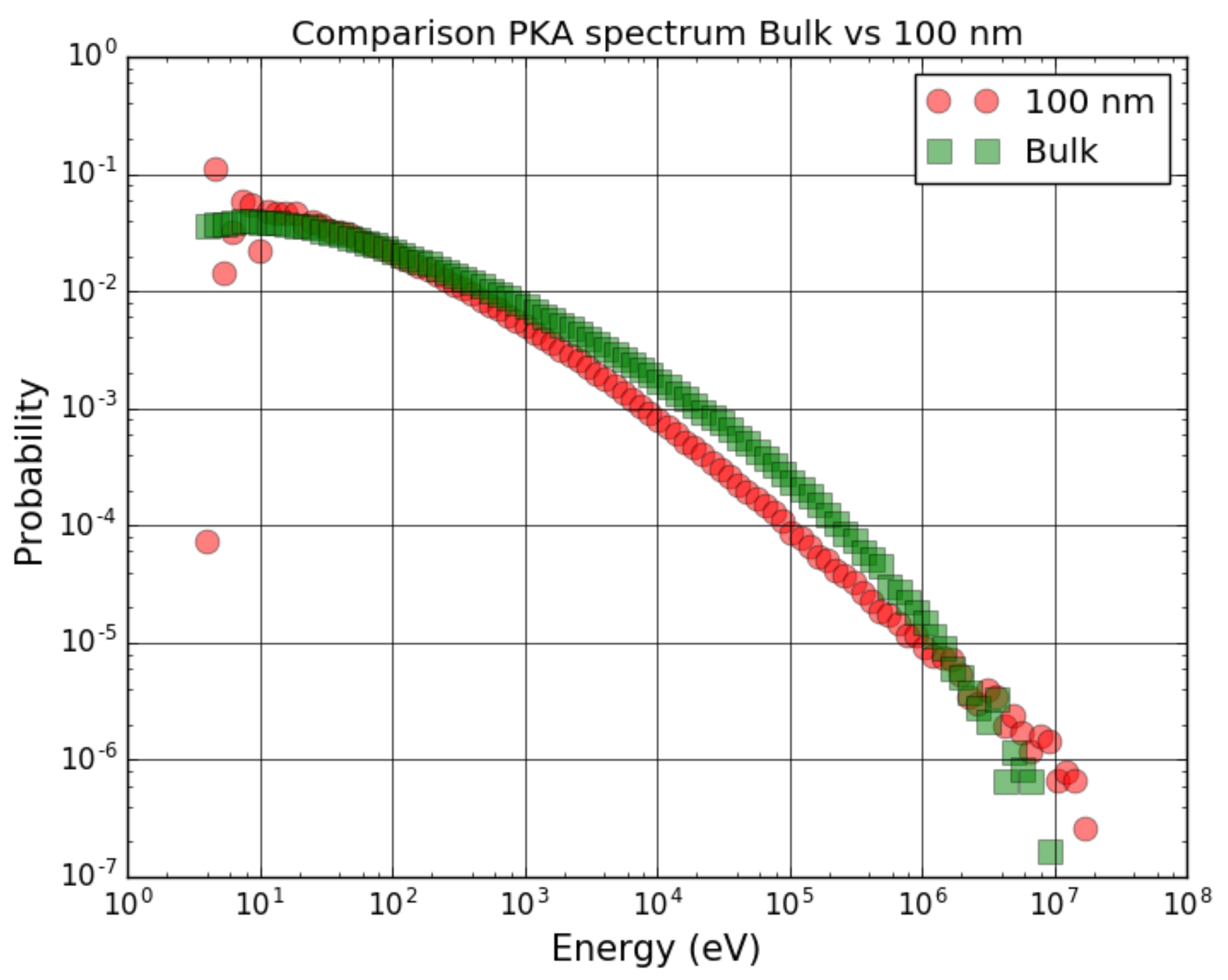
3.1. Simulation
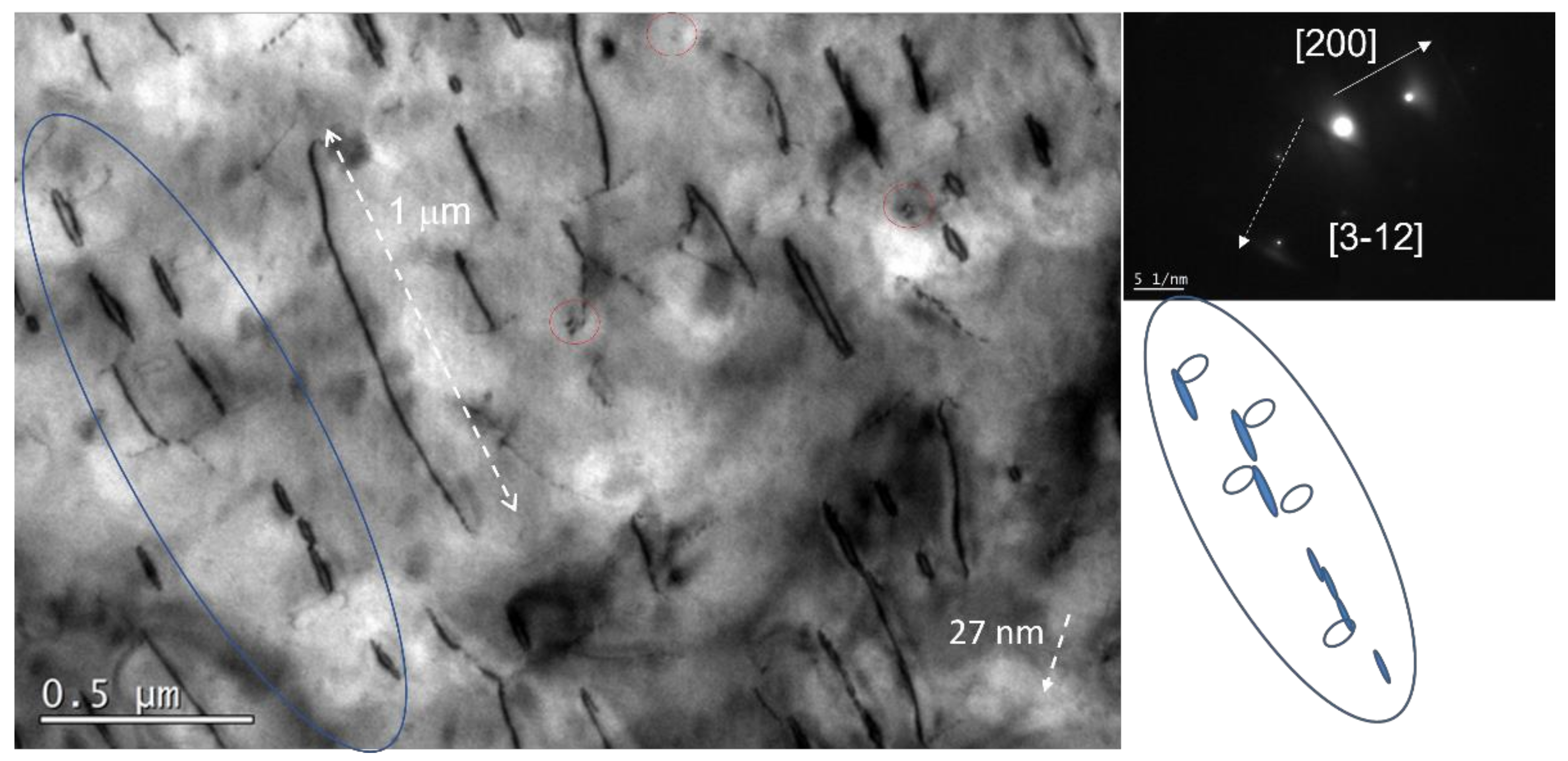
3.2. Bulk Specimens
3.3. Thin-Film Specimens
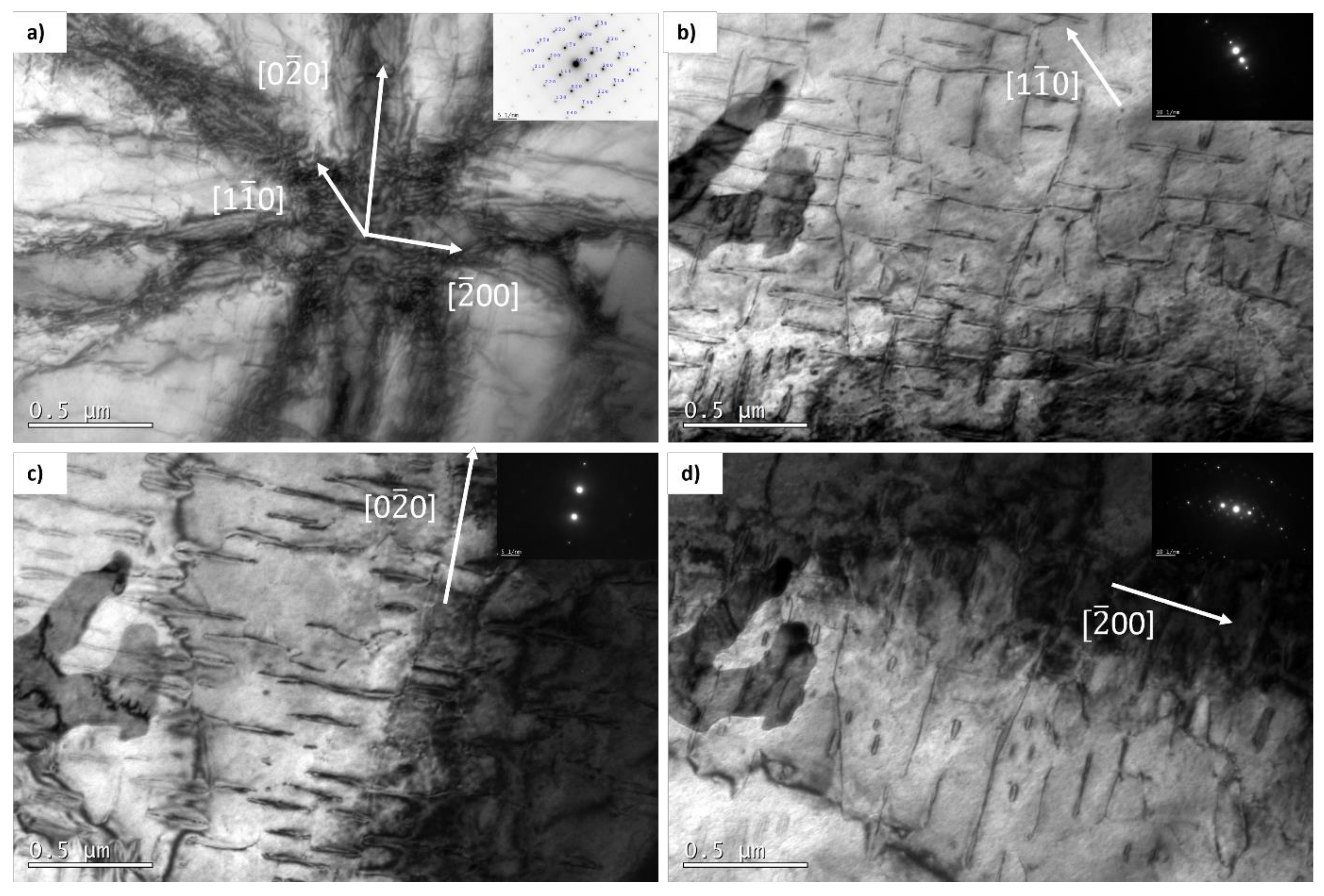
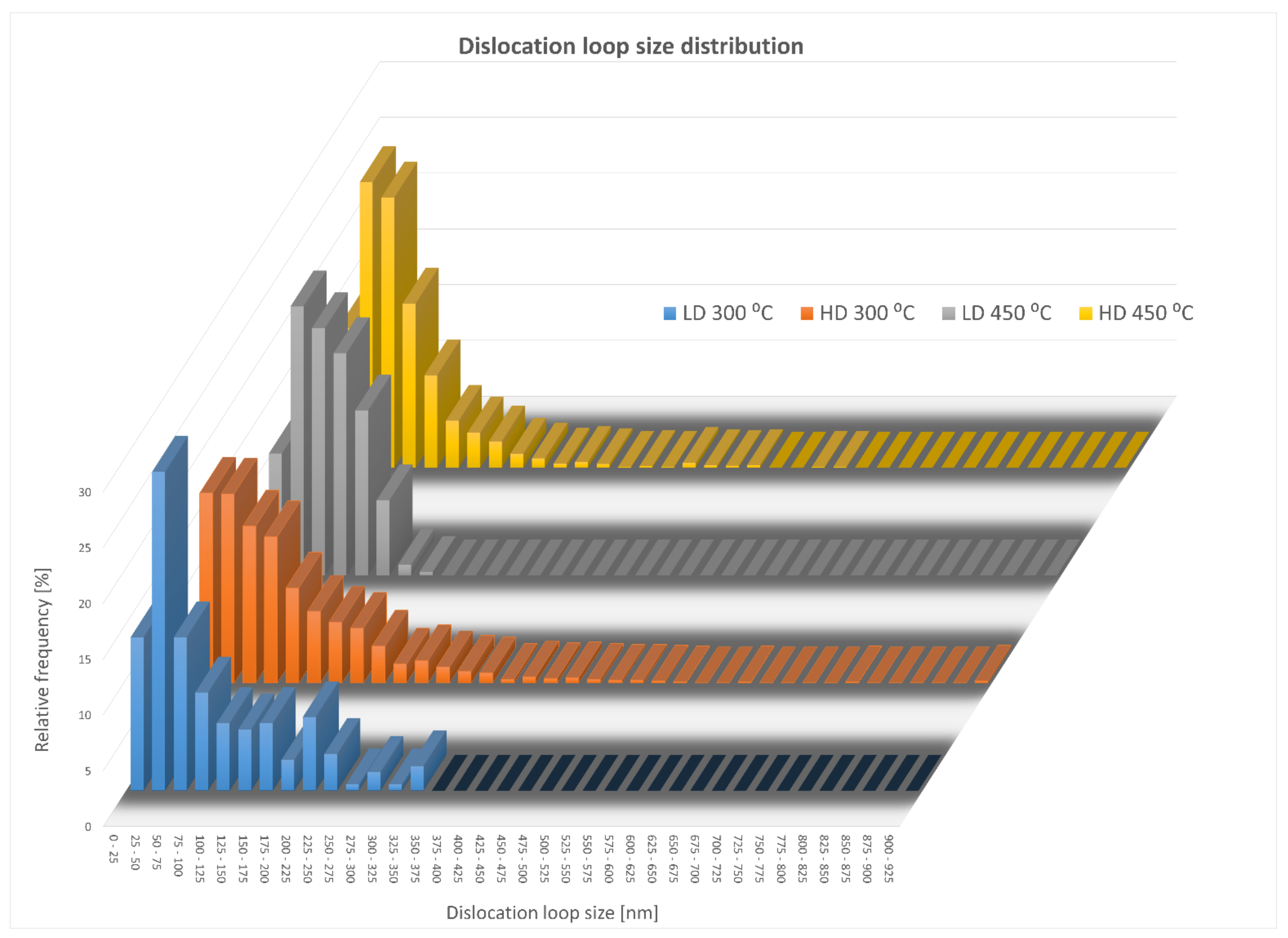
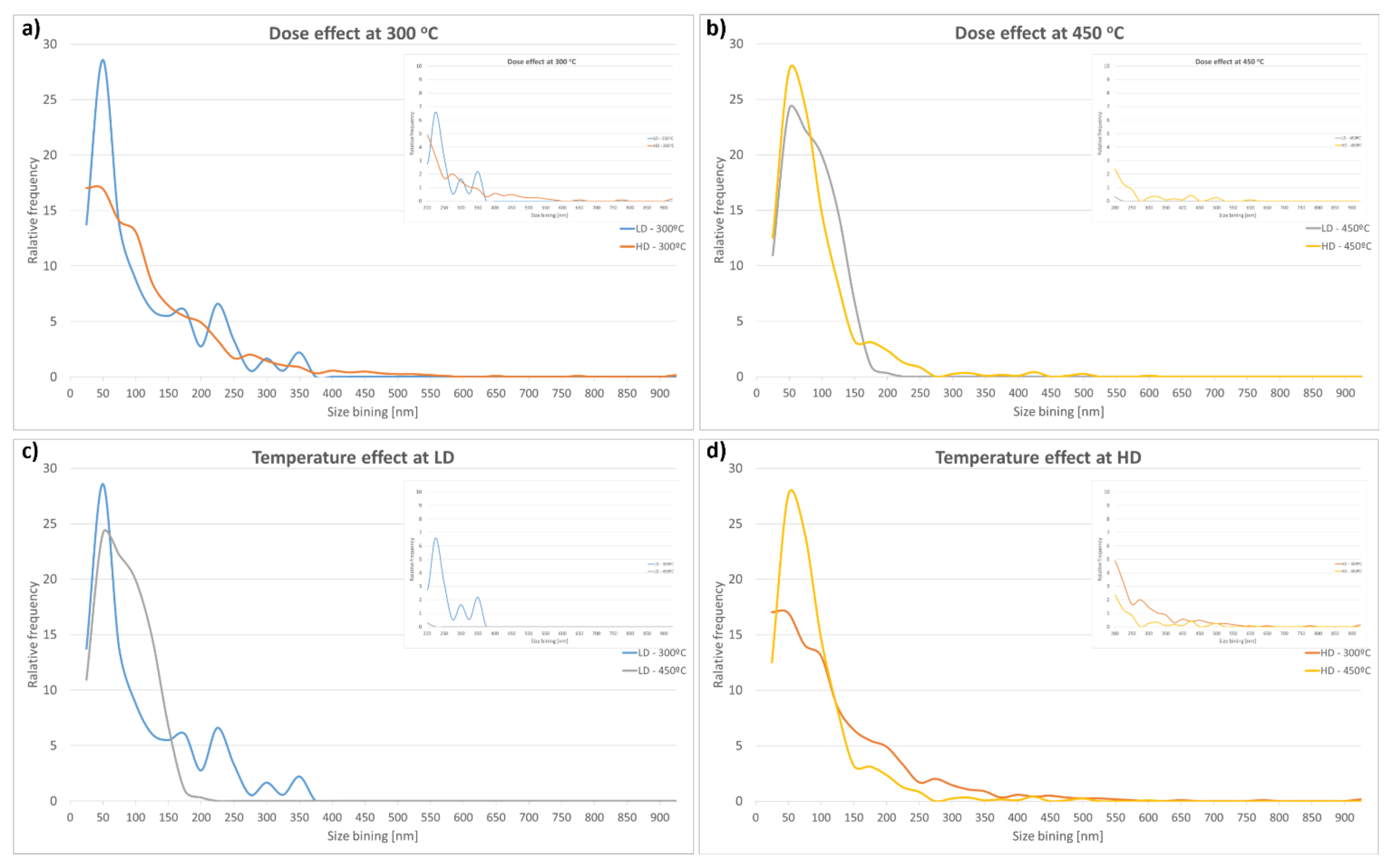
3.3.1. Loop Size Distribution
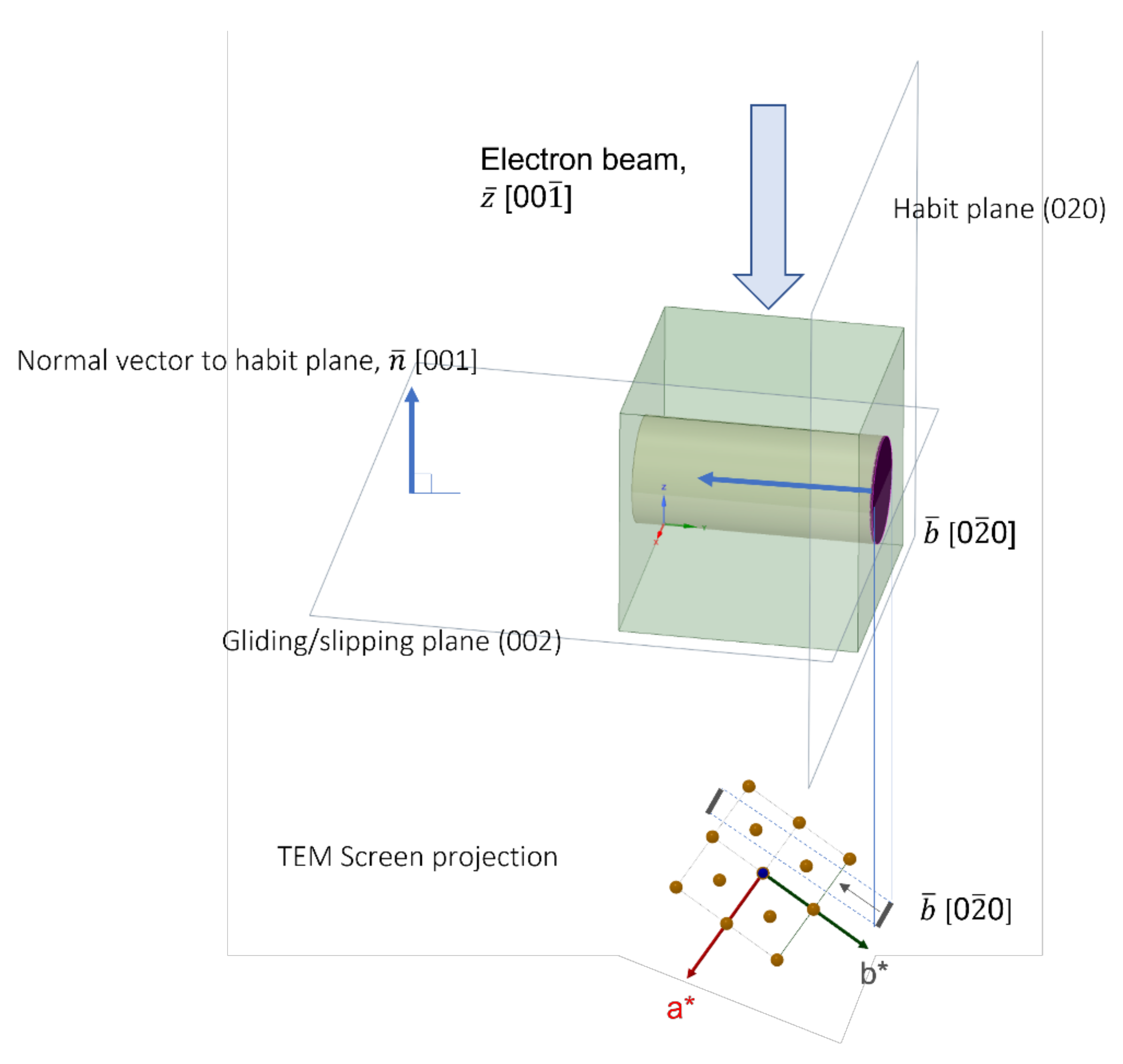
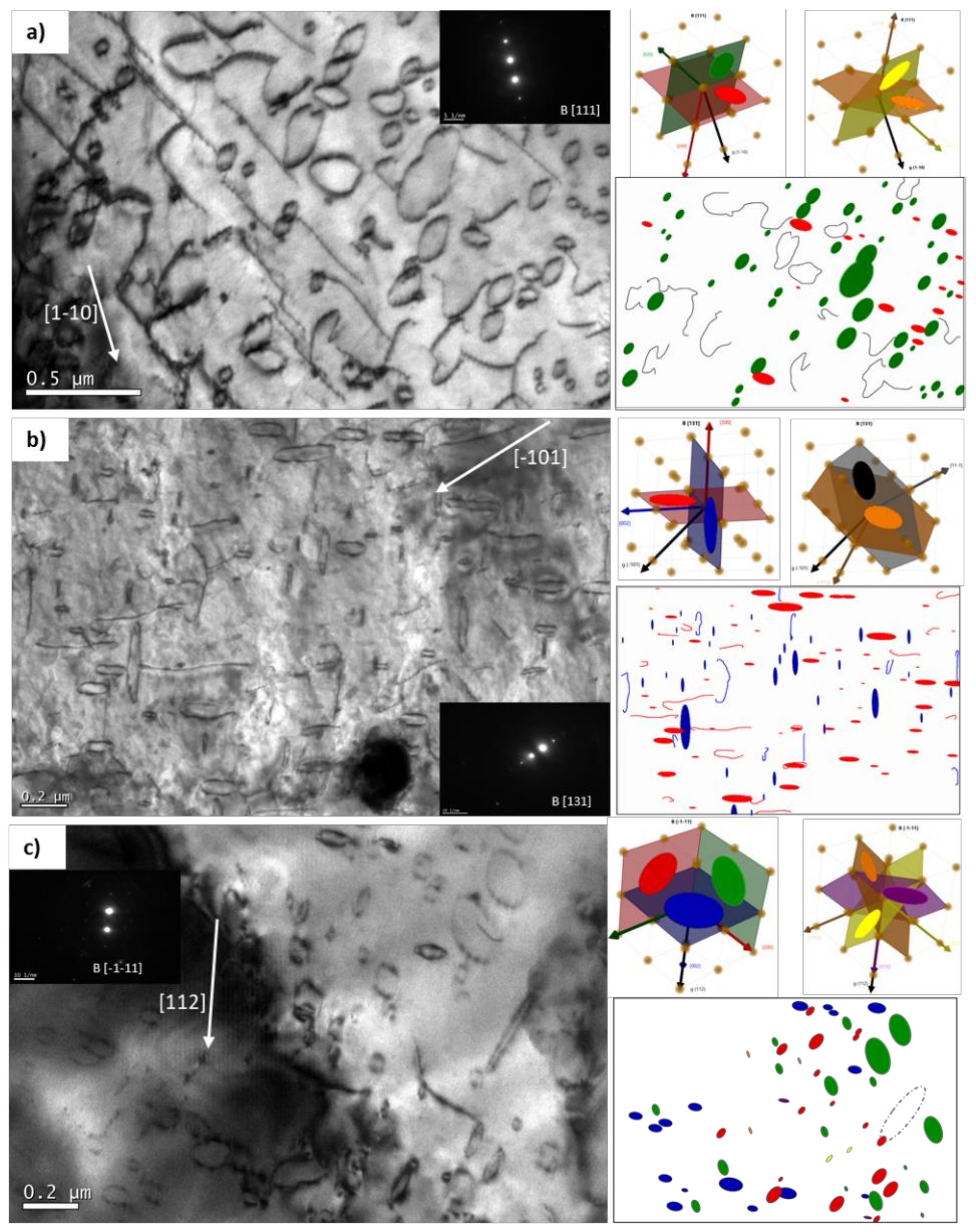
3.3.2. Loop Habit Plane
Low Dose (4.25 × 1015 ion/cm2) at 300 °C
High Dose (8.5 × 1015 ion/cm2) at 300 °C
Low Dose (4.25 × 1015 ion/cm2) at 450 °C
High Dose (8.5 × 1015 ion/cm2) at 450 °C
Analysis of the Results
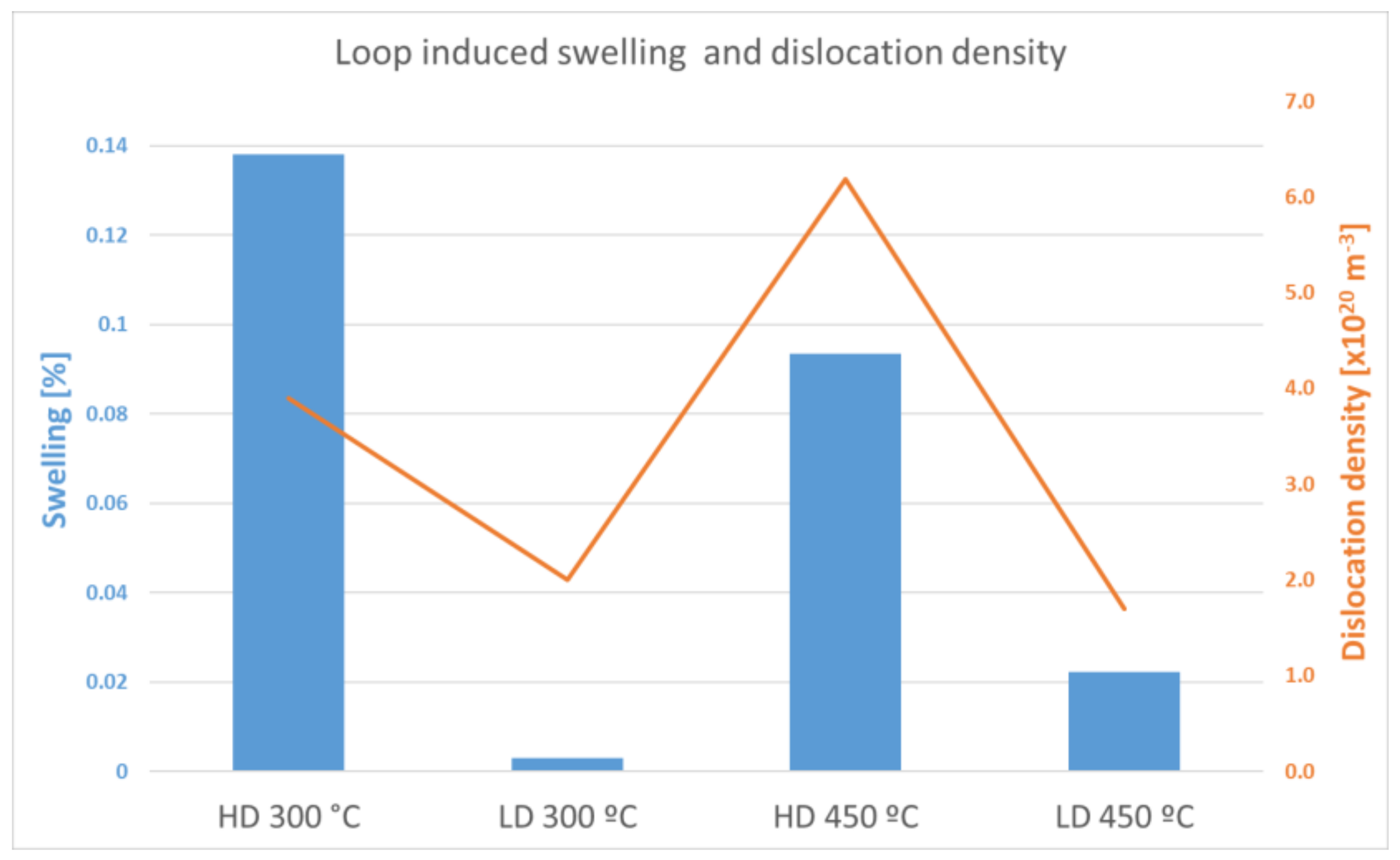
3.3.3. Swelling
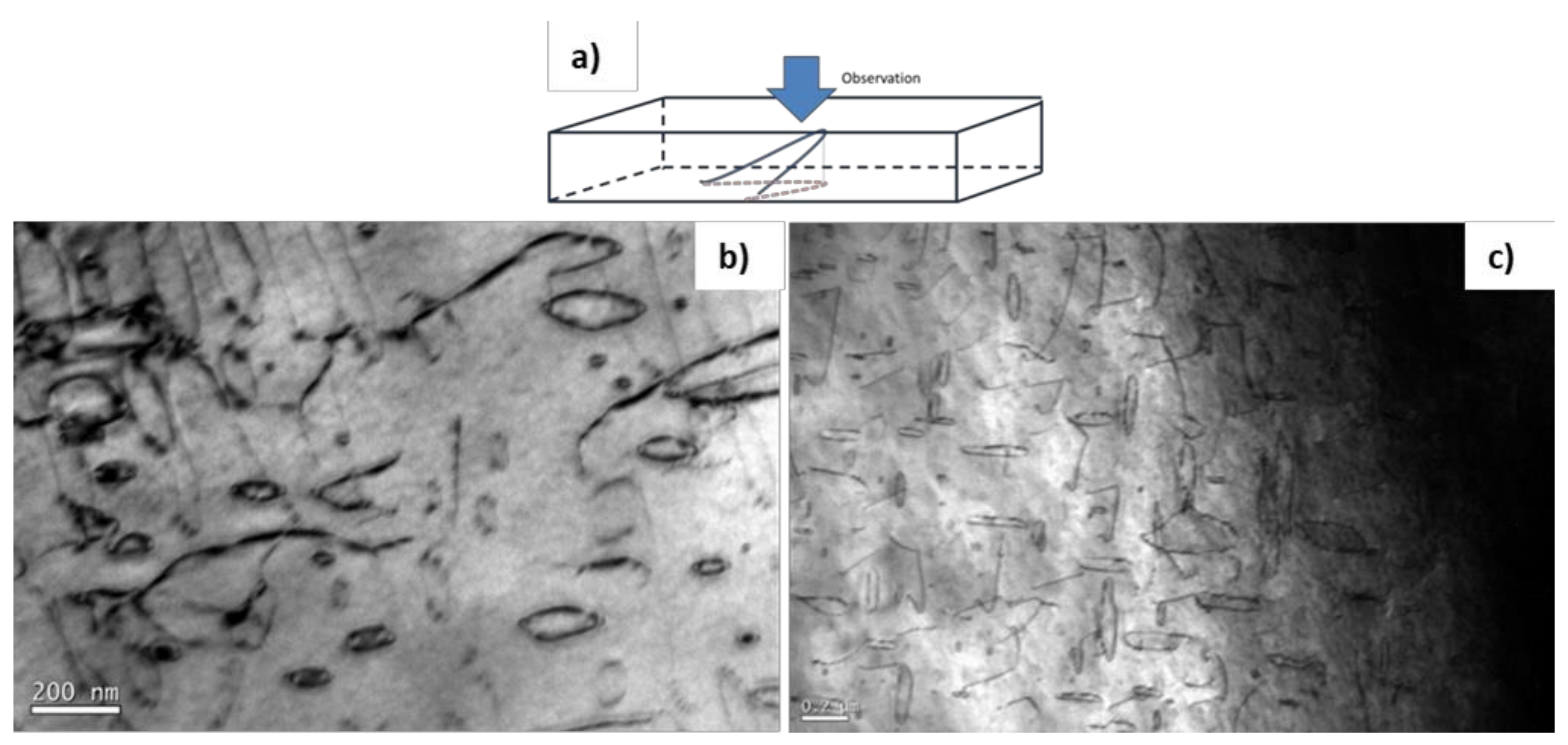
3.3.4. Additional Observation
Effect of Film Thickness
Open Loops
4. Discussion
4.1. Defect Generation during Irradiation
4.2. Effect of Temperature and Dose on Loop Size
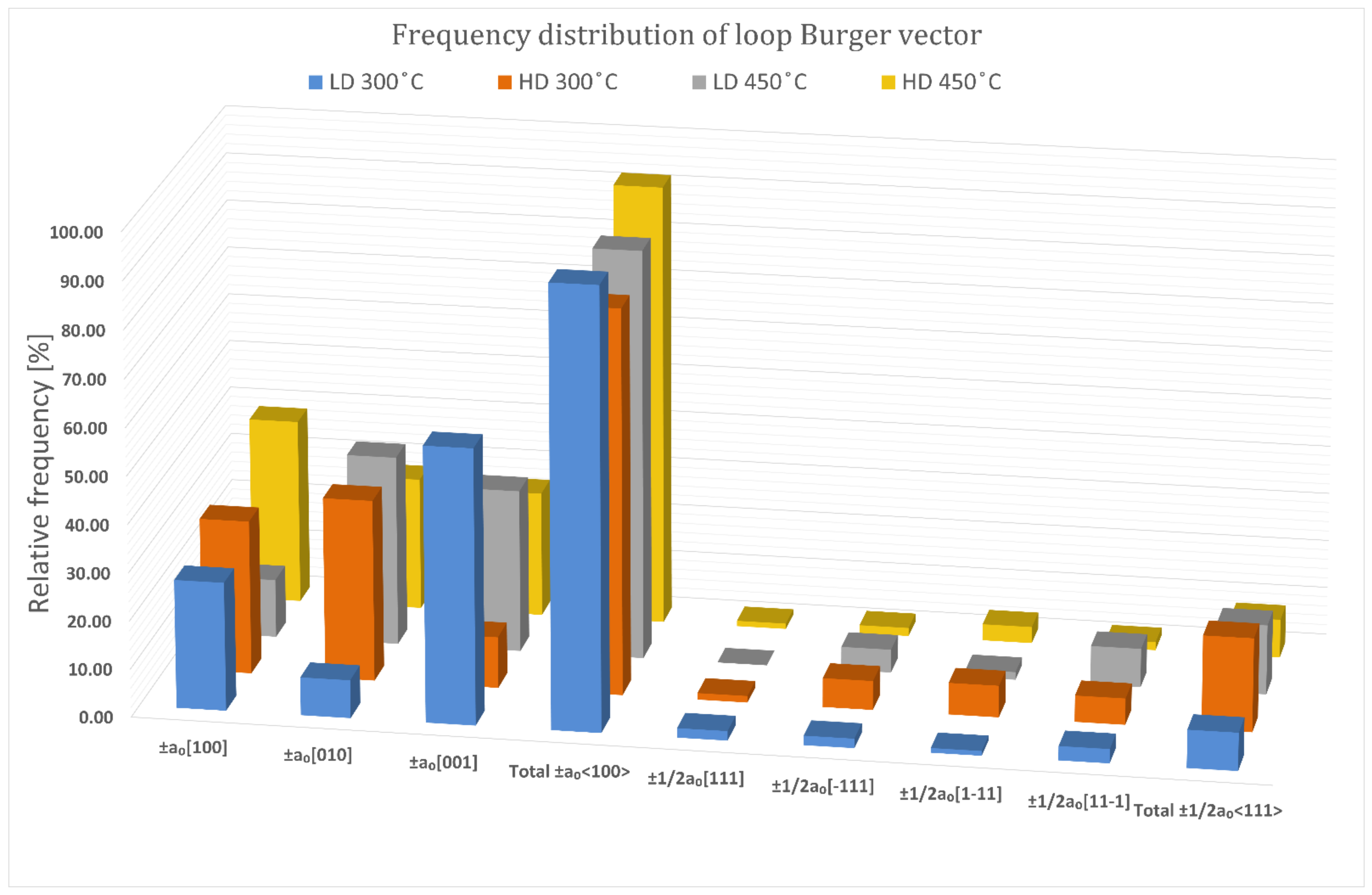
4.3. Burger Vector and Habit Planes
4.4. Open Loops and Free Surfaces
4.5. Nature of Loops (Vacancy or Interstitial)
5. Conclusions
- Apparent differences were found between thin foil irradiation and the first nm in bulk specimens in terms of dislocation loops. There is an evident effect of the reduced volume available for the defects to recombine in thin-film specimens.
- Understanding the complex diffusion mechanism of ±a0<100> loops is a critical step in further exploring the mechanical properties of Fe and Fe-based alloys associated with the formation of ±a0<100> dislocation loops by deformation or radiation.
- Most of the loops identified in all four experimental conditions were b ±a0<100> type, between 80% and 92% in total. With regard to the literature, those dislocations at 300 °C should be ±½a0<111>, and as the irradiation temperature increases, should also be the ±a0<100> loop population. However, in this research, the observations indicated otherwise.
- The highest average loop size value was found for HD 300 °C, and the largest loop, 907 nm, corresponded to nine times the sample thickness. In addition, this experimental condition produced the biggest loop swelling, 0.14%.
- Free surfaces orientation must be taken into consideration to determine the importance of this parameter in terms of defect annihilation or image forces.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Knaster, J. An assessment of the available alternatives for fusion relevant neutron sources. Nucl. Fusion 2018, 58, 095001. [Google Scholar] [CrossRef]
- Haley, J.C.; Briggs, S.A.; Edmondson, P.D.; Sridharan, K.; Roberts, S.G.; Lozano-Perez, S.; Field, K.G. Dislocation loop evolution during in-situ ion irradiation of model FeCrAl alloys. Acta Mater. 2017, 136, 390–401. [Google Scholar] [CrossRef]
- Kaoumi, D.; Adamson, J.; Kirk, M. Microstructure evolution of two model ferritic/martensitic steels under in situ ion irradiation at low doses (0–2dpa). J. Nucl. Mater. 2014, 445, 12–19. [Google Scholar] [CrossRef]
- Kaoumi, D.; Adamson, J. Self-ordered defect structures in two model F/M steels under in situ ion irradiation. J. Nucl. Mater. 2014, 448, 233–238. [Google Scholar] [CrossRef]
- Yang, Z.; Sakaguchi, N.; Watanabe, S.; Kawai, M. Dislocation Loop Formation and Growth under In Situ Laser and/or Electron Irradiation. Sci. Rep. 2011, 1, 190. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Birtcher, R.; Kirk, M.; Furuya, K.; Lumpkin, G.; Ruault, M.-O. In situ Transmission Electron Microscopy Investigation of Radiation Effects. J. Mater. Res. 2005, 20, 1654–1683. [Google Scholar] [CrossRef]
- Kirk, M.A.; Baldo, P.M.; Liu Amelia, C.Y.; Ryan, E.A.; Birtcher, R.C.; Yao, Z.; Xu, L.S.; Jenkins, M.M.; Hernandez-Mayoral, D.; Kaoumi, T.; et al. In situ transmission electron microscopy and ion irradiation of ferritic materials. Microsc. Res. Tech. 2009, 72, 182–186. [Google Scholar] [CrossRef]
- Jenkins, M.L.; Yao, Z.; Hernández-Mayoral, M.; Kirk, M.A. Dynamic observations of heavy-ion damage in Fe and Fe-Cr alloys. J. Nucl. Mater. 2009, 389, 197–202. [Google Scholar] [CrossRef]
- Yao, Z.; Jenkins, M.L.; Hernández-Mayoral, M.; Kirk, M.A. The temperature dependence of heavy-ion damage in iron: A microstructural transition at elevated temperatures. Philos. Mag. 2010, 90, 4623–4634. [Google Scholar] [CrossRef]
- Prokhodtseva, A.; Décamps, B.; Schäublin, R. Comparison between bulk and thin foil ion irradiation of ultra high purity Fe. J. Nucl. Mater. 2013, 442 (Suppl. 1), S786–S789. [Google Scholar] [CrossRef]
- Prokhodtseva, A.; Décamps, B.; Ramar, A.; Schäublin, R. Impact of He and Cr on defect accumulation in ion-irradiated ultrahigh-purity Fe(Cr) alloys. Acta Mater. 2013, 61, 6958–6971. [Google Scholar] [CrossRef]
- Roldán, M.; Fernández, P.; Rams, J.; Jiménez-Rey, D.; Materna-Morris, E.; Klimenkov, M. Comparative study of helium effects on EU-ODS EUROFER and EUROFER97 by nanoindentation and TEM. J. Nucl. Mater. 2015, 460, 226–234. [Google Scholar] [CrossRef]
- Chen, J.; Duval, F.; Jung, P.; Schäublin, R.; Gao, N.; Barthe, M.-F. Dislocation loops in ultra-high purity Fe(Cr) alloys after 7.2 MeV proton irradiation. J. Nucl. Mater. 2018, 503, 81–90. [Google Scholar] [CrossRef]
- Nordlund, K.; Zinkle, S.J.; Sand, A.E.; Granberg, F.; Averback, R.S.; Stoller, R.E.; Suzudo, T.; Malerba, L.; Banhart, F.; Weber, W.J.; et al. Primary radiation damage: A review of current understanding and models. J. Nucl. Mater. 2018, 512, 450–479. [Google Scholar] [CrossRef]
- Fikar, J.; Gröger, R. Interactions of prismatic dislocation loops with free surfaces in thin foils of body-centered cubic iron. Acta Mater. 2015, 99, 392–401. [Google Scholar] [CrossRef]
- Stoller, R. The effect of free surfaces on cascade damage production in iron. J. Nucl. Mater. 2002, 307–311, 935–940. [Google Scholar] [CrossRef]
- Korchuganov, A.V.; Zolnikov, K.P.; Kryzhevich, D.S.; Psakhie, S.G. Primary Ion-Irradiation Damage of BCC-Iron Surfaces. Russ. Phys. J. 2017, 60, 170–174. [Google Scholar] [CrossRef]
- Knaster, J.; Moeslang, A.; Muroga, T. Materials research for fusion. Nat. Phys. 2016, 12, 424–434. [Google Scholar] [CrossRef]
- Tan, L.; Snead, L.; Katoh, Y. Development of new generation reduced activation ferritic-martensitic steels for advanced fusion reactors. J. Nucl. Mater. 2016, 478, 42–49. [Google Scholar] [CrossRef] [Green Version]
- Fernández, P.; Hoffmann, J.; Rieth, M.; Roldán, M.; Gómez-Herrero, A. TEM characterisation on new 9% Cr advanced steels thermomechanical treated after tempering. J. Nucl. Mater. 2018, 500, 1–10. [Google Scholar] [CrossRef]
- Roldán, M.; Galán, P.; Sánchez, F.J.; García-Cortés, I.; Jiménez-Rey, D.; Fernández, P. Ion Beam Experiments to Emulate Nuclear Fusion Environment on Structural Materials at CMAM; IntechOpen: London, UK, 2018. [Google Scholar]
- Jenkins, M.L.; Yao, Z.; Hernández-Mayoral, M.; Kirk, M.A. Direct in-situ electron microscope observations of the dynamics of irradiation damage effects in Fe and FeCr alloys. J. Nucl. Mater. 2009, 389, 197–202. [Google Scholar] [CrossRef]
- Le Coze, J. Procurement of Pure Fe Metal and Fe-Based Alloys with Controlled Chemical Alloying Element Contents and Microstructure; Final Report on Model Alloy Preparation; Armines Ecole Nationale Superieure des Mines: Saint Etienne, France, 2007. [Google Scholar]
- Roldán, M.; Fernández, P.; Vila, R.; Gómez-Herrero, A.; Sánchez, F.J. The effect of triple ion beam irradiation on cavity formation on pure EFDA iron. J. Nucl. Mater. 2016, 479, 100–111. [Google Scholar] [CrossRef]
- Saavedra, R.; Jiménez-Rey, D.; Martin, P.; Vila, R. Ionoluminescence of fused silica under swift ion irradiation. Nucl. Instrum. Methods Phys. Res. Sect. B 2016, 382, 96–100. [Google Scholar] [CrossRef]
- Stoller, R.E.; Toloczko, M.B.; Was, G.S.; Certain, A.G.; Dwaraknath, S.; Garner, F.A. On the use of SRIM for computing radiation damage exposure. Nucl. Instrum. Methods Phys. Res. Sect. B 2013, 310, 75–80. [Google Scholar] [CrossRef]
- Kato, N.I. Reducing focused ion beam damage to transmission electron microscopy samples. J. Electron Microsc. 2004, 53, 451–458. [Google Scholar] [CrossRef] [PubMed]
- Howie, A.; Whelan, M.J. Diffraction contrast of electron microscope images of crystal lattice defects. III. Results and experimental confirmation of the dynamical theory of dislocation image contrast. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1962, 267, 206–230. [Google Scholar]
- Yao, B.; Edwards, D.J.; Kurtz, R.J. TEM characterisation of dislocation loops in irradiated bcc Fe-based steels. J. Nucl. Mater. 2013, 434, 402–410. [Google Scholar] [CrossRef]
- Qing, L. An equation to determine the practical tilt angle of a double-tilt specimen holder and its application to transmission electron microscopy. Micron Microsc. Acta 1989, 20, 261–264. [Google Scholar] [CrossRef]
- Maher, D.M.; Eyre, B.L. Neutron irradiation damage in molybdenum. Philos. Mag. 1971, 23, 409–438. [Google Scholar] [CrossRef]
- Eyre, B.L.; Perrin, R.C.; Maher, D.M. Electron microscope image contrast from small dislocation loops. I. Theoretical predictions for edge dislocation loops in a BCC crystal. J. Phys. F Met. Phys. 1977, 7, 1359–1369. [Google Scholar] [CrossRef]
- Williams, D.B.; Barry, C.C. Transmission Electron Microscopy: A Textbook for Materials; Springer: Berlin/Heidelberg, Germany, 2009; p. 779. [Google Scholar]
- Robinson, M.T.; Torrens, I.M. Computer simulation of atomic-displacement cascades in solids in the binary-collision approximation. Phys. Rev. B 1974, 12, 5008–5024. [Google Scholar] [CrossRef]
- Robinson, M.T. Slowing-down time of energetic atoms in solids. Phys. Rev. B 1989, 40, 10717–10726. [Google Scholar] [CrossRef]
- Broeders, C.; Konobeyev, A. Defect production efficiency in metals under neutron irradiation. J. Nucl. Mater. 2004, 328, 197–214. [Google Scholar] [CrossRef]
- Domain, C.; Becquart, C.S. Ab initio calculations of defects in Fe and dilute Fe-Cu alloys. Phys. Rev. B 2001, 65, 024103. [Google Scholar] [CrossRef]
- Willaime, C.-C.F.F.; Ordejón, P. Stability and Mobility of Mono- and Di-Interstitials in alpha-Fe. Phys. Rev. Lett. 2004, 92, 175503. [Google Scholar]
- Fu, C.-C.; Torre, J.D.; Willaime, F.; Bocquet, J.-L.; Barbu, A. Multiscale modelling of defect kinetics in irradiated iron. Nat. Mater. 2004, 4, 68–74. [Google Scholar] [CrossRef]
- Heald, P.T. The preferential trapping of interstitials at dislocations. Philos. Mag. J. Theor. Exp. Appl. Phys. 1975, 31, 551–558. [Google Scholar] [CrossRef]
- Aliaga, M.; Schäublin, R.; Löffler, J.F.; Caturla, M. Surface-induced vacancy loops and damage dispersion in irradiated Fe thin films. Acta Mater. 2015, 101, 22–30. [Google Scholar] [CrossRef]
- Hales, R.; Smallman, R.E.; Dobson, P.S. The Formation and Growth of Vacancy Loops in Magnesium. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1968, 307, 71–81. [Google Scholar]
- Terentyev, D.A.; Klaver, T.P.C.; Olsson, P.; Marinica, M.-C.; Willaime, F.; Domain, C.; Malerba, L. Self-Trapped Interstitial-Type Defects in Iron. Phys. Rev. Lett. 2008, 100, 145503. [Google Scholar] [CrossRef]
- Hernández-Mayoral, M.; Yao, Z.; Jenkins, M.; Kirk, M. Heavy-ion irradiations of Fe and Fe-Cr model alloys Part 2: Damage evolution in thin-foils at higher doses. Philos. Mag. 2008, 88, 2881–2897. [Google Scholar] [CrossRef]
- Gilbert, M.; Dudarev, S.L.; Derlet, P.M.; Pettifor, D.G. Structure and metastability of mesoscopic vacancy and interstitial loop defects in iron and tungsten. J. Phys. Condens. Matter 2008, 20, 345214. [Google Scholar] [CrossRef]
- Dai, C.; Long, F.; Saidi, P.; Béland, L.K.; Yao, Z.; Daymond, M.R. Primary damage production in the presence of extended defects and growth of vacancy-type dislocation loops in hcp zirconium. Phys. Rev. Mater. 2019, 3, 043602. [Google Scholar] [CrossRef] [Green Version]
- Fikar, J.; Schäublin, R.; Mason, D.R.; Nguyen-Manh, D. Nano-sized prismatic vacancy dislocation loops and vacancy clusters in tungsten. Nucl. Mater. Energy 2018, 16, 60–65. [Google Scholar] [CrossRef]
- Byggmästar, J.; Granberg, F. Dynamical stability of radiation-induced C15 clusters in iron. J. Nucl. Mater. 2019, 528, 151893. [Google Scholar] [CrossRef]
- Granberg, F.; Byggmästar, J.; Nordlund, K. Defect accumulation and evolution during prolonged irradiation of Fe and FeCr alloys. J. Nucl. Mater. 2019, 528, 151843. [Google Scholar] [CrossRef]
- Arakawa, K.; Amino, T.; Mori, H. Direct observation of the coalescence process between nanoscale dislocation loops with different Burgers vectors. Acta Mater. 2011, 59, 141–145. [Google Scholar] [CrossRef]
- Grammatikopoulos, P.; Bacon, D.J.; Osetsky, Y.N. Simulation of the interaction between an edge dislocation and ⟨111⟩ interstitial dislocation loops in α-iron. Radiat. Eff. Defects Solids 2019, 174, 329–338. [Google Scholar] [CrossRef]
- Hull, D.; Bacon, D.J. Introduction to Dislocations; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Gao, N.; Yao, Z.W.; Lu, G.H.; Deng, H.Q.; Gao, F. Mechanisms for interstitial dislocation loops to diffuse in BCC iron. Nat. Commun. 2021, 12, 225. [Google Scholar] [CrossRef]
- Alexander, R.; Proville, L.; Becquart, C.S.; Goryeava, A.M.; Dérès, J.; Lapointe, C.; Marinica, M.C. Interatomic potentials for irradiation-induced defects in iron. J. Nucl. Mater. 2020, 535, 152141. [Google Scholar] [CrossRef]
- Byggmästar, J.; Granberg, F.; Sand, A.E.; Pirttikoski, A.; Alexander, R.; Marinica, M.-C.; Nordlund, K. Collision cascades overlapping with self-interstitial defect clusters in Fe and W. J. Phys. Condens. Matter 2019, 31, 245402. [Google Scholar] [CrossRef] [Green Version]
- Stoller, R.E. The role of cascade energy and temperature in primary defect formation in iron. J. Nucl. Mater. 2000, 276, 22–32. [Google Scholar] [CrossRef] [Green Version]
- Zinkle, S.J. Microstructures and mechanical properties of irradiated metals and alloys. In Materials Issues for Generation IV Systems; Ghetta, D.V., Gorse, D.M., Pontikis, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 227–244. [Google Scholar]
- Li, Y.; Boleininger, M.; Robertson, C.; Dupuy, L.; Dudarev, S.L. Diffusion and interaction of prismatic dislocation loops simulated by stochastic discrete dislocation dynamics. Phys. Rev. Mater. 2019, 3, 073805. [Google Scholar] [CrossRef]
- Jenkins, M.; Kirk, M.; Phythian, W. Experimental studies of cascade phenomena in metals. J. Nucl. Mater. 1993, 205, 16–30. [Google Scholar] [CrossRef] [Green Version]
- Souidi, A.; Hou, M.; Becquart, C.S.; Domain, C. Atomic displacement cascade distributions in iron. J. Nucl. Mater. 2001, 295, 179–188. [Google Scholar] [CrossRef]
- Kirk, M.; Robertson, I.; Vetrano, J.; Jenkins, M.; Funk, L. The Collapse of Defect Cascades to Dislocation Loops during Self-Ion Irradiations of Iron, Nickel, and Copper at 30, 300, and 600 K; ASTM: West Conshohocken, PA, USA, 1987. [Google Scholar]
- Kim, Y.S. Primary radiation damage characterisation of α-iron under irradiation temperature for various PKA energies. Mater. Res. Express 2018, 5, 046518. [Google Scholar]
- Straalsund, J.; Powell, R.; Chin, B. An overview of neutron irradiation effects in LMFBR materials. J. Nucl. Mater. 1982, 108–109, 299–305. [Google Scholar] [CrossRef]
- Brailsford, A.; Mansur, L. Effect of self-ion injection in simulation studies of void swelling. J. Nucl. Mater. 1977, 71, 110–116. [Google Scholar] [CrossRef]
- Cawthorne, C.; Fulton, E.J. Voids in Irradiated Stainless Steel. Nature 1967, 216, 575–576. [Google Scholar] [CrossRef]
- Garner, F.A. Radiation-induced damage in austenitic structural steels used in nuclear reactors. In Comprehensive Nuclear Materials, 2nd ed.; Konings, R.J.M., Stoller, R.E., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 57–168. [Google Scholar]
- Hashimoto, N.; Kasada, R.; Raj, B.; Vijayalakshmi, M. Radiation effects in ferritic steels and advanced ferritic-martensitic steels. In Comprehensive Nuclear Materials, 2nd ed.; Konings, R.J.M., Stoller, R.E., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 226–254. [Google Scholar]
- Golubov, S.; Singh, B.; Trinkaus, H. Defect accumulation in fcc and bcc metals and alloys under cascade damage conditions—Towards a generalisation of the production bias model. J. Nucl. Mater. 2000, 276, 78–89. [Google Scholar] [CrossRef]
- Becquart, C.S.; Domain, C.; Legris, A.; van Duysen, J.C. Influence of the interatomic potentials on molecular dynamics simulations of displacement cascades. J. Nucl. Mater. 2000, 280, 73–85. [Google Scholar] [CrossRef]
- Kuramoto, E.; Ohsawa, K.; Imai, J.; Obata, K.; Tsutsumi, T. Bias Mechanism and Its Effects for Fundamental Process of Irradiation Damage. Mater. Trans. 2004, 45, 34–39. [Google Scholar] [CrossRef]
- Swinburne, T.D.; Arakawa, K.; Mori, H.; Yasuda, H.; Isshiki, M.; Mimura, K.; Uchikoshi, M.; Dudarev, S.L. Fast, vacancy-free climb of prismatic dislocation loops in bcc metals. Sci. Rep. 2016, 6, 30596. [Google Scholar] [CrossRef] [PubMed]
- Arakawa, K.; Amino, T.; Yasuda, H.; Mori, H. <110>Dislocation Junction Formation via the Coalescence between Nanoscale 1/2 <111> Prismatic Dislocation Loops in Iron. ISIJ Int. 2017, 57, 2065–2069. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Stoller, R.E.; Osetsky, Y.N.; Terentyev, D. Solving the Puzzle of ⟨100⟩ Interstitial Loop Formation in bcc Iron. Phys. Rev. Lett. 2013, 110, 265503. [Google Scholar] [CrossRef] [Green Version]
- Yao, Z.; Hernández-Mayoral, M.; Jenkins, M.L.; Kirk, M.A. Heavy-ion irradiations of Fe and Fe-Cr model alloys Part 1: Damage evolution in thin-foils at lower doses. Philos. Mag. 2008, 88, 2851–2880. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.-R.; Chen, W.-Y.; Li, M.; Henry, J.; Zinkle, S.J. Dynamic observation of dual-beam irradiated Fe and Fe-10Cr alloys at 435 °C. Acta Mater. 2021, 209, 116793. [Google Scholar] [CrossRef]
- Zinkle, S.; Singh, B. Microstructure of neutron-irradiated iron before and after tensile deformation. J. Nucl. Mater. 2006, 351, 269–284. [Google Scholar] [CrossRef]
- Eyre, B.L.; Bartlett, A.F. An electron microscope study of neutron irradiation damage in alpha-iron. Philos. Mag. J. Theor. Exp. Appl. Phys. 1965, 12, 261–272. [Google Scholar] [CrossRef]
- Horton, L.L.; Bentley, J.; Farrell, K. TEM study of neutron-irradiated iron. J. Nucl. Mater. 1982, 108–109, 222–233. [Google Scholar] [CrossRef] [Green Version]
- Matijasevic, M.; van Renterghem, W.; Almazouzi, A. Characterisation of irradiated single crystals of Fe and Fe-15Cr. Acta Mater. 2009, 57, 1577–1585. [Google Scholar] [CrossRef]
- Konobeev, Y.V.; Dvoriashin, A.M.; Porollo, S.I.; Garner, F.A. Garner, Swelling and microstructure of pure Fe and Fe-Cr alloys after neutron irradiation to ∼26 dpa at 400 °C. J. Nucl. Mater. 2006, 355, 124–130. [Google Scholar] [CrossRef]
- Hernández-Mayoral, M.; Gómez-Briceño, D. Transmission electron microscopy study on neutron irradiated pure iron and RPV model alloys. J. Nucl. Mater. 2010, 399, 146–153. [Google Scholar] [CrossRef]
- Chang, Z.; Terentyev, D.; Sandberg, N.; Samuelsson, K.; Olsson, P. Anomalous bias factors of dislocations in bcc iron. J. Nucl. Mater. 2015, 461, 221–229. [Google Scholar] [CrossRef] [Green Version]
- Loretto, M.H. Electron Beam Analysis of Materials; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Kirk, M.; Yi, X.; Jenkins, M. Characterisation of irradiation defect structures and densities by transmission electron microscopy. J. Mater. Res. 2015, 30, 1195–1201. [Google Scholar] [CrossRef]
- Johnson, R.A. Interstitials and Vacancies in α Iron. Phys. Rev. 1964, 134, A1329–A1336. [Google Scholar] [CrossRef]
- Surh, M.P.; Sturgeon, J.B.; Wolfer, W.G. Void nucleation, growth, and coalescence in irradiated metals. J. Nucl. Mater. 2008, 378, 86–97. [Google Scholar] [CrossRef] [Green Version]
- Cottrell, G.A. Void migration, coalescence and swelling in fusion materials. Fusion Eng. Design 2003, 66–68, 253–257. [Google Scholar] [CrossRef]
- Li, X.; Liu, W.; Xu, Y.; Liu, C.; Pan, B.; Liang, Y.; Fang, Q.; Chen, J.-L.; Luo, G.-N.; Lu, G.-H.; et al. Energetic and kinetic dataset on interaction of the vacancy and self-interstitial atom with the grain boundary in α-iron. Data Brief. 2016, 7, 798–813. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Robertson, I.M.; Jenkins, M.L.; English, C.A. Low-dose neutron-irradiation damage in alfa iron. J. Nucl. Mater. 1982, 108, 12. [Google Scholar]
- Marian, J.; Wirth, B.D.; Schäublin, R.; Perlado, J.M.; de la Rubia, T.D. <100>-Loop characterisation in α-Fe: Comparison between experiments and modeling. J. Nucl. Mater. 2002, 307, 871–875. [Google Scholar] [CrossRef]




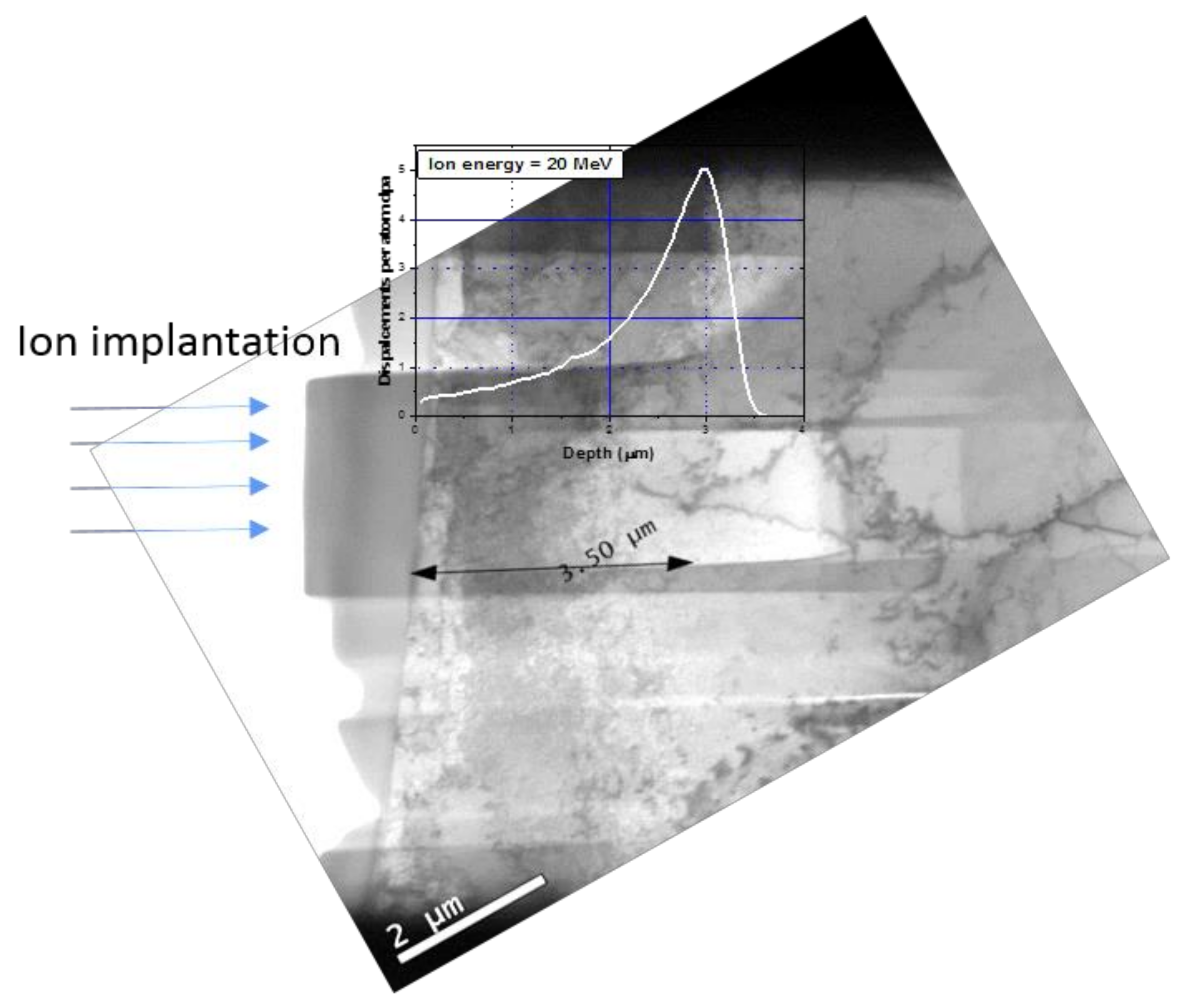

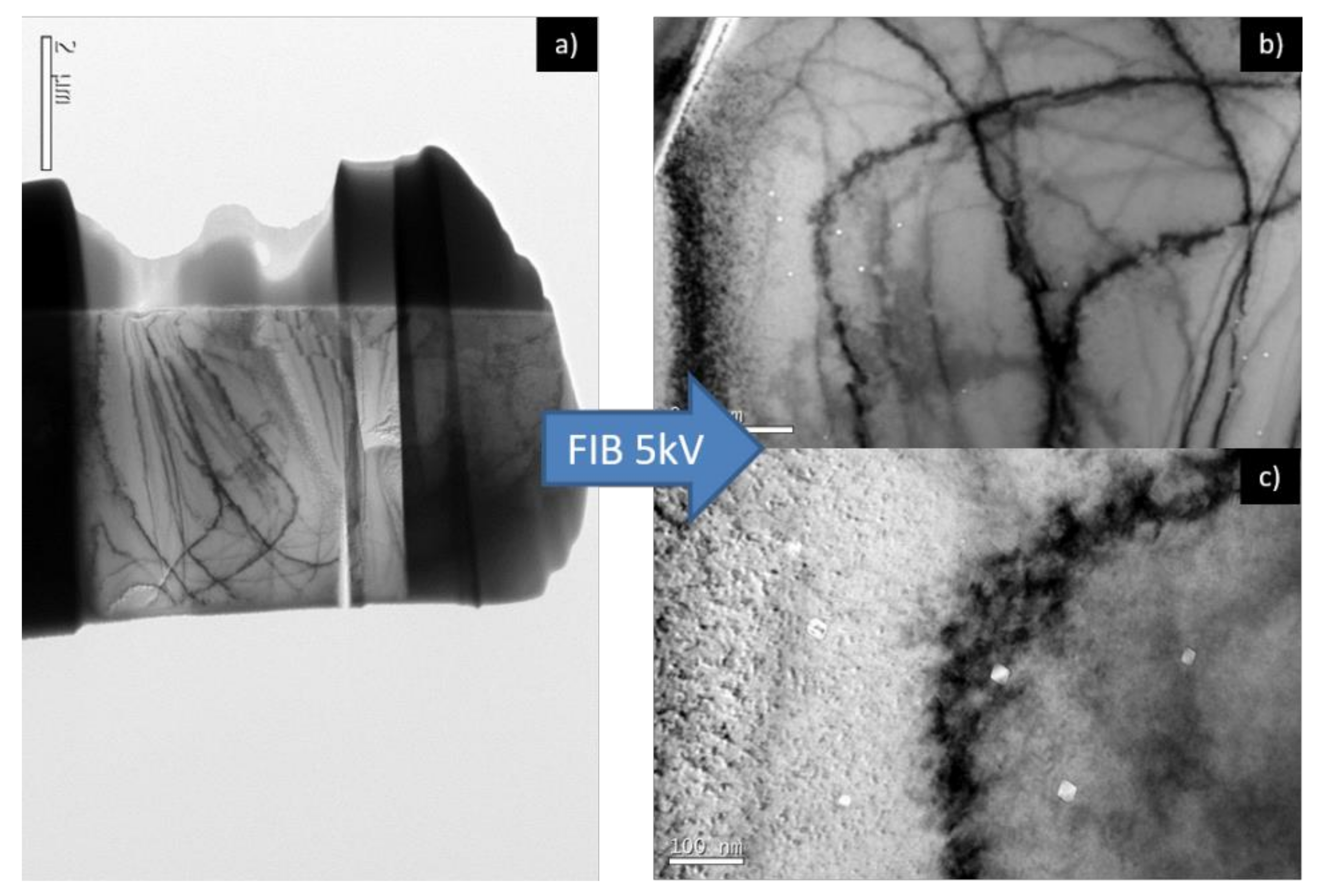
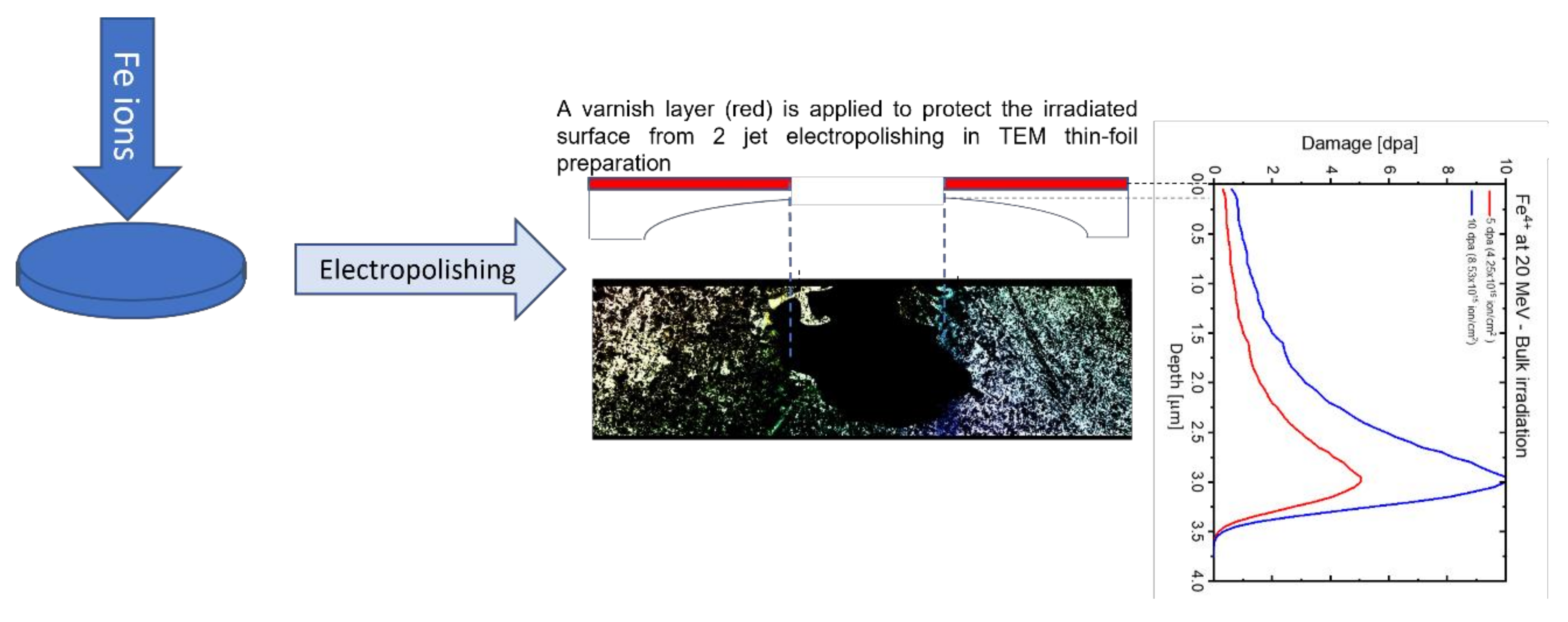
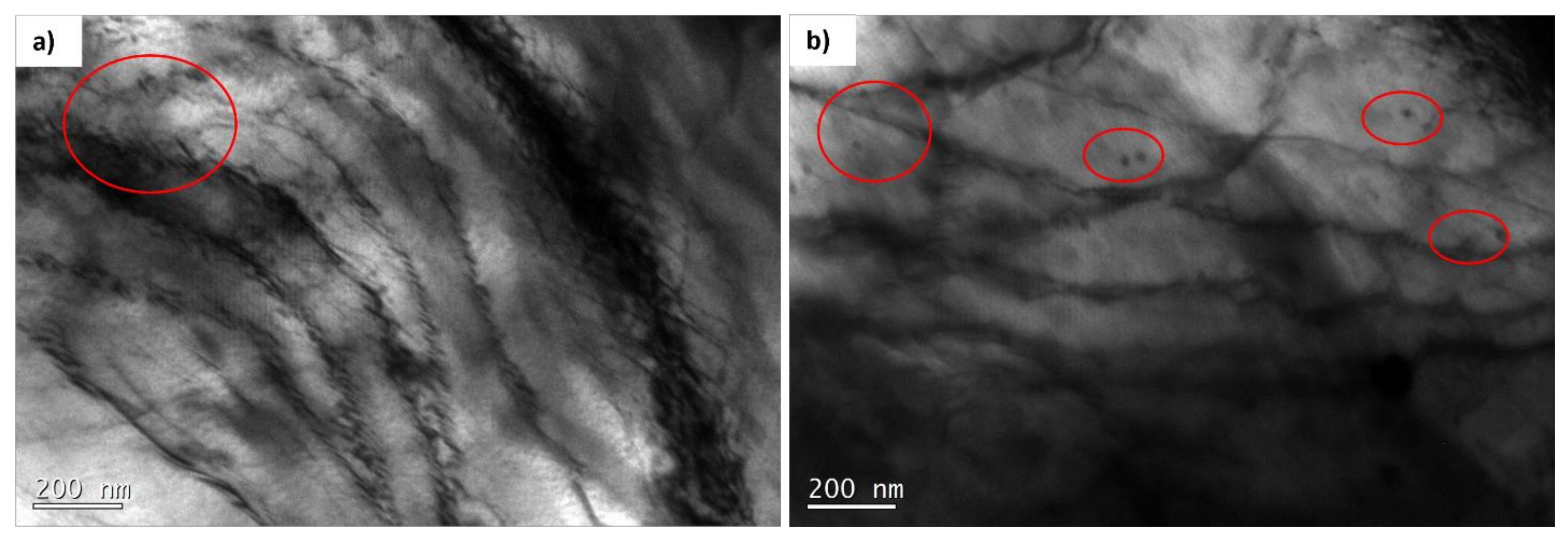









| C | S | O | N | P | Cr | |
|---|---|---|---|---|---|---|
| (wt ppm) | 4.3 | 1.3 | 4 | 3.6 | 0.03 | 0.03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roldán, M.; Sánchez, F.J.; Fernández, P.; Ortiz, C.J.; Gómez-Herrero, A.; Rey, D.J. Dislocation Loop Generation Differences between Thin Films and Bulk in EFDA Pure Iron under Self-Ion Irradiation at 20 MeV. Metals 2021, 11, 2000. https://doi.org/10.3390/met11122000
Roldán M, Sánchez FJ, Fernández P, Ortiz CJ, Gómez-Herrero A, Rey DJ. Dislocation Loop Generation Differences between Thin Films and Bulk in EFDA Pure Iron under Self-Ion Irradiation at 20 MeV. Metals. 2021; 11(12):2000. https://doi.org/10.3390/met11122000
Chicago/Turabian StyleRoldán, Marcelo, Fernando José Sánchez, Pilar Fernández, Christophe J. Ortiz, Adrián Gómez-Herrero, and David Jiménez Rey. 2021. "Dislocation Loop Generation Differences between Thin Films and Bulk in EFDA Pure Iron under Self-Ion Irradiation at 20 MeV" Metals 11, no. 12: 2000. https://doi.org/10.3390/met11122000
APA StyleRoldán, M., Sánchez, F. J., Fernández, P., Ortiz, C. J., Gómez-Herrero, A., & Rey, D. J. (2021). Dislocation Loop Generation Differences between Thin Films and Bulk in EFDA Pure Iron under Self-Ion Irradiation at 20 MeV. Metals, 11(12), 2000. https://doi.org/10.3390/met11122000







