Defectoscopic and Geometric Features of Defects That Occur in Sheet Metal and Their Description Based on Statistical Analysis
Abstract
:1. Introduction
- −
- Identifying technological reasons for the formation of defects during rolling;
- −
- Studying and systematizing the morphological description of defects of different shapes and determining their description’s parameter ranges.
2. Technological and Morphological Prerequisites for Classification
Technological Defects and Causes of Their Occurrence
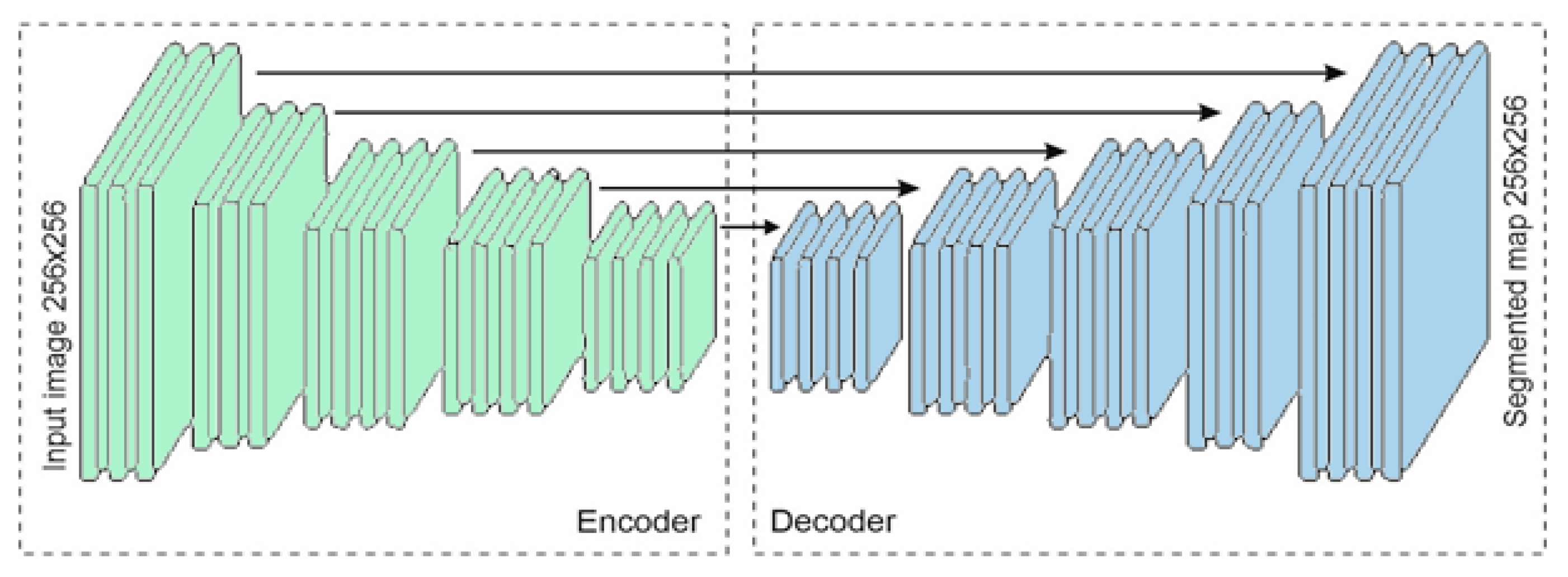
3. Method for Detecting Defective Zones
4. Defect Geometry Analysis
5. Morphological Analysis Results
6. Attribute Selection
- −
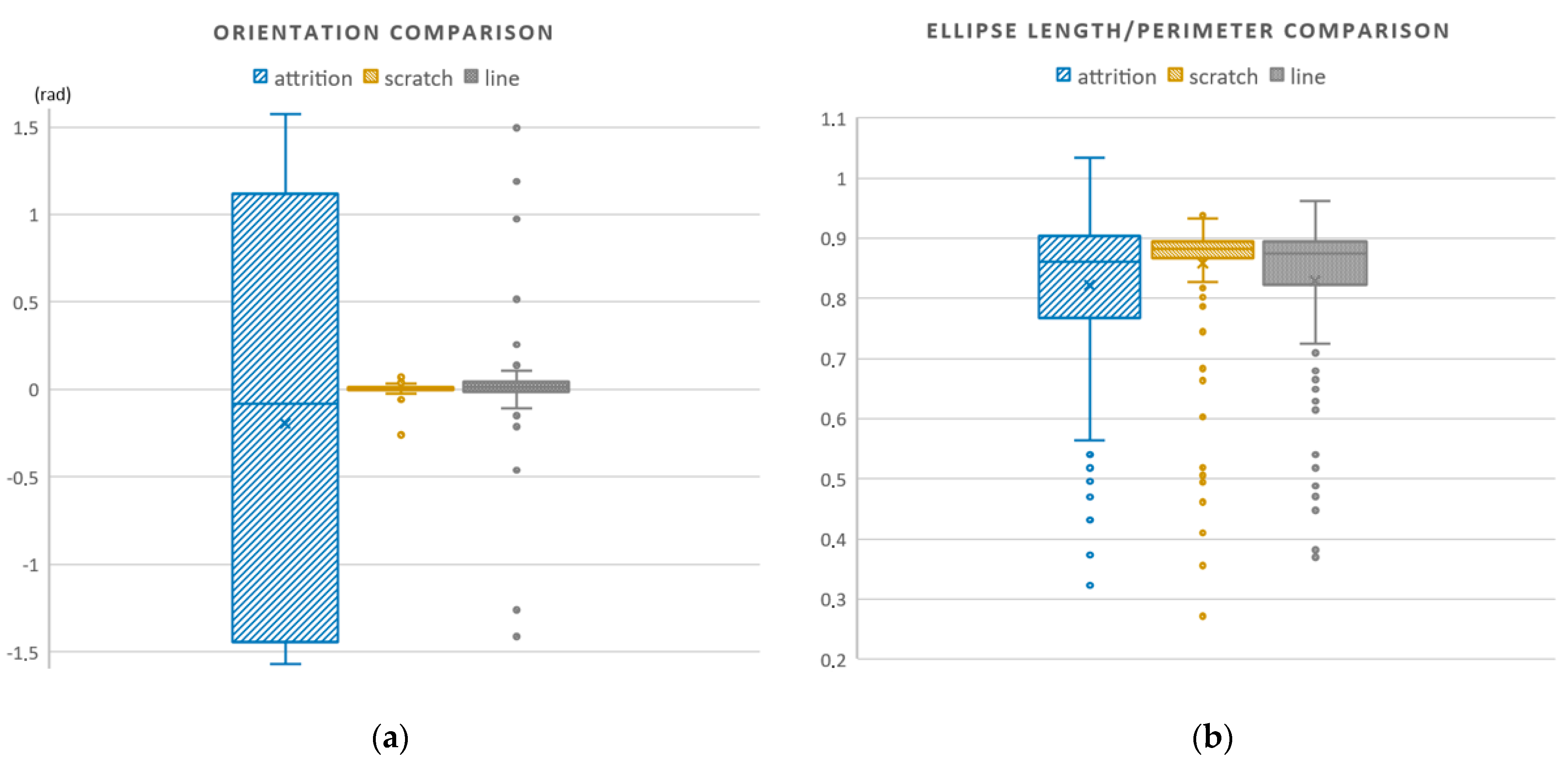
- Eccentricity of the defect ellipse, which shows the proximity of its shape to the circle (Eccentricity);
- −
- The angle (in radians) that forms the main axis of the defect ellipse in the strip rolling direction (Orientation);
- −
- Defect ellipse length versus defect perimeter ratio (El_len/Per);
- −
- The minor axis versus the major axis of the defect ellipse ratio (Min_A/Maj_A).
6.1. Selection of Classifiers
6.2. Classification Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Mazur, V.L.; Timoshenko, V.I.; Prikhod’ko, I.Y. Stability loss and defects in coils cold-rolled strip. Steel Transl. 2019, 49, 58–65. [Google Scholar] [CrossRef]
- Mazur, I.P. Monitoring the surface quality in sheet rolling. Steel Transl. 2011, 41, 326. [Google Scholar] [CrossRef]
- Hao, R.; Lu, B.; Cheng, Y.; Li, X.; Huang, B. A steel surface defect inspection approach towards smart industrial monitoring. J. Intell. Manuf. 2020, 32, 1833–1843. [Google Scholar] [CrossRef]
- Wang, S.; Xia, X.; Ye, L.; Yang, B. Automatic detection and classification of steel surface defect using deep convolutional neural networks. Metals 2021, 11, 388. [Google Scholar] [CrossRef]
- Neven, R.; Goedemé, T. A multi-branch U-Net for steel surface defect type and severity segmentation. Metals 2021, 11, 870. [Google Scholar] [CrossRef]
- Feng, X.; Gao, X.; Luo, L. X-SDD: A new benchmark for hot rolled steel strip surface defects detection. Symmetry 2021, 13, 706. [Google Scholar] [CrossRef]
- Zhao, W.; Chen, F.; Huang, H.; Li, D.; Cheng, W. A new steel defect detection algorithm based on deep learning. Comput. Intell. Neurosci. 2021, 2021, 5592878. [Google Scholar] [CrossRef]
- Jiang, X.; Hao, Y.; Xu, G. Equivalent circular defect model of real defect outlines in the IC manufacturing process. IEEE Trans. Semicond. Manuf. 1998, 11, 432–441. [Google Scholar] [CrossRef] [Green Version]
- Hess, C.; Stroele, A.P. Modeling of real defect outlines and parameter extraction using a checkerboard test structure to localize defects. IEEE Trans. Semicond. Manuf. 1994, 7, 284–292. [Google Scholar] [CrossRef]
- Borghese, N.A.; Fomasi, M. Automatic defect classification on a production line. Intell. Ind. Syst. 2015, 1, 373–393. [Google Scholar] [CrossRef]
- Psuj, G. Utilization of multisensor data fusion for magnetic nondestructive evaluation of defects in steel elements under Various operation strategies. Sensors 2018, 18, 2091. [Google Scholar] [CrossRef] [Green Version]
- Detecting Scratch on Image with Much Noise. Available online: https://stackoverflow.com/questions/33227202/detecting-scratch-on-image-with-much-noise (accessed on 12 November 2021).
- Becker, D.; Bierwirth, J.; Brachthäuser, N.; Döpper, R.; Thülig, T. Zero-Defect-Strategy in the Cold Rolling Industry. Possibilities and Limitations of Defect Avoidance and Defect Detection in the Production of Cold-Rolled Steel Strip; Fachvereinigung Kaltwalzwerke e.V., CIELFFA: Düsseldorf, Germany, 2019; p. 16. [Google Scholar]
- Brezinová, J.; Vináš, J.; Maruschak, P.; Guzanová, A.; Draganovská, D.; Vrabel’, M. Sustainable Renovation within Metallurgical Production; RAM-Verlag: Lüdenscheid, Germany, 2017; p. 215. [Google Scholar]
- Kaggle Severstal: Steel Defect Detection. Can. You Detect. and Classify Defects in Steel? 2019. Available online: https://www.kaggle.com/c/severstal-steel-defect-detection (accessed on 4 October 2021).
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. arXiv 2015, arXiv:1505.04597v1. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. arXiv 2014, arXiv:1411.4038. [Google Scholar]
- Tran, S.-T.; Cheng, C.-H.; Nguyen, T.-T.; Le, M.-H.; Liu, D.-G. TMD-Unet: Triple-Unet with multi-scale input features and dense skip connection for medical image segmentation. Healthcare 2021, 9, 54. [Google Scholar] [CrossRef]
- Hou, Y.; Liu, Z.; Zhang, T.; Li, Y. C-UNet: Complement UNet for remote sensing road extraction. Sensors 2021, 21, 2153. [Google Scholar] [CrossRef]
- Jiao, L.; Huo, L.; Hu, C.; Tang, P. Refined UNet: UNet-based refinement network for cloud and shadow precise segmentation. Remote Sens. 2020, 12, 2001. [Google Scholar] [CrossRef]
- Jing, J.; Wang, Z.; Rätsch, M.; Zhang, H. Mobile-Unet: An efficient convolutional neural network for fabric defect detection. Text. Res. J. 2020, 21, 1427–1435. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167v3. [Google Scholar]
- Konovalenko, I.; Maruschak, P.; Brezinová, J.; Viňáš, J.; Brezina, J. Steel surface defect classification using deep residual neural network. Metals 2020, 10, 846. [Google Scholar] [CrossRef]
- Qian, K. Automated detection of steel defects via machine learning based on real-time semantic segmentation. In Proceedings of the 3rd International Conference on Video and Image Processing (ICVIP 2019), Shanghai, China, 20–23 December 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 42–46. [Google Scholar] [CrossRef]
- Yu, H.; Li, X.; Song, K.; Shang, E.; Liu, H.; Yan, Y. Adaptive depth and receptive field selection network for defect semantic segmentation on castings X-rays. NDT E Int. 2020, 116, 102345. [Google Scholar] [CrossRef]
- Zhu, Y.; Yang, R.; He, Y.; Ma, J.; Guo, H.; Yang, Y.; Zhang, L. A Lightweight Multiscale Attention Semantic Segmentation Algorithm for Detecting Laser Welding Defects on Safety Vent of Power Battery. IEEE Access 2021, 9, 39245–39254. [Google Scholar] [CrossRef]
- Aslam, Y.; Santhi, N.; Ramasamy, N.; Ramar, K. Localization and segmentation of metal cracks using deep learning. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 4205–4213. [Google Scholar] [CrossRef]
- Kim, H.; Lee, S.; Han, S. Railroad Surface Defect Segmentation Using a Modified Fully Convolutional Network. KSII Trans. Internet Inf. Syst. 2020, 14, 12. [Google Scholar]
- Allan, G.A.; Walton, A.J. Efficient critical area estimation for arbitrary defect shapes. In Proceedings of the 1997 IEEE International Symposium on Defect and Fault Tolerance in VLSI Systems, Paris, France, 20–22 October 1997; pp. 20–28. [Google Scholar] [CrossRef]
- Talapatra, S.N.; Chaudhuri, R.; Ghosh, S. Cell Profiler and WEKA tools: Image Analysis for fish erythrocytes shape and machine learning model algorithm accuracy prediction of dataset. World Sci. News 2021, 154, 101–116. [Google Scholar]
- Penumuru, D.P.; Muthuswamy, S.; Karumbu, P. Identification and classification of materials using machine vision and machine learning in the context of industry 4.0. J. Intell. Manuf. 2020, 31, 1229–1241. [Google Scholar] [CrossRef]
- Konovalenko, I.; Maruschak, P.; Brevus, V.; Prentkovskis, O. Recognition of scratches and abrasions on metal surfaces using a classifier based on a convolutional neural network. Metals 2021, 11, 549. [Google Scholar] [CrossRef]
- Konovalenko, I.; Maruschak, P.; Brevus, V. Steel surface defect detection using an ensemble of deep residual neural networks. J. Comput. Inf. Sci. Eng. 2022, 22, 014501. [Google Scholar] [CrossRef]
- Konovalenko, I.; Hutsaylyuk, V.; Maruschak, P. Classification of surface defects of rolled metal using deep neural network ResNet50. In Proceedings of the 13th International Conference on Intelligent Technologies in Logistics and Mechatronics Systems, Panevezys, Lithuania, 1 October 2020; pp. 41–48. [Google Scholar]
- Fleiss, J.L. Statistical Methods for Rates and Proportions, 2nd ed.; John Wiley: New York, NY, USA, 1981; p. 336. [Google Scholar]

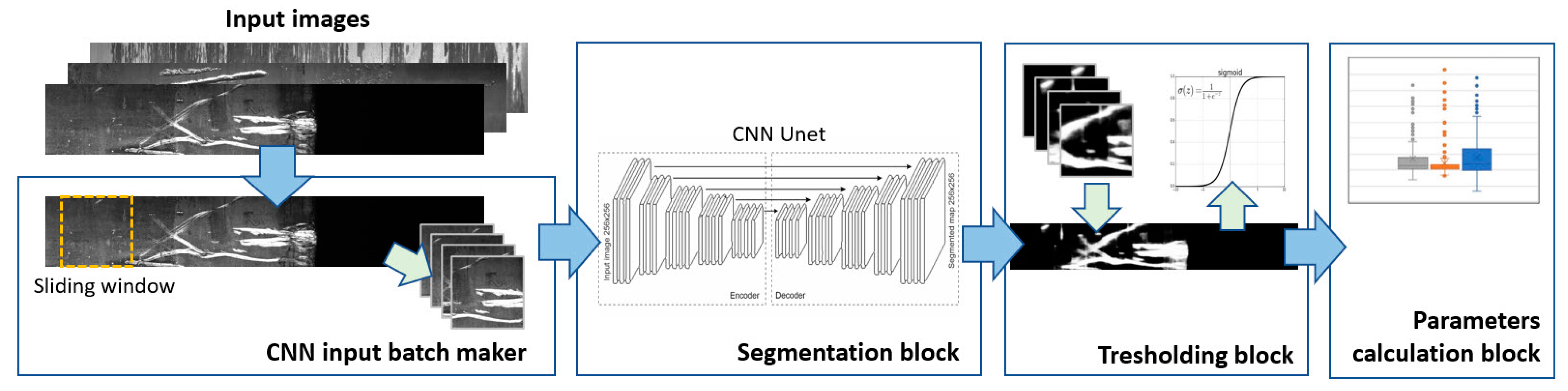

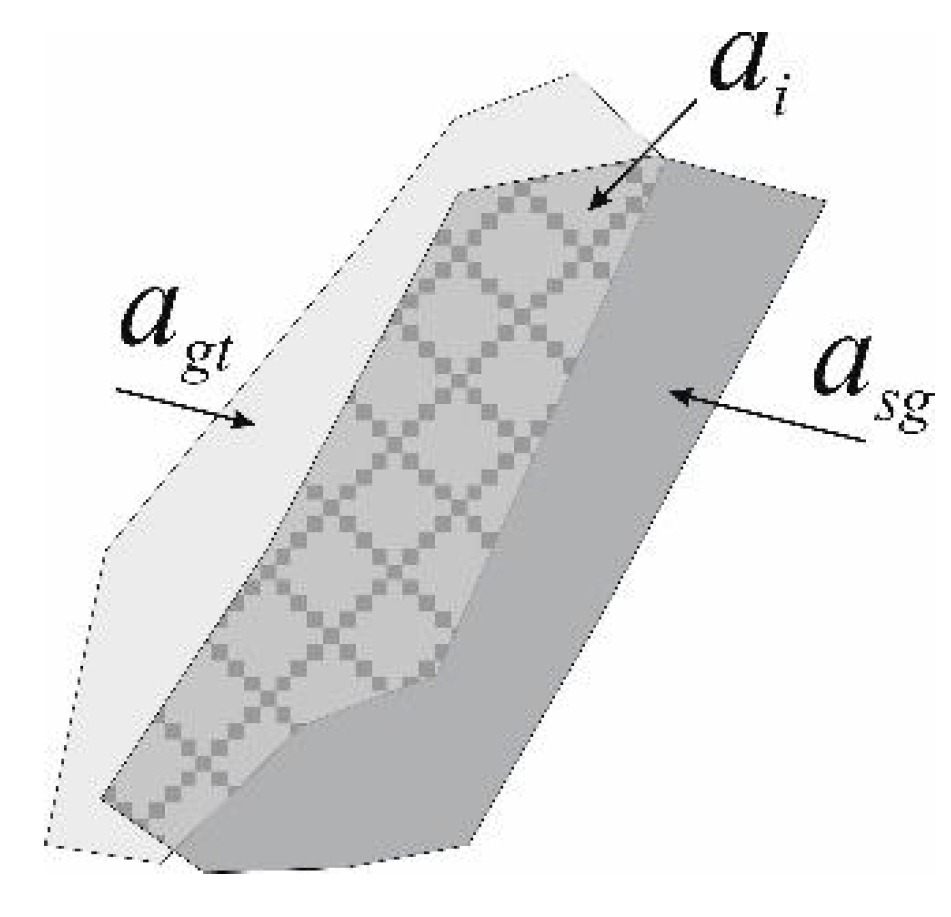




| Model | DSC | IoU |
|---|---|---|
| Developed model | 0.912 | 0.894 |
| Kun Qian [24] | 0.915 and 0.905 | – |
| Han Yu et al. [25] | – | 0.86 |
| Y. Zhu et al. [26] | – | 0.847 |
| Aslam, Y. et al. [27] | 0.917 | – |
| Hyeonho Kim [28] | – | 0.854 and 0.846 |
| Parameter Name | Parameter Geometry | Geometric Content Description |
|---|---|---|
| Orientation |  | Defect orientation relative to the strip rolling direction |
| Area |  | Defect area |
| Perimeter | 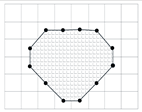 | Defect perimeter shows the development of its edge |
| Eccentricity | 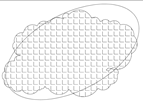 | Eccentricity shows the degree of “elongation” of the defect shape |
| Maximum and minimum axes of the defect when describing its ellipse | 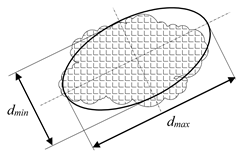 | Allows the defect size and shape to be established |
| Defect Subclass | Causes of Formation | The Scheme of the Analyzed Defects | Morphological Description of Defects Analyzed |
|---|---|---|---|
| Scratches | Jamming and actuation of individual rollers and harnessing | 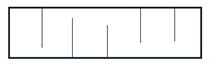 | Defects are oriented parallel to the strip movement direction. They have a clear-cut thin thread-like front that runs through the entire image. |
| Lines | Adhesion of metal particles to the roll surface and their sliding on the strip surface |  | Defects are oriented parallel to the strip movement direction but less clearly than cracks. They have a rough front, the edges of which show “cuts”, and plastically deformed microzones due to scratching of the metal. |
| Attritions | Strip friction against the drive parts of the process equipment |  | Defects of arbitrary orientation. They have a matte surface and a large area. The defect color may be inhomogeneous across its area due to depth differences in different areas. |
| Attribute Selection | |||
|---|---|---|---|
| Attribute | Expert Opinion | Statistical Methods | Weka |
| Eccentricity | ✓ | ✓ | ✓ |
| Orientation | ✓ | ✓ | ✓ |
| El_len/Per | ✓ | ||
| Min_A/Maj_A | ✓ | ✓ | ✓ |
| Major_Axis_Length | ✓ | ||
| Statistical Values of Attributes | ||||
|---|---|---|---|---|
| Attribute | Minimum | Maximum | Mean | STD |
| Eccentricity | 0.404 | 1.000 | 0.966 | 0.077 |
| Major_axis_length | 13.621 | 1632.084 | 180.683 | 161.164 |
| Orientation | −1.570 | 1.570 | −0.053 | 0.647 |
| El_len/Per | 0.271 | 1.156 | 0.838 | 0.114 |
| Min_A/Maj_A | 0.020 | 0.915 | 0.174 | 0.173 |
| Classifiers Models Quality Comparison | |||
|---|---|---|---|
| Attribute | Correctly Classified Instances | Kappa Statistics | Mean Absolute Error |
| J48 | 69.36% | 0.533 | 0.239 |
| REPTree | 70.83% | 0.558 | 0.239 |
| LMT | 73.21% | 0.593 | 0.226 |
| Random forest | 73.95% | 0.605 | 0.230 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konovalenko, I.; Maruschak, P.; Kozbur, H.; Brezinová, J.; Brezina, J.; Guzanová, A. Defectoscopic and Geometric Features of Defects That Occur in Sheet Metal and Their Description Based on Statistical Analysis. Metals 2021, 11, 1851. https://doi.org/10.3390/met11111851
Konovalenko I, Maruschak P, Kozbur H, Brezinová J, Brezina J, Guzanová A. Defectoscopic and Geometric Features of Defects That Occur in Sheet Metal and Their Description Based on Statistical Analysis. Metals. 2021; 11(11):1851. https://doi.org/10.3390/met11111851
Chicago/Turabian StyleKonovalenko, Ihor, Pavlo Maruschak, Halyna Kozbur, Janette Brezinová, Jakub Brezina, and Anna Guzanová. 2021. "Defectoscopic and Geometric Features of Defects That Occur in Sheet Metal and Their Description Based on Statistical Analysis" Metals 11, no. 11: 1851. https://doi.org/10.3390/met11111851
APA StyleKonovalenko, I., Maruschak, P., Kozbur, H., Brezinová, J., Brezina, J., & Guzanová, A. (2021). Defectoscopic and Geometric Features of Defects That Occur in Sheet Metal and Their Description Based on Statistical Analysis. Metals, 11(11), 1851. https://doi.org/10.3390/met11111851










