Hot Deformation Behavior of a Beta Metastable TMZF Alloy: Microstructural and Constitutive Phenomenological Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material Characterization
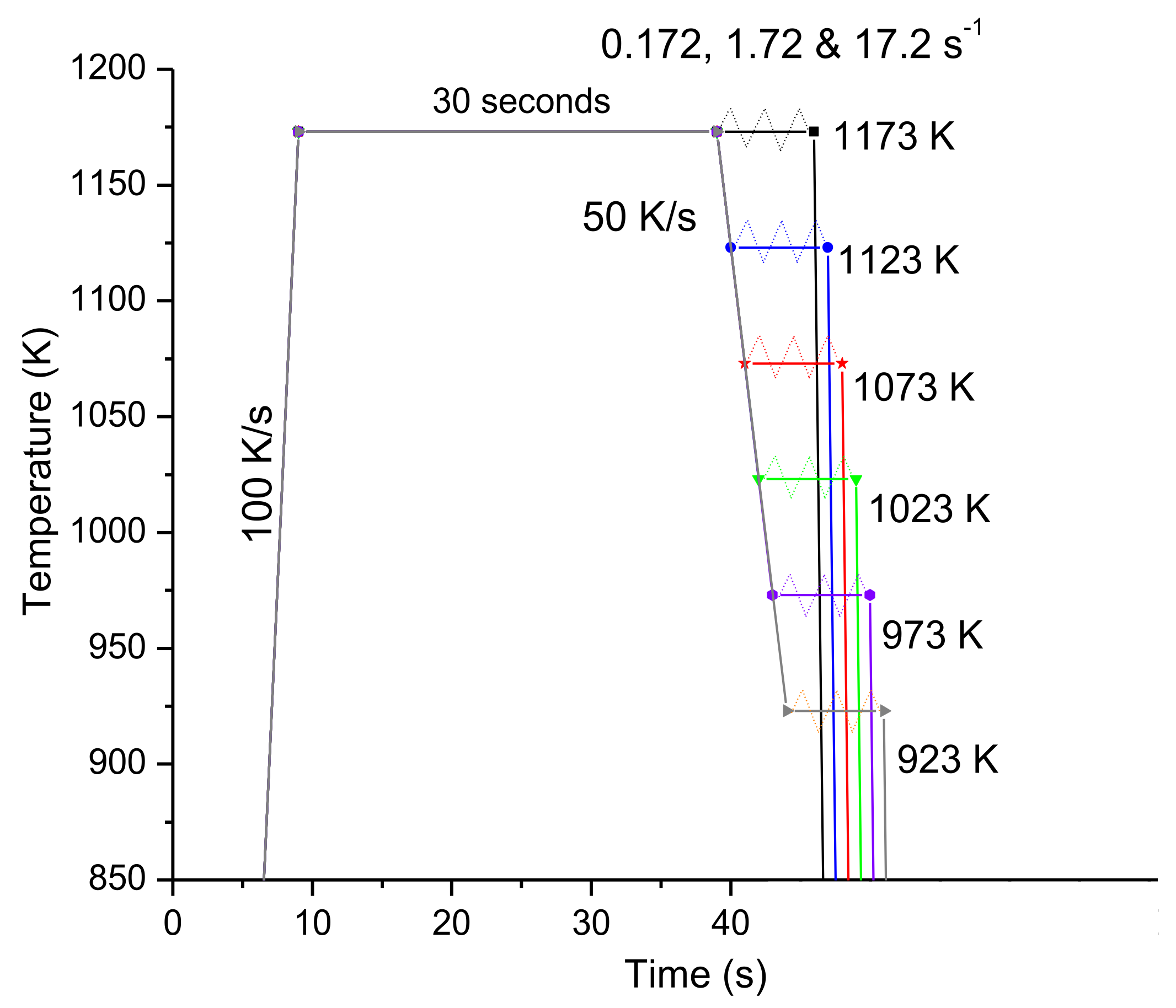
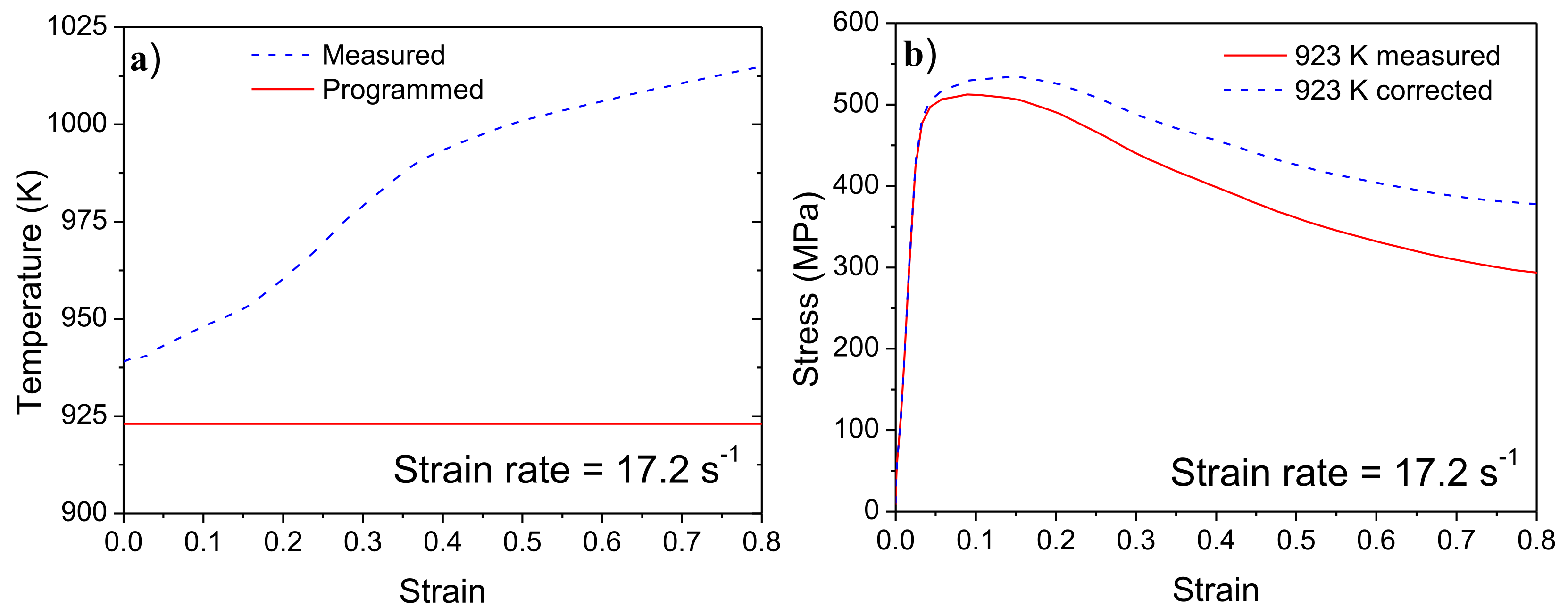
2.2. Compression Tests
2.3. Constitutive Equation Constant Determination
2.3.1. Strain-Compensated Arrhenius-Type Equation
2.3.2. Modified Johnson–Cook Model
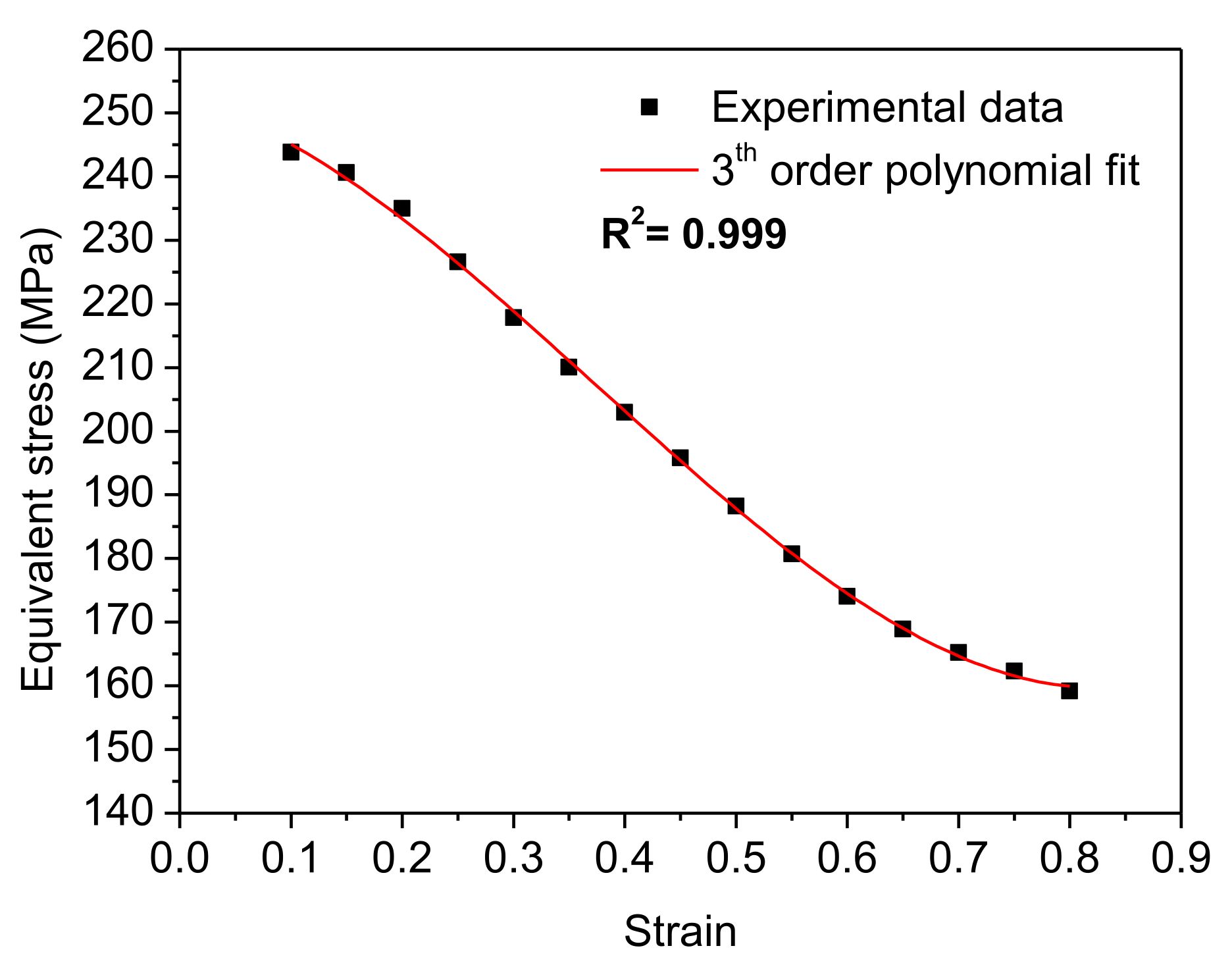
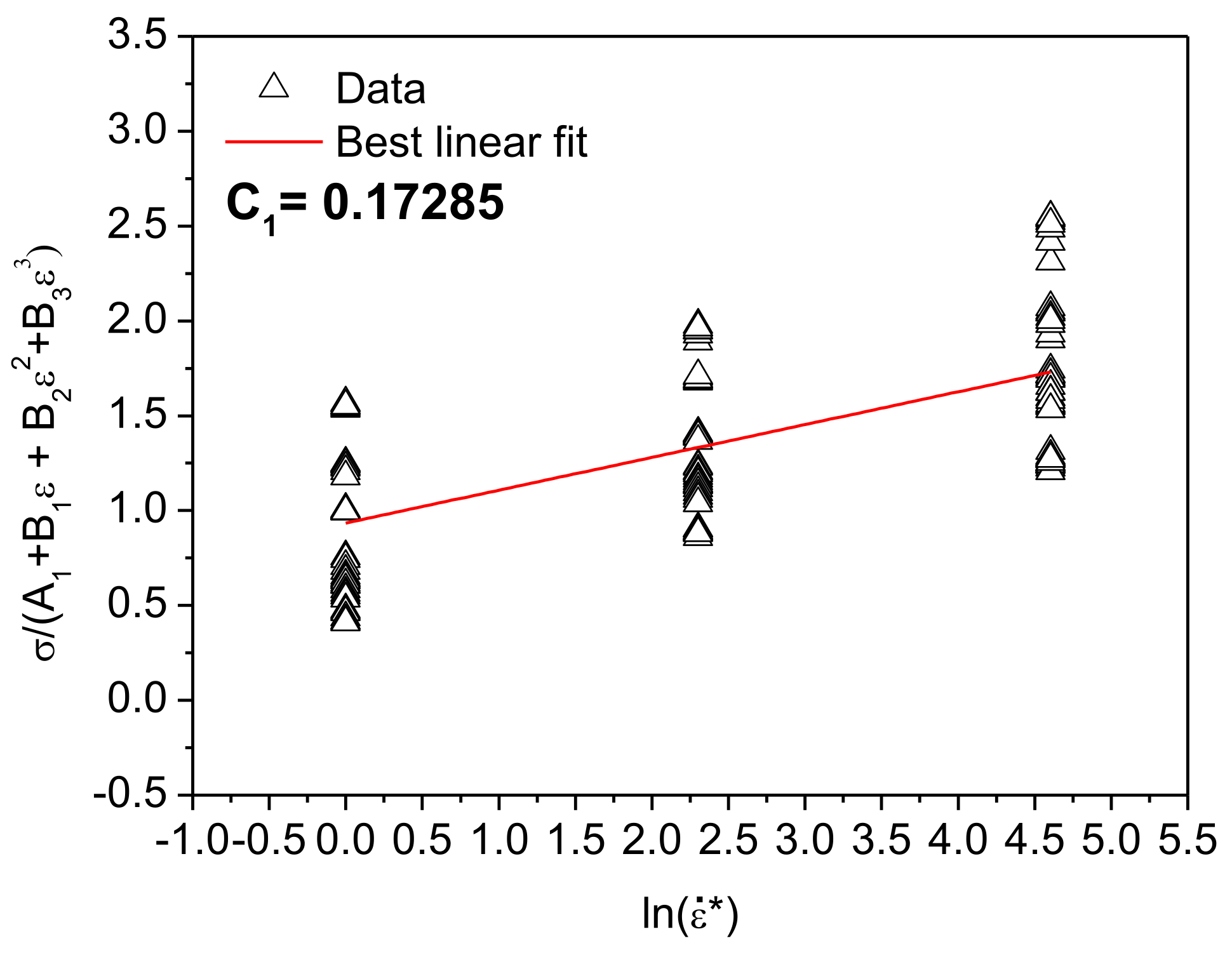
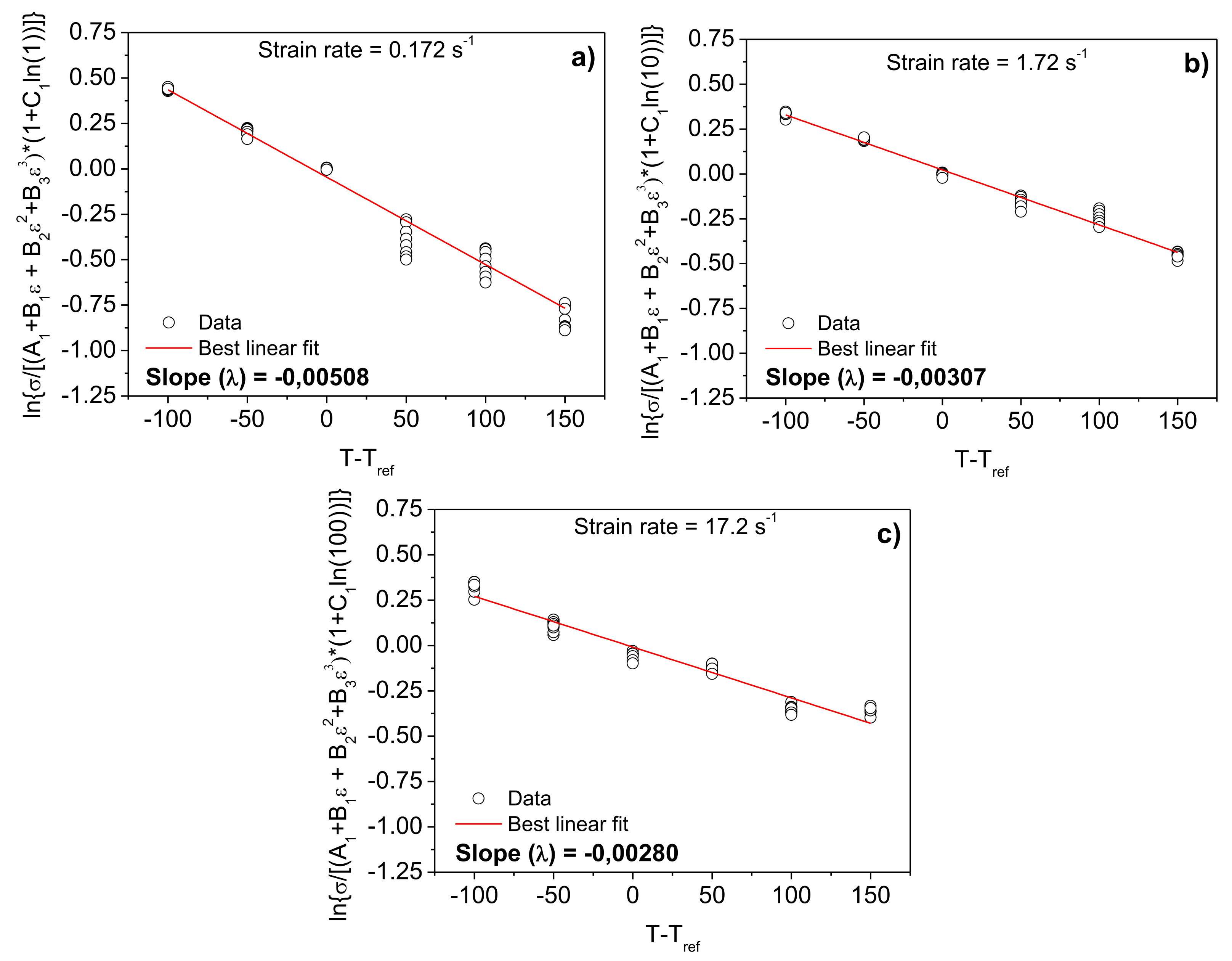
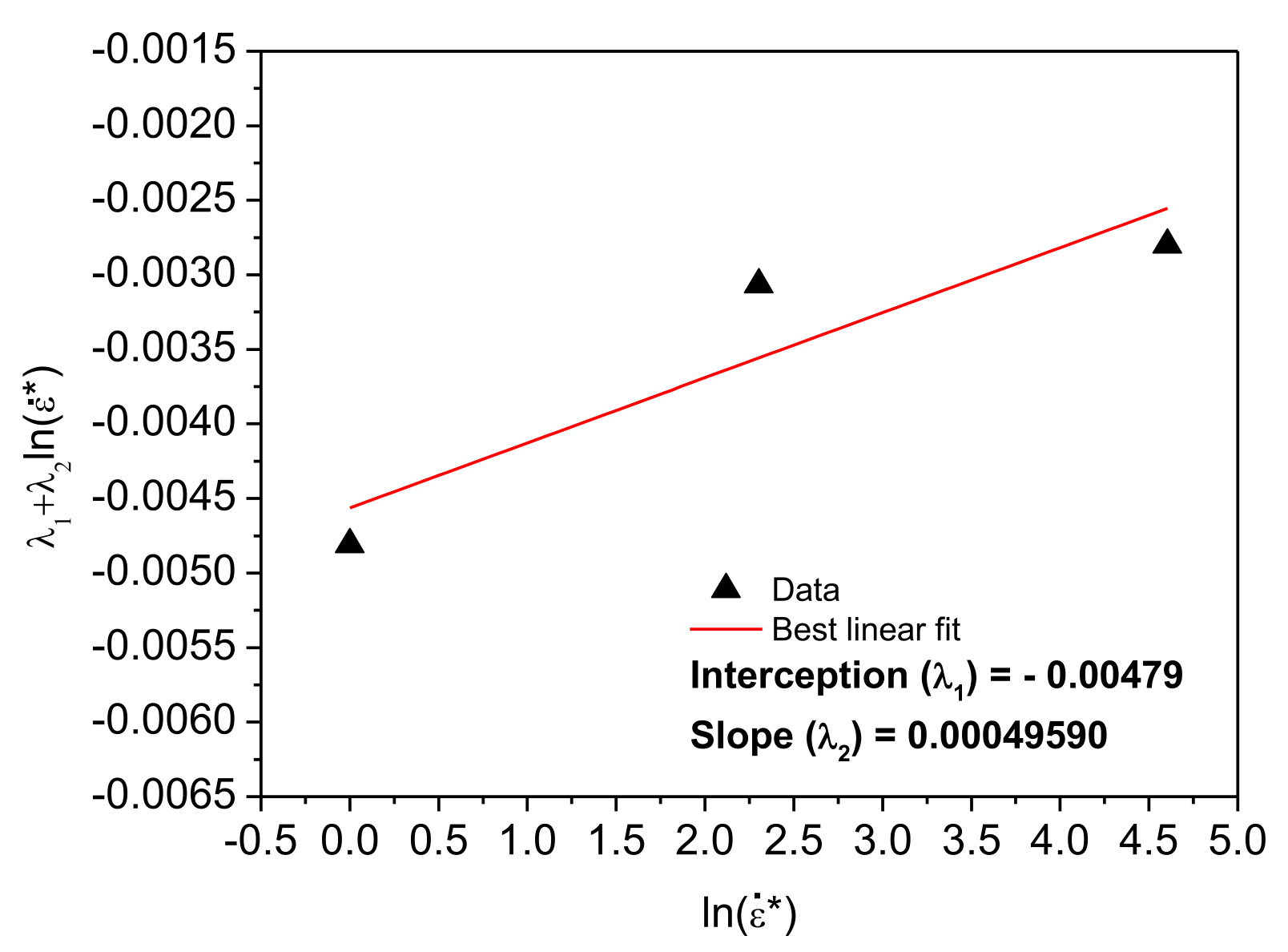
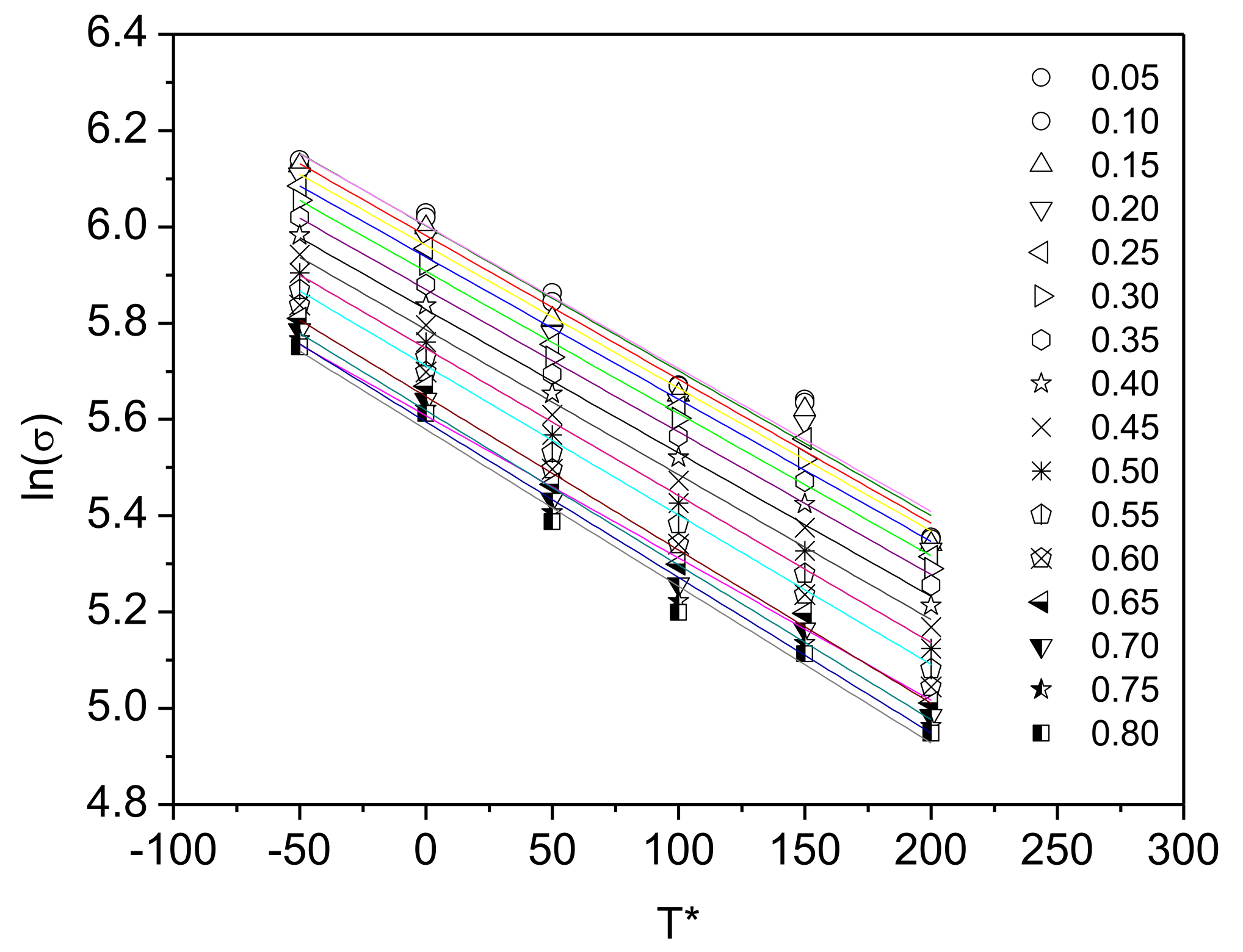
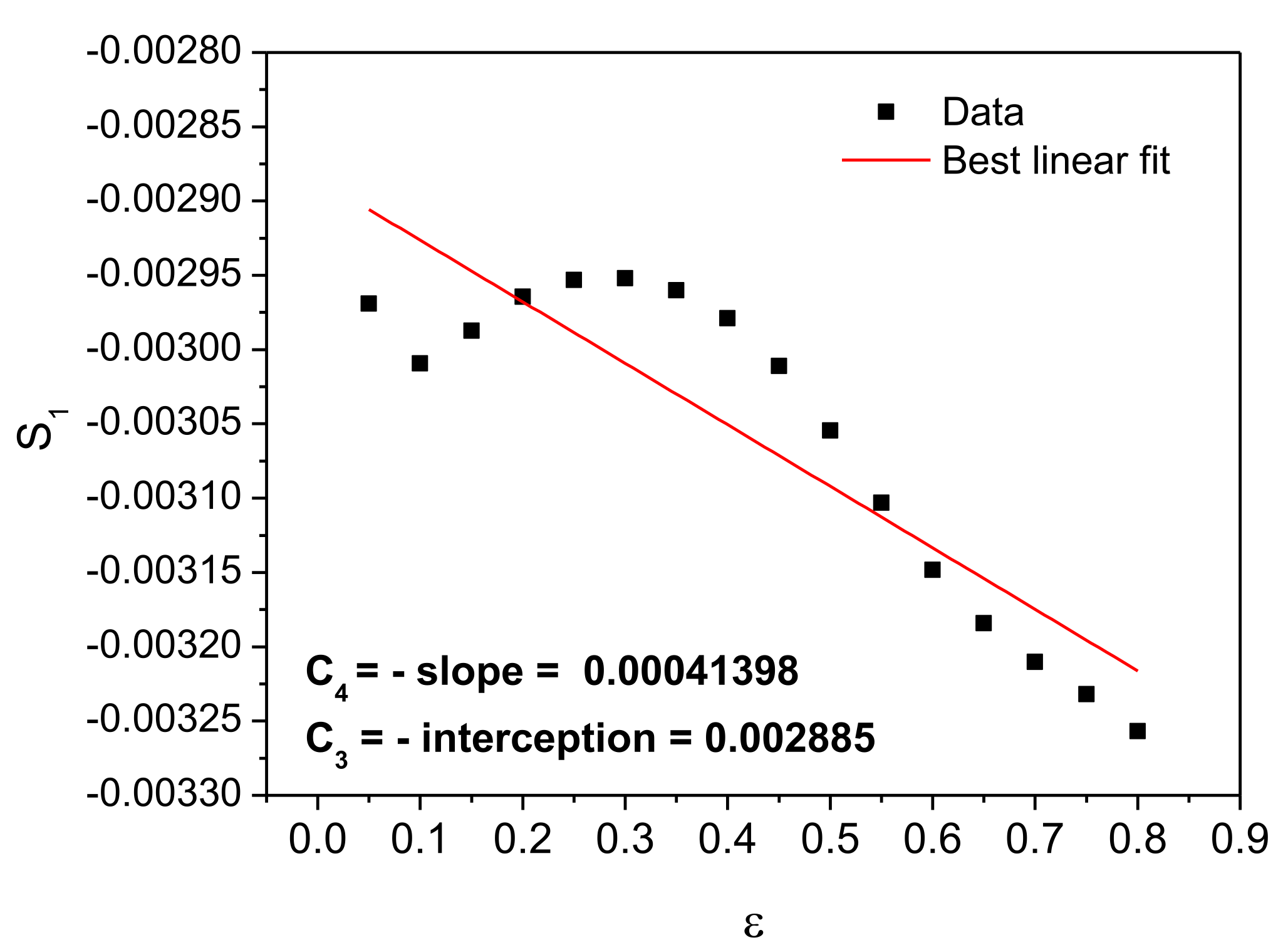
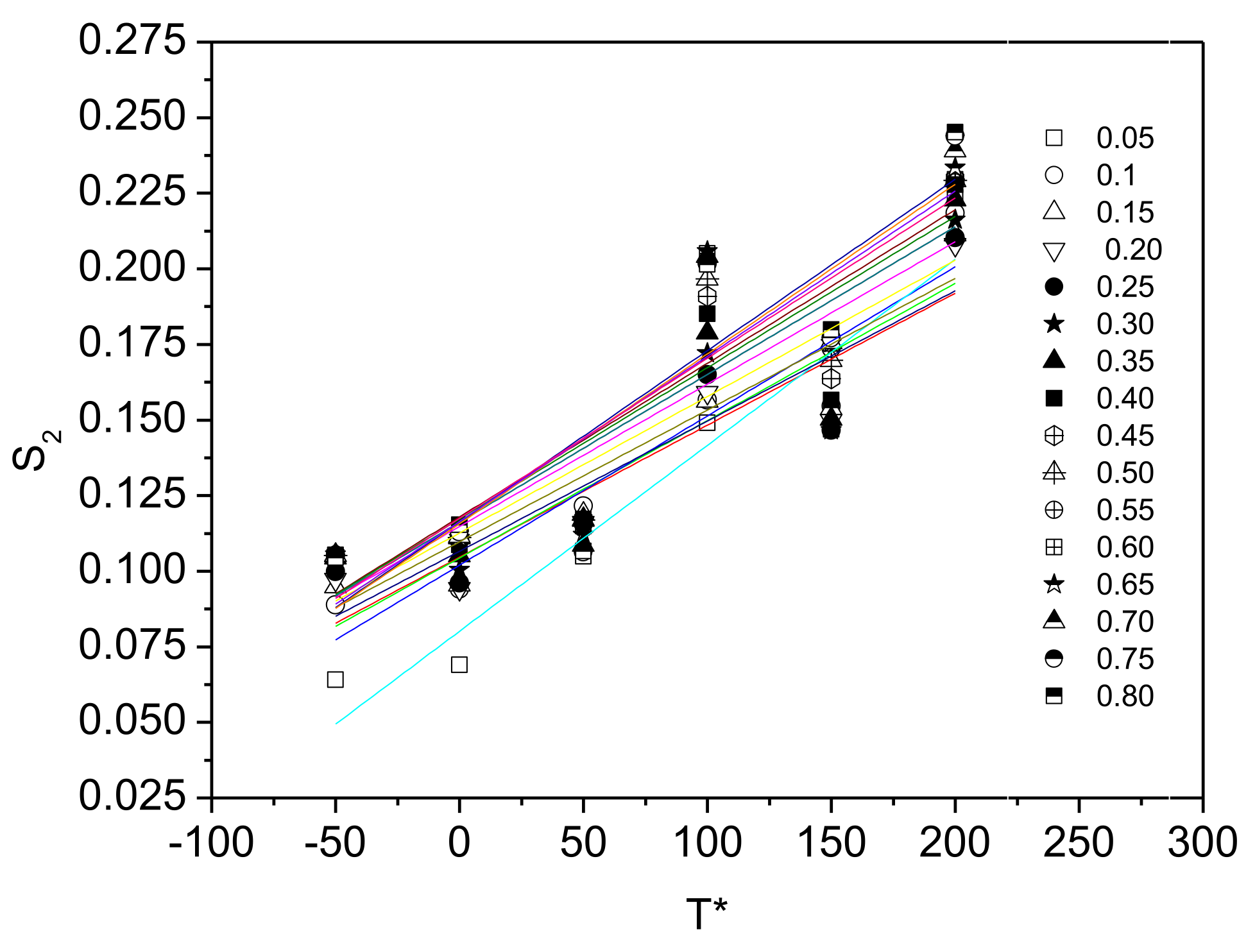
2.3.3. Modified Zerilli–Armstrong Model
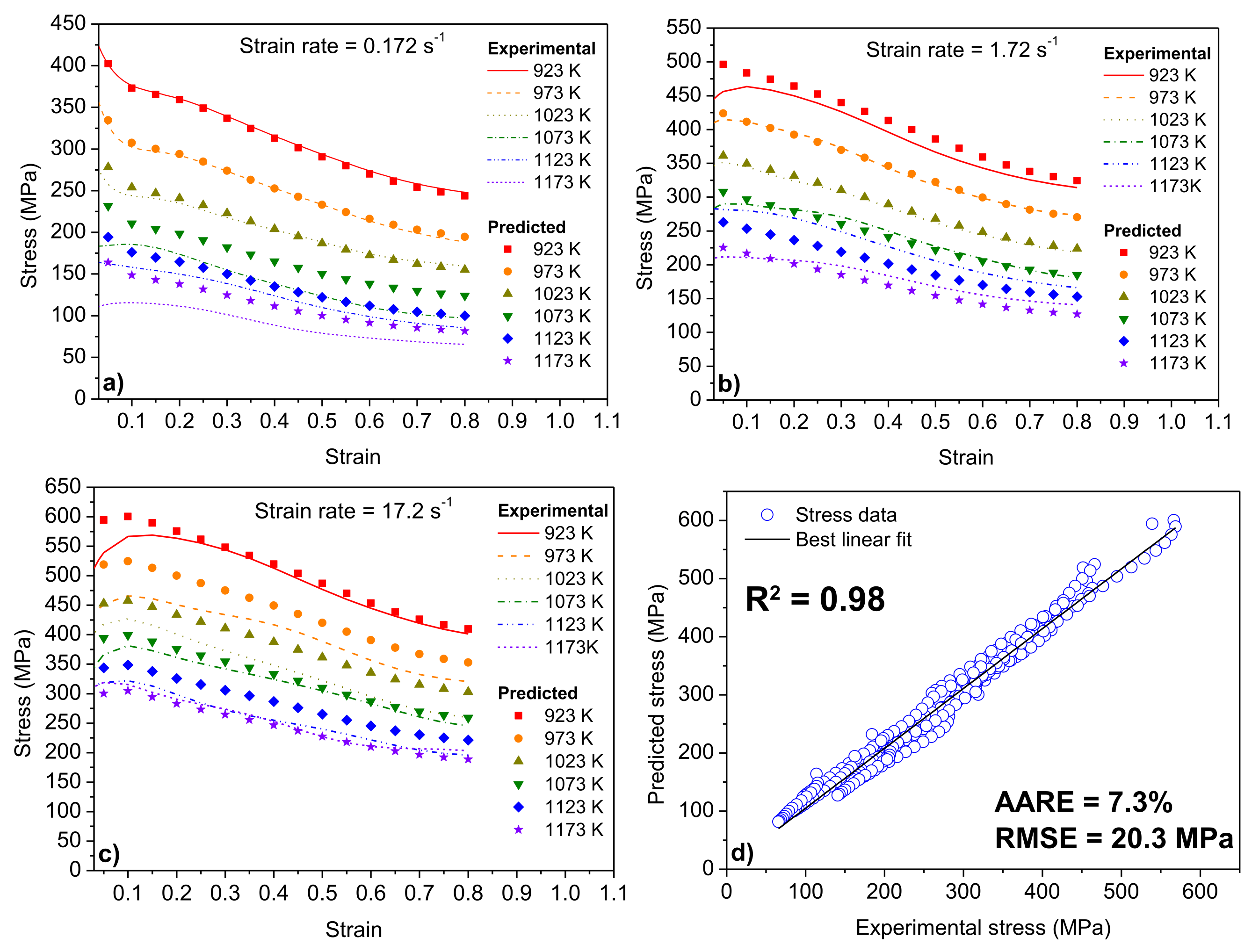
2.4. Predictability Comparison
2.5. Processing Maps
3. Results and Discussion
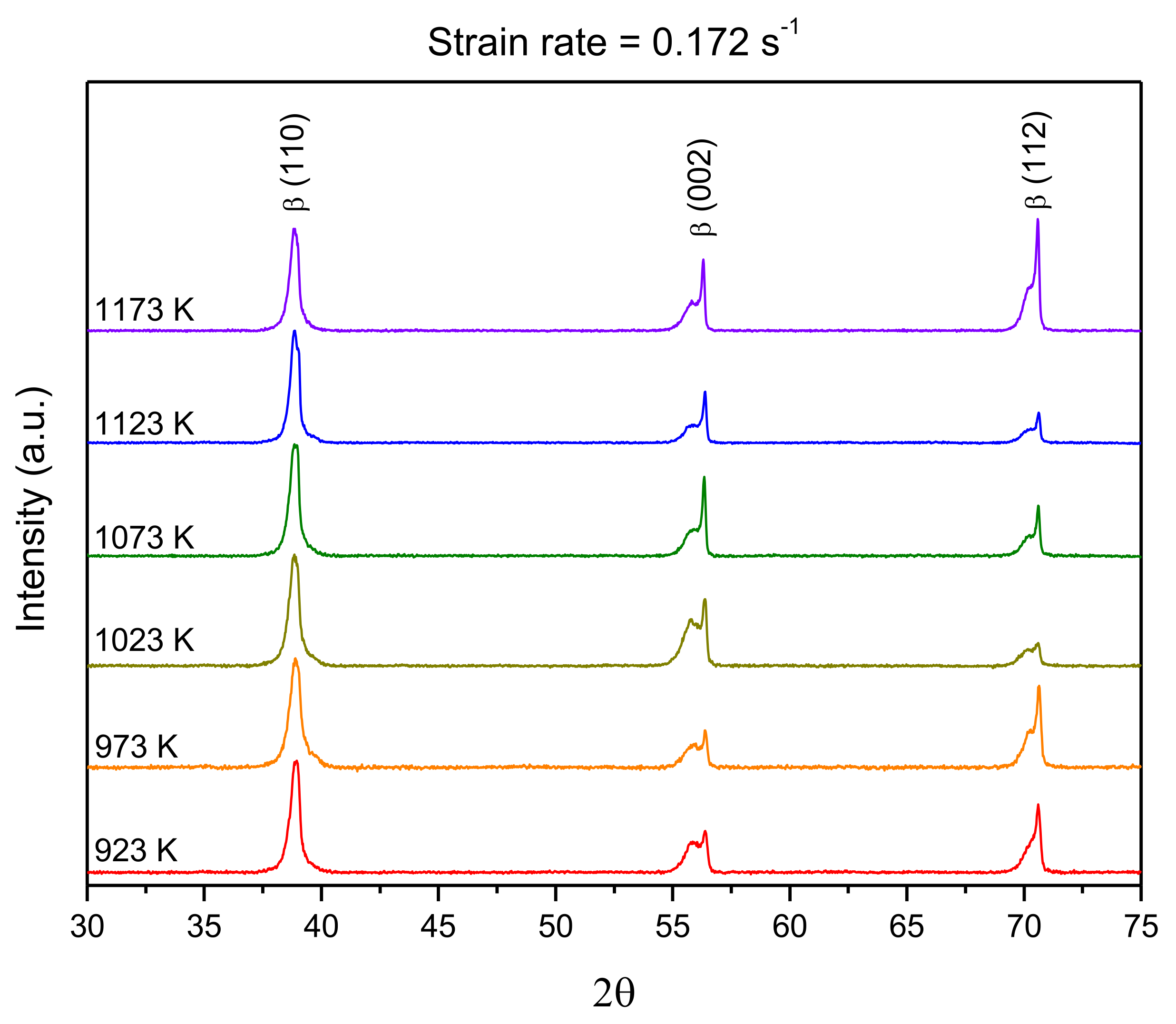
3.1. Initial Material Characterization
3.2. Compressive Flow Stress Curves
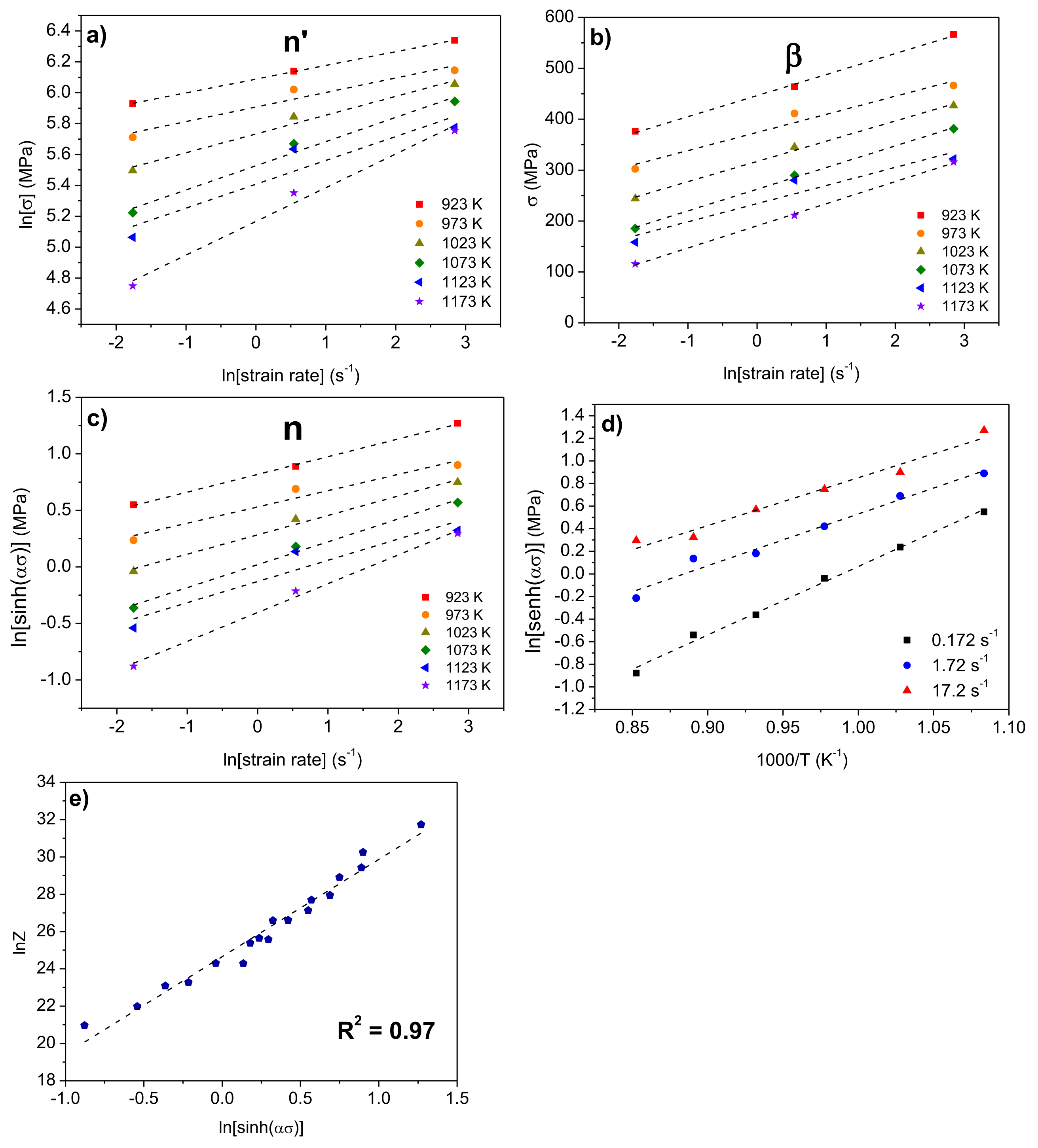
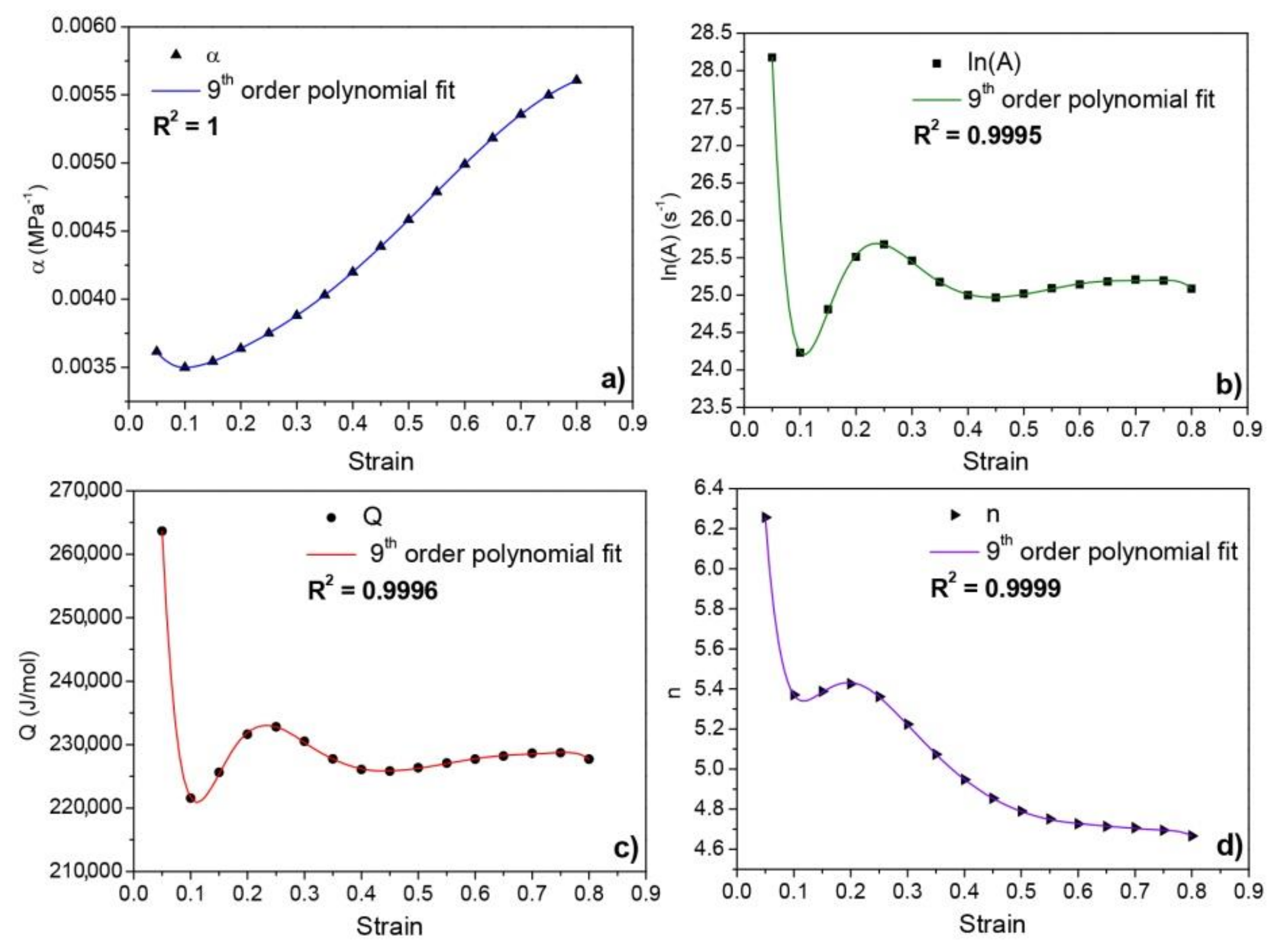
3.3. Arrhenius-Type Equation: Determination of the Material’s Constants
3.4. Modified Johnson–Cook Model
3.5. Modified Zerilli–Armstrong Model
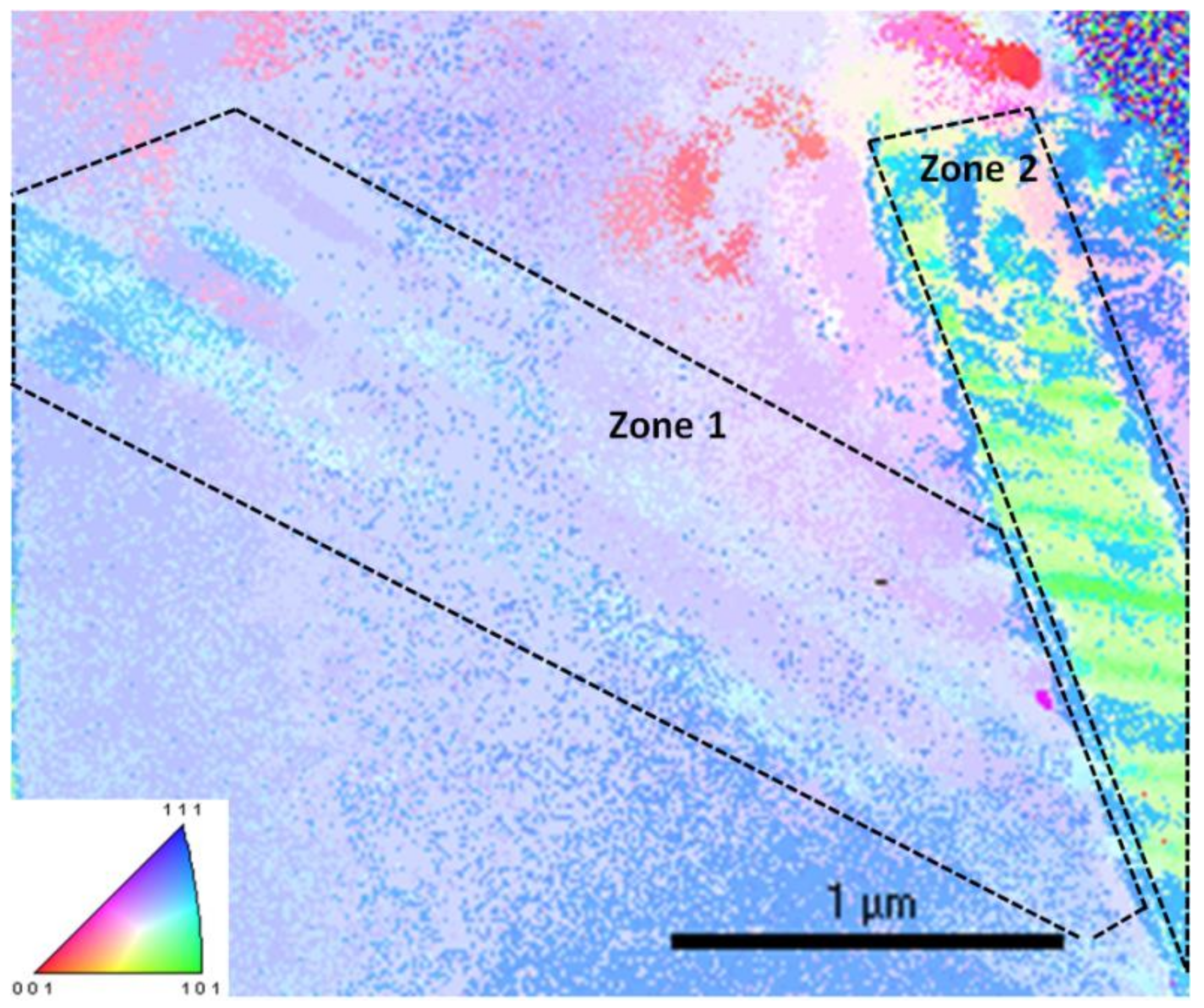
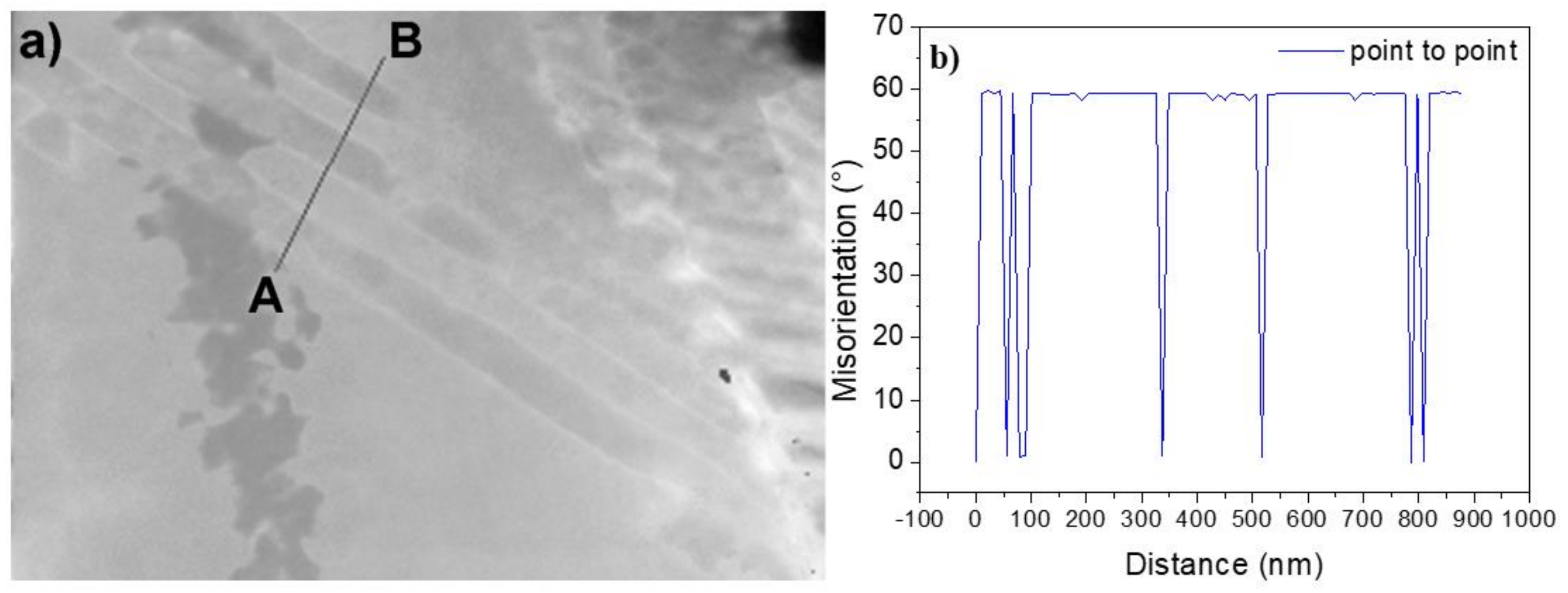
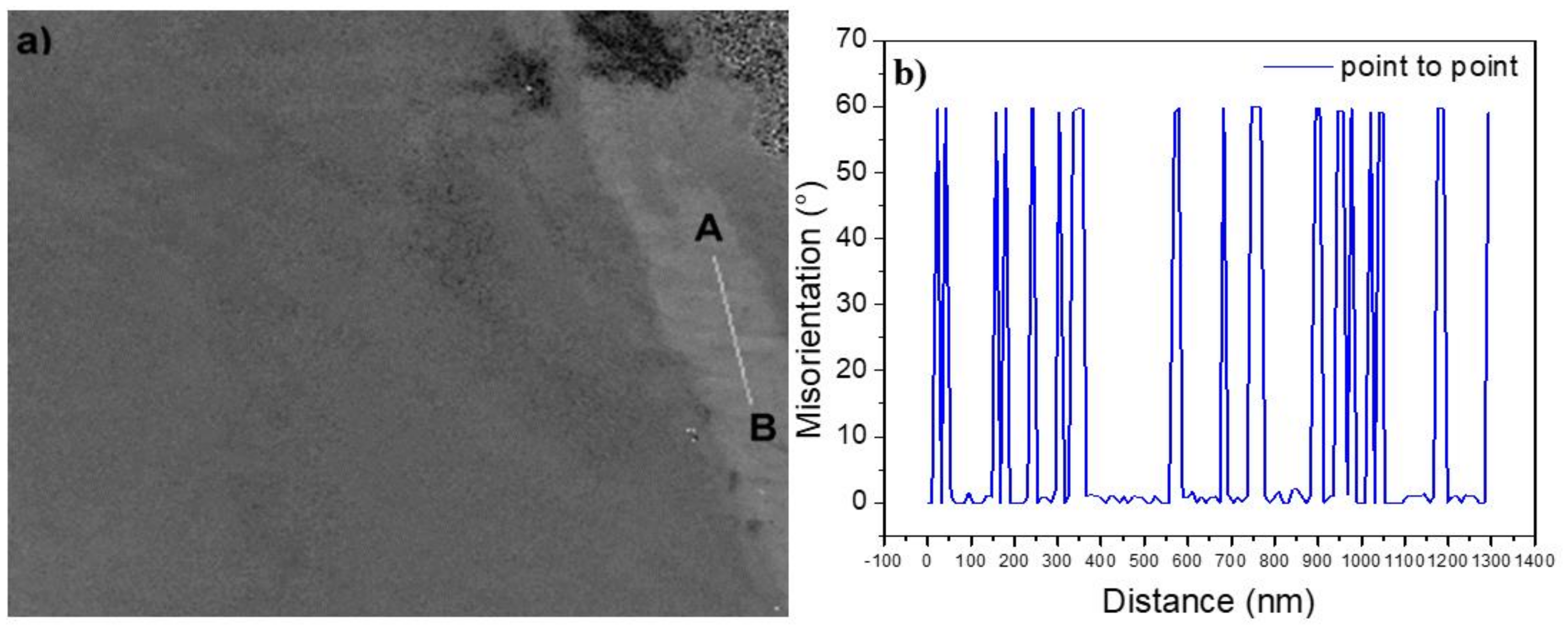
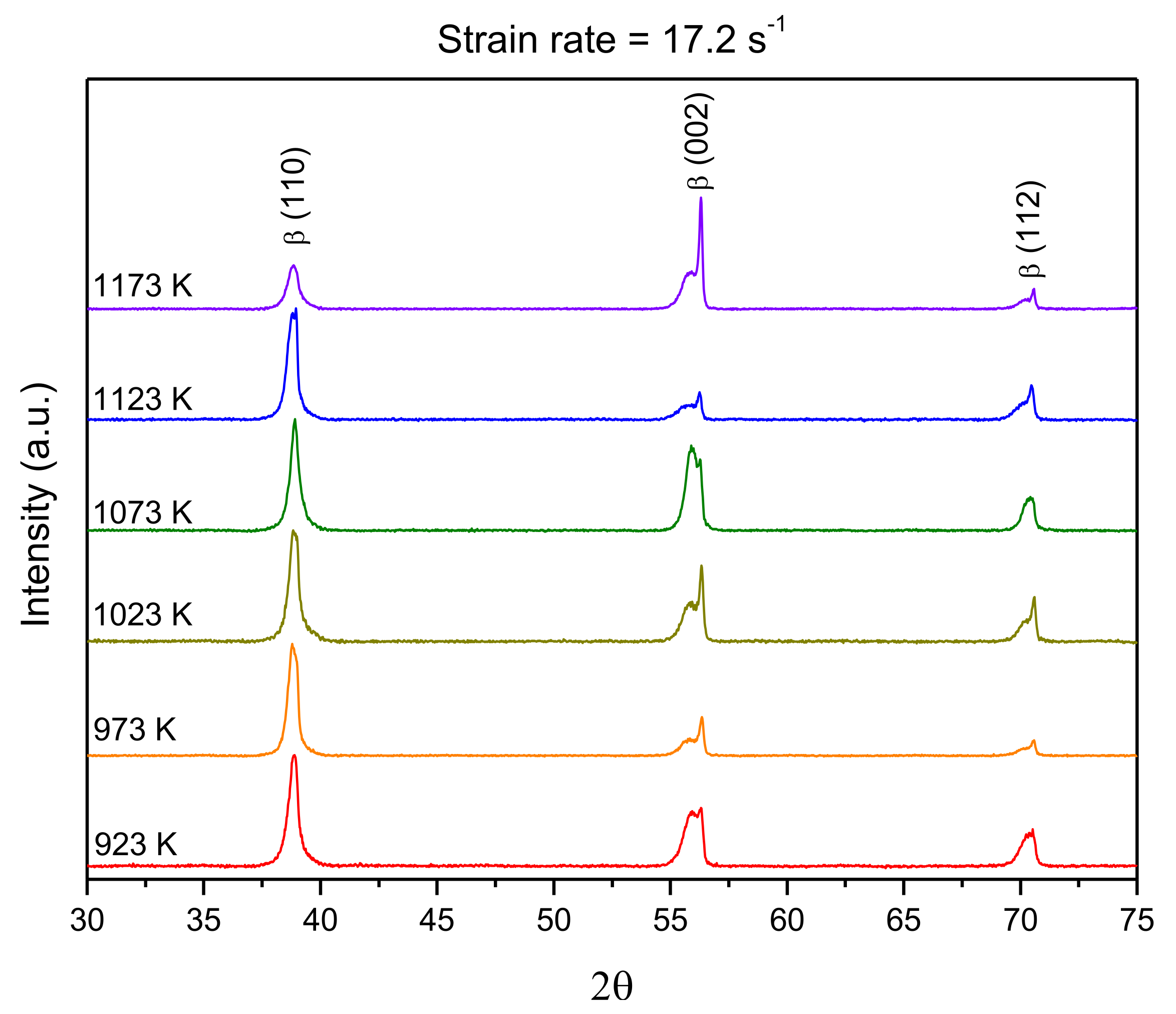
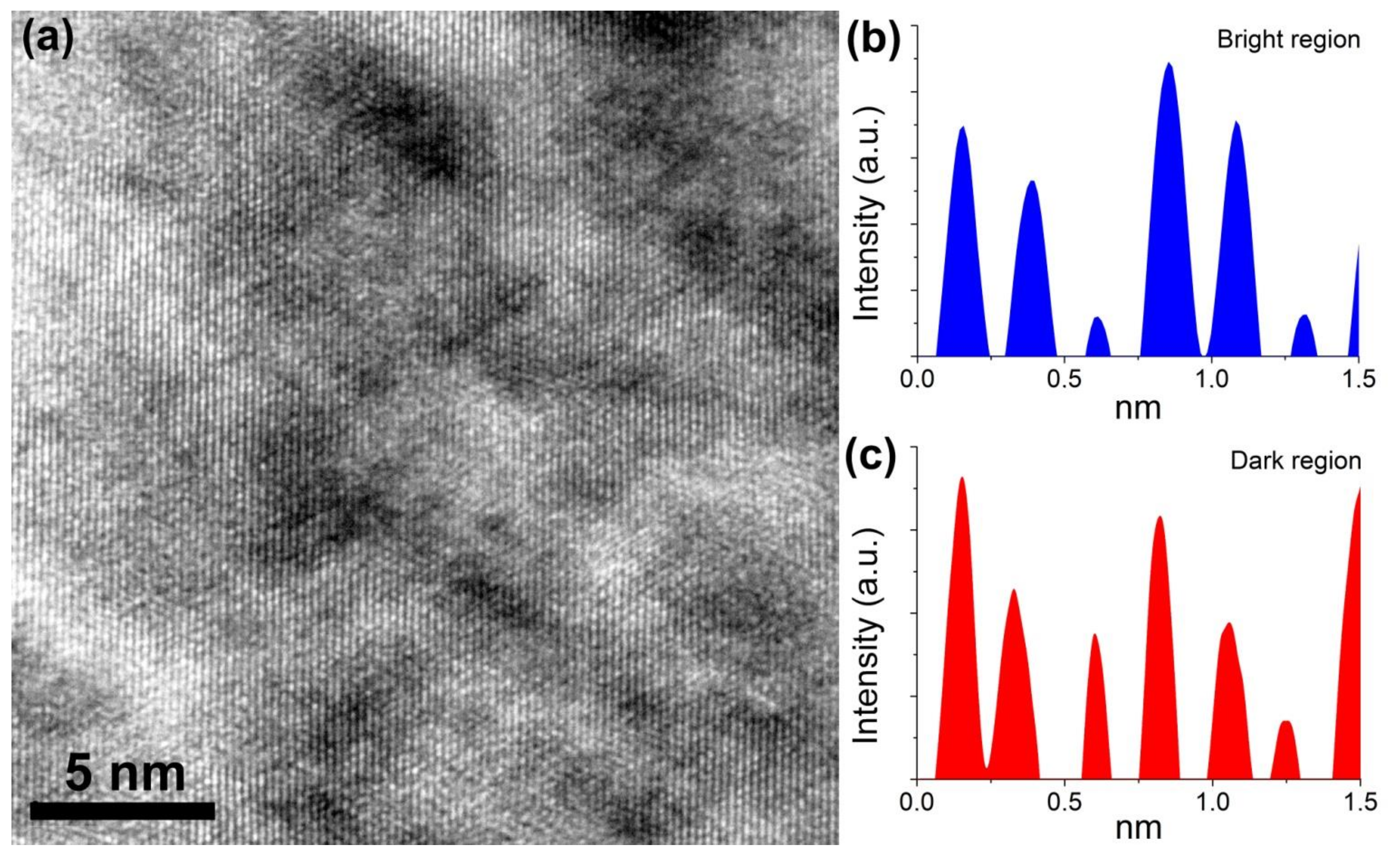
3.6. Microstructure Characterization after Processing
3.7. Structural Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Soundararajan, S.R.; Vishnu, J.; Manivasagam, G.; Muktinutalapati, N.R. Titanium Alloys–Novel Aspects of Their Manufacturing and Processing; Motyka, M., Ziaka, W., Sieniawski, J., Eds.; IntechOpen Limited: London, UK, 2018. [Google Scholar]
- Quadros, F.D.F.; Kuroda, P.A.B.; Sousa, K.D.S.J.; Donato, T.A.G.; Grandini, C.R. Preparation, structural and microstructural characterization of Ti-25Ta-10Zr alloy for biomedical applications. J. Mater. Res. Technol. 2019, 8, 4108–4114. [Google Scholar] [CrossRef]
- Song, Y.H.; Kim, M.K.; Park, E.J.; Song, H.J.; Anusavice, K.J.; Park, Y.J. Cytotoxicity of alloying elements and experimental titanium alloys by WST-1 and agar overlay tests. Dent. Mater. 2014, 30, 977–983. [Google Scholar] [CrossRef] [PubMed]
- Warchomicka, F.; Poletti, C.; Stockinger, M. Study of the hot deformation behaviour in Ti-5Al-5Mo-5V-3Cr-1Zr. Mater. Sci. Eng. A 2011, 528, 8277–8285. [Google Scholar] [CrossRef]
- Weiss, I.; Semiatin, S.L. Thermomechanical processing of beta titanium alloys—An overview. Mater. Sci. Eng. A 1999, 263, 243–256. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater. Des. 2011, 32, 1733–1759. [Google Scholar] [CrossRef]
- Gourdet, S.; Montheillet, F. A model of continuous dynamic recrystallization. Acta Mater. 2003, 51, 2685–2699. [Google Scholar] [CrossRef]
- Huang, K.; Logé, R.E. A review of dynamic recrystallization phenomena in metallic materials. JMADE 2016, 111, 548–574. [Google Scholar] [CrossRef]
- Duerig, T.W.; Terlinde, G.T.; Williams, J.C. The Omega Phase Reaction in Titanium Alloy; Defense Technical Information Center: Fort Belvoir, VA, USA, 1980; Volume 2, pp. 1299–1300. [Google Scholar]
- Leyens, C.; Peters, M. Titanium and Titanium Alloys. Fundamentals and Applications, 1st ed.; Leyens, C., Peters, M., Eds.; WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim: Köln, Germany, 2003; ISBN 3527305343. [Google Scholar]
- George, A.; Divakar, R. Evidence for spinodal decomposition in Ti-15Mo quenched alloy using transmission electron microscopy. Micron 2019, 121, 43–52. [Google Scholar] [CrossRef] [PubMed]
- Biesiekierski, A.; Ping, D.; Li, Y.; Lin, J.; Munir, K.S.; Yamabe-Mitarai, Y.; Wen, C. Extraordinary high strength Ti-Zr-Ta alloys through nanoscaled, dual-cubic spinodal reinforcement. Acta Biomater. 2017, 53, 549–558. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Niinomi, M.; Hieda, J.; Nakai, M.; Cho, K. Deformation-induced ω phase in modified Ti-29Nb-13Ta-4.6Zr alloy by Cr addition. Acta Biomater. 2013, 9, 8027–8035. [Google Scholar] [CrossRef]
- Chen, W.; Cao, S.; Zhang, J.; Zha, Y.; Hu, Q.; Sun, J. New insights into formation mechanism of interfacial twin boundary ω-phase in metastable β-Ti alloys. Mater. Charact. 2020, 164, 110363. [Google Scholar] [CrossRef]
- Wu, S.Q.; Ping, D.H.; Yamabe-Mitarai, Y.; Xiao, W.L.; Yang, Y.; Hu, Q.M.; Li, G.P.; Yang, R. {112} <111> Twinning during ω to body-centered cubic transition. Acta Mater. 2015, 62, 122–128. [Google Scholar] [CrossRef]
- Ettouney, O.; Hardt, D.E. A method for in-process failure prediction in cold upset forging. J. Eng. Ind. 1983, 105, 161–167. [Google Scholar] [CrossRef]
- Dieter, G.E.; Kuhn, H.A.; Semiatin, S.L. Handbook of Workability and Process Design; ASM International: Materials Park, OH, USA, 2003; ISBN 0871707780. [Google Scholar]
- Hickman, B.S. Omega phase precipitation in alloys of titanium with transition metals. Trans. TMS-AIME 1969, 245, 1329–1335. [Google Scholar]
- Samantaray, D.; Mandal, S.; Borah, U.; Bhaduri, A.K.; Sivaprasad, P.V. A thermo-viscoplastic constitutive model to predict elevated-temperature flow behaviour in a titanium-modified austenitic stainless steel. Mater. Sci. Eng. A 2009, 526, 1–6. [Google Scholar] [CrossRef]
- Han, Y.; Zeng, W.; Qi, Y.; Zhao, Y. Optimization of forging process parameters of Ti600 alloy by using processing map. Mater. Sci. Eng. A 2011, 529, 393–400. [Google Scholar] [CrossRef]
- Hickman, B.S. The formation of omega phase in titanium and zirconium alloys: A review. J. Mater. Sci. 1969, 4, 554–563. [Google Scholar] [CrossRef]
- Silcock, J.M. An X-ray examination of the to phase in TiV, TiMo and TiCr alloys. Acta Metall. 1958, 6, 481–493. [Google Scholar] [CrossRef]
- Momeni, A.; Abbasi, S.M.; Morakabati, M.; Akhondzadeh, A. Yield point phenomena in TIMETAL 125 beta Ti alloy. Mater. Sci. Eng. A 2015, 643, 142–148. [Google Scholar] [CrossRef]
- McQueen, H.J.; Bourell, D.L. Formability and metallurgical structure. In Proceedings of the TMS, Warrendale, PA, USA, 5–9 October 1986; Sachdev, A.K., Embury, J.D., Eds.; pp. 344–368. [Google Scholar]
- Santos, N.B.D. Avaliação de um Critério de Equivalência entre Dados de Tração a Quente e Fluência em Aços. Ph.D. Thesis, Universidade Federal de São Carlos, São Carlos, SP, Brazil, 2007. [Google Scholar]
- Mcqueen, H.J.; Jonas, J.J. Recent advances in hot working: Fundamental dynamic softening mechanisms. J. Appl. Metalwork. 1984, 3, 233–241. [Google Scholar] [CrossRef]
- Lucci, A.; Riontino, G.; Tabasso, M.C.; Tamanim, M.; Venturello, G. Recrystallization and stored energy of dilute copper solid solutions with substitutional transition elements of the 4th period. Acta Metall. 1978, 26, 615–622. [Google Scholar] [CrossRef]
- Trump, A.M. Recrystallization and Grain Growth Kinetics in Binary Alpha Titanium-Aluminum Alloys. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2017. [Google Scholar]













Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerra, A.P.d.B.; Jorge, A.M., Jr.; Roche, V.; Bolfarini, C. Hot Deformation Behavior of a Beta Metastable TMZF Alloy: Microstructural and Constitutive Phenomenological Analysis. Metals 2021, 11, 1769. https://doi.org/10.3390/met11111769
Guerra APdB, Jorge AM Jr., Roche V, Bolfarini C. Hot Deformation Behavior of a Beta Metastable TMZF Alloy: Microstructural and Constitutive Phenomenological Analysis. Metals. 2021; 11(11):1769. https://doi.org/10.3390/met11111769
Chicago/Turabian StyleGuerra, Ana Paula de Bribean, Alberto Moreira Jorge, Jr., Virginie Roche, and Claudemiro Bolfarini. 2021. "Hot Deformation Behavior of a Beta Metastable TMZF Alloy: Microstructural and Constitutive Phenomenological Analysis" Metals 11, no. 11: 1769. https://doi.org/10.3390/met11111769
APA StyleGuerra, A. P. d. B., Jorge, A. M., Jr., Roche, V., & Bolfarini, C. (2021). Hot Deformation Behavior of a Beta Metastable TMZF Alloy: Microstructural and Constitutive Phenomenological Analysis. Metals, 11(11), 1769. https://doi.org/10.3390/met11111769









