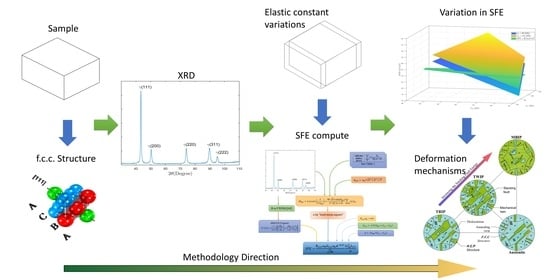
Stacking Fault Energy Determination in Fe-Mn-Al-C Austenitic Steels by X-ray Diffraction
Abstract
:1. Introduction
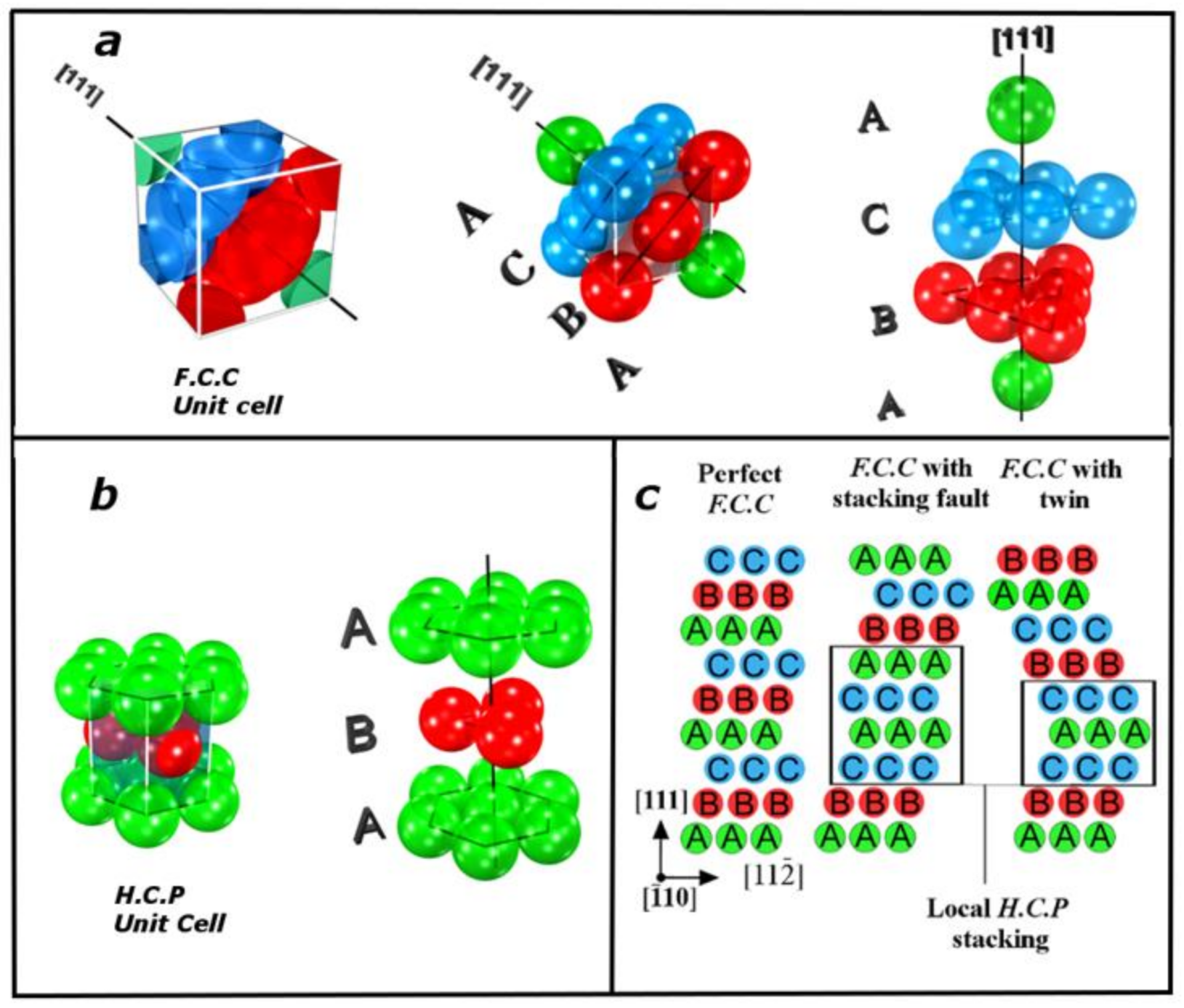
2. About the Stacking Fault and Stacking Fault Energy
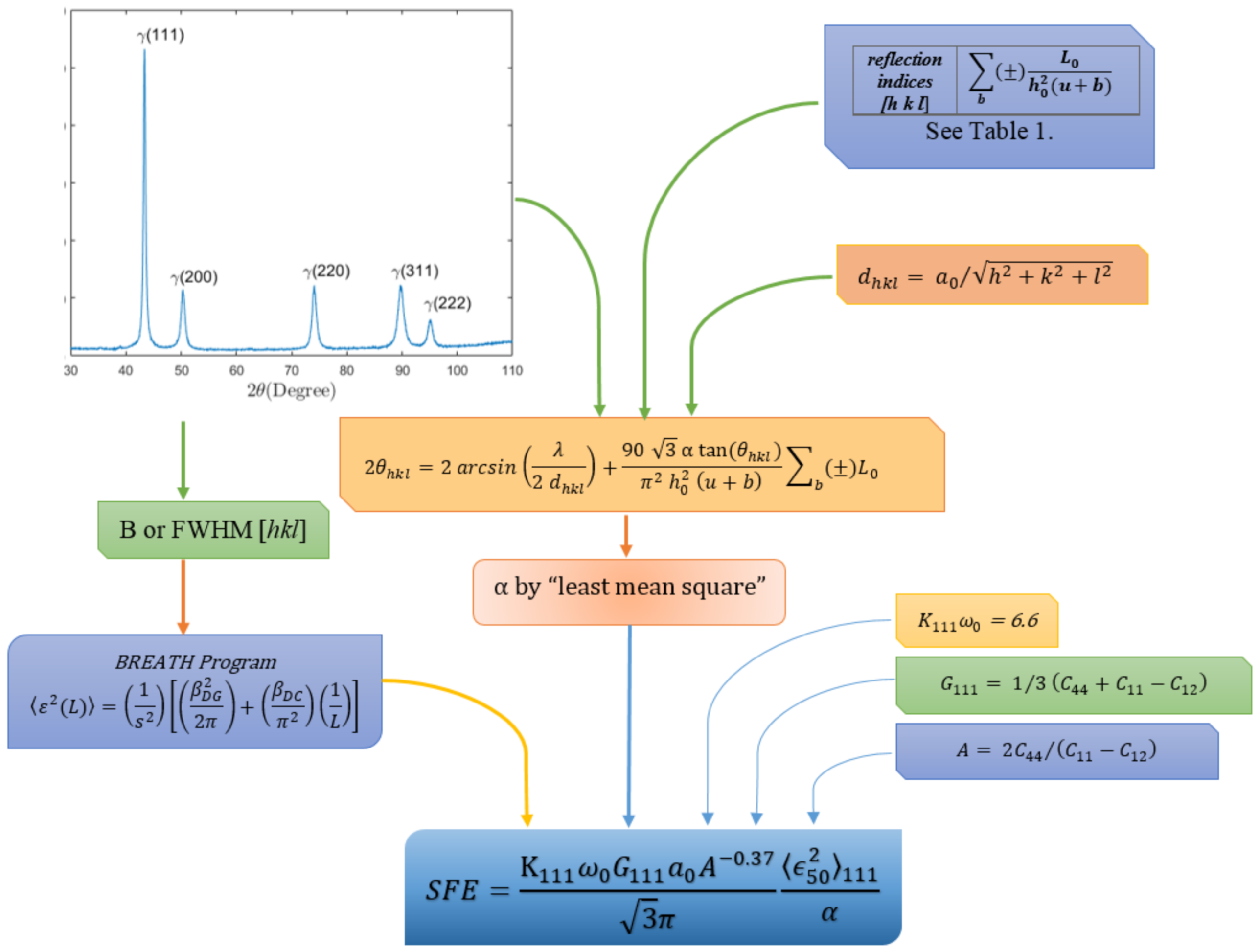
3. About the X-ray Diffraction Technique for Determining the SFE
- = stacking fault energy (mJ/m2)
- = 6.6 (constant value)
- , A is the Zener elastic anisotropy and are elastic stiffness coefficients
- is the shear modulus in <111> direction (GPa.)
- = lattice constant ()
- = root mean square microstrain in the <111> direction averaged over the distance of 50
- = stacking fault probability
3.1. XRD Background Setting
3.2. XRD Determination of the Mean Square Microstrain
3.3. Determination of Peak Positions
3.4. Stacking Fault Probability
- = change in the position of the diffraction lines
- = the diffraction angle for each peak
- = constant specific to each h k l reflection (Table 1)
3.5. Elastic Constants
4. Experimental Procedure
4.1. Specimen Preparation
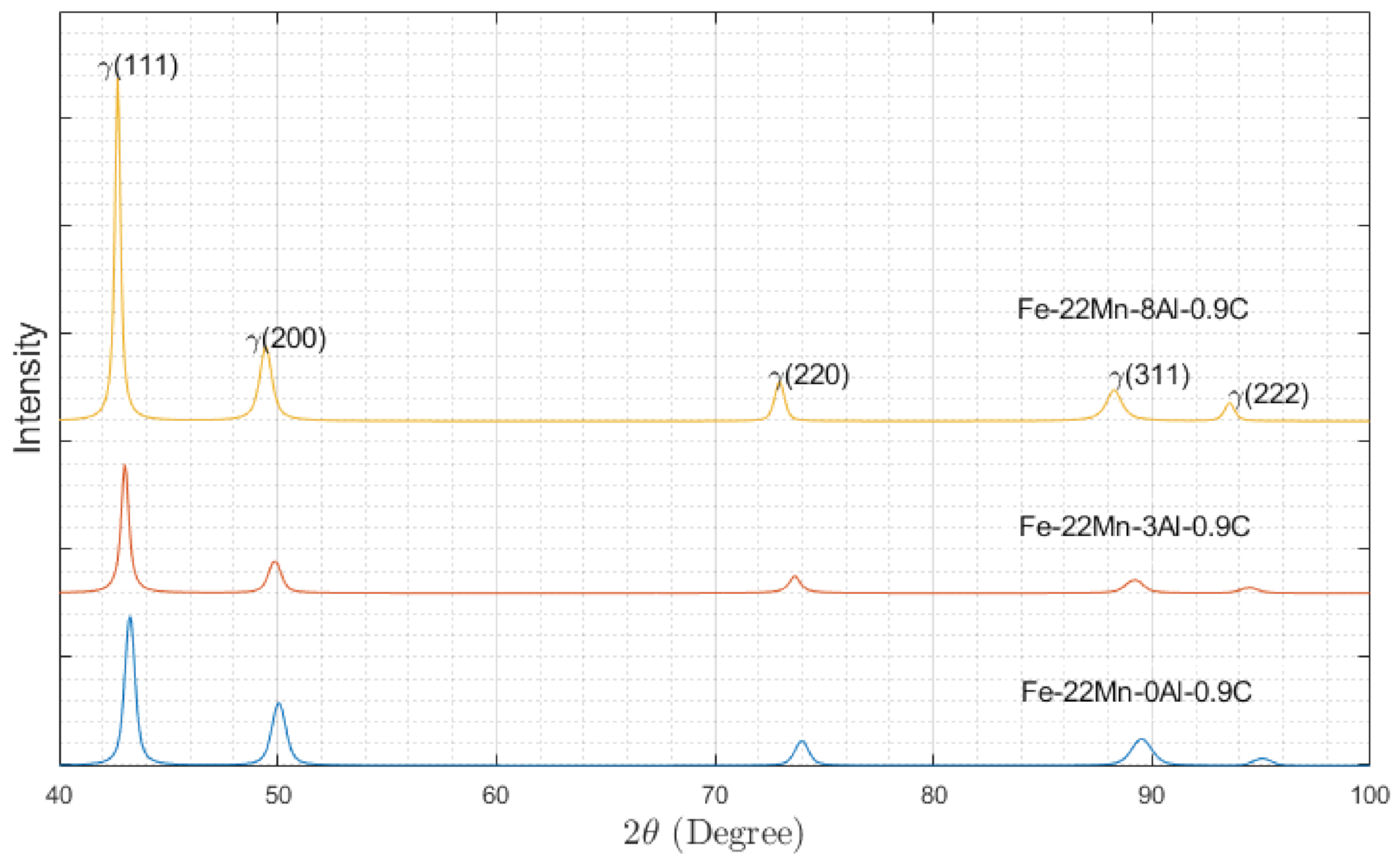
4.2. X-ray Diffraction
4.3. Determination of the SFE
5. Results and Discussions
6. Conclusions
- The flow diagram presents the calculation of the SFE using data obtained by XRD in addition to values of the elastic constants. The procedure was verified with a widely used commercial Hadfield-type alloy, where the values obtained were within the range established by previous investigations.
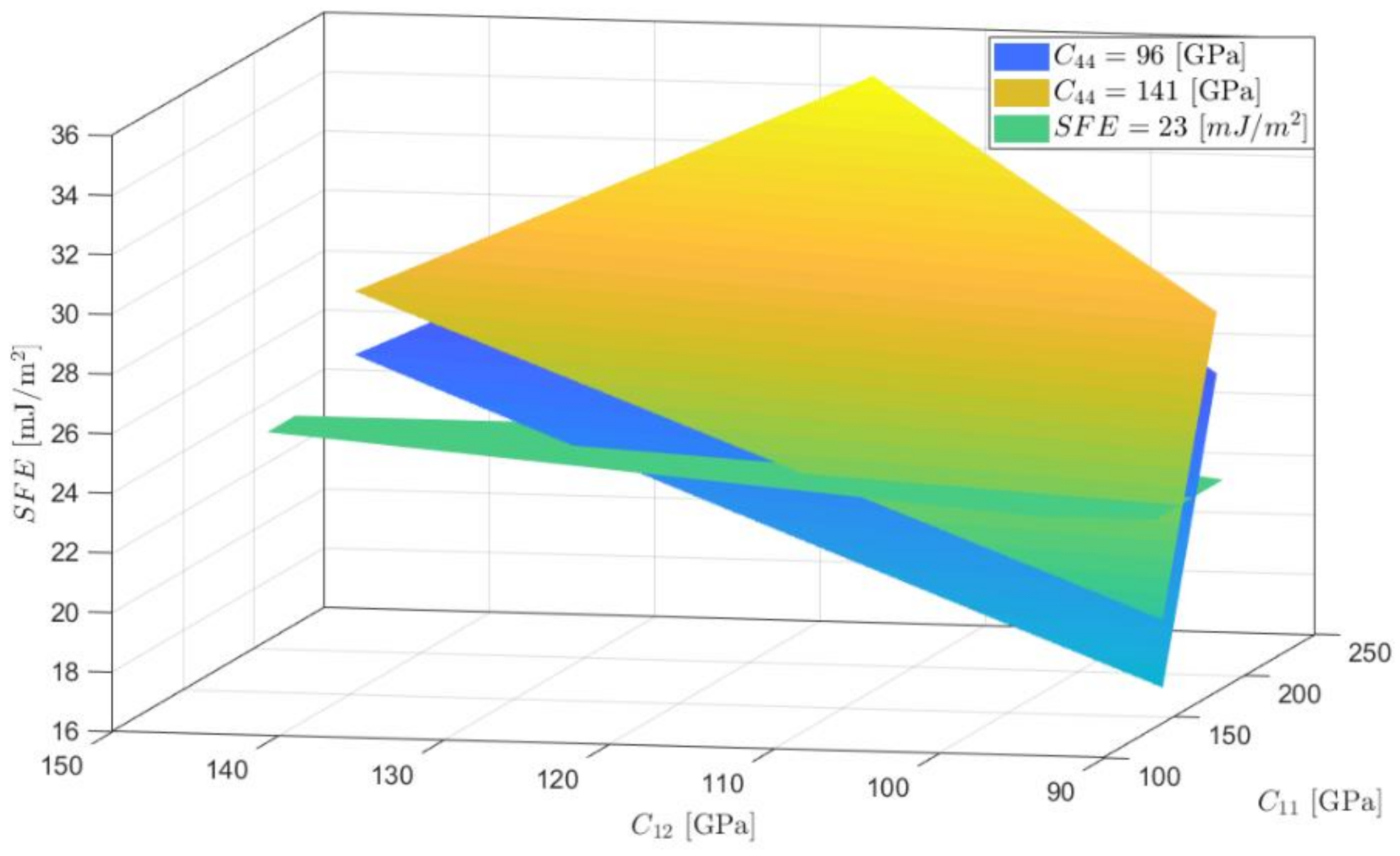
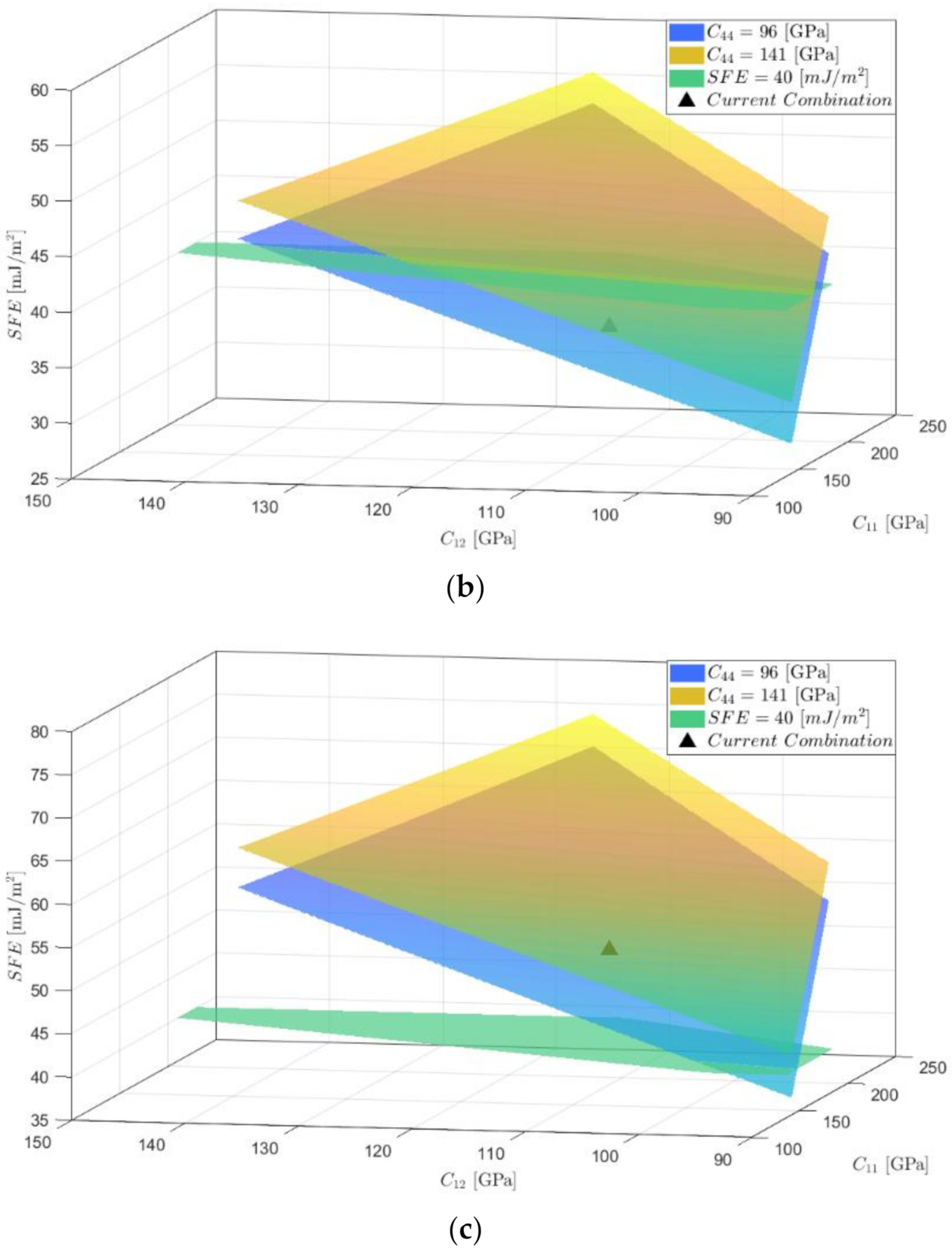
- Average SFE reference values can be obtained using elastic constants of alloys with similar compositions, which serve an alternative when it is not possible to retrieve the values from experimental tests or computational calculations. However, for Hadfield steel, the variation of the elastic constants in the range in which they have been reported generates a variation in the calculated SFE of 30%.
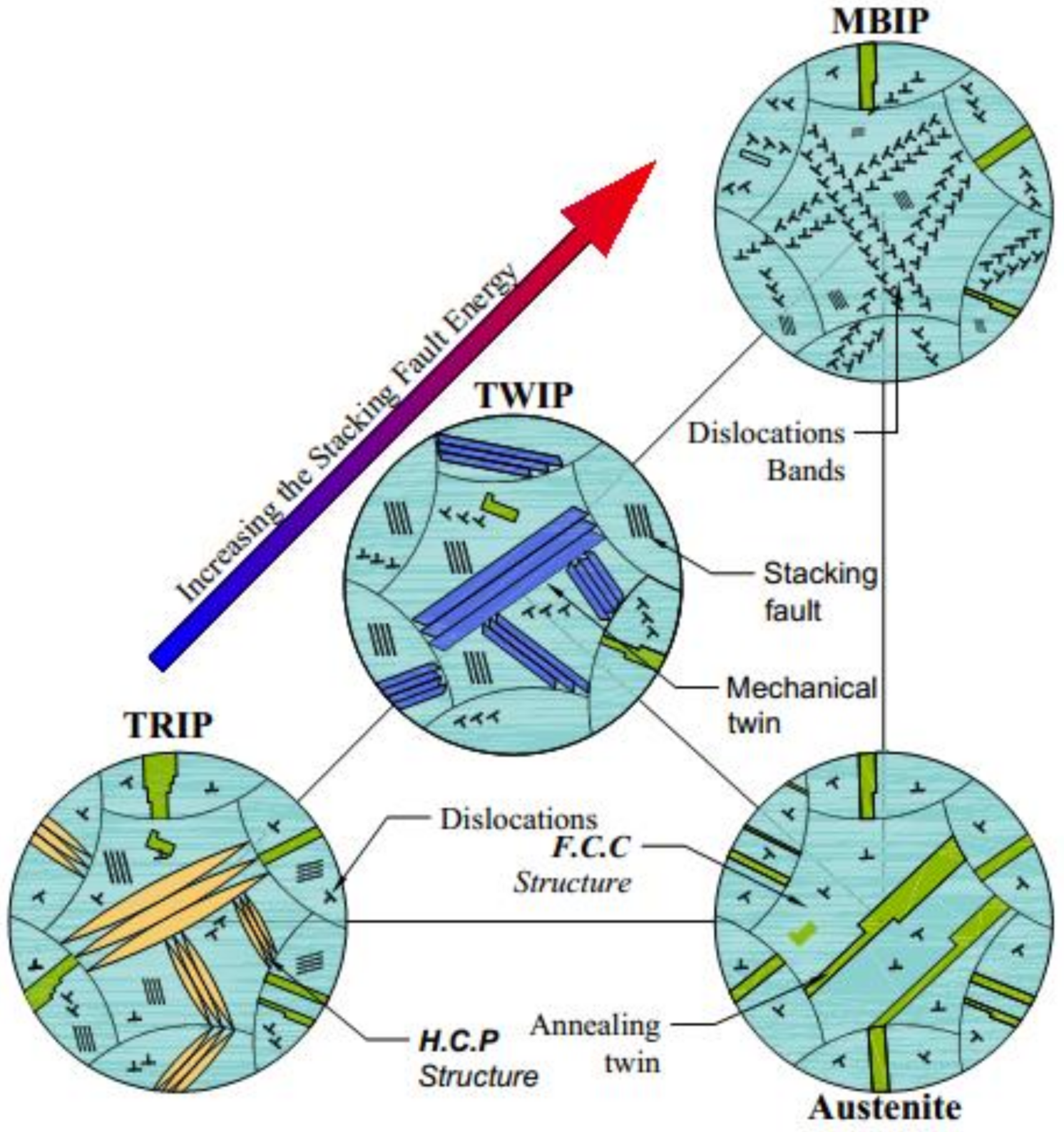
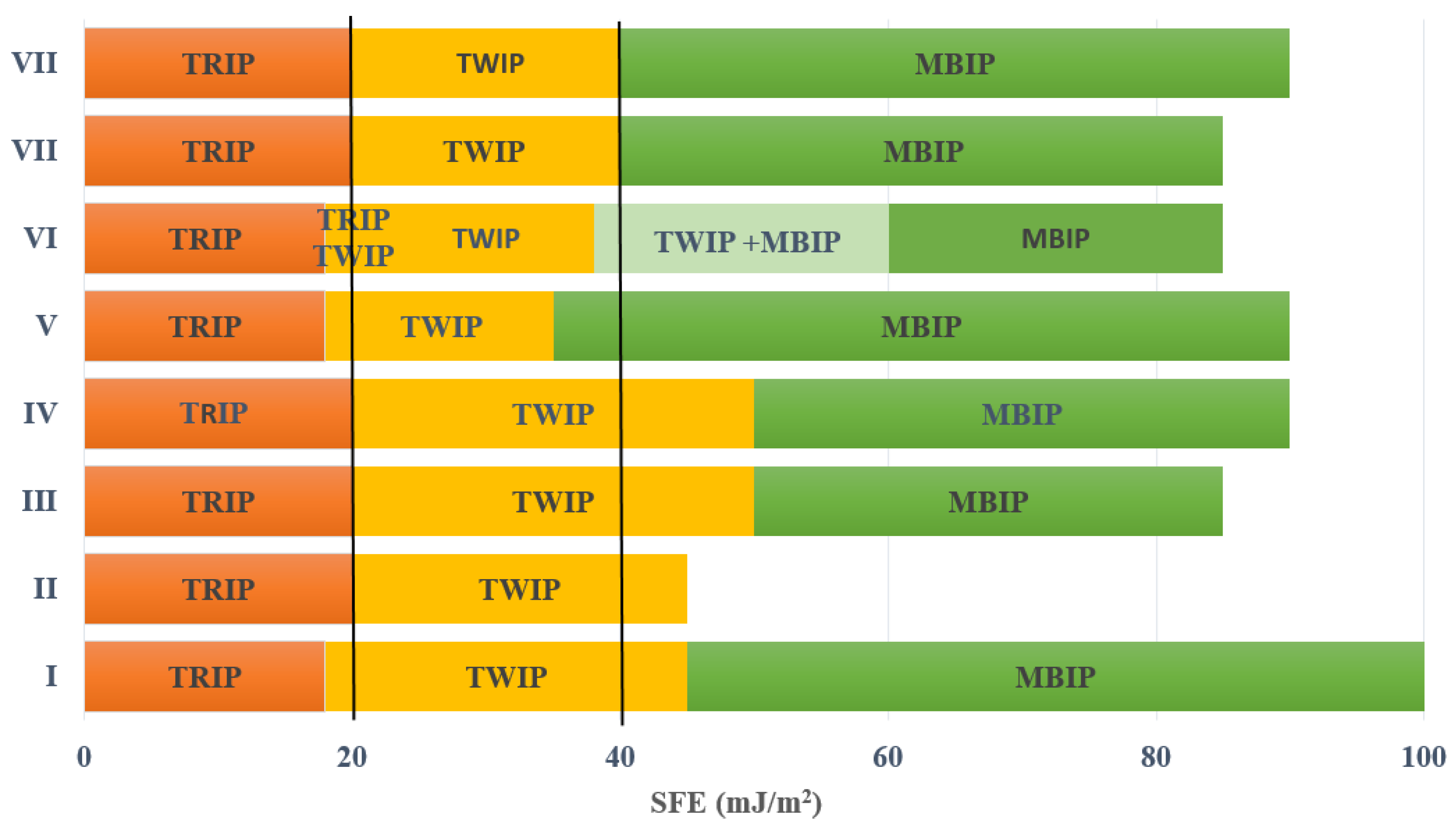
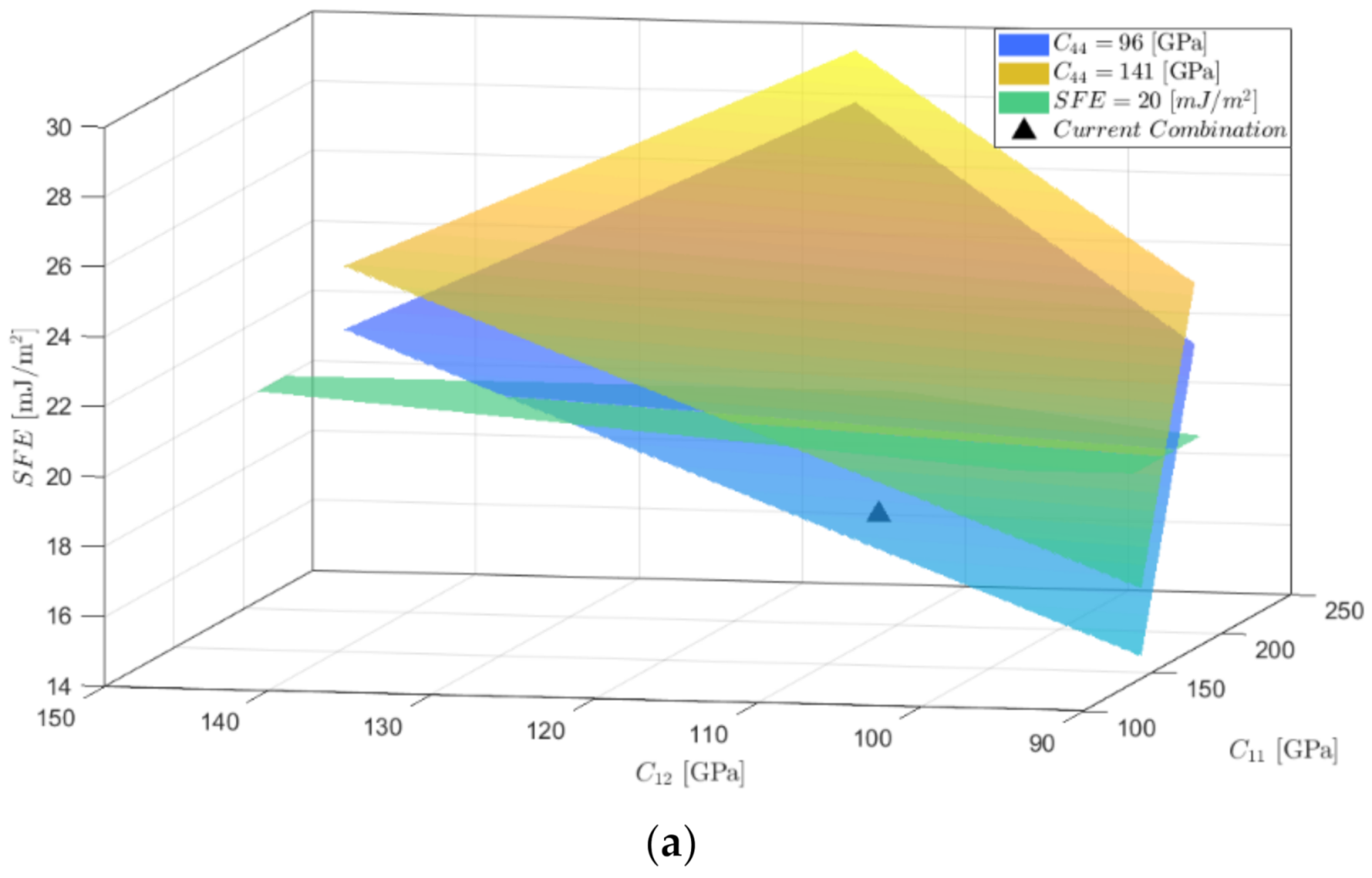
- and are within the ranges reported for austenitic steels generates variations of 36.6%, 28%, and 28.4% in the value of the SFE for the Fe-22Mn-XAl-0.9C alloys studied with 0%, 3%, and 8% Al, respectively; representing the possibility that these alloys present TRIP or TWIP deformation mechanisms for the case of 0% and TWIP or MBIP for 3% Al content. In the case of the alloy with 8% Al, the probable deformation mechanism is MBIP even with the variation in SFE.
- The SFE variation is 11.6%, 12.3%, and 11.5% for alloys with 0%, 3%, and 8% Al, respectively. When changing between the extreme values reported for this constant reflected in a smaller effect concerning the variations of and .
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| SFE | Stacking fault energy, mJ/m2 |
| SFP | Stacking fault probability |
| MSM | Mean square microstrain |
| A | Zener elastic anisotropy |
| G | Shear modulus |
| β | Integral Breadth o FWHM |
References
- Zambrano, O.A.; Valdés, J.; Rodriguez, L.; Reyes, D.; Snoeck, E.; Rodríguez, S.; Coronado, J. Elucidating the role of κ-carbides in FeMnAlC alloys on abrasion wear. Tribol. Int. 2019, 135, 421–431. [Google Scholar] [CrossRef]
- Zambrano, O. A Review on the Effect of Impact Toughness and Fracture Toughness on Impact-Abrasion Wear. J. Mater. Eng. Perform. 2021, 30, 7101–7116. [Google Scholar] [CrossRef]
- Suh, D.-W.; Kim, S.-J. Medium Mn transformation-induced plasticity steels: Recent progress and challenges. Scr. Mater. 2017, 126, 63–67. [Google Scholar] [CrossRef]
- Frommeyer, G.; Brüx, U. Microstructures and Mechanical Properties of High-Strength Fe-Mn-Al-C Light-Weight TRIPLEX Steels. Steel Res. Int. 2006, 77, 627–633. [Google Scholar] [CrossRef]
- Yoo, J.D.; Park, K.-T. Microband-induced plasticity in a high Mn-Al-C light steel. Mater. Sci. Eng. A 2008, 496, 417–424. [Google Scholar] [CrossRef]
- Zambrano, O.A. A general perspective of Fe-Mn-Al-C steels. J. Mater. Sci. 2018, 53, 14003–14062. [Google Scholar] [CrossRef] [Green Version]
- Zambrano, O.A.; Valdés, J.; Aguilar, Y.; Coronado, J.; Rodríguez, S.; Logé, R.E. Hot deformation of a Fe-Mn-Al-C steel susceptible of κ-carbide precipitation. Mater. Sci. Eng. A 2017, 689, 269–285. [Google Scholar] [CrossRef]
- Li, Y.-P.; Song, R.-B.; Wen, E.-D.; Yang, F.-Q. Hot deformation and dynamic recrystallization behavior of austenite-based low-density Fe-Mn-Al-C steel. Acta Metall. Sin. (Engl. Lett.) 2016, 29, 441–449. [Google Scholar] [CrossRef] [Green Version]
- Wan, P.; Kang, T.; Li, F.; Gao, P.; Zhang, L.; Zhao, Z. Dynamic recrystallization behavior and microstructure evolution of low-density high-strength Fe-Mn-Al-C steel. J. Mater. Res. Technol. 2021, 15, 1059–1068. [Google Scholar] [CrossRef]
- Durán, J.; Pérez, G.; Rodríguez, J.; Aguilar, Y.; Logé, R.; Zambrano, O.A. Microstructural Evolution Study of Fe-Mn-Al-C Steels Through Variable Thermomechanical Treatments. Met. Mater. Trans. A 2021, 52, 4785–4799. [Google Scholar] [CrossRef]
- Saeed-Akbari, A.; Imlau, J.; Prahl, U.; Bleck, W. Derivation and variation in composition-dependent stacking fault energy maps based on subregular solution model in high-manganese steels. Met. Mater. Trans. A 2009, 40, 3076–3090. [Google Scholar] [CrossRef]
- Curtze, S.; Kuokkala, V.-T. Dependence of tensile deformation behavior of TWIP steels on stacking fault energy, temperature and strain rate. Acta Mater. 2010, 58, 5129–5141. [Google Scholar] [CrossRef]
- Zambrano, O.A. Stacking Fault Energy Maps of Fe-Mn-Al-C-Si Steels: Effect of Temperature, Grain Size, and Variations in Compositions. J. Eng. Mater. Technol. 2016, 138, 041010. [Google Scholar] [CrossRef]
- Nakano, J.; Jacques, P.J. Effects of the thermodynamic parameters of the hcp phase on the stacking fault energy calculations in the Fe-Mn and Fe-Mn-C systems. Calphad 2010, 34, 167–175. [Google Scholar] [CrossRef]
- Kumar, D. Design of high manganese steels: Calculation of Sfe and Ms temperature. In HSLA Steels 2015, Microalloying 2015 & Offshore Engineering Steels 2015; Springer: Berlin/Heidelberg, Germany, 2016; pp. 857–863. [Google Scholar]
- Pierce, D.T.; Jiménez, J.A.; Bentley, J.; Raabe, D.; Wittig, J.E. The influence of stacking fault energy on the microstructural and strain-hardening evolution of Fe-Mn-Al-Si steels during tensile deformation. Acta Mater. 2015, 100, 178–190. [Google Scholar] [CrossRef]
- Idrissi, H.; Ryelandt, L.; Veron, M.; Schryvers, D.; Jacques, P.J. Is there a relationship between the stacking fault character and the activated mode of plasticity of Fe-Mn-based austenitic steels? Scr. Mater. 2009, 60, 941–944. [Google Scholar] [CrossRef]
- Lehnhoff, G.; Findley, K.; De Cooman, B. The influence of silicon and aluminum alloying on the lattice parameter and stacking fault energy of austenitic steel. Scr. Mater. 2014, 92, 19–22. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, P.; Sarkar, A.; Barat, P.; Bandyopadhyay, S.; Sen, P.; Chattopadhyay, S.; Chatterjee, P.; Chatterjee, S.; Mitra, M. Deformation characteristics of rolled zirconium alloys: A study by X-ray diffraction line profile analysis. Acta Mater. 2004, 52, 5687–5696. [Google Scholar] [CrossRef]
- Pierce, D.T.; Jiménez, J.A.; Bentley, J.; Raabe, D.; Oskay, C.; Wittig, J. The influence of manganese content on the stacking fault and austenite/ε-martensite interfacial energies in Fe-Mn-(Al-Si) steels investigated by experiment and theory. Acta Mater. 2014, 68, 238–253. [Google Scholar] [CrossRef]
- Mahato, B.; Shee, S.; Sahu, T.; Chowdhury, S.G.; Sahu, P.; Porter, D.; Karjalainen, L. An effective stacking fault energy viewpoint on the formation of extended defects and their contribution to strain hardening in a Fe-Mn-Si-Al twinning-induced plasticity steel. Acta Mater. 2015, 86, 69–79. [Google Scholar] [CrossRef]
- Medvedeva, N.; Park, M.; Van Aken, D.C.; Medvedeva, J.E. First-principles study of Mn, Al and C distribution and their effect on stacking fault energies in fcc Fe. J. Alloys Compd. 2014, 582, 475–482. [Google Scholar] [CrossRef]
- Zambrano, O.A.; Castaneda, J.A.; Camargo, M. Towards the comprehension of the stacking fault energy in Fe-Mn-Al-C steels. In Proceedings of the 6th European Conference on Computational Mechanics (ECCM 6), 7th European Conference on Computational Fluid Dynamics (ECFD 7), Glasgow, UK, 11–15 June 2018; Volume 1, pp. 3126–3134. [Google Scholar]
- Pierce, D.; Nowag, K.; Montagne, A.; Jiménez, J.; Wittig, J.; Ghisleni, R. Single crystal elastic constants of high-manganese transformation-and twinning-induced plasticity steels determined by a new method utilizing nanoindentation. Mater. Sci. Eng. A 2013, 578, 134–139. [Google Scholar] [CrossRef]
- Rafaja, D.; Krbetschek, C.; Ullrich, C.; Martin, S. Stacking fault energy in austenitic steels determined by using in situ X-ray diffraction during bending. J. Appl. Crystallogr. 2014, 47, 936–947. [Google Scholar] [CrossRef]
- Reed, R.; Schramm, R. Relationship between stacking-fault energy and x-ray measurements of stacking-fault probability and microstrain. J. Appl. Phys. 1974, 45, 4705–4711. [Google Scholar] [CrossRef]
- Ichikawa, R.; Martinez, L.; Imakuma, K.; Turrillas, X. Development of a methodology for the application of the Warren-Averbach method. In V Scientific Meeting of Applied Physics; Blucher: Sao Paulo, Brazil, 2015. [Google Scholar]
- Williamson, G.; Hall, W. X-ray line broadening from filed aluminium and wolfram. Acta Metall. 1953, 1, 22–31. [Google Scholar] [CrossRef]
- Schramm, R.; Reed, R. Stacking fault energies of seven commercial austenitic stainless steels. Metall. Trans. A 1975, 6, 1345. [Google Scholar] [CrossRef]
- Chaudhary, N.; Abu-Odeh, A.; Karaman, I.; Arróyave, R. A data-driven machine learning approach to predicting stacking faulting energy in austenitic steels. J. Mater. Sci. 2017, 52, 11048–11076. [Google Scholar] [CrossRef]
- Paterson, M.S. X-ray diffraction by face-centered cubic crystals with deformation faults. J. Appl. Phys. 1952, 23, 805–811. [Google Scholar] [CrossRef]
- Christian, J.W.; Mahajan, S. Deformation twinning. Prog. Mater. Sci. 1995, 39, 1–157. [Google Scholar] [CrossRef]
- Li, Z.; Pradeep, K.G.; Deng, Y.; Raabe, D.; Tasan, C.C. Metastable high-entropy dual-phase alloys overcome the strength–ductility trade-off. Nature 2016, 534, 227–230. [Google Scholar] [CrossRef]
- Grässel, O.; Frommeyer, G.; Derder, C.; Hofmann, H. Phase transformations and mechanical properties of Fe-Mn-Si-Al TRIP-steels. Le J. De Phys. IV 1997, 7, C5-383–C5-388. [Google Scholar] [CrossRef] [Green Version]
- Ding, H.; Han, D.; Cai, Z.; Wu, Z. Microstructures and mechanical behavior of Fe-18Mn-10Al-(0.8-1.2) C steels. JOM 2014, 66, 1821–1827. [Google Scholar] [CrossRef]
- Hua, D.; Huaying, L.; Zhiqiang, W.; Mingli, H.; Haoze, L.; Qibin, X. Microstructural Evolution and Deformation Behaviors of Fe-M n-Al-C Steels with DifferSent Stacking Fault Energies. Steel Res. Int. 2013, 84, 1288–1293. [Google Scholar] [CrossRef]
- Yoo, J.; Hwang, S.; Park, K.-T. Origin of extended tensile ductility of a Fe-28Mn-10Al-1C steel. Met. Mater. Trans. A 2009, 40, 1520–1523. [Google Scholar] [CrossRef]
- Marandi, A.; Zarei-Hanzaki, R.; Zarei-Hanzaki, A.; Abedi, H. Dynamic recrystallization behavior of new transformation–twinning induced plasticity steel. Mater. Sci. Eng. A 2014, 607, 397–408. [Google Scholar] [CrossRef]
- Welsch, E.; Ponge, D.; Haghighat, S.H.; Sandlöbes, S.; Choi, P.; Herbig, M.; Zaefferer, S.; Raabe, D. Strain hardening by dynamic slip band refinement in a high-Mn lightweight steel. Acta Mater. 2016, 116, 188–199. [Google Scholar] [CrossRef]
- Smallman, R.; Westmacott, K. Stacking faults in face-centred cubic metals and alloys. Philos. Mag. 1957, 2, 669–683. [Google Scholar] [CrossRef]
- Otte, H.; Welch, D. Formation of stacking faults in polycrystalline silicon bronze under tensile deformation. Philos. Mag. 1964, 9, 299–313. [Google Scholar] [CrossRef]
- Adler, R.; Otte, H. Dislocation configurations in wire-drawn polycrystalline copper alloys: A study by x-ray diffraction. Mater. Sci. Eng. 1966, 1, 222–238. [Google Scholar] [CrossRef]
- Otte, H.M. Measurement of Stacking-Fault Energies by X-Ray Diffraction. J. Appl. Phys. 1967, 38, 217–222. [Google Scholar] [CrossRef]
- Gallagher, P. The influence of alloying, temperature, and related effects on the stacking fault energy. Metall. Trans. 1970, 1, 2429–2461. [Google Scholar]
- Delhez, R.; De Keijser, T.H.; Mittemeijer, E. Determination of crystallite size and lattice distortions through X-ray diffraction line profile analysis. Fresenius’ Z. Anal. Chem. 1982, 312, 1–16. [Google Scholar] [CrossRef]
- Ungár, T.; Gubicza, J.; Ribárik, G.; Borbély, A. Crystallite size distribution and dislocation structure determined by diffraction profile analysis: Principles and practical application to cubic and hexagonal crystals. J. Appl. Crystallogr. 2001, 34, 298–310. [Google Scholar] [CrossRef] [Green Version]
- Warren, B. X-Ray Diffraction; Courier Corporation: North Chelmsford, MA, USA, 1990. [Google Scholar]
- Hsu, Y.G.Z.S.T. X-ray peak-shift determination of deformation fault probability in Fe-Mn-Si alloys. J. Mater. Sci. Technol. 2002, 5, 459–461. [Google Scholar]
- Huang, S.; Li, N.; Wen, Y.; Teng, J.; Ding, S.; Xu, Y. Effect of Si and Cr on stacking fault probability and damping capacity of Fe-Mn alloy. Mater. Sci. Eng. A 2008, 479, 223–228. [Google Scholar] [CrossRef]
- Chandan, A.K.; Mishra, G.; Mahato, B.; Chowdhury, S.; Kundu, S.; Chakraborty, J. Stacking Fault Energy of Austenite Phase in Medium Manganese Steel. Met. Mater. Trans. A 2019, 50, 4851–4866. [Google Scholar] [CrossRef]
- Ribárik, G.; Ungár, T.; Gubicza, J. MWP-fit: A program for multiple whole-profile fitting of diffraction peak profiles by ab initio theoretical functions. J. Appl. Crystallogr. 2001, 34, 669–676. [Google Scholar] [CrossRef] [Green Version]
- Adler, R.; Otte, H.; Wagner, C. Determination of dislocation density and stacking fault probability from x-ray powder pattern peak profiles. Metall. Trans. 1970, 1, 2375–2382. [Google Scholar]
- Tian, X.; Li, H.; Zhang, Y. Effect of Al content on stacking fault energy in austenitic Fe-Mn-Al-C alloys. J. Mater. Sci. 2008, 43, 6214–6222. [Google Scholar] [CrossRef]
- Rhodes, C.G.; Thompson, A.W. The composition dependence of stacking fault energy in austenitic stainless steels. Metall. Trans. A 1977, 8, 1901–1906. [Google Scholar] [CrossRef]
- Langford, J.I. A rapid method for analysing the breadths of diffraction and spectral lines using the Voigt function. J. Appl. Crystallogr. 1978, 11, 10–14. [Google Scholar] [CrossRef]
- Bakshi, S.D.; Sinha, D.; Chowdhury, S.G. Anisotropic broadening of XRD peaks of α′-Fe: Williamson-Hall and Warren-Averbach analysis using full width at half maximum (FWHM) and integral breadth (IB). Mater. Charact. 2018, 142, 144–153. [Google Scholar] [CrossRef]
- Larson, A.; Von Dreele, R. General Structure Analysis System (GSAS) Manual; LANSCE, MS-H805, Los Alamos National Laborator: Los Alamos, NM, USA, 1994; p. 87545. [Google Scholar]
- Langford, J. Accuracy of Crystallite Size and Strain Determined from the Integral Breadth of Powder Diffraction Lines; NBS Special Publication: Gaithersburg, MD, USA, 1980; p. 255. [Google Scholar]
- Warren, B. X-ray studies of deformed metals. Progr. Met. Phys. 1959, 8, 147–202. [Google Scholar] [CrossRef]
- Ungár, T. Dislocation model of strain anisotropy. Powder Diffr. 2008, 23, 125–132. [Google Scholar] [CrossRef] [Green Version]
- Delhez, R.; de Keijser, T.; Mittemeijer, E.; Langford, J. Size and strain parameters from peak profiles: Sense and nonsense. Aust. J. Phys. 1988, 41, 213–228. [Google Scholar] [CrossRef] [Green Version]
- Balzar, D.; Ledbetter, H. Voigt-function modeling in Fourier analysis of size-and strain-broadened X-ray diffraction peaks. J. Appl. Crystallogr. 1993, 26, 97–103. [Google Scholar] [CrossRef]
- Warren, B.; Averbach, B. The effect of cold-work distortion on X-ray patterns. J. Appl. Phys. 1950, 21, 595–599. [Google Scholar] [CrossRef]
- Howard, S.; Snyder, R. The use of direct convolution products in profile and pattern fitting algorithms. I. Development of algorithms. J. Appl. Crystallogr. 1989, 22, 238–243. [Google Scholar] [CrossRef]
- Balzar, D. BREADTH–a program for analyzing diffraction line broadening. J. Appl. Crystallogr. 1995, 28, 244–245. [Google Scholar] [CrossRef]
- Prevey, P.S. X-ray diffraction residual stress techniques. ASM Int. ASM Handbook 1986, 10, 380–392. [Google Scholar]
- Martinez, L.G. Desenvolvimento e Implantacao de Uma Tecnica de Analise de Perfis de Difracao de Raios x Para a Determinacao da Energia de Falha de Empilhamento de Metais e Ligas de Estrutura CFC. Ph.D. Thesis, University of Sao Paulo, Sao Paulo, Brazil, 1989. [Google Scholar]
- Talonen, J.; Hänninen, H. Formation of shear bands and strain-induced martensite during plastic deformation of metastable austenitic stainless steels. Acta Mater. 2007, 55, 6108–6118. [Google Scholar] [CrossRef]
- Barman, H.; Hamada, A.; Sahu, T.; Mahato, B.; Talonen, J.; Shee, S.; Sahu, P.; Porter, D.; Karjalainen, L. A stacking fault energy perspective into the uniaxial tensile deformation behavior and microstructure of a Cr-Mn austenitic steel. Met. Mater. Trans. A 2014, 45, 1937–1952. [Google Scholar] [CrossRef]
- Curtze, S.; Kuokkala, V.-T.; Oikari, A.; Talonen, J.; Hänninen, H. Thermodynamic modeling of the stacking fault energy of austenitic steels. Acta Mater. 2011, 59, 1068–1076. [Google Scholar] [CrossRef]
- Lee, T.-H.; Shin, E.; Oh, C.-S.; Ha, H.-Y.; Kim, S.-J. Correlation between stacking fault energy and deformation microstructure in high-interstitial-alloyed austenitic steels. Acta Mater. 2010, 58, 3173–3186. [Google Scholar] [CrossRef]
- Muslov, S.; Lotkov, A.; Arutyunov, S. Extrema of Elastic Properties of Cubic Crystals. Russ. Phys. J. 2019, 62, 1417–1427. [Google Scholar] [CrossRef]
- Gebhardt, T.; Music, D.; Kossmann, D.; Ekholm, M.; Abrikosov, I.A.; Vitos, L.; Schneider, J.M. Elastic properties of fcc Fe-Mn-X (X = Al, Si) alloys studied by theory and experiment. Acta Mater. 2011, 59, 3145–3155. [Google Scholar] [CrossRef]
- Zhang, H.; Johansson, B.; Vitos, L. Ab initio calculations of elastic properties of bcc Fe-Mg and Fe-Cr random alloys. Phys. Rev. B 2009, 79, 224201. [Google Scholar] [CrossRef]
- Jung, I.; Lee, S.-J.; De Cooman, B.C. Influence of Al on internal friction spectrum of Fe–18Mn–0.6 C twinning-induced plasticity steel. Scr. Mater. 2012, 66, 729–732. [Google Scholar] [CrossRef]
- King, H.; Peters, M. Predictive Equations for Martensitic and Antiferromagnetic Transformations in Fe-Mn-Al-Si Alloys. Can. Metall. Q. 1997, 36, 137–141. [Google Scholar]
- Cankurtaran, M.; Saunders, G.; Ray, P.; Wang, Q.; Kawald, U.; Pelzl, J.; Bach, H. Relationship of the elastic and nonlinear acoustic properties of the antiferromagnetic fcc Fe 60 Mn 40 single-crystal alloy to Invar behavior. Phys. Rev. B 1993, 47, 3161. [Google Scholar] [CrossRef] [PubMed]
- Rietveld, H. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 1969, 2, 65–71. [Google Scholar] [CrossRef]
- Zambrano, O.A.; Tressia, G.; Souza, R. Failure analysis of a crossing rail made of Hadfield steel after severe plastic deformation induced by wheel-rail interaction. Eng. Fail. Anal. 2020, 30, 104621. [Google Scholar] [CrossRef]
- Dastur, Y.; Leslie, W. Mechanism of work hardening in Hadfield manganese steel. Metall. Trans. A 1981, 12, 749–759. [Google Scholar] [CrossRef]
- Adler, P.; Olson, G.; Owen, W. Strain hardening of Hadfield manganese steel. Metall. Mater. Trans. A 1986, 17, 1725–1737. [Google Scholar] [CrossRef]
- Kim, T.; Bourdillon, A. Influence of carbon on development of deformation microstructures in Hadfield steels. Mater. Sci. Technol. 1992, 8, 1011–1022. [Google Scholar] [CrossRef]
- Music, D.; Takahashi, T.; Vitos, L.; Asker, C.; Abrikosov, I.A.; Schneider, J.M. Elastic properties of Fe-Mn random alloys studied by ab initio calculations. Appl. Phys. Lett. 2007, 91, 191904. [Google Scholar] [CrossRef] [Green Version]
- Bampton, C.; Jones, I.; Loretto, M. Stacking fault energy measurements in some austenitic stainless steels. Acta Metall. 1978, 26, 39–51. [Google Scholar] [CrossRef]
- Endoh, Y.; Noda, Y.; Iizumi, M. Lattice dynamics and invar properties in fcc FeMn alloy. J. Phys. Soc. Jpn. 1981, 50, 469–475. [Google Scholar] [CrossRef]
- Lenkkeri, J. Measurements of elastic moduli of face-centred cubic alloys of transition metals. J. Phys. F Met. Phys. 1981, 11, 1991. [Google Scholar] [CrossRef]
- Stinville, J.; Tromas, C.; Villechaise, P.; Templier, C. Anisotropy changes in hardness and indentation modulus induced by plasma nitriding of 316L polycrystalline stainless steel. Scr. Mater. 2011, 64, 37–40. [Google Scholar] [CrossRef]
- Paszkiewicz, T.; Wolski, S. Elastic properties of cubic crystals: Every’s versus Blackman’s diagram. J. Phys. Conf. Ser. 2008, 104, 012038. [Google Scholar] [CrossRef]
- Chen, S.; Rana, R.; Haldar, A.; Ray, R.K. Current state of Fe-Mn-Al-C low density steels. Prog. Mater. Sci. 2017, 89, 345–391. [Google Scholar] [CrossRef]

| Indices of Reflection [H K L] | |
|---|---|
| 1 1 0 | |
| 2 0 0 | |
| 2 2 0 | |
| 3 1 1 | |
| 2 2 2 | |
| 4 0 0 |
| Alloy | Fe (% wt) | Mn (% wt) | Al (% wt) | C (% wt) |
|---|---|---|---|---|
| Fe-22Mn-0.9C-0Al | Balance | 20.5 | 0 | 0.87 |
| Fe-22Mn-0.9C-3Al | Balance | 22.2 | 3.5 | 0.84 |
| Fe-22Mn-0.9C-8Al | Balance | 22.1 | 8.3 | 0.89 |
| Reference | Composition of Alloys (wt. pc) | Methodology | C11 [GPa] | C12 [GPa] | C44 [GPa] | Determined SFE of the Hadfield Using These Elastic Constants (mJ/m2) |
|---|---|---|---|---|---|---|
| Music, et al. [83] | Fe-10Mn | ab initio | 210 | 153 | 135 | 20.53 |
| Bampton, et al. [84] | Fe-18Cr-12N-3Mo | Crystal Grown | 235 | 138.5 | 117 | 29.2 |
| Endoh, et al. [85] | Fe-30Mn | Atomic Force | 200 ± 9 | 127 ± 6 | 130 ± 3 | 24.1 ± 0.9 |
| Gebhardt, Music, Kossmann, Ekholm, Abrikosov, Vitos and Schneider [73] | Fe-25Mn-2Al | ab initio | 153.6 | 105 | 135.5 | 18.5 |
| Pierce, Nowag, Montagne, Jiménez, Wittig and Ghisleni [24] | Fe-18Mn-1.5Al-0.6C | Nanoindentation | 169 ± 6 | 82 ± 3 | 96 ± 4 | 26.9 ± 1 |
| Lenkkeri [86] | Fe-38.5Mn | Ultrasound | 169.2 | 97.7 | 140.1 | 25.9 |
| Cankurtaran, Saunders, Ray, Wang, Kawald, Pelzl and Bach [77] | Fe-40Mn | Ultrasound | 170 | 98 | 141 | 24.27 |
| Stinville, et al. [87] | 316L | Nanoindentation | 196 | 129 | 116 | 21.9 |
| Pierce, Nowag, Montagne, Jiménez, Wittig and Ghisleni [24] | Fe-22Mn-3Al-3Si | Nanoindentation | 175 ± 7 | 83 ± 3 | 97 ± 4 | 27.3 ± 1.1 |
| Alloy | Phase | ± 0.005 | X2 | F2(R) | |
|---|---|---|---|---|---|
| Fe-22Mn-0.9C-0Al | 3.627 | 47.713 | 5.8 | 0.0431 | |
| Fe-22Mn-0.9C-3Al | 3.634 | 47.990 | 3.9 | 0.0383 | |
| Fe-22Mn-0.9C-8Al | 3.671 | 49.471 | 5.2 | 0.0523 |
| Alloy | SFPx104 | SFE * (mJ/m2) | SFE ** (mJ/m2) | |
|---|---|---|---|---|
| Fe-22Mn-0.9C-0Al | 9.62 ± 2.68 | 8.92 | 17.53 ± 2.47 | 10.99 |
| Fe-22Mn-0.9C-3Al | 6.52 ± 2.96 | 13.56 | 35.61 ± 4.76 | 33.42 |
| Fe-22Mn-0.9C-8Al | 7.48 ± 3.24 | 21.86 | 50.76 ± 6.73 | 53.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castañeda, J.A.; Zambrano, O.A.; Alcázar, G.A.; Rodríguez, S.A.; Coronado, J.J. Stacking Fault Energy Determination in Fe-Mn-Al-C Austenitic Steels by X-ray Diffraction. Metals 2021, 11, 1701. https://doi.org/10.3390/met11111701
Castañeda JA, Zambrano OA, Alcázar GA, Rodríguez SA, Coronado JJ. Stacking Fault Energy Determination in Fe-Mn-Al-C Austenitic Steels by X-ray Diffraction. Metals. 2021; 11(11):1701. https://doi.org/10.3390/met11111701
Chicago/Turabian StyleCastañeda, Jaime A., Oscar A. Zambrano, Germán A. Alcázar, Sara A. Rodríguez, and John J. Coronado. 2021. "Stacking Fault Energy Determination in Fe-Mn-Al-C Austenitic Steels by X-ray Diffraction" Metals 11, no. 11: 1701. https://doi.org/10.3390/met11111701
APA StyleCastañeda, J. A., Zambrano, O. A., Alcázar, G. A., Rodríguez, S. A., & Coronado, J. J. (2021). Stacking Fault Energy Determination in Fe-Mn-Al-C Austenitic Steels by X-ray Diffraction. Metals, 11(11), 1701. https://doi.org/10.3390/met11111701