Simulation of Quasi-Static Crack Propagation by Adaptive Finite Element Method
Abstract
1. Introduction
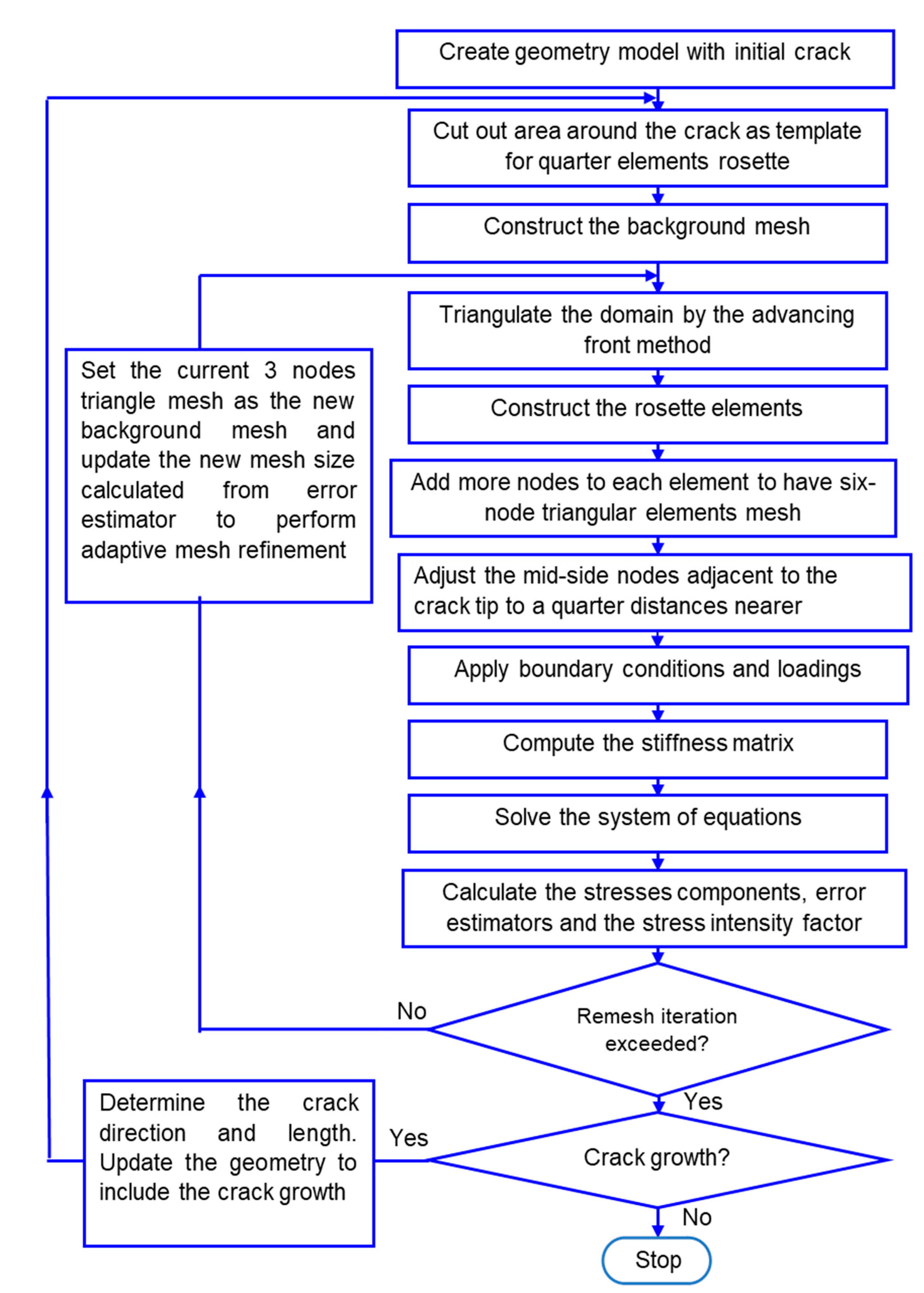
2. Developed Program Framework
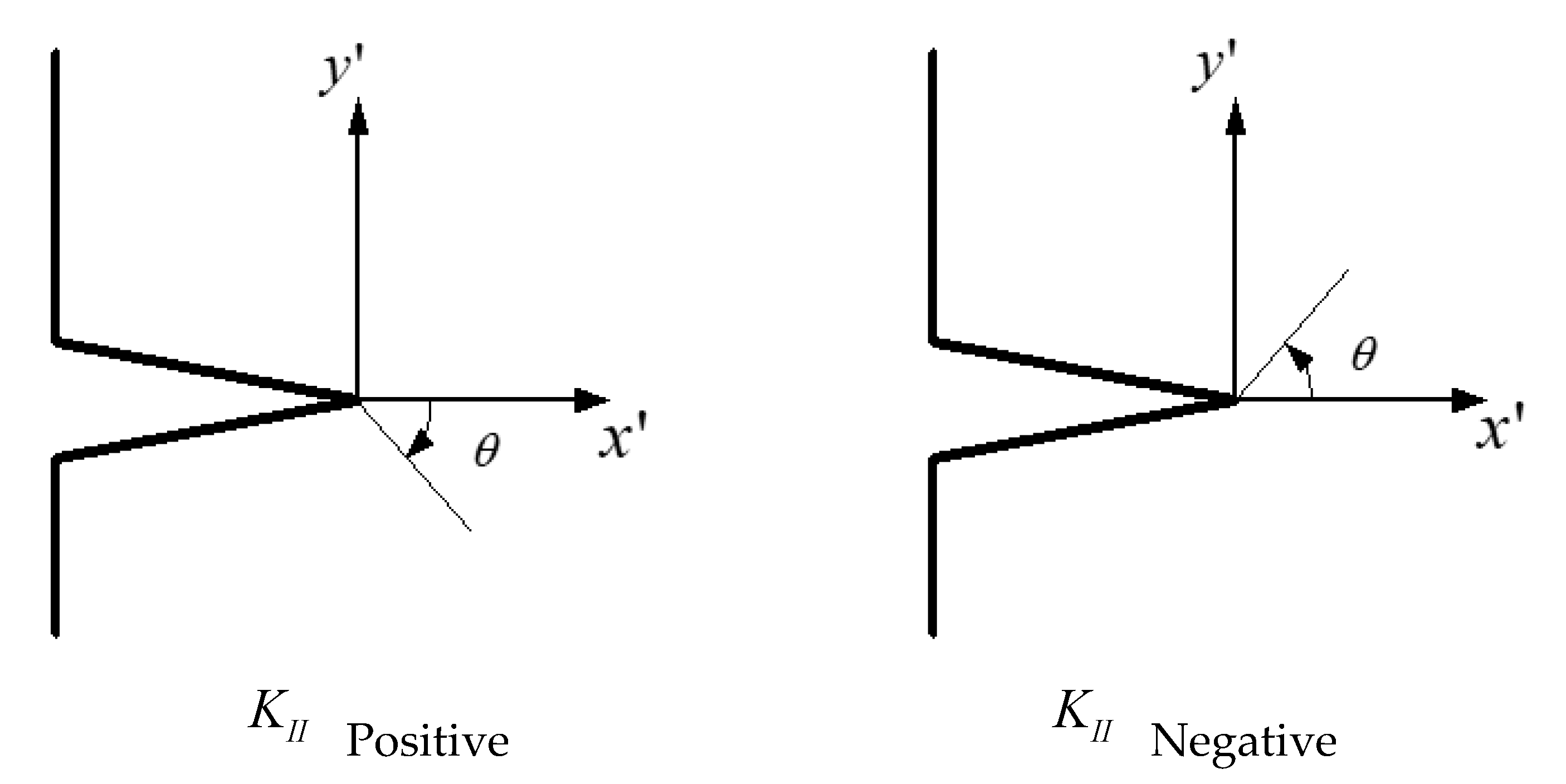
2.1. Displacement Extrapolation Technique (DET)
2.2. Adaptive Mesh Refinement
2.3. Crack Growth Analysis
3. Numerical Results and Discussion
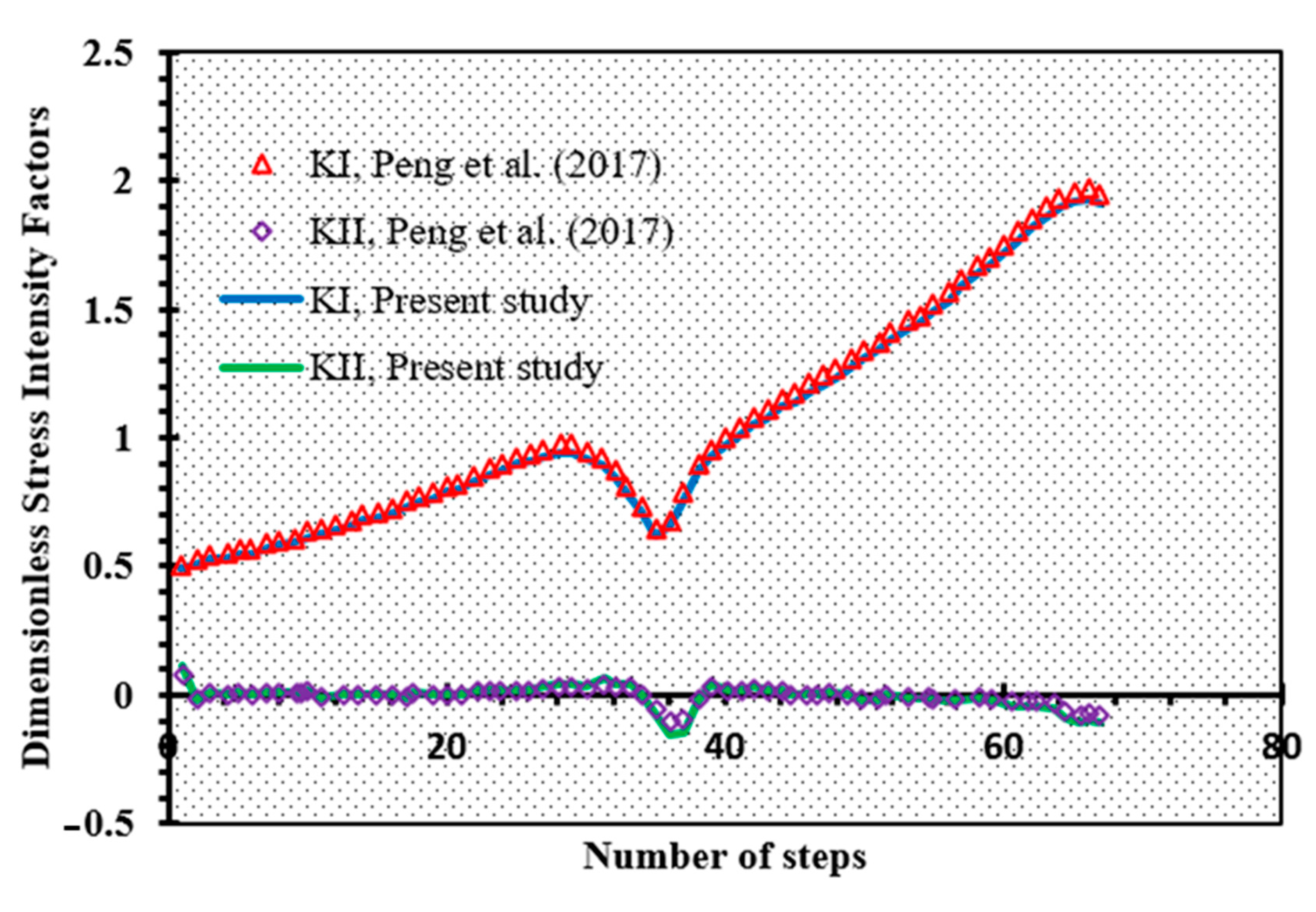
3.1. Two Internal Non-Colinear Cracks
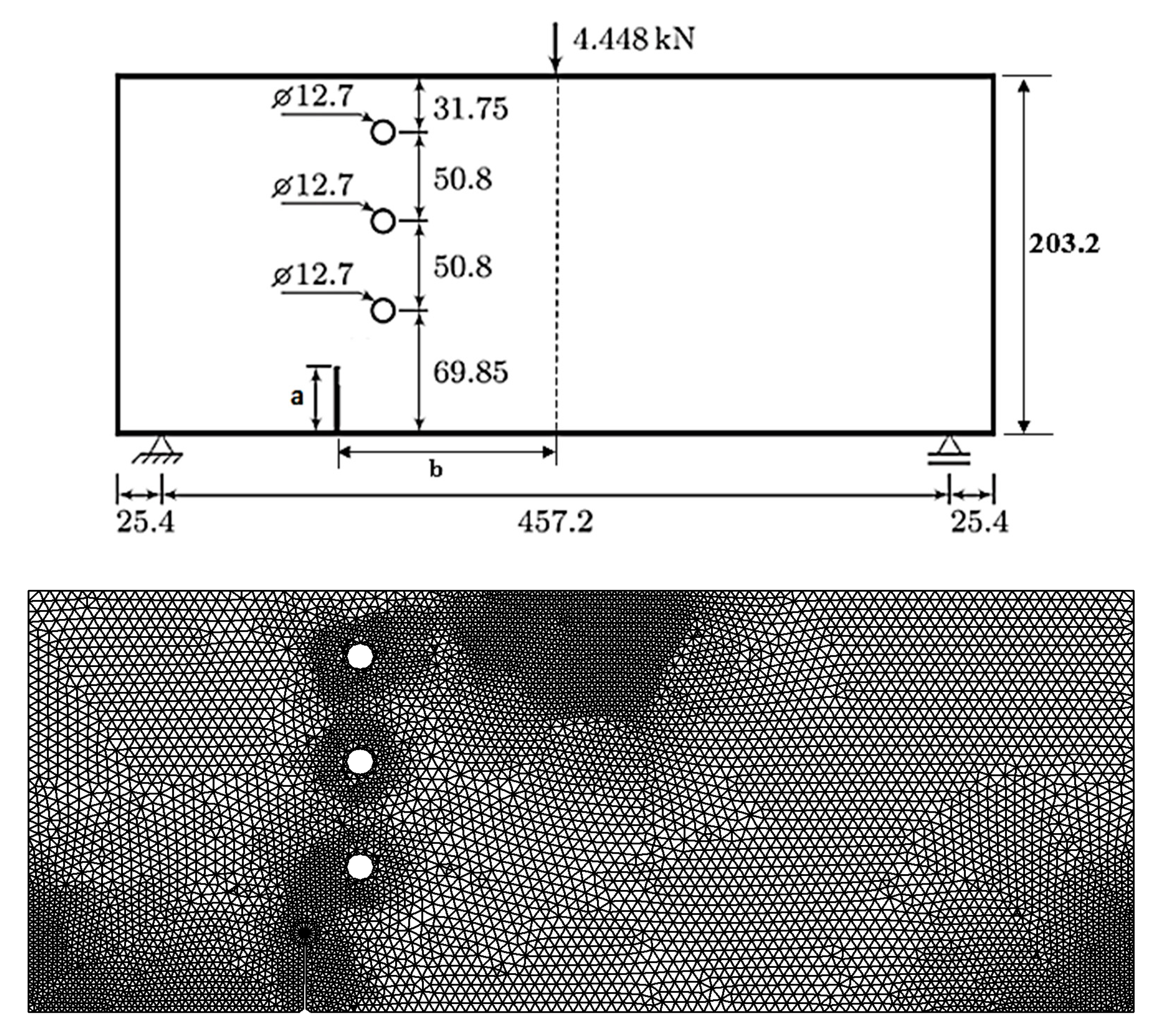
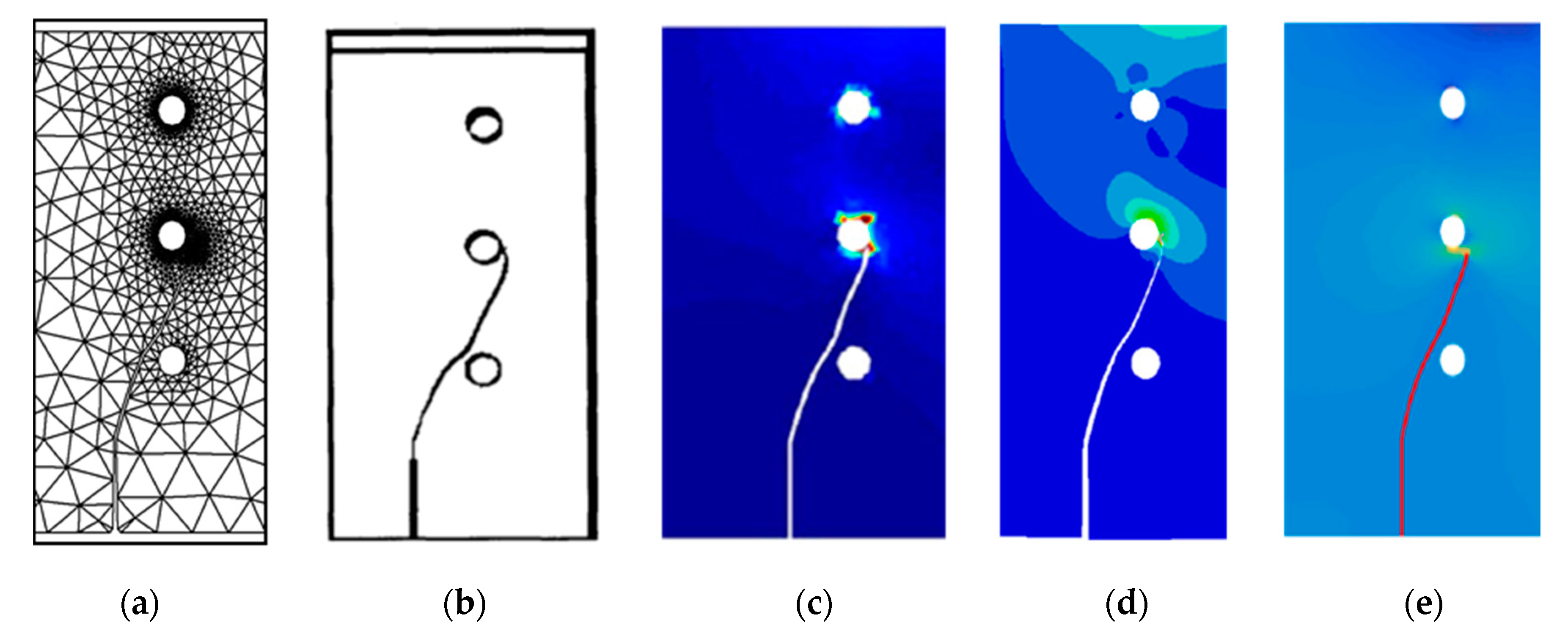
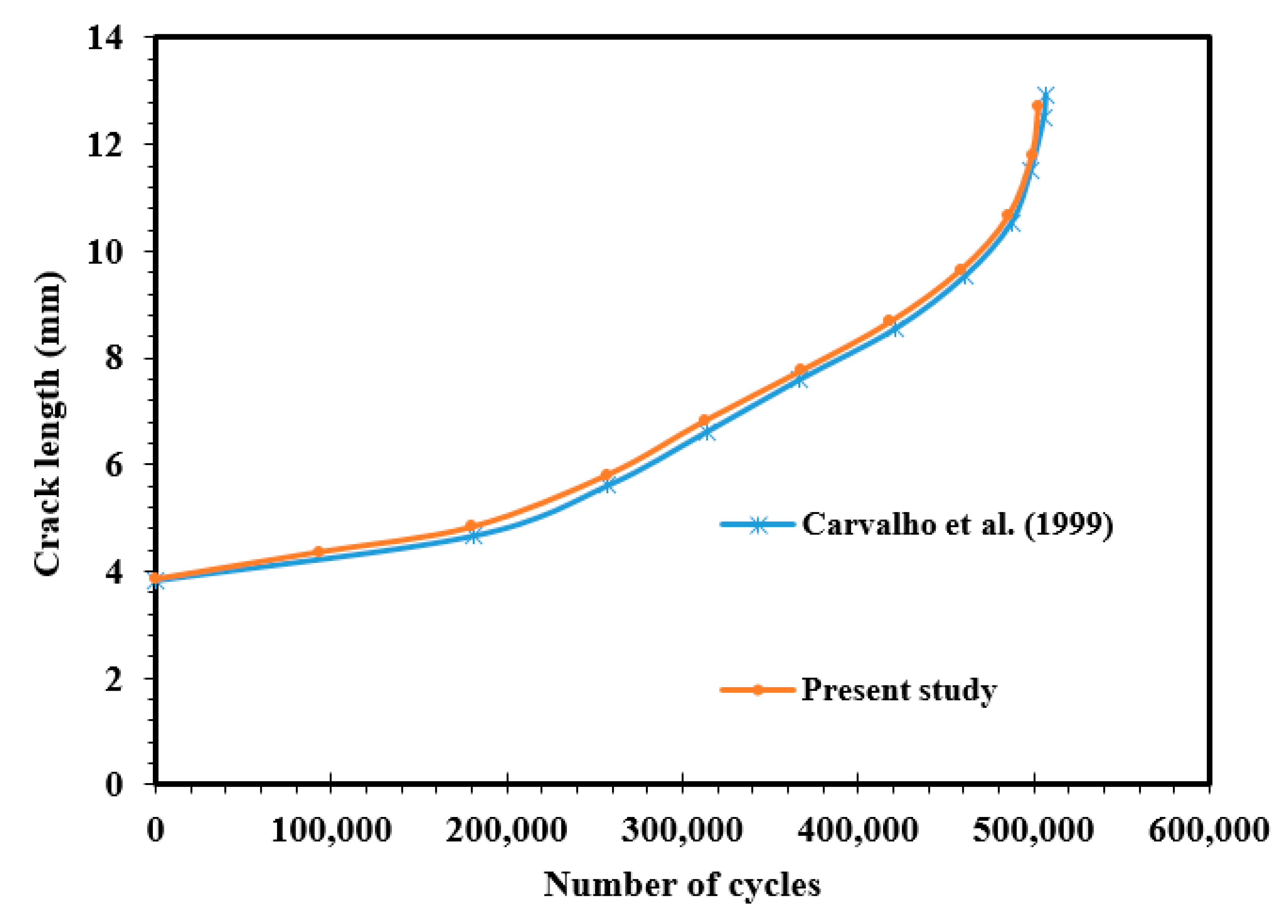
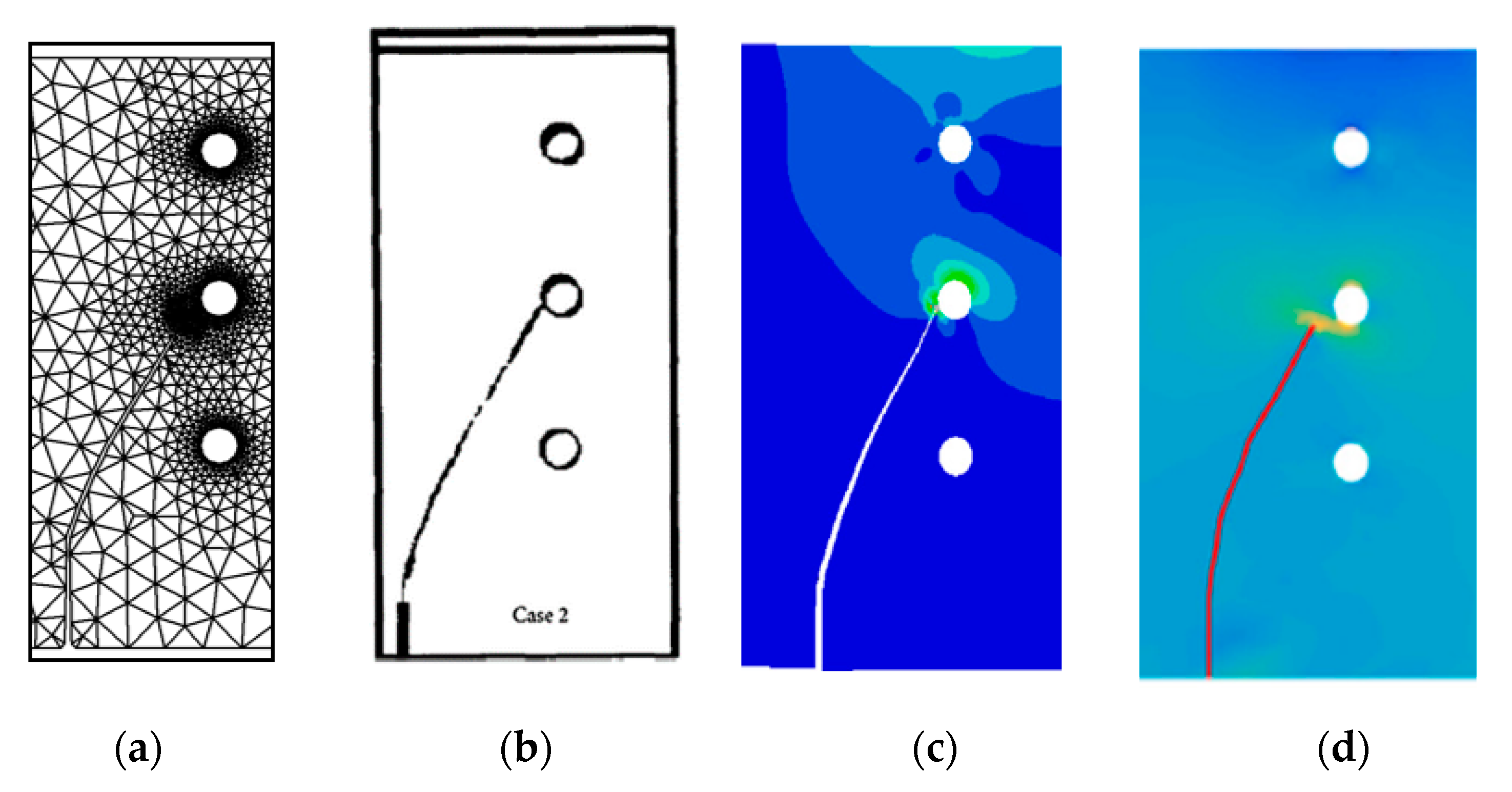
3.2. PMMA Beam Specimen
3.2.1. Case I
3.2.2. Case II
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, A.F. Mechanics and Mechanisms of Fracture: An Introduction; ASM International: Geauga County, OH, USA, 2005. [Google Scholar]
- ANSYS. Academic Research Mechanical, Release 19.2, Help System. In Coupled Field Analysis Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Manual, A.U. Abaqus User Manual; Abacus: Waltham, MA, USA, 2020. [Google Scholar]
- Lebaillif, D.; Recho, N. Brittle and ductile crack propagation using automatic finite element crack box technique. Eng. Fract. Mech. 2007, 74, 1810–1824. [Google Scholar] [CrossRef]
- Duflot, M.; Nguyen-Dang, H. Fatigue crack growth analysis by an enriched meshless method. J. Comput. Appl. Math. 2004, 168, 155–164. [Google Scholar] [CrossRef]
- Yan, X. Automated simulation of fatigue crack propagation for two-dimensional linear elastic fracture mechanics problems by boundary element method. Eng. Fract. Mech. 2007, 74, 2225–2246. [Google Scholar] [CrossRef]
- Zhao, T.; Zhang, J.; Jiang, Y. A study of fatigue crack growth of 7075-T651 aluminum alloy. Int. J. Fatigue 2008, 30, 1169–1180. [Google Scholar] [CrossRef]
- Miranda, A.C.D.O.; Meggiolaro, M.A.; Martha, L.F.; Castro, J. Stress intensity factor predictions: Comparison and round-off error. Comput. Mater. Sci. 2012, 53, 354–358. [Google Scholar] [CrossRef]
- Ingraffea, A.R.; de Borst, R. Computational Fracture mechanics. In Encyclopedia of Computational Mechanics, 2nd ed.; John Wiley & Sons, Ltd.: West Sussex, UK, 2017; pp. 1–26. [Google Scholar]
- Liu, Z.; Wang, X.; Miller, R.E.; Hu, J.; Chen, X. Ductile fracture properties of 16MND5 bainitic forging steel under different in-plane and out-of-plane constraint conditions: Experiments and predictions. Eng. Fract. Mech. 2021, 241, 107359. [Google Scholar] [CrossRef]
- Alshoaibi, A.M. Finite element procedures for the numerical simulation of fatigue crack propagation under mixed mode loading. Struct. Eng. Mech. 2010, 35, 283–299. [Google Scholar] [CrossRef]
- Alshoaibi, A.M. An Adaptive Finite Element Framework for Fatigue Crack Propagation under Constant Amplitude Loading. Int. J. Appl. Sci. Eng. 2015, 13, 261–270. [Google Scholar]
- Alshoaibi, A. Finite element-based model for crack propagation in linear elastic materials. Eng. Solid Mech. 2020, 8, 131–142. [Google Scholar] [CrossRef]
- Alshoaibi, A.M.; Hadi, M.; Ariffin, A. Two-dimensional numerical estimation of stress intensity factors and crack propagation in linear elastic Analysis. J. Struct. Durab. Health Monit. 2007, 3, 15–27. [Google Scholar]
- Fageehi, Y.A.; Alshoaibi, A.M. Nonplanar Crack Growth Simulation of Multiple Cracks Using Finite Element Method. Adv. Mater. Sci. Eng. 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Alshoaibi, A.M.; Ariffin, A. Finite element modeling of fatigue crack propagation using a self adaptive mesh strategy. Int. Rev. Aerosp. Eng. 2015, 8, 209–215. [Google Scholar] [CrossRef]
- Alshoaibi, A.M.; Ariffin, A. Fatigue life and crack path prediction in 2D structural components using an adaptive finite element strategy. Int. J. Mech. Mater. Eng. 2008, 3, 97–104. [Google Scholar]
- Alshoaibi, A.M.; Ariffin, A.K. Finite element simulation of stress intensity factors in elastic-plastic crack growth. J. Zhejiang Univ. Sci. A 2006, 7, 1336–1342. [Google Scholar] [CrossRef]
- Alshoaibi, A.M. A two dimensional Simulation of crack propagation using Adaptive Finite Element Analysis. J. Comput. Appl. Mech. 2018, 49, 335–341. [Google Scholar]
- Alshoaibi, A.M.; Fageehi, Y.A. Fageehi, 2D finite element simulation of mixed mode fatigue crack propagation for CTS specimen. J. Mater. Res. Technol. 2020, 9, 7850–7861. [Google Scholar] [CrossRef]
- Bashiri, A.H.; Alshoaibi, A.M. Adaptive Finite Element Prediction of Fatigue Life and Crack Path in 2D Structural Components. Metals 2020, 10, 1316. [Google Scholar] [CrossRef]
- Barsoum, R.S. Application of quadratic isoparametric finite elements in linear fracture mechanics. Int. J. Fract. 1974, 10, 603–605. [Google Scholar] [CrossRef]
- Henshell, R.D.; Shaw, K.G. Crack tip finite elements are unnecessary. Int. J. Numer. Methods Eng. 1975, 9, 495–507. [Google Scholar] [CrossRef]
- Phongthanapanich, S.; Dechaumphai, P. Adaptive Delaunay triangulation with object-oriented programming for crack propagation analysis. Finite Elements Anal. Des. 2004, 40, 1753–1771. [Google Scholar] [CrossRef]
- Erdogan, F.; Sih, G.C. On the crack extension in plates under plane loading and transverse shear. J. Basic Eng. 1963, 85, 519–525. [Google Scholar] [CrossRef]
- Zienkiewicz, O.; Taylor, R.; Zhu, J. The Finite Element Method: Its Basis and Fundamentals; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Cavendish, J.C. Automatic triangulation of arbitrary planar domains for the finite element method. Int. J. Numer. Methods Eng. 1974, 8, 679–696. [Google Scholar] [CrossRef]
- Andersen, M.R. Fatigue Crack Initiation and Growth in Ship Structures; Department of Naval Architecture and Offshore Engineering, Technical University of Denmark: Lyngby, Denmark, 1998. [Google Scholar]
- Surendran, M.; Bordas, S.; Palani, G.; Bordas, S. Linear smoothed extended finite element method for fatigue crack growth simulations. Eng. Fract. Mech. 2019, 206, 551–564. [Google Scholar] [CrossRef]
- Tu, S.; Cai, R. A coupling of boundary elements and singular integral equation for the solution of the fatigue cracked body. Stress Anal. 1993, 3, 239–247. [Google Scholar]
- Bittencourt, T.; Wawrzynek, P.; Ingraffea, A.; Sousa, J. Quasi-automatic simulation of crack propagation for 2D LEFM problems. Eng. Fract. Mech. 1996, 55, 321–334. [Google Scholar] [CrossRef]
- Ingraffea, A.R.; Grigoriu, M. Probabilistic Fracture Mechanics: A Validation of Predictive Capability; Cornell University Ithaca Ny Depterment of Structural Engineering: Ithaca, NY, USA, 1990. [Google Scholar]
- Huynh, H.D.; Nguyen, M.N.; Cusatis, G.; Tanaka, S.; Bui, T.Q. A polygonal XFEM with new numerical integration for linear elastic fracture mechanics. Eng. Fract. Mech. 2019, 213, 241–263. [Google Scholar] [CrossRef]
- Dirik, H.; Yalçinkaya, T. Crack path and life prediction under mixed mode cyclic variable amplitude loading through XFEM. Int. J. Fatigue 2018, 114, 34–50. [Google Scholar] [CrossRef]
- Ma, W.; Liu, G.; Wang, W. A coupled extended meshfree–Smoothed meshfree method for crack growth simulation. Theor. Appl. Fract. Mech. 2020, 107, 102572. [Google Scholar] [CrossRef]
- Carvalho, C.V.; de Araújo, T.D.P.; Cavalcante, J.B.; Martha, L.F.; Bittencourt, T. Automatic Fatigue Crack Propagation Using a Self-Adaptative Strategy. In Proceedings of the PACAM VI––Sixth Pan-American Congress of Applied Mechanics, Rio de Janeiro, Brazial; 1999. Available online: file:///C:/Users/MDPI/AppData/Local/Temp/Automatic_fatigue_crack_propagation_using_a_self-a.pdf (accessed on 15 October 2020).
- Peng, X.; Kulasegaram, S.; Wu, S.; Bordas, S. An extended finite element method (XFEM) for linear elastic fracture with smooth nodal stress. Comput. Struct. 2017, 179, 48–63. [Google Scholar] [CrossRef]








| Property | Value in Metric Unit |
|---|---|
| Modulus of elasticity, E | 74 GPa |
| Poisson’s ratio, υ | 0.3 |
| Fracture toughness, KIC | |
| Threshold stress intensity factor, Kth | |
| Paris law coefficient, C | 2.087136 × 10−13 |
| Paris law exponent m | 3.32 |
| Specimen | a | b |
|---|---|---|
| Case I | 25.4 | 152.4 |
| Case II | 38.1 | 127 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshoaibi, A.M.; Fageehi, Y.A. Simulation of Quasi-Static Crack Propagation by Adaptive Finite Element Method. Metals 2021, 11, 98. https://doi.org/10.3390/met11010098
Alshoaibi AM, Fageehi YA. Simulation of Quasi-Static Crack Propagation by Adaptive Finite Element Method. Metals. 2021; 11(1):98. https://doi.org/10.3390/met11010098
Chicago/Turabian StyleAlshoaibi, Abdulnaser M., and Yahya Ali Fageehi. 2021. "Simulation of Quasi-Static Crack Propagation by Adaptive Finite Element Method" Metals 11, no. 1: 98. https://doi.org/10.3390/met11010098
APA StyleAlshoaibi, A. M., & Fageehi, Y. A. (2021). Simulation of Quasi-Static Crack Propagation by Adaptive Finite Element Method. Metals, 11(1), 98. https://doi.org/10.3390/met11010098






