On the CFD Modelling of Slamming of the Metal Melt in High-Pressure Die Casting Involving Lost Cores
Abstract
1. Introduction
2. Model Equations and Simulation Methodology
2.1. Model Equations
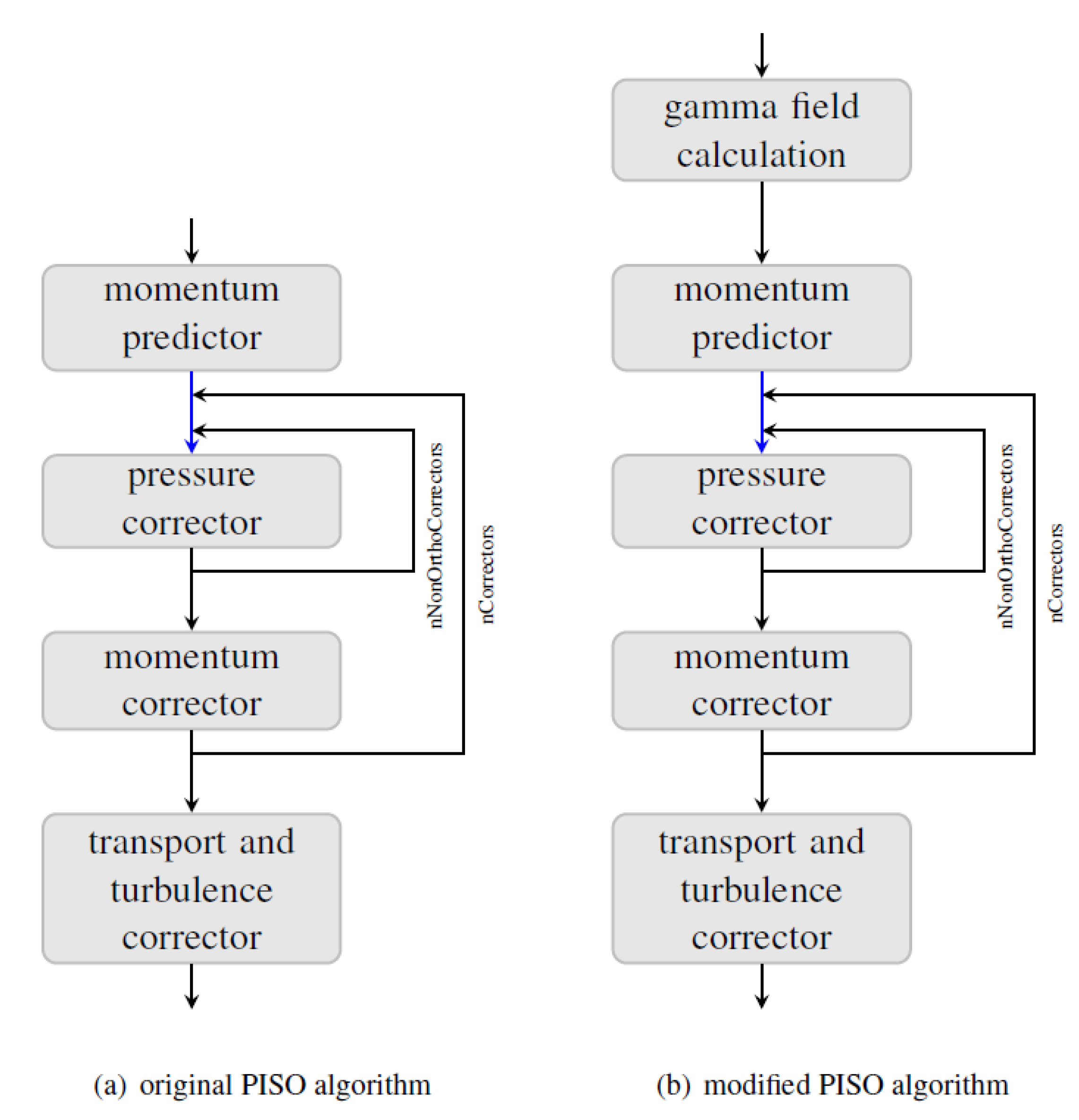
2.2. Simulation Methodology
3. Results and Discussion
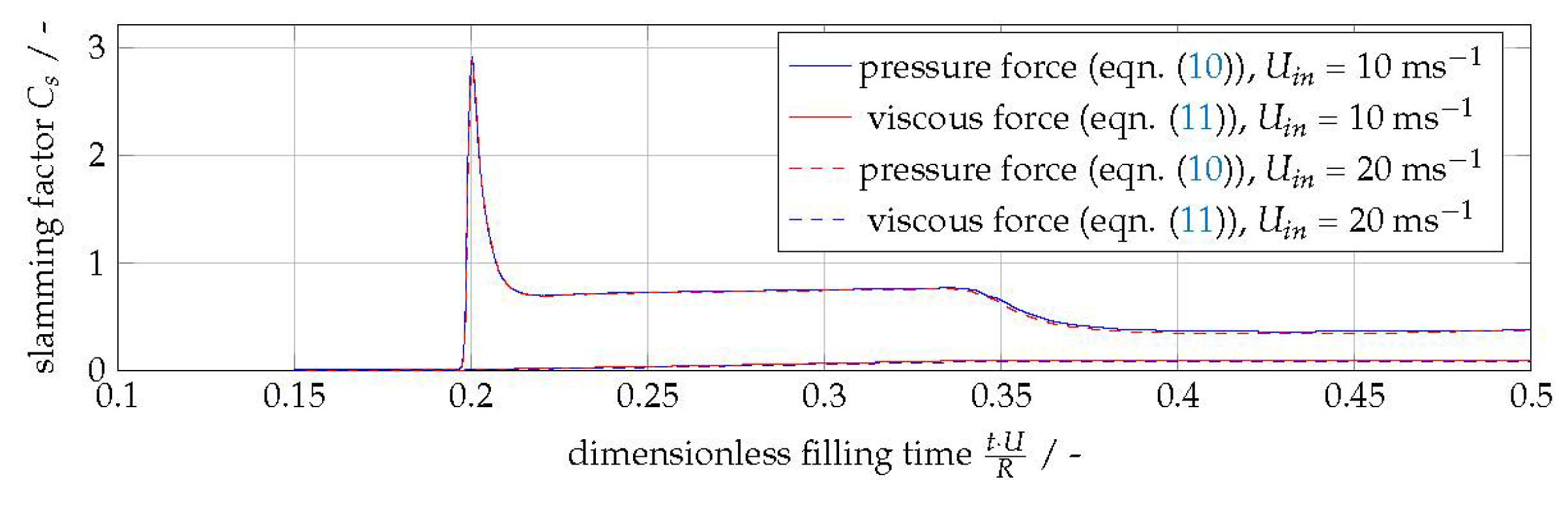
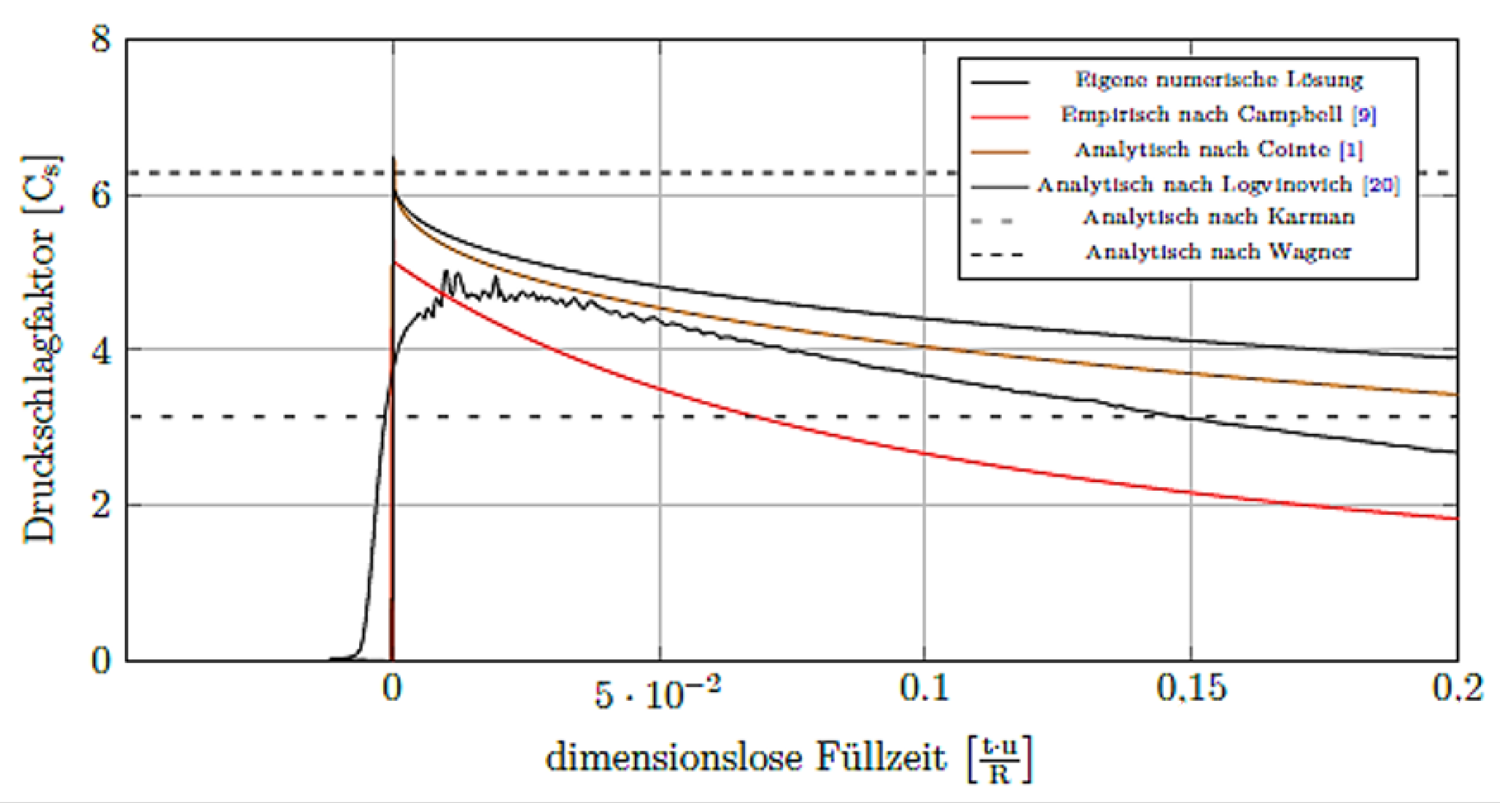
3.1. The Concept of the Dimensionless Slamming Factor
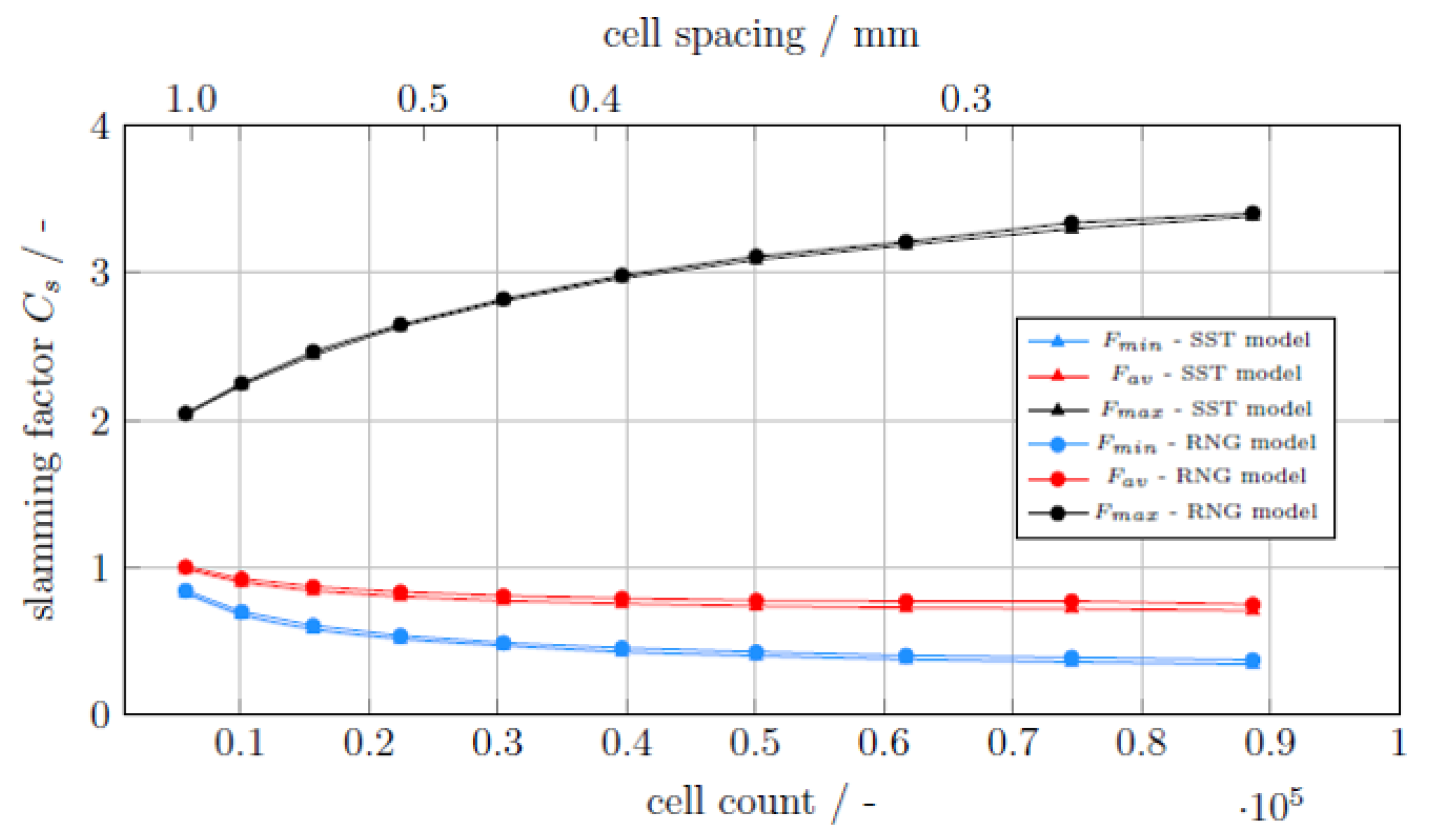
3.2. Determining the Slamming Factor with Respect to Mesh Resolution
3.3. Effect of Turbulence
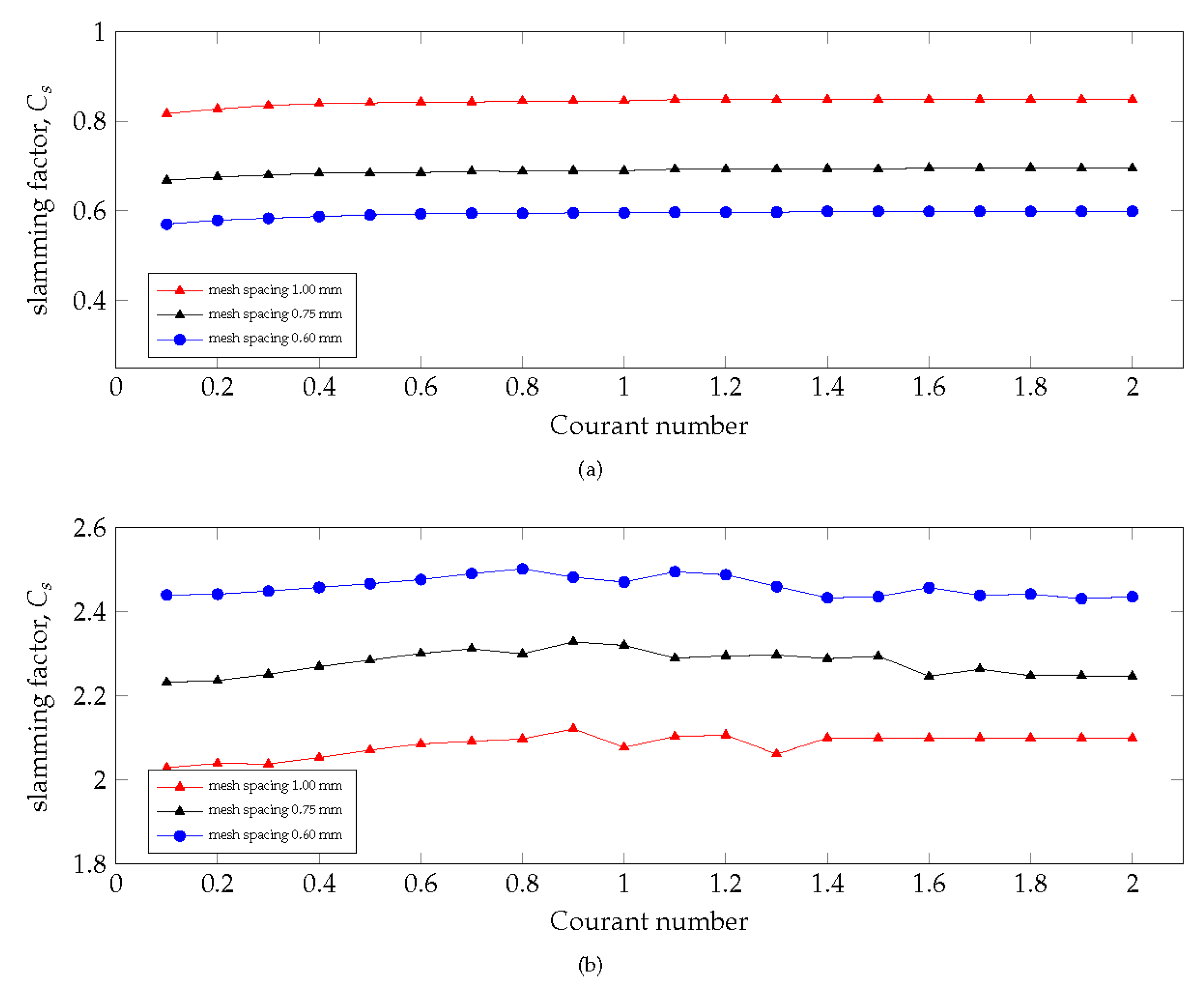
3.4. Effect of Courant Number
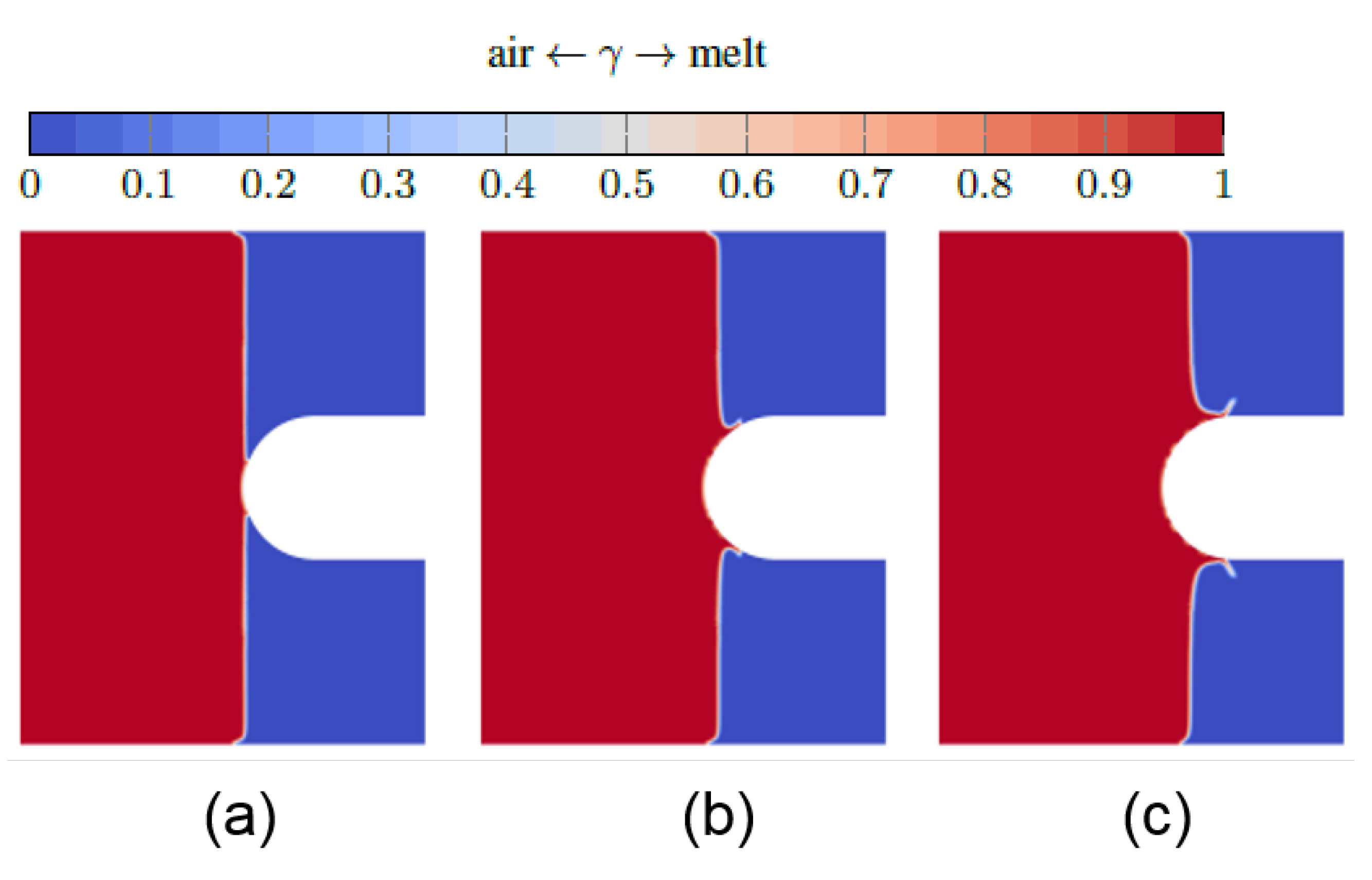
3.5. Response of the Core to the Spike-Like Force Impact
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Menter SST k-ω Model (Menter 1994)
References
- Kaufmann, H.; Uggowitzer, P. Metallurgy and Processing of High-Integrity Light Metal Pressure Castings; Schiele & Schön: Berlin, Germany, 2007. [Google Scholar]
- Nogowizin, B. Theorie und Praxis des Druckgusses, 1st ed.; Schiele & Schoen: Berlin, Germany, 2010. [Google Scholar]
- Brunnhuber, E. Praxis der Druckgussfertigung; Schiele & Schoen: Berlin, Germany, 1991. [Google Scholar]
- Campbell, J. Complete Casting Handbook: Metal Casting Processes, Metallurgy, Techniques and Design; Elsevier Science: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Jelínek, P.; Adámková, E. Lost cores for high-pressure die casting. Arch. Foundry Eng. 2014, 14, 101–104. [Google Scholar] [CrossRef]
- Kohlstädt, S.; Rabus, U.; Goeke, S.; Kuckenburg, S. Verfahren zur Herstellung Eines Metallischen Druckgussbauteils Unter Verwendung Eines Salzkerns Mit Integrierter Stützstruktur und Hiermit Hergestelltes Druckgussbauteil. DE Patent DE10,201,410,221,359A1, 21 April 2016. [Google Scholar]
- Schneider, T.; Kohlstädt, S.; Rabus, U. Gehäuse mit Druckgussbauteil zur Anordnung Eines Elektrischen Fahrmotors in Einem Kraftfahrzeug und Verfahren zur Herstellung eines Druckgussbauteils. DE Patent DE10,201,410,221,358A1, 21 April 2016. [Google Scholar]
- Graf, E.; Soell, G. Vorrichtung zur Herstellung Eines Druckgussbauteils mit Einem Kern und Einem Einlegeteil. DE Patent DE10,145,876A1, 10 April 2003. [Google Scholar]
- Graf, E.; Söll, G. Verfahren zur Herstellung Eines Zylinderkurbelgehäuses. WO Patent WO2,008,138,508A1, 20 November 2008. [Google Scholar]
- Fuchs, B.; Körner, C. Mesh resolution consideration for the viability prediction of lost salt cores in the high pressure die casting process. Prog. Comput. Fluid Dyn. 2014, 14, 24–30. [Google Scholar] [CrossRef]
- Kohlstädt, S.; Vynnycky, M.; Gebauer-Teichmann, A. Experimental and numerical CHT-investigations of cooling structures formed by lost cores in cast housings for optimal heat transfer. Heat Mass Trans. 2018, 54, 3445–3459. [Google Scholar] [CrossRef]
- Kohlstädt, S.; Vynnycky, M.; Neubauer, A.; Gebauer-Teichmann, A. Comparative RANS turbulence modelling of lost salt core viability in high pressure die casting. Prog. Comput. Fluid Dyn. 2019, 19, 316–327. [Google Scholar] [CrossRef]
- Fuchs, B.; Eibisch, H.; Körner, C. Core viability simulation for salt core technology in high-pressure die casting. Int. J. Met. 2013, 7, 39–45. [Google Scholar] [CrossRef]
- Fuchs, V. Numerische Modellierung von Fluid-Struktur-Wechselwirkungen an Wellenbeaufschlagten Strukturen; Kassel University Press GmbH: Kassel, Germany, 2014. [Google Scholar]
- Campbell, T.; Weynberg, P. Measurement of Parameters Affecting Slamming—Final Report; Technical Report, Wolfson Marine Craft Unit Report No. 440; University of Southampton: Southampton, UK, 1980. [Google Scholar]
- Abrate, S. Hull slamming. Appl. Mech. Rev. 2011, 64, 060803. [Google Scholar] [CrossRef]
- Kohlstädt, S.; Vynnycky, M.; Jäckel, J. Towards the modelling of fluid-structure interactive lost core deformation in high-pressure die casting. Appl. Math. Mod. 2020, 20, 319–333. [Google Scholar] [CrossRef]
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Dahle, A.; Arnberg, L. The rheological properties of solidifying aluminum foundry alloys. JOM 1996, 48, 34–37. [Google Scholar] [CrossRef]
- Ferrer, P.; Causon, D.; Qian, L.; Mingham, C.; Ma, Z. A multi-region coupling scheme for compressible and incompressible flow solvers for two-phase flow in a numerical wave tank. Comput. Fluids 2016, 125, 116–129. [Google Scholar] [CrossRef]
- Mayon, R.; Sabeur, Z.; Tan, M.Y.; Djidjeli, K. Free surface flow and wave impact at complex solid structures. In Proceedings of the 12th International Conference on Hydrodynamics, Egmond aan Zee, NL, USA, 18–23 September 2016; 10p. [Google Scholar]
- Brackbill, J.; Kothe, D.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Versteeg, H.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education Limited: London, UK, 2007. [Google Scholar]
- Menter, F. 2-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Koch, M.; Lechner, C.; Reuter, F.; Köhler, K.; Mettin, R.; Lauterborn, W. Numerical modeling of laser generated cavitation bubbles with the finite volume and volume of fluid method, using OpenFOAM. Comput. Fluids 2016, 126, 71–90. [Google Scholar] [CrossRef]
- White, F. Fluid Mechanics, 7th ed.; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Assael, M.; Kakosimos, K.; Banish, R.; Brillo, J.; Egry, I.; Brooks, R.; Quested, P.; Mills, K.; Nagashima, A.; Sato, Y.; et al. Reference data for the density and viscosity of liquid aluminum and liquid iron. J. Phys. Chem. Ref. Data 2006, 35, 285–300. [Google Scholar] [CrossRef]
- Jasak, H.; Jemcov, A.; Tukovic, Z. OpenFOAM: A C++ Library for Complex Physics Simulations. In Proceedings of the International Workshop on Coupled Methods in Numerical Dynamics IUC, Dubrovnik, Croatia, 19–21 September 2007. [Google Scholar]
- Jasak, H. OpenFOAM: Open source CFD in research and industry. Int. J. Naval Archit. Ocean Eng. 2009, 1, 89–94. [Google Scholar]
- Weller, H.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object orientated techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Maric, T.; Höpken, J.; Mooney, K. Openfoam Technology Primer; Stan Mott: Hannover, Germany, 2014. [Google Scholar]
- Chen, G.; Xiong, Q.; Morris, P.; Paterson, E.; Sergeev, A.; Wang, Y. OpenFOAM for computational fluid dynamics. Not. AMS 2014, 61, 354–363. [Google Scholar] [CrossRef]
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. Ph.D. Thesis, Imperial College London (University of London), London, UK, 1996. [Google Scholar]
- Droniou, J. Finite volume schemes for diffusion equations: Introduction to and review of modern methods. Math. Model. Methods Appl. Sci. 2014, 24, 1575–1619. [Google Scholar] [CrossRef]
- Robertson, E.; Choudhury, V.; Bhushan, S.; Walters, D. Validation of OpenFOAM numerical methods and turbulence models for incompressible bluff body flows. Comput. Fluids 2015, 123, 122–145. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.; Losada, I. Simulating coastal engineering processes with OpenFOAM®. Coast. Eng. 2013, 71, 119–134. [Google Scholar] [CrossRef]
- Issa, R. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Patankar, S.; Spalding, D. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Elsevier: Berlin/Heidelberg, Germany, 1983; pp. 54–73. [Google Scholar]
- von Karman, T.H. The Impact on Seaplane Floats during Landing; Technical Report; National Advisory Committee on Aeronautics: Washington, DC, USA, 1929; p. 8. [Google Scholar]
- Wagner, H. Über Stoß- und Gleitvorgänge an der Oberfläche von Flüssigkeiten. Zamm J. Appl. Math. Mech. Angew. Math. Und Mech. 1932, 12, 193–215. [Google Scholar] [CrossRef]
- Wienke, J. Druckschlagbelastung auf schlanke zylindrische Bauwerke durch brechende Wellen: Theoretische und großmaßstäbliche Laboruntersuchungen. Ph.D. Thesis, TU Braunschweig, Braunschweig, Germany, 2001. [Google Scholar]
- Campbell, T.; Weynberg, P. An Investigation into Wave Slamming Loads on Cylinders; Technical Report, Wolfson Marine Craft Unit Report No. 317; University of Southampton: Southampton, UK, 1977. [Google Scholar]
- Bodily, K.; Carlson, S.; Truscott, T. The water entry of slender axisymmetric bodies. Phys. Fluids 2014, 26, 072108. [Google Scholar] [CrossRef]
- Wienke, J.; Sparboom, U.; Oumeraci, H. Breaking wave impact on a slender cylinder. In Coastal Engineering 2000; ASCE: Reston, VA, USA, 2001; pp. 1787–1798. [Google Scholar]
- Ghadimi, P.; Dashtimanesh, A.; Djeddi, S.R. Study of water entry of circular cylinder by using analytical and numerical solutions. J. Braz. Soc. Mech. Sci. Eng. 2012, 34, 225–232. [Google Scholar] [CrossRef][Green Version]
- Cointe, R.; Armand, J.L. Hydrodynamic impact analysis of a cylinder. J. Offshore Mech. Arct. Eng. 1987, 109, 237–243. [Google Scholar] [CrossRef]
- Logvinovich, G. Hydrodynamics of Free-Boundary Flows; Israel Program for Scientific Translation: Jerusalem, Israel, 1972. [Google Scholar]
- Duff, G.; Naylor, D. Differential Equations of Applied Mathematics; Wiley: New York, NY, USA, 1966. [Google Scholar]
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D. Thesis, Imperial College London (University of London), London, UK, 2003. [Google Scholar]
- Bo, W.; Grove, J.W. A volume of fluid method based ghost fluid method for compressible multi-fluid flows. Comput. Fluids 2014, 90, 113–122. [Google Scholar] [CrossRef]
- Fedkiw, R.; Aslam, T.; Merriman, B.; Osher, S. A non-oscillatory Eulerian approach to interfaces in multimaterial flows (the ghost fluid method). J. Comput. Phys. 1999, 152, 457–492. [Google Scholar] [CrossRef]
- Roenby, J.; Bredmose, H.; Jasak, H. A computational method for sharp interface advection. R. Soc. Open Sci. 2016, 3, 160405. [Google Scholar] [CrossRef]
- Vukčević, V. Numerical Modelling of Coupled Potential and Viscous Flow for Marine Applications. Ph.D. Thesis, Fakultet strojarstva i brodogradnje, Sveučilište u Zagrebu, Zagreb, Croatia, 2016. [Google Scholar]
- Menter, F.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Yakhot, V.; Orszag, S.A.; Thangam, S.; Gatski, T.B.; Speziale, C.G. Development of turbulence models for shear flows by a double expansion technique. Phys. Fluids A Fluid Dyn. 1992, 4, 1510–1520. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.; Lewy, H. On the partial difference equations of mathematical physics. IBM J. Res. Dev. 1967, 11(2), 215–234. [Google Scholar] [CrossRef]
- Beitz, W.; Shields, M.; Dubbel, H.; Davies, B.; Küttner, K. DUBBEL—Handbook of Mechanical Engineering; Springer: London, UK, 2013. [Google Scholar]
- Salencon, J.; Lyle, S. Handbook of Continuum Mechanics: General Concepts—Thermoelasticity; Physics and Astronomy Online Library; Springer: Berlin, Germany, 2001. [Google Scholar]
- Groezinger, D. Water-Soluble Salt Cores. U.S. Patent US8,403,028B2, 26 March 2013. [Google Scholar]
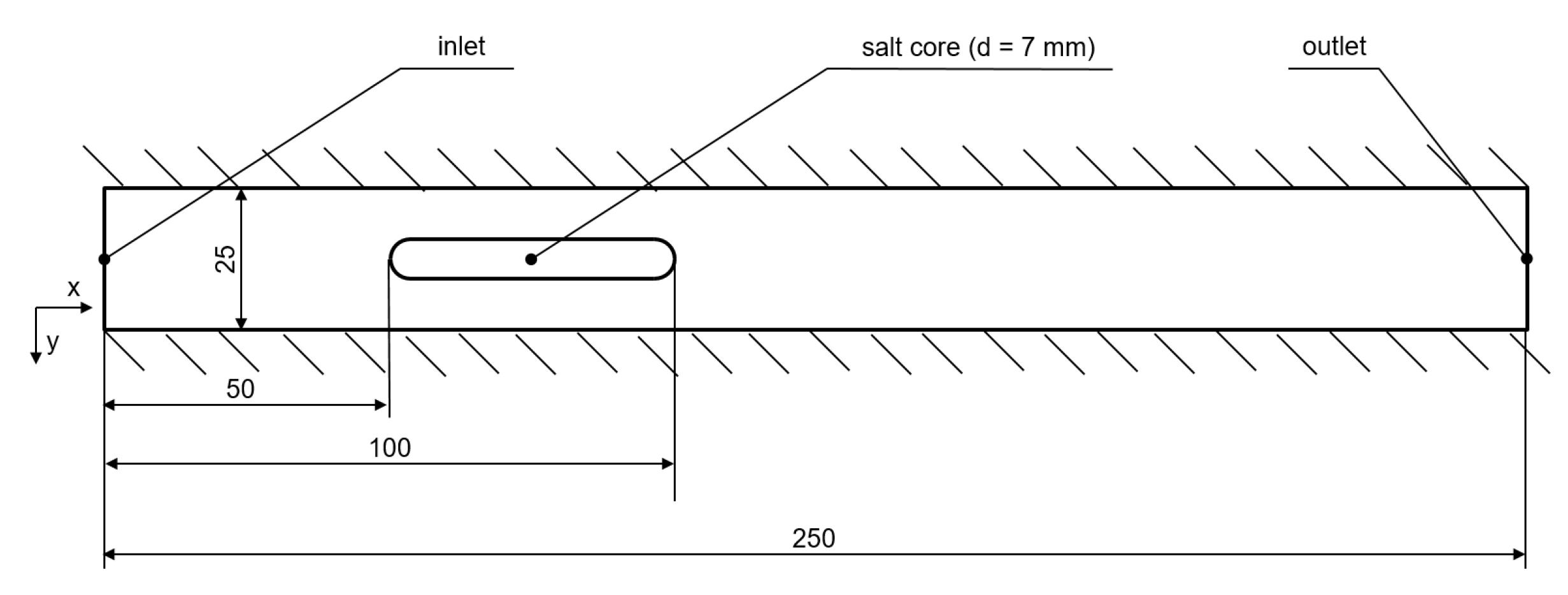


| Boundary | U/ms | p/Pa | T/K | |||||
|---|---|---|---|---|---|---|---|---|
| inlet | = 1 | = | = 0 | T | = | |||
| outlet | = 0 | = 0 | p | = | = 0 | |||
| salt core | = 0 | = 0 | = | = 0 | ||||
| wall | = 0 | = 0 | = | = 0 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kohlstädt, S.; Vynnycky, M.; Goeke, S. On the CFD Modelling of Slamming of the Metal Melt in High-Pressure Die Casting Involving Lost Cores. Metals 2021, 11, 78. https://doi.org/10.3390/met11010078
Kohlstädt S, Vynnycky M, Goeke S. On the CFD Modelling of Slamming of the Metal Melt in High-Pressure Die Casting Involving Lost Cores. Metals. 2021; 11(1):78. https://doi.org/10.3390/met11010078
Chicago/Turabian StyleKohlstädt, Sebastian, Michael Vynnycky, and Stephan Goeke. 2021. "On the CFD Modelling of Slamming of the Metal Melt in High-Pressure Die Casting Involving Lost Cores" Metals 11, no. 1: 78. https://doi.org/10.3390/met11010078
APA StyleKohlstädt, S., Vynnycky, M., & Goeke, S. (2021). On the CFD Modelling of Slamming of the Metal Melt in High-Pressure Die Casting Involving Lost Cores. Metals, 11(1), 78. https://doi.org/10.3390/met11010078





