Charge Plan Model for Steelmaking-Continuous Casting Section

Abstract

Pursuing the intellectualization of a steelmaking plant and developing a charge plan of the steelmaking-continuous casting section are critical in metallurgy engineering. Herein, we aim to develop a charge plan model based on the operation of the steelmaking-continuous casting section to minimize the penalty values of residual materials; of a contract not selected and the penalty values that is caused by the difference in steel grades, the width and the delivery time between slabs in the same charge. We introduce an improved elitist genetic algorithm (IEGA), define the matching chromosome coding and decoding strategies, and suggest improving the selection, crossover, and mutation operators. Finally, we verify the proposed model and algorithm on the production data of a real enterprise. We clarify the applicability of developing a charge plan based on model analysis and demonstrate the effectiveness of the IEGA through algorithm analysis.

1. Introduction

A batch plan for a steelmaking-continuous casting section (SM-CC) primarily comprises of a charge plan and a cast plan and is located in a transition layer between a contract plan and an operation plan. It should not only rely on a production contract pool after preparing the contract plan but also consider the slab width, production process, delivery time, and other constraints to realize continuous production at a steel plant. In SM-CC, the steelmaking procedure is the starting point of the overall production wherein a charge is considered as the minimum unit of production. Therefore, defining a relevant and accurate charge plan is necessary. A charge plan for SM-CC implies combining and optimizing slabs of different steel grades and specifications to obtain different charges according to the constraints of steelmaking production and to prepare the background for a subsequent cast plan.

Scholars worldwide have conducted extensive research on the development of a charge plan for SM-CC. Quelhadj et al. [1] first hypothesized that the SM-CC production process could serve as an important link in steel production and that the optimization of a steelmaking charge plan could save costs and increase the benefits in steel enterprises. In addition, the charge plan optimization problem of a steelmaking process was formulated as an integer programming model and solved using the Tabu search algorithm. Yan [2] proposed a flexible charge plan. Although the number of unselected slabs was reduced therein, the difficulty of solving the model simultaneously increased, and the final results were listed carelessly. Tang et al. [3,4] established a charge plan model with a known number of the charge and incomplete contract arrangements considering the preselection of a contract pool and then applied a genetic algorithm to solve it. Huang et al. [5] formulated a mathematical model to minimize residual materials and the steel-grade replacement costs. In addition, they identified the weight factors of different optimization objectives to promote on-site decision-making and solved the problem using a dynamic programming algorithm. Considering two flows of continuous machine casting and assuming the possibility of producing slabs with different widths, Cheng et al. [6] developed a charge plan model to minimize the number of casts and the difference in adjacent slab widths of charges. Then, they solved this model using the variable neighborhood search combined with a simulated annealing algorithm.

In existing studies focused on the development of a charge plan, researchers mainly considered two approaches: one corresponded to an establishment method of a model and the other one corresponded to a solution method of a model. Concerning the former, several research works could be mentioned as examples. Ma et al. [7] compared the task of charge plan formulation with the one-dimensional packing problem. This analogy method allowed fitting a conventional problem with a practical one and the degree of fit between these two problems directly influenced the results of modeling and solving. Ouelhadj et al. [8] adopted a multi-agent system, and Wang et al. [9] utilized Petri nets and other intelligent modeling methods. The use of such methods provides certain advantages. It allows the overcoming of the fixed rationale of conventional modeling methods and understanding the essence of a problem. However, in the current related research, certain limitations still exist. The complexity of SM-CC production planning is a limitation associated with a modeling method. In steel mills, the actual information is constantly updated, and various scenarios may occur. Therefore, researchers seek to identify the most effective approaches to address such a complex situation and model a real situation with high accuracy. A similar purpose is pursued in the present study.

Concerning the solving methods of a model, early studies introduced methods such as heuristic methods [10] and operations research methods [11]. However, with the development of computer intelligence techniques, researchers have begun utilizing more intelligent algorithms. For example, Lu et al. [12] and Tang et al. [13] applied the Tabu search algorithm to solve an optimization problem corresponding to a steelmaking process. Yuan et al. [14] and Gong [15] employed a genetic search algorithm to solve a multi-objective production optimization problem in SM-CC under different constraints. Chen [16] proposed a method combining the immune and genetic algorithms that effectively prevented premature convergence of the genetic algorithm. Liu et al. [17] summarized numerous research methods that were mainly divided into static and dynamic scheduling; however, they could not be separated from the improvement of solving algorithm. Evidently, intelligent algorithms are deemed more convenient than conventional solution methods as they improve the calculation speed and save manpower as well as material resources. However, defining an appropriate intelligent algorithm is necessary to apply specific changes to adapt a specific model and to address the premature or local optimum problem of an algorithm itself.

Existing research on a charge plan in SM-CC is too extensive to consider in its entirety. However, the global metallurgical industry field determines the status of relatively few foreign researchers. Existing research mainly suggests applying the simulation method to actual steel mills, i.e., they promote the development of intelligent approaches for investigating heavy industry. Based on the aforementioned observations, herein, we first clarify the specific problem of charge plan definition, and subsequently develop a concrete charge plan model and solve it using a proposed improved elitist genetic algorithm (IEGA).

2. Development of a Charge Plan Model for SM-CC

2.1. Problem Description

To facilitate the mathematical formulation of a charge plan problem, explaining its goal and constraints is necessary. Concerning SM-CC, the input condition for a charge plan needs to be identified based on a provided contract pool. The main constraint condition corresponds to the steelmaking process constraint. The purpose of this constraint is to optimize and combine the preselected contract pool according to a certain number of charges. The requirements corresponding to different contracts are not specifically consistent. There may be differences in the steel grade, specification, physical characteristics, delivery time, and other factors. Therefore, to ensure the minimum smelting furnace capacity is attained, the development of a charge plan aims to attain the minimum delivery time difference, the maximum finished material rate, the lowest production cost, and the minimum used residual material.

2.2. Charge Plan Model

(1)

Application conditions

(1) Contracts may not be arranged in real production. However, to avoid the presence of abnormal contracts, the following conditions can be checked: lack of product data, forcibly arranging the slab width, and the delivery time or product steel grade in those contracts that do not match with the other contracts. However, based on the actual situation, the model can reasonably arrange the contracts that need to be maintained. The actual situation in the steel production is rather complicated and can change rapidly. It is neither practical nor meaningful to have numerous production contracts fully arranged.

(2) The number of charges is known. This is the premise condition that is required to arrange a charge plan.

(3) A single contract requirement is smaller than the furnace capacity and is not decomposable due to the furnace capacity limitation. However, if the demand for a single contract is greater than the furnace capacity, the model will decompose this contract. This part corresponds to the definition of a contract plan that is considered as a default step in the present study and is not included in the research scope.

(4) The furnace capacity is constant. This describes the actual requirements, meaning that the furnace capacity needs to be fixed.

(2)

Symbol definition

Table 1 provides all symbol definitions used to define the proposed model.

Table 1. Symbol definition table.

Symbol	Definition
Xik/Xjk	=1. Charge k includes contract i/j.
	=0. Charge k does not include contract i/j.
Yk	Residual material quantity of charge k.
L	Total number of charges to be planned.
N	Total number of contracts.
W	Furnace capacity.
gi	Weight of contract i.
PR	Penalty cost of residual material.
PiU	Penalty cost of the contract i not selected.
Pijc/Pijw/Pijd	When contracts i and j form a charge, the penalty cost caused by the difference in steel grade, width, and delivery time.
Pc/Pw/Pd	Penalty cost coefficient caused by the difference in steel grade, width, and delivery time when contracts i and j form a charge.
ci/wi/di	Steel grade, width, and delivery time of contract i.
Rc	Maximum difference in steel grade in the same charge.
Rw	Maximum width adjustment range of the contract in the same charge.
Rd	Maximum delivery time interval between contracts in the same charge.
α1/α2/α3	Weight coefficients of the three objective functions whose sum is 1, which are equal to 1/3 in this article.

(3)

Mathematical model

(1) The objective function can be defined as follows.

$$minZ={\alpha }_1{Z}_1+{\alpha }_2{Z}_2+{\alpha }_3{Z}_3$$

(1)

$$Z_1={\displaystyle \sum }_{k=1}^L{\displaystyle \sum }_{i=1}^N{\displaystyle \sum }_{j=1}^N\left\{P_{ij}^c+P_{ij}^w+P_{ij}^d\right\}\cdot X_{ik}\cdot X_{jk}$$

(2)

$$Z_2={\displaystyle \sum }_{k=1}^L(P^R\cdot Y_k)$$

(3)

$$Z_3={\displaystyle \sum }_{k=1}^L\left(1-X_{ik}\right)P_i{}^U$$

(4)

here, $Z_1$ is the penalty value caused by the difference in the steel grade, width, and delivery time between the contracts in the same charge; $Z_2$ is the penalty value of a residual material; and $Z_3$ is the penalty value of the contract not selected. The objective function is to minimize the sum of the weights of $Z_1$, $Z_2$, and $Z_3$.

(2) Constraints can be defined as follows:

$${\displaystyle \sum }_{k=1}^L{X}_{ik}\le 1\left(i=1,2,\cdots ,N\right)$$

(5)

The implication is that each contract can only be arranged into a maximum of one charge as follows:

$${\displaystyle \sum }_{i=1}^N(g_i\cdot X_{ik})+Y_k=W\left(k=1,2,\cdots ,L\right)$$

(6)

$$Y_k\ge 0\left(k=1,2,\cdots ,L\right)$$

(7)

Thus, the sum of the contract weight within charge k shall not exceed the furnace capacity, and the difference between these two is defined as the residual material quantity $Y_k$ in charge k:

$$X_{ik}\in \left\{0,1\right\}\left(i=1,2,\cdots ,N;k=1,2,\cdots ,L\right)$$

(8)

here, $X_{ik}$ is a discrete variable that can adopt the values 0 or 1 such that contract i exists in charge k when $X_{ik}$ is 1 and it does not exist when $X_{ik}$ is 0.

$$P_{ij}^c=\{\begin{array}{cc}{P}^c|c_i-c_j|,& \mathrm{if}0\le |c_i-c_j|<R_c\\ +\infty & \mathrm{otherwise}\end{array}$$

(9)

$$P_{ij}^w=\{\begin{array}{cc}{P}^w|w_i-w_j|,& \mathrm{if}0\le f{w}_i-w_j|<R_w\\ +\infty & \mathrm{otherwise}\end{array}$$

(10)

$$P_{ij}^d=\{\begin{array}{cc}{P}^d|d_i-d_j|,\hfill & \mathrm{if}0\le f{d}_i-d_j|<R_d\\ +\infty & \mathrm{otherwise}\end{array}$$

(11)

This equation defines the penalty value of contracts i and j due to differences in the steel grade, width, and delivery time within the same charge.

3. Process of Solving the Charge Plan Model for SM-CC

A charge plan is typically solved in the form of a large-scale combinatorial optimization problem. The complexity of the problem is often related to the number of contracts and charges. In the production process at steel mills, the number of contracts and charges are large. Accordingly, the general search method is difficult to apply. Therefore, herein, we propose an improved elitist genetic algorithm (IEGA) to solve the charge plan model. The algorithm flow can be described as follows.

(1)

Read the basic data of the preselected contract pool, including the contract number, weight, steel grade, and delivery time.

(2)

Initialize algorithm parameters, including the iteration time, population size, crossover probability, and conventional mutation probability.

(3)

Initialize the population of N individuals according to the permutation coding rule.

(4)

Decode the chromosomes of the population.

(5)

Calculate the objective function values of the current populations and record the optimal individuals and their chromosomes.

(6)

Calculate the fitness values of the current populations and record the maximum fitness, average fitness, etc.

(7)

Determine whether the maximum number of iterations has been attained. If yes, end the iteration and output the result. If not, proceed to the next step.

(8)

According to the introduced improvement in the algorithm, judge whether the operation on a large variation probability is required and output the matching variation probability.

(9)

During the first selection operation, independently select N parent chromosomes from the current population.

(10)

Independently perform partial matching and crossover operations on the selected N parent chromosomes.

(11)

Independently perform chromosome fragment reversal mutation operations on the N individuals after crossover.

(12)

Obtain a population of size 2N by merging the parent population with the offspring population. Perform the second selection operation, choosing N individuals from 2N individuals to obtain a new generation of the population.

(13)

Go back to step 5, continue the iteration process until the iteration is complete.

3.1. Chromosome Encoding

The final solution of a charge plan model is expected to have such a characteristic that all contract numbers should differ from each other. Therefore, we implement the encoding method of permutation coding to construct chromosomes. The charge plan uses the contract number to represent the gene value in a chromosome coding string. Chromosome coding can be expressed as $\left\{a_1,\dots ,a_i,\dots ,a_N\right\}$. The chromosome length is the total number of precompiled contracts N, and a_i represents the contract number, $a_i\in \left\{1,2,\dots ,N\right\}$. In the encoding scheme, gene positions $a_i$ in the same chromosome are natural numbers without repetition.

3.2. Chromosome Decoding

The example provided in Figure 1 represents the chromosome coding of the charge plan, illustrating its feasible solution. The numbers 1–10 denote the contract numbers and the total number 10 corresponds to the total number of preselected contracts. The steps of chromosome decoding in the charge plan are as follows:

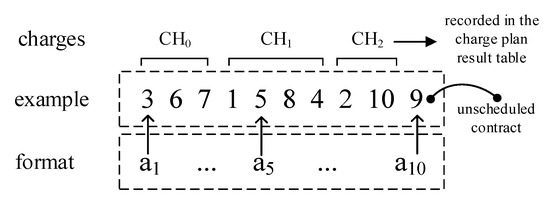
Figure 1. Schematic of chromosome encoding and decoding in a charge plan.

Step (1)

Start a cycle according to chromosome length N.

Step (2)

In each cycle, accumulate weight g_i of contract a_i corresponding to gene position i of the current chromosome.

Step (3)

Determine whether the accumulated weight exceeds the furnace capacity. If not, record the contract a_i.

Step (4)

If yes, subtract weight g_i from the accumulated weight and record the accumulated contract as the number of charges in the charge plan result table.

Step (5)

Run the next cycle until the algorithm iterates N times.

3.3. Calculation of the Fitness Function

In the proposed model, the fitness function adopts the fitness distribution method based on the linear ordering of the objective function value [18] and can be written as follows:

$$\mathrm{Fit}\left(Pos\right)=2-SP+2\times \left(SP-1\right)\times \left(Pos-1\right)/\left(Nind-1\right)$$

(12)

here, Nind represents the number of individuals in the population; Pos represents the ranking position of individuals in the population; SP denotes the selection pressure that is generally taken as [1.0, 2.0]. When using the fitness distribution function, an objective function value of each individual in the population must be calculated in advance and these values must be arranged in descending order to obtain a ranking position of the corresponding individual. Then, according to Equation (12), the algorithm can derive the fitness of each individual by following the convention that the higher the value of the objective function, the smaller the fitness. Accordingly, in the iterative process, the algorithm can select better individuals from the population.

3.4. Genetic Operators

Generally, genetic operators include selection operators, crossover operators, and mutation operators. The selection of an operator considerably influences the convergence of an algorithm.

(1)

Selection operators

Herein, we consider two types of selection operators that first calculate the fitness value of each chromosome according to Equation (12) and then make the selection.

After performing statistical analysis on the current population, the algorithm makes the first selection to choose independently N parent chromosomes from the current population. To this end, the algorithm adopts the elitism and tournament selection method [19], based on the conventional tournament selection method to select a certain number of individuals from the population; however, the method of improving elite individuals must be selected.

After executing the crossover and mutation operations, the algorithm completes the second selection and merges the parent and offspring populations. The purpose here is to select N chromosomes from the combined 2N chromosomes as the new generation population. To realize this, the algorithm adopts the direct copy selection method based on fitness ordering. After calculating the fitness value of 2N chromosomes, the algorithm sorts them in descending order according to fitness and then directly copies N chromosomes corresponding to the highest fitness value as a new generation population.

(2)

Crossover operators

In this study, the proposed algorithm is based on a partial matching crossover operator [20]. Figure 2 illustrates the crossover process, which includes four steps.

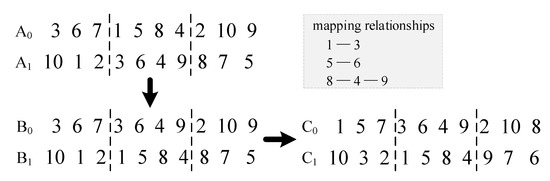
Figure 2. Schematic of the crossover operator.

Step (1)

All chromosomes are paired in the order in which they exist in the population. If the number of chromosomes is odd, the last chromosome is copied directly and does not participate in the crossover operation.

Step (2)

The starting and ending positions of the genes to be swapped in a pair of parental chromosomes (A₀\A₁) are generated randomly.

Step (3)

Intermediate chromosomes (B₀\B₁) are obtained by swapping the genes of two chromosomes and scrambling the sequences, respectively.

Step (4)

Conflict detection. The algorithm establishes the mapping relationships between two groups of genes that need to be exchanged in A₀\A₁. Then, it replaces a conflicting gene in B₀\B₁ according to the mapping relationship. Finally, a new pair of progeny chromosomes (C₀\C₁) is formed.

(3)

Mutation operators

As shown in Figure 3, the proposed algorithm utilizes a chromosome fragment reversal operator [21] to randomly select two reversal points on individual chromosome A₀. Then, a sequence of genes between two points is reversed to obtain new progeny chromosome C₀.

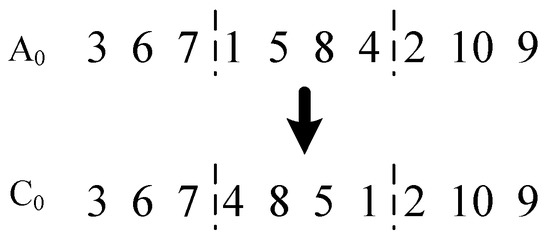
Figure 3. Schematic of the mutation operator.

During the present study, we found that in the late iteration period, the population lacked the diversity of chromosomes and in particular cases, fell into the local optimal solution. Therefore, we incorporated the method of large mutation probability while using the reversal operator. The idea of the large mutation probability operation [22,23] is that when all individuals in a generation are relatively concentrated, the algorithm performs a mutation operation with a probability much larger than the usual mutation probability. The mutation operation with a large mutation probability can randomly and independently produce new individuals, thereby diversifying the population. However, this large variation probability operation can be applied only to a charge plan model involving a large amount of data.

When maximum fitness Fit_max and average fitness Fit_ave of a certain generation of a population satisfy the following formula, the algorithm performs a mutation operation with a large mutation probability as follows:

$$\mathsf{\alpha }Fi{t}_{max}<Fi{t}_{ave}$$

(13)

here, $\mathsf{\alpha }\in \left(0.5,1\right)$ is the density factor that represents the concentration degree of an individual. In addition, we require the model to maintain the optimal objective function value at least ten times continuously during iteration, and therefore, the algorithm must adopt a great variation operation.

4. Application Case and Analysis

4.1. Application Case

To verify the developed charge plan model and the proposed algorithm for SM-CC, we utilized the production data of a real iron and steel enterprise as an example to conduct experimental verification. To this end, among the data corresponding to 300 contracts planned to be input for production on a certain day, the model randomly chose 40 preselected contract data points as the input set of the charge plan model and arranged ten charges.

As shown in Table 2, the last row corresponds to the penalty coefficient and other parameters involved in the model. We defined the experimental parameters as follows: the population number popsize = 500; the number of iterations maxgen = 1000; the crossover probability Pc = 0.95; and the mutation probability Pm = 0.10/0.50. The experimental environment was implemented using Python3.7, and the computing platform was PyCharm (Version 2019.2.1, JetBrains, Prague, Czech Republic).

Table 2. Basic parameters of the charge plan model.

Contract No.	Official Number	Steel Grade Code	Steel Grade	Width/mm	Delivery Time/d	Weight/t	Cancellation Penalty
1	6179921	BQ37701F	24	1495	30	70	10
2	6179928	BQ69200F	24	1533	30	63	10
3	6172135	BN37704F	21	1525	30	75	10
4	6172233	CG61100F	23	1505	30	75	10
5	6156607	CB61200F	24	1474	30	72	10
6	6172129	BQ37704F	24	1474	30	65	10
7	6172242	BN47701F	22	1474	30	75	10
8	6180591	BQ38701F	23	1472	30	91	10
9	6172242	CB61200F	22	1472	30	75	10
10	6180591	AC06300R	11	1494	30	91	10
11	6180572	AC06300R	12	1488	30	81	10
12	6180570	AC06300F	11	1476	30	73	10
13	6180352	AC06300R	11	1474	30	91	10
14	6179558	AC06300R	12	1476	30	74	10
15	6180330	AC06300R	11	1472	30	61	10
16	6180615	AC06300R	11	1472	30	61	10
17	6180619	AC06300F	12	1472	30	61	10
18	6180009	AC06300R	11	1471	30	74	10
19	6180193	AC06300R	11	1471	30	72	10
20	6176823	AC06300R	12	1470	30	74	10
21	6177181	AC06300R	12	1470	30	72	10
22	6177184	AC06300F	10	1464	30	76	10
23	6180189	AC13500R	11	1464	30	62	10
24	6176670	AC13500R	10	1258	15	74	10
25	6178762	AC13500R	10	1255	15	64	10
26	6180571	AC06900F	10	1243	30	81	10
27	6180578	AC10400F	10	1243	30	61	10
28	6179559	BC06800F	12	1241	15	85	10
29	6179987	BC06800F	11	1241	15	65	10
30	6180618	AC05400F	11	1241	30	81	10
31	6122828	AK43701F	23	1569	30	66	10
32	6180060	BQ37704F	24	1525	30	73	10
33	6179923	BQ69200F	24	1524	30	65	10
34	6169455	BH02900F	15	1471	20	74	10
35	6174345	BC06900F	12	1270	15	87	100
36	6154910	AC06300R	12	1270	15	93	100
37	6179629	AC06300R	12	1269	15	93	100
38	6179877	AC06300F	12	1269	15	93	100
39	6178809	AC06300F	12	1268	15	87	100
40	6178952	AC06300R	10	1268	15	77	100

W = 300, P^c = 1.0, P^w = 0.02, P^d = 1.0, P^R = 0.2, R_c = 2, R_w = 100, R_d = 5.

4.2. Discussion and Analysis of Results

Table 3 presents the results obtained after ten cycles of the case described above. The optimal solution was obtained at the second iteration; the optimal objective function value (OOFV) reached 123.10; the total amount of residual materials was 294 t, and the solving time was 587.10 s. Herein, we discuss and analyze the experimental results from two aspects: proposed model and proposed algorithm.

Table 3. Results of the charge plan model development.

Times	Residual Materials	OOFV of the Charge Plan	Solving Time/s
1	294	123.18	635.68
2	294	123.10	587.10
3	362	144.98	637.23
4	313	128.62	559.05
5	360	146.64	610.30
6	294	123.10	649.24
7	572	306.28	552.84
8	445	171.46	571.05
9	369	148.44	660.87
10	275	125.76	663.73
mean	357.8	154.16	612.71

(1)

Proposed model

Table 4 provides the specific results of the second optimal solution presented in Table 3. There were 40 contracts in the preselected contract pool, but only 36 of them were arranged in the charge plan, and contracts 3, 21, 22, and 34 were not included. In addition, the limit of the number of charges had to be defined. This is because when these and other contracts were combined into one charge, their steel grade, slab width, or delivery time could be rather different from the parameters of the other contracts. For example, when contracts 3 and 34 were combined with any other contracts into one charge, a large penalty was imposed on the steel grade difference. In addition, due to the early delivery time of contracts 35–40 and the penalty of contract cancellation being relatively large, the result arranged these six contracts into one plan. These observations indicate that the penalty coefficient setting in the charge plan model developed herein is reasonable, and the algorithm improvement is relevant. Moreover, the observed calculation efficiency and degree of automation were high.

Table 4. Optimal solution result of the charge plan model.

Charge No.	Contract No.	Official Number	Steel Grade Code	Steel Grade	Width/mm	Delivery Time/d	Weight/t	Residual Material/t
1	4	6172233	CG61100F	23	1505	30	75	18
	1	6179921	BQ37701F	24	1495	30	70
	6	6172129	BQ37704F	24	1474	30	65
	5	6156607	CB61200F	24	1474	30	72
2	28	6179559	BC06800F	12	1241	15	85	35
	39	6178809	AC06300F	12	1268	15	87
	37	6179629	AC06300R	12	1269	15	93
3	26	6180571	AC06900F	10	1243	30	81	77
	27	6180578	AC10400F	10	1243	30	61
	30	6180618	AC05400F	11	1241	30	81
4	8	6180591	BQ38701F	23	1472	30	91	59
	9	6172242	CB61200F	22	1472	30	75
	7	6172242	BN47701F	22	1474	30	75
5	29	6179987	BC06800F	11	1241	15	65	20
	25	6178762	AC13500R	10	1255	15	64
	24	6176670	AC13500R	10	1258	15	74
	40	6178952	AC06300R	10	1268	15	77
6	2	6179928	BQ69200F	24	1533	30	63	33
	32	6180060	BQ37704F	24	1525	30	73
	33	6179923	BQ69200F	24	1524	30	65
	31	6122828	AK43701F	23	1569	30	66
7	38	6179877	AC06300F	12	1269	15	93	27
	35	6174345	BC06900F	12	1270	15	87
	36	6154910	AC06300R	12	1270	15	93
8	11	6180572	AC06300R	12	1488	30	81	10
	14	6179558	AC06300R	12	1476	30	74
	20	6176823	AC06300R	12	1470	30	74
	17	6180619	AC06300F	12	1472	30	61
9	13	6180352	AC06300R	11	1474	30	91	1
	23	6180189	AC13500R	11	1464	30	62
	19	6180193	AC06300R	11	1471	30	72
	18	6180009	AC06300R	11	1471	30	74
10	12	6180570	AC06300F	11	1476	30	73	14
	15	6180330	AC06300R	11	1472	30	61
	16	6180615	AC06300R	11	1472	30	61
	10	6180591	AC06300R	11	1494	30	91

Optimal objective function value (OOFV) of the charge plan = 123.10.

(2)

Proposed algorithm

Figure 4 presents the iteration curve of the proposed charge plan (the iteration curve of the second result) solved using IEGA. The vertical axis represents the model objective function value, and the horizontal axis denotes iteration times. In Figure 4, after 500 iterations of solving the charge plan model, the optimization result was 123.10. During each iteration of IEGA, the value of the objective function gradually converged to a smaller direction, indicating the high efficiency of the proposed algorithm.

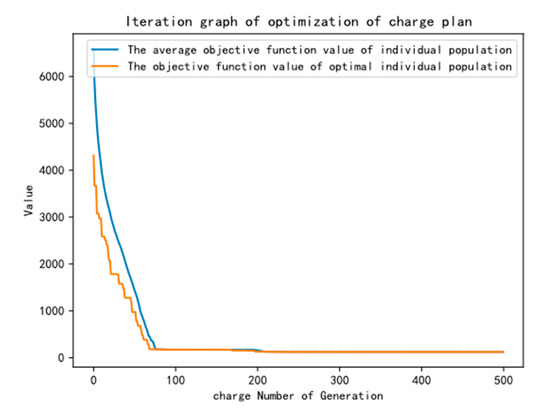
Figure 4. Iteration curve of the charge plan model solved using improved elitist genetic algorithm (IEGA).

In addition, to demonstrate the validity of the proposed algorithm against alternative approaches, we applied the elitist genetic algorithm (EGA) [24] and the simple genetic algorithm (SGA) [25] to solve the considered problem and compared the corresponding results as follows (Table 5).

Table 5. Comparison of the solution results obtained using alternative methods.

Methods	Population Size	Iterations	Vo1	To2	Mo3	Vc4	Tc5	Mc6
IEGA	1000	500	123.10	587.10	294	138.03	615.06	336.8
EGA	1000	1000	123.10	754.84	294	162.54	1095.56	348.5
SGA	2000	1000	2279.2	2163.27	447	2377.88	4173.17	511.20

¹ OOFV of the charge plan. ² OOFV corresponding to solving time/s. ³ OOFV corresponding to residual material/t. ⁴ Mean of the objective function solved in multiple cycles. ⁵ Mean of the solving time for multiple cycles/s. ⁶ Mean of the amount of residual material solved in multiple cycles/t.

(1) When using SGA to solve this model, the achieved result was not ideal. Although the population size and the number of iterations were greater, V_o was 2279.2, which is much larger than the value obtained using the other two methods. This is mainly because the genetic operators in SGA have little effect on determining the optimal solution. In each iteration process, the population difference is not big; hence, the optimization cannot be performed quickly.

(2) When using EGA to solve this model, V_o was 123.10. However, this result was obtained at the 519th iteration. Compared with IEGA, finding a solution through EGA required more iterations and therefore, larger solving time.

(3) As a result of iteratively solving the problem and comparing the statistical data of EGA and IEGA, we observed that V_c, T_c, and M_c obtained using EGA were greater than those obtained using IEGA.

In the process of solving the model, each iteration of IEGA needs to be selected twice. The first selection preserves the elite chromosomes in each generation, and the second selection preserves the population with high fitness in each generation. Partial matching crossover operation enhances the difference between individuals in each generation of population. The chromosome fragment reversal mutation operation increases the chromosome richness; in particular, in the late iteration, when the chromosomes in the population tend to be consistent, the combination of the great variation operation increases the chromosome richness to avoid the algorithm tending to the local optimal solution. Therefore, we concluded that the proposed IEGA was superior over EGA and SGA in solving the charge plan model for SM-CC.

4.3. Practical Examples

Considering the model and algorithm proposed herein, combined with some other studies and using C# language, an SM-CC production planning system was developed and applied to a steel plant. The application effect results are listed in Table 6.

Table 6. System application effect comparison.

Contrast Items	Processing Time of SM-CC/min	The Number of Times the Broken Casting	Residual Materials/t
System application	183.5	0.3	2.3
No system application	206.4	0.8	11.2

The data listed in Table 6 are the average values of the corresponding statistics after 10 consecutive charges. Thus, the application of the proposed system shortens the processing time of the SM-CC by about 20 min, and the broken casting times of the continuous casting machine decreased from 0.8 to 0.3. This is because the model and algorithm proposed herein can minimize the difference in steel grade, width, and delivery time between contracts within the same charge, considerably reduce the adjustment between charges, and make the process more stable and smooth. Additionally, the residual materials are reduced from 11.2 t to 2.3 t, which reduces the cost incurred by inventory and improves the competitiveness of enterprises.

5. Conclusions and Future Prospects

In the present study, we thoroughly investigated the development of a charge plan model of SM-CC, formulated a suitable model, improved the conventional genetic algorithm, and successfully solved the problem based on the specific situation of the considered model. According to the characteristics of the model, we introduced an IEGA based on the permutation encoding method and proposed the corresponding chromosome decoding strategy. Based on the above research, we draw the following conclusions:

(1)

The results of model analysis confirmed the correctness of the developed charge plan model. We found that the optimal objective function value was 123.10, the total amount of the residual material was 294 t, and the solving time was 587.10 s.

(2)

Through algorithm analysis, we demonstrated that IEGA is more effective than EGA and SGA. In the process of solving the model, each iteration of IEGA requires two selection operations, one crossover operation and one mutation operation, which improves the speed of searching for the optimal solution of the algorithm and prevents the algorithm from tending to the local optimal solution.

(3)

Using the SM-CC production planning system, the processing time in the SM-CC was shortened by about 20 min. The average number of broken casting times was reduced from 0.8 to 0.3, and the residual materials decreased from 11.2 t to 2.3 t.

Thus, this study evidences the rationality of the proposed model and algorithm, but its practicability needs to be further verified. In this regard, future works will include the following subjects: (1) development and improvement of the SM-CC production planning system with increased versatility; (2) relatively independent research on the charge and casting plans, with further research on the close relationship between them.