Setting the Basis for the Interpretation of Temperature First Order Reversal Curve (TFORC) Distributions of Magnetocaloric Materials
Abstract
1. Introduction
2. Methods
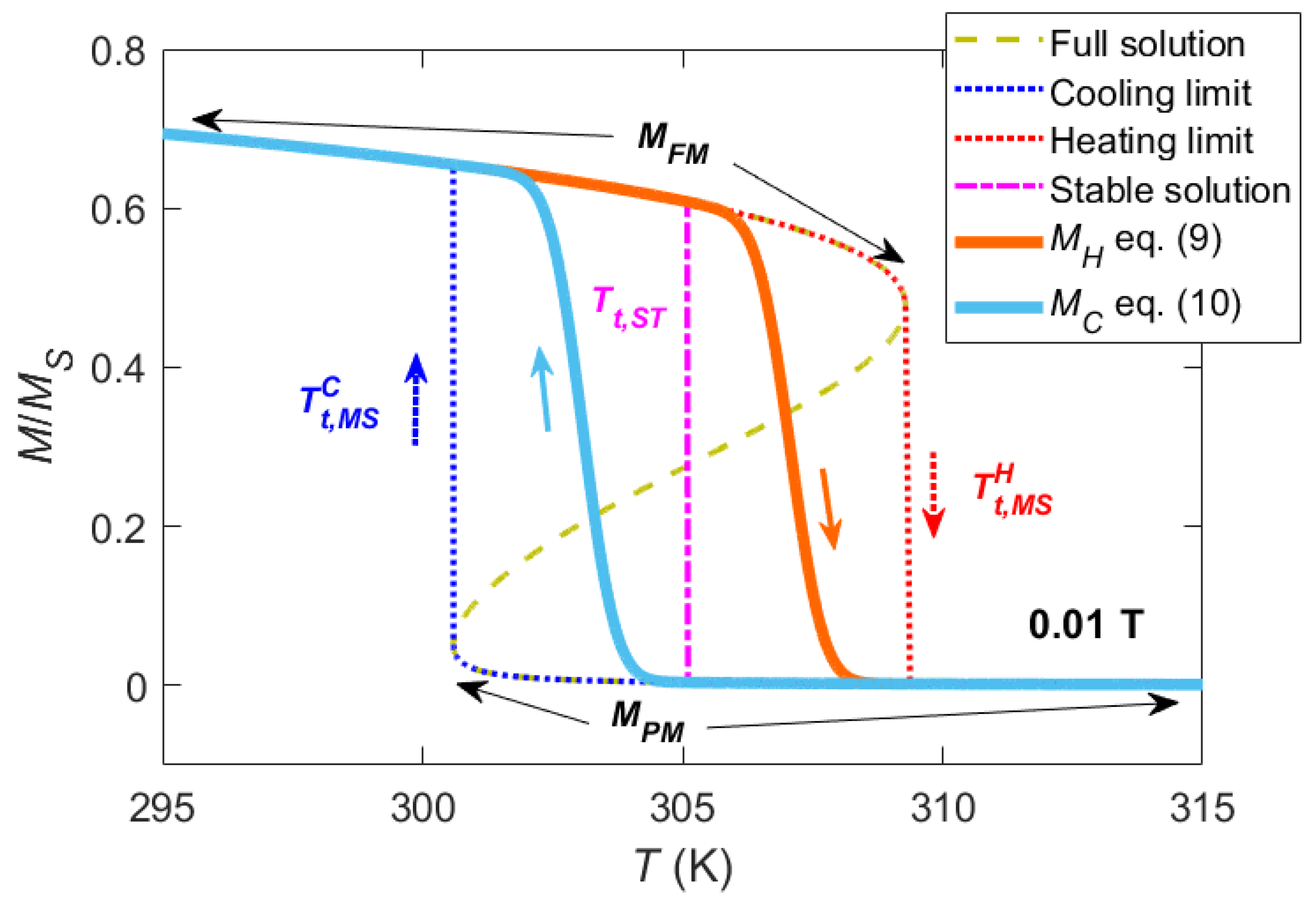
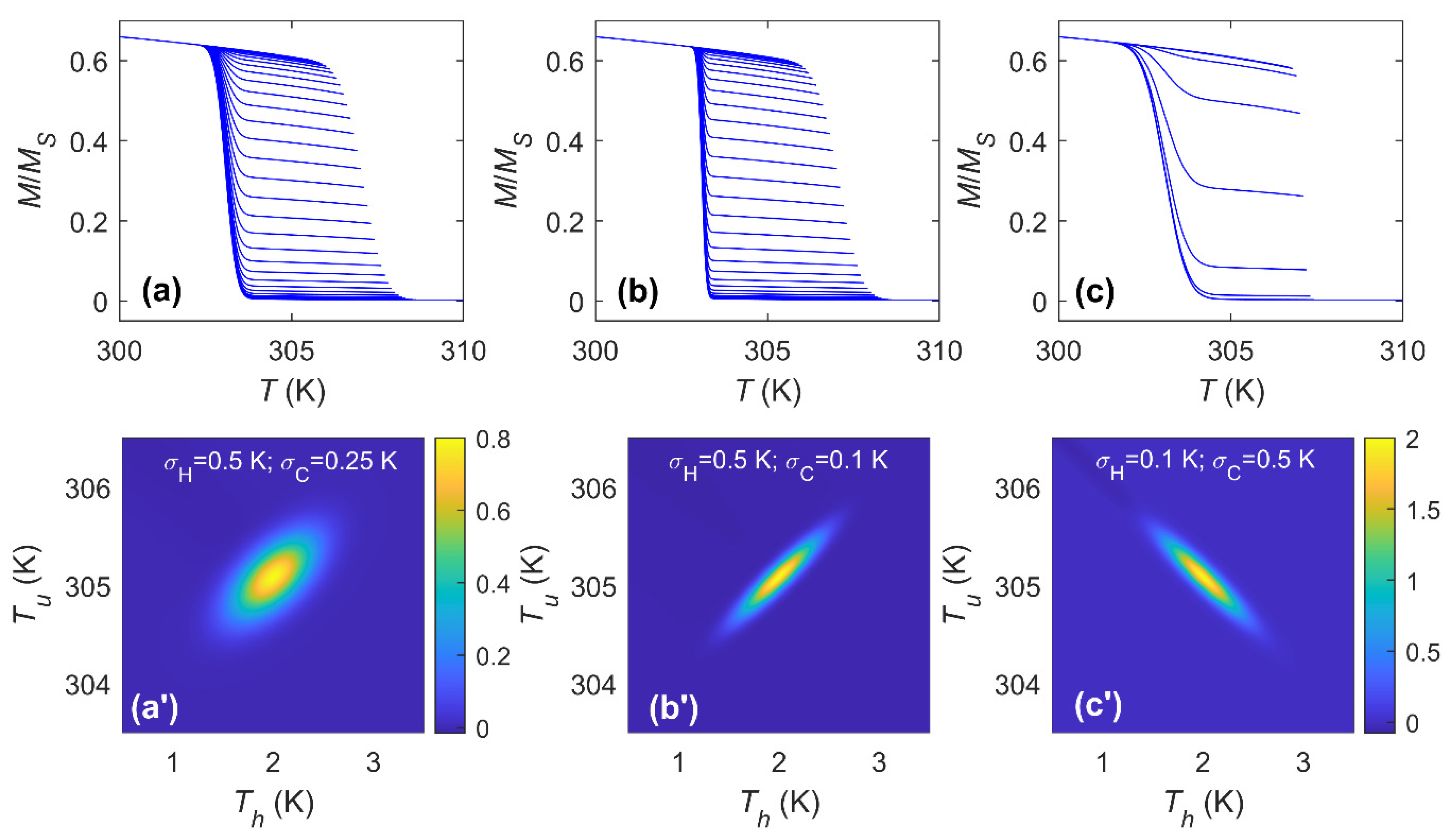
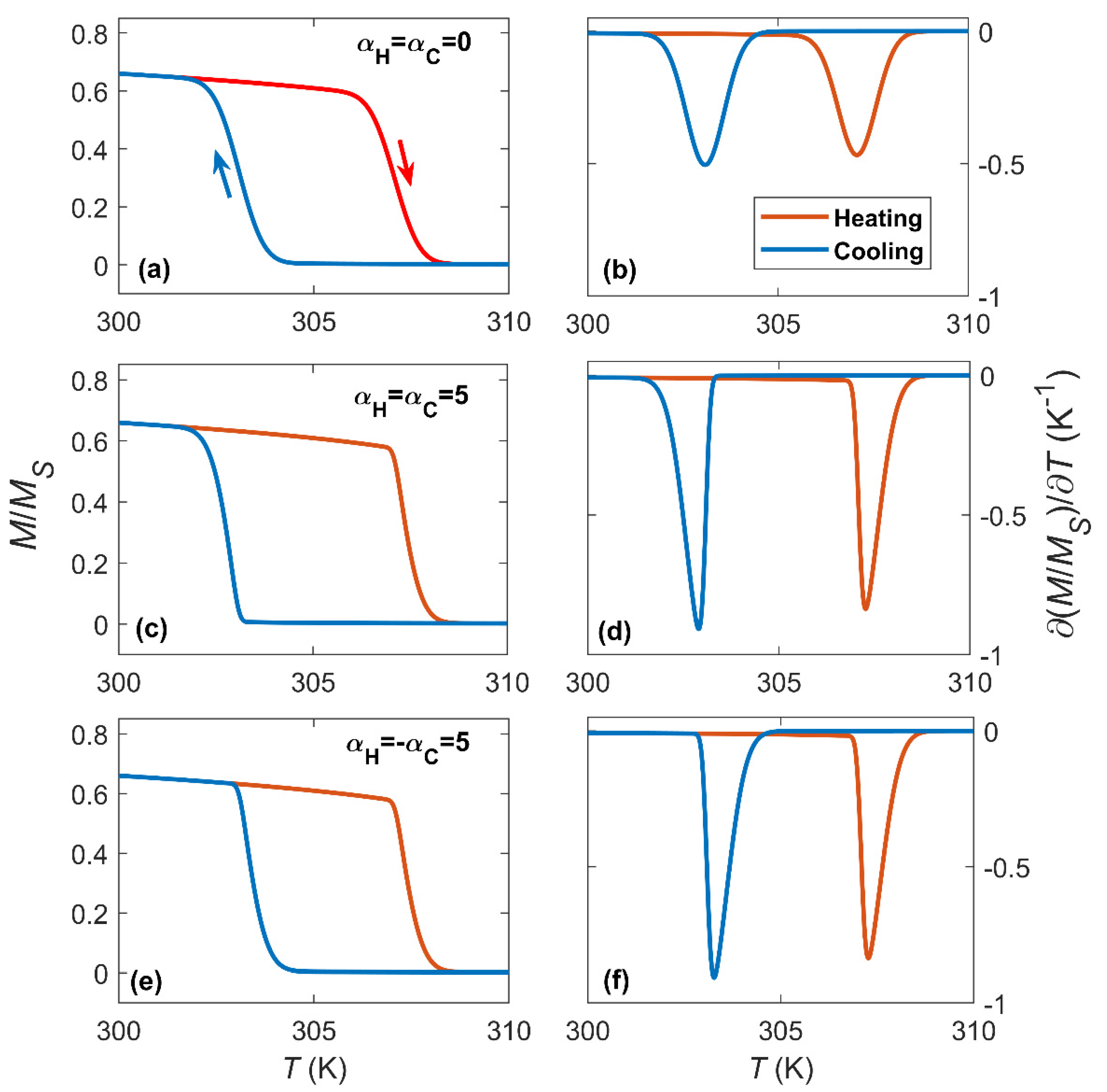
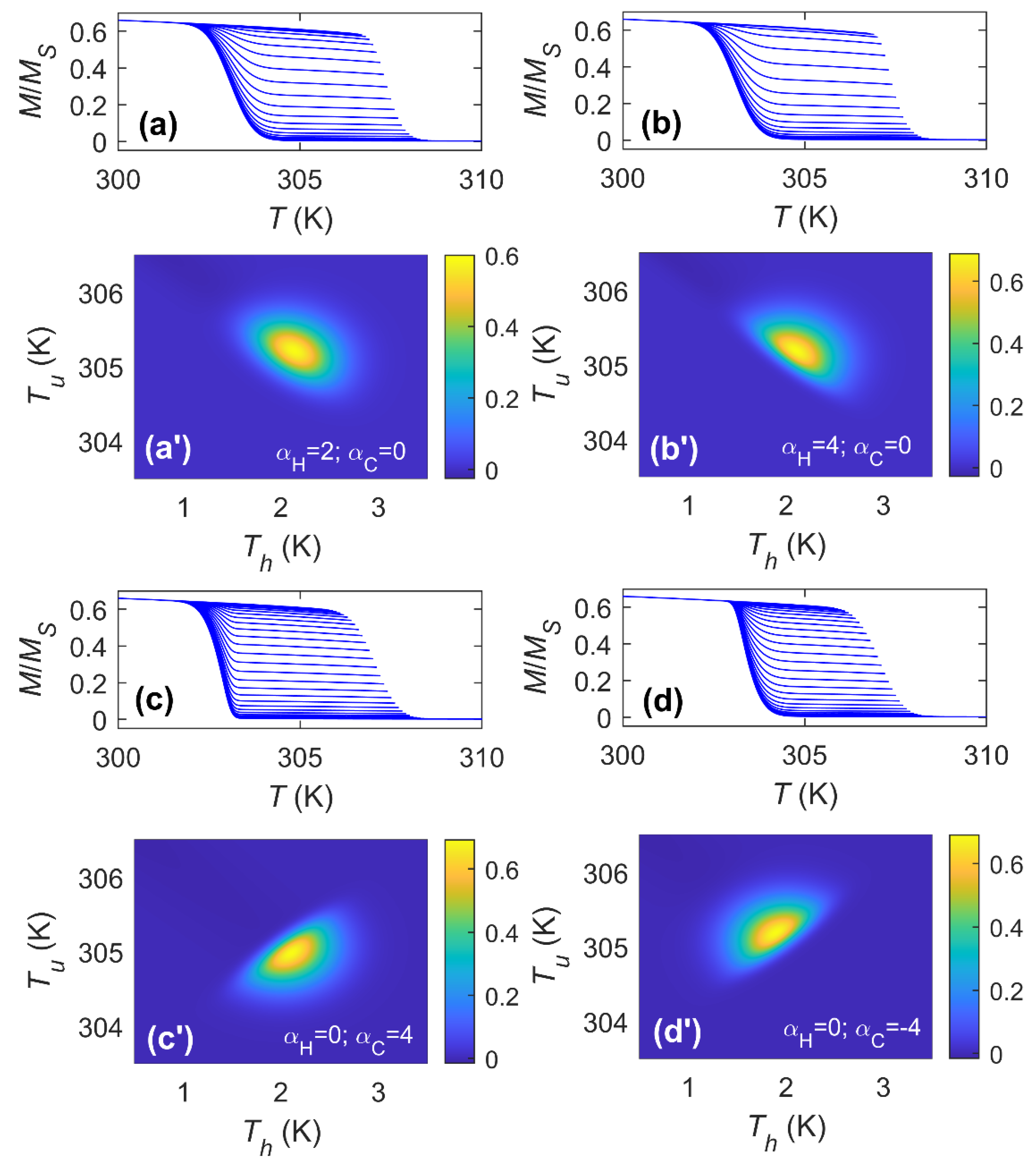
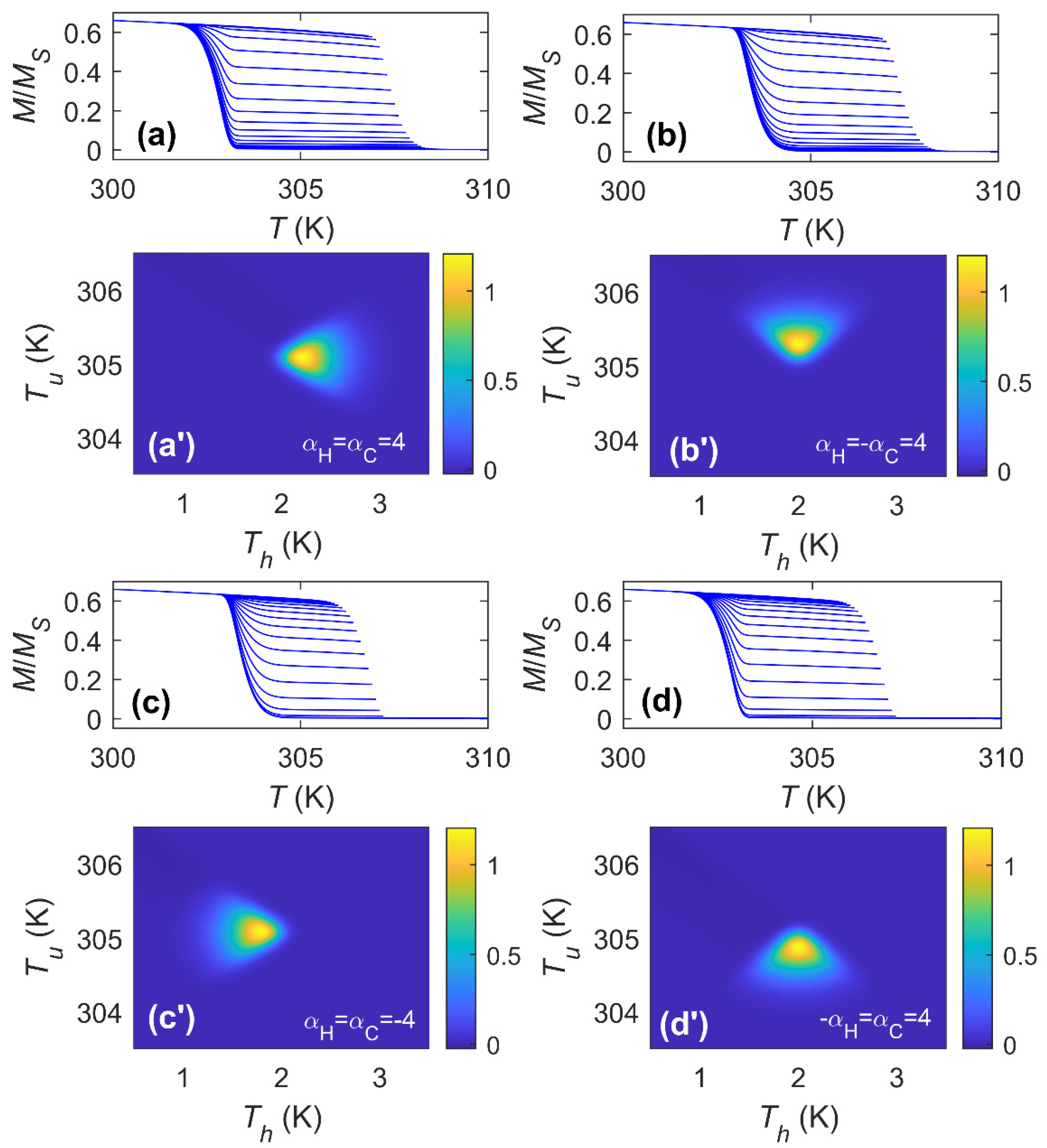
3. Results and Discussion
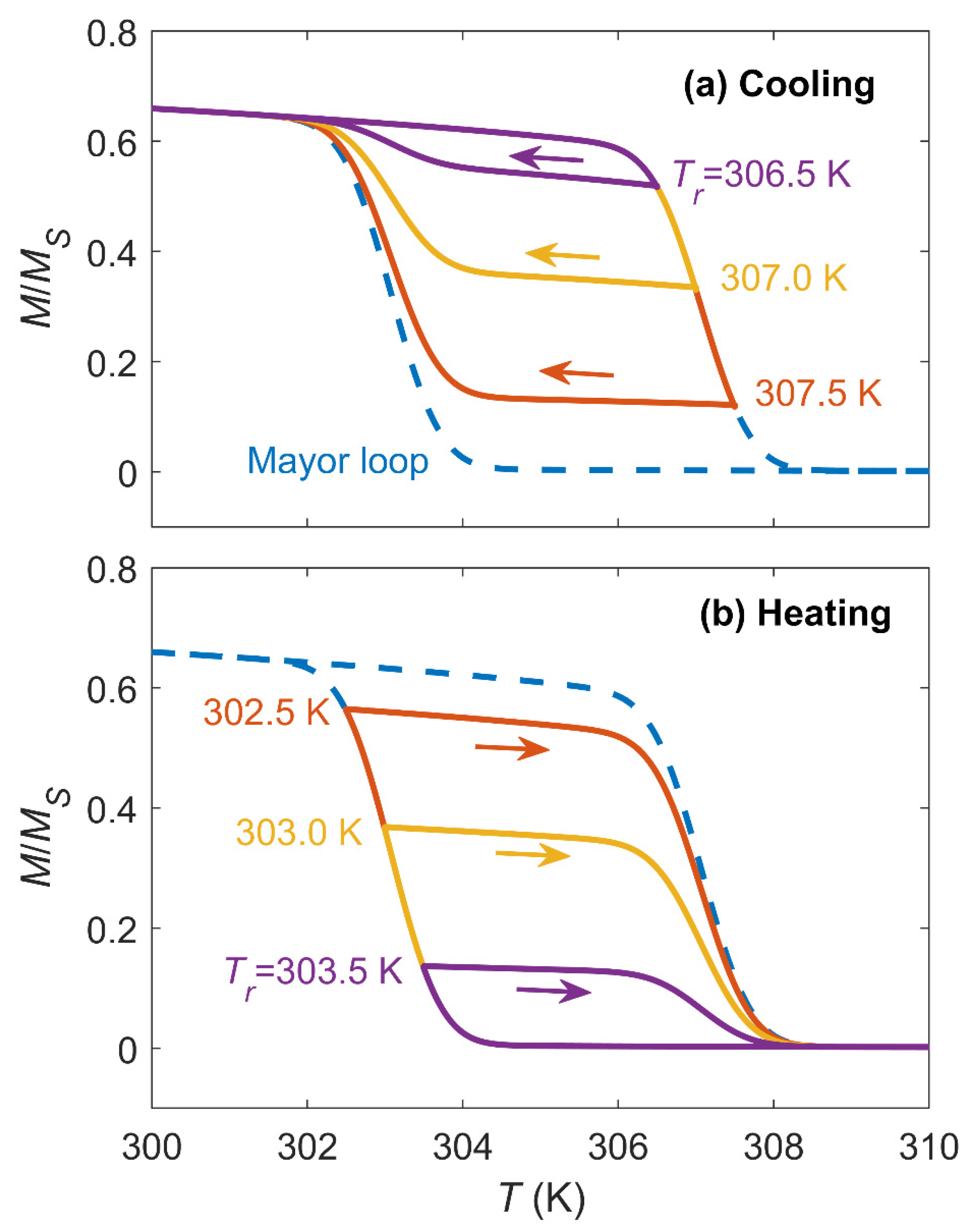
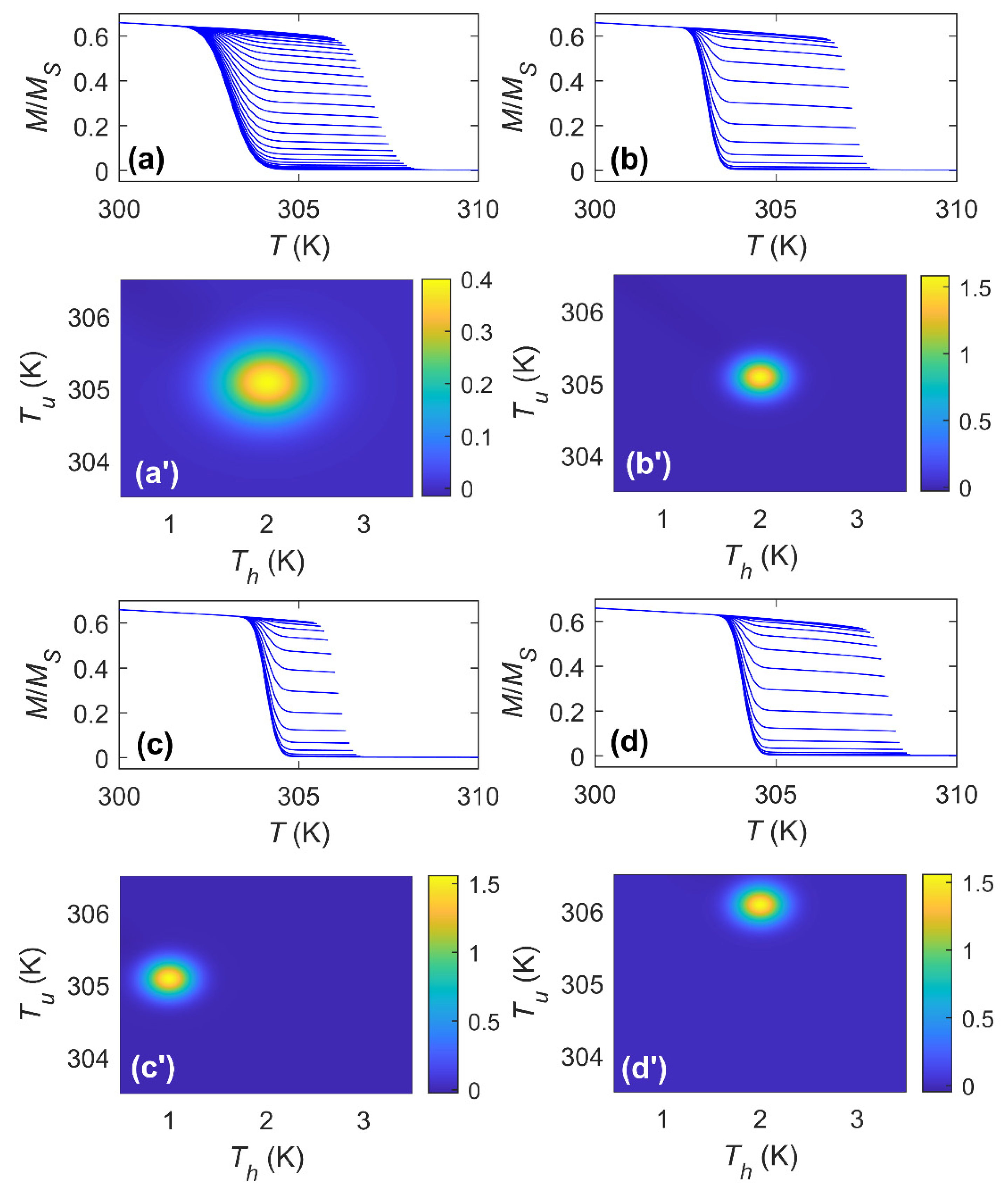
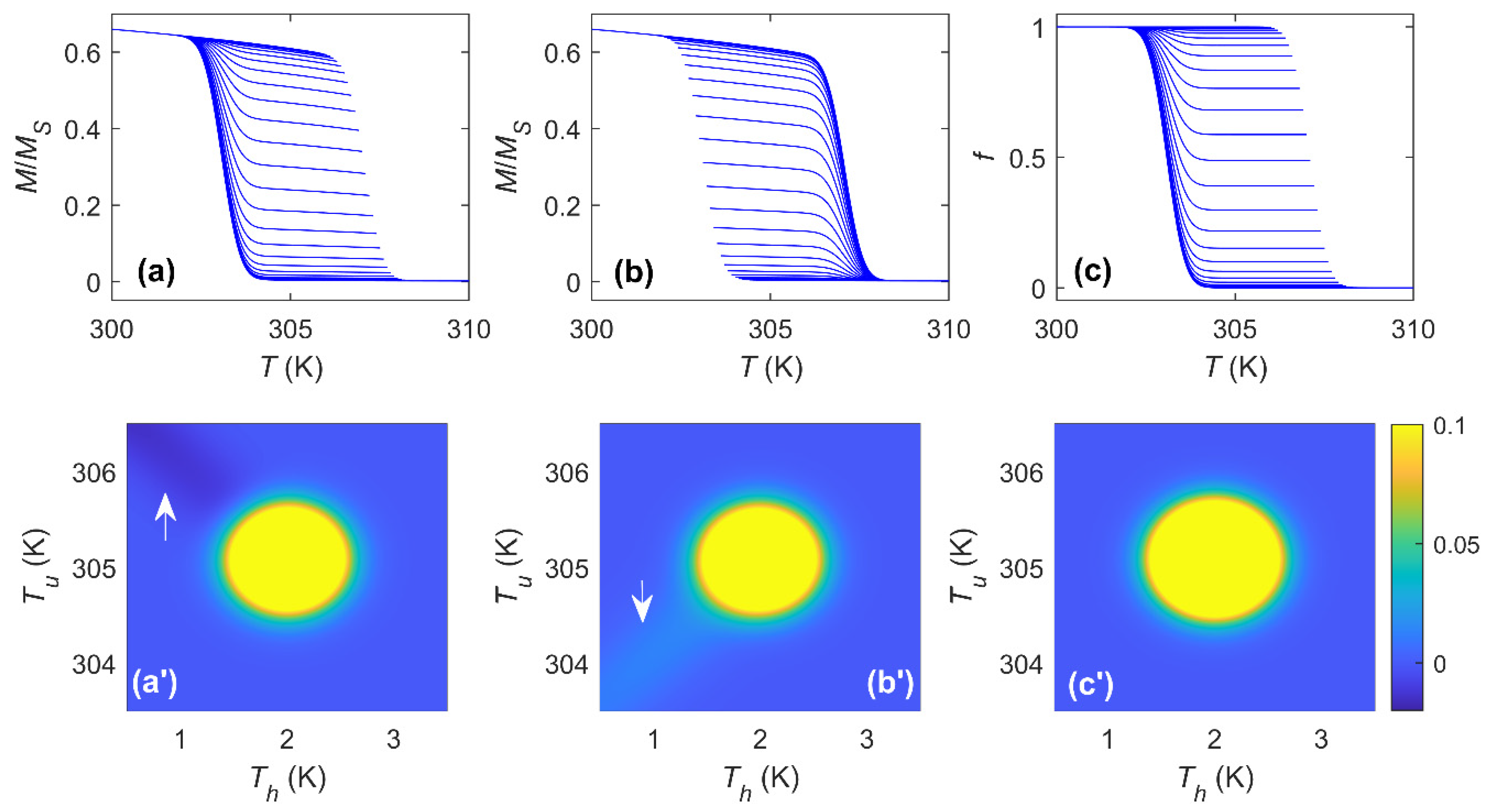
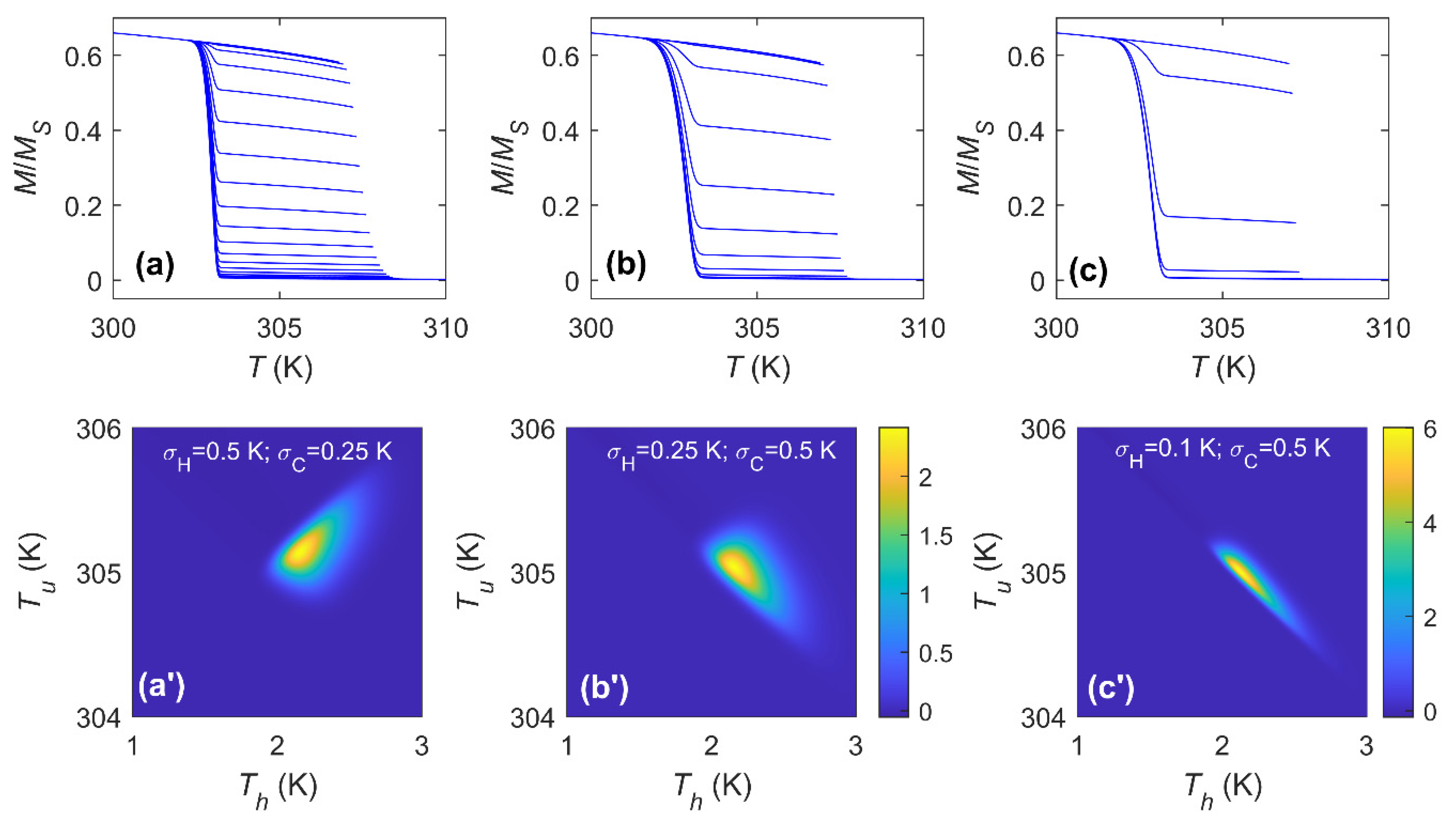
3.1. Symmetric Transformations
3.2. Asymmetric Transformations
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Franco, V.; Blázquez, J.S.; Ipus, J.J.; Law, J.Y.; Moreno-Ramírez, L.M.; Conde, A. Magnetocaloric effect: From materials research to refrigeration devices. Prog. Mater. Sci. 2018, 93, 112–232. [Google Scholar] [CrossRef]
- Yu, B.; Liu, M.; Egolf, P.W.; Kitanovski, A. A review of magnetic refrigerator and heat pump prototypes built before the year 2010. Int. J. Refrig. 2010, 33, 1029–1060. [Google Scholar] [CrossRef]
- Kitanovski, A.; Tušek, J.; Tomc, U.; Plaznik, U.; Ozbolt, M.; Poredoš, A. Magnetocaloric Energy Conversion; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-08741-2. [Google Scholar]
- Jaeger, G. The Ehrenfest Classification of Phase Transitions: Introduction and Evolution. Arch. Hist. Exact Sci. 1998, 53, 51–81. [Google Scholar] [CrossRef]
- Brown, G. V Magnetic heat pumping near room temperature. J. Appl. Phys. 1976, 47, 3673–3680. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Giant Magnetocaloric Effect in Gd5(Si2Ge2). Phys. Rev. Lett. 1997, 78, 4494–4497. [Google Scholar] [CrossRef]
- Biswas, A.; Mudryk, Y.; Pathak, A.K.; Zhou, L.; Pecharsky, V.K. Managing hysteresis of Gd5Si2Ge2 by magnetic field cycling. J. Appl. Phys. 2019, 126, 243902. [Google Scholar] [CrossRef]
- Fujita, A.; Fujieda, S.; Hasegawa, Y.; Fukamichi, K. Itinerant-electron metamagnetic transition and large magnetocaloric effects in La(Fex,Si1-x)13 compounds and their hydrides. Phys. Rev. B 2003, 67, 104416. [Google Scholar] [CrossRef]
- Moreno-Ramírez, L.M.; Romero-Muñiz, C.; Law, J.Y.; Franco, V.; Conde, A.; Radulov, I.A.; Maccari, F.; Skokov, K.P.; Gutfleisch, O. Tunable first order transition in La(Fe,Cr,Si)13 compounds: Retaining magnetocaloric response despite a magnetic moment reduction. Acta Mater. 2019, 175, 406–414. [Google Scholar] [CrossRef]
- Tegus, O.; Brück, E.; Buschow, K.H.J.; de Boer, F.R. Transition-metal-based magnetic refrigerants for room-temperature applications. Nature 2002, 415, 150–152. [Google Scholar] [CrossRef]
- Hu, S.; Miao, X.; Liu, J.; Ou, Z.; Cong, M.; Haschuluu, O.; Gong, Y.; Qian, F.; You, Y.; Zhang, Y.; et al. Small hysteresis and giant magnetocaloric effect in Nb-substituted (Mn,Fe)2(P, Si) alloys. Intermetallics 2019, 114, 106602. [Google Scholar] [CrossRef]
- Planes, A.; Mañosa, L.; Moya, X.; Krenke, T.; Acet, M.; Wassermann, E.F. Magnetocaloric effect in Heusler shape-memory alloys. J. Magn. Magn. Mater. 2007, 310, 2767–2769. [Google Scholar] [CrossRef]
- Neves-Bez, H.; Pathak, A.K.; Biswas, A.; Zarkevich, N.; Balema, V.; Mudryk, Y.; Johnson, D.D.; Pecharsky, V.K. Giant enhancement of the magnetocaloric response in Ni–Co–Mn–Ti by rapid solidification. Acta Mater. 2019, 173, 225–230. [Google Scholar] [CrossRef]
- Kaeswurm, B.; Franco, V.; Skokov, K.P.; Gutfleisch, O. Assessment of the magnetocaloric effect in La,Pr(Fe,Si) under cycling. J. Magn. Magn. Mater. 2016, 406, 259–265. [Google Scholar] [CrossRef]
- Gutfleisch, O.; Gottschall, T.; Fries, M.; Benke, D.; Radulov, I.; Skokov, K.P.; Wende, H.; Gruner, M.; Acet, M.; Entel, P.; et al. Mastering hysteresis in magnetocaloric materials. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150308. [Google Scholar] [CrossRef] [PubMed]
- Mayergoyz, I. Mathematical models of hysteresis. IEEE Trans. Magn. 1986, 22, 603–608. [Google Scholar] [CrossRef]
- Pike, C.R.; Roberts, A.P.; Verosub, K.L. Characterizing interactions in fine magnetic particle systems using first order reversal curves. J. Appl. Phys. 1999, 85, 6660–6667. [Google Scholar] [CrossRef]
- Dobrotă, C.-I.; Stancu, A. What does a first-order reversal curve diagram really mean? A study case: Array of ferromagnetic nanowires. J. Appl. Phys. 2013, 113, 43928. [Google Scholar] [CrossRef]
- Franco, V.; Gottschall, T.; Skokov, K.P.; Gutfleisch, O. First-Order Reversal Curve (FORC) Analysis of Magnetocaloric Heusler-Type Alloys. IEEE Magn. Lett. 2016, 7, 1–4. [Google Scholar] [CrossRef]
- Franco, V. Temperature-FORC analysis of a magnetocaloric Heusler alloy using a unified driving force approach (T*FORC). J. Appl. Phys. 2020, 127, 133902. [Google Scholar] [CrossRef]
- Atitoaie, A.; Tanasa, R.; Stancu, A.; Enachescu, C. Study of spin crossover nanoparticles thermal hysteresis using FORC diagrams on an Ising-like model. J. Magn. Magn. Mater. 2014, 368, 12–18. [Google Scholar] [CrossRef]
- Preisach, F. Über die magnetische Nachwirkung. Z. Für Phys. 1935, 94, 277–302. [Google Scholar] [CrossRef]
- Pike, C.R.; Roberts, A.P.; Dekkers, M.J.; Verosub, K.L. An investigation of multi-domain hysteresis mechanisms using FORC diagrams. Phys. Earth Planet. Inter. 2001, 126, 11–25. [Google Scholar] [CrossRef]
- Roberts, A.P.; Verosub, K.L. First-order reversal curve diagrams and thermal relaxation effects in magnetic particles. Geophys. J. Int. 2001, 145, 721–730. [Google Scholar]
- Stancu, A.; Pike, C.; Stoleriu, L.; Postolache, P.; Cimpoesu, D. Micromagnetic and Preisach analysis of the First Order Reversal Curves (FORC) diagram. J. Appl. Phys. 2003, 93, 6620–6622. [Google Scholar] [CrossRef]
- Muxworthy, A.; Heslop, D.; Williams, W. Influence of magnetostatic interactions on first-order-reversal-curve (FORC) diagrams: A micromagnetic approach. Geophys. J. Int. 2004, 158, 888–897. [Google Scholar] [CrossRef]
- Newell, A.J. A high-precision model of first-order reversal curve (FORC) functions for single-domain ferromagnets with uniaxial anisotropy. Geochem. Geophys. Geosyst. 2005, 6, Q05010. [Google Scholar] [CrossRef]
- Bean, C.P.; Rodbell, D.S. Magnetic Disorder as a First-Order Phase Transformation. Phys. Rev. 1962, 126, 104–115. [Google Scholar] [CrossRef]
- Piazzi, M.; Bennati, C.; Curcio, C.; Kuepferling, M.; Basso, V. Modeling specific heat and entropy change in La(Fe–Mn–Si)13–H compounds. J. Magn. Magn. Mater. 2016, 400, 349–355. [Google Scholar] [CrossRef]
- Karpenkov, D.Y.; Karpenkov, A.Y.; Skokov, K.P.; Radulov, I.A.; Zheleznyi, M.; Faske, T.; Gutfleisch, O. Pressure Dependence of Magnetic Properties in La(Fe,Si)13: Multistimulus Responsiveness of Caloric Effects by Modeling and Experiment. Phys. Rev. Appl. 2020, 13, 34014. [Google Scholar] [CrossRef]
- Von Ranke, P.J.; de Campos, A.; Caron, L.; Coelho, A.A.; Gama, S.; de Oliveira, N.A. Calculation of the giant magnetocaloric effect in the MnFeP0.45As0.55 compound. Phys. Rev. B 2004, 70, 94410. [Google Scholar] [CrossRef]
- Wang, G.F.; Song, L.; Ou, Z.Q.; Zhao, Z.R.; Tegus, O. Calculation of the magnetization and magnetocaloric effect in the MnFeP0.45As0.55 compound. Acta Metall. Sin. (Engl. Lett.) 2007, 20, 265–269. [Google Scholar] [CrossRef]
- Azzalini, A. The Skew-Normal and Related Families; Cambridge University Press: Cambridge, UK, 2013; ISBN 9781107029279. [Google Scholar]
- Moreno-Ramírez, L.M.; Blázquez, J.S.; Radulov, I.A.; Skokov, K.P.; Gutfleisch, O.; Franco, V.; Conde, A. Combined Kinetic and Bean-Rodbell approach for describing field-induced transitions in LaFe11.6Si1.4 alloys. Submitt. Scr. Mater. 2020. submitted for publication. [Google Scholar]
- Waske, A.; Giebeler, L.; Weise, B.; Funk, A.; Hinterstein, M.; Herklotz, M.; Skokov, K.; Fähler, S.; Gutfleisch, O.; Eckert, J. Asymmetric first-order transition and interlocked particle state in magnetocaloric La(Fe,Si)13. Phys. Status Solidi Rapid Res. Lett. 2015, 9, 136–140. [Google Scholar] [CrossRef]
- Diestel, A.; Niemann, R.; Schleicher, B.; Schwabe, S.; Schultz, L.; Fähler, S. Field-temperature phase diagrams of freestanding and substrate-constrained epitaxial Ni-Mn-Ga-Co films for magnetocaloric applications. J. Appl. Phys. 2015, 118, 23908. [Google Scholar] [CrossRef]
| Heating Transformation | Cooling Transformation | TFORC Distribution Shape | TFORC Distribution Orientation |
|---|---|---|---|
| Circle | - | ||
| Ellipse | 45° (major symmetry axis) | ||
| Ellipse | −45° (major symmetry axis) | ||
| Semi-circle | 45° (reflection axis) | ||
| Semi-circle | 135° (reflection axis) | ||
| Semi-circle | 225° (reflection axis) | ||
| Semi-circle | 315° (reflection axis) | ||
| Isosceles Triangle | 0° (reflection axis) | ||
| Isosceles Triangle | 90° (reflection axis) | ||
| Isosceles Triangle | 180° (reflection axis) | ||
| Isosceles Triangle | 270° (reflection axis) | ||
| Combination of previous shapes: scalene triangle or skew ellipse | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno-Ramírez, L.M.; Franco, V. Setting the Basis for the Interpretation of Temperature First Order Reversal Curve (TFORC) Distributions of Magnetocaloric Materials. Metals 2020, 10, 1039. https://doi.org/10.3390/met10081039
Moreno-Ramírez LM, Franco V. Setting the Basis for the Interpretation of Temperature First Order Reversal Curve (TFORC) Distributions of Magnetocaloric Materials. Metals. 2020; 10(8):1039. https://doi.org/10.3390/met10081039
Chicago/Turabian StyleMoreno-Ramírez, Luis M., and Victorino Franco. 2020. "Setting the Basis for the Interpretation of Temperature First Order Reversal Curve (TFORC) Distributions of Magnetocaloric Materials" Metals 10, no. 8: 1039. https://doi.org/10.3390/met10081039
APA StyleMoreno-Ramírez, L. M., & Franco, V. (2020). Setting the Basis for the Interpretation of Temperature First Order Reversal Curve (TFORC) Distributions of Magnetocaloric Materials. Metals, 10(8), 1039. https://doi.org/10.3390/met10081039






