Comparison of Bayesian Methods on Parameter Identification for a Viscoplastic Model with Damage
Abstract
1. Introduction
2. Model Problem
3. Bayesian Identification
3.1. Transitional Markov Chain Monte Carlo Method
Transitional MCMC Algorithm
- In the first step, is set and from a set of N samples are picked up.
- should be selected in a way that the coefficient of variation of where is equal to a prescribed value. Accordingly, the coefficient of variation serves as an indicator of how close is to .
- The plausibility weight is calculated for and the parameter is computed.
- Samples for are provided from by Metropolis-Hastings algorithm. In other words, the k-th sample is picked up from a Markov Chain that starts from one of the samples where which is selected randomly. The i-th initial sample is chosen with probability . As proposal distribution, a Gaussian which is centered at the current sample in the k-th chain is applied in Metropolis-Hastings algorithm. Also, the covariance matrix:wherein which is a prescribed scaling factor which is used as the rejection rate in Metropolis-Hastings algorithm.
- Steps two to four are repeated until . At the final step, samples for are distributed according to and it is turned out that is asymptotically unbiased for .
3.2. Gauss-Markov-Kalman Filter Using Functional Approximation
3.2.1. The Linear Filter
3.2.2. Sequential Gauss-Markov-Kalman Filter
3.2.3. Sampling
3.2.4. Functional Approximation
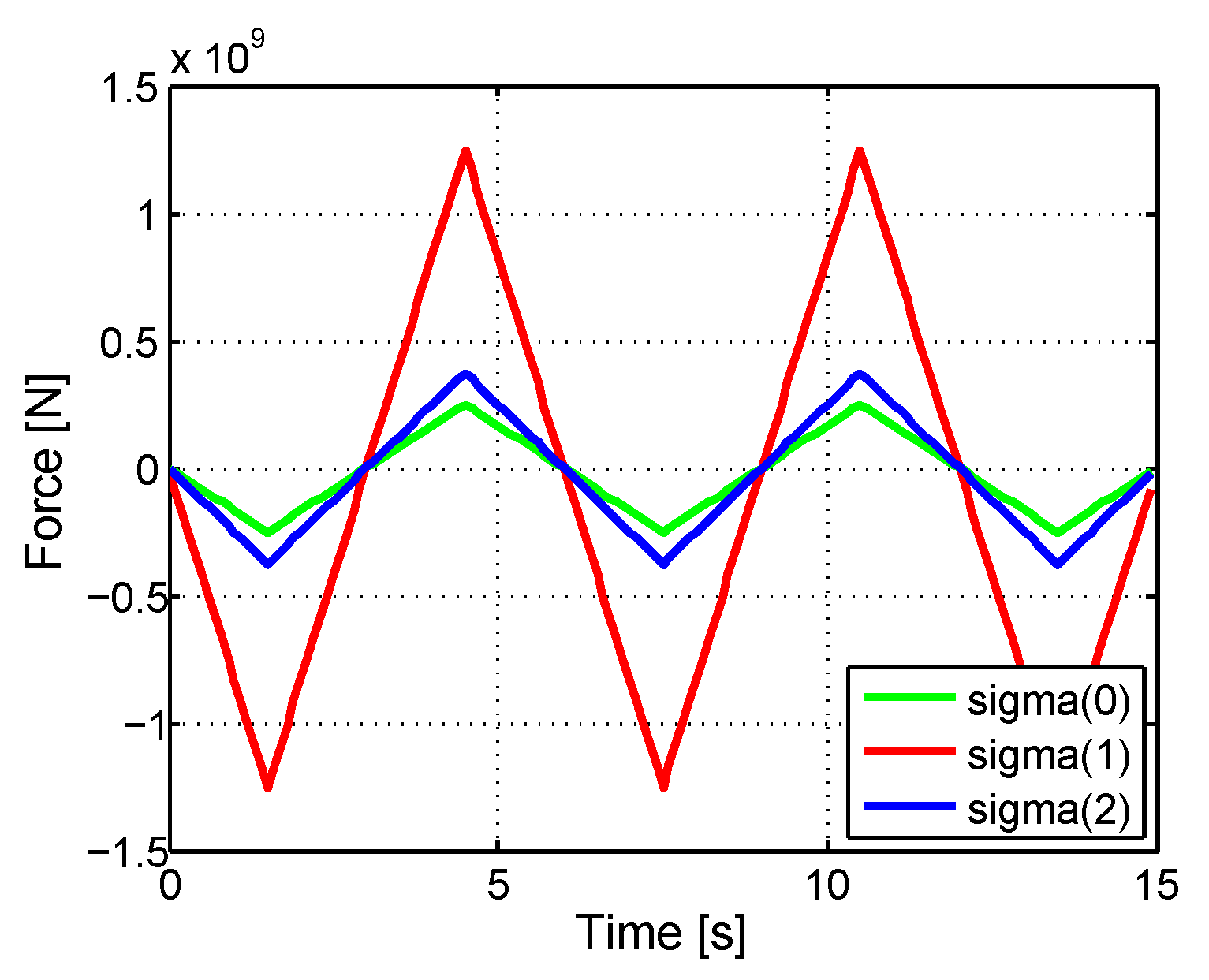
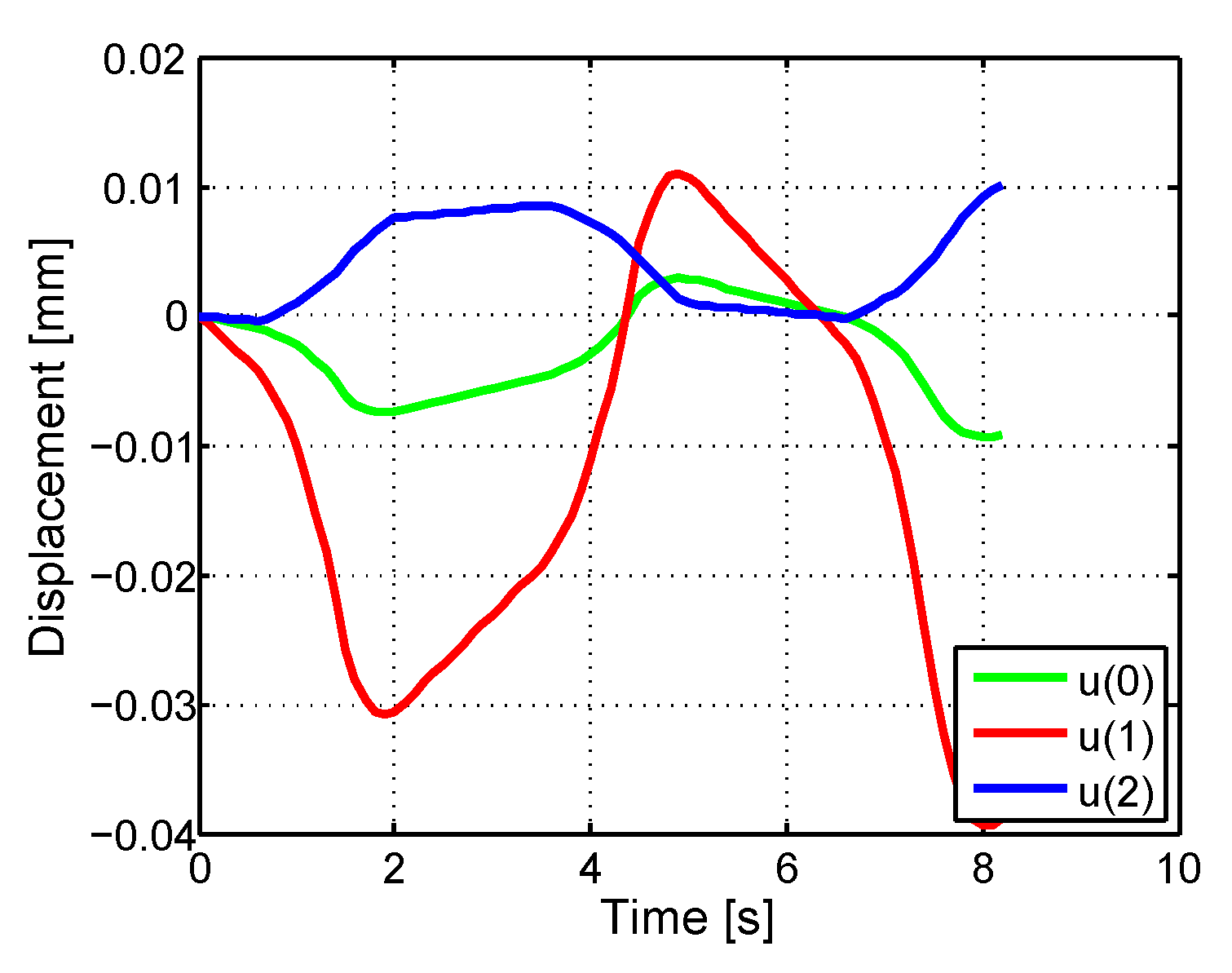
4. Numerical Results
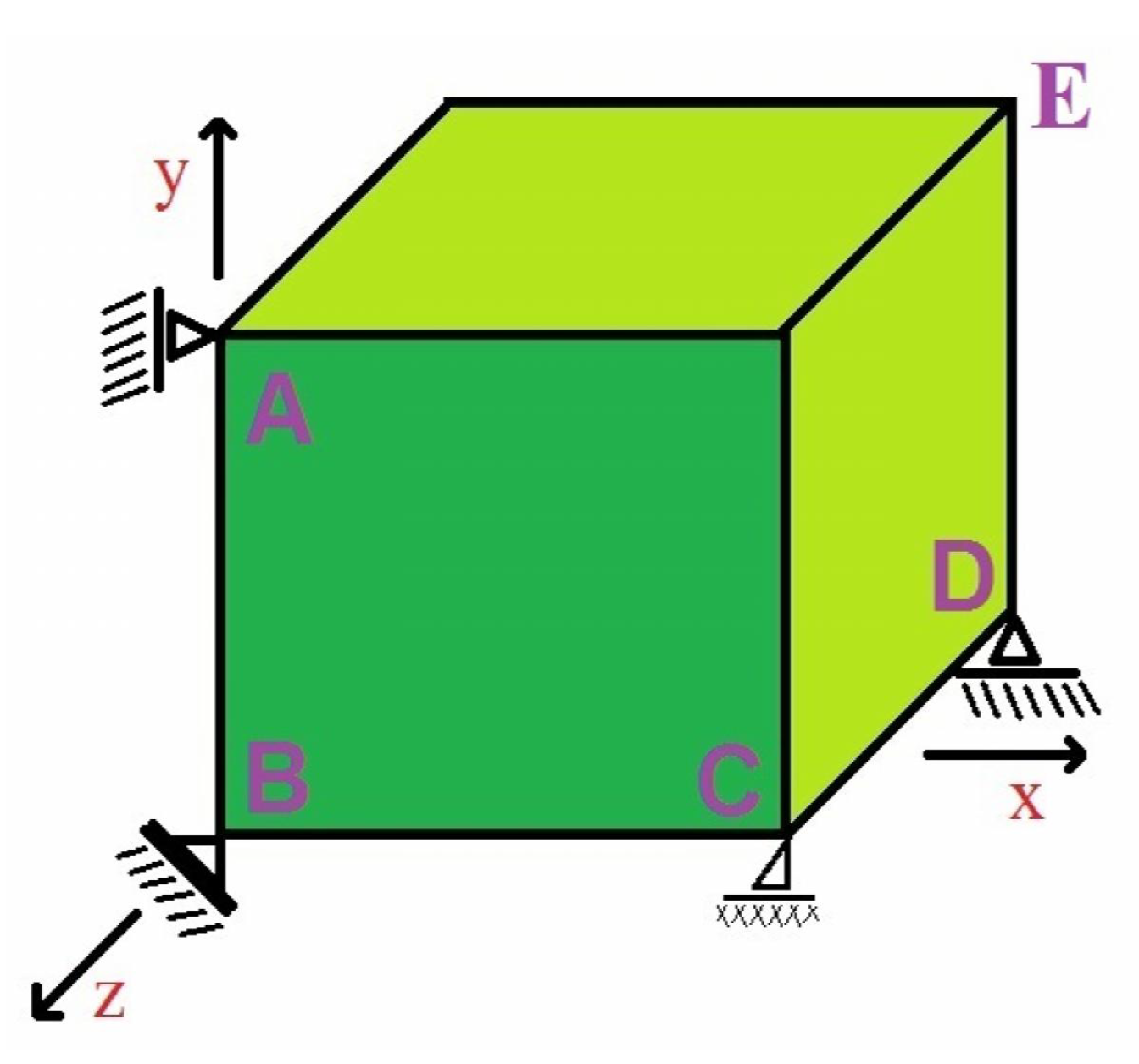
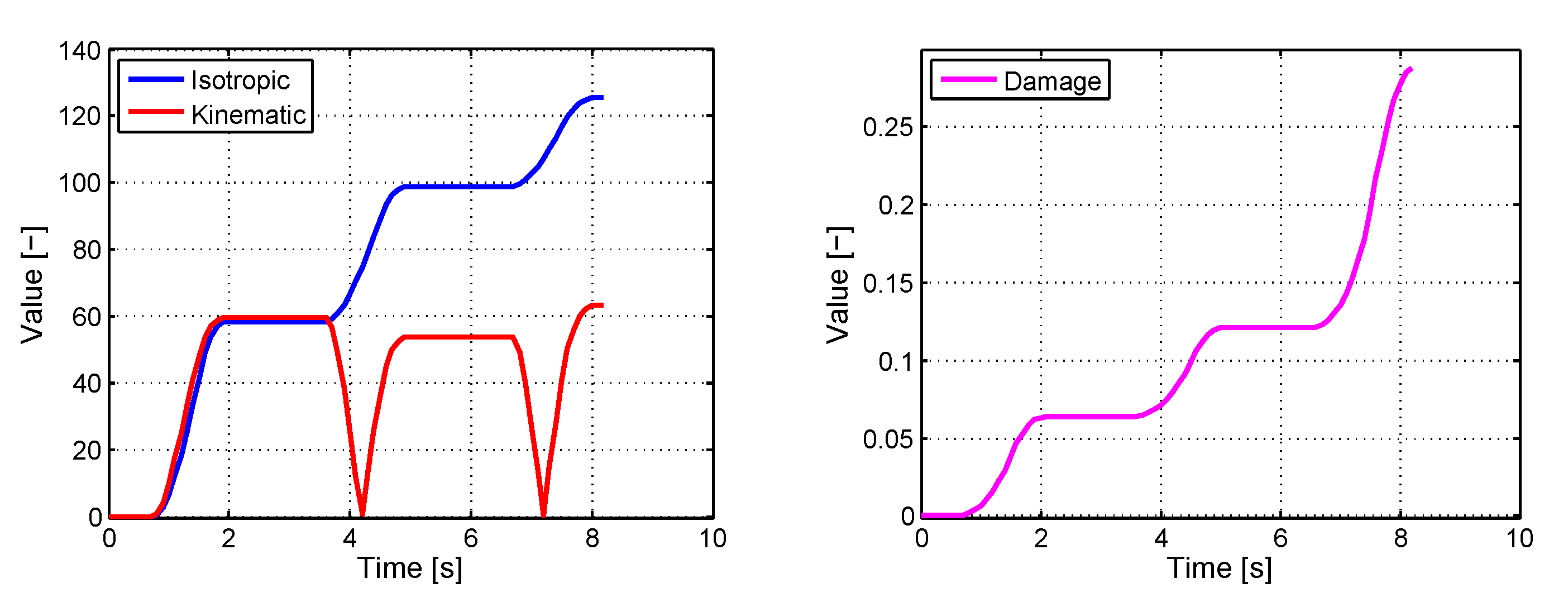
Validation Procedure for Viscoplasticity Model with Isotropic and Kinematic Hardening Behavior
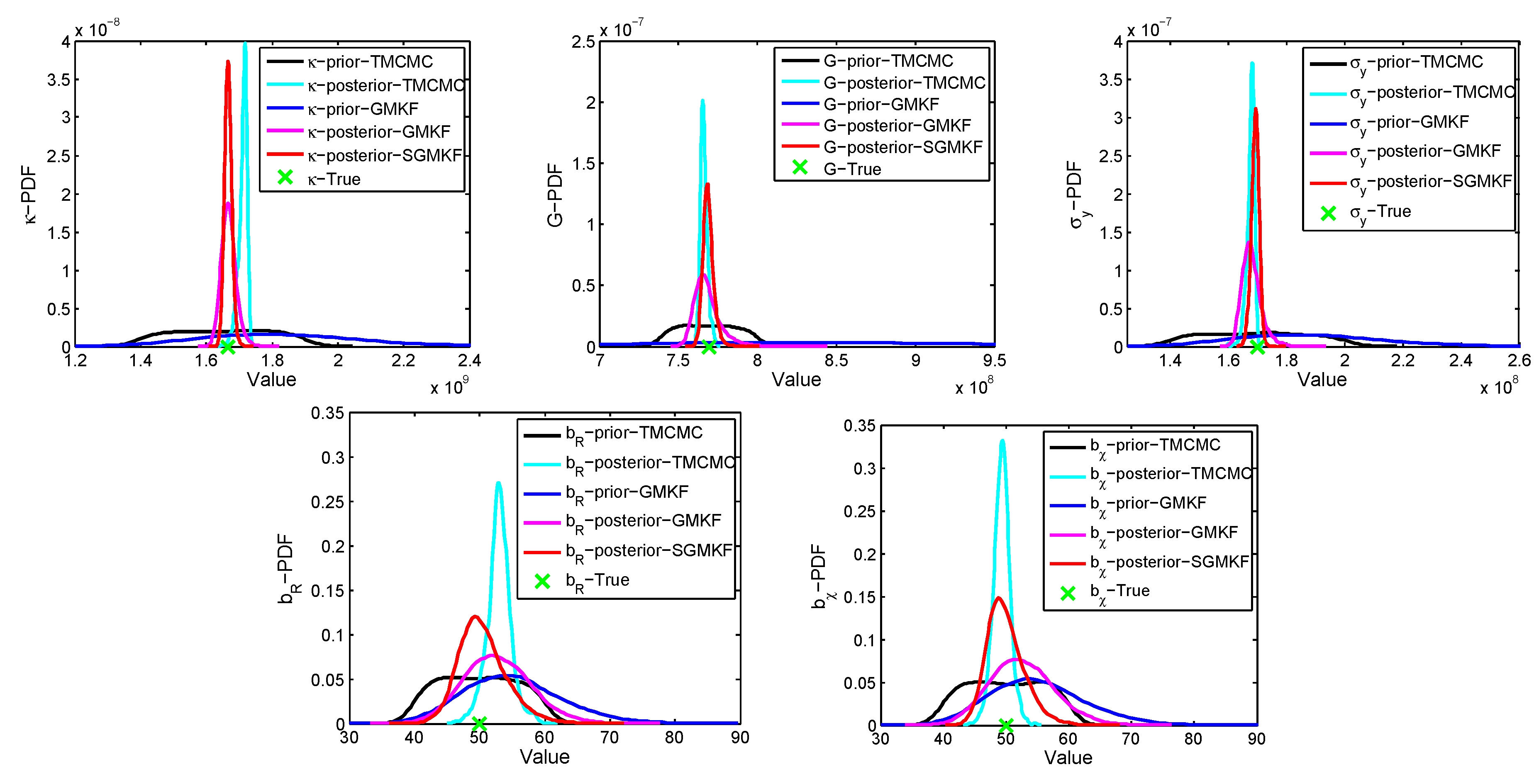
5. Discussion and Comparison
5.1. Validation Procedure on Viscoplastic-Damage Model with Isotropic and Kinematic Hardening
6. Conclusions
7. Summary
Author Contributions
Funding
Conflicts of Interest
Appendix A. Elasto-Viscoplastic Constitutive Laws
Appendix B. Gauss-Markov-Kalman Filter
Appendix B.1. Conditional Expectation
Appendix B.2. Constructing a Posterior Random Variable
Appendix B.3. Updating Random Variables
Appendix B.4. Correcting the Mean
Appendix B.5. Building the Filter
References
- Adeli, E.; Rosić, B.V.; Matthies, H.G.; Reinstädler, S.; Dinkler, D. Comparison of Bayesian Methods on Parameter Identification for a Viscoplastic Model with Damage. J. Comput. Mech. 2019. [Google Scholar] [CrossRef]
- Pacheco, C.; Dulikravich, G.S.; Vesenjak, M.; Borovinsek, M.; Duarte, I.M.A.; Jha, R.; Reddy, S.R.; Orlande, H.R.B.; Colaco, M.J. Inverse parameter identification in solid mechanics using Bayesian statistics, response surfaces and minimization. Tech. Mech. 2016, 36, 120–131. [Google Scholar]
- Słonski, M. Bayesian identification of elastic parameters in composite laminates applying lamb waves monitoring. In Proceedings of the Fifth ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete Island, Greece, 25–27 May 2015. [Google Scholar]
- Zhang, E.; Chazot, J.D.; Antoni, J. Parametric identification of elastic modulus of polymeric material in laminated glasses. In Proceedings of the 16th IFAC Symposium on System Identification, The International Federation of Automatic Control, Brussels, Belgium, 11–13 July 2012. [Google Scholar]
- Gallina, A.; Ambrozinski, L.; Packo, P.; Pieczonka, L.; Uhl, T.; Staszewski, W.J. Bayesian parameter identification of orthotropic composite materials using lamb waves dispersion curves measurement. J. Vibr. Control 2017, 23, 2656–2671. [Google Scholar] [CrossRef]
- Pieczonka, L.; Gallina, A.; Ambrozinski, L.; Packo, P.; Uhl, T.; Staszewski, W.J. Parameters identification of composite materials using Bayesian approach and guided ultrasonic waves. In Proceedings of the ISMA 2016—International Conference on Noise and Vibration Engineering and USD2016, Leuven, Belgium, 19–21 September 2016. [Google Scholar]
- Arnst, M.; Ghanem, R.; Soize, C. Identification of Bayesian posteriors for coefficients of chaos expansions. J. Comput. Phys. 2010, 229, 3134–3154. [Google Scholar] [CrossRef][Green Version]
- Rappel, H.; Beex, L.A.A.; Noels, L.; Bordas, S.P.A. Identifying elastoplastic parameters with Bayes’ theorem considering double error sources and model uncertainty. J. Prob. Eng. Mech. 2018. [Google Scholar] [CrossRef]
- An, D.; Cho, J.; Kim, N.H. Identification of correlated damage parameters under noise and bias using Bayesian inference. Struct. Health Monit. 2011, 11, 293–303. [Google Scholar] [CrossRef]
- Hernandez, W.P.; Borges, F.C.L.; Castello, D.A.; Roitman, N.; Magluta, C. Bayesian inference applied on model calibration of a fractional derivative viscoelastic model. In Proceedings of the XVII International Symposium on Dynamic Problems of Mechanics, Natal, Brazil, 22–27 February 2015. [Google Scholar]
- Mahnken, R. Identification of material parameters for constitutive equations. In Encyclopedia of Computational Mechanics, 2nd ed.; Part 2. Solids and Structures; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2017; pp. 1–21. [Google Scholar]
- Zheng, W.; Yu, Y. Bayesian probabilistic framework for damage identification of steel truss bridges under joint uncertainties. Adv. Civ. Eng. 2013, 1–13. [Google Scholar] [CrossRef]
- Nichols, J.M.; Moore, E.Z.; Murphy, K.D. Bayesian identification of a cracked plate using a population-based Markov Chain Monte Carlo method. J. Comput. Struct. 2011, 89, 1323–1332. [Google Scholar] [CrossRef]
- Madireddy, S.; Sista, B.; Vemaganti, K. A Bayesian approach to selecting hyperelastic constitutive models of soft tissue. J. Comput. Appl. Math. 2015, 291, 102–122. [Google Scholar] [CrossRef]
- Wang, J.; Zabaras, N. A Bayesian inference approach to the inverse heat conduction problem. Int. J. Heat Mass Trans. 2004, 47, 3927–3941. [Google Scholar] [CrossRef]
- Oh, C.K.; Beck, J.L.; Yamada, M. Bayesian learning using automatic relevance determination prior with an application to earthquake early warning. J. Eng. Mech. 2008, 134, 1013–1020. [Google Scholar] [CrossRef]
- Alvin, K. Finite element model update via Bayesian estimation and minimization of dynamic residuals. Am. Inst. Aeronaut. Astronaut. J. 1997, 135, 879–886. [Google Scholar] [CrossRef]
- Marwala, T.; Sibusiso, S. Finite element model updating using Bayesian framework and modal properties. J. Aircraft 2005, 42, 275–278. [Google Scholar] [CrossRef]
- Daghia, F.; de Miranda, S.; Ubertini, F.; Viola, E. Estimation of elastic constants of thick laminated plates within a Bayesian framework. J. Compos. Struct. 2007, 80, 461–473. [Google Scholar] [CrossRef]
- Abhinav, S.; Manohar, C. Bayesian parameter identification in dynamic state space models using modified measurement equations. Int. J. Non-Linear Mech. 2015, 71, 89–103. [Google Scholar] [CrossRef]
- Gogu, C.; Yin, W.; Haftka, R.; Ifju, P.; Molimard, J.; le Riche, R.; Vautrin, A. Bayesian identification of elastic constants in multi-directional laminate from Moire interferometry displacement fields. J. Exp. Mech. 2013, 53, 635–648. [Google Scholar] [CrossRef]
- Gogu, C.; Haftka, R.; Molimard, J.; Vautrin, A. Introduction to the Bayesian approach applied to elastic constants identification. Am. Inst. Aeronaut. Astronaut. J. 2010, 48, 893–903. [Google Scholar] [CrossRef]
- Koutsourelakis, P.S. A novel Bayesian strategy for the identification of spatially varying material properties and model validation: An application to static elastography. Int. J. Num. Methods Eng. 2012, 91, 249–268. [Google Scholar] [CrossRef]
- Koutsourelakis, P.S. A multi-resolution, non-parametric, Bayesian framework for identification of spatially-varying model parameters. J. Comput. Phys. 2009, 228, 6184–6211. [Google Scholar] [CrossRef]
- Fitzenz, D.D.; Jalobeanu, A.; Hickman, S.H. Integrating laboratory creep compaction data with numerical fault models: A Bayesian framework. J. Geophys. Res. Solid Earth 2007, 112, B08410. [Google Scholar] [CrossRef]
- Most, T. Identification of the parameters of complex constitutive models: Least squares minimization vs. Bayesian updating. In Reliability and Optimization of Structural Systems; Straub, D., Ed.; CRC Press: Boca Raton, FL, USA, 2010; pp. 119–130. [Google Scholar]
- Sarkar, S.; Kosson, D.S.; Mahadevan, S.; Meeussen, J.C.L.; Sloot, H.v.; Arnold, J.R.; Brown, K.G. Bayesian calibration of thermodynamic parameters for geochemical speciation modeling of cementitious materials. J. Cement Concr. Res. 2012, 42, 889–902. [Google Scholar] [CrossRef]
- Zhang, E.; Chazot, J.D.; Antoni, J.; Hamdi, M. Bayesian characterization of Young’s modulus of viscoelastic materials in laminated structures. J. Sound Vibr. 2013, 332, 3654–3666. [Google Scholar] [CrossRef]
- Mehrez, L.; Kassem, E.; Masad, E.; Little, D. Stochastic identification of linear-viscoelastic models of aged and unaged asphalt mixtures. J. Mater. Civ. Eng. 2015, 27, 04014149. [Google Scholar] [CrossRef]
- Miles, P.; Hays, M.; Smith, R.; Oates, W. Bayesian uncertainty analysis of finite deformation viscoelasticity. J. Mech. Mater. 2015, 91, 35–49. [Google Scholar] [CrossRef]
- Zhao, X.; Pelegri, A.A. A Bayesian approach for characterization of soft tissue viscoelasticity in acoustic radiation force imaging. Int. J. Num. Methods Biomed. Eng. 2016, 32, E02741. [Google Scholar] [CrossRef] [PubMed]
- Kenz, Z.R.; Banks, H.T.; Smith, R.C. Comparison of frequentist and Bayesian confidence analysis methods on a viscoelastic stenosis model. SIAM/ASA J. Uncertain. Quant. 2013, 1, 348–369. [Google Scholar] [CrossRef][Green Version]
- An, D.; Choi, J.; Kim, N.H.; Pattabhiraman, S. Fatigue life prediction based on Bayesian approach to incorporate field data into probability model. J. Struct. Eng. Mech. 2011, 37, 427–442. [Google Scholar] [CrossRef]
- Hoshi, T.; Kobayashi, Y.; Kawamura, K.; Fujie, M.G. Developing an intraoperative methodology using the finite element method and the extended Kalman filter to identify the material parameters of an organ model. In Proceedings of the 29th Annual International Conference of the IEEE EMBS Cité Internationale, Lyon, France, 23–26 August 2007. [Google Scholar]
- Furukawa, T.; Pan, J.W. Stochastic identification of elastic constants for anisotropic materials. Int. J. Num. Methods Eng. 2010, 81, 429–452. [Google Scholar] [CrossRef]
- Conte, J.P.; Astroza, R.; Ebrahimian, H. Bayesian methods for nonlinear system identification of civil structures. MATEC Web Conf. 2015, 24, 03002. [Google Scholar] [CrossRef]
- Hendriks, M.A.N. Identification of the Mechanical Behavior of Solid Materials. Ph.D. Thesis, Department of Mechanical Engineering, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 1991. [Google Scholar]
- Bolzon, G.; Fedele, R.; Maier, G. Parameter identification of a cohesive crack model by Kalman filter. J. Comput. Methods Appl. Mech. Eng. 2002, 191, 2847–2871. [Google Scholar] [CrossRef]
- Astroza, R.; Nguyen, L.T.; Nestorović, T. Finite element model updating using simulated annealing hybridized with unscented Kalman filter. J. Comput. Struct. 2016, 177, 176–191. [Google Scholar] [CrossRef]
- Mahmoudi, E.; König, M.; Schanz, T. Probabilistic analysis of a gas storage cavity mined in a spatially random rock salt medium. In Proceedings of the Coupled Problems 2017, Rhodes, Greece, 12–14 June 2017. [Google Scholar]
- Mahmoudi, E.; Khaledi, K.; König, D.; Schanz, T. Probabilistic analysis of a rock salt cavern with application to energy storage systems, using subset simulation methodology. In Energy Geotechnics; Wuttke, F., Bauer, S., Sanchez, M., Eds.; CRC Press: Boca Rotan, FL, USA, 2016; pp. 609–615. [Google Scholar]
- Wall, O.; Holst, J. Estimation of parameters in viscoplastic and creep material models. SIAM J. Appl. Math. 2001, 61, 2080–2103. [Google Scholar] [CrossRef]
- Nakamura, T.; Gu, Y. Identification of elastic-plastic anisotropic parameters using instrumented indentation and inverse analysis. J. Mech. Mater. 2007, 39, 340–356. [Google Scholar] [CrossRef]
- Agmell, M.; Ahadi, A.; Stahl, J. Identification of plasticity constants from orthogonal cutting and inverse analysis. J. Mech. Mater. 2014, 77, 43–51. [Google Scholar] [CrossRef]
- Sevieri, G.; Andreini, M.; Falco, A.D.; Matthies, H.G. Concrete gravity dams model parameters updating using static measurements. Eng. Struct. 2019, 196. [Google Scholar] [CrossRef]
- Sevieri, G.; Falco, A.D. Dynamic structural health monitoring for concrete gravity dams based on the Bayesian inference. J. Civil Struct. Health Monit. 2020, 10, 235–250. [Google Scholar] [CrossRef]
- Sevieri, G.; Falco, A.D.; Marmo, G. Shedding Light on the Effect of Uncertainties in the Seismic Fragility Analysis of Existing Concrete Dams. Infrastructures 2020, 5, 22. [Google Scholar] [CrossRef]
- Marsili, F.; Croce, P.; Friedman, N.; Formichi, P.; Landi, F. Seismic reliability assessment of a concrete water tank based on the Bayesian updating of the finite element model. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2017, 3, 021004. [Google Scholar] [CrossRef]
- Marsili, F.; Croce, P.; Friedman, N.; Formichi, P.; Landi, F. On Bayesian identification methods for the analysis of existing structures. In Proceedings of the IABSE Congress Stockholm, Challenges in Design and Construction of an Innovative and Sustainable Built Environment, Stockholm, Sweden, 21–23 September 2016; pp. 116–123. [Google Scholar]
- Croce, P.; Landi, F.; Formichi, P. Probabilistic Seismic Assessment of Existing Masonry Buildings. Buildings 2019, 9, 237. [Google Scholar] [CrossRef]
- Croce, P.; Formichi, P.; Landi, F. A Bayesian hierarchical model for climatic loads under climate change. Eccomas Proc. UNCECOMP 2019, 298–308. [Google Scholar] [CrossRef]
- Croce, P.; Marsili, F.; Klawonn, F.; Formichi, P.; Landi, F. Evaluation of statistical parameters of concrete strength from secondary experimental test data. Constr. Build. Mater. 2018, 163, 343–359. [Google Scholar] [CrossRef]
- Bocciarelli, M.; Bolzon, G.; Maier, G. A constitutive model of metal-ceramic functionally graded material behavior: Formulation and parameter identification. J. Comput. Mater. Sci. 2008, 43, 16–26. [Google Scholar] [CrossRef]
- Gu, Y.; Nakamura, T.; Prchlik, L.; Sampath, S.; Wallace, J. Micro-indentation and inverse analysis to characterize elastic-plastic graded materials. J. Mater. Sci. Eng. A 2003, 345, 223–233. [Google Scholar] [CrossRef]
- Corigliano, A.; Mariani, S. Parameter identification of a time-dependent elastic-damage interface model for the simulation of debonding in composites. J. Compos. Sci. Technol. 2001, 61, 191–203. [Google Scholar] [CrossRef]
- Corigliano, A.; Mariani, S. Simulation of damage in composites by means of interface models: Parameter identification. J. Compos. Sci. Technol. 2001, 61, 2299–2315. [Google Scholar] [CrossRef]
- Ebrahimian, H.; Astroza, R.; Conte, J.P.; de Callafon, R.A. Nonlinear finite element model updating for damage identification of civil structures using batch Bayesian estimation. J. Mech. Syst. Signal Process. 2017, 84, 194–222. [Google Scholar] [CrossRef]
- Ebrahimian, H.; Astroza, R.; Conte, J.P. Parametric Identification of Hysteretic Material Constitutive Laws in Nonlinear Finite Element Models using Extended Kalman Filter; Department of Structural Engineering, University of California: San Diego, CA, USA, 2014. [Google Scholar]
- Ebrahimian, H.; Astroza, R.; Conte, J.P. Extended Kalman filter for material parameter estimation in nonlinear structural finite element models using direct differentiation method. Earthq. Eng. Struct. Dyn. 2015, 44, 1495–1522. [Google Scholar] [CrossRef]
- Astroza, R.; Ebrahimian, H.; Conte, J.P. Material parameter identification in distributed plasticity FE models of frame-type structures using nonlinear stochastic filtering. J. Eng. Mech. 2015, 141, 04014149. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Heshmati, M.; Boodagh, P.; Salamon, J.W. Probabilistic Identification of Seismic Response Mechanism in a Class of Similar Arch Dams. Infrastructures 2019, 4, 44. [Google Scholar] [CrossRef]
- Saouma, V.E.; Hariri-Ardebili, M.A. Probabilistic Cracking, Aging and Shaking of Concrete Dams. In Proceedings of the 5th International Symposiumon Dam Safety, Istanbul, Turkey, 27–31 October 2018; pp. 44–56. [Google Scholar]
- Yan, A.; de Boe, P.; Golinval, J. Structural damage diagnosis by Kalman model based on stochastic subspace identification. Int. J. Struct. Health Monit. 2004, 3, 103–119. [Google Scholar] [CrossRef]
- Ghannadi, P.; Kourehli, S.S. Model updating and damage detection in multi-story shear frames using salp swarm algorithm. Earthq. Struct. 2019, 17, 63–73. [Google Scholar]
- Ghannadi, P.; Kourehli, S.S.; Noori, M.; Altabey, W.A. Efficiency of grey wolf optimization algorithm for damage detection of skeletal structures via expanded mode shapes. Adv. Struct. Eng. 2020. [Google Scholar] [CrossRef]
- Gharehbaghi, V.; Nguyen, A.; Farsangi, E.N.; Yang, T.Y. Supervised damage and deterioration detection in building structures using an enhanced autoregressive time-series approach. J. Build. Eng. 2020. [Google Scholar] [CrossRef]
- Ching, J.; Chen, Y.C. Transitional Markov Chain Monte Carlo method for Bayesian model updating, model class selection and model averaging. J. Eng. Mech. 2007, 133, 816–832. [Google Scholar] [CrossRef]
- Ching, J.; Wang, J. Application of the Transitional Markov Chain Monte Carlo algorithm to probabilistic site characterization. J. Eng. Geol. 2016, 203, 151–167. [Google Scholar] [CrossRef]
- Matthies, H.G.; Zander, E.; Rosić, B.V.; Litvinenko, A.; Pajonk, O. Inverse problems in a Bayesian setting. J. Comput. Methods Solids Fluids 2016, 245–286. [Google Scholar]
- Matthies, H.G.; Zander, E.; Rosić, B.V.; Litvinenko, A. Parameter estimation via conditional expectation: A Bayesian inversion. Adv. Model. Simulat. Eng. Sci. 2016, 3, 24. [Google Scholar] [CrossRef]
- Matthies, H.G.; Litvinenko, A.; Rosić, B.V.; Zander, E. Bayesian parameter estimation via filtering and functional approximations. Tech. Gazette 2016, 23, 1–8. [Google Scholar]
- Pajonk, O.; Rosić, B.V.; Litvinenko, A.; Matthies, H.G. A deterministic filter for non-Gaussian Bayesian estimation—Applications to dynamical system estimation with noisy measurements. Phys. D Nonlinear Phenomena 2012, 241, 775–788. [Google Scholar] [CrossRef]
- Simo, J.C.; Hughes, T.J.R. Computational Inelasticity, 7th ed.; Springer: New York, NY, USA, 1998. [Google Scholar]
- Kowalsky, U.; Meyer, J.; Heinrich, S.; Dinkler, D. A nonlocal damage model for mild steel under inelastic cyclic straining. Comput. Mater. Sci. 2012, 63, 28–34. [Google Scholar] [CrossRef]
- Pirondi, A.; Bonora, N. Modeling ductile damage under fully reversed cycling. Comput. Mater. Sci. 2003, 26, 129–141. [Google Scholar] [CrossRef]
- Hughes, T.; Hulbert, G. Space-time finite element methods for elastodynamics: Formulations and error estimates. Comput. Methods Appl. Mech. Eng. 1988, 66, 339–363. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 6th ed.; Elsevier Butterworth-Heinemann: Oxford, UK, 2005; ISBN 978-1-85617-633-0. [Google Scholar]
- Wang, J.; Katafygiotis, L.S.; Noori, M.N. Transitional Markov Chain Monte Carlo simulation for reliability-based optimization. In Safety, Reliability, Risk and Life-Cycle Performance of Structures & Infrastructures; Deodatis, G., Ellingwood, B.R., Frangopol, D.M., Eds.; CRC Press: Boca Raton, FL, USA, 2014; pp. 1593–1599. [Google Scholar]
- McGrayne, S.B. The Theory That Would Not Die; Yale University Press: New Haven, CT, USA, 2011. [Google Scholar]
- Luenberger, D.G. Optimization by Vector Space Methods; Wiley: Chichester, UK, 1969. [Google Scholar]
- Grewal, M.S.; Andrews, A.P. Kalman Filtering: Theory and Practice Using MATLAB; Wiley: Chichester, UK, 2008. [Google Scholar]
- Evensen, G. Data Assimilation—The Ensemble Kalman Filter; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Pajonk, O. Stochastic Spectral Methods for Linear Bayesian Inference. Ph.D. Thesis, Institut für Wissenschaftliches Rechnen, Technische Universität Braunschweig, Braunschweig, Germany, 2012. [Google Scholar]
- Matthies, H.G. Stochastic finite elements: Computational Approaches to Stochastic Partial Differential Equations. J. Appl. Math. Mech. 2008, 88, 849–873. [Google Scholar] [CrossRef]
- Xiu, D. Numerical Methods for Stochastic Computations: A Spectral Method Approach; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Wiener, N. The homogeneous chaos. Am. J. Math. 1938, 60, 897–936. [Google Scholar] [CrossRef]
- Ghanem, R.; Spanos, P.D. Stochastic Finite Eements—A Spectral Approach; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Adeli, E.; Rosić, B.V.; Matthies, H.G.; Reinstädler, S. Bayesian parameter identification in plasticity. In Proceedings of the XIV International Conference on Computational Plasticity, Fundamentals and Applications COMPLAS XIV, Barcelona, Spain, 5–7 September 2017. [Google Scholar]
- Adeli, E.; Rosić, B.V.; Matthies, H.G.; Reinstädler, S. Effect of Load Path on Parameter Identification for Plasticity Models using Bayesian Methods. In Lecture Notes in Computational Science and Engineering; Nature Springer, 2018; Available online: http://arxiv.org/abs/1906.07246 (accessed on 17 June 2019).
- Adeli, E.; Matthies, H.G. Parameter Identification in Viscoplasticity using Transitional Markov Chain Monte Carlo Method. Available online: http://arxiv.org/abs/1906.10647 (accessed on 21 June 2019).
- Felippa, C. Introduction to FEM, FEM Modeling: Mesh, Loads and BCs; University of Colorado: Boulder, CO, USA, 2016. [Google Scholar]
- Adeli, E. Viscoplastic-Damage Model Parameter Identification via Bayesian Methods. Ph.D. Dissertation, Institut für Wissenschaftliches Rechnen, Technische Universität Braunschweig, Braunschweig, Germany, 2019. [Google Scholar] [CrossRef]
- Adeli, E.; Rosić, B.V.; Matthies, H.G.; Reinstädler, S.; Dinkler, D. Bayesian Parameter Determination of a CT-Test Described by a Viscoplastic-Damage Model Considering the Model Error. 2019. Available online: https://www.researchgate.net/publication/334537857_Bayesian_Parameter_Determination_of_a_CT-Test_described_by_a_Viscoplastic-Damage_Model_considering_the_Model_Error (accessed on 21 June 2019).
- Bonet, J.; Wood, R.D. Nonlinear Continuum Mechanics for Finite Element Analysis; Cambridge University Press: Cambridge, UK, 1997; ISBN 9780521572729. [Google Scholar]
- Chaboche, J.L.; Rousselier, G. On the plastic and viscoplastic constitutive equations—Part 1: Rules developed with internal variable concept. J. Press. Vessel Technol. 1983, 105, 153–158. [Google Scholar] [CrossRef]
- Chaboche, J.L.; Rousselier, G. On the plastic and viscoplastic constitutive equations—Part 2: Application of internal variable concepts to the 316 stainless steel. J. Press. Vessel Technol. 1983, 105, 159–164. [Google Scholar] [CrossRef]
- Bobrowski, A. Functional Analysis for Probability and Stochastic Processes; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Pritchard, C. The Changing Shape of Geomtetry; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Rao, M. Conditional Measures and Applications; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Rao, M.; Swift, R.J. Probability Theory with Applications. Mathematics and Its Applications, Band 582; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; SIAM: Philadelphia, PA, USA, 2004. [Google Scholar]
- Jaynes, E.T. Probability Theory, the Logic of Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Aster, R.C.; Borchers, B.; Thurber, C.H. Parameter Estimation and Inverse Problems, 2nd ed.; Academic Press: Cambridge, MA, USA, 2012; ISBN 978-0-12-804651-7. [Google Scholar]
- Dashti, M.; Stuart, A.M. The Bayesian Approach to Inverse Problems. In Handbook of Uncertainty Quantification; Springer Nature: Cham, Switzerland, 2015; pp. 1–118. [Google Scholar]
- Bosq, D. Linear processes in function spaces, theory and applications. In Lecture Notes in Statistics 149; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]




| Elastic strains |
| with |
| Viscoplastic strains |
| Isotropic and kinematic hardening |
| Local damage |
| Initial conditions |
| , , , and |
| Parameters and their units |
| G, , (elastic strains) |
| , k, n, (viscoplastic strains) |
| , , , , (hardening) |
| , , , , (local damage) |
| G | n | k | ||||||
|---|---|---|---|---|---|---|---|---|
| 1.66 × 109 | 7.69 × 108 | 1.7 × 108 | 1 | 1.5 × 108 | 50 | 2.75 × 108 | 50 | 2.75 × 108 |
| Param. | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1.66 × 109 | 1.71 × 109 | 1.33 × 107 | 1.66 × 109 | 2.28 × 107 | 1.66 × 109 | 1.13 × 107 | ||
| G | 7.69 × 108 | 7.66 × 108 | 2.24 × 106 | 7.68 × 108 | 9.09 × 106 | 7.68 × 108 | 3.47 × 106 | |
| 50 | 53.00 | 1.83 | 54.78 | 5.16 | 52.36 | 3.71 | ||
| 50 | 49.30 | 1.32 | 54.58 | 5.15 | 52.04 | 3.01 | ||
| 1.7 × 108 | 1.67 × 108 | 1.37 × 106 | 1.67 × 108 | 3.48 × 106 | 1.69 × 108 | 1.35 × 106 |
| G | n | k | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.66 × 105 | 7.69 × 104 | 266 | 1 | 23,500 | 298.6 | 117.2 | 100 | 150 | 7 | 8 | −80 |
| Param. | |||||
|---|---|---|---|---|---|
| 1.66 × 105 | 1.66 × 105 | 2.03 × 103 | 1.66 × 105 | 937.87 | |
| G | 7.69 × 104 | 7.70 × 104 | 710.34 | 7.70 × 104 | 430.05 |
| 266 | 264.75 | 1.81 | 265.1 | 1.07 | |
| 298.6 | 304.75 | 29.02 | 300.35 | 7.06 | |
| 100 | 103.12 | 11.18 | 102.98 | 2.77 | |
| 7 | 7.07 | 0.82 | 6.84 | 0.65 | |
| 8 | 7.82 | 0.70 | 8.13 | 0.57 | |
| −80 | −86.29 | 10.29 | −79.98 | 3.34 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adeli, E.; Rosić, B.; Matthies, H.G.; Reinstädler, S.; Dinkler, D. Comparison of Bayesian Methods on Parameter Identification for a Viscoplastic Model with Damage. Metals 2020, 10, 876. https://doi.org/10.3390/met10070876
Adeli E, Rosić B, Matthies HG, Reinstädler S, Dinkler D. Comparison of Bayesian Methods on Parameter Identification for a Viscoplastic Model with Damage. Metals. 2020; 10(7):876. https://doi.org/10.3390/met10070876
Chicago/Turabian StyleAdeli, Ehsan, Bojana Rosić, Hermann G. Matthies, Sven Reinstädler, and Dieter Dinkler. 2020. "Comparison of Bayesian Methods on Parameter Identification for a Viscoplastic Model with Damage" Metals 10, no. 7: 876. https://doi.org/10.3390/met10070876
APA StyleAdeli, E., Rosić, B., Matthies, H. G., Reinstädler, S., & Dinkler, D. (2020). Comparison of Bayesian Methods on Parameter Identification for a Viscoplastic Model with Damage. Metals, 10(7), 876. https://doi.org/10.3390/met10070876




