Interaction of Process Parameters, Forming Mechanisms, and Residual Stresses in Single Point Incremental Forming
Abstract
1. Introduction
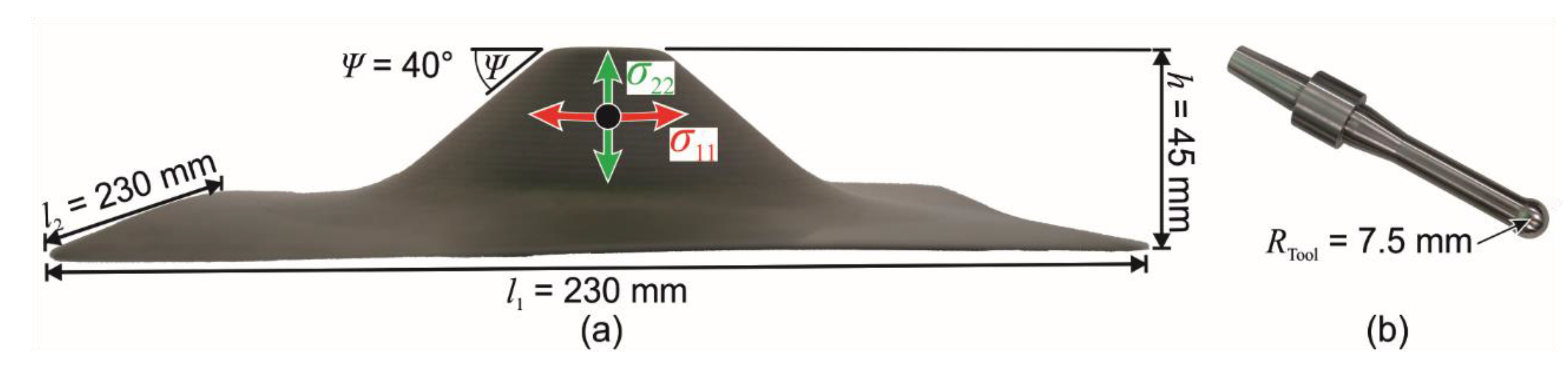
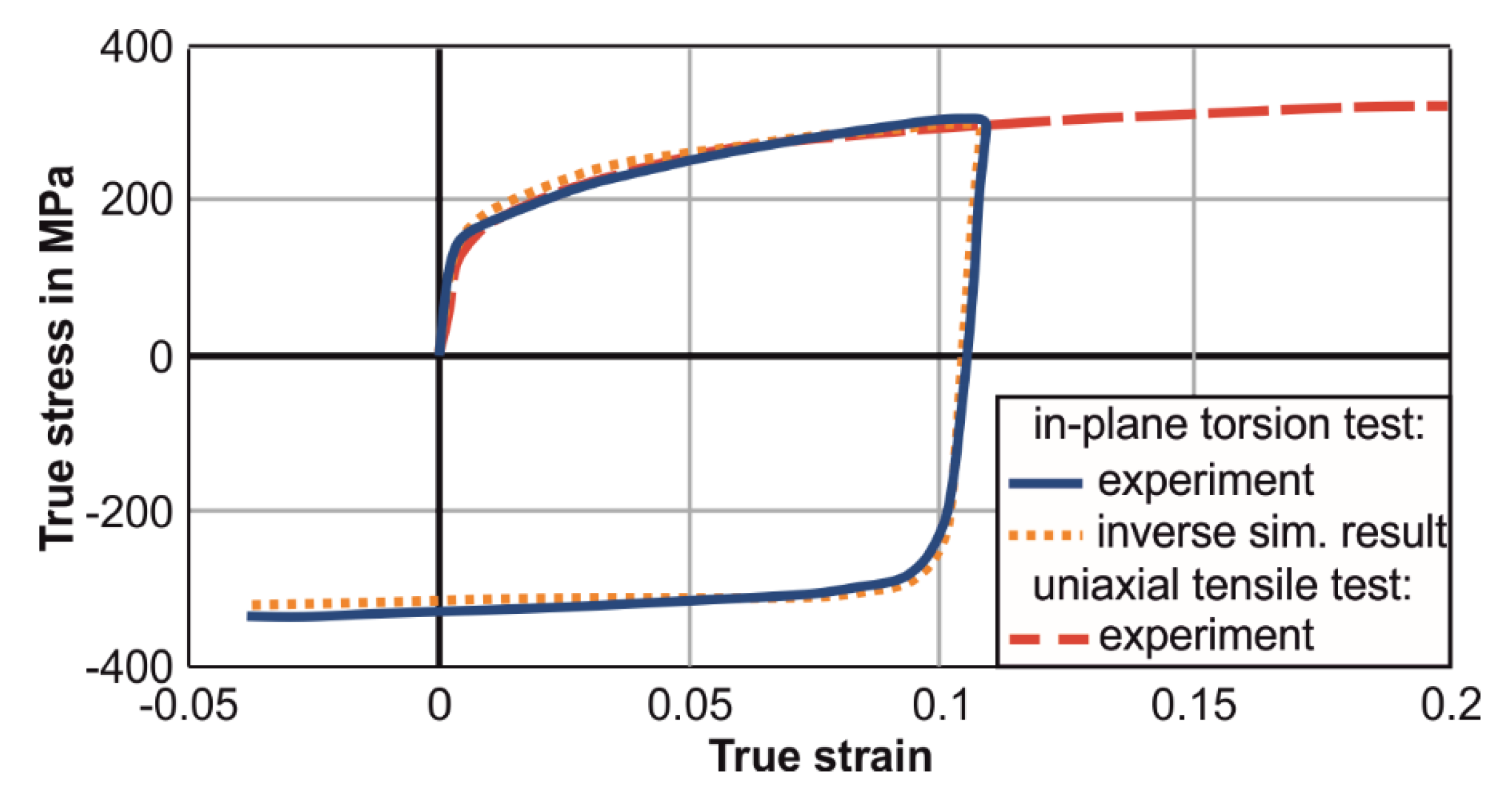
2. Materials and Methods
3. Results
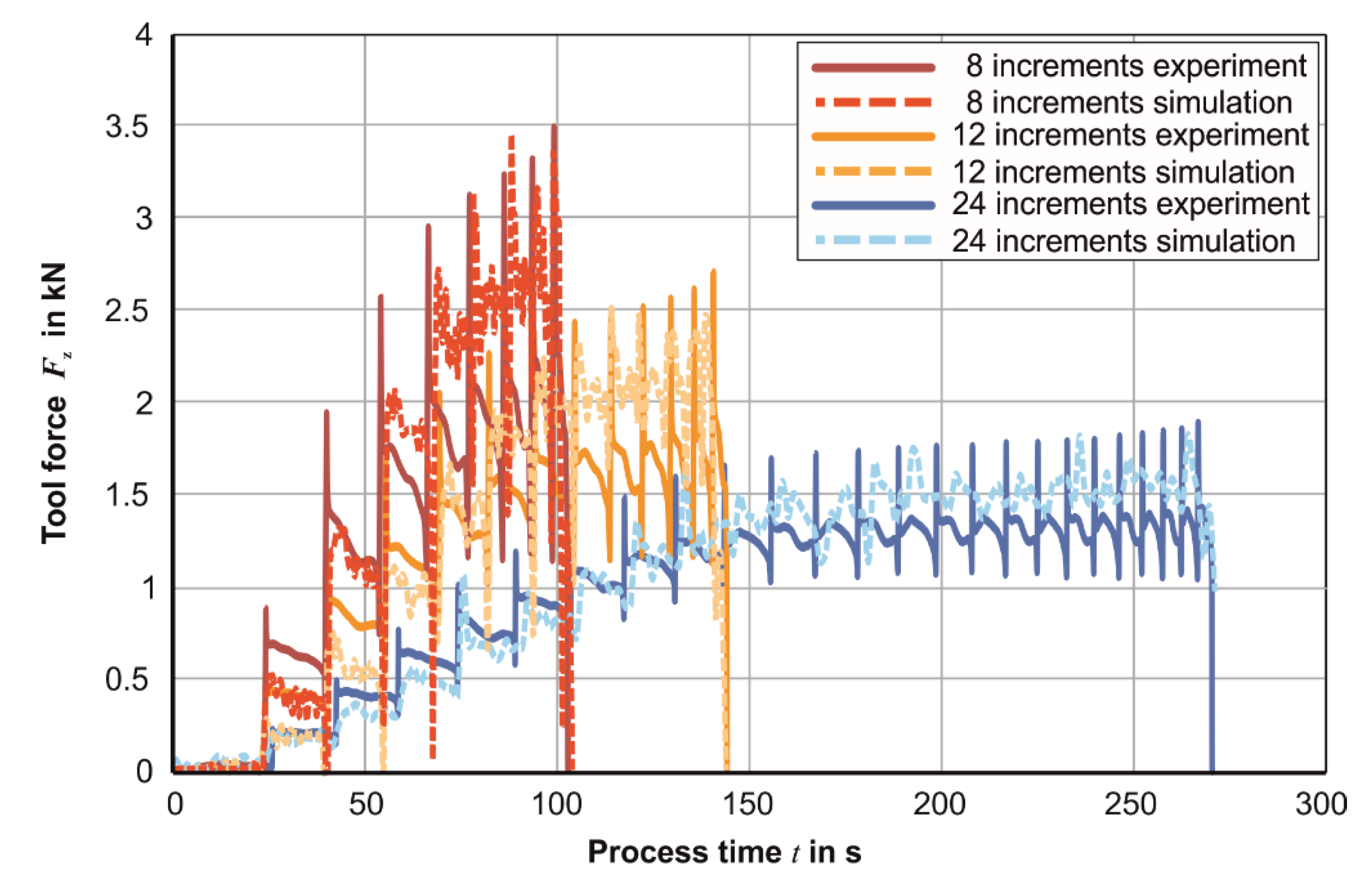
3.1. Process Force
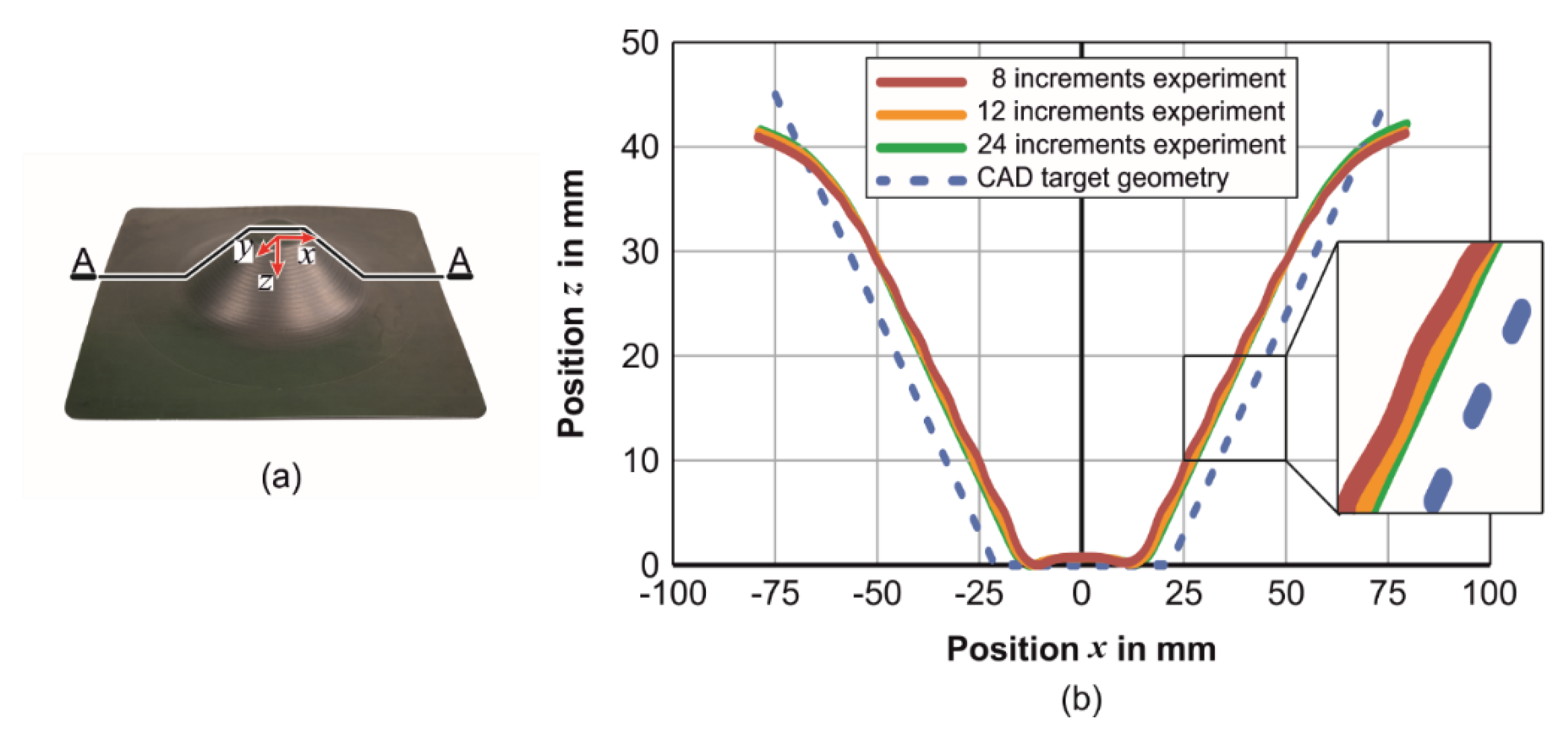
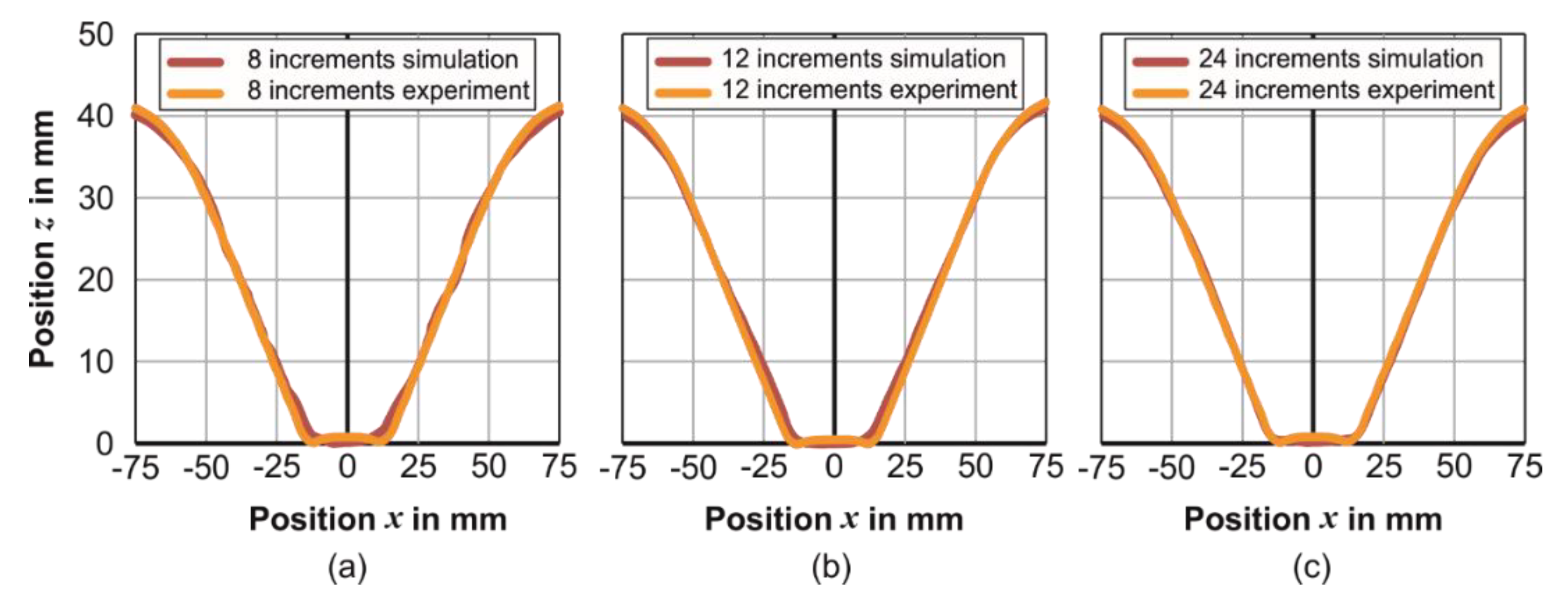
3.2. Geometry
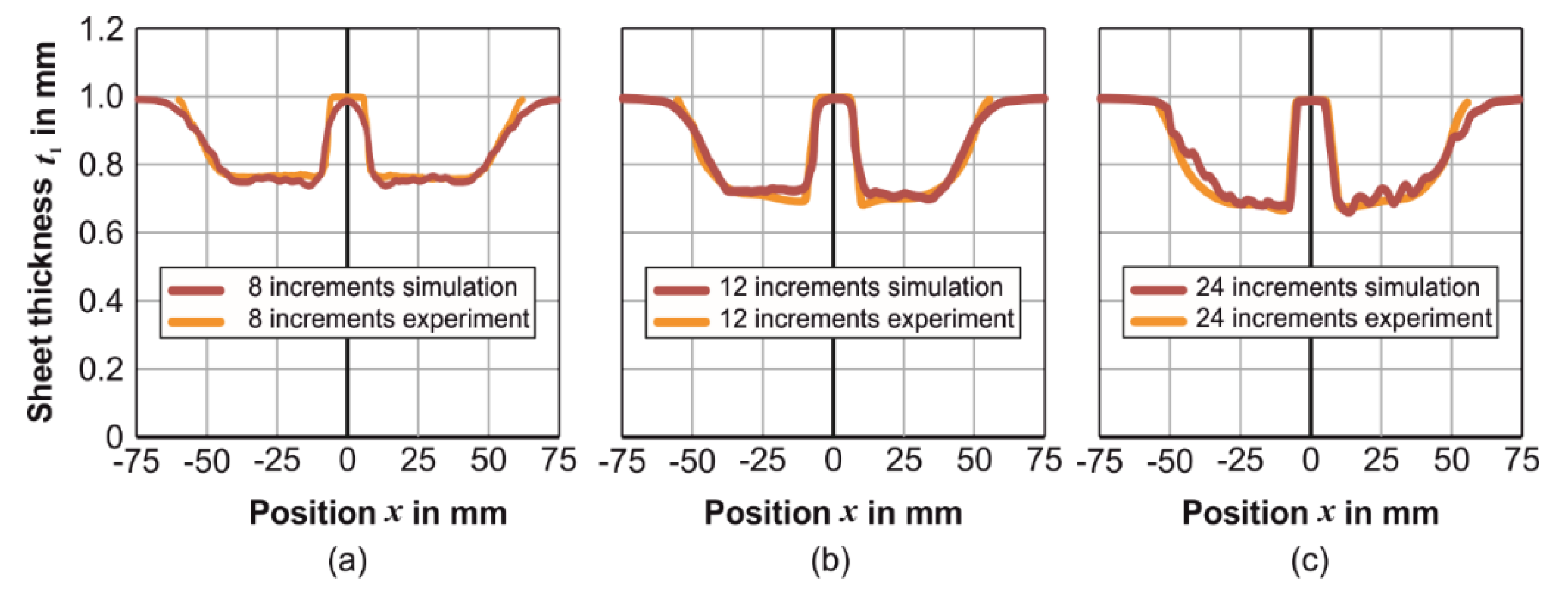
3.3. Sheet Thickness
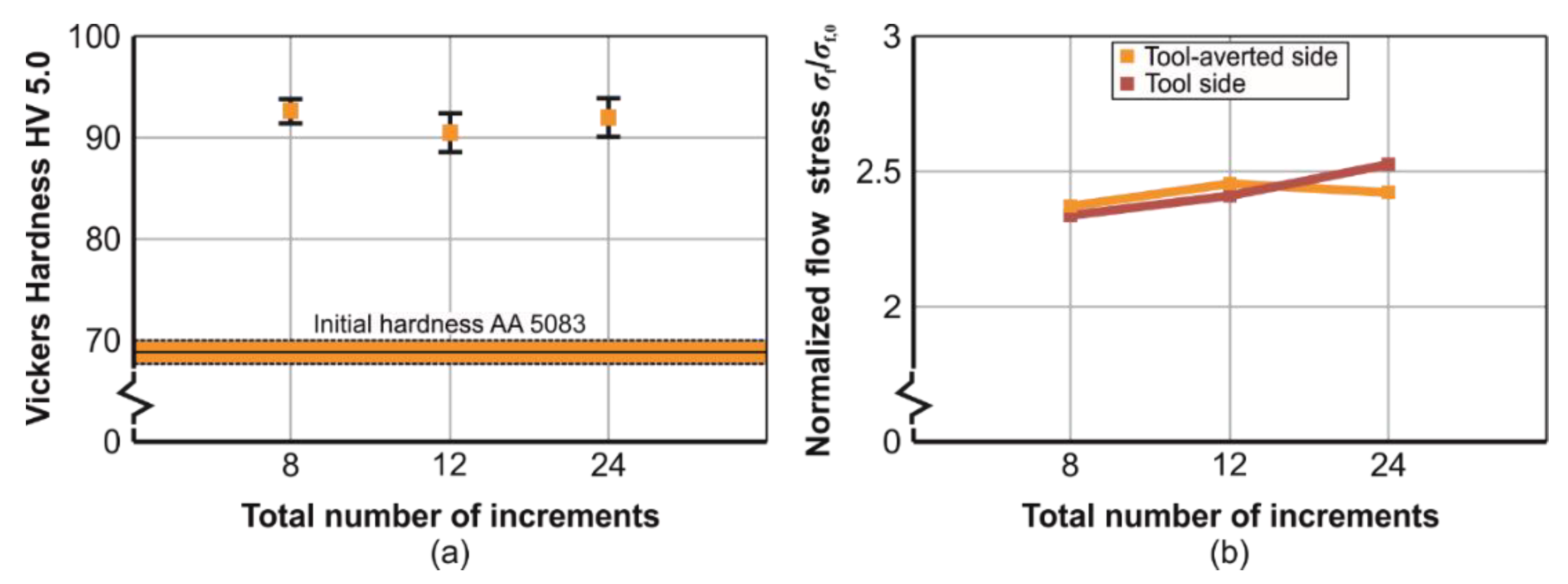
3.4. Hardness
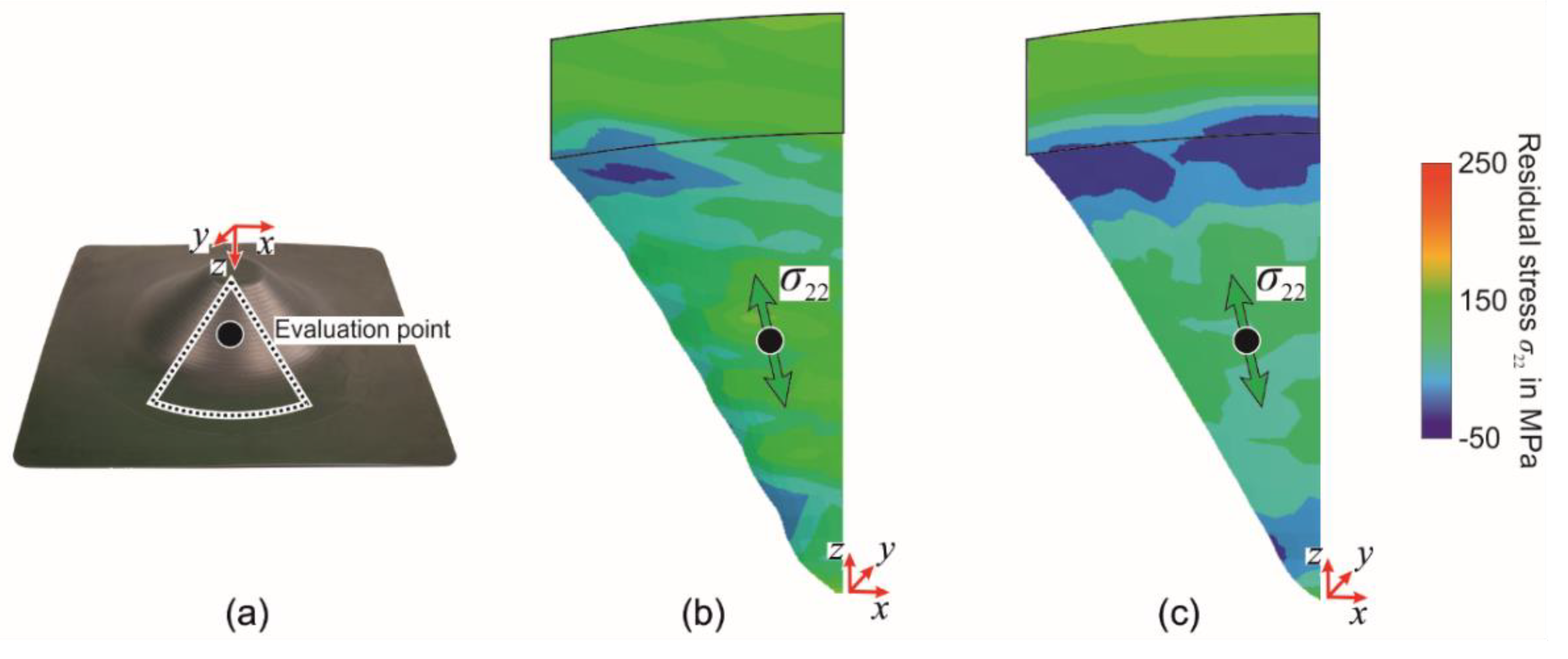
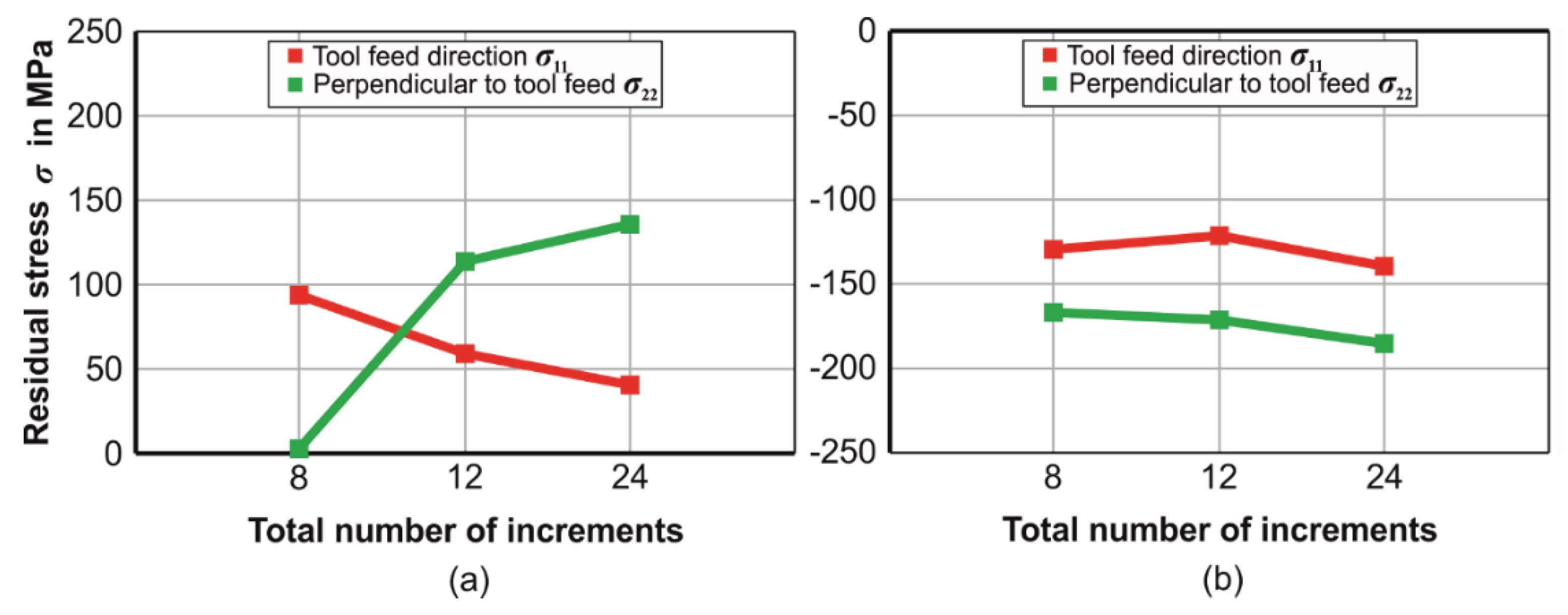
3.5. Residual Stresses
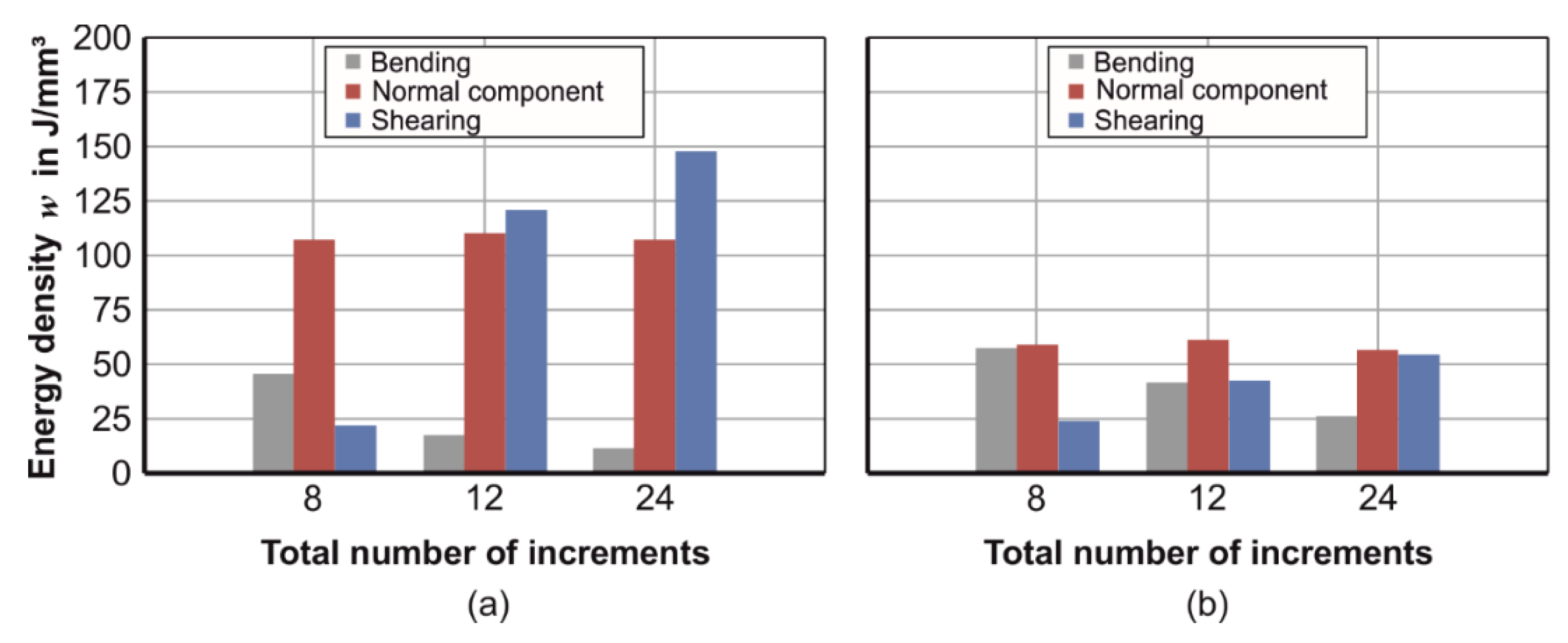
3.6. Forming Mechanisms
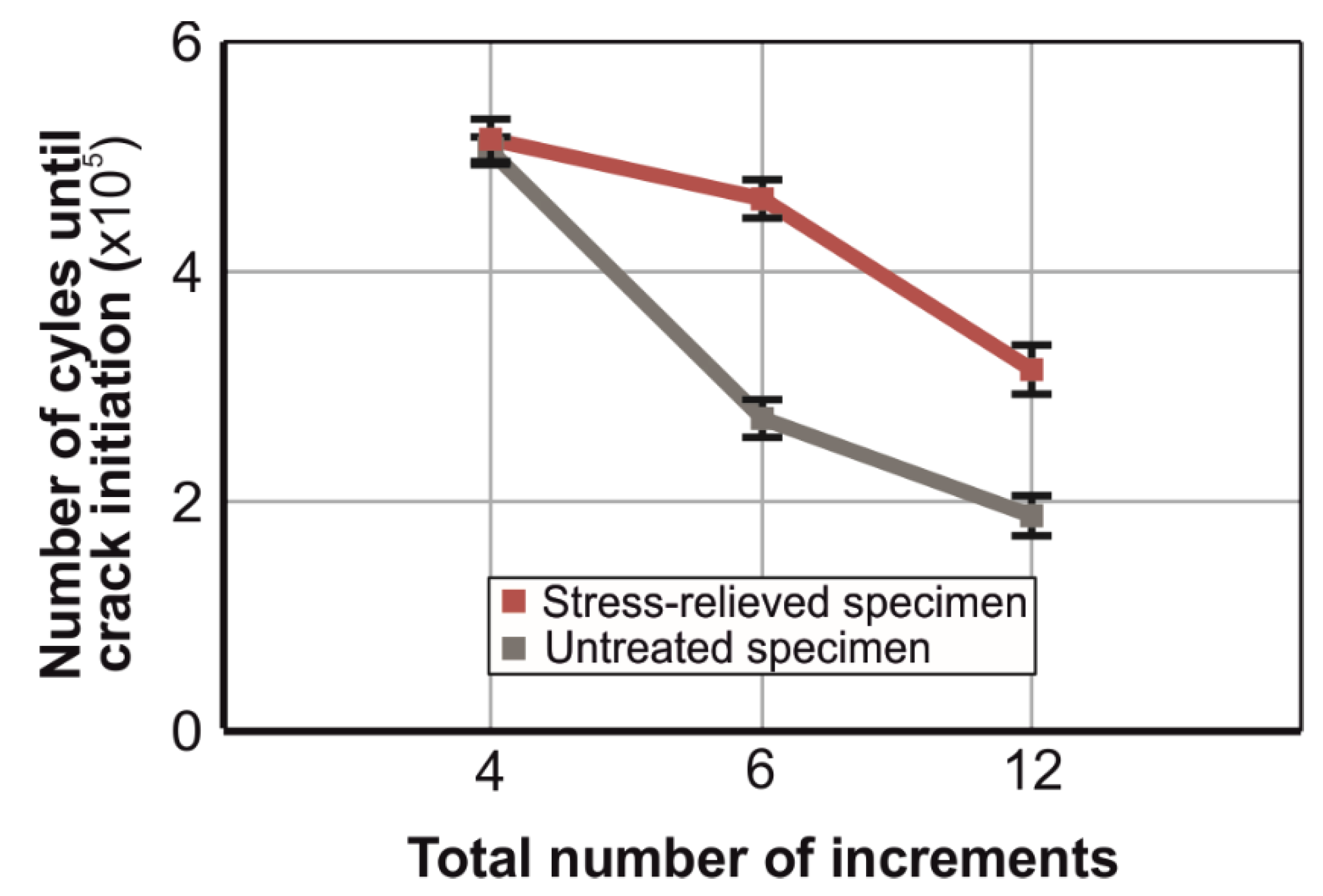
4. Discussion
5. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Emmens, W.; van den Boogaard, A. An overview of stabilizing deformation mechanisms in incremental sheet forming. J. Mater. Process. Technol. 2009, 209, 3688–3695. [Google Scholar] [CrossRef]
- Silva, M.B.; Skjødt, M.; Atkins, A.; Bay, N.; Martins, P.A.F. Single-point incremental forming and formability—Failure diagrams. J. Strain. Anal. Eng. 2008, 43, 15–35. [Google Scholar] [CrossRef]
- Sebastiani, G. Erweiterung der Prozessgrenzen inkrementeller Blechumformverfahren Mittels Flexibler Werkzeuge; Shaker Verlag: Aachen, Germany, 2016; pp. 85–102. [Google Scholar]
- Maqbool, F.; Bambach, M. Revealing the dominant forming mechanism of single point incremental forming (SPIF) by splitting plastic energy dissipation. Procedia Eng. 2017, 183, 188–193. [Google Scholar] [CrossRef]
- Klocke, F.; König, W. Fertigungsverfahren 4: Umformen, 5rd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Bambach, M.; Ames, J.; Azaouzi, J.; Campagne, M.; Hirt, G.; Batoz, J. Initial experimental and numerical investigations into a class of new strategies for single point incremental forming (SPIF). In Proceedings of the 8th Int. ESAFORM Conference on Material Forming, Cluj-Napoca, Romania, 27–29 April 2005; pp. 671–674. [Google Scholar]
- Hagan, E.; Jeswiet, J. A review of conventional and modern single-point sheet metal forming methods. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2003, 217, 213–225. [Google Scholar] [CrossRef]
- Kim, T.; Yang, D. Improvement of formability for the incremental sheet metal forming process. Int. J. Mech. Sci. 2000, 42, 1271–1286. [Google Scholar] [CrossRef]
- Tekkaya, A.E. Equivalent strain and stress history in torsion tests. Steel Res. Int. 1994, 65, 65–70. [Google Scholar] [CrossRef]
- Emmens, W.C. Formability—A Review of Parameters and Processes that Control, Limit or Enhance the Formability of Sheet Metal; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Eyckens, P.; Moreau, J.; Duflou, J.; Van Bael, A.; Van Houtte, P. MK modelling of sheet formability in the incremental sheet forming process, taking into account through-thickness shear. Int. J. Mater. Form. 2009, 2, 379. [Google Scholar] [CrossRef]
- Jackson, K.; Allwood, J. The mechanics of incremental sheet forming. J. Mater. Process. Technol. 2009, 209, 1158–1174. [Google Scholar] [CrossRef]
- Martins, P.A.F.; Bay, N.; Skjødt, M.; Silva, M. Theory of single point incremental forming. CIRP Ann. 2008, 57, 247–252. [Google Scholar] [CrossRef]
- Maaß, F.; Gies, S.; Dobecki, M.; Brömmelhoff, K.; Tekkaya, A.E.; Reimers, W. Analysis of residual stress state in sheet metal parts processed by single point incremental forming. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2018; Volume 1960, p. 160017. [Google Scholar]
- Lemaitre, J.; Chaboche, J.L. Mechanics of Solid Materials, 1st ed.; Cambridge University Press: Cambridge, UK, 1990; pp. 226–252. [Google Scholar]
- Ambrogio, G.; Costantino, I.; De Napoli, L.; Filice, L.; Fratini, L.; Muzzupappa, M. On the influence of some relevant process parameters on the dimensional accuracy in Incremental Forming: A numerical and experimental investigation. J. Mater Process. Technol. 2003, 153, 501–507. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Maneesh, K.; Venkata, N.; Cao, J. Formability and surface finish studies in single point incremental forming. J. Manuf. Sci. Eng. 2011, 133, 621–627. [Google Scholar] [CrossRef]
- Maaß, F.; Hahn, M.; Tekkaya, A.E.; Dobecki, M.; Poeche, A.; Brömmelhoff, K.; Reimers, W. Forming mechanisms-related residual stress development in single point incremental forming. Prod. Eng. 2019, 13, 149–156. [Google Scholar] [CrossRef]
- Svensson, N. Anisotropy and the Bauschinger effect in cold rolled aluminum. J. Mech. Eng. Sci. 1966, 8, 162–172. [Google Scholar] [CrossRef]
- Maaß, F.; Dobecki, M.; Hahn, M.; Reimers, W.; Tekkaya, A.E. Setting Component Properties in Incremental Forming. In Proceedings of the Contributed Papers from Materials Science and Technology, Portland, OR, USA, 29 September–3 October 2019; pp. 1176–1182. [Google Scholar] [CrossRef]


| Process Parameters | 8 Increments | 12 Increments | 24 Increments |
|---|---|---|---|
| Tool radius RTool | 7.5 mm | 7.5 mm | 7.5 mm |
| Step-down increment Δz | 5.625 mm | 3.75 mm | 1.875 mm |
| Relative tool step-down Δz/RTool | 0.75 | 0.5 | 0.25 |
| Tool feed vTool | 1500 mm/min | 1500 mm/min | 1500 mm/min |
| Tool rotation θTool | 300 RPM | 300 RPM | 300 RPM |
| Young’s Modulus E | Poisson’s Ratio υ | k | Q | b | C | γ |
|---|---|---|---|---|---|---|
| 73,000 MPa | 0.33 | 120 MPa | 83 MPa | 9.88 | 30,000 | 330 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maaß, F.; Hahn, M.; Tekkaya, A.E. Interaction of Process Parameters, Forming Mechanisms, and Residual Stresses in Single Point Incremental Forming. Metals 2020, 10, 656. https://doi.org/10.3390/met10050656
Maaß F, Hahn M, Tekkaya AE. Interaction of Process Parameters, Forming Mechanisms, and Residual Stresses in Single Point Incremental Forming. Metals. 2020; 10(5):656. https://doi.org/10.3390/met10050656
Chicago/Turabian StyleMaaß, Fabian, Marlon Hahn, and A. Erman Tekkaya. 2020. "Interaction of Process Parameters, Forming Mechanisms, and Residual Stresses in Single Point Incremental Forming" Metals 10, no. 5: 656. https://doi.org/10.3390/met10050656
APA StyleMaaß, F., Hahn, M., & Tekkaya, A. E. (2020). Interaction of Process Parameters, Forming Mechanisms, and Residual Stresses in Single Point Incremental Forming. Metals, 10(5), 656. https://doi.org/10.3390/met10050656





