Uncertainty Quantification in Small-Timescale Model-Based Fatigue Crack Growth Analysis Using a Stochastic Collocation Method
Abstract
1. Introduction
2. Stochastic Collocation Method for Uncertainty Quantification
2.1. Stochastic Systems and Interpolation Formulation
2.2. Full Tensor Product Collocation
2.3. Smolyak Sparse Grid Collocation
3. Uncertainty Quantification in FCG Analysis
3.1. Description of Small-Timescale FCG Model
3.2. Uncertainty Quantification in FCG
3.3. The Remaining Useful Life Prediction
4. Results and Discussion
4.1. FCG Analysis of A Metal Plate
4.2. The Stochastic Collocation Method for Remaining Useful Life Prediction
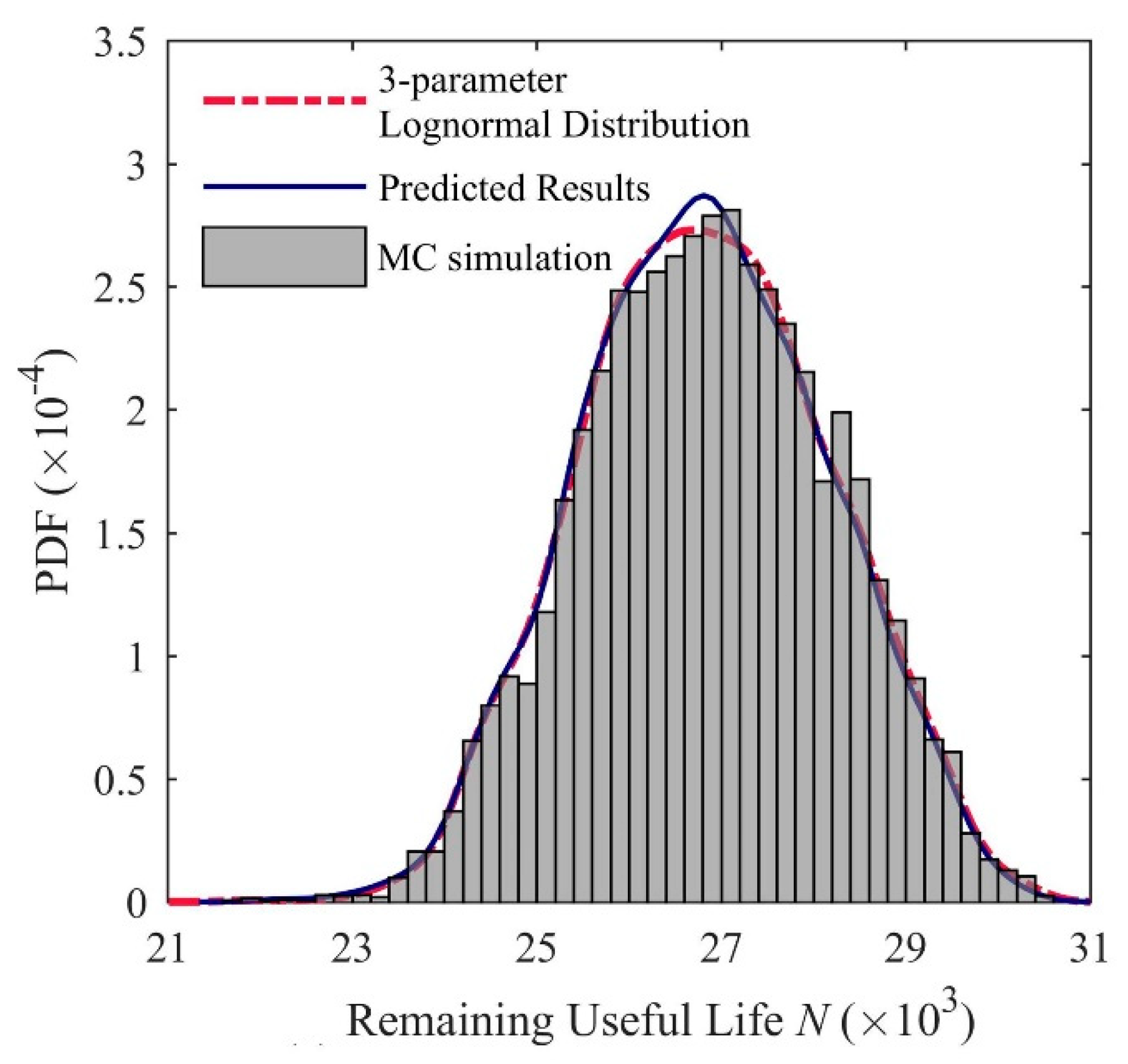
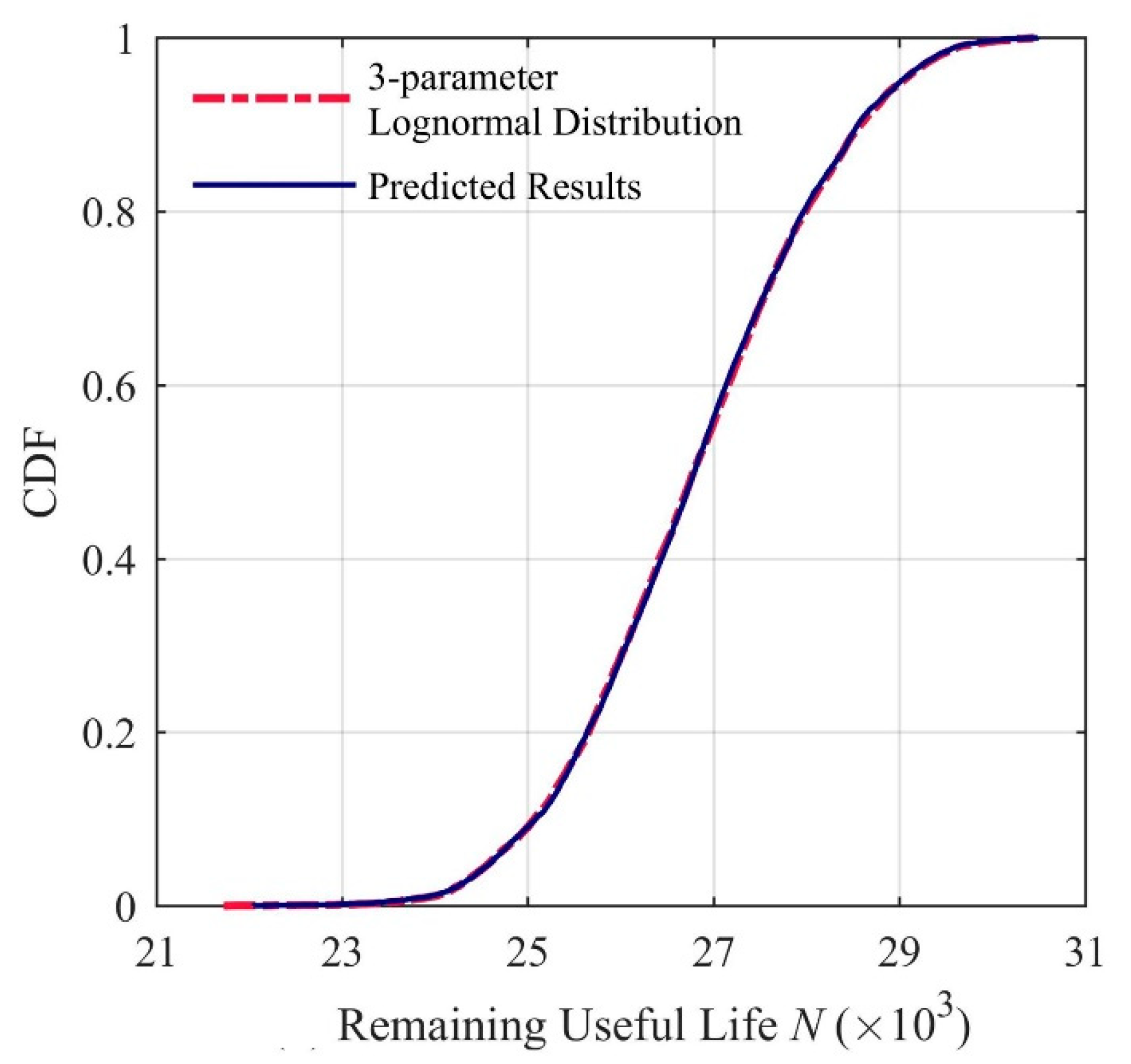
4.3. Results of Remaining Useful Life Prediction
5. Conclusions
- (1)
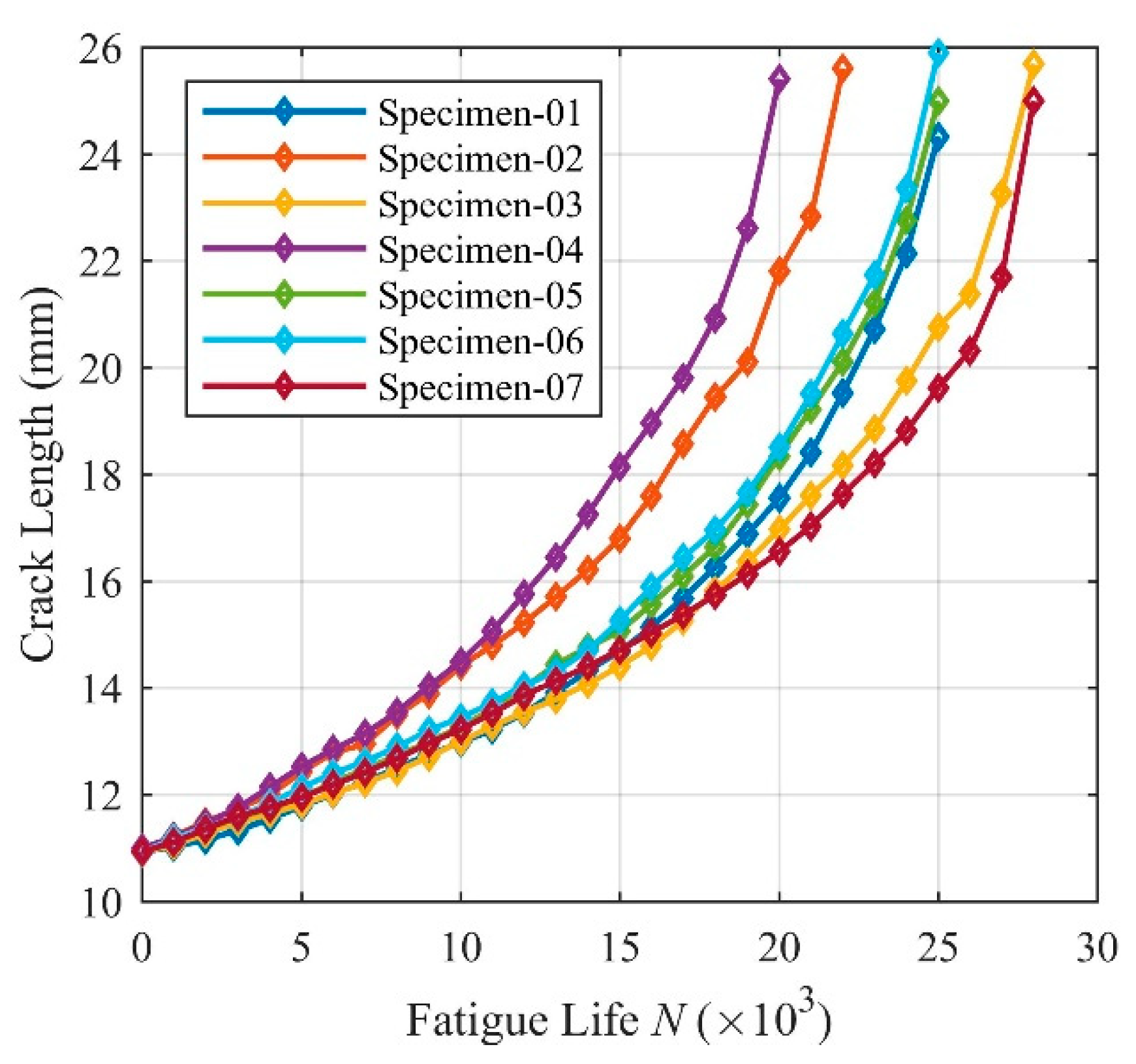
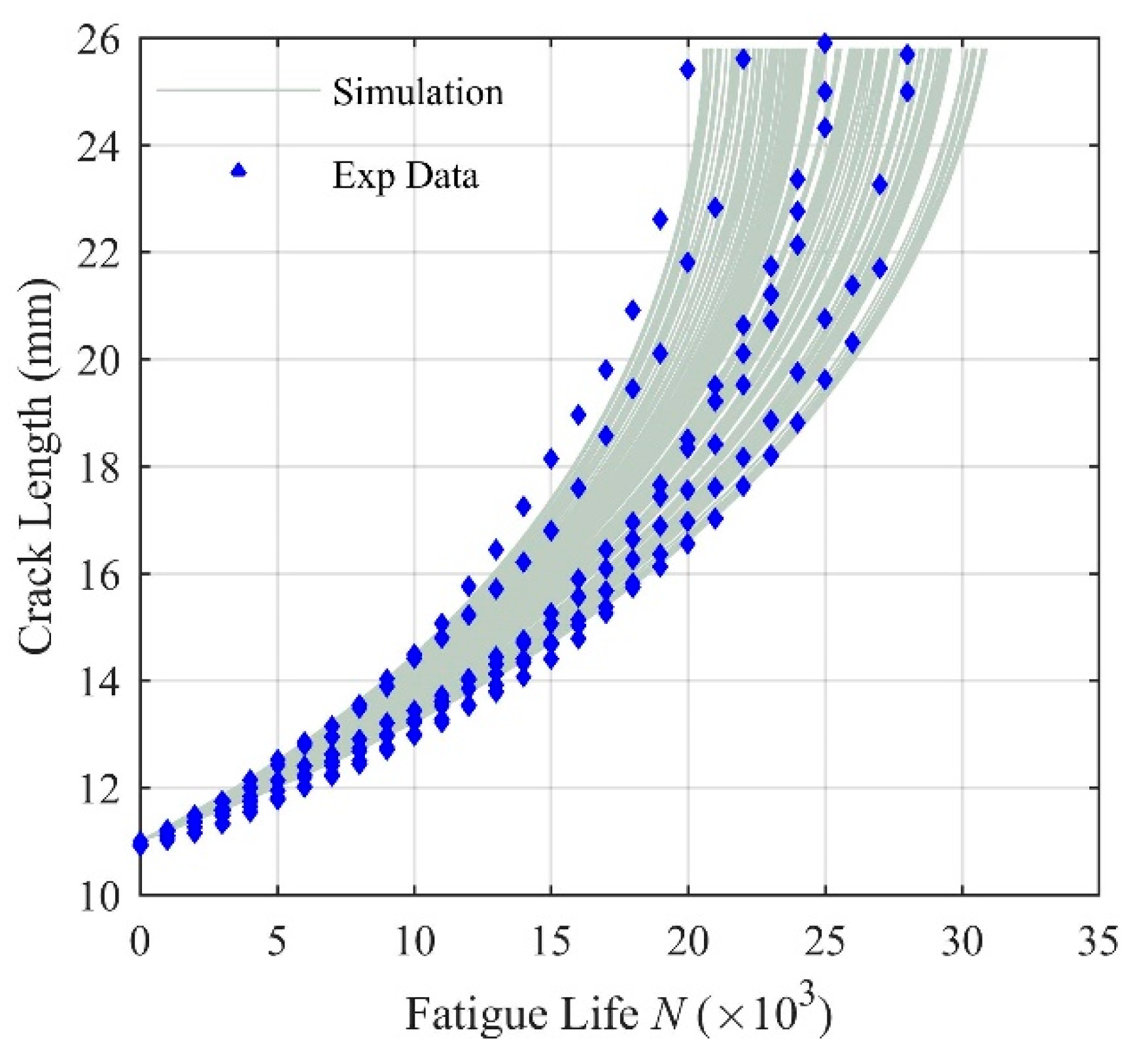
- The FCG curves predicted by the Monte Carlo simulation of the small-timescale model considering the uncertainty parameters agreed well with the experimental data under constant amplitude loading. It can be observed that parameter uncertainties do exist in FCG analysis. Besides, the small-timescale model shows a continuous relationship between the fatigue crack length and the loading history.
- (2)
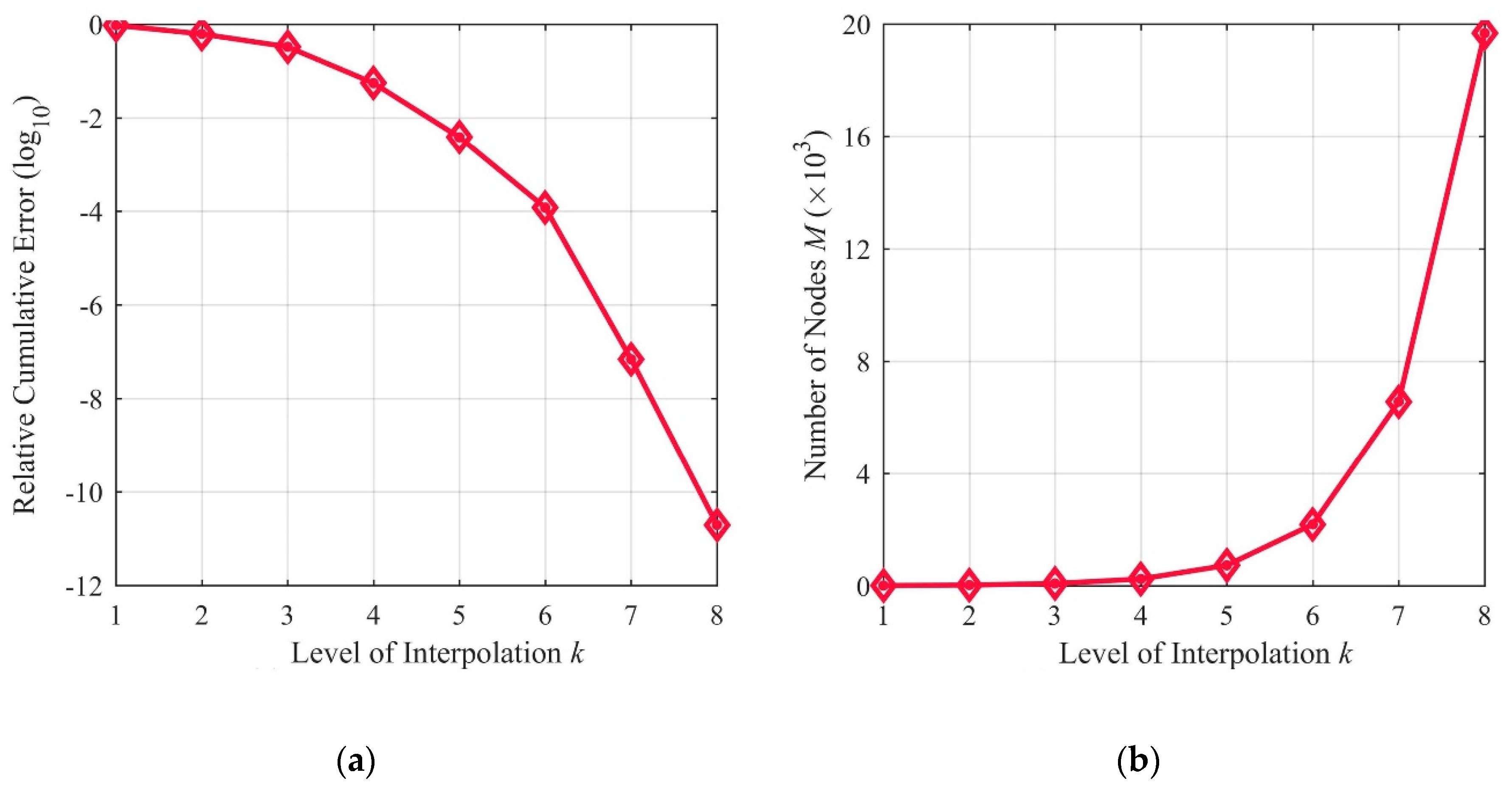
- The remaining useful life predictions obtained from the proposed approach were compared with the Monte Carlo simulation results for the plate specimen. The comparisons show that the proposed approach can greatly improve the efficiency and accuracy for uncertainty quantification in FCG analysis by utilizing the stochastic collocation method.
- (3)
- The significant computation efficiency of this uncertainty quantification approach for FCG can be potentially applied to much more complicated multi-dimensional problems for crack and damage propagations. Moreover, this study focuses on the material uncertainty quantification and other types of uncertainties can be involved in potential applications.
Author Contributions
Funding
Conflicts of Interest
References
- Farrar, C.R.; Lieven, N.A. Damage prognosis: The future of structural health monitoring. Philos. Trans. Math. Phys. Eng. Sci. 2007, 365, 623–632. [Google Scholar] [CrossRef] [PubMed]
- Novak, E.; Ritter, K. High dimensional integration of smooth functions over cubes. Numer. Math. 1996, 75, 79–97. [Google Scholar] [CrossRef]
- Jallouf, S.; Casavola, K.; Pappalettere, C.; Pluvinage, G. Assessment of undercut defect in a laser welded plate made of Ti–6Al–4V titanium alloy with probabilistic domain failure assessment diagram. Eng. Fail. Anal. 2016, 59, 17–27. [Google Scholar] [CrossRef]
- Long, X.Y.; Liu, K.; Jiang, C.; Xiao, Y.; Wu, S.C. Uncertainty propagation method for probabilistic fatigue crack growth life prediction. Theor. Appl. Fract. Mech. 2019, 103, 102–268. [Google Scholar] [CrossRef]
- Lin, Y.; Ding, Z.; Zio, E. Fatigue crack growth assessment method subject to model uncertainty. Eng. Fract. Mech. 2019, 219, 106–624. [Google Scholar] [CrossRef]
- Liu, Y.; Mahadevan, S. Probabilistic fatigue life prediction using an equivalent initial flaw size distribution. Int. J. Fatigue 2009, 31, 476–487. [Google Scholar] [CrossRef]
- Chen, M.; Fang, W.; Yang, C.; Xie, L. Bayesian prediction and probabilistic model of fatigue cracks in steel structures. Eng. Fail. Anal. 2019, 103, 335–346. [Google Scholar] [CrossRef]
- Shiao, M.; Chen, T.; Mao, Z. Probabilistic Maintenance-Free Operating Period via Bayesian Filter with Markov Chain Monte Carlo (MCMC) Simulations and Subset Simulation. In Model Validation and Uncertainty Quantification; Springer: Cham, Switzerland, 2019; Volume 3, pp. 225–234. [Google Scholar]
- Bäck, J.; Nobile, F.; Tamellini, L.; Tempone, R. Stochastic Spectral Galerkin and Collocation Methods for PDEs with Random Coefficients: A Numerical Comparison; Springer: Berlin, Heidelberg, Germany, 2011; pp. 43–62. [Google Scholar]
- Xiu, D.; Hesthaven, J.S. High-order collocation methods for differential equations with random inputs. Siam. J. Sci. Comput. 2005, 27, 1118–1139. [Google Scholar] [CrossRef]
- Najm, H.N. Uncertainty quantification and polynomial chaos techniques in computational fluid dynamics. Annu. Rev. Fluid Mech. 2009, 41, 35–52. [Google Scholar] [CrossRef]
- Reagan, M.T.; Najm, H.N.; Debusschere, B.J.; Le Maître, O.P.; Knio, O.M.; Ghanem, R.G. Spectral stochastic uncertainty quantification in chemical systems. Combust. Theor. Model. 2004, 8, 607–632. [Google Scholar] [CrossRef]
- Li, H.; Zhang, D. Probabilistic collocation method for flow in porous media: Comparisons with other stochastic methods. Water Resour. Res. 2007, 43, W09409. [Google Scholar] [CrossRef]
- Foo, J.; Yosibash, Z.; Karniadakis, G.E. Stochastic simulation of riser-sections with uncertain measured pressure loads and/or uncertain material properties. Comput. Method Appl. Mech. 2007, 196, 4250–4271. [Google Scholar] [CrossRef]
- He, J.; Gao, S.; Gong, J. A sparse grid stochastic collocation method for structural reliability analysis. Struct. Saf. 2014, 51, 29–34. [Google Scholar] [CrossRef]
- Riahi, H.; Bressolette, P.; Chateauneuf, A. Random fatigue crack growth in mixed mode by stochastic collocation method. Eng. Fract. Mech. 2010, 77, 3292–3309. [Google Scholar] [CrossRef]
- Zhao, F.; Tian, Z.; Zeng, Y. A stochastic collocation approach for efficient integrated gear health prognosis. Mech. Syst. Signal Process. 2013, 39, 372–387. [Google Scholar] [CrossRef]
- Beck, A.T.; Gomes, W.J.D.S. Stochastic fracture mechanics using polynomial chaos. Probabilistic Eng. Mech. 2013, 34, 26–39. [Google Scholar] [CrossRef]
- Sankararaman, S.; Ling, Y.; Mahadevan, S. Uncertainty quantification and model validation of fatigue crack growth prediction. Eng. Fract. Mech. 2011, 78, 1487–1504. [Google Scholar] [CrossRef]
- Tang, H.; Li, D.; Li, J.; Xue, S. Epistemic uncertainty quantification in metal fatigue crack growth analysis using evidence theory. Int. J. Fatigue 2017, 99, 163–174. [Google Scholar] [CrossRef]
- Long, X.Y.; Jiang, C.; Liu, K.; Han, X.; Gao, W.; Li, B.C. An interval analysis method for fatigue crack growth life prediction with uncertainty. Comput. Struct. 2018, 210, 1–11. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A critical analysis crack propagation laws. J. Basic Eng. 1963, 85, 528–534. [Google Scholar] [CrossRef]
- Forman, R.G.; Kearney, V.E.; Engle, R.M. Numerical analysis of crack propagation in cyclic-loaded structures. J. Basic Eng. 1967, 89, 459–463. [Google Scholar] [CrossRef]
- Wolf, E. Fatigue crack closure under cyclic tension. Eng. Fract. Mech. 1970, 2, 37–45. [Google Scholar] [CrossRef]
- Chang, T.; Li, G.; Hou, J. Effects of applied stress level on plastic zone size and opening stress ratio of a fatigue crack. Int. J. Fatigue 2005, 27, 519–526. [Google Scholar] [CrossRef]
- Newman, J.C. A crack opening stress equation for fatigue crack growth. Int. J. Fract. 1984, 24, R131–R135. [Google Scholar] [CrossRef]
- Vasudevan, A.K.; Sadananda, K.; Louat, N. Reconsideration of fatigue crack closure. Scr. Metall. Mater. 1992, 27, 1673–1678. [Google Scholar] [CrossRef]
- Zhang, J.Z.; He, X.D.; Tang, H.; Du, S.Y. Direct high resolution in situ SEM observations of small fatigue crack opening profiles in the ultra-fine grain aluminium alloy. Mater. Sci. Eng. 2008, 485, 115–118. [Google Scholar] [CrossRef]
- Lu, Z.; Liu, Y. Small time scale fatigue crack growth analysis. Int. J. Fatigue 2010, 32, 1306–1321. [Google Scholar] [CrossRef]
- Lu, Z.; Liu, Y. Concurrent fatigue crack growth simulation using extended finite element method. Front. Archit. Civ. Eng. China 2010, 4, 339–347. [Google Scholar] [CrossRef]
- Lu, Z.; Liu, Y. A comparative study between a small time scale model and the two driving force model for fatigue analysis. Int. J. Fatigue 2012, 42, 57–70. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, W.; Zhang, J.; Dai, W.; Zhao, Y. Investigative method for fatigue crack propagation based on a small time scale. Materials 2018, 11, 774. [Google Scholar] [CrossRef]
- Huo, J.; Zhu, D.; Hou, N.; Sun, W.; Dong, J. Application of a small-timescale fatigue, crack-growth model to the plane stress/strain transition in predicting the lifetime of a tunnel-boring-machine cutter head. Eng. Fail. Anal. 2017, 71, 11–30. [Google Scholar] [CrossRef]
- Ye, H.; Wang, T.; Wu, C.; Duan, Z.; Liu, C. A comparative analysis of driving force models for fatigue crack propagation of CFRP-reinforced steel structure. Int. J. Fatigue 2020, 130, 105266. [Google Scholar] [CrossRef]
- Lu, Z.; Liu, Y. Experimental investigation of random loading sequence effect on fatigue crack growth. Mater. Des. 2011, 32, 4773–4785. [Google Scholar] [CrossRef]
- Barthelmann, V.; Novak, E.; Ritter, K. High dimensional polynomial interpolation on sparse grids. ADV Comput. Math. 2000, 12, 273–288. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Kawagoishi, N.; Chen, Q. Fatigue and fracture behaviour of structural Al-alloys up to very long life regimes. Int. J. Fatigue 2006, 28, 1572–1576. [Google Scholar] [CrossRef]


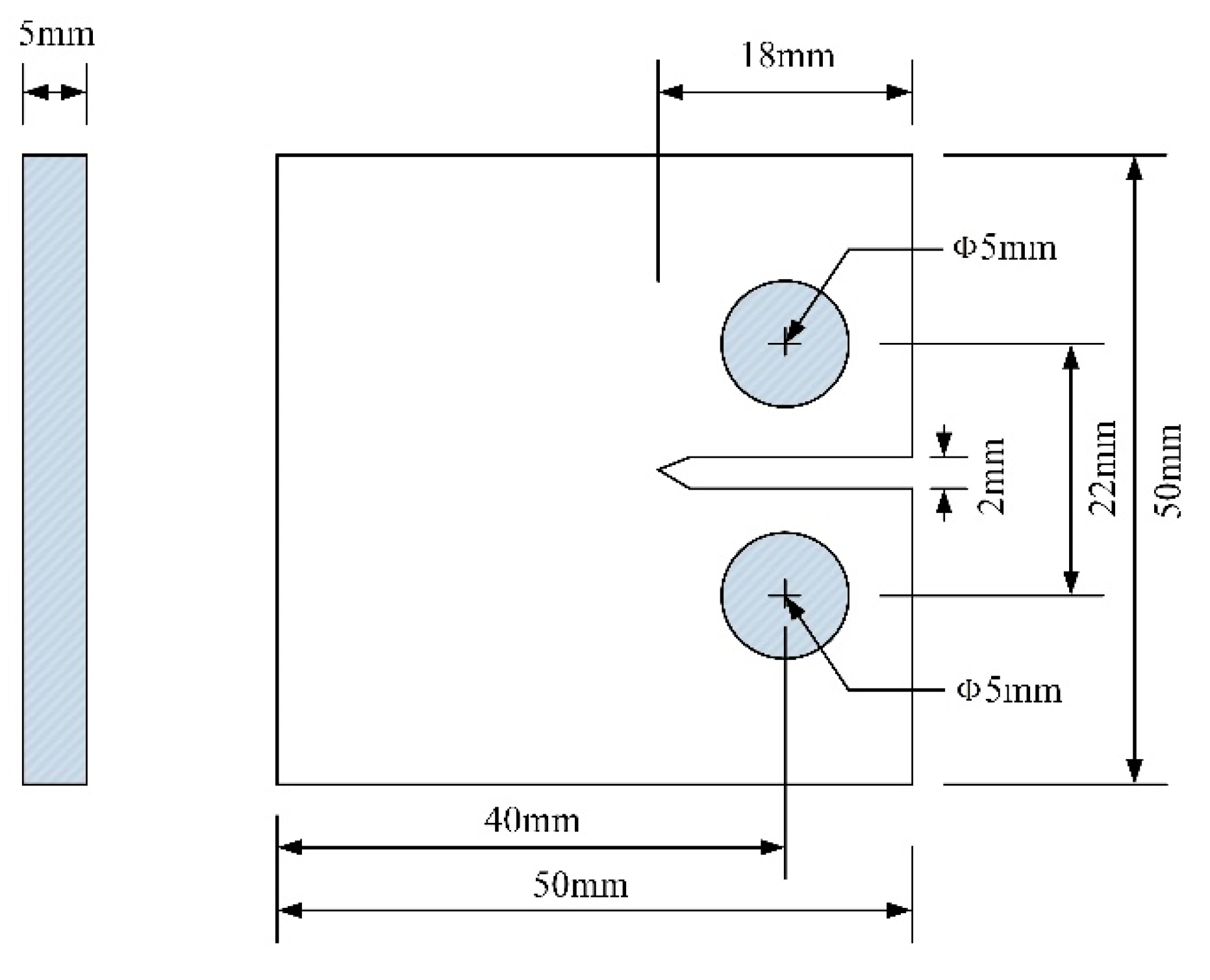
| Specimen Material | Ultimate Strength (MPa) | Yield Strength (MPa) | Young’s Modulus (MPa) | Plate Width (mm) | Plate Thickness (mm) |
|---|---|---|---|---|---|
| Al 7075-T6 | 573~582 | 502~516 | 71.7 | 40 | 5 |
| Specimen | 01 | 02 | 03 | 04 | 05 | 06 | 07 |
|---|---|---|---|---|---|---|---|
| N | a (mm) | a (mm) | a (mm) | a (mm) | a (mm) | a (mm) | a (mm) |
| 0 | 10.921 | 10.913 | 10.921 | 10.992 | 10.921 | 10.921 | 10.931 |
| 1000 | 11.024 | 11.216 | 11.056 | 11.201 | 11.102 | 11.178 | 11.102 |
| 2000 | 11.153 | 11.486 | 11.266 | 11.452 | 11.344 | 11.376 | 11.353 |
| 3000 | 11.326 | 11.733 | 11.476 | 11.750 | 11.569 | 11.580 | 11.589 |
| 4000 | 11.545 | 11.993 | 11.638 | 12.137 | 11.734 | 11.837 | 11.755 |
| 5000 | 11.778 | 12.416 | 11.814 | 12.521 | 11.947 | 12.128 | 11.946 |
| 6000 | 12.005 | 12.778 | 12.020 | 12.843 | 12.224 | 12.400 | 12.184 |
| 7000 | 12.237 | 12.939 | 12.216 | 13.141 | 12.478 | 12.618 | 12.412 |
| 8000 | 12.491 | 13.484 | 12.435 | 13.541 | 12.724 | 12.890 | 12.671 |
| 9000 | 12.747 | 13.882 | 12.698 | 14.031 | 12.983 | 13.200 | 12.956 |
| 10,000 | 12.967 | 14.414 | 12.990 | 14.497 | 13.262 | 13.435 | 13.216 |
| 11,000 | 13.210 | 14.797 | 13.277 | 15.069 | 13.598 | 13.714 | 13.517 |
| 12,000 | 13.523 | 15.222 | 13.536 | 15.755 | 14.005 | 14.040 | 13.850 |
| 13,000 | 13.904 | 15.707 | 13.780 | 16.443 | 14.441 | 14.314 | 14.132 |
| 14,000 | 14.290 | 16.214 | 14.070 | 17.249 | 14.762 | 14.699 | 14.407 |
| 15,000 | 14.681 | 16.797 | 14.413 | 18.141 | 15.060 | 15.260 | 14.708 |
| 16,000 | 15.145 | 17.587 | 14.780 | 18.953 | 15.569 | 15.889 | 15.033 |
| 17,000 | 15.678 | 18.561 | 15.256 | 19.801 | 16.094 | 16.439 | 15.373 |
| 18,000 | 16.260 | 19.440 | 15.820 | 20.910 | 16.641 | 16.960 | 15.735 |
| 19,000 | 16.878 | 20.103 | 16.363 | 22.602 | 17.436 | 17.651 | 16.130 |
| 20,000 | 17.555 | 21.790 | 16.964 | 25.404 | 18.335 | 18.503 | 16.549 |
| 21,000 | 18.400 | 22.818 | 17.600 | 19.209 | 19.500 | 17.033 | |
| 22,000 | 19.521 | 25.601 | 18.167 | 20.095 | 20.627 | 17.625 | |
| 23,000 | 20.714 | 18.840 | 21.195 | 21.723 | 18.197 | ||
| 24,000 | 22.124 | 19.741 | 22.749 | 23.361 | 18.808 | ||
| 25,000 | 24.323 | 20.748 | 24.992 | 25.890 | 19.616 | ||
| 26,000 | 21.374 | 20.313 | |||||
| 27,000 | 23.258 | 21.681 | |||||
| 28,000 | 25.682 | 24.986 |
| Variable | |||
|---|---|---|---|
| Mean value | 0.8 | 32 | 520 |
| Standard deviation | 0.011 | 2.72 | 30.32 |
| The Type of Distribution | K-S Distance | Critical Distance | The Level of Significance |
|---|---|---|---|
| Uniform distribution | 0.289 | 0.0136 | 0 |
| Normal distribution | 0.017 | 0.0136 | 0.008 |
| 2-parameter lognormal distribution | 0.016 | 0.0136 | 0.012 |
| 3-parameter lognormal distribution | 0.007 | 0.0136 | 0.689 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, H.; Guo, X.; Xue, S. Uncertainty Quantification in Small-Timescale Model-Based Fatigue Crack Growth Analysis Using a Stochastic Collocation Method. Metals 2020, 10, 646. https://doi.org/10.3390/met10050646
Tang H, Guo X, Xue S. Uncertainty Quantification in Small-Timescale Model-Based Fatigue Crack Growth Analysis Using a Stochastic Collocation Method. Metals. 2020; 10(5):646. https://doi.org/10.3390/met10050646
Chicago/Turabian StyleTang, Hesheng, Xueyuan Guo, and Songtao Xue. 2020. "Uncertainty Quantification in Small-Timescale Model-Based Fatigue Crack Growth Analysis Using a Stochastic Collocation Method" Metals 10, no. 5: 646. https://doi.org/10.3390/met10050646
APA StyleTang, H., Guo, X., & Xue, S. (2020). Uncertainty Quantification in Small-Timescale Model-Based Fatigue Crack Growth Analysis Using a Stochastic Collocation Method. Metals, 10(5), 646. https://doi.org/10.3390/met10050646





