Numerical Simulation of Buckling and Post-Buckling Behavior of a Central Notched Thin Aluminum Foil with Nonlinearity in Consideration
Abstract
1. Introduction
2. Problem Definition
Critical Buckling Stress
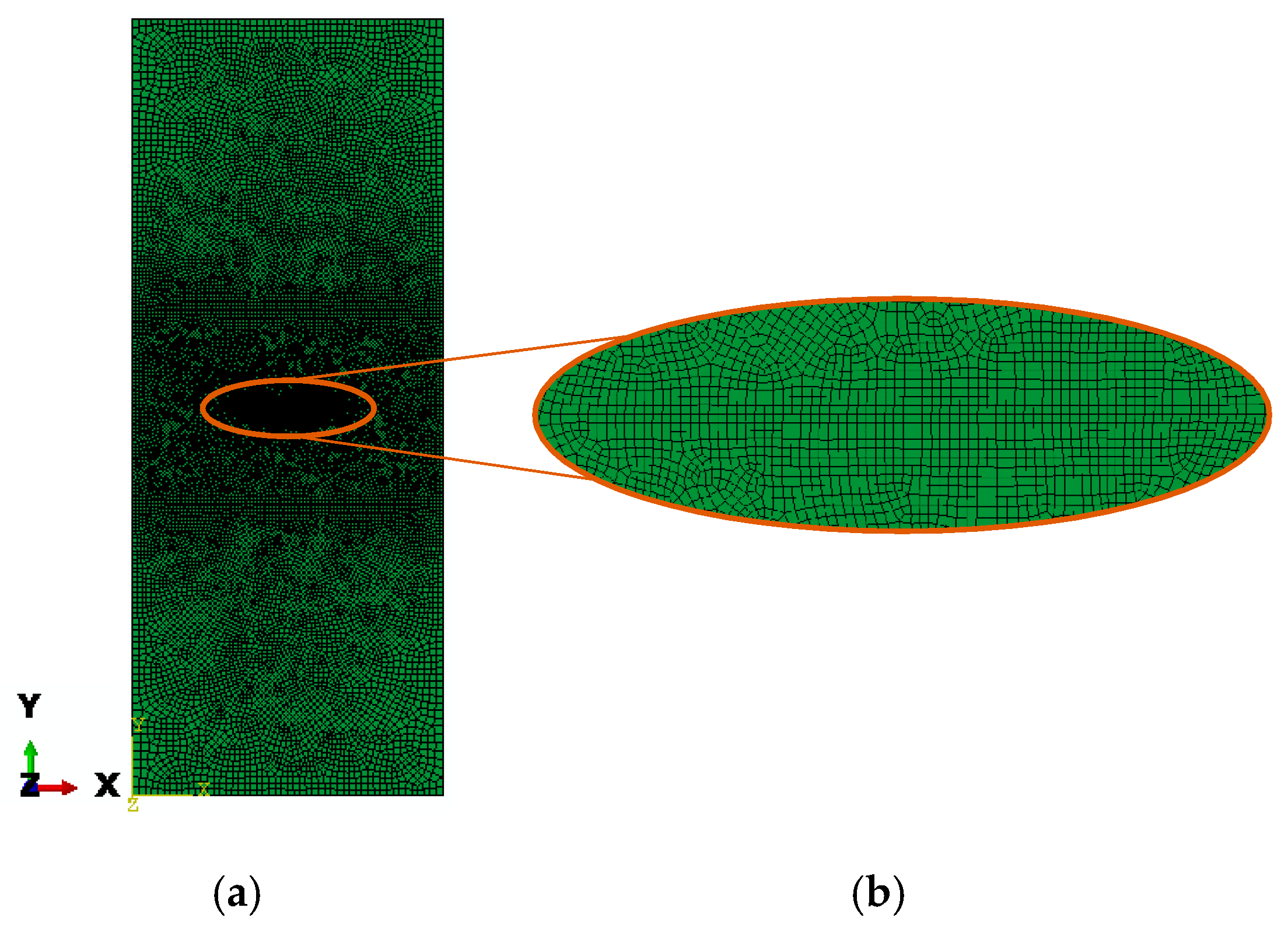
3. Numerical Model
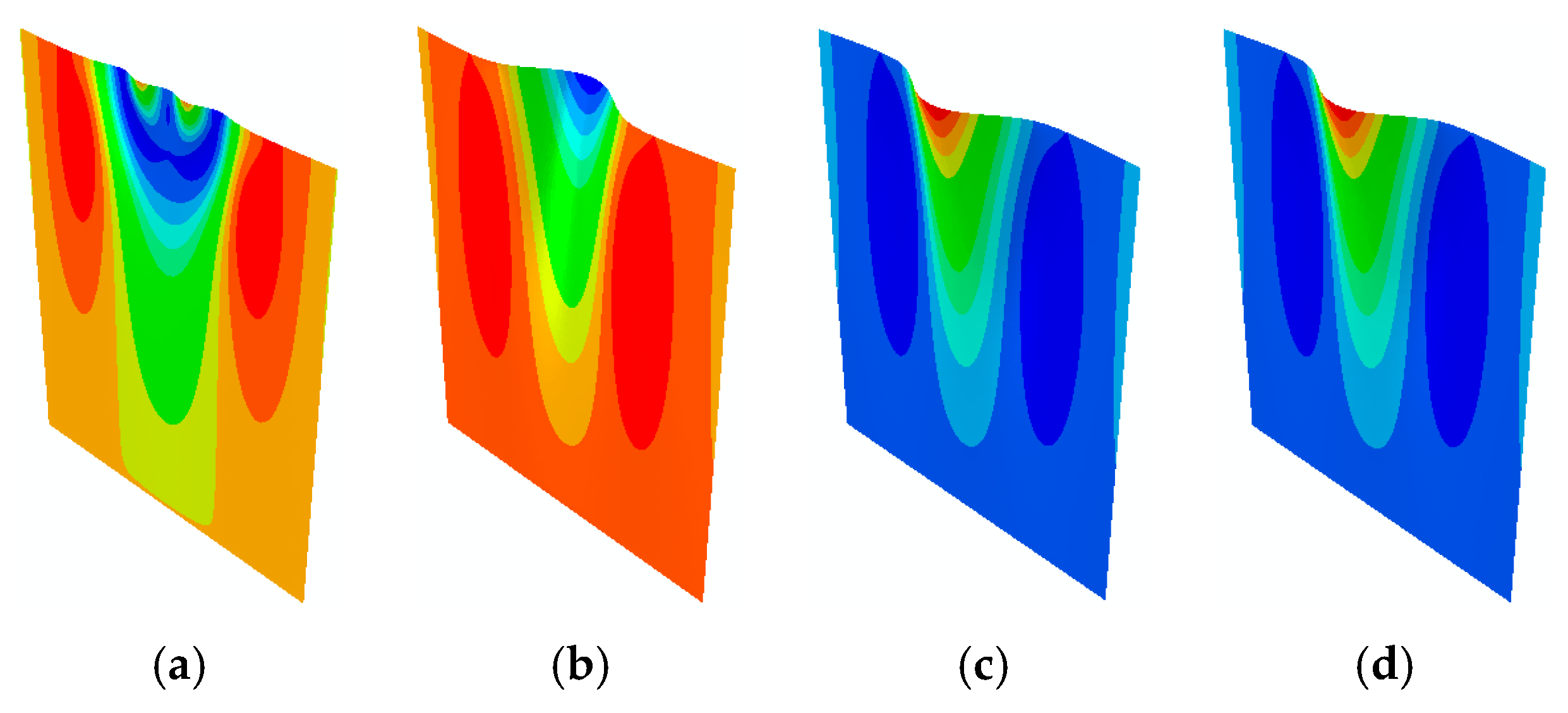
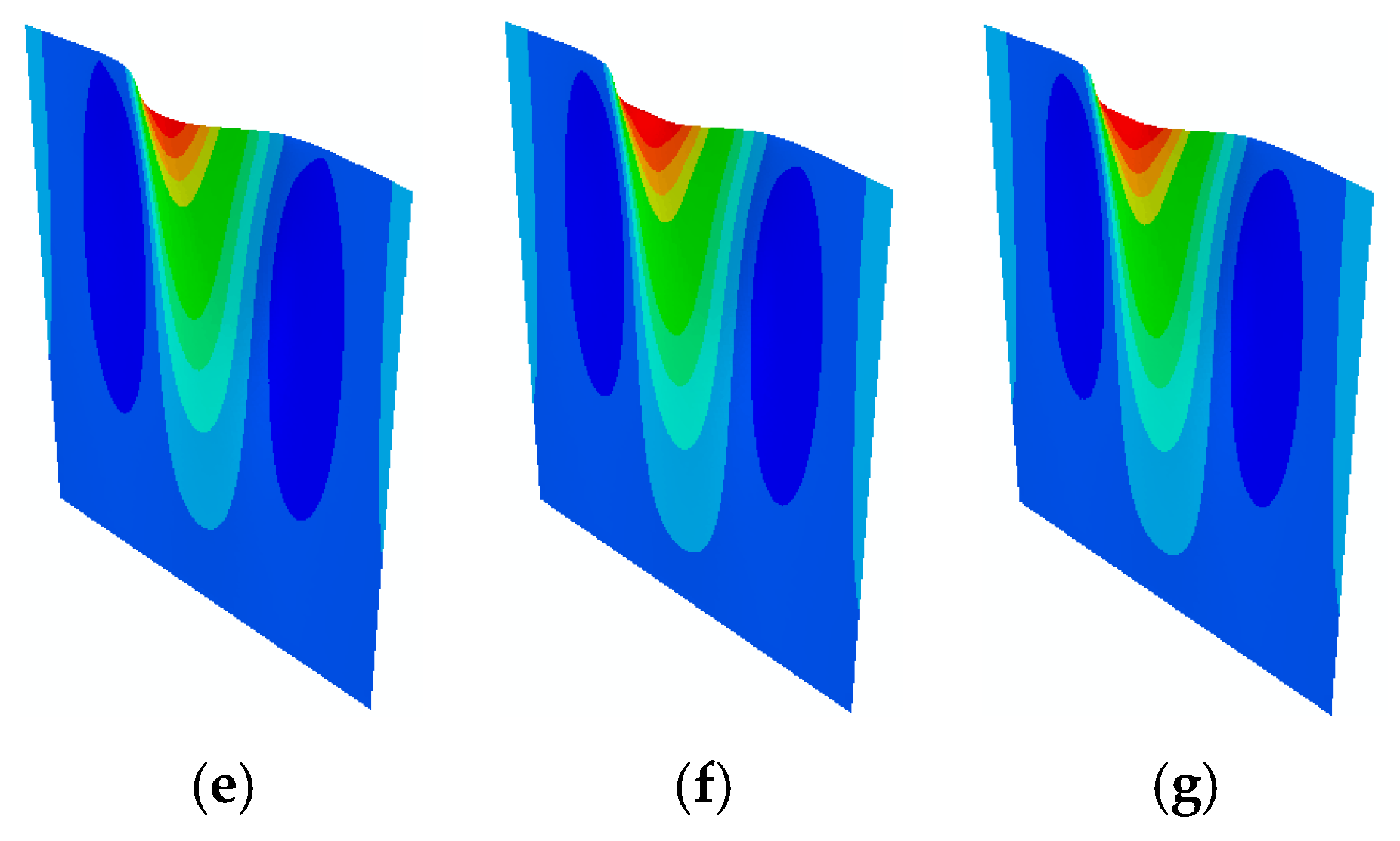
4. Results and Discussion
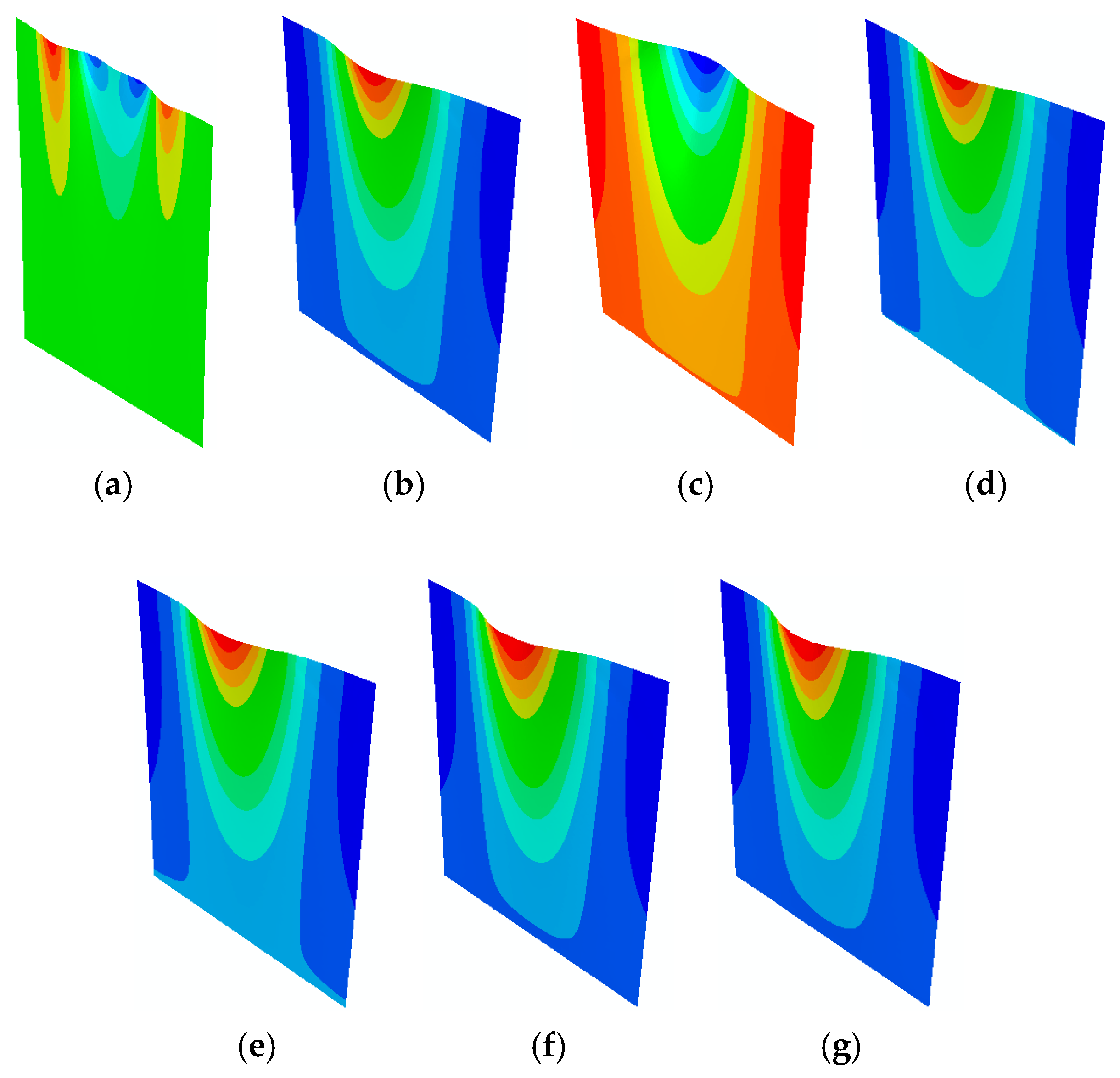
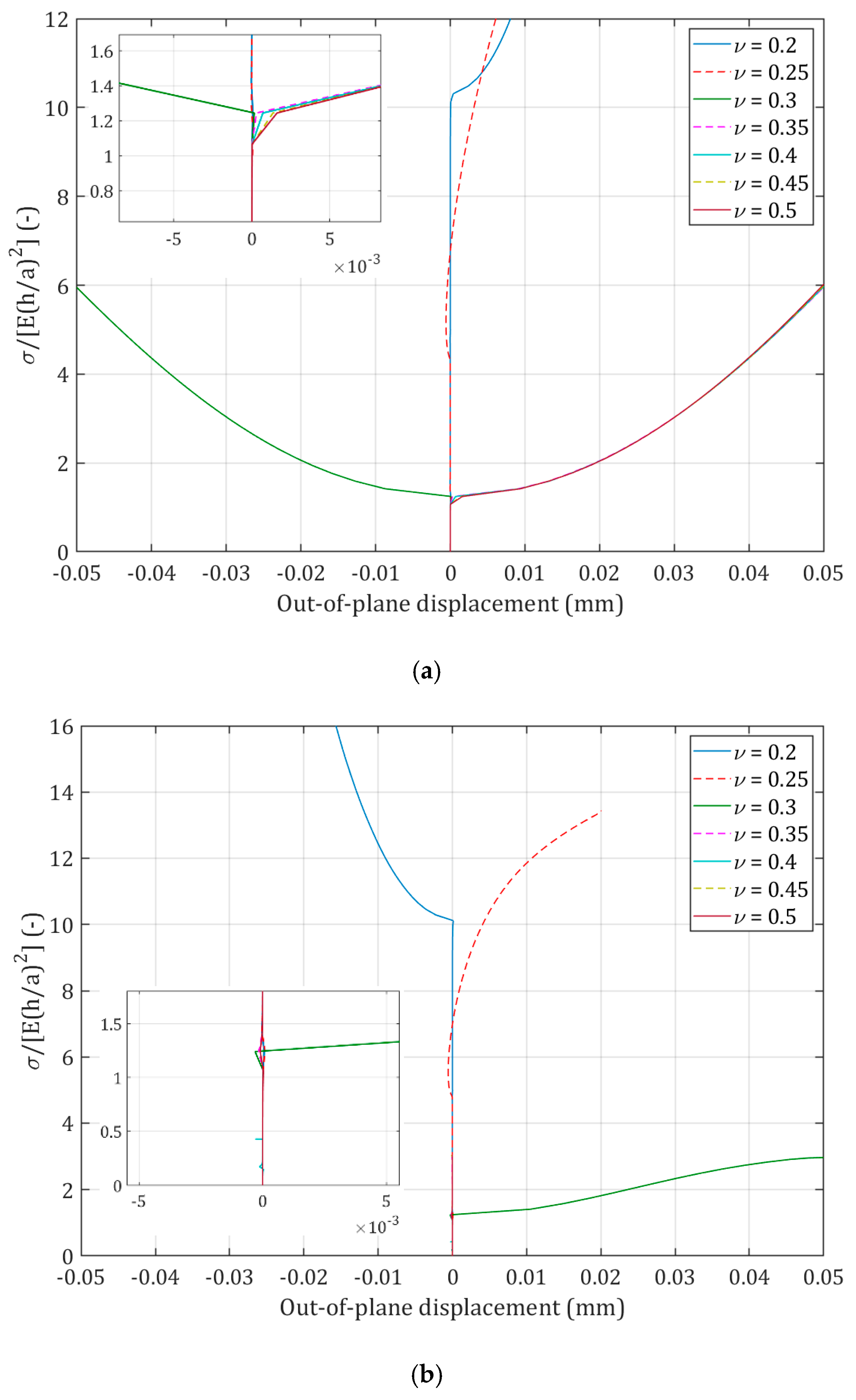
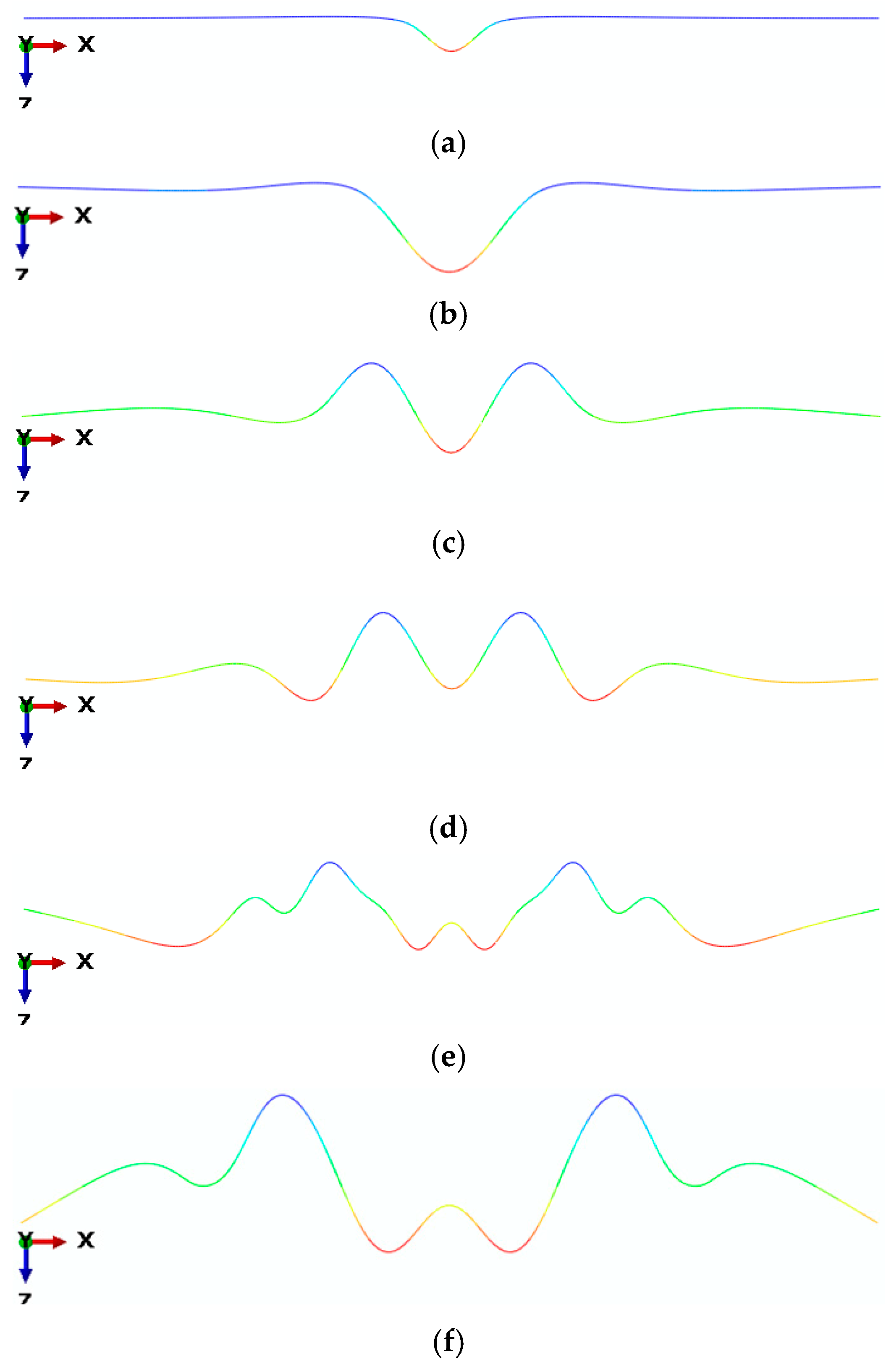
4.1. Influence of Poisson’s Ratio
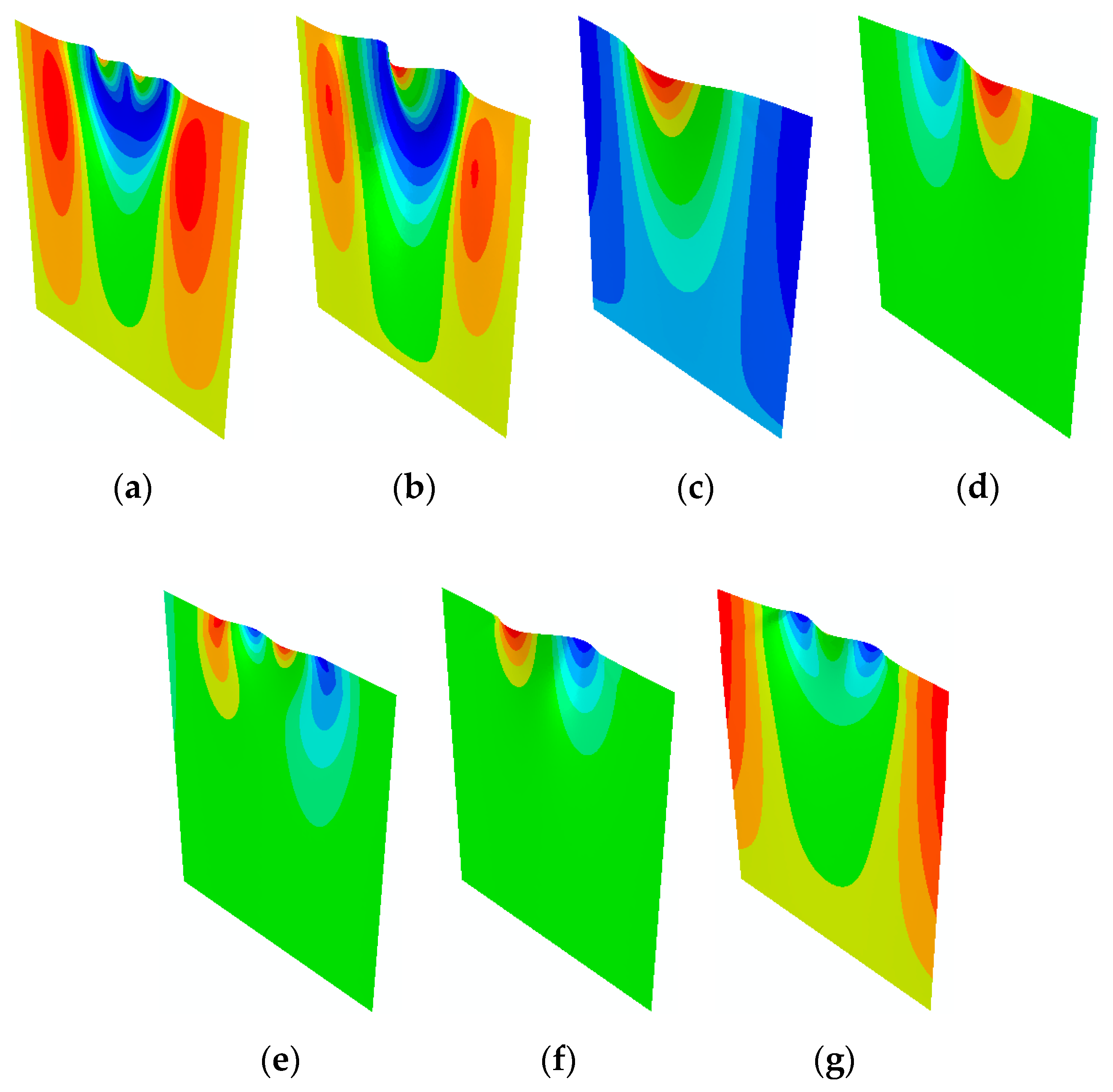
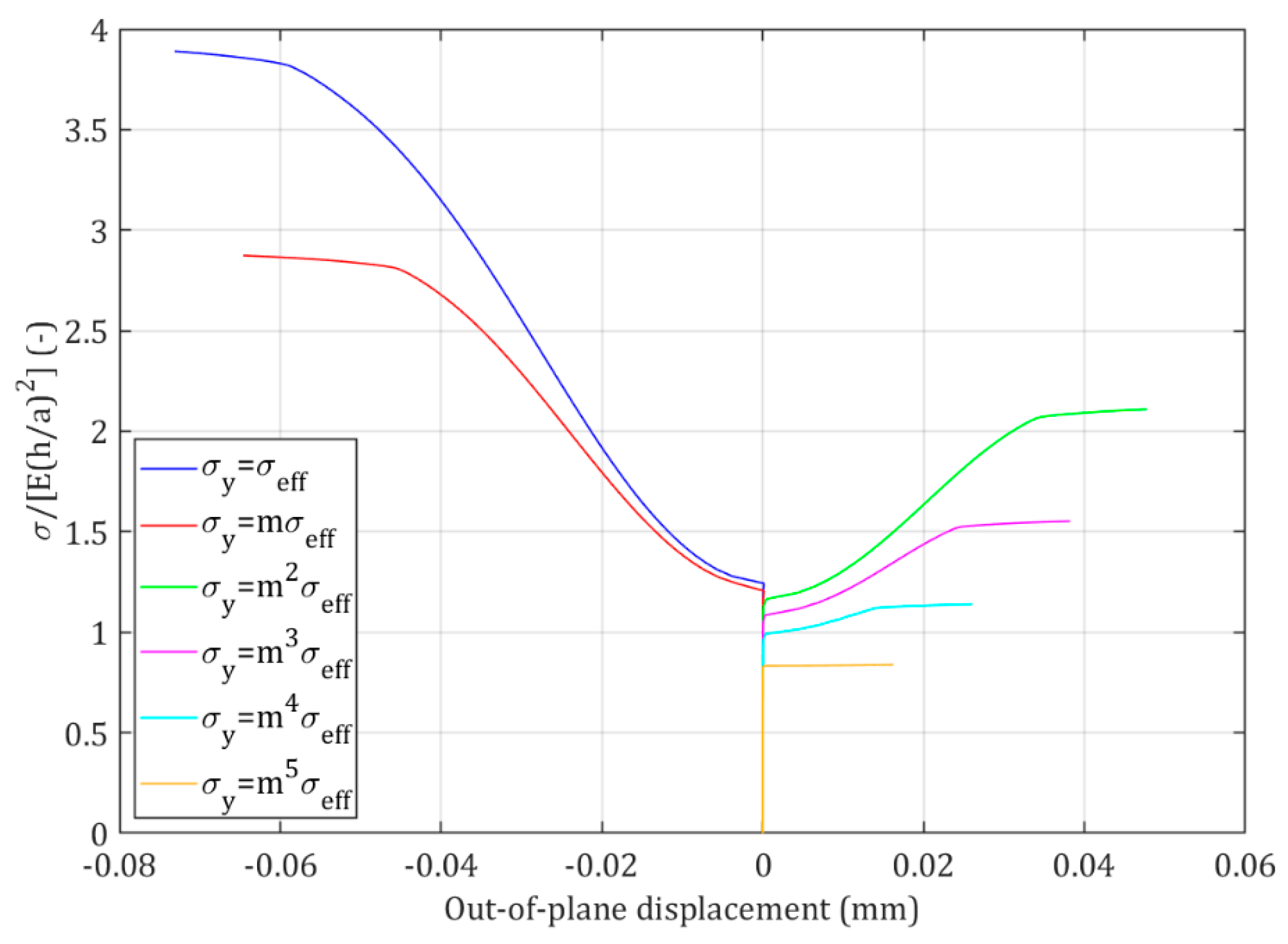
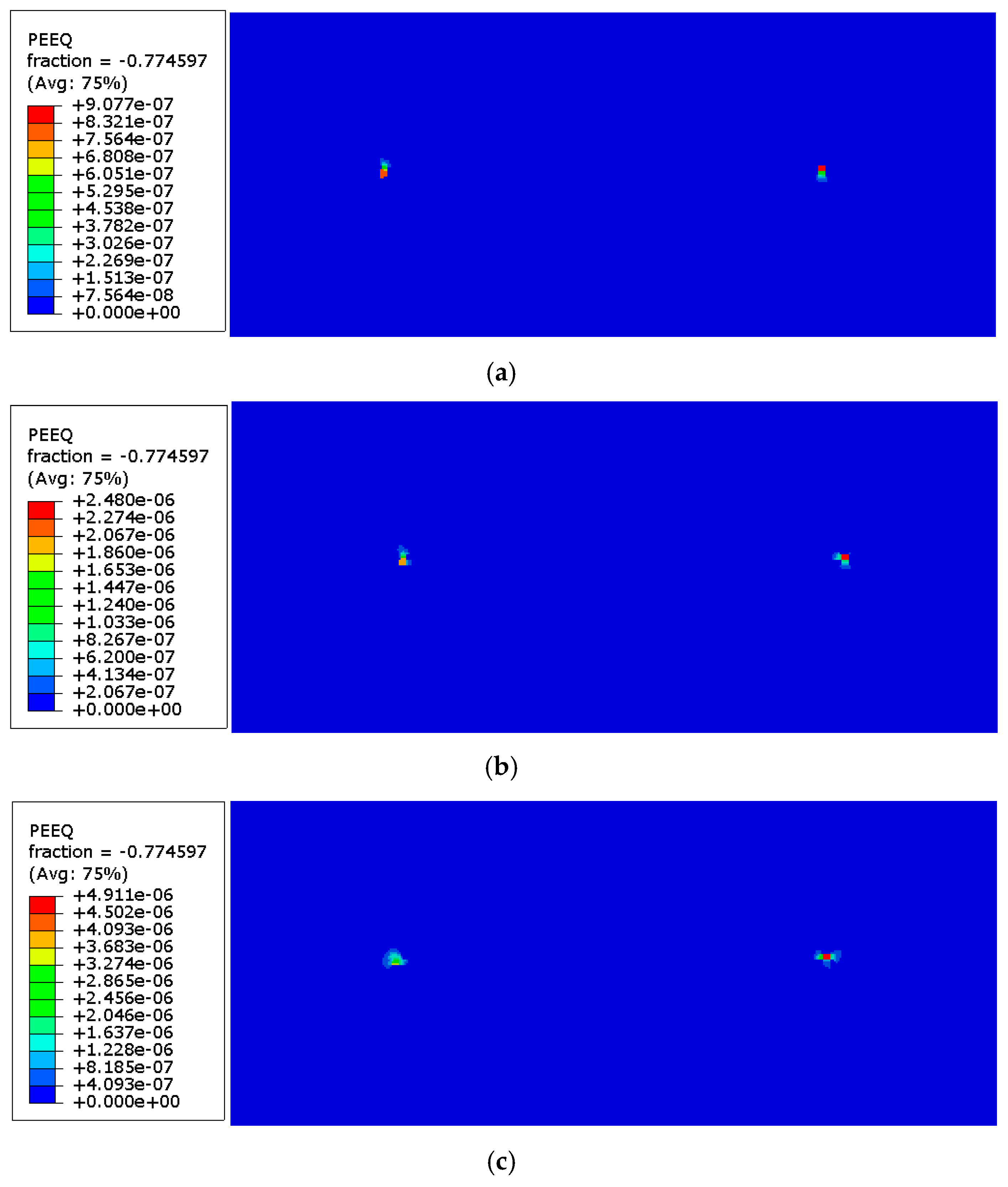
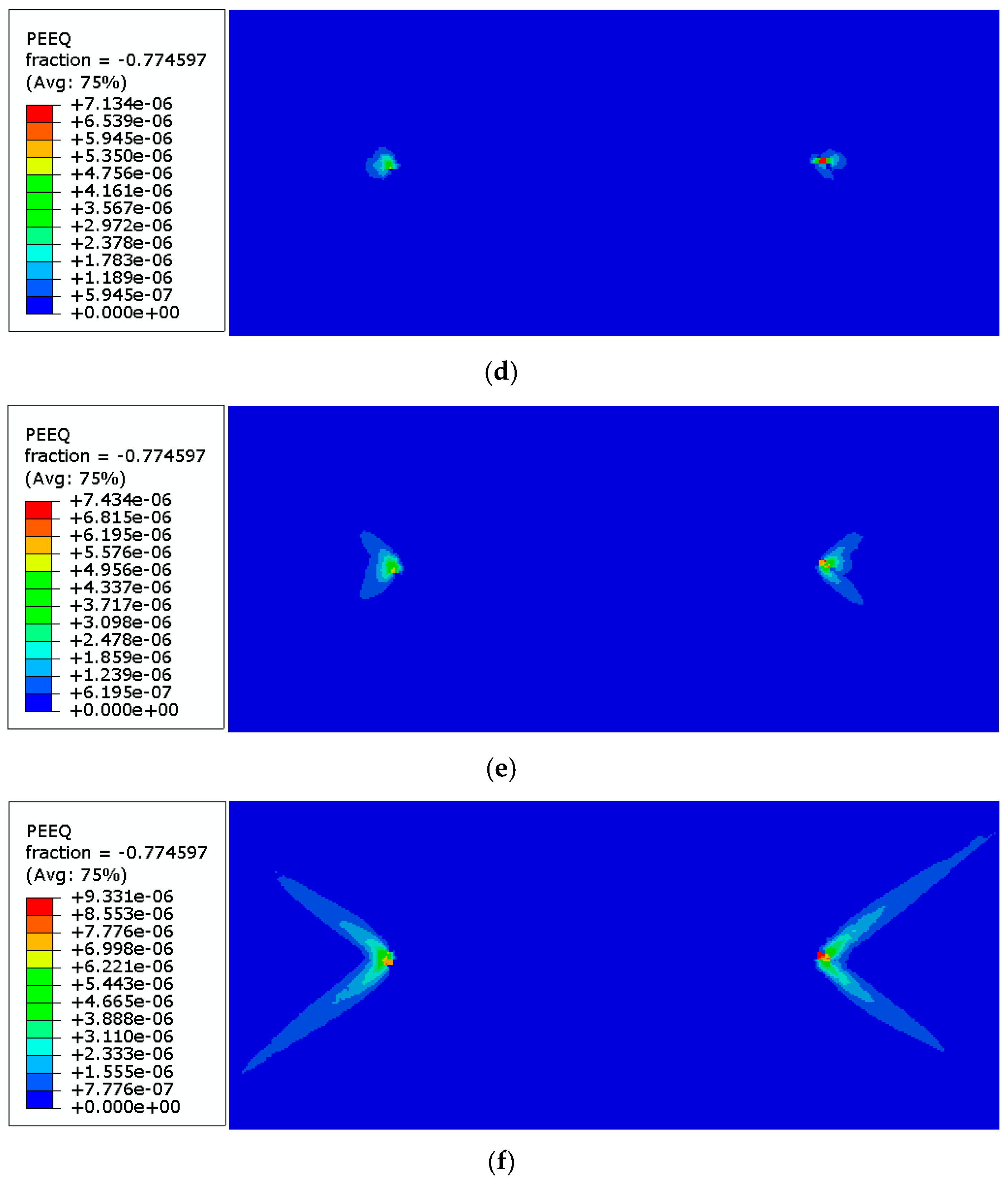
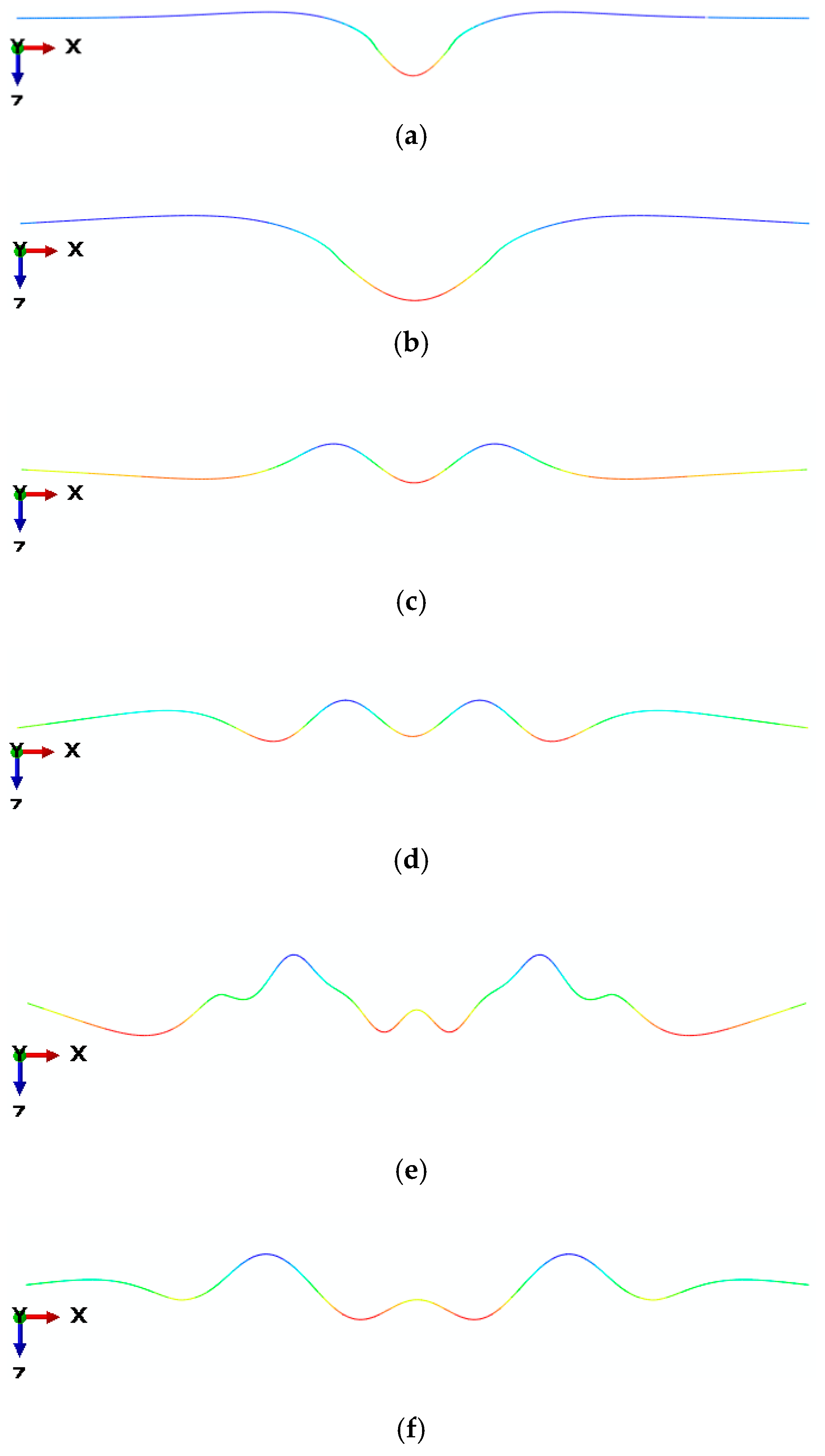
4.2. Influence of Yield Limit
4.3. Influence of Crack Length-to-Sheet Width
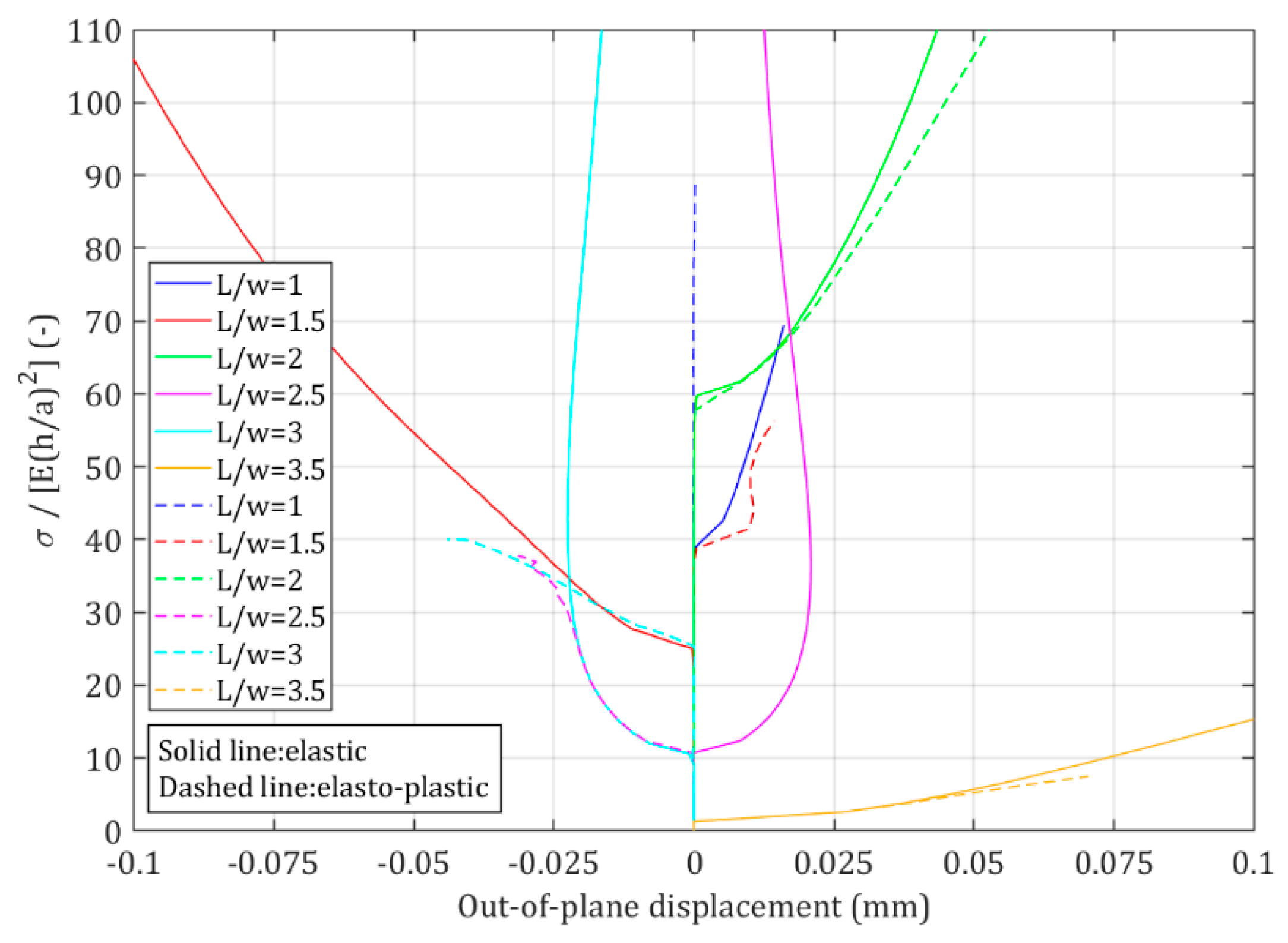
4.4. Influence of the Sheet Aspect Ratio
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bolzon, G.; Shahmardani, M.; Liu, R.; Zappa, E. Failure analysis of thin metal foils. Frat. Integr. Strutt. 2017, 11, 328–336. [Google Scholar] [CrossRef]
- Puntel, E.; Deseri, L.; Fried, E. Wrinkling of a stretched thin sheet. J. Elast. 2011, 105, 137–170. [Google Scholar] [CrossRef]
- Kao-Walter, S. On the Fracture of Thin Laminates. Ph.D. Thesis, Series No. 2004:07. Dep. Mech. Eng., Blekinge Institute of Technology, Karlskrona, Sweden, 2004. [Google Scholar]
- Fu, C.; Wang, T.; Xu, F.; Huo, Y.; Potier-Ferry, M. A modeling and resolution framework for wrinkling in hyperelastic sheets at finite membrane strain. J. Mech. Phys. Solids 2019, 124, 446–470. [Google Scholar] [CrossRef]
- Kim, T.-Y.; Puntel, E.; Fried, E. Numerical study of the wrinkling of a stretched thin sheet. Int. J. Solids Struct. 2012, 49, 771–782. [Google Scholar] [CrossRef]
- Bolzon, G.; Shahmardani, M.; Liu, R.; Zappa, E. A combined experimental-numerical investigation of the failure mode of thin metal foils. Procedia Struct. Integr. 2017, 3, 168–171. [Google Scholar] [CrossRef]
- Bolzon, G.; Shahmardani, M. Numerical simulation of non-standard tensile tests of thin metal foils. AIP Conf. Proc. 2018, 1922, 080011. [Google Scholar]
- Najarzadeh, L.; Movahedian, B.; Azhari, M. Stability analysis of the thin plates with arbitrary shapes subjected to non-uniform stress fields using boundary element and radial integration methods. Eng. Anal. Bound. Elem. 2018, 87, 111–121. [Google Scholar] [CrossRef]
- Nguyen-Thoi, T.; Bui-Xuan, T.; Phung-Van, P.; Nguyen-Xuan, H.; Ngo-Thanh, P. Static, free vibration and buckling analyses of stiffened plates by CS-FEM-DSG3 using triangular elements. Comp. Struct. 2013, 125, 100–113. [Google Scholar] [CrossRef]
- Mo, J.; Cheung, P.T.; Sherman, C.P.; Das, R. Chapter 11 - Thin Plate Deflection. Demystifying Numer. Models 2019, 235–255. [Google Scholar]
- Bolzon, G.; Shahmardani, M. Macroscopic response and decohesion models of metal-polymer laminates. Eng. Trans. 2017, 65, 53–59. [Google Scholar]
- Andreasson, E.; Kao-Walter, S.; Ståhle, P. Micro-mechanisms of a laminated packaging material during fracture. Eng. Frac. Mech. 2014, 127, 313–326. [Google Scholar] [CrossRef]
- Davidovitch, B.; Schroll, R.D.; Vella, D.; Adda-Bedia, M.; Cerdad, E.A. Prototypical model for tensional wrinkling in thin sheets. PNAS 2011, 108, 18227–18232. [Google Scholar] [CrossRef] [PubMed]
- Valente de Carvalho, R. Wrinkling of Thin Sheets under Tension. Master’s Thesis, Técnico Lisboa, Lisbon, Portugal, November 2015. [Google Scholar]
- Datta, P.K.; Biswas, S. Research advances on tension buckling behaviour of aerospace structures: A review. Int. J. Aeronaut. Space. 2011, 12, 1–15. [Google Scholar] [CrossRef]
- Markstrӧm, K.; Stoåkers, B. Buckling of cracked members under tension. Int. J. Solids Struct. 1980, 16, 217–229. [Google Scholar] [CrossRef]
- Shaw, D.; Huang, Y.H. Buckling behavior of a central cracked thin plate under tension. Eng. Frac. Mech. 1990, 35, 1019–1027. [Google Scholar] [CrossRef]
- Riks, E.; Rankin, C.C.; Brogan, F.A. The buckling behavior of a central crack in a plate under tension. Eng. Frac. Mech. 1992, 43, 529–548. [Google Scholar] [CrossRef]
- Brighenti, R. Buckling of cracked thin-plates under tension or compression. Thin Walled Struct. 2005, 43, 209–224. [Google Scholar] [CrossRef]
- Seif, A.E.; Kabir, M.Z. An efficient analytical model to evaluate the first two local buckling modes of finite cracked plate under tension. Lat. Am. J. Solids Struct. 2015, 12, 2078–2093. [Google Scholar] [CrossRef]
- Rammerstorfer, F.G. Buckling of elastic structures under tensile loads. Acta Mech. 2018, 229, 881–900. [Google Scholar] [CrossRef]
- Amiri Rad, A.; Panahandeh-Shahraki, D. Buckling of cracked functionally graded plates under tension. Thin Walled Struct. 2014, 84, 26–33. [Google Scholar] [CrossRef]
- Wang, T.; Fu, C.; Xu, F.; Huo, Y.; Potier-Ferry, M. On the wrinkling and restabilization of highly stretched sheets. Int. J. Eng. Sci. 2019, 136, 1–16. [Google Scholar] [CrossRef]
- Brighenti, R. Buckling sensitivity analysis of cracked thin plates under membrane tension or compression loading. Nucl. Eng. Des. 2009, 239, 965–980. [Google Scholar] [CrossRef]
- Guz, A.N.; Dyshel’, M.S.; Nazarenko, V.M. Fracture and stability of materials and structural members with cracks: Approaches and results. Int. Appl. Mech. 2004, 40, 1323–1359. [Google Scholar] [CrossRef]
- Dyshel, M.S. Stability and fracture of plates with a central and an edge crack under tension. Int. Appl. Mech. 2002, 38, 472–476. [Google Scholar] [CrossRef]
- Ståhle, P.; Li, C.; Bjerkén, C. Crack tip singularity in a buckling thin sheet. In Proceedings of the 19th Nordic Seminar on Computational Mechanics, Lund, Sweden, 20–21 October 2006; pp. 43–46. [Google Scholar]
- Isida, M. Effect of Width and Length on Stress Intensity Factors of Internally Cracked Plates Under Various Boundary Conditions. Int. J. Fract. 1971, 7, 301–316. [Google Scholar] [CrossRef]
- HKS Inc. ABAQUS/Standard, Theory and User’s Manuals, Version 2019; HKS Inc.: Pawtucket, RI, USA, 2019. [Google Scholar]
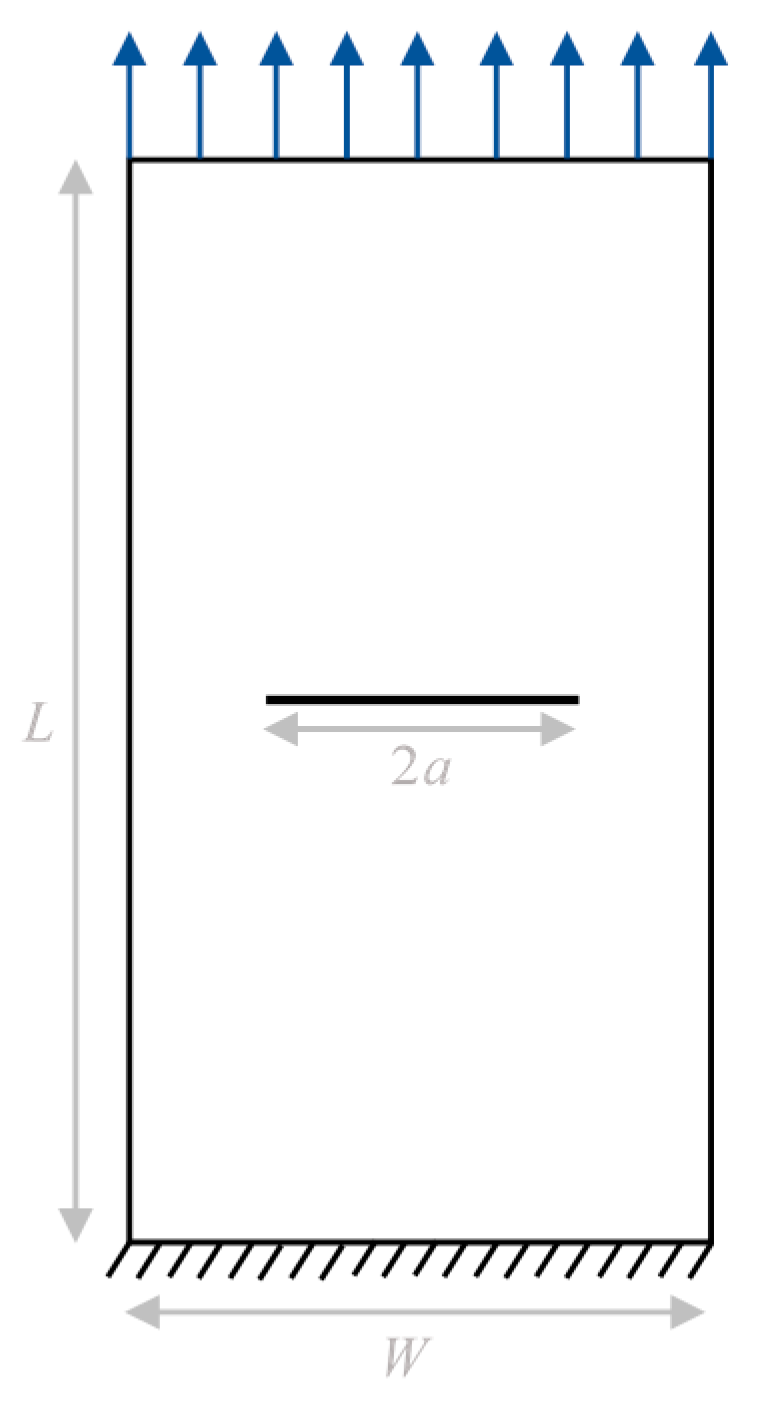






| Length (L, mm) | Width (W, mm) | Thickness (h, mm) | Crack Length (2a, mm) |
|---|---|---|---|
| 250 | 100 | 0.009 | 40 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahmardani, M.; Ståhle, P.; Islam, M.S.; Kao-Walter, S. Numerical Simulation of Buckling and Post-Buckling Behavior of a Central Notched Thin Aluminum Foil with Nonlinearity in Consideration. Metals 2020, 10, 582. https://doi.org/10.3390/met10050582
Shahmardani M, Ståhle P, Islam MS, Kao-Walter S. Numerical Simulation of Buckling and Post-Buckling Behavior of a Central Notched Thin Aluminum Foil with Nonlinearity in Consideration. Metals. 2020; 10(5):582. https://doi.org/10.3390/met10050582
Chicago/Turabian StyleShahmardani, Mahdieh, Per Ståhle, Md Shafiqul Islam, and Sharon Kao-Walter. 2020. "Numerical Simulation of Buckling and Post-Buckling Behavior of a Central Notched Thin Aluminum Foil with Nonlinearity in Consideration" Metals 10, no. 5: 582. https://doi.org/10.3390/met10050582
APA StyleShahmardani, M., Ståhle, P., Islam, M. S., & Kao-Walter, S. (2020). Numerical Simulation of Buckling and Post-Buckling Behavior of a Central Notched Thin Aluminum Foil with Nonlinearity in Consideration. Metals, 10(5), 582. https://doi.org/10.3390/met10050582





