Carbon Impact Mitigation of the Iron Ore Direct Reduction Process through Computer-Aided Optimization and Design Changes
Abstract
1. Introduction
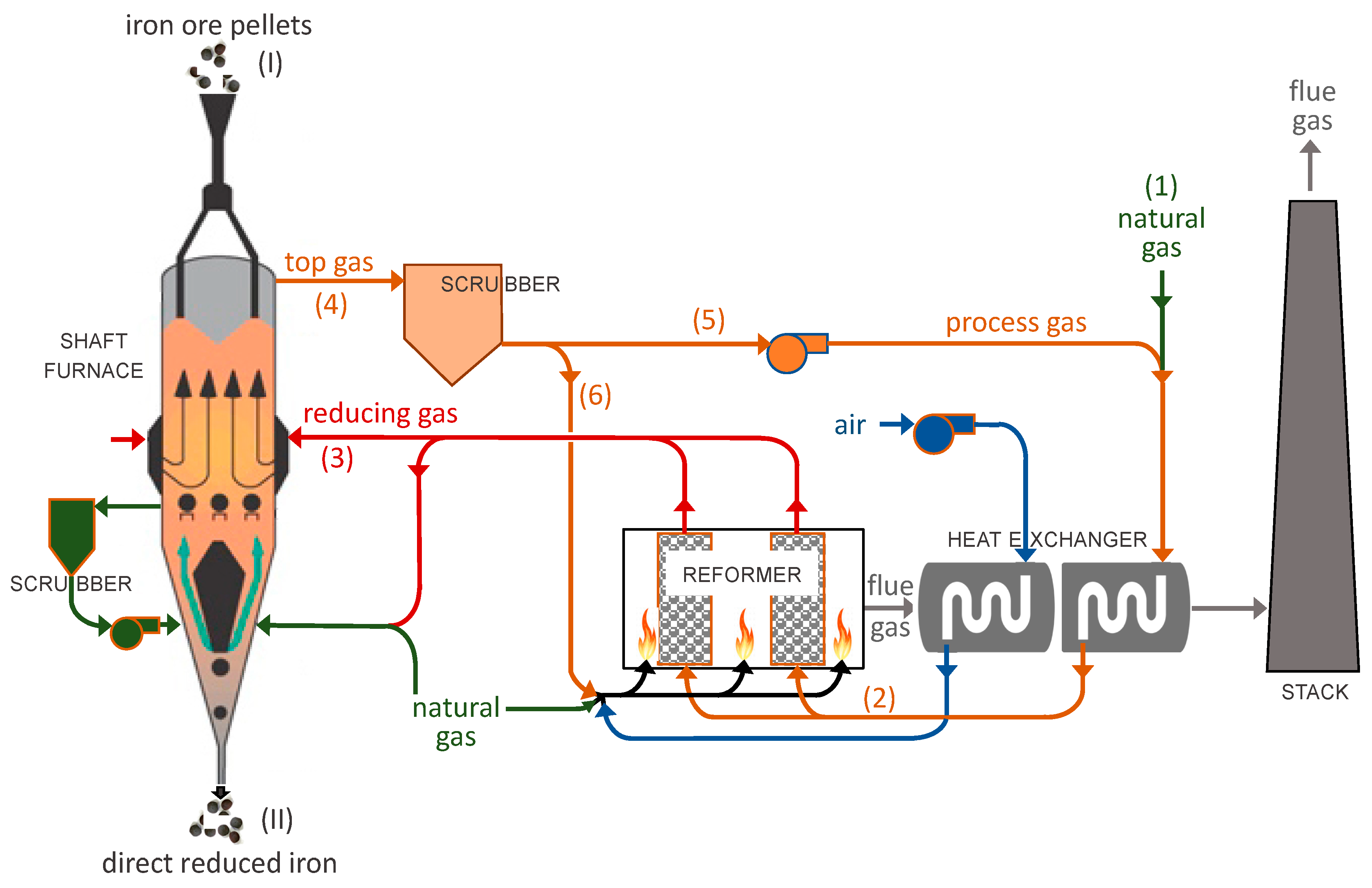
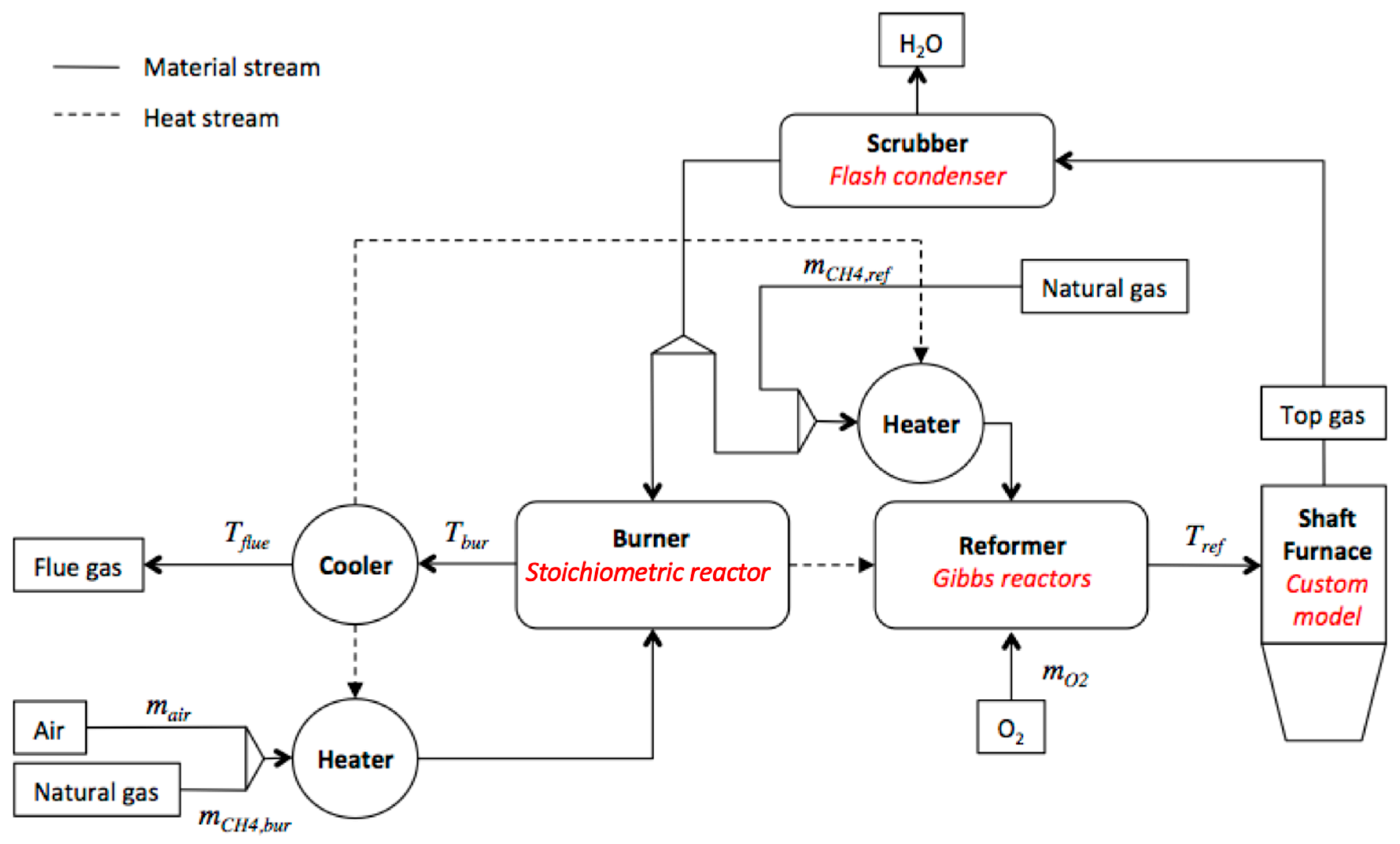
2. Modeling Scheme
- The reducing gas characteristics (composition, temperature), pellet properties (diameter, flow rate) and the reactor dimensions are considered as model inputs, with the cooling gas specified.
- The split of input pellets between Zone 1 and Zone 2 is calculated based on the given reducing and cooling gas flow rates.
- The shaft outputs are calculated and the DRI as well as top gas properties are determined.
- The gas loop is calculated with top gas as input with the goal of having a converged recycling. The convergence is obtained when the calculated heated outlet reformed gas characteristics are sufficiently close to the inlet reducing gas characteristics.
3. Process Computer-Aided Optimization
3.1. Definition of the Optimization Problem
- The first term is the normalized carbon emissions that need to be minimized. This term was multiplied by a power (a = 0.5) of the relative wustite reduction height . hreac is the reactor height and hFeO is the height where wustite rate falls below a low value (10−6 kg h−1). This was done in order to keep a good column performance.
- Two other terms were added to ensure the feasibility of the proposed modifications. The middle term drives the convergence of the gas loop (feasibility), ensured when the H2 flowrate at the reformer outlet is equal to that at the shaft inlet: . The last term was added to get similar metallization rates, via the input pellet split between original and optimized cases: .
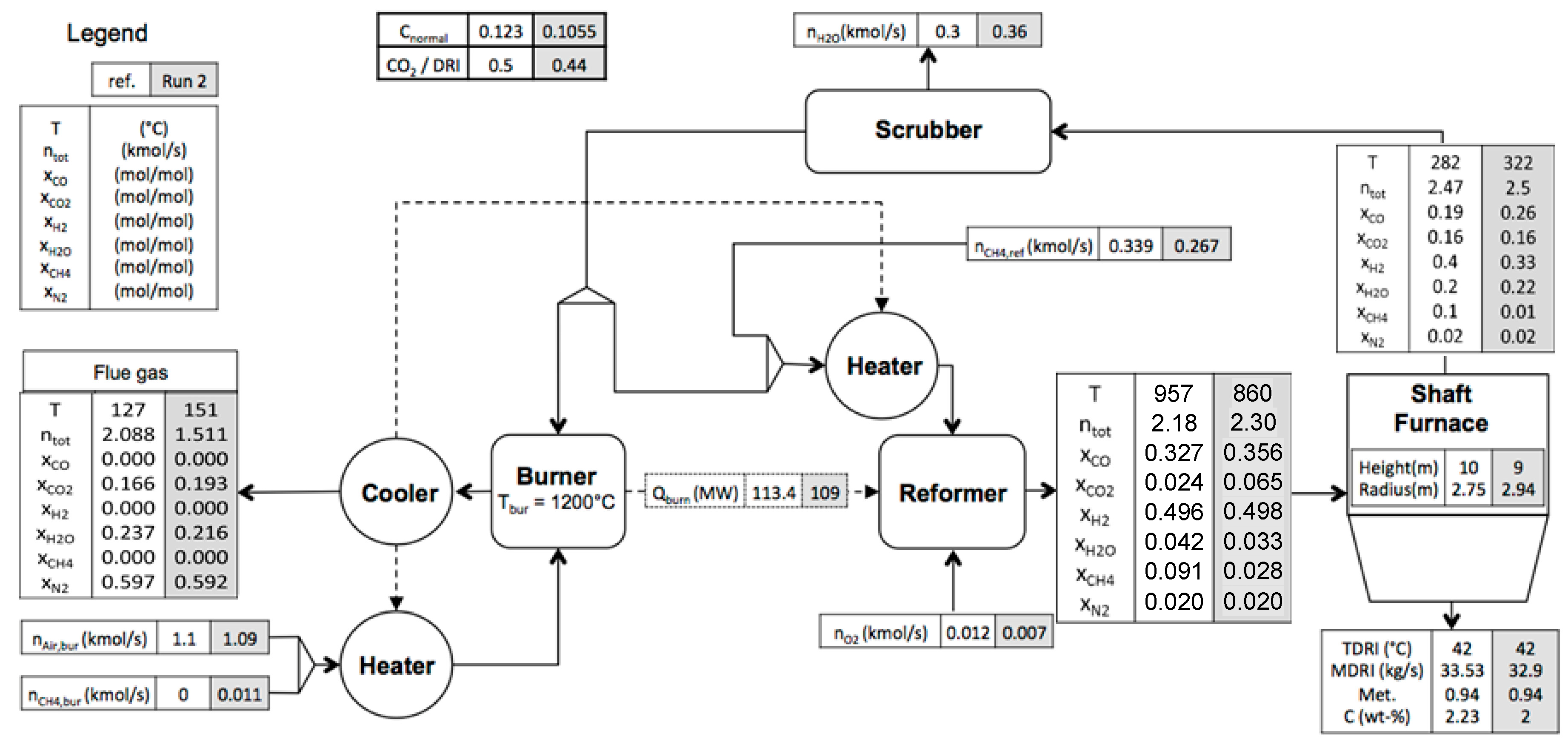
3.2. Launching of Optimization Runs
3.3. Results Analysis
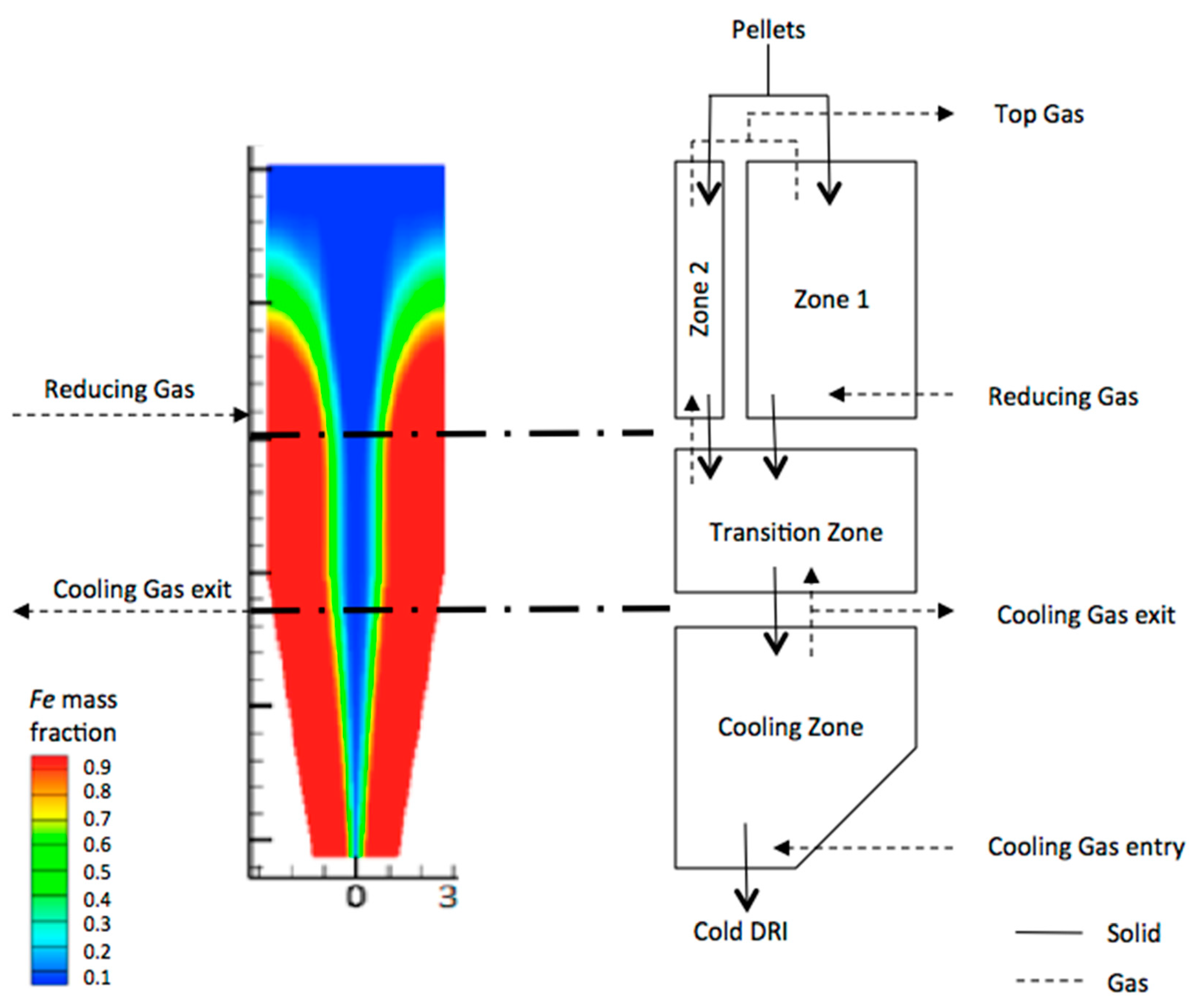
3.4. Comparison of Profiles in the Reduction Zone (Zone 1)
3.5. Comparison with Previous Literature Works
3.6. Techno-Economic Remarks
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Quader, M.A.; Ahmed, S.; Ghazilla, R.A.R.; Ahmed, S.; Dahari, M. A comprehensive review on energy efficient CO2 breakthrough technologies for sustainable green iron and steel manufacturing. Renew. Sustain. Energy Rev. 2015, 50, 594–614. [Google Scholar] [CrossRef]
- van Ruijven, B.J.; van Vuuren, D.P.; Boskaljon, W.; Neelis, M.L.; Saygin, D.; Patel, M.K. Long-term model-based projections of energy use and CO2 emissions from the global steel and cement industries. Resour. Conserv. Recycl. 2016, 112, 15–36. [Google Scholar] [CrossRef]
- Song, J.; Jiang, Z.; Bao, C.; Xu, A. Comparison of Energy Consumption and CO2 Emission for Three Steel Production Routes-Integrated Steel Plant Equipped with Blast Furnace, Oxygen Blast Furnace or COREX. Metals 2019, 9, 364. [Google Scholar] [CrossRef]
- Xu, C.; Cang, D. A Brief Overview of Low CO2 Emission Technologies for Iron and Steel Making. J. Iron Steel Res. Int. 2010, 17, 1–7. [Google Scholar] [CrossRef]
- Müller, N.; Herz, G.; Reichelt, E.; Jahn, M. CO2 emission reduction potential in the steel industry by integration of a direct reduction process into existing steel mills. In Proceedings of the Challenges for Petrochemicals and Fuels: Integration of Value Chains and Energy Transition DGMK Conference, Berlin, Germany, 10–12 October 2018. [Google Scholar]
- Buergler, T.; Kofler, I. Direct reduction technology as a flexible tool to reduce the CO2 intensity of iron and steelmaking. BHM Berg-und Hüttenmännische Monatshefte 2017, 162, 14–19. [Google Scholar] [CrossRef]
- Huitu, K.; Helle, M.; Helle, H.; Kekkonen, M.; Saxen, H. Optimization of Midrex Direct Reduced Iron Use in Ore-Based Steelmaking. Steel Res. Int. 2015, 86, 456–465. [Google Scholar] [CrossRef]
- Midrex. World Direct Reduction Statistics. 2019. Available online: https://www.midrex.com/wp-content/uploads/Midrex_STATSbookprint_2018Final-1.pdf (accessed on 7 February 2020).
- Bechara, R.; Hamadeh, H.; Mirgaux, O.; Patisson, F. Optimization of the Iron Ore Direct Reduction Process through Multiscale Process Modeling. Materials 2018, 11, 1094. [Google Scholar] [CrossRef] [PubMed]
- Nogare, D.D.; Zugliano, A.; Primavera, A.; Melchiori, T.; Canu, P. Multiphysics simulation of a DRP shaft furnace. In Proceedings of the STEELSIM 2013 International Conference on Modelling and Simulation of Metallurgical Processes in Steelmaking, Ostrava, Czech Republic, 10–12 September 2013. [Google Scholar]
- Hamadeh, H.; Mirgaux, O.; Patisson, F. Detailed Modeling of the Direct Reduction of Iron Ore in a Shaft Furnace. Materials 2018, 11, 1865. [Google Scholar] [CrossRef] [PubMed]
- Parisi, D.; Laborde, M.A. Modelling of Counter Current Moving Bed Gas-Solid Reactor Used in Direct Reduction of Iron Ore. Chem. Eng. J. 2004, 104, 35–43. [Google Scholar] [CrossRef]
- Alamsari, B.; Torii, S.; Trianto, A.; Bindar, Y. Study of the Effect of Reduced Iron Temperature Rising on Total Carbon Formation in Iron Reactor Isobaric and Cooling Zone. Adv. Mech. Eng. 2010, 2, 192430. [Google Scholar] [CrossRef]
- Nouri, S.M.M.; Ebrahim, H.A.; Jamshidi, E. Simulation of direct reduction reactor by the grain model. Chem. Eng. J. 2011, 166, 704–709. [Google Scholar] [CrossRef]
- Shams, A.; Moazeni, F. Modeling and Simulation of the MIDREX Shaft Furnace: Reduction, Transition and Cooling Zones. JOM 2015, 67, 2681–2689. [Google Scholar] [CrossRef]
- Ajbar, A.; Alhumaizi, K.; Soliman, M.A.; Ali, E. Model-based energy analysis of an integrated Midrex-based iron/steel plant. Chem. Eng. Commun. 2014, 201, 1686–1704. [Google Scholar] [CrossRef]
- Ghadi, A.Z.; Valipour, M.S.; Biglari, M. CFD simulation of two-phase gas-particle flow in the Midrex shaft furnace: The effect of twin gas injection system on the performance of the reactor. Int. J. Hydrog. Energy 2017, 42, 103–118. [Google Scholar] [CrossRef]
- Hamadeh, H. Modélisation mathématique détaillée du procédé de réduction directe du minerai de fer. Ph.D. Thesis, Université de Lorraine, Nancy, France, 2017. Available online: https://tel.archives-ouvertes.fr/tel-01740462/ (accessed on 7 February 2020).
- Duarte, P.E.; Becerra, J. Reducing greenhouse gas emissions with Energiron non-selective carbon-free emissions scheme. Stahl und Eisen Zeitschrift fuer die Herstellung und Verarbeitung von Eisen und Stahl 2011, 131, S85–S86, S88–S90, S92–S94. [Google Scholar]
- Tanaka, H. Potential for CO2 Emissions Reduction in MIDREX Direct Reduction Process. In Proceedings of the IEA (International Energy Agency) Greenhouse Gas R&D workshop, Tokyo, Japan, 5–7 November 2013; Available online: https://ieaghg.org/2-uncategorised/392-iron-steel-workshop (accessed on 7 February 2020).
- Knop, K.; Ångström, S. Process for Production of Direct Reduced Iron. U.S. Patent No. 8,709,128, 29 April 2014. [Google Scholar]
- Ranzani da Costa, A.; Wagner, D.; Patisson, F. Modelling a new, low CO2 emissions, hydrogen steelmaking process. J. Clean. Prod. 2013, 46, 27–35. [Google Scholar] [CrossRef]
- Al-Malah, K.I.M. Aspen Plus: Chemical Engineering Applications; John Wiley & Sons: Hoboke, NJ, USA, 2016; ISBN 978-1-119-13123-6. [Google Scholar]
- Navid, A.; Khalilarya, S.; Abbasi, M. Diesel engine optimization with multi-objective performance characteristics by non-evolutionary Nelder-Mead algorithm: Sobol sequence and Latin hypercube sampling methods comparison in DoE process. Fuel 2018, 228, 349–367. [Google Scholar] [CrossRef]
- Ang, S.M.C.; Brett, D.J.L.; Fraga, E.S. A multi-objective optimisation model for a general polymer electrolyte membrane fuel cell system. J. Power Sources 2010, 195, 2754–2763. [Google Scholar] [CrossRef]
- Yildiz, A.R. A novel hybrid whale-Nelder-Mead algorithm for optimization of design and manufacturing problems. Int. J. Adv. Manuf. Technol. 2019, 105, 5091–5104. [Google Scholar] [CrossRef]
- Box, M.J. A new method of constrained optimization and a comparison with other methods. Comput. J. 1965, 8, 42–52. [Google Scholar] [CrossRef]
- Ölvander, J. Available online: https://complexmethod.readthedocs.io/en/latest/index.html (accessed on 7 February 2020).

| Hematite reduction | |
| Magnetite reduction | |
| Wustite reduction | |
| Water gas shift | |
| Steam methane reforming | |
| Methane cracking | |
| Boudouard reaction |
| Variable Number | Variable Name | Description | Original Value/Range |
|---|---|---|---|
| 1 | nCO,red | Component molar flow rates in the reducing gas inlet (kmol/s) | 0.7/[0.65–1.2] |
| 2 | nH2,red | 1.08/[0.8–1.2] | |
| 3 | nH2O,red | 0.09/[0.02–0.3] | |
| 4 | nCO2,red | 0.05/[0.02–0.3] | |
| 5 | nCH4,red | 0.19/[0.02–0.25] | |
| 6 | Treducing gas | Reducing gas temperature (°C) | 957/[850–970] |
| 7 | mpellet | Pellet mass flow rate (kg/s) | 45.54/[42.5–54] |
| 8 | rreac | Radius of the shaft furnace (m) | 2.75/[2.25–3.25] |
| 9 | hreac | Height of shaft furnace * | 10/[6–14] |
| 10 | dp | Pellet diameter (m) | 0.015/[0.01–0.016] |
| Variables | Reference | Run 1 | Run 2 | |
|---|---|---|---|---|
| 1 | 0.71 | 0.98 | 0.82 | |
| 2 | 1.08 | 1.07 | 1.146 | |
| 3 | 0.0916 | 0.096 | 0.075 | |
| 4 | 0.05 | 0.12 | 0.15 | |
| 5 | 0.1981 | 0.167 | 0.064 | |
| 6 | 957 | 882 | 860 | |
| 7 | 45.54 | 45.54 | 44.9 | |
| 8 | (m) | 2.75 | 2.75 | 2.94 |
| 9 | (m) | 10 | 10 | 9 |
| 10 | dp (m) | 0.015 | 0.015 | 0.0145 |
| Objective | ||||
| (kg/kg) | 0.123 | 0.105 | 0.105 | |
| Results | ||||
| 33.527 | 33.53 | 32.90 | ||
| Metallization (%) | 94.2 | 94.1 | 94.2 | |
| Carbon mass fraction in DRI | 0.0235 | 0.0237 | 0.02 | |
| 1.51 | 1.09 | 1.39 | ||
| 12 | 9.4 | 8.7 | ||
| Recycling ratio * | 0.63 | 0.77 | 0.73 | |
| 2.178 | 2.479 | 2.29 | ||
| 30.35 | 40.44 | 35.34 | ||
| (kmol/s) | 0.339 | 0.285 | 0.267 | |
| (kmol/s) | 0 | 0.008 | 0.01 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Béchara, R.; Hamadeh, H.; Mirgaux, O.; Patisson, F. Carbon Impact Mitigation of the Iron Ore Direct Reduction Process through Computer-Aided Optimization and Design Changes. Metals 2020, 10, 367. https://doi.org/10.3390/met10030367
Béchara R, Hamadeh H, Mirgaux O, Patisson F. Carbon Impact Mitigation of the Iron Ore Direct Reduction Process through Computer-Aided Optimization and Design Changes. Metals. 2020; 10(3):367. https://doi.org/10.3390/met10030367
Chicago/Turabian StyleBéchara, Rami, Hamzeh Hamadeh, Olivier Mirgaux, and Fabrice Patisson. 2020. "Carbon Impact Mitigation of the Iron Ore Direct Reduction Process through Computer-Aided Optimization and Design Changes" Metals 10, no. 3: 367. https://doi.org/10.3390/met10030367
APA StyleBéchara, R., Hamadeh, H., Mirgaux, O., & Patisson, F. (2020). Carbon Impact Mitigation of the Iron Ore Direct Reduction Process through Computer-Aided Optimization and Design Changes. Metals, 10(3), 367. https://doi.org/10.3390/met10030367





