Insight into the Role and Mechanism of Nano MgO on the Hot Compressive Deformation Behavior of Mg-Zn-Ca Alloys
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Initial Microstructure Analysis
3.2. Flow Curves
3.3. Constitutive Analysis
3.4. Processing Maps
4. Discussion
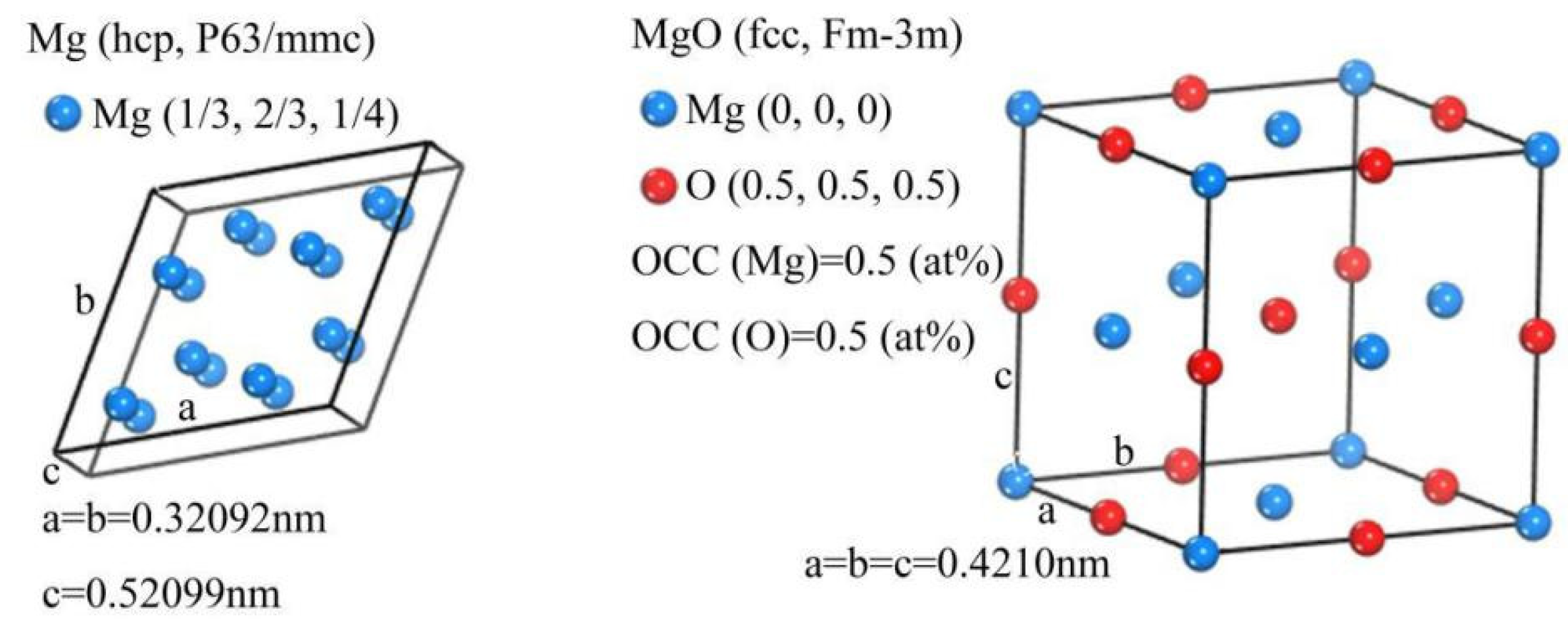
4.1. Crystal Analysis
4.2. Flow Behavior
4.3. Deformation Mechanism
4.4. Microstructure Evolution
5. Conclusions
- (1)
- The crystal structure analysis showed that MgO particles can be used as effective and stable nucleation cores of a Mg matrix, and a fine and more homogeneous microstructure of MZCM was formed with the addition of nano MgO particles.
- (2)
- The flow stress of MZC and MZCM showed typical DRX features, and the flow stress of MZCM is lower than that of MZC during deformation at 523–623 K but this result is the opposite at 673 K and 0.1–1 s−1. The average εc/εp value of MZCM is lower than that of MZC, revealing that the addition of nano MgO promotes the DRX of MZC. This result is consistent with microstructure evolution.
- (3)
- The constitutive equation of MZCM was developed; the n and m value show that dislocation climb is the dominate compressive deformation mechanism for MZC and MZCM, but the higher m value of MZCM might be attributed to the grain boundary sliding mechanism. The n and Q values of MZCM were lower than those of MZC under the same deformation condition, but the m value showed a reverse trend, which implies that the addition of nano MgO particles decreases the stress sensitivity and deformation resistance for thermal deformation and improves the plasticity of MZC.
- (4)
- According to the processing maps, compared with MZC, MZCM exhibits higher power dissipation efficiency, a larger DRX region and smaller instability regions, but the area of the low-temperature high strain-rate instability region for MZCM is larger and the area of the low-temperature high strain-rate instability region instability region for MZCM is smaller. Combined with microstructure evolution, a relatively lower Z value means sufficient DRX occurred in MZCM, and the optimum hot working condition for MZCM was determined to be 623–653 K and 0.01–0.001 s−1.
Author Contributions
Funding
Conflicts of Interest
References
- Ahmad, R.; Wu, Z.X.; Curtin, W.A. Analysis of double cross-slip of pyramidal I <c + a> screw dislocations and implications for ductility in Mg alloys. Acta Mater. 2020, 183, 228–241. [Google Scholar] [CrossRef]
- Bommal, V.K.; Krishn, M.G.; Rao, C.T. Magnesium matrix composites for biomedical applications: A review. J. Magn. Alloys 2019, 7, 72–79. [Google Scholar] [CrossRef]
- Zheng, Y.F.; Gu, X.N.; Xi, Y.L.; Chai, D.L. In vitro degradation and cytotoxicity of Mg/Ca composites produced by powder metallurgy. Acta Biomater. 2010, 6, 1783–1791. [Google Scholar] [CrossRef] [PubMed]
- Pollock, T. Weight Loss with Magnesium Alloys. Science 2010, 328, 986–987. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.R.; Li, Z.; You, C.; Chen, M.F. Effects of MgO modified β-TCP nanoparticles on the microstructure and properties of β-TCP/Mg-Zn-Zr composites. Bioact. Mater. 2017, 2, 1–9. [Google Scholar] [CrossRef]
- Chen, Y.W.; Moussi, J.; Drury, J.L.; Wataha, J.C. Zirconia in Biomedical Applications. Expert Rev. Med. Devices 2016, 13, 945–963. [Google Scholar] [CrossRef]
- Mounib, M.; Pavese, M.; Badini, C.; Lefebvre, W.; Dieringa, H. Reactivity and Microstructure of Al2O3-Reinforced Magnesium-Matrix Composites. Adv. Mater. Sci. Eng. 2014, 2014, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Lei, T.; Tang, W.; Cai, S.H.; Feng, F.F.; Li, N.F. On the corrosion behaviour of newly developed biodegradable Mg-based metal matrix composites produced by in situ reaction. Corros. Sci. 2012, 54, 270–277. [Google Scholar] [CrossRef]
- Meenashisundaram, G.K.; Seetharaman, S.; Gupta, M. Enhancing overall tensile and compressive response of pure Mg using nano-TiB2 particulates. Mater. Charact. 2014, 94, 178–188. [Google Scholar] [CrossRef]
- Goh, C.S.; Gupta, M.; Wei, J.; Lee, L.C. Characterization of High Performance Mg/MgO Nanocomposites. J. Compos. Mater. 2007, 41, 2325–2335. [Google Scholar] [CrossRef]
- Lin, G.Y.; Liu, D.D.; Chen, M.F.; You, C.; Li, Z.; Wang, Y. Preparation and characterization of biodegradable Mg-Zn-Ca/MgO nanocomposites for biomedical applications. Mater. Charact. 2018, 144, 120–130. [Google Scholar] [CrossRef]
- Shahin, M.; Munir, K.; Wen, C.; Li, Y. Magnesium matrix nanocomposites for orthopedic applications: A review from mechanical, corrosion, and biological perspectives. Acta Biomater. 2019, 96, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.R.; Li, Z.; Chen, M.F.; You, C.; Liu, D. The effect of nano β-TCP on hot compression deformation behavior and microstructure evolution of the biomedical Mg-Zn-Zr alloy. Mater. Sci. Eng. A 2018, 715, 205–213. [Google Scholar] [CrossRef]
- Xiao, P.; Gao, Y.M.; Xu, F.X.; Yang, S.; Li, Y.; Li, B. Hot deformation behavior of in-situ nanosized TiB2 particulate reinforced AZ91 Mg matrix composite. J. Alloys Compd. 2019, 798, 1–11. [Google Scholar] [CrossRef]
- Raj, R. Development of a Processing Map for Use in Warm-Forming and Hot-Forming Processes. Metall. Trans. A 1981, 12, 1089–1097. [Google Scholar] [CrossRef]
- Łyszkowski, R.; Bystrzycki, J. Hot deformation and processing maps of a Fe-Al intermetallic alloy. Mater. Charact. 2014, 96, 196–205. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Q.; Liu, G.; Guo, W.; Jiang, H.; Ding, W. Effect of SiC particles and the particulate size on the hot deformation and processing map of AZ91 magnesium matrix composites. Mater. Sci. Eng. A 2017, 707, 315–324. [Google Scholar] [CrossRef]
- Fan, Z.; Zuo, Y.B.; Jiang, B. A new technology for treating liquid metals with intensive melt shearing. Mater. Sci. Forum 2011, 690, 141–144. [Google Scholar] [CrossRef]
- Cheng, W.L.; Bai, Y.; Ma, S.C.; Wang, L.; Wang, H.; Yu, H. Hot deformation behavior and workability characteristic of a fine-grained Mg-8Sn-2Zn-2Al alloy with processing map. J. Mater. Sci. Tech. 2019, 35, 1198–1209. [Google Scholar] [CrossRef]
- Hao, J.Q.; Zhang, J.S.; Xu, C.X.; Ni, K. Optimum parameters and kinetic analysis for hot working of a solution-treated Mg-Zn-Y-Mn magnesium alloy. J. Alloys Compd. 2018, 754, 283–296. [Google Scholar] [CrossRef]
- Chadha, K.; Shahriari, D.; Tremblay, R.; BHATTACHARJEE, P.P.; JAHAZI, M. Deformation and Recrystallization Behavior of the Cast Structure in Large Size, High Strength Steel Ingots: Experimentation and Modeling. Metall. Mater. Trans. A 2017, 48, 4297–4313. [Google Scholar] [CrossRef]
- Tahreen, N.; Zhang, D.F.; Pan, F.S.; Jiang, Q.; Li, C.; Li, D.Y. Characterization of hot deformation behavior of an extruded Mg-Zn-Mn-Y alloy containing LPSO phase. J. Alloys Compd. 2015, 644, 814–823. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Seshacharyulu, T. Processing maps for hot working of titanium alloys. Mater. Sci. Eng. A 1998, 243, 82–88. [Google Scholar] [CrossRef]
- Ansari, N.; Tran, B.; Poole, W.J.; Singh, S.S.; Krishnaswamy, H.; Jain, J. High temperature deformation behavior of Mg-5wt.%Y binary alloy: Constitutive analysis and processing maps. Mater. Sci. Eng. A 2020, 777, 139051. [Google Scholar] [CrossRef]
- Kwak, T.Y.; Kim, W.J. Effect of refinement of grains and icosahedral phase on hot compressive deformation and processing maps of Mg-Zn-Y magnesium alloys with different volume fractions of icosahedral phase. J. Mater. Sci. Tech. 2019, 35, 181–191. [Google Scholar] [CrossRef]
- Suttona, S.C.; Luo, A.A. Constitutive behavior and processing maps of a new wrought magnesium alloy ZE20 (Mg-2Zn-0.2Ce). J. Magn. Alloys 2020, 8, 111–126. [Google Scholar] [CrossRef]
- Wang, W.Y.; Tang, B.; Shang, S.L.; Wang, J.; Li, S.; Wang, Y. Local lattice distortion mediated formation of stacking faults in Mg alloys. Acta Mater. 2019, 170, 231–239. [Google Scholar] [CrossRef] [Green Version]
- Bramfitt, B.L. The effect of carbide and nitride additions on the heterogeneous nucleation behavior of liquid iron. Metall. Trans. 1970, 1, 1987–1995. [Google Scholar] [CrossRef]
- Li, L.; Wang, Y.; Li, H.; Jiang, W.; Wang, T.; Zhang, C.C.; Wang, F.; Garmestani, H. Effect of the Zener-Hollomon parameter on the dynamic recrystallization kinetics of Mg-Zn-Zr-Yb magnesium alloy. Comp. Mater. Sci. 2019, 166, 221–229. [Google Scholar] [CrossRef]
- He, D.G.; Lin, Y.C.; Chen, J.; Chen, D.D.; Huang, J.; Tang, Y. Microstructural evolution and support vector regression model for an aged Ni-based superalloy during two-stage hot forming with stepped strain rates. Mater. Des. 2018, 154, 51–62. [Google Scholar] [CrossRef]
- Queen, H.J.; Ryan, N.D. Constitutive analysis in hot working. Mater. Sci. Eng. A 2002, 322, 43–63. [Google Scholar]
- Xia, X.S.; Chen, Q.; Huang, S.H.; Lin, J.; Hu, C.; Zhao, Z. Hot deformation behavior of extruded Mg-Zn-Y-Zr alloy. J. Alloys Compd. 2015, 644, 308–316. [Google Scholar] [CrossRef]
- Tahreen, N.; Zhang, D.F.; Pan, F.S.; Jiang, X.Q.; Li, D.Y.; Chen, D.L. Hot deformation and processing map of an as-extruded Mg-Zn-Mn-Y alloy containing I and W phases. Mater. Des. 2015, 87, 245–255. [Google Scholar] [CrossRef]
- Xia, X.; Chen, Q.; Zhang, K.; Zhao, Z.; Ma, M.; Li, X. Hot deformation behavior and processing map of coarse-grained Mg-Gd-Y-Nd-Zr alloy. Mater. Sci. Eng. A 2013, 587, 283–290. [Google Scholar] [CrossRef]
- Poliak, E.I.; Jonas, J.J. Initiation of Dynamic Recrystallization in Constant Strain Rate Hot Deformation. ISIJ Int. 2003, 43, 684–691. [Google Scholar] [CrossRef] [Green Version]
- Jonas, J.J.; Quelennec, X.; Jiang, L.; Martin, E. The Avrami kinetics of dynamic recrystallization. Acta Mater. 2009, 57, 2748–2756. [Google Scholar] [CrossRef]
- Barnett, M.R. Hot Working Microstructure Map for Magnesium AZ31. Mater. Sci. Forum 2003, 426, 515–520. [Google Scholar] [CrossRef]
- Park, S.H.; Jung, J.G.; Kim, Y.M.; You, B.S. A new high-strength extruded Mg-8Al-4Sn-2Zn alloy. Mater. Lett. 2015, 139, 35–38. [Google Scholar] [CrossRef]
- Sherby, O.D.; Wadsworth, J. Superplasticity-Recent advances and future directions. Prog. Mater. Sci. 1989, 33, 169–221. [Google Scholar] [CrossRef]
- Mabuchi, M.; Ameyama, K.; Iwasaki, H.; Higashi, K. Low temperature superplasticity of AZ91 magnesium alloy with non-equilibrium grain boundaries. Acta Mater. 1999, 47, 2047–2057. [Google Scholar] [CrossRef]
- Panicker, R.; Chokshi, A.H.; Mishra, R.K.; Verma, R.; Krajewski, P.E. Microstructural evolution and grain boundary sliding in a superplastic magnesium AZ31 alloy. Acta Mater. 2009, 57, 3683–3693. [Google Scholar] [CrossRef]
- Tong, L.B.; Zheng, M.Y.; Zhang, D.P.; Gan, W.M.; Brokmeier, H.G.; Meng, J. Compressive deformation behavior of Mg-Zn-Ca alloy at elevated temperature. Mater. Sci. Eng. A 2013, 586, 71–77. [Google Scholar] [CrossRef]
- Yue, C.X.; Zhang, L.W.; Liao, S.L.; Pei, J.B.; Gao, H.J.; Jia, Y.W. Research on the dynamic recrystallization behavior of GCr15 steel. Mater. Sci. Eng. A 2009, 499, 177–181. [Google Scholar] [CrossRef]















| Materials. | Zn | Ca | MgO | Mg |
|---|---|---|---|---|
| Mg-Zn-Ca (MZC) | 3 | 0.2 | - | Balance |
| n-MgO/Mg-Zn-Ca (MZCM) | 3 | 0.2 | - | Balance |
| Spectrums | Mg | Ca | Zn | O |
|---|---|---|---|---|
| #1 | 36.58 (57.08) | 16.68 (15.79) | 46.74 (27.13) | - |
| #2 | 36.73 (58.76) | 1.56 (1.28) | 60.71 (38.96) | - |
| #3 | 68.71 (59.10) | - | - | 31.29 (40.90) |
| #4 | 46.91 (58.93) | 13.88 (14.27) | 49.21 (36.80) | - |
| #5 | 45.77 (67.70) | 2.13 (1.39) | 52.10 (30.91) | - |
| Number | Mg | MgO | δ/% | ||
|---|---|---|---|---|---|
| d/nm | (hkl) | d/nm | (hkl) | ||
| 1 | 0.13867 | (200) | 0.14891 | (220) | 1.87 |
| 2 | 0.13613 | (112) | 0.21056 | (200) | 1.07 |
| 3 | 0.13396 | (201) | 0.14891 | (220) | 2.91 |
| 4 | 0.13613 | (112) | 0.14891 | (220) | 1.05 |
| Temperature/K | /s‒1 | MZC | MZCM | ||||
|---|---|---|---|---|---|---|---|
| εc | εp | εc/εp | εc | εp | εc/εp | ||
| 523 | 0.001 | 0.195 | 0.267 | 0.730 | 0.193 | 0.265 | 0.728 |
| 0.01 | 0.207 | 0.296 | 0.699 | 0.208 | 0.305 | 0.682 | |
| 0.1 | 0.215 | 0.325 | 0.662 | 0.218 | 0.338 | 0.645 | |
| 1 | 0.229 | 0.338 | 0.678 | 0.239 | 0.342 | 0.699 | |
| 573 | 0.001 | 0.093 | 0.122 | 0.762 | 0.099 | 0.161 | 0.615 |
| 0.01 | 0.139 | 0.295 | 0.471 | 0.200 | 0.294 | 0.680 | |
| 0.1 | 0.211 | 0.322 | 0.655 | 0.215 | 0.314 | 0.685 | |
| 1 | 0.220 | 0.336 | 0.654 | 0.226 | 0.327 | 0.691 | |
| 623 | 0.001 | 0.087 | 0.110 | 0.791 | 0.073 | 0.117 | 0.624 |
| 0.01 | 0.102 | 0.149 | 0.685 | 0.099 | 0.176 | 0.563 | |
| 0.1 | 0.178 | 0.281 | 0.633 | 0.211 | 0.284 | 0.743 | |
| 1 | 0.191 | 0.284 | 0.673 | 0.220 | 0.289 | 0.761 | |
| 673 | 0.001 | 0.057 | 0.065 | 0.877 | 0.054 | 0.067 | 0.806 |
| 0.01 | 0.070 | 0.078 | 0.897 | 0.076 | 0.093 | 0.817 | |
| 0.1 | 0.074 | 0.079 | 0.937 | 0.088 | 0.140 | 0.629 | |
| 1 | 0.086 | 0.092 | 0.935 | 0.203 | 0.277 | 0.733 | |
| /s‒1 | MZC | MZCM | ||||||
|---|---|---|---|---|---|---|---|---|
| 523 K | 573 K | 623 K | 673 K | 523 K | 573 K | 623 K | 673 K | |
| 1 | 45.3 | 41.4 | 38.1 | 35.2 | 34.6 | 31.6 | 29.0 | 26.9 |
| 0.1 | 43.0 | 39.1 | 35.8 | 32.9 | 32.3 | 29.3 | 26.7 | 24.6 |
| 0.01 | 40.7 | 36.8 | 33.5 | 30.6 | 29.9 | 26.9 | 24.4 | 22.3 |
| 0.001 | 38.4 | 34.5 | 31.2 | 28.3 | 27.7 | 24.6 | 22.1 | 19.9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, H.; Yu, L.; Lyu, S.; You, C.; Chen, M. Insight into the Role and Mechanism of Nano MgO on the Hot Compressive Deformation Behavior of Mg-Zn-Ca Alloys. Metals 2020, 10, 1357. https://doi.org/10.3390/met10101357
Zheng H, Yu L, Lyu S, You C, Chen M. Insight into the Role and Mechanism of Nano MgO on the Hot Compressive Deformation Behavior of Mg-Zn-Ca Alloys. Metals. 2020; 10(10):1357. https://doi.org/10.3390/met10101357
Chicago/Turabian StyleZheng, Haoran, LeiTing Yu, Shaoyuan Lyu, Chen You, and Minfang Chen. 2020. "Insight into the Role and Mechanism of Nano MgO on the Hot Compressive Deformation Behavior of Mg-Zn-Ca Alloys" Metals 10, no. 10: 1357. https://doi.org/10.3390/met10101357
APA StyleZheng, H., Yu, L., Lyu, S., You, C., & Chen, M. (2020). Insight into the Role and Mechanism of Nano MgO on the Hot Compressive Deformation Behavior of Mg-Zn-Ca Alloys. Metals, 10(10), 1357. https://doi.org/10.3390/met10101357




