Flow Stress of bcc Metals over a Wide Range of Temperature and Strain Rates
Abstract
1. Introduction
2. Materials and Methods
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kuehmann, C.J.; Olson, G.B. Computational materials design and engineering. Mater. Sci. Technol. 2009, 25, 472–478. [Google Scholar] [CrossRef]
- Allen, D.H.; Harris, C.E. A Review of Nonlinear Constitutive Models for Metals; Langley Research Center: Hampton, VA, USA, 1990. [Google Scholar]
- Bodner, S.R. Review of a unified elastic—Viscoplastic theory. In Unified Constitutive Equations for Creep and Plasticity; Springer: Dordrecht, The Netherlands, 1987; pp. 273–301. [Google Scholar] [CrossRef]
- Cowper, G.R.; Symonds, P.S. Strain-Hardening and Strain-Rate Effects in the Impact Loading of Cantilever Beams; Brown University: Providence, RI, USA, 1957. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Bodner, S.R.; Partom, Y. Constitutive equations for elastic-viscoplastic strain-hardening materials. J. Appl. Mech. 1975, 42, 385–389. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Li, Y. Flow stress of fcc polycrystals with application to OFHC Cu. Acta Mater. 1998, 46, 565–577. [Google Scholar] [CrossRef]
- Surek, T.; Luton, M.; Jonas, J. Dislocation glide controlled by linear elastic obstacles: A thermodynamic analysis. Philos. Mag. A J. Theor. Exp. Appl. Phys. 1973, 27, 425–440. [Google Scholar] [CrossRef]
- Kocks, U.; Argon, A.; Ashby, M. Thermodynamics and kinetics of slip. Prog. Mater. Sci. 1975, 19, 1–281. [Google Scholar]
- Follansbee, P.; Kocks, U. A constitutive description of the deformation of copper based on the use of the mechanical threshold stress as an internal state variable. Acta Metall. 1988, 36, 81–93. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Abed, F.H. Microstructural based models for bcc and fcc metals with temperature and strain rate dependency. Mech. Mater. 2005, 37, 355–378. [Google Scholar] [CrossRef]
- Taylor, G. Thermally-activated deformation of BCC metals and alloys. Prog. Mater. Sci. 1992, 36, 29–61. [Google Scholar] [CrossRef]
- Cosrad, H. Effect of temperature on yield and flow stress of BCC metals. Philos. Mag. 1960, 5, 745–751. [Google Scholar] [CrossRef]
- Kawata, K.; Hashimoto, S.; Kurokawa, K. Analyses of high velocity tension of bars of finite length of BCC and FCC metals with their own constitutive equations. In High Velocity Deformation of Solids; Springer: Berlin/Heidelberg, Germany, 1979; pp. 1–15. [Google Scholar]
- Zerilli, F.J.; Armstrong, R.W. Dislocation-mechanics-based constitutive relations for material dynamics calculations. J. Appl. Phys. 1987, 61, 1816–1825. [Google Scholar] [CrossRef]
- Klepaczko, J.R. Constitutive modeling in dynamic plasticity based on physical state variables-A review. Le Journal de Physique Colloques 1988, 49, C3-553–C3-560. [Google Scholar] [CrossRef]
- Bonora, N.; Milella, P.P. Constitutive modeling for ductile metals behavior incorporating strain rate, temperature and damage mechanics. Int. J. Impact Eng. 2001, 26, 53–64. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Abed, F.H. A coupled temperature and strain rate dependent yield function for dynamic deformations of bcc metals. Int. J. Plast. 2006, 22, 1398–1431. [Google Scholar] [CrossRef]
- Rusinek, A.; Klepaczko, J. Shear testing of a sheet steel at wide range of strain rates and a constitutive relation with strain-rate and temperature dependence of the flow stress. Int. J. Plast. 2001, 17, 87–115. [Google Scholar] [CrossRef]
- Rusinek, A.; Rodríguez-Martínez, J.A.; Arias, A. A thermo-viscoplastic constitutive model for FCC metals with application to OFHC copper. Int. J. Mech. Sci. 2010, 52, 120–135. [Google Scholar] [CrossRef]
- Bonora, N.; Testa, G.; Ruggiero, A.; Iannitti, G.; Mortazavi, N.; Hörnqvist, M. Numerical simulation of dynamic tensile extrusion test of ofhc copper. J. Dyn. Behav. Mater. 2015, 1, 136–152. [Google Scholar] [CrossRef][Green Version]
- Liang, R.; Khan, A.S. A critical review of experimental results and constitutive models for BCC and FCC metals over a wide range of strain rates and temperatures. Int. J. Plast. 1999, 15, 963–980. [Google Scholar] [CrossRef]
- Khan, A.S.; Liang, R. Behaviors of three BCC metal over a wide range of strain rates and temperatures: Experiments and modeling. Int. J. Plast. 1999, 15, 1089–1109. [Google Scholar] [CrossRef]
- Huh, H.; Ahn, K.; Lim, J.H.; Kim, H.W.; Park, L.J. Evaluation of dynamic hardening models for BCC, FCC, and HCP metals at a wide range of strain rates. J. Mater. Process. Technol. 2014, 214, 1326–1340. [Google Scholar] [CrossRef]
- Salvado, F.C.; Teixeira-Dias, F.; Walley, S.M.; Lea, L.J.; Cardoso, J.B. A review on the strain rate dependency of the dynamic viscoplastic response of FCC metals. Prog. Mater. Sci. 2017, 88, 186–231. [Google Scholar] [CrossRef]
- Gray III, G.T. High-strain-rate deformation: Mechanical behavior and deformation substructures induced. Annu. Rev. Mater. Res. 2012, 42, 285–303. [Google Scholar] [CrossRef]
- Conrad, H. Thermally activated deformation of metals. JOM 1964, 16, 582–588. [Google Scholar] [CrossRef]
- Klepaczko, J. A general approach to rate sensitivity and constitutive modeling of FCC and BCC metals. Impact Eff. Fast Transient Load. 1988, 3–35. [Google Scholar]
- Rusinek, A.; Zaera, R.; Klepaczko, J.R. Constitutive relations in 3-D for a wide range of strain rates and temperatures–application to mild steels. Int. J. Solids Struct. 2007, 44, 5611–5634. [Google Scholar] [CrossRef]
- Kumar, A.; Hauser, F.; Dorn, J. Viscous drag on dislocations in aluminum at high strain rates. Acta Metall. 1968, 16, 1189–1197. [Google Scholar] [CrossRef]
- Vreeland, T., Jr.; Lau, S. Study of Dislocation Mobility and Density in Metallic Crystals; Technical report; WM Keck Lab. of Engineering Materials; California Institute of Technology: Pasadena, CA, USA, 1974. [Google Scholar]
- Nabarro, F.R.; Duesbery, M.S. Dislocations in Solids; Elsevier: Amsterdam, The Netherlands, 2002; Volume 11. [Google Scholar]
- Kruml, T.; Coddet, O.; Martin, J. About the determination of the thermal and athermal stress components from stress-relaxation experiments. Acta Mater. 2008, 56, 333–340. [Google Scholar] [CrossRef]
- Johnston, W.G.; Gilman, J.J. Dislocation velocities, dislocation densities, and plastic flow in lithium fluoride crystals. J. Appl. Phys. 1959, 30, 129–144. [Google Scholar] [CrossRef]
- Vineyard, G.H. Frequency factors and isotope effects in solid state rate processes. J. Phys. Chem. Solids 1957, 3, 121–127. [Google Scholar] [CrossRef]
- Tanibayashi, M. A Method to Determine the Internal Stress and the Stress Exponent m of the Dislocation Velocity. Phys. Status Solidi (A) 1990, 120, K19–K23. [Google Scholar] [CrossRef]
- Arsenault, R.; Li, J.C. Thermally activated dislocation motion in a periodic internal stress field. Philos. Mag. A J. Theor. Exp. Appl. Phys. 1967, 16, 1307–1311. [Google Scholar] [CrossRef]
- Campbell, J.; Ferguson, W. The temperature and strain-rate dependence of the shear strength of mild steel. Philos. Mag. 1970, 21, 63–82. [Google Scholar] [CrossRef]
- Gurrutxaga-Lerma, B.; Balint, D.; Dini, D.; Sutton, A. The mechanisms governing the activation of dislocation sources in aluminum at different strain rates. J. Mech. Phys. Solids 2015, 84, 273–292. [Google Scholar] [CrossRef]
- Tanguy, B.; Besson, J.; Piques, R.; Pineau, A. Ductile to brittle transition of an A508 steel characterized by Charpy impact test: Part II: Modeling of the Charpy transition curve. Eng. Fract. Mech. 2005, 72, 413–434. [Google Scholar] [CrossRef]
- Chapuliot, S.; Lacire, M.; Marie, S.; Nédélec, M. Thermomechanical analysis of thermal shock fracture in the brittle/ductile transition zone. Part I: Description of tests. Eng. Fract. Mech. 2005, 72, 661–673. [Google Scholar] [CrossRef]
- Reytier, M.; Chapuliot, S.; Marie, S.; Ferry, L.; Nedelec, M. Study of cleavage initiation under thermal shock by tests on cracked rings and thermomechanical calculations. Nucl. Eng. Des. 2006, 236, 1039–1050. [Google Scholar] [CrossRef]
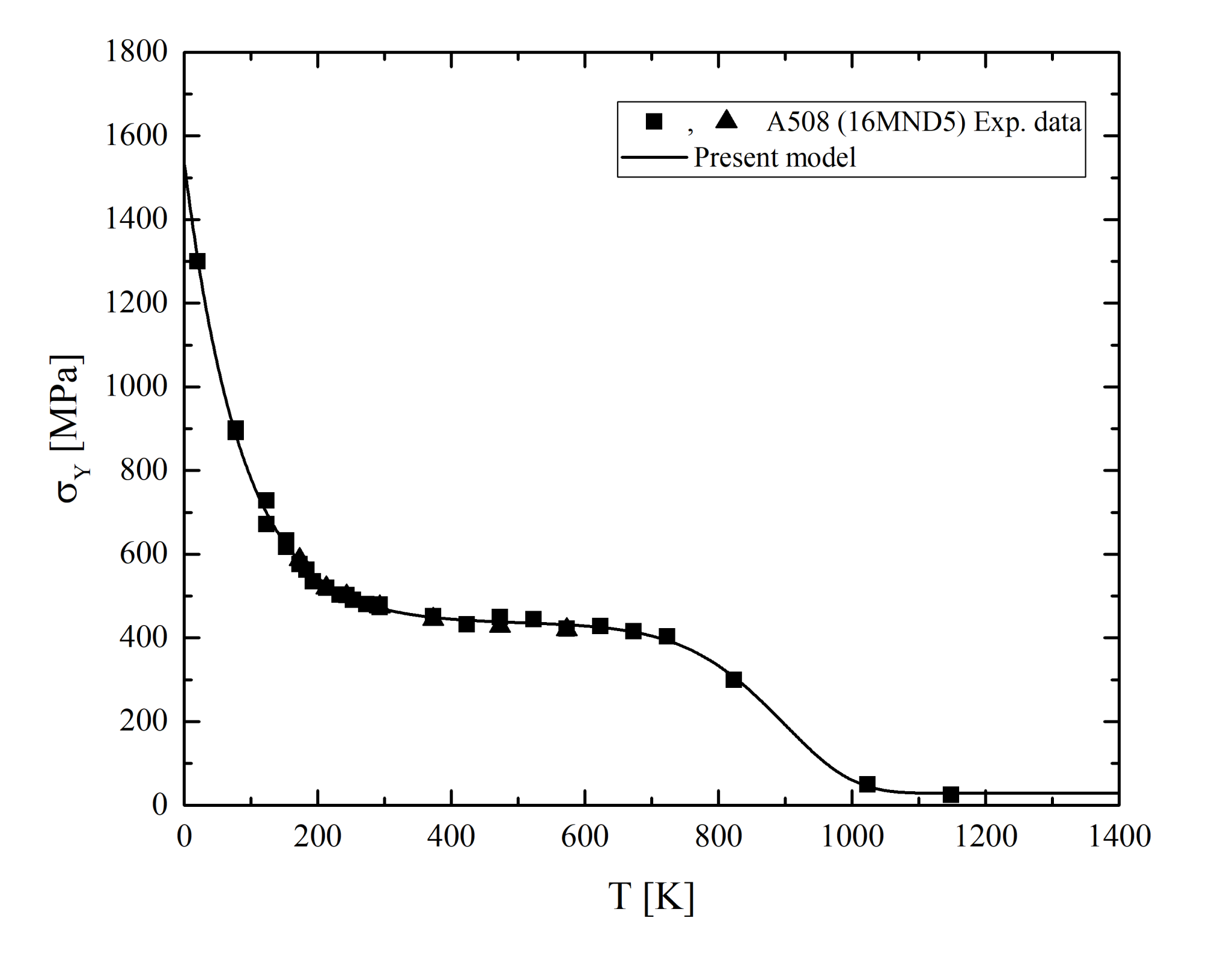
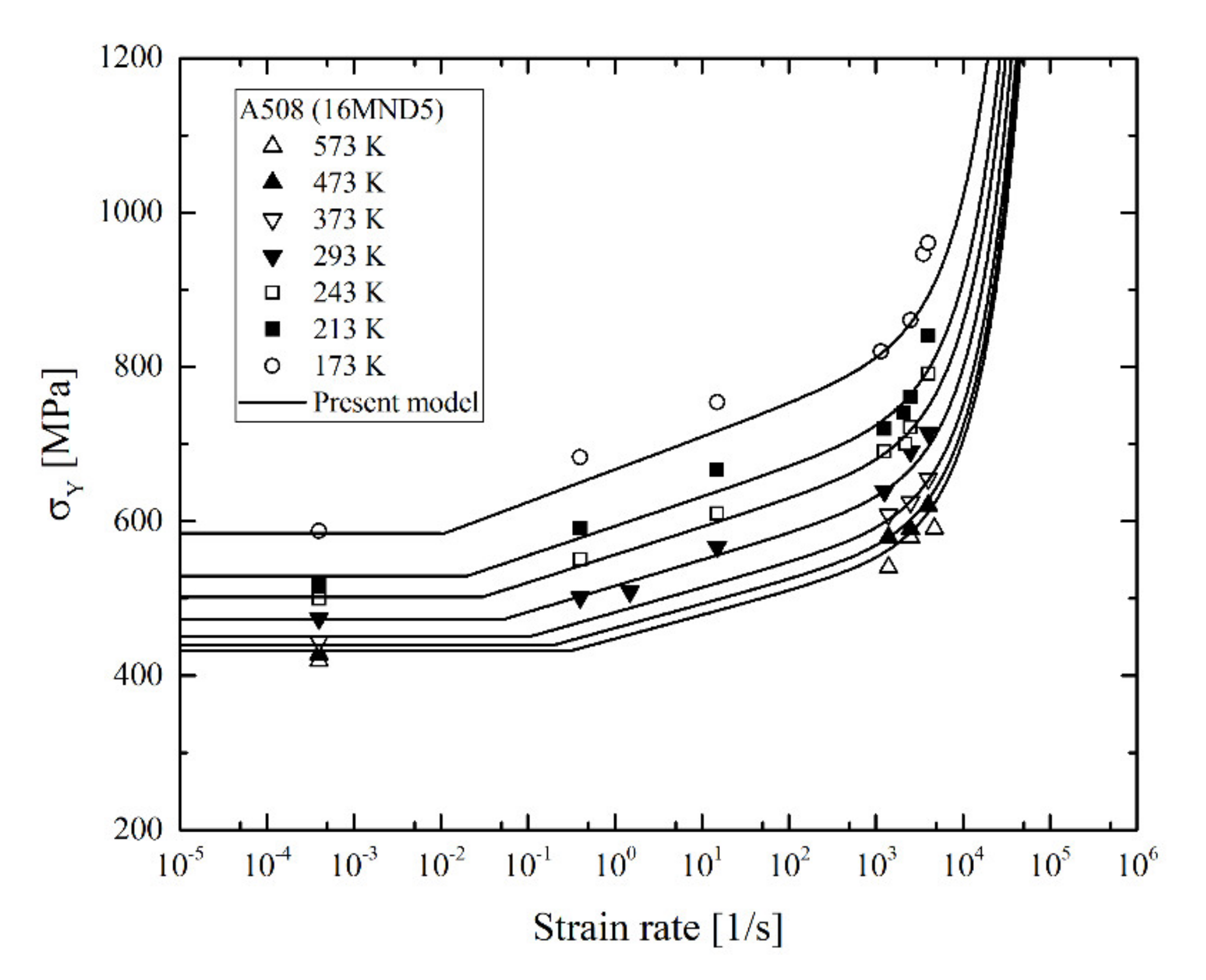
| Element | C | S | P | Si | Mn | Ni | Cr | Mo | Cu | Co |
|---|---|---|---|---|---|---|---|---|---|---|
| wt.% | 0.16 | 0.005 | 0.006 | 0.19 | 1.35 | 0.74 | 0.18 | 0.51 | 0.007 | 0.01 |
| Parameter | A | T1 [K] | T2 [K] | m | λ | Tm [K] | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Value | 28.7 | 407.0 | 2.7 | 86.5 | 908.5 | 9.83 | 0.033 | 1623 | 106 | 5 × 10-3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Testa, G.; Bonora, N.; Ruggiero, A.; Iannitti, G. Flow Stress of bcc Metals over a Wide Range of Temperature and Strain Rates. Metals 2020, 10, 120. https://doi.org/10.3390/met10010120
Testa G, Bonora N, Ruggiero A, Iannitti G. Flow Stress of bcc Metals over a Wide Range of Temperature and Strain Rates. Metals. 2020; 10(1):120. https://doi.org/10.3390/met10010120
Chicago/Turabian StyleTesta, Gabriel, Nicola Bonora, Andrew Ruggiero, and Gianluca Iannitti. 2020. "Flow Stress of bcc Metals over a Wide Range of Temperature and Strain Rates" Metals 10, no. 1: 120. https://doi.org/10.3390/met10010120
APA StyleTesta, G., Bonora, N., Ruggiero, A., & Iannitti, G. (2020). Flow Stress of bcc Metals over a Wide Range of Temperature and Strain Rates. Metals, 10(1), 120. https://doi.org/10.3390/met10010120






