Applications of the Critical Power Model to Dynamic Constant External Resistance Exercise: A Brief Review of the Critical Load Test
Abstract
1. Introduction
Historical Perspective: The Influence of Dr. Herbert A. deVries
2. The Modeling of Human Performance
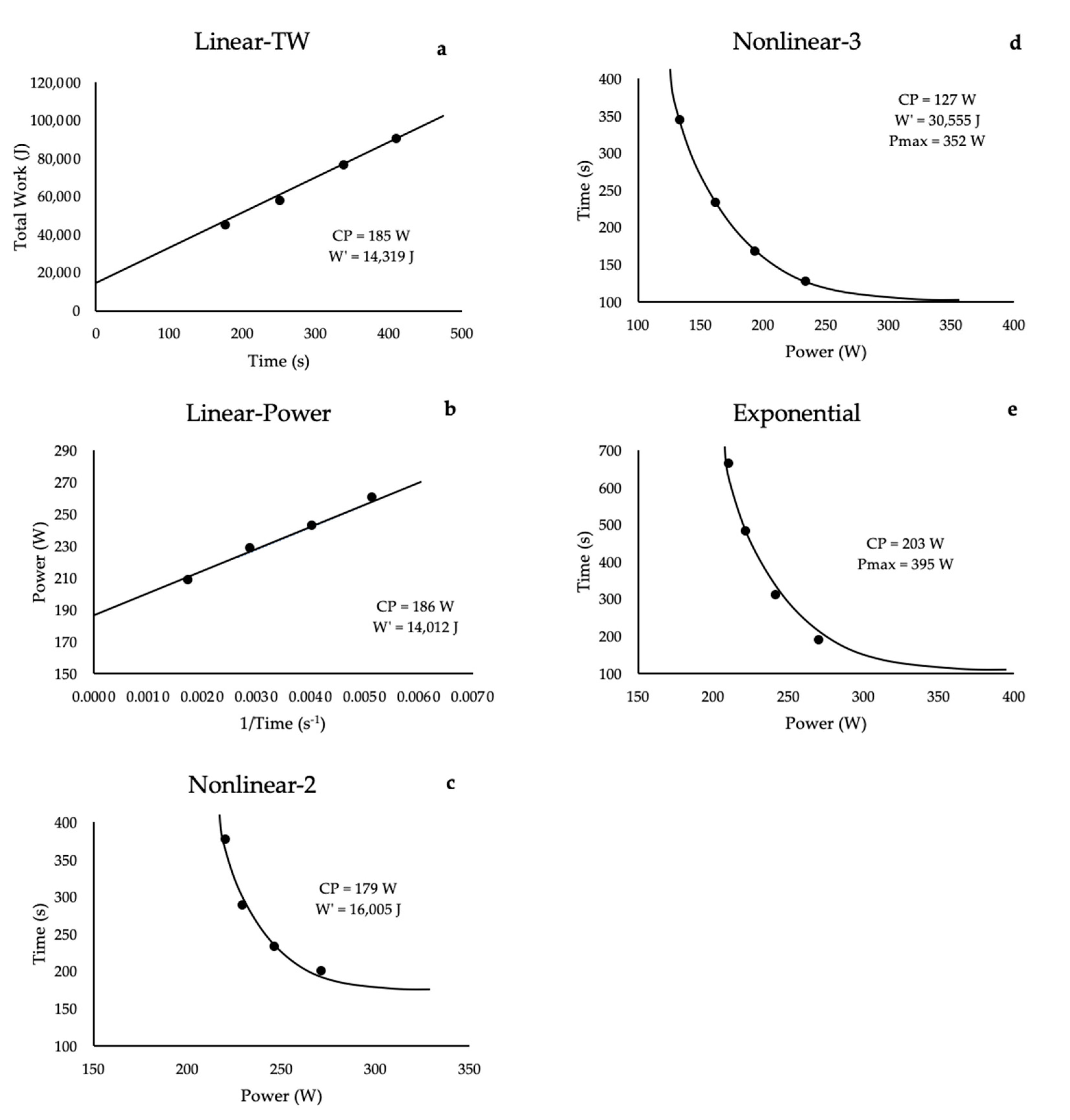
3. The Critical Power Test
4. Critical Power Test Parameters
5. Methodological Considerations
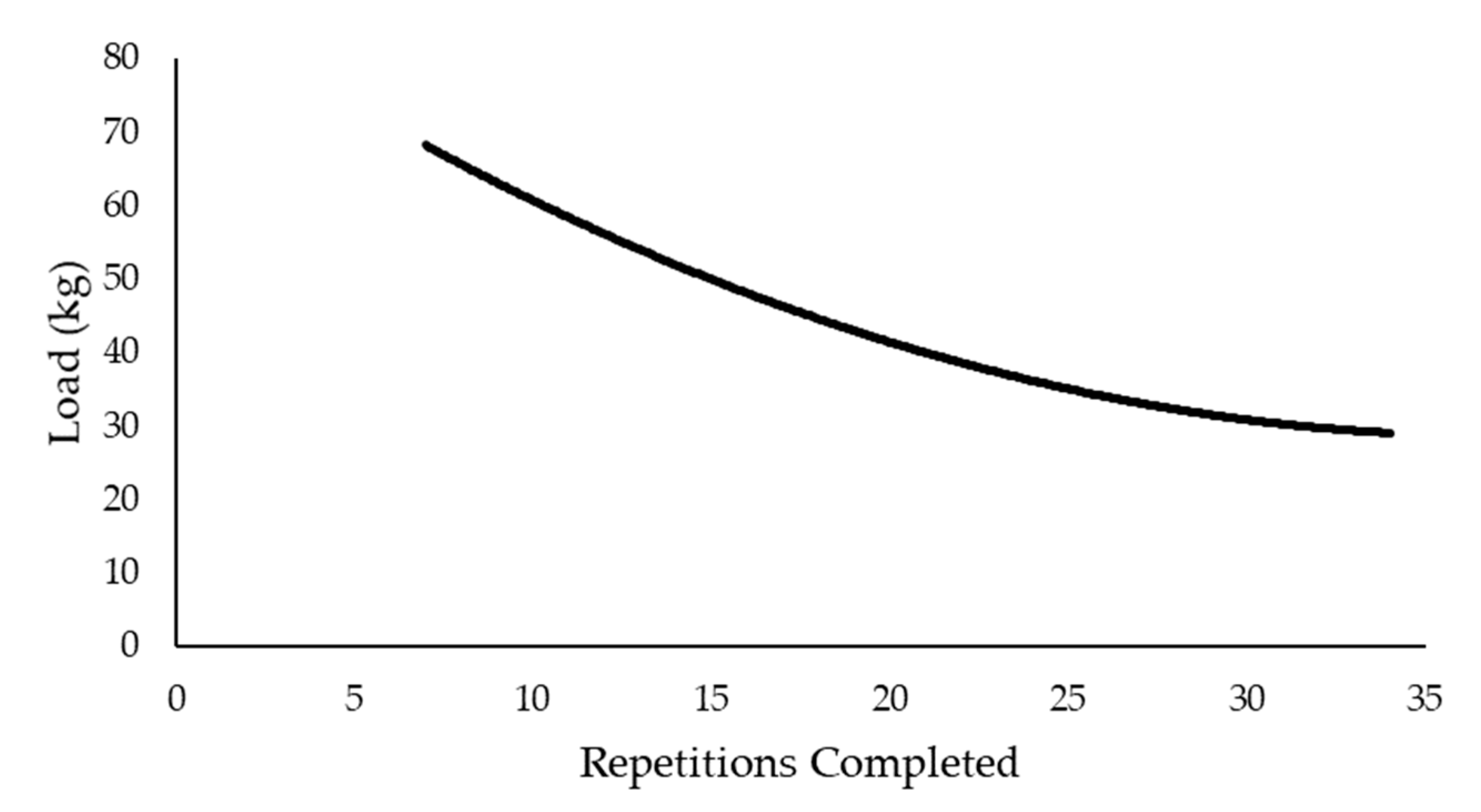
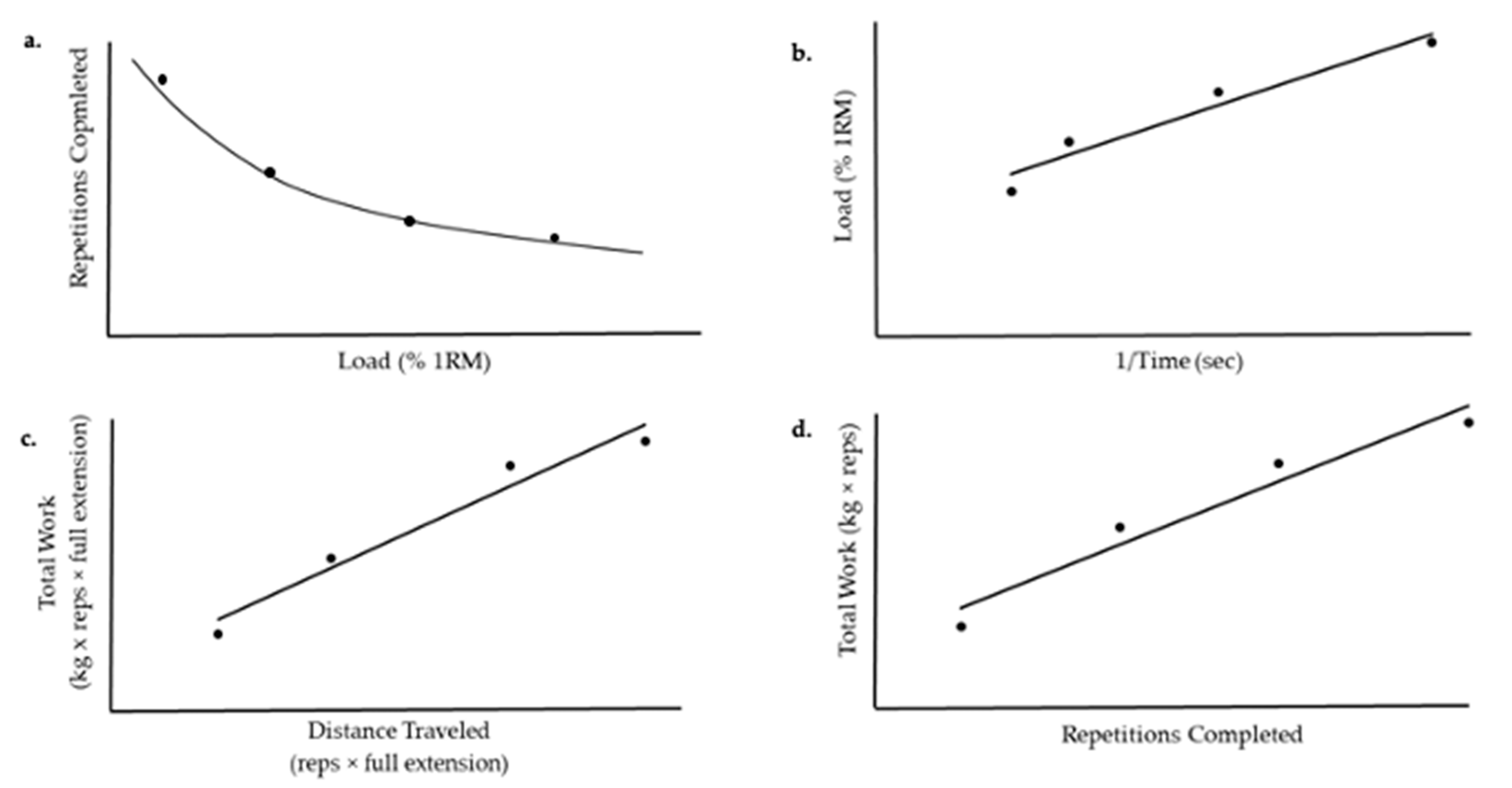
6. Progression of the Modeling across Exercise Modalities: Applications of the Critical Power Model to DCER Exercises
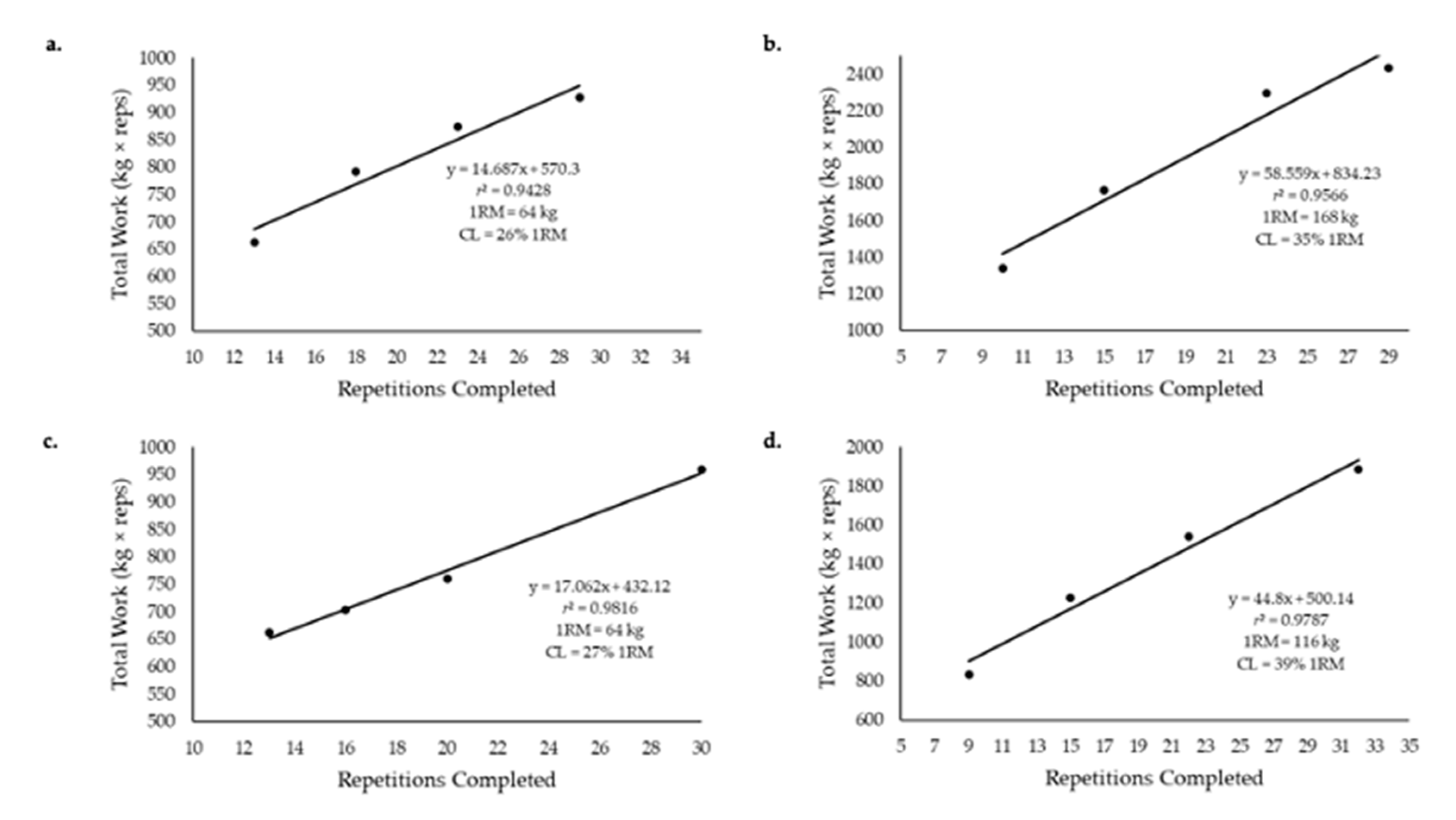
7. Additional Methodological Considerations for the Determination of the CL Test Parameters
8. Test Parameters: Critical Load and the y-Intercept (L′)
9. Research and Training Applications of the Critical Load Model
10. Recommendations for the Determination of the Critical Load
- At least four loads are recommended for the determination of the CL and L′, and each load used in the mathematical model should be greater than the CL. At this time, 50% 1RM or greater is recommended for the lowest load, and under most conditions, increases in loads should be made at increments of 10% (i.e., 50%, 60%, 70%, 80% 1RM).
- A cadence should be selected specific to each movement and standardized across subjects. This cadence should allow for successful completion of repetitions through the full range of motion for the lowest and highest loads.
- For subjects unfamiliar with performing repetitions to failure, a familiarization session at a submaximal load around 50–60% may improve the accuracy of the modeling.
- The model should be examined for each subject, and the r2 of the total work versus repetition relationship should be at least 0.75 or greater.
- If an r2 is lower than 0.75 or the lowest load used in the model is lower than the CL for an individual subject, that load should be eliminated and an additional load setting greater than 50% 1RM should be performed and used in the analyses.
- The CL and L′ can be estimated using the linear, 2-parameter total work (load (kg) × repetitions) versus duration relationship, the linear, 2-parameter load versus the inverse duration, or the nonlinear, 3-parameter model, and the duration should be expressed as repetitions.
- The mean and range of r2 and standard error of the estimate (SEE) values from the regression model should be reported in all future works.
11. Future Research on the Critical Load Model
- Load selections—A wider range (e.g., 35–40% 1RM to 95% 1RM) of relative load settings should be examined across whole-body, upper-body, and lower-body, unilateral and bilateral muscle actions to determine the effects of the load setting on the mathematical modeling.
- Number of loads—The effects of using two loads versus three, four, or five loads on the parameter estimates CL and L′ from the linear and non-linear mathematical models should be examined.
- Effects of cadence—The effect of various cadences, including a self-selected cadence, on the estimation of the CL and L′ should be examined.
- Reliability—Future studies should examine the reliability of the CL and L′ for various DCER exercises.
- Muscle specific thresholds—The CL model should be examined for agonist versus antagonist muscle actions, bilateral versus unilateral muscle actions, and upper- versus lower-body muscle groups to determine if the mathematical model is sensitive to detect muscle group-specific fatigue characteristics.
- Mode-specific thresholds—Studies should compare the parameter estimates for isometric versus DCER movements in the same muscle group.
- Physiological underpinnings—Further investigation is warranted to examine the potential metabolic and circulatory factors underlying the determination of the CL and L′ as well as the prediction of performance using the CL model.
- Training studies—Training adaptations for strength and hypertrophy should be examined for loads prescribed above and below the CL for each individual.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- De Vries, H.A. Physiology of physical conditioning for the elderly. In Guide to Fitness After Fifty; Springer: Boston, MA, USA, 1977; pp. 47–52. [Google Scholar]
- DeVries, H.A. Tranquilizer effect of exercise: A critical review. Phys. Sportsmed. 1981, 9, 46–55. [Google Scholar] [CrossRef] [PubMed]
- DeVries, H.A.; Moritani, T.; Nagata, A.; Magnussen, K. The relation between critical power and neuromuscular fatigue as estimated from electromyographic data. Ergonomics 1982, 25, 783–791. [Google Scholar] [CrossRef] [PubMed]
- DeVries, H.A.; Brodowicz, G.R.; Robertson, L.D.; Svoboda, M.D.; Schendel, J.S.; Tichy, A.M.; Tichy, M.W. Estimating physical working capacity and training changes in the elderly at the fatigue threshold (PWCft). Ergonomics 1989, 32, 967–977. [Google Scholar] [CrossRef]
- Moritani, T.; DeVries, H.A. Neural factors versus hypertrophy in the time course of muscle strength gain. Am. J. Phys. Med. 1979, 58, 115. [Google Scholar] [PubMed]
- Monod, H.; Scherrer, J. The work capacity of a synergic muscular group. Ergonomics 1965, 8, 329–338. [Google Scholar] [CrossRef]
- Moritani, T.; Nagata, A.; DeVries, H.A. Critical power as a measure of physical work capacity and anaerobic threshold. Ergonomics 1981, 24, 339–350. [Google Scholar] [CrossRef]
- Hill, D.W. The critical power concept. Sports Med. 1993, 16, 237–254. [Google Scholar] [CrossRef]
- Jones, A.M.; Vanhatalo, A.; Burnley, M.; Morton, R.H.; Poole, D.C. Critical power: Implications for determination of VO2max and exercise tolerance. Med. Sci. Sports Exerc. 2010, 42, 1876–1890. [Google Scholar] [CrossRef]
- Poole, D.C.; Burnley, M.; Vanhatalo, A.; Rossiter, H.B.; Jones, A.M. Critical power: An important fatigue threshold in exercise physiology. Med. Sci. Sports Exerc. 2016, 48, 2320. [Google Scholar] [CrossRef]
- Vanhatalo, A.; Jones, A.M.; Burnley, M. Application of critical power in sport. Int. J. Sports Physiol. Perform. 2011, 6, 128–136. [Google Scholar] [CrossRef]
- Hill, A.V. The physiological bases of athletic records. Sci. Mon. 1925, 21, 409–428. [Google Scholar]
- Hughson, R.L.; Orok, C.J.; Staudt, L.E. A high velocity treadmill running test to assess endurance running potential. Int. J. Sports Med. 1984, 5, 23–25. [Google Scholar] [CrossRef] [PubMed]
- Poole, D.C.; Ward, S.A.; Gardner, G.W.; Whipp, B.J. Metabolic and respiratory profile of the upper limit for prolonged exercise in man. Ergonomics 1988, 31, 1265–1279. [Google Scholar] [CrossRef]
- Whipp, B.J.; Huntsman, D.J.; Storer, T.W.; Lamarra, N.; Wasserman, K. A constant which determines the duration of tolerance to high-intensity work. Fed. Amer. Soc. Exp. Biol. 1982, 41, 1591. [Google Scholar]
- Gaesser, G.A.; Poole, D.C. The slow component of oxygen uptake kinetics in humans. Exerc. Sport Sci. Rev. 1996, 24, 35–70. [Google Scholar] [CrossRef]
- Billat, V.; Binsee, V.; Petit, B.; Koralsztein, J.P. High level runners are able to maintain a VO2 steady state below VO2max in all-out run over their critical velocity. Arch. Physiol. Biochem. 1998, 106, 38–45. [Google Scholar] [CrossRef]
- Pethick, J.; Winter, S.L.; Burnley, M. Physiological evidence that the critical torque is a phase transition not a threshold. Med. Sci. Sports Exerc. 2020, 52, 2390–2401. [Google Scholar] [CrossRef] [PubMed]
- Housh, D.J.; Housh, T.J.; Bauge, S.M. The accuracy of the critical power test for predicting time to exhaustion during cycle ergometry. Ergonomics 1989, 32, 997–1004. [Google Scholar] [CrossRef]
- Bull, A.J.; Housh, T.J.; Johnson, G.O.; Perry, S.R. Effect of mathematical modeling on the estimation of critical power. Med. Sci. Sports Exerc. 2000, 32, 526–530. [Google Scholar] [CrossRef]
- Morton, R. A 3-parameter critical power model. Ergonomics 1996, 39, 611–619. [Google Scholar] [CrossRef]
- Bergstrom, H.C.; Housh, T.J.; Zuniga, J.M.; Traylor, D.A.; Lewis, R.W., Jr.; Camic, C.L.; Schmidt, R.J.; Johnson, G.O. Differences among estimates of critical power and anaerobic work capacity derived from five mathematical models and the 3-min all-out test. J. Strength Cond. Res. 2014, 28, 592–600. [Google Scholar] [CrossRef] [PubMed]
- Bull, A.J.; Housh, T.J.; Johnson, G.O.; Rana, S.R. Physiological responses at five estimates of critical velocity. Eur. J. Appl. Physiol. 2008, 102, 711–720. [Google Scholar] [CrossRef] [PubMed]
- Bull, A.J.; Housh, T.J.; Johnson, G.O.; Perry, S.R. Electromyographic and mechanomyographic responses at critical power. Can. J. Appl. Physiol. 2000, 25, 262–270. [Google Scholar] [CrossRef] [PubMed]
- Housh, D.J.; Housh, T.J.; Bauge, S.M. A methodological consideration for the determination of critical power and anaerobic work capacity. Res. Q. Exerc. Sport 1990, 61, 406–409. [Google Scholar] [CrossRef]
- Switalla, J.R.; Byrd, M.T.; Abel, M.G.; Fleenor, B.S.; Bergstrom, H.C. Can experienced runners accurately estimate performance capabilities to derive the parameters of the critical velocity model? Int. J Phys. Ed. Sports Health 2017, 4, 204–209. [Google Scholar]
- Brim, H.H., III; Abel, M.G.; Wallace, B.J.; Byrd, M.T.; Eastman, J.E.; Bergstrom, H.C. Can critical velocity and anaerobic swimming capacity be determined from estimated performance times in collegiate swimmers? J. Exerc. Physiol. Online 2017, 20, 23–32. [Google Scholar]
- Burnley, M.; Doust, J.H.; Vanhatalo, A. A 3-min all-out test to determine peak oxygen update and maximal steady state. Med. Sci. Sports Exerc. 2006, 38, 1995–2003. [Google Scholar] [CrossRef]
- Vanhatalo, A.; Doust, J.; Burnley, M. Determination of critical power using a 3-min all-out cycling test. Med. Sci. Sports Exerc. 2007, 39, 548–555. [Google Scholar] [CrossRef]
- Bergstrom, H.C.; Housh, T.J.; Zuniga, J.M.; Camic, C.L.; Traylor, D.A.; Schmidt, R.J.; Johnson, G.O. A new single work bout test to estimate critical power and anaerobic work capacity. J. Strength Cond. Res. 2012, 26, 656–663. [Google Scholar] [CrossRef]
- Clark, I.E.; Murray, S.R.; Pettitt, R.W. Alternative procedures for the 3-min all-out exercise test. J. Strength Cond. Res. 2013, 27, 2104–2112. [Google Scholar] [CrossRef]
- Wakayoshi, K.; Ikuta, K.; Yoshida, T.; Udo, M.; Moritani, T.; Mutoh, Y.; Miyashita, M. Determination and validity of critical velocity as an index of swimming performance in the competitive swimmer. Eur. J. Appl. Physiol. Occup. Physiol. 1992, 64, 153–157. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, M.D.; Bell, G.J. A comparison of critical velocity estimates to actual velocities in predicting simulated rowing performance. Can. J. Appl. Physiol. 2000, 25, 223–235. [Google Scholar] [CrossRef][Green Version]
- Morton, R.H.; Redstone, M.D.; Laing, D.J. The critical power concept and bench press: Modeling 1RM and repetitions to failure. Int. J. Exerc. Sci. 2014, 7, 6. [Google Scholar]
- Arakelian, V.M.; Mendes, R.G.; Trimer, R.; Rossi Caruso, F.C.; de Sousa, N.M.; Borges, V.C.; do Valle Gomes Gatto, C.; Baldissera, V.; Arena, R.; Borghi-Silva, A. Critical load: A novel approach to determining a sustainable intensity during resistance exercise. J. Sports Med. Phys. Fitness 2017, 57, 556–564. [Google Scholar]
- Dinyer, T.K.; Byrd, M.T.; Vesotsky, A.N.; Succi, P.J.; Bergstrom, H.C. Applying the critical power model to a full-body resistance-training movement. Int. J. Sports Physiol. Perform. 2019, 14, 1364–1370. [Google Scholar] [CrossRef] [PubMed]
- Dinyer, T.K.; Byrd, M.T.; Succi, P.J.; Bergstrom, H.C. The timecourse of changes in neuromuscular responses during the performance of leg extension repetitions to failure below and above critical resistance in women. J. Strength Cond. Res. 2020. [Google Scholar] [CrossRef] [PubMed]
- Dinyer, T.K.; Byrd, M.T.; Vesotsky, A.N.; Succi, P.J.; Bergstrom, H.C. Linear and nonlinear modeling of critical load. J. Exerc. Physiol. Online 2020, 23, 1–13. [Google Scholar]
- Hendrix, C.R.; Housh, T.J.; Johnson, G.O.; Mielke, M.; Camic, C.L.; Zuniga, J.M.; Schmidt, R.J. Comparison of critical force to EMG fatigue thresholds during isometric leg extension. Med. Sci. Sports Exerc. 2009, 41, 956–964. [Google Scholar] [CrossRef]
- Moss, A.C.; Dinyer, T.K.; Abel, M.G.; Bergstrom, H.C. Methodological considerations for the determination of the critical load for the deadlift. J. Strength Cond. Res. 2020. [Google Scholar] [CrossRef]
- Dinyer, T.K.; Byrd, M.T.; Vesotsky, A.N.; Succi, P.J.; Clasey, J.L.; Bergstrom, H.C. The sensitivity of the critical resistance model to detect sex-related differences in fatigue during submaximal muscular contractions. J. Sci. Sport Exerc. 2019, 1, 151–158. [Google Scholar] [CrossRef]
- Dinyer, T.K.; Byrd, M.T.; Garver, M.J.; Ricard, A.J.; Miller, W.M.; Burns, S.; Clasey, J.L.; Bergstrom, H.C. Low-load vs. high-load resistance training to failure on one repetition maximum strength and body composition in untrained women. J. Strength Cond. Res. 2019, 33, 1737–1744. [Google Scholar] [CrossRef]
- Jenkins, N.D.M.; Housh, T.J.; Buckner, S.L.; Bergstrom, H.C.; Cochrane, K.C.; Hill, E.C.; Smith, C.M.; Schmidt, R.J.; Johnson, G.O.; Cramer, J.T. Neuromuscular adaptations after 2 and 4 weeks of 80% versus 30% 1 repetition maximum resistance training to failure. J. Strength Cond. Res. 2016, 30, 2174–2185. [Google Scholar] [CrossRef]
- Mitchell, C.J.; Churchward-Venne, T.A.; West, D.W.D.; Burd, N.A.; Breen, L.; Baker, S.K.; Phillips, S.M. Resistance exercise load does not determine training-mediated hypertrophic gains in young men. J. Appl. Physiol. 2012, 113, 71–77. [Google Scholar] [CrossRef]
- Morton, R.W.; Oikawa, S.Y.; Wavell, C.G.; Mazara, N.; McGlory, C.; Quadrilatero, J.; Baechler, B.L.; Baker, S.K.; Phillips, S.M. Neither load nor systemic hormones determine resistance training-mediated hypertrophy or strength gains in resistance-trained young men. J. Appl. Physiol. 2016, 121, 129–138. [Google Scholar] [CrossRef]
- Schoenfeld, B.J.; Peterson, M.D.; Ogborn, D.; Contreras, B.; Sonmez, G.T. Effects of low- vs. high-load resistance training on muscle strength and hypertrophy in well-trained men. J. Strength Cond. Res. 2015, 29, 254–2963. [Google Scholar] [CrossRef]
- Sheppard, J.M.; Triplett, N.T. Program design for resistance training. In Essentials of Strength and Conditioning, 4th ed.; Haff, G.G., Triplett, N.T., Eds.; Human Kinetics: Champaign, IL, USA, 2013; pp. 453–458. [Google Scholar]
- Jenkins, N.D.M.; Housh, T.J.; Bergstrom, H.C.; Cochrane, K.C.; Hill, E.C.; Smith, C.M.; Johnson, G.O.; Schmidt, R.J.; Cramer, J.T. Muscle activation during three sets to failure at 80 vs. 30% 1RM resistance exercise. Eur. J. Appl. Physiol. 2015, 115, 2335–2347. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bergstrom, H.C.; Dinyer, T.K.; Succi, P.J.; Voskuil, C.C.; Housh, T.J. Applications of the Critical Power Model to Dynamic Constant External Resistance Exercise: A Brief Review of the Critical Load Test. Sports 2021, 9, 15. https://doi.org/10.3390/sports9020015
Bergstrom HC, Dinyer TK, Succi PJ, Voskuil CC, Housh TJ. Applications of the Critical Power Model to Dynamic Constant External Resistance Exercise: A Brief Review of the Critical Load Test. Sports. 2021; 9(2):15. https://doi.org/10.3390/sports9020015
Chicago/Turabian StyleBergstrom, Haley C., Taylor K. Dinyer, Pasquale J. Succi, Caleb C. Voskuil, and Terry J. Housh. 2021. "Applications of the Critical Power Model to Dynamic Constant External Resistance Exercise: A Brief Review of the Critical Load Test" Sports 9, no. 2: 15. https://doi.org/10.3390/sports9020015
APA StyleBergstrom, H. C., Dinyer, T. K., Succi, P. J., Voskuil, C. C., & Housh, T. J. (2021). Applications of the Critical Power Model to Dynamic Constant External Resistance Exercise: A Brief Review of the Critical Load Test. Sports, 9(2), 15. https://doi.org/10.3390/sports9020015



