Validation of Inertial Sensor to Measure Barbell Kinematics across a Spectrum of Loading Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Approach to the Problem
2.2. Subjects
2.3. Procedures
2.4. Data Processing
2.5. Statistical Analyses
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- DeWeese, B.H.; Hornsby, G.; Stone, M.; Stone, M.H. The Training Process: Planning for Strength—Power Training in Track and Field. Part 1: Theoretical Aspects. J. Sport Health Sci. 2015, 4, 308–317. [Google Scholar] [CrossRef]
- Halson, S.L. Monitoring Training Load to Understand Fatigue in Athletes. Sports Med. 2014, 44 (Suppl. 2), S139–S147. [Google Scholar] [CrossRef] [PubMed]
- García-Ramos, A.; Padial, P.; Haff, G.G.; Argüelles-Cienfuegos, J.; García-Ramos, M.; Conde-Pipó, J.; Feriche, B. Effect of Different Interrepetition Rest Periods on Barbell Velocity Loss During the Ballistic Bench Press Exercise. J. Strength Cond. Res. 2015, 29, 2388–2396. [Google Scholar] [CrossRef]
- Sanchez-Medina, L.; González-Badillo, J.J. Velocity Loss as an Indicator of Neuromuscular Fatigue During Resistance Training. Med. Sci. Sports Exerc. 2011, 43, 1725–1734. [Google Scholar] [CrossRef] [PubMed]
- Mann, J.B.; Ivey, P.A.; Sayers, S.P. Velocity-Based Training in Football. J. Strength Cond. 2015, 37, 52–57. [Google Scholar] [CrossRef]
- Wilson, K.M.; Helton, W.S.; de Joux, N.R.; Head, J.R.; Weakley, J.J. Real-Time Quantitative Performance Feedback During Strength Exercise Improves Motivation, Competitiveness, Mood, and Performance. Proc. Hum. Factors Ergon. Soc. Annu. Meet. 2017, 61, 1546–1550. [Google Scholar] [CrossRef]
- Kawamori, N.; Haff, G.G. The Optimal Training Load for the Development of Muscular Power. J. Strength Cond. Res. 2004, 18, 675–684. [Google Scholar]
- Behm, D.G.; Sale, D.G. Intended Rather Than Actual Movement Velocity Determines Velocity-Specific Training Response. J. Appl. Physiol. 1993, 74, 359–368. [Google Scholar] [CrossRef]
- Jovanović, M.; Flanagan, E.P. Researched Applications of Velocity Based Strength Training. J. Aust. Strength Cond. 2014, 22, 58–69. [Google Scholar]
- Cormie, M.P.; Deane, M.R.; McBride, M.J. Methodological Concerns for Determining Power Output in the Jump Squat. J. Strength Cond. Res. 2007, 21, 424–430. [Google Scholar] [CrossRef]
- Balsalobre-Fernández, C.; Marchante, D.; Muñoz-López, M.; Jiménez, S.L. Validity and Reliability of a Novel Iphone App for the Measurement of Barbell Velocity and 1rm on the Bench-Press Exercise. J. Sports Sci. 2018, 36, 64–70. [Google Scholar] [CrossRef] [PubMed]
- Drinkwater, J.E.; Galna, J.B.; McKenna, H.M.; Hunt, B.P.; Pyne, B.D. Validation of an Optical Encoder During Free Weight Resistance Movements and Analysis of Bench Press Sticking Point Power During Fatigue. J. Strength Cond. Res. 2007, 21, 510–517. [Google Scholar] [CrossRef][Green Version]
- Mitter, B.; Hölbling, D.; Bauer, P.; Stöckl, M.; Baca, A.; Tschan, H. Concurrent Validity of Field-Based Diagnostic Technology Monitoring Movement Velocity in Powerlifting Exercises. J. Strength Cond. Res. 2019. [Google Scholar] [CrossRef] [PubMed]
- Wen, K.; Yu, K.; Li, Y.; Zhang, S.; Zhang, W. A New Quaternion Kalman Filter Based Foot-Mounted Imu and Uwb Tightly-Coupled Method for Indoor Pedestrian Navigation. IEEE Trans. Veh. Technol. 2020, 69, 4340–4352. [Google Scholar] [CrossRef]
- Sato, L.K.; Smith, L.S.; Sands, A.W. Validation of an Accelerometer for Measuring Sport Performance. J. Strength Cond. Res. 2009, 23, 341–347. [Google Scholar] [CrossRef]
- Sato, K.; Carroll, K.M.; Wagle, J.P.; Lang, H.M.; Smith, A.P.; Abbott, J.C.; Hierholzer, K.M.; Stone, M.H. Validation of Inertial Sensor to Measure Velocity of Medicine Balls. J. Trainol. 2018, 7, 16–20. [Google Scholar] [CrossRef]
- Matuszak, M.E.; Fry, A.C.; Weiss, L.W.; Ireland, T.R.; McKnight, M.M. Effect of Rest Interval Length on Repeated 1 Repetition Maximum Back Squats. J. Strength Cond. Res. 2003, 17, 634–637. [Google Scholar]
- Urquhart, B.G.; Moir, G.L.; Graham, S.M.; Connaboy, C. Reliability of 1rm Split-Squat Performance and the Efficacy of Assessing Both Bilateral Squat and Split-Squat 1rm in a Single Session for Non–Resistance-Trained Recreationally Active Men. J. Strength Cond. Res. 2015, 29, 1991–1998. [Google Scholar] [CrossRef][Green Version]
- Chandler, T.J.; Stone, M.H. The Squat Exercise in Athletic Conditioning: A Position Statement and Review of the Literature. Chiropr. Sports Med. 1992, 6, 105. [Google Scholar]
- Appleby, B.B.; Banyard, H.; Cormie, P.; Cormack, S.J.; Newton, R.U. Validity and Reliability of Methods to Determine Barbell Displacement in Heavy Back Squats: Implications for Velocity-Based Training. J. Strength Cond. Res. 2018. Publish Ahead of Print. [Google Scholar] [CrossRef]
- Sato, K.; Fortenbaugh, D.; Hydock, D.S. Kinematic Changes Using Weightlifting Shoes on Barbell Back Squat. J. Strength Cond. Res. 2012, 26, 28–33. [Google Scholar] [CrossRef] [PubMed]
- Banyard, H.G.; Nosaka, K.; Sato, K.; Haff, G.G. Validity of Various Methods for Determining Velocity, Force, and Power in the Back Squat. Int. J. Sports Physiol. Perform. 2017, 12, 1170–1176. [Google Scholar] [CrossRef] [PubMed]
- García-Ramos, A.; Pestaña-Melero, F.L.; Pérez-Castilla, A.; Rojas, F.J.; Haff, G.G. Mean Velocity vs. Mean Propulsive Velocity vs. Peak Velocity: Which Variable Determines Bench Press Relative Load with Higher Reliability? J. Strength Cond. Res. 2018, 32, 1273–1279. [Google Scholar] [CrossRef]
- A New View of Statistics: A Scale of Magnitudes for Effect Statistics. Available online: https://www.sportsci.org/resource/stats/effectmag.html (accessed on 28 June 2020).
- Balsalobre-Fernández, C.; Kuzdub, M.; Poveda-Ortiz, P.; del Campo-Vecino, J. Validity and Reliability of the Push Wearable Device to Measure Movement Velocity During the Back Squat Exercise. J. Strength Cond. Res. 2016, 30, 1968–1974. [Google Scholar] [CrossRef]
- Carroll, K.M.; Sato, K.; Bazyler, C.D.; Triplett, N.T.; Stone, M.H. Increases in Variation of Barbell Kinematics Are Observed with Increasing Intensity in a Graded Back Squat Test. Sports 2017, 5, 51. [Google Scholar] [CrossRef]
- Tillaar, R.V.D. Effect of Descent Velocity Upon Muscle Activation and Performance in Two-Legged Free Weight Back Squats. Sports 2019, 7, 15. [Google Scholar] [CrossRef]
- Kompf, J.; Arandjelović, O. The Sticking Point in the Bench Press, the Squat, and the Deadlift: Similarities and Differences, and Their Significance for Research and Practice. Sports Med. 2017, 47, 631–640. [Google Scholar] [CrossRef]
- Van den Tillaar, R.; Ettema, G. A Comparison of Successful and Unsuccessful Attempts in Maximal Bench Pressing. Med. Sci. Sports Exerc. 2009, 41, 2056–2063. [Google Scholar] [CrossRef] [PubMed]
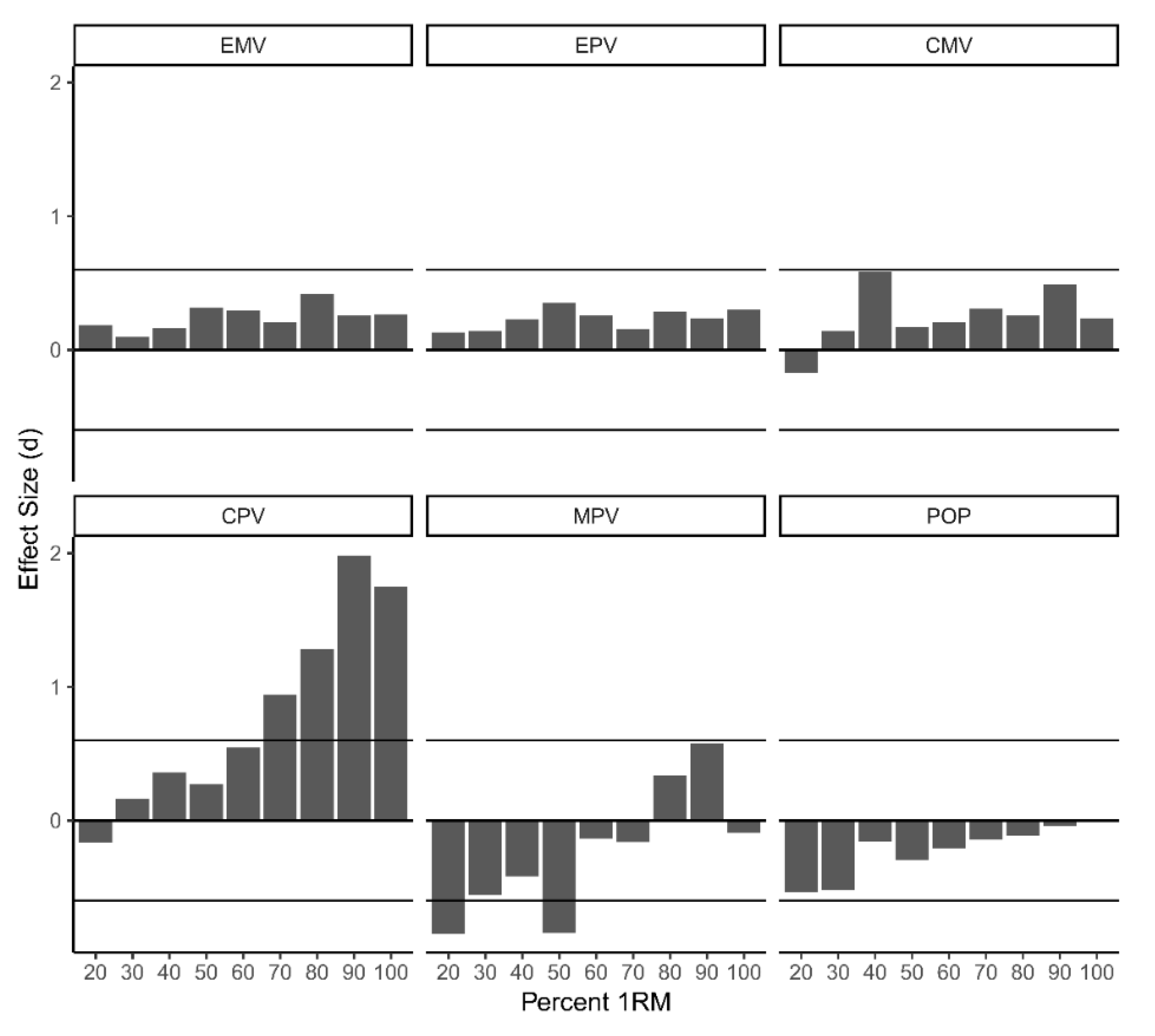
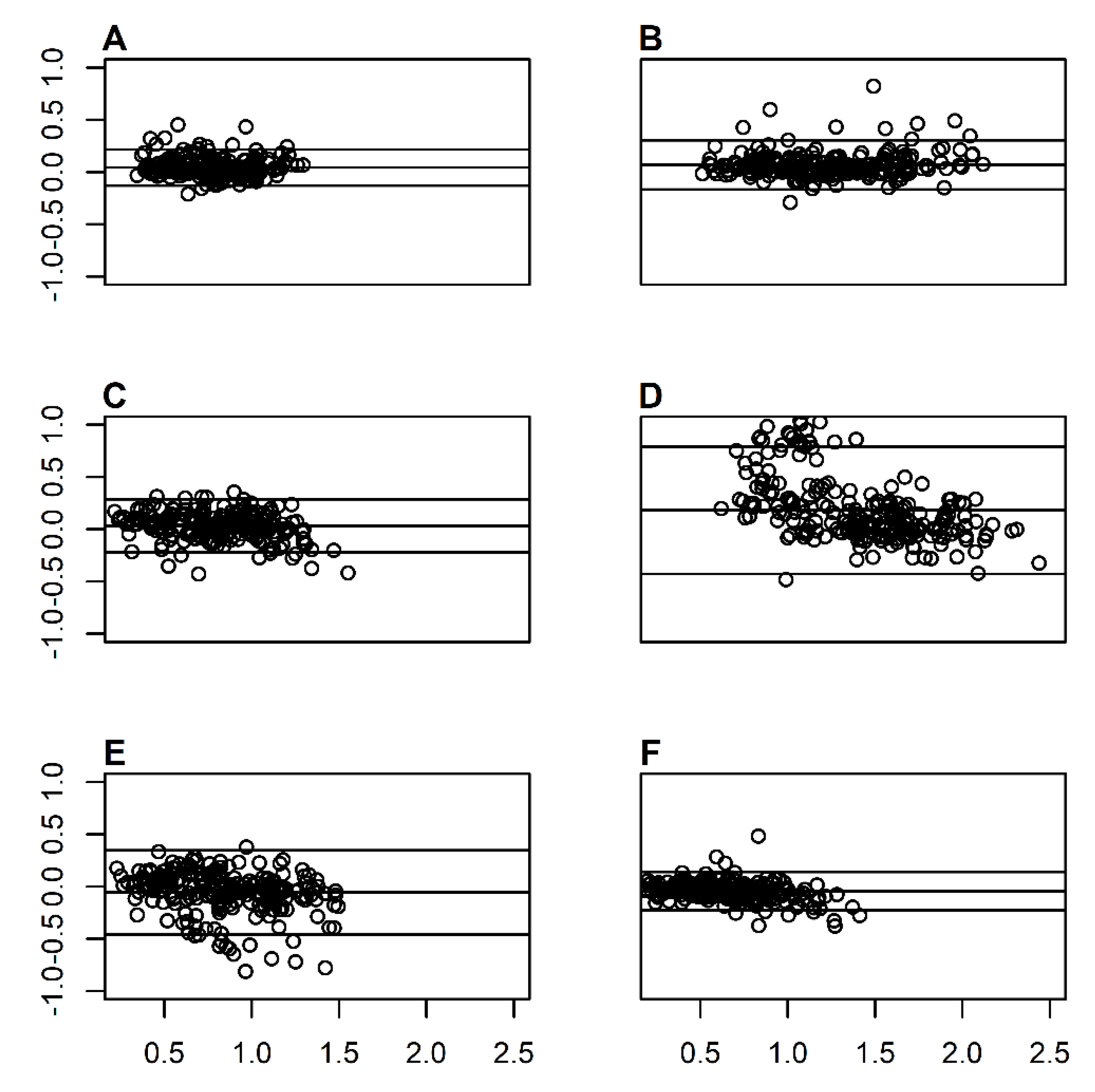

| Percent 1RM | Device | EMV | EPV | CPV | CMV | MPV | POP-100 |
|---|---|---|---|---|---|---|---|
| 20% | IMU | 0.91 ± 0.24 | 1.47 ± 0.38 | 1.94 ± 0.27 | 1.18 ± 0.22 | 1.32 ± 0.2 | 1.04 ± 0.25 |
| 3DMOCAP | 0.96 ± 0.23 | 1.52 ± 0.39 | 1.89 ± 0.29 | 1.15 ± 0.15 | 1.2 ± 0.17 | 0.91 ± 0.22 | |
| 30% | IMU | 0.92 ± 0.21 | 1.48 ± 0.32 | 1.81 ± 0.22 | 1.1 ± 0.17 | 1.26 ± 0.2 | 0.98 ± 0.22 |
| 3DMOCAP | 0.94 ± 0.2 | 1.53 ± 0.38 | 1.84 ± 0.2 | 1.12 ± 0.12 | 1.17 ± 0.14 | 0.88 ± 0.18 | |
| 40% | IMU | 0.84 ± 0.17 | 1.31 ± 0.3 | 1.62 ± 0.22 | 0.93 ± 0.16 | 1.08 ± 0.17 | 0.8 ± 0.18 |
| 3DMOCAP | 0.87 ± 0.21 | 1.38 ± 0.34 | 1.69 ± 0.17 | 1.02 ± 0.11 | 1.05 ± 0.12 | 0.77 ± 0.17 | |
| 50% | IMU | 0.8 ± 0.19 | 1.24 ± 0.32 | 1.57 ± 0.24 | 0.92 ± 0.19 | 1.03 ± 0.18 | 0.73 ± 0.18 |
| 3DMOCAP | 0.85 ± 0.18 | 1.36 ± 0.36 | 1.63 ± 0.21 | 0.94 ± 0.11 | 0.96 ± 0.13 | 0.67 ± 0.16 | |
| 60% | IMU | 0.77 ± 0.18 | 1.21 ± 0.28 | 1.39 ± 0.25 | 0.82 ± 0.16 | 0.9 ± 0.18 | 0.66 ± 0.18 |
| 3DMOCAP | 0.83 ± 0.18 | 1.28 ± 0.3 | 1.51 ± 0.2 | 0.85 ± 0.12 | 0.87 ± 0.13 | 0.63 ± 0.17 | |
| 70% | IMU | 0.72 ± 0.18 | 1.13 ± 0.29 | 1.13 ± 0.27 | 0.7 ± 0.13 | 0.72 ± 0.14 | 0.57 ± 0.14 |
| 3DMOCAP | 0.75 ± 0.16 | 1.18 ± 0.29 | 1.36 ± 0.21 | 0.73 ± 0.1 | 0.73 ± 0.11 | 0.55 ± 0.15 | |
| 80% | IMU | 0.6 ± 0.17 | 0.97 ± 0.3 | 0.95 ± 0.3 | 0.6 ± 0.15 | 0.6 ± 0.15 | 0.47 ± 0.13 |
| 3DMOCAP | 0.67 ± 0.16 | 1.06 ± 0.29 | 1.28 ± 0.21 | 0.63 ± 0.11 | 0.62 ± 0.11 | 0.45 ± 0.15 | |
| 90% | IMU | 0.56 ± 0.13 | 0.87 ± 0.22 | 0.74 ± 0.25 | 0.45 ± 0.13 | 0.45 ± 0.11 | 0.38 ± 0.13 |
| 3DMOCAP | 0.59 ± 0.13 | 0.92 ± 0.22 | 1.21 ± 0.23 | 0.51 ± 0.1 | 0.49 ± 0.1 | 0.38 ± 0.15 | |
| 100% | IMU | 0.57 ± 0.14 | 0.91 ± 0.24 | 0.63 ± 0.27 | 0.34 ± 0.15 | 0.39 ± 0.13 | 0.37 ± 0.13 |
| 3DMOCAP | 0.61 ± 0.15 | 0.98 ± 0.26 | 1.08 ± 0.24 | 0.37 ± 0.09 | 0.35 ± 0.09 | 0.36 ± 0.15 |
| Percent 1RM | Device | EMV | EPV | CPV | CMV | MPV | POP-100 |
|---|---|---|---|---|---|---|---|
| 20% | IMU | 26.63 (20.41–38.47) | 26.03 (19.96–37.54) | 14.17 (11.04–20.05) | 18.97 (14.64–27.02) | 15.42 (12–21.84) | 23.7 (18.22–34.03) |
| 3DMOCAP | 23.94 (18.4–34.39) | 25.8 (19.79–37.19) | 15.53 (12.09–22) | 13.09 (10.2–18.49) | 18.89 (14.58–26.89) | 24.44 (18.78–35.15) | |
| 30% | IMU | 22.85 (17.66–32.46) | 21.83 (16.89–30.95) | 12.44 (9.74–17.41) | 15.79 (12.34–22.19) | 15.73 (12.3–22.1) | 22.7 (17.55–32.24) |
| 3DMOCAP | 21.21 (16.41–30.04) | 24.82 (19.15–35.39) | 10.61 (8.32–14.83) | 10.38 (8.14–14.5) | 23.57 (18.21–33.53) | 20.98 (16.24–29.71) | |
| 40% | IMU | 19.78 (15.46–27.51) | 23.22 (18.1–32.48) | 13.39 (10.57–18.47) | 17.58 (13.81–24.38) | 16.13 (12.71–22.33) | 23.08 (17.99–32.27) |
| 3DMOCAP | 24.34 (18.95–34.11) | 24.48 (19.07–34.33) | 10.28 (8.13–14.15) | 10.4 (8.22–14.31) | 22.48 (17.53–31.4) | 22.52 (17.57–31.47) | |
| 50% | IMU | 24.04 (18.57–34.24) | 26 (20.04–37.16) | 15.38 (12.03–21.6) | 20.89 (16.17–29.58) | 17.98 (13.95–25.34) | 25.29 (19.5–36.09) |
| 3DMOCAP | 21.07 (16.31–29.84) | 26.15 (20.15–37.39) | 12.56 (9.84–17.59) | 11.82 (9.27–16.54) | 24.47 (18.89–34.87) | 23.97 (18.51–34.12) | |
| 60% | IMU | 22.9 (17.85–32.01) | 23.42 (18.25–32.77) | 17.86 (13.98–24.77) | 19.24 (15.05–26.74) | 20.2 (15.79–28.12) | 27.35 (21.23–38.55) |
| 3DMOCAP | 21.33 (16.65–29.74) | 23.01 (17.94–32.18) | 13.34 (10.53–18.41) | 13.73 (10.83–18.95) | 14.82 (11.69–20.48) | 26.5 (20.6–37.3) | |
| 70% | IMU | 24.88 (19.59–34.18) | 25.36 (19.96–34.87) | 23.97 (18.89–32.89) | 18.82 (14.89–25.63) | 19.21 (15.2–26.17) | 24.89 (19.6–34.2) |
| 3DMOCAP | 21.71 (17.14–29.67) | 24.79 (19.52–34.05) | 15.66 (12.48–21.24) | 14.27 (11.38–19.32) | 22.31 (17.61–30.52) | 27.89 (21.9–38.53) | |
| 80% | IMU | 28.25 (22.09–39.31) | 30.75 (23.99–43.01) | 31.43 (24.5–44.03) | 25.51 (20.01–35.32) | 25.71 (20.16–35.61) | 28.05 (21.95–39.03) |
| 3DMOCAP | 24.27 (19.05–33.53) | 27.9 (21.83–38.79) | 16.6 (13.18–22.68) | 17.49 (13.88–23.92) | 18.92 (14.91–25.92) | 33.58 (26.11–47.26) | |
| 90% | IMU | 22.87 (17.51–33.11) | 24.84 (18.98–36.1) | 33.36 (25.24–49.47) | 29.94 (22.75–44.01) | 25.58 (19.53–37.23) | 34.88 (26.34–51.94) |
| 3DMOCAP | 21.7 (16.62–31.34) | 23.69 (18.12–34.34) | 19.19 (14.73–27.59) | 19.56 (15.01–28.14) | 20.45 (15.68–29.46) | 39.7 (29.79–59.97) | |
| 100% | IMU | 24.1 (17.57–38.56) | 26.12 (19–42.02) | 43.77 (31.05–75.29) | 43.02 (30.56–73.74) | 34.59 (24.9–57.24) | 35.54 (25.55–59.03) |
| 3DMOCAP | 24.73 (18.02–39.63) | 26.42 (19.22–42.54) | 22.51 (16.44–35.86) | 24.79 (18.06–39.73) | 26.16 (19.03–42.08) | 42.17 (30–72.01) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbott, J.C.; Wagle, J.P.; Sato, K.; Painter, K.; Light, T.J.; Stone, M.H. Validation of Inertial Sensor to Measure Barbell Kinematics across a Spectrum of Loading Conditions. Sports 2020, 8, 93. https://doi.org/10.3390/sports8070093
Abbott JC, Wagle JP, Sato K, Painter K, Light TJ, Stone MH. Validation of Inertial Sensor to Measure Barbell Kinematics across a Spectrum of Loading Conditions. Sports. 2020; 8(7):93. https://doi.org/10.3390/sports8070093
Chicago/Turabian StyleAbbott, John C., John P. Wagle, Kimitake Sato, Keith Painter, Thaddeus J. Light, and Michael H. Stone. 2020. "Validation of Inertial Sensor to Measure Barbell Kinematics across a Spectrum of Loading Conditions" Sports 8, no. 7: 93. https://doi.org/10.3390/sports8070093
APA StyleAbbott, J. C., Wagle, J. P., Sato, K., Painter, K., Light, T. J., & Stone, M. H. (2020). Validation of Inertial Sensor to Measure Barbell Kinematics across a Spectrum of Loading Conditions. Sports, 8(7), 93. https://doi.org/10.3390/sports8070093






