Fatigue-Mediated Loss of Complexity is Contraction-Type Dependent in Vastus Lateralis Electromyographic Signals
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects
2.2. Protocol
2.3. Session One
2.4. Session Two
2.5. Sessions Three–Five
2.6. Electromyographic Measurements and Signal Processing
2.7. Data Analysis
3. Results
3.1. Fatigue Status, Contraction Type, and Fatigue Protocol
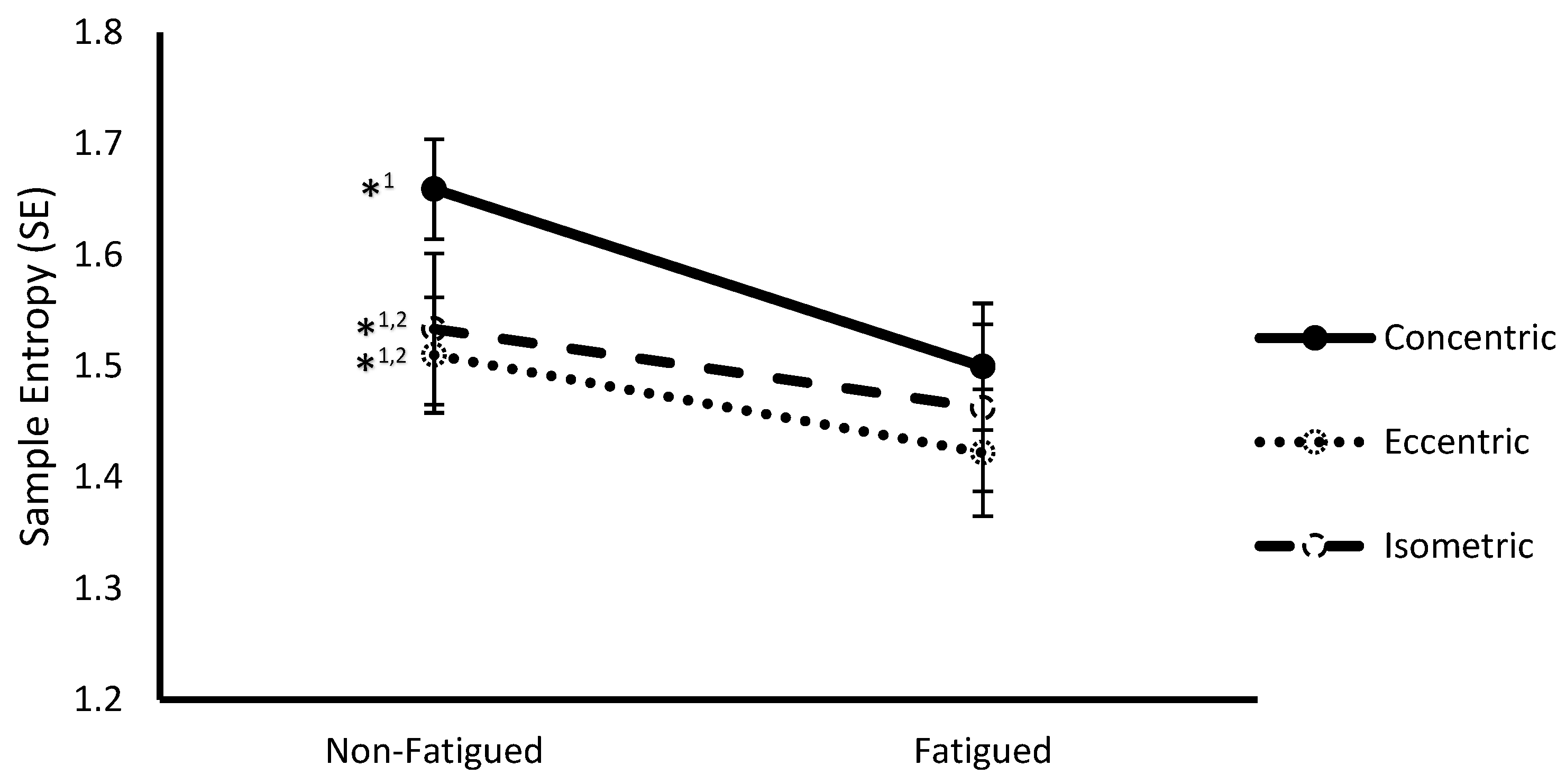
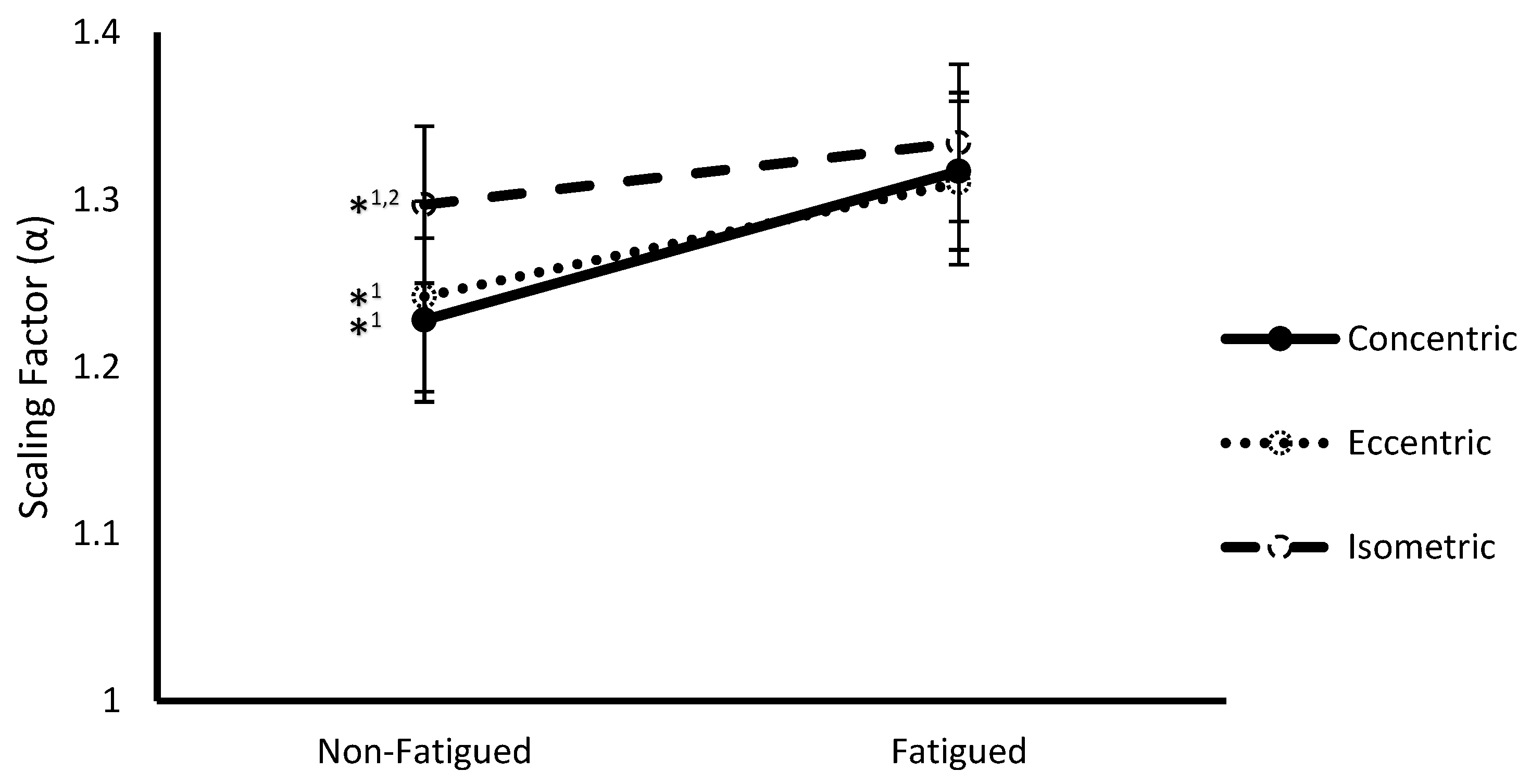
3.2. Fatigue State * Contraction Type Interaction
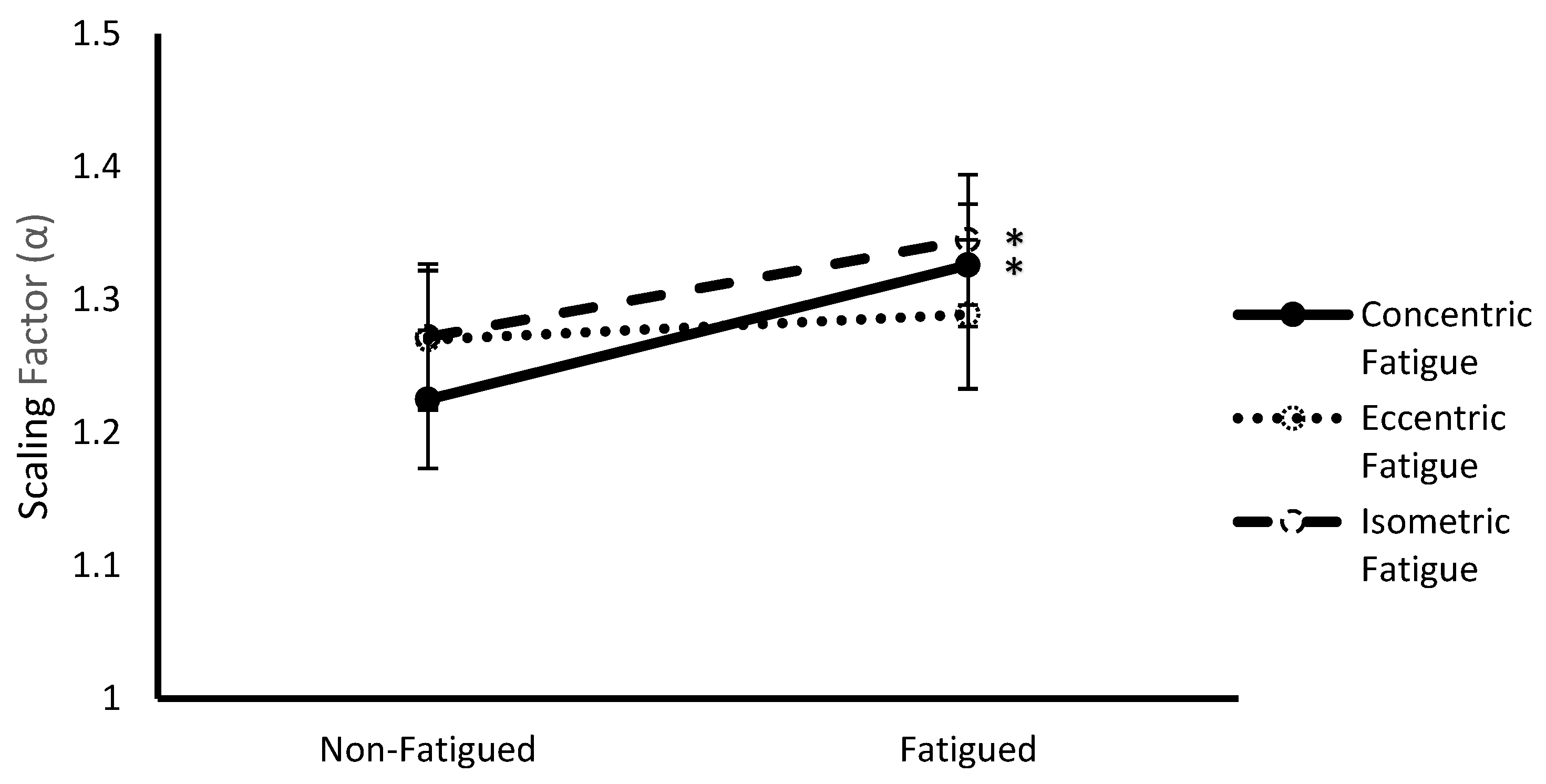
3.3. Fatigue Protocol * Fatigue Status Interaction
4. Discussion
4.1. Effect of Fatigue Status
4.2. Effect of Contraction Type
4.3. Effect of Fatigue Protocol
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Goldberger, A.L.; Peng, C.K.; Lipsitz, L.A. What is physiologic complexity and how does it change with aging and disease? Neurobiol. Aging 2002, 23, 23–26. [Google Scholar] [CrossRef]
- Manor, B.; Lipsitz, L.A. Physiologic complexity and aging: Implications for physical function and rehabilitation. Prog. Neuropsychopharmacol. Biol. Psychiatry 2013, 45, 287–293. [Google Scholar] [CrossRef]
- Lipsitz, L. Dynamics of stability: The physiologic basis of functional health and frailty. J. Gerontol. A Biol. Sci. Med. Sci. 2002, 57, 115–125. [Google Scholar] [CrossRef]
- Suda, E.Y.; Madeleine, P.; Hirata, R.P.; Samani, A.; Kawamura, T.T.; Sacco, I.C. Reduced complexity of force and muscle activity during low level isometric contractions of the ankle in diabetic individuals. Clin. Biomech. 2017, 42, 38–46. [Google Scholar] [CrossRef] [PubMed]
- Fino, P.C.; Nussbaum, M.A.; Brolinson, P.G. Decreased high-frequency center-of-pressure complexity in recently concussed asymptomatic athletes. Gait Posture 2016, 50, 69–74. [Google Scholar] [CrossRef] [PubMed]
- Pethick, J.; Winter, S.L.; Burnley, M. Fatigue reduces the complexity of knee extensor torque fluctuations during maximal and submaximal intermittent isometric contractions in man: Loss of complexity in torque during fatiguing muscle contractions. J. Physiol. 2015, 593, 2085–2096. [Google Scholar] [CrossRef] [PubMed]
- West, B.J. Fractal physiology and the fractional calculus: A perspective. Front. Physiol. 2010, 1, 12. [Google Scholar] [CrossRef]
- Stergiou, N.; Harbourne, R.T.; Cavanaugh, J.T. Optimal movement variability: A new theoretical perspective for neurologic physical therapy. J. Neurol. Phys. Ther. 2006, 30, 120–129. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Peng, C.K.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 1995, 5, 82–87. [Google Scholar] [CrossRef] [PubMed]
- Kantelhardt, J.W.; Koscielny-Bunde, E.; Rego, H.H.; Havlin, S.; Bunde, A. Detecting long-range correlations with detrended fluctuation analysis. Physica A 2001, 295, 441–454. [Google Scholar] [CrossRef]
- Hausdorff, J.M. Gait dynamics, fractals and falls: Finding meaning in the stride-to-stride fluctuations of human walking. Hum. Mov. Sci. 2007, 26, 555–589. [Google Scholar] [CrossRef]
- Monto, S.; Vanhatalo, S.; Holmes, M.D.; Palva, J.M. Epileptogenic neocortical networks are revealed by abnormal temporal dynamics in seizure-free subdural EEG. Cereb. Cortex 2007, 17, 1386–1393. [Google Scholar] [CrossRef]
- Hardstone, R.; Poil, S.S.; Schiavone, G.; Jansen, R.; Nikulin, V.V.; Mansvelder, H.D.; Linkenkaer-Hansen, K. Detrended fluctuation analysis: A scale-free view on neuronal oscillations. Front. Physiol. 2012, 3, 450. [Google Scholar] [CrossRef] [PubMed]
- Nieminen, H.; Takala, E.P. Evidence of deterministic chaos in the myoelectric signal. Electromyogr. Clin. Neurophysiol. 1996, 36, 49–58. [Google Scholar] [PubMed]
- Cashaback, J.G.; Cluff, T.; Potvin, J.R. Muscle fatigue and contraction intensity modulates the complexity of surface electromyography. J. Electromyogr. Kinesiol. 2013, 23, 78–83. [Google Scholar] [CrossRef] [PubMed]
- Karthick, P.A.; Makaram, N.; Ramakrishnan, S. Analysis of progression of fatigue conditions in biceps brachii muscles using surface electromyography signals and complexity based features. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2014, 3276–3279. [Google Scholar] [CrossRef]
- Beretta-Piccoli, M.; D’Antona, G.; Barbero, M.; Fisher, B.; Dieli-Conwright, C.M.; Clijsen, R.; Cescon, C. Evaluation of central and peripheral fatigue in the quadriceps using fractal dimension and conduction velocity in young females. PLoS ONE 2015, 10, e0123921. [Google Scholar] [CrossRef] [PubMed]
- Boccia, G.; Dardanello, D.; Beretta-Piccoli, M.; Cescon, C.; Coratella, G.; Rinaldo, N.; Barbero, M.; Lanza, M.; Schena, F.; Rainoldi, A. Muscle fiber conduction velocity and fractal dimension of EMG during fatiguing contractions of young and elderly men. Physiol. Meas. 2016, 37, 162–174. [Google Scholar] [CrossRef]
- Gupta, V.; Suryanarayanan, S.; Reddy, N.P. Fractal analysis of surface EMG signals from the biceps. Int. J. Med. Inform. 1997, 45, 185–192. [Google Scholar] [CrossRef]
- Sun, R.; Song, R.; Tong, K. Complexity Analysis of EMG Signals for Patients After Stroke During Robot-Aided Rehabilitation Training Using Fuzzy Approximate Entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 1013–1019. [Google Scholar] [CrossRef] [PubMed]
- Beck, T.W.; Housh, T.J.; Cramer, J.T.; Weir, J.P. The effects of interelectrode distance over the innervation zone and normalization on the electromyographic amplitude and mean power frequency versus concentric, eccentric, and isometric torque relationships for the vastus lateralis muscle. J. Kinesiol. Electromyogr. 2009, 19, 219–231. [Google Scholar] [CrossRef]
- Yoon, T.S.; Park, D.S.; Kang, S.W.; Chun, S.I.; Shin, J.S. Isometric and isokinetic curves at the knee joint. Yonsei Med. J. 1991, 32, 33–43. [Google Scholar] [CrossRef] [PubMed]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. Physiobank, physiotoolkit, and physionet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Yentes, J.M.; Hunt, N.; Schmid, K.K.; Kaipust, J.P.; McGrath, D.; Stergiou, N. The appropriate use of approximate entropy and sample entropy with short data sets. Ann. Biomed. Eng. 2013, 41, 349–365. [Google Scholar] [CrossRef] [PubMed]
- Pethick, J.; Winter, S.L.; Burnley, M. Loss of knee extensor torque complexity during fatiguing isometric muscle contractions occurs exclusively above the critical torque. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2016, 310, R1144–R1153. [Google Scholar] [CrossRef]
- Pethick, J.; Winter, S.L.; Burnley, M. Caffeine ingestion attenuates fatigue-induced loss of muscle torque complexity. Med. Sci. Sports Exerc. 2018, 50, 236–245. [Google Scholar] [CrossRef]
- Peters, E.J.; Fuglevand, A.J. Cessation of human motor unit discharge during sustained maximal voluntary contraction. Neurosci. Lett. 1999, 274, 66–70. [Google Scholar] [CrossRef]
- Lindinger, M.I. Potassium regulation during exercise and recovery in humans: Implications for skeletal and cardiac muscle. J. Mol. Cell. Cardiol. 1995, 27, 1011–1022. [Google Scholar] [CrossRef]
- Camic, C.L.; Housh, T.J.; Zuniga, J.M.; Russell Hendrix, C.; Bergstrom, H.C.; Traylor, D.A.; Schmidt, R.J.; Johnson, G.O. Electromyographic and mechanomyographic responses across repeated maximal isometric and concentric muscle actions of the leg extensors. J. Electromyogr. Kinesiol. 2013, 23, 342–348. [Google Scholar] [CrossRef]
- Babault, N.; Pousson, M.; Ballay, Y.; Van Hoecke, J. Activation of human quadriceps femoris during isometric, concentric, and eccentric contractions. J. Appl. Physiol. 2001, 91, 2628–2634. [Google Scholar] [CrossRef]
- Duchateau, J.; Baudry, S. Insights into the neural control of eccentric contractions. J. Appl. Physiol. 2014, 116, 1418–1425. [Google Scholar] [CrossRef]
- Kay, D.; St. Clair Gibson, A.; Mitchell, M.; Lambert, M.; Noakes, T. Different neuromuscular recruitment patterns during eccentric, concentric and isometric contractions. J. Electromyogr. Kinesiol. 2000, 10, 425–431. [Google Scholar] [CrossRef]
- Coburn, J.W.; Housh, T.J.; Cramer, J.T.; Weir, J.P.; Miller, J.M.; Beck, T.W.; Malek, M.H.; Johnson, G.O. Mechanomyographic and electromyographic responses of the vastus medialis muscle during isometric and concentric muscle actions. J. Strength Cond. Res. 2005, 19, 412. [Google Scholar] [CrossRef] [PubMed]
- Vaillancourt, D.E.; Newell, K.M. Changing complexity in human behavior and physiology through aging and disease. Neurobiol. Aging 2002, 23, 1–11. [Google Scholar] [CrossRef]
- Hultborn, H.; Lindström, S.; Wigström, H. On the function of recurrent inhibition in the spinal cord. Exp. Brain Res. 1979, 37, 399–403. [Google Scholar] [CrossRef] [PubMed]
- Barrué-Belou, S.; Marque, P.; Duclay, J. Recurrent inhibition is higher in eccentric compared to isometric and concentric maximal voluntary contractions. Acta Physiol. 2018, 223, e13064. [Google Scholar] [CrossRef]
- Duclay, J.; Pasquet, B.; Martin, A.; Duchateau, J. Specific modulation of corticospinal and spinal excitabilities during maximal voluntary isometric, shortening and lengthening contractions in synergist muscles: Corticospinal and spinal excitabilities during lengthening contraction. J. Physiol. 2011, 589, 2901–2916. [Google Scholar] [CrossRef]
- Duchateau, J.; Enoka, R.M. Neural control of lengthening contractions. J. Exp. Biol. 2016, 219, 197–204. [Google Scholar] [CrossRef]
- Pasquet, B.; Carpentier, A.; Duchateau, J.; Hainaut, K. Muscle fatigue during concentric and eccentric contractions. Muscle Nerve. 2000, 23, 1727–1735. [Google Scholar] [CrossRef]
- Poole, D.C.; Burnley, M.; Vanhatalo, A.; Rossiter, H.B.; Jones, A.M. Critical power: an important fatigue threshold in exercise physiology. Med. Sci. Sports Exerc. 2016, 48, 2320–2334. [Google Scholar] [CrossRef] [PubMed]
| Condition | Sample Entropy | Scaling Factor (α) | |
|---|---|---|---|
| Fatigue Status | Non-fatigued | 1.57 ± 0.05 | 1.26 ± 0.05 |
| Fatigued | 1.46 ± 0.06 * | 1.32 ± 0.05 * | |
| Contraction Type | Concentric | 1.58 ± 0.05 | 1.27 ± 0.05 |
| Eccentric | 1.47 ± 0.07 ** | 1.28 ± 0.05 | |
| Isometric | 1.50 ± 0.05 ** | 1.32 ± 0.05 ** | |
| Fatigue Protocol | Concentric | 1.53 ± 0.07 | 1.28 ± 0.05 |
| Eccentric | 1.50 ± 0.06 | 1.28 ± 0.05 | |
| Isometric | 1.52 ± 0.06 | 1.31 ± 0.05 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernandez, L.R.; Camic, C.L. Fatigue-Mediated Loss of Complexity is Contraction-Type Dependent in Vastus Lateralis Electromyographic Signals. Sports 2019, 7, 78. https://doi.org/10.3390/sports7040078
Hernandez LR, Camic CL. Fatigue-Mediated Loss of Complexity is Contraction-Type Dependent in Vastus Lateralis Electromyographic Signals. Sports. 2019; 7(4):78. https://doi.org/10.3390/sports7040078
Chicago/Turabian StyleHernandez, Luis R., and Clayton L. Camic. 2019. "Fatigue-Mediated Loss of Complexity is Contraction-Type Dependent in Vastus Lateralis Electromyographic Signals" Sports 7, no. 4: 78. https://doi.org/10.3390/sports7040078
APA StyleHernandez, L. R., & Camic, C. L. (2019). Fatigue-Mediated Loss of Complexity is Contraction-Type Dependent in Vastus Lateralis Electromyographic Signals. Sports, 7(4), 78. https://doi.org/10.3390/sports7040078






