Validity and Reliability of a Commercially-Available Velocity and Power Testing Device
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Approach to the Problem
2.2. Participants
2.3. Familiarization and 1 RM Determination
2.4. Experimental Trials
2.5. Kinetic and Kinematic Data Acquisition and Processing
2.6. Statistical Analyses
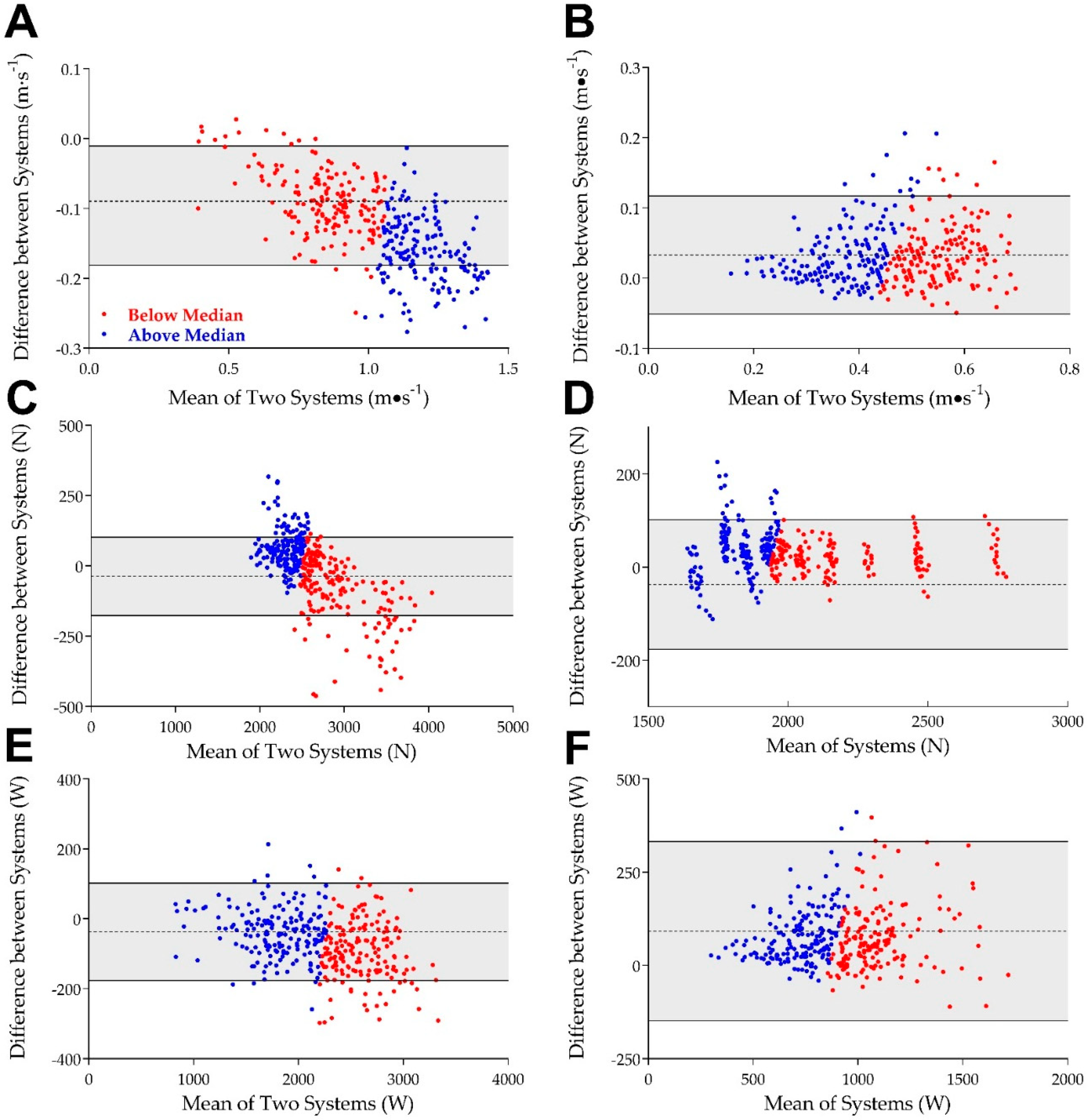
3. Results
3.1. Overall Validity and Reliability
3.2. Analysis of High and Low Values
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Garnacho-Castaño, M.V.; López-Lastra, S.; Maté-Muñoz, J.L. Reliability and validity assessment of a linear position transducer. J. Sports Sci. Med. 2015, 14, 128. [Google Scholar] [PubMed]
- Mann, J.B.; Ivey, P.A.; Sayers, S.P. Velocity-based training in football. Strength Cond. J. 2015, 37, 52–57. [Google Scholar] [CrossRef]
- González-Badillo, J.; Marques, M.; Sánchez-Medina, L. The importance of movement velocity as a measure to control resistance training intensity. J. Hum. Kinet. 2011, 29, 15–19. [Google Scholar] [CrossRef] [PubMed]
- González-Badillo, J.J.; Sánchez-Medina, L. Movement velocity as a measure of loading intensity in resistance training. Int. J. Sports Med. 2010, 31, 347–352. [Google Scholar] [CrossRef] [PubMed]
- Oliver, J.M.; Kreutzer, A.; Jenke, S.C.; Phillips, M.D.; Mitchell, J.B.; Jones, M.T. Velocity drives greater power observed during back squat using cluster sets. J. Strength Cond. Res 2016, 30, 235–243. [Google Scholar] [CrossRef]
- Smart, D.J.; Hopkins, W.G.; Gill, N.D. Differences and changes in the physical characteristics of professional and amateur rugby union players. J. Strength Cond. Res. 2013, 27, 3033–3044. [Google Scholar] [CrossRef]
- Cormie, P.; McBride, J.M.; McCaulley, G.O. Validation of power measurement techniques in dynamic lower body resistance exercises. J. Appl. Biomechan. 2007, 23, 103–118. [Google Scholar] [CrossRef]
- Ebben, W.P.; Hintz, M.J.; Simenz, C.J. Strength and conditioning practices of Major League Baseball strength and conditioning coaches. J. Strength Cond. Res. 2005, 19, 538. [Google Scholar]
- Ebben, W.P.; Carroll, R.M.; Simenz, C.J. Strength and conditioning practices of National Hockey League strength and conditioning coaches. J. Strength Cond. Res. 2004, 18, 889–897. [Google Scholar]
- Craft, J. Survey: Football core exercises of selected universities. Strength Cond. J. 1992, 14, 34–38. [Google Scholar] [CrossRef]
- Jackson, A.S.; Pollock, M.L. Generalized equations for predicting body density of men. Br. J. Nutr. 1978, 40, 497–504. [Google Scholar] [CrossRef] [PubMed]
- Siri, W. Body composition from fluid spaces and density: Analysis of methods. 1961. Nutrition 1993, 9, 480. [Google Scholar] [PubMed]
- Oliver, J.M.; Jagim, A.R.; Sanchez, A.C.; Mardock, M.A.; Kelly, K.A.; Meredith, H.J.; Smith, G.L.; Greenwood, M.; Parker, J.L.; Riechman, S.E. Greater gains in strength and power with intraset rest intervals in hypertrophic training. J. Strength Cond. Res. 2013, 27, 3116–3131. [Google Scholar] [CrossRef]
- Banyard, H.G.; Nosaka, K.; Sato, K.; Haff, G.G. Validity of various methods for determining velocity, force, and power in the back squat. Int. J. Sports Physiol. Perform. 2017, 12, 1170–1176. [Google Scholar] [CrossRef] [PubMed]
- Bland, J.M.; Altman, D. Statistical methods for assessing agreement between two methods of clinical measurement. Int. J. Nurs. Stud. 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Hopkins, W. Linear models and effect magnitudes for research, clinical and practical applications. Sportscience 2010, 14, 49–57. [Google Scholar]
- Hopkins, W.G. Spreadsheets for Analysis of Validity and Reliability. Sportscience 2017, 21, 36–44. [Google Scholar]
- Koo, T.K.; Li, M.Y. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef]
- Cronin, J.B.; Hing, R.D.; McNair, P.J. Reliability and validity of a linear position transducer for measuring jump performance. J. Strength Cond. Res. 2004, 18, 590–593. [Google Scholar]
- Walmsley, R.P.; Amell, T.K. The application and interpretation of intraclass correlations in the assessment of reliability in isokinetic dynamometry. Isokinet. Exerc. Sci. 1996, 6, 117–124. [Google Scholar] [CrossRef]
- Crewther, B.; Kilduff, L.; Cunningham, D.; Cook, C.; Owen, N.; Yang, G. Validating two systems for estimating force and power. Int. J. Sports Med. 2011, 32, 254. [Google Scholar] [CrossRef] [PubMed]
- O’Donnell, S.; Tavares, F.; McMaster, D.; Chambers, S.; Driller, M. The validity and reliability of the GymAware linear position transducer for measuring counter-movement jump performance in female athletes. Meas. Phys. Educ. Exerc. Sci. 2018, 22, 101–107. [Google Scholar] [CrossRef]
- Orange, S.T.; Metcalfe, J.W.; Marshall, P.; Vince, R.V.; Madden, L.A.; Liefeith, A. Test-retest reliability of a commercial linear position transducer (GymAware PowerTool) to measure velocity and power in the back squat and bench press. J. Strength Cond. Res. 2018. [Google Scholar] [CrossRef] [PubMed]
- Drinkwater, E.J.; Galna, B.; McKenna, M.J.; Hunt, P.H.; Pyne, D.B. Validation of an optical encoder during free weight resistance movements and analysis of bench press sticking point power during fatigue. J. Strength Cond. Res. 2007, 21, 510–517. [Google Scholar] [PubMed]
- Dorrell, H.F.; Moore, J.M.; Smith, M.F.; Gee, T.I. Validity and reliability of a linear positional transducer across commonly practised resistance training exercises. J. Sports Sci. 2018, 37, 67–73. [Google Scholar] [CrossRef] [PubMed]
| PV (m·s−1) | Mean Bias | Cohen’s d | ICC | SEE |
|---|---|---|---|---|
| Below Median | −0.09 (−0.12, −0.06) | −0.59 (−0.80, −0.38) | 0.975 (0.967, 0.982) | 0.04 (0.04, 0.05) |
| Above Median | −0.16 (−0.18, −0.14) | −1.46 (−1.69, −1.22) | 0.953 (0.936, 0.965) | 0.05 (0.04, 0.05) |
| All Values | −0.12 (−0.16, −0.09) | −0.57 (−0.72, −0.42) | 0.982 (0.978, 0.985) | 0.05 (0.04, 0.05) |
| AV (m·s−1) | ||||
| Below Median | 0.03 (0.02, 0.05) | 0.43 (0.22, 0.64) | 0.914 (0.884, 0.937) | 0.03 (0.03, 0.04) |
| Above Median | 0.03 (0.02, 0.04) | 0.48 (0.26, 0.69) | 0.894 (0.957, 0.921) | 0.03 (0.03, 0.04) |
| All Values | 0.03 (0.01, 0.05) | 0.28 (0.13, 0.43) | 0.966 (0.958, 0.973) | 0.04 (0.04, 0.04) |
| PF (N) | ||||
| Below Median | 63.05 (30.0, 96.1) | 0.40 (0.19, 0.61) | 0.948 (0.930, 0.961) | 69.3 (64.6, 77.4) |
| Above Median | −85.6 (−167.6, −3.6) | −0.22 (−0.42, −0.01) | 0.976 (0.968, 0.982) | 110.6 (103.0, 123.4) |
| All Values | −11.48 (−74.4, 51.4) | −0.03 (−0.17, 0.12) | 0.979 (0.974, 0.983) | 101.5 (94.5, 109.5) |
| AF (N) | ||||
| Below Median | 38.5 (18.4, 58.6) | 0.40 (0.19, 0.61) | 0.911 (0.881, 0.934) | 48.5 (45.2, 54.2) |
| Above Median | 20.9 (−29.9, 71.7) | 0.09 (−0.12, 0.29) | 0.996 (0.994, 0.997) | 31.7 (29.5, 35.3) |
| All Values | 29.7 (−8.6, 68.0) | 0.11 (−0.03, 0.26) | 0.992 (0.990, 0.994) | 45.8 (42.6, 49.4) |
| PP (W) | ||||
| Below Median | −37.4 (−107.3, 32.5) | −0.11 (−0.32, 0.10) | 0.989 (0.985, 0.992) | 71.2 (66.4, 79.5) |
| Above Median | −93.4 (−146.3, −40.5) | −0.37 (−0.58, −0.16) | 0.972 (0.962, 0.979) | 83.9 (78.1, 93.6) |
| All Values | −65.5 (−138.9, 8.0) | −0.13 (−0.28, 0.02) | 0.993 (0.992, 0.994) | 80.3 (74.8, 86.7) |
| AP (W) | ||||
| Below Median | 77.9 (48.2, 107.7) | 0.55 (0.34, 0.77) | 0.927 (0.901, 0.946) | 60.2 (56.1, 67.4) |
| Above Median | 73.2 (35.8, 110.6) | 0.41 (0.20, 0.63) | 0.935 (0.912, 0.952) | 81.2 (75.6, 90.8) |
| All Values | 75.6 (38.9, 112.3) | 0.31 (0.16, 0.46) | 0.972 (0.966, 0.978) | 77.4 (72.1, 83.7) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Askow, A.T.; Stone, J.D.; Arndts, D.J.; King, A.C.; Goto, S.; Hannon, J.P.; Garrison, J.C.; Bothwell, J.M.; Esposito, P.E.; Jagim, A.R.; et al. Validity and Reliability of a Commercially-Available Velocity and Power Testing Device. Sports 2018, 6, 170. https://doi.org/10.3390/sports6040170
Askow AT, Stone JD, Arndts DJ, King AC, Goto S, Hannon JP, Garrison JC, Bothwell JM, Esposito PE, Jagim AR, et al. Validity and Reliability of a Commercially-Available Velocity and Power Testing Device. Sports. 2018; 6(4):170. https://doi.org/10.3390/sports6040170
Chicago/Turabian StyleAskow, Andrew T., Jason D. Stone, Daniel J. Arndts, Adam C. King, Shiho Goto, Joseph P. Hannon, J. Craig Garrison, James M. Bothwell, Phil E. Esposito, Andrew R. Jagim, and et al. 2018. "Validity and Reliability of a Commercially-Available Velocity and Power Testing Device" Sports 6, no. 4: 170. https://doi.org/10.3390/sports6040170
APA StyleAskow, A. T., Stone, J. D., Arndts, D. J., King, A. C., Goto, S., Hannon, J. P., Garrison, J. C., Bothwell, J. M., Esposito, P. E., Jagim, A. R., Jones, M. T., Jennings, W., & Oliver, J. M. (2018). Validity and Reliability of a Commercially-Available Velocity and Power Testing Device. Sports, 6(4), 170. https://doi.org/10.3390/sports6040170






