The Value of the First Repetition: Force, Impulse, and Linear Velocity in Flywheel Deadlifts and Their Link to Maximal Free-Weight Strength
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Research Design
2.3. Flywheel Deadlifts
2.4. Mean Force, Velocity, Impulse, and Time-Under-Tension During Flywheel Deadlifts
2.5. Free-Weight 1-RM Deadlift Assessment
2.6. Main Trials on the Flywheel Device
2.7. Statistical Analysis
3. Results
3.1. Mean and Peak Concentric Velocity
3.2. Mean Eccentric Velocity
3.3. Impulse and Time Under Tension
3.4. Mean Force (MF)
3.5. Correlations Between Velocity Metrics and 1-RM Across Inertia Levels
3.6. Correlations Between Impulse and 1-RM Across Inertia Loads and Repetitions
3.7. Correlations Between Mean Force and 1-RM Across Inertia Loads and Repetitions
3.8. Inertial Load vs. Response Relationships: Slopes, Correlations, and Fisher’s Z for Flywheel Deadlift Variables
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Inertial Load (kg∙m2) | Rep 1 | Rep 2 | Rep 3 | Rep 4 | Rep 5 | Rep 6 | Rep 1–6 |
|---|---|---|---|---|---|---|---|
| 0.025 | 0.76 | 0.56 | 0.42 | 0.64 | 0.69 | 0.65 | 0.69 |
| p = 0.003 | p = 0.045 | p = 0.154 | p = 0.018 | p = 0.009 | p = 0.016 | p = 0.010 | |
| 0.050 | 0.35 | 0.27 | 0.49 | 0.59 | 0.48 | 0.59 | 0.50 |
| p = 0.247 | p = 0.374 | p = 0.090 | p = 0.035 | p = 0.098 | p = 0.033 | p = 0.081 | |
| 0.075 | 0.2647 | 0.3609 | 0.3024 | 0.2268 | 0.3585 | 0.4322 | 0.3431 |
| p = 0.382 | p = 0.226 | p = 0.315 | p = 0.456 | p = 0.229 | p = 0.140 | p = 0.251 | |
| 0.100 | 0.373 | 0.56 | 0.71 | 0.70 | 0.77 | 0.64 | 0.73 |
| p = 0.209 | p = 0.045 | p = 0.006 | p = 0.008 | p = 0.002 | p = 0.019 | p = 0.004 | |
| 0.125 | 0.80 | 0.69 | 0.81 | 0.82 | 0.83 | 0.81 | 0.83 |
| p = 0.001 | p = 0.009 | p = 0.001 | p = 0.001 | p = 0.000 | p = 0.001 | p = 0.000 | |
| 0.145 | 0.71 | 0.71 | 0.66 | 0.67 | 0.73 | 0.77 | 0.79 |
| p = 0.006 | p = 0.006 | p = 0.015 | p = 0.013 | p = 0.004 | p = 0.002 | p = 0.001 |
| Inertial Load (kg∙m2) | Rep 1 | Rep 2 | Rep 3 | Rep 4 | Rep 5 | Rep 6 | Rep 1–6 |
|---|---|---|---|---|---|---|---|
| 0.025 | 0.67 | 0.51 | 0.43 | 0.54 | 0.52 | 0.59 | 0.60 |
| p = 0.012 | p = 0.075 | p = 0.142 | p = 0.054 | p = 0.066 | p = 0.035 | p = 0.029 | |
| 0.050 | 0.40 | 0.21 | 0.45 | 0.45 | 0.34 | 0.48 | 0.41 |
| p = 0.171 | p = 0.484 | p = 0.121 | p = 0.123 | p = 0.250 | p = 0.098 | p = 0.160 | |
| 0.075 | 0.2865 | 0.3372 | 0.3937 | 0.2086 | 0.3292 | 0.3646 | 0.3315 |
| p = 0.343 | p = 0.260 | p = 0.183 | p = 0.494 | p = 0.272 | p = 0.221 | p = 0.269 | |
| 0.100 | 0.61 | 0.66 | 0.69 | 0.55 | 0.69 | 0.37 | 0.63 |
| p = 0.028 | p = 0.015 | p = 0.010 | p = 0.050 | p = 0.009 | p = 0.216 | p = 0.022 | |
| 0.125 | 0.73 | 0.74 | 0.81 | 0.85 | 0.74 | 0.83 | 0.82 |
| p = 0.004 | p = 0.004 | p = 0.001 | p = 0.000 | p = 0.004 | p = 0.000 | p = 0.001 | |
| 0.145 | 0.85 | 0.72 | 0.58 | 0.70 | 0.74 | 0.77 | 0.77 |
| p < 0.001 | p = 0.006 | p = 0.040 | p = 0.008 | p = 0.004 | p = 0.002 | p = 0.002 |
| Inertial Load (kg∙m2) | Rep 1 | Rep 2 | Rep 3 | Rep 4 | Rep 5 | Rep 6 | Rep 1–6 | Total Impulse |
|---|---|---|---|---|---|---|---|---|
| 0.025 | 0.62 | 0.79 | 0.37 | 0.50 | 0.65 | 0.21 | 0.63 | 0.00 |
| p = 0.023 | p = 0.001 | p = 0.217 | p = 0.081 | p = 0.015 | p = 0.490 | p = 0.022 | p = 0.997 | |
| 0.050 | 0.62 | 0.42 | 0.42 | 0.39 | 0.17 | 0.45 | 0.46 | 0.46 |
| p = 0.024 | p = 0.153 | p = 0.151 | p = 0.186 | p = 0.583 | p = 0.123 | p = 0.110 | p = 0.110 | |
| 0.075 | 0.49 | 0.60 | 0.66 | 0.58 | 0.49 | 0.60 | 0.63 | 0.63 |
| p = 0.087 | p = 0.031 | p = 0.015 | p = 0.039 | p = 0.088 | p = 0.030 | p = 0.021 | p = 0.021 | |
| 0.100 | 0.57 | 0.56 | 0.59 | 0.58 | 0.57 | 0.72 | 0.67 | 0.67 |
| p = 0.042 | p = 0.048 | p = 0.034 | p = 0.039 | p = 0.044 | p = 0.006 | p = 0.012 | p = 0.012 | |
| 0.125 | 0.79 | 0.66 | 0.64 | 0.46 | 0.62 | 0.53 | 0.66 | 0.66 |
| p = 0.001 | p = 0.014 | p = 0.019 | p = 0.109 | p = 0.024 | p = 0.061 | p = 0.014 | p = 0.014 | |
| 0.145 | 0.58 | 0.30 | 0.39 | 0.56 | 0.38 | 0.58 | 0.52 | 0.52 |
| p = 0.039 | p = 0.313 | p = 0.182 | p = 0.046 | p = 0.201 | p = 0.039 | p = 0.068 | p = 0.068 |
| Inertial Load (kg∙m2) | Rep 1 | Rep 2 | Rep 3 | Rep 4 | Rep 5 | Rep 6 | Rep 1–6 |
|---|---|---|---|---|---|---|---|
| 0.025 | 0.52 | 0.45 | 0.30 | 0.40 | 0.44 | 0.30 | 0.41 |
| p = 0.067 | p = 0.126 | p = 0.322 | p = 0.173 | p = 0.128 | p = 0.325 | p = 0.165 | |
| 0.050 | 0.57 | 0.52 | 0.54 | 0.52 | 0.46 | 0.41 | 0.51 |
| p = 0.042 | p = 0.067 | p = 0.057 | p = 0.068 | p = 0.114 | p = 0.164 | p = 0.073 | |
| 0.075 | 0.77 | 0.84 | 0.90 | 0.90 | 0.90 | 0.89 | 0.88 |
| p = 0.002 | p = 0.000 | p = 0.000 | p = 0.000 | p = 0.000 | p = 0.000 | p = 0.000 | |
| 0.100 | 0.79 | 0.92 | 0.89 | 0.87 | 0.86 | 0.89 | 0.90 |
| p = 0.001 | p = 0.000 | p = 0.000 | p = 0.000 | p = 0.000 | p = 0.000 | p = 0.000 | |
| 0.125 | 0.83 | 0.76 | 0.79 | 0.72 | 0.78 | 0.74 | 0.78 |
| p = 0.000 | p = 0.002 | p = 0.001 | p = 0.006 | p = 0.002 | p = 0.004 | p = 0.002 | |
| 0.145 | 0.79 | 0.82 | 0.83 | 0.82 | 0.82 | 0.84 | 0.83 |
| p = 0.001 | p = 0.001 | p = 0.000 | p = 0.001 | p = 0.001 | p = 0.000 | p = 0.000 |
References
- Martinez-Hernandez, D. Flywheel Eccentric Training: How to Effectively Generate Eccentric Overload. Strength Cond. J. 2024, 46, 234–250. [Google Scholar] [CrossRef]
- Tesch, P.A.; Fernandez-Gonzalo, R.; Lundberg, T.R. Clinical applications of iso-inertial, eccentric-overload (YoYoTM) resistance exercise. Front. Physiol. 2017, 8, 241. [Google Scholar] [CrossRef]
- Berg, H.E.; Tesch, P.A. A gravity-independent ergometer to be used for resistance training in space. Aviat. Sp. Environ. Med. 1994, 65, 752–756. [Google Scholar]
- Vicens-Bordas, J.; Esteve, E.; Fort-Vanmeerhaeghe, A.; Bandholm, T.; Thorborg, K. Is inertial flywheel resistance training superior to gravity-dependent resistance training in improving muscle strength? A systematic review with meta-analyses. J. Sci. Med. Sport 2018, 21, 75–83. [Google Scholar] [CrossRef]
- Muñoz-López, A.; Nakamura, F.Y.; Beato, M. Eccentric overload differences between loads and training variables on flywheel training. Biol. Sport 2023, 40, 1151–1158. [Google Scholar] [CrossRef]
- Beato, M.; Raya-González, J.; Hernandez-Davo, J.L.; Maroto-Izquierdo, S. Editorial: The science of flywheel training: Exercise physiology and practical applications. Front. Physiol. 2023, 14, 1241529. [Google Scholar] [CrossRef]
- Petré, H.; Wernstål, F.; Mattsson, C.M. Effects of Flywheel Training on Strength-Related Variables: A Meta-analysis. Sports Med.-Open 2018, 4, 55. [Google Scholar] [CrossRef]
- Maroto-Izquierdo, S.; García-López, D.; Fernandez-Gonzalo, R.; Moreira, O.C.; González-Gallego, J.; de Paz, J.A. Skeletal muscle functional and structural adaptations after eccentric overload flywheel resistance training: A systematic review and meta-analysis. J. Sci. Med. Sport 2017, 20, 943–951. [Google Scholar] [CrossRef]
- Beato, M.; de Keijzer, K.L.; Muñoz-Lopez, A.; Raya-González, J.; Pozzo, M.; Alkner, B.A.; Dello Iacono, A.; Vicens-Bordas, J.; Coratella, G.; Maroto-Izquierdo, S.; et al. Current Guidelines for the Implementation of Flywheel Resistance Training Technology in Sports: A Consensus Statement. Sports Med. 2024, 54, 541–556. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-López, A.; De Souza Fonseca, F.; Ramírez-Campillo, R.; Gantois, P.; Javier Nuñez, F.; Nakamura, F.Y. The use of real-time monitoring during flywheel resistance training programmes: How can we measure eccentric overload? A systematic review and meta-analysis. Biol. Sport 2021, 38, 639–652. [Google Scholar] [CrossRef] [PubMed]
- Allen, W.J.C.; De Keijzer, K.L.; Raya-González, J.; Castillo, D.; Coratella, G.; Beato, M. Chronic effects of flywheel training on physical capacities in soccer players: A systematic review. Res. Sports Med. 2023, 31, 228–248. [Google Scholar] [CrossRef]
- de Keijzer, K.L.; Gonzalez, J.R.; Beato, M. The effect of flywheel training on strength and physical capacities in sporting and healthy populations: An umbrella review. PLoS ONE 2022, 17, e0264375. [Google Scholar] [CrossRef] [PubMed]
- Suchomel, T.J.; Wagle, J.P.; Douglas, J.; Taber, C.B.; Harden, M.; Haff, G.G.; Stone, M.H. Implementing Eccentric Resistance Training—Part 1: A Brief Review of Existing Methods. J. Funct. Morphol. Kinesiol. 2019, 4, 38. [Google Scholar] [CrossRef] [PubMed]
- Gonzalo-Skok, O.; Tous-Fajardo, J.; Valero-Campo, C.; Berzosa, C.C.; Bataller, A.V.; Arjol-Serrano, J.L.J.L.; Moras, G.; Mendez-Villanueva, A. Eccentric-overload training in team-sport functional performance: Constant bilateral vertical versus variable unilateral multidirectional movements. Int. J. Sports Physiol. Perform. 2017, 12, 951–958. [Google Scholar] [CrossRef] [PubMed]
- Carroll, K.M.; Wagle, J.P.; Sato, K.; Taber, C.B.; Yoshida, N.; Bingham, G.E.; Stone, M.H. Characterising overload in inertial flywheel devices for use in exercise training. Sports Biomech. 2019, 18, 390–401. [Google Scholar] [CrossRef]
- Spudić, D.; Smajla, D.; Šarabon, N. Validity and reliability of force–velocity outcome parameters in flywheel squats. J. Biomech. 2020, 107, 109824. [Google Scholar] [CrossRef]
- Spudić, D.; Cvitkovič, R.; Šarabon, N. Assessment and evaluation of force–velocity variables in flywheel squats: Validity and reliability of force plates, a linear encoder sensor, and a rotary encoder sensor. Appl. Sci. 2021, 11, 10541. [Google Scholar] [CrossRef]
- Muñoz-López, A.; Floría, P.; Sañudo, B.; Pecci, J.; Pérez, J.C.; Pozzo, M. The maximum flywheel load: A novel index to monitor loading intensity of flywheel devices. Sensors 2021, 21, 8124. [Google Scholar] [CrossRef]
- McErlain-Naylor, S.A.; Beato, M. Concentric and eccentric inertia–velocity and inertia–power relationships in the flywheel squat. J. Sports Sci. 2021, 39, 1136–1143. [Google Scholar] [CrossRef]
- Martín-Rivera, F.; Beato, M.; Alepuz-Moner, V.; Maroto-Izquierdo, S. Use of concentric linear velocity to monitor flywheel exercise load. Front. Physiol. 2022, 13, 961572. [Google Scholar] [CrossRef]
- Zhu, Z.; Chen, J.; Sun, R.; Wang, R.; He, J.; Zhang, W.; Lin, W.; Li, D. An investigation of the load-velocity relationship between flywheel eccentric and barbell training methods. Front. Public Health 2025, 13, 1579291. [Google Scholar] [CrossRef]
- Martinez-Aranda, L.M.; Fernandez-Gonzalo, R. Effects of inertial setting on power, force, work, and eccentric overload during flywheel resistance exercise in women and men. J. Strength Cond. Res. 2017, 31, 1653–1661. [Google Scholar] [CrossRef]
- Scherrer, D.; Nunley, B.; Eggleston, J.; Harry, J. Deadlift Biomechanics across Multiple Sets in Resistance Trained Males. Int. J. Strength Cond. 2023, 3. [Google Scholar] [CrossRef]
- Bezodis, N.E.; Willwacher, S.; Salo, A.I.T. The Biomechanics of the Track and Field Sprint Start: A Narrative Review. Sports Med. 2019, 49, 1345–1364. [Google Scholar] [CrossRef]
- Tsoukos, A.; Tsoukala, M.; Mirto Papadimitriou, D.; Terzis, G.; Bogdanis, G.C. Acute Effects of Low vs. High Inertia During Flywheel Deadlifts with Equal Force Impulse on Vertical Jump Performance. Sensors 2025, 25, 1125. [Google Scholar] [CrossRef]
- Maroto-Izquierdo, S.; García-López, D.; Beato, M.; Bautista, I.J.; Hernández-Davó, J.L.; Raya-González, J.; Martín-Rivera, F. Force Production and Electromyographic Activity during Different Flywheel Deadlift Exercises. Sports 2024, 12, 95. [Google Scholar] [CrossRef]
- Thompson, B.J.; Stock, M.S.; Shields, J.E.; Luera, M.J.; Munayer, I.K.; Mota, J.A.; Carrillo, E.C.; Olinghouse, K.D. Barbell deadlift training increases the rate of torque development and vertical jump performance in novices. J. Strength Cond. Res. 2015, 29, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Martín-Fuentes, I.; Oliva-Lozano, J.M.; Muyor, J.M. Electromyographic activity in deadlift exercise and its variants. A systematic review. PLoS ONE 2020, 15, e0229507. [Google Scholar] [CrossRef] [PubMed]
- Brien, J.; Browne, D.; Earls, D.; Lodge, C. Investigation into the Optimal Number of Repetitions Needed to Maintain Power Output in the Flywheel Romanian Deadlift Exercise. Eur. J. Sport Sci. 2023, 2, 29–33. [Google Scholar] [CrossRef]
- Brien, J.O.; Browne, D.; Earls, D.; Lodge, C. The effects of varying inertial loadings on power variables in the flywheel romanian deadlift exercise. Biol. Sport 2022, 39, 499–503. [Google Scholar] [CrossRef]
- Brien, J.O.; Browne, D.; Earls, D.; Lodge, C. The Relationship between Bodyweight, Maximum and Relative Strength, and Power Variables during Flywheel Inertial Training. Biomechanics 2023, 3, 291–298. [Google Scholar] [CrossRef]
- Gallo, C.A.; Thompson, W.K.; Godfrey, A.P.; Lewandowski, B.E.; DeWitt, J.K. Influence of Load Profile on Biomechanics of the Squat and Deadlift. Available online: https://ntrs.nasa.gov/citations/20180004675 (accessed on 15 September 2025).
- Chiu, L.Z.F.; Salem, G.J. Comparison of joint kinetics during free weight and flywheel resistance exercise. J. Strength Cond. Res. 2006, 20, 555–562. [Google Scholar] [CrossRef]
- Haff, G.; Triplett, N.T. Essentials of Strength Training and Conditioning; Haff, G.G., Triplett, T.N., Eds.; Human Kinetics: Champaign, IL, USA, 2016. [Google Scholar]
- Tsoukos, A.; Krzysztofik, M.; Wilk, M.; Zajac, A.; Panagiotopoulos, M.G.; Psarras, I.I.; Petraki, D.P.; Terzis, G.; Bogdanis, G.C. Fatigue and Metabolic Responses during Repeated Sets of Bench Press Exercise to Exhaustion at Different Ranges of Motion by. J. Hum. Kinet. 2024, 91, 61–76. [Google Scholar] [CrossRef] [PubMed]
- Bogdanis, G.C.; Tsoukos, A.; Veligekas, P.; Tsolakis, C.; Terzis, G. Effects of muscle action type with equal impulse of conditioning activity on postactivation potentiation. J. Strength Cond. Res. 2014, 28, 2521–2528. [Google Scholar] [CrossRef]
- Tsoukos, A.; Brown, L.E.; Terzis, G.; Wilk, M.; Zajac, A.; Bogdanis, G.C. Changes in EMG and movement velocity during a set to failure against different loads in the bench press exercise. Scand. J. Med. Sci. Sports 2021, 31, 2071–2082. [Google Scholar] [CrossRef]
- Tsoukos, A.; Wilk, M.; Krzysztofik, M.; Zajac, A.; Bogdanis, G.C. The Impact of Range of Motion on Applied Force Characteristics and Electromyographic Activity during Repeated Sets of Bench Press Exercise. J. Hum. Kinet. 2024, 91, 189–204. [Google Scholar] [CrossRef]
- Tsoukos, A.; Brown, L.E.; Veligekas, P.; Terzis, G.; Bogdanis, G.C. Postactivation potentiation of bench press throw performance using velocity-based conditioning protocols with low and moderate loads. J. Hum. Kinet. 2019, 68, 81–98. [Google Scholar] [CrossRef] [PubMed]
- Tsoukos, A.; Bogdanis, G.C. Effects of Transducer Placement on Load–Velocity Relationships in Smith Machine and Free Weight Squats in Trained Women. J. Funct. Morphol. Kinesiol. 2025, 10, 178. [Google Scholar] [CrossRef]
- Tsoukos, A.; Bogdanis, G.C. Lower Fatigue in the Eccentric than the Concentric Phase of a Bench Press Set Executed with Maximum Velocity to Failure Against Both Heavy and Light Loads. J. Hum. Kinet. 2023, 88, 119–129. [Google Scholar] [CrossRef]
- Wilk, M.; Zajac, A.; Tufano, J.J. The Influence of Movement Tempo During Resistance Training on Muscular Strength and Hypertrophy Responses: A Review. Sports Med. 2021, 51, 1629–1650. [Google Scholar] [CrossRef] [PubMed]
- Cormie, P.; McGuigan, M.R.; Newton, R.U. Adaptations in athletic performance after ballistic power versus strength training. Med. Sci. Sports Exerc. 2010, 42, 1582–1598. [Google Scholar] [CrossRef] [PubMed]
- Haff, G.G.; Carlock, J.M.; Hartman, M.J.; Kilgore, J.L.; Kawamori, N.; Jackson, J.R.; Morris, R.T.; Sands, W.A.; Stone, M.H. Force-time curve characteristics of dynamic and isometric muscle actions of elite women olympic weightlifters. J. Strength Cond. Res. 2005, 19, 741–748. [Google Scholar] [CrossRef] [PubMed]
- Behm, D.G.; Konrad, A.; Nakamura, M.; Alizadeh, S.; Culleton, R.; Anvar, S.H.; Pearson, L.T.; Ramirez-Campillo, R.; Sale, D.G. A narrative review of velocity-based training best practice: The importance of contraction intent versus movement speed. Appl. Physiol. Nutr. Metab. 2025, 50, 1–9. [Google Scholar] [CrossRef] [PubMed]
- da Silva, J.B.; Lima, V.P.; da Silva Novaes, J.; de Castro, J.B.P.; Nunes, R.d.A.M.; de Souza Vale, R.G.S. Time under tension, muscular activation, and blood lactate responses to perform 8, 10, and 12RM in the bench press exercise. J. Exerc. Physiol. Online 2017, 20, 41–54. [Google Scholar]
- Neuendorf, T.; Kaden, M.; Wachler, E.; Schumann, M.; Nitzsche, N. Metabolic Responses of Eccentric Accentuated Flywheel Squats by a Multi-set Protocol with Increasing Loads. J. Sci. Sport Exerc. 2025. [Google Scholar] [CrossRef]
- Mak, M.C.W.; Bishop, C.; Beato, M. Validity and Reliability of Flywheel Resistance Technology as an Assessment Method and Its Association with Sports Performance and Asymmetry: A Systematic Review. J. Strength Cond. Res. 2025, 39, e930–e948. [Google Scholar] [CrossRef]
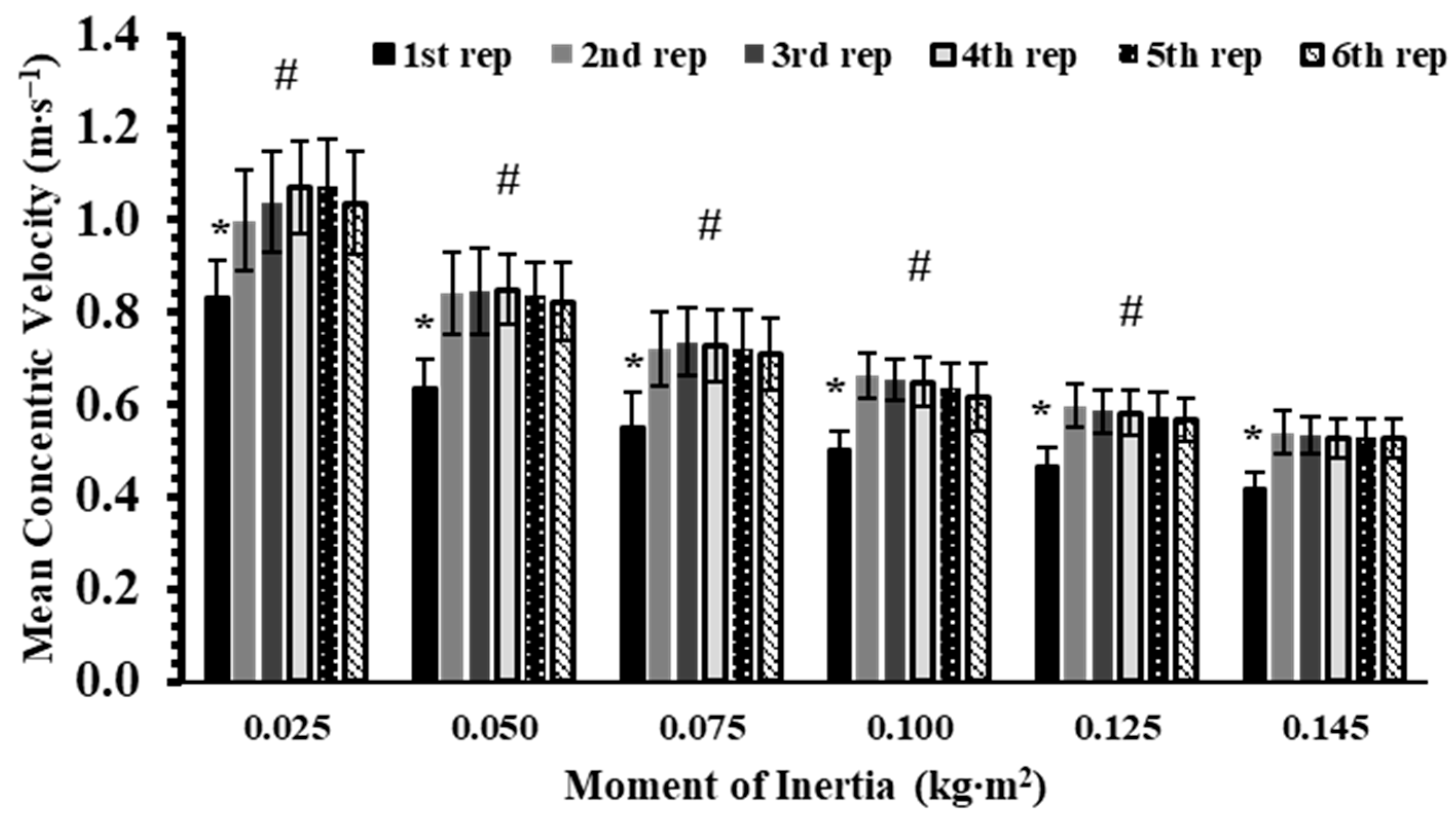

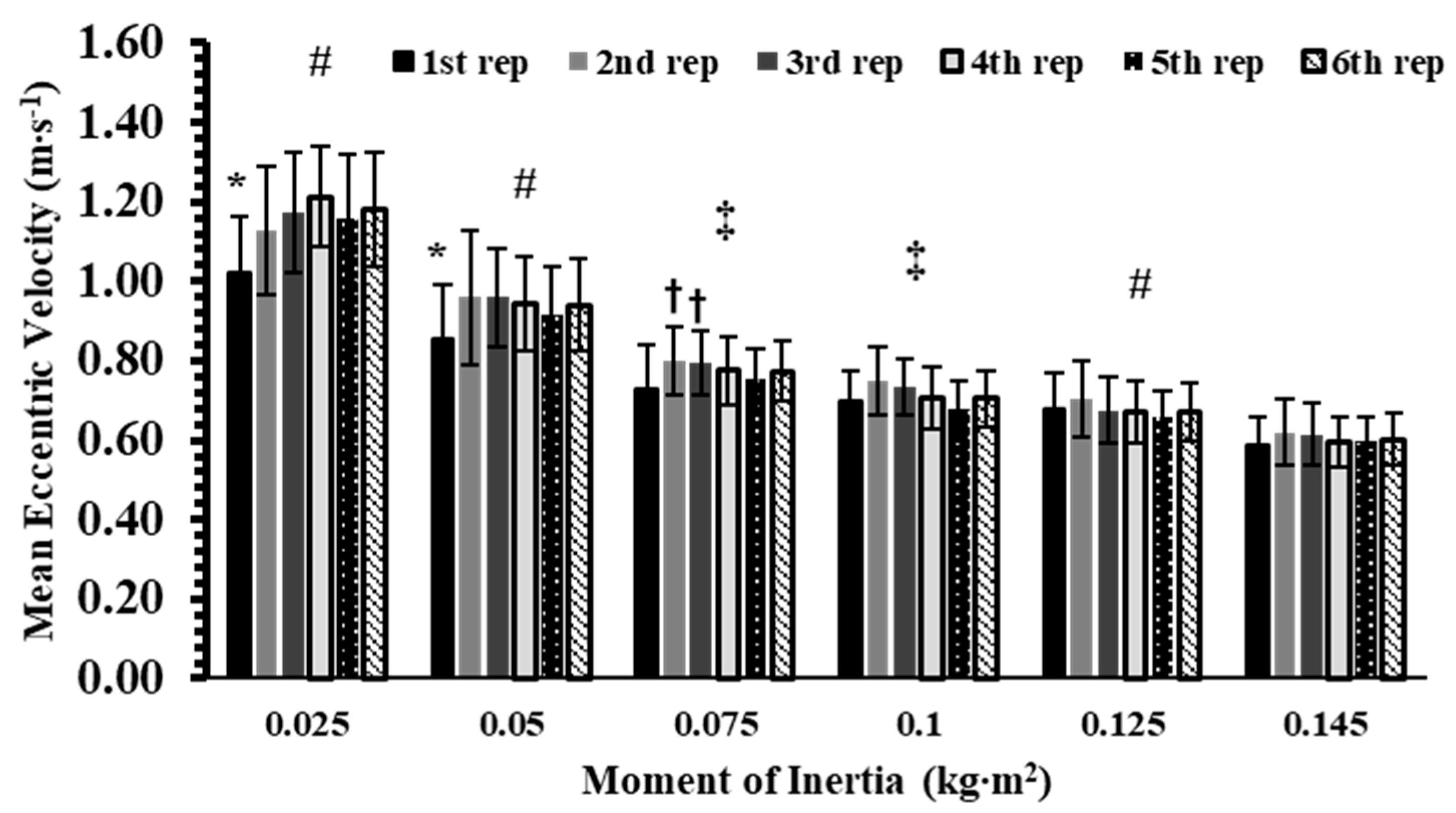
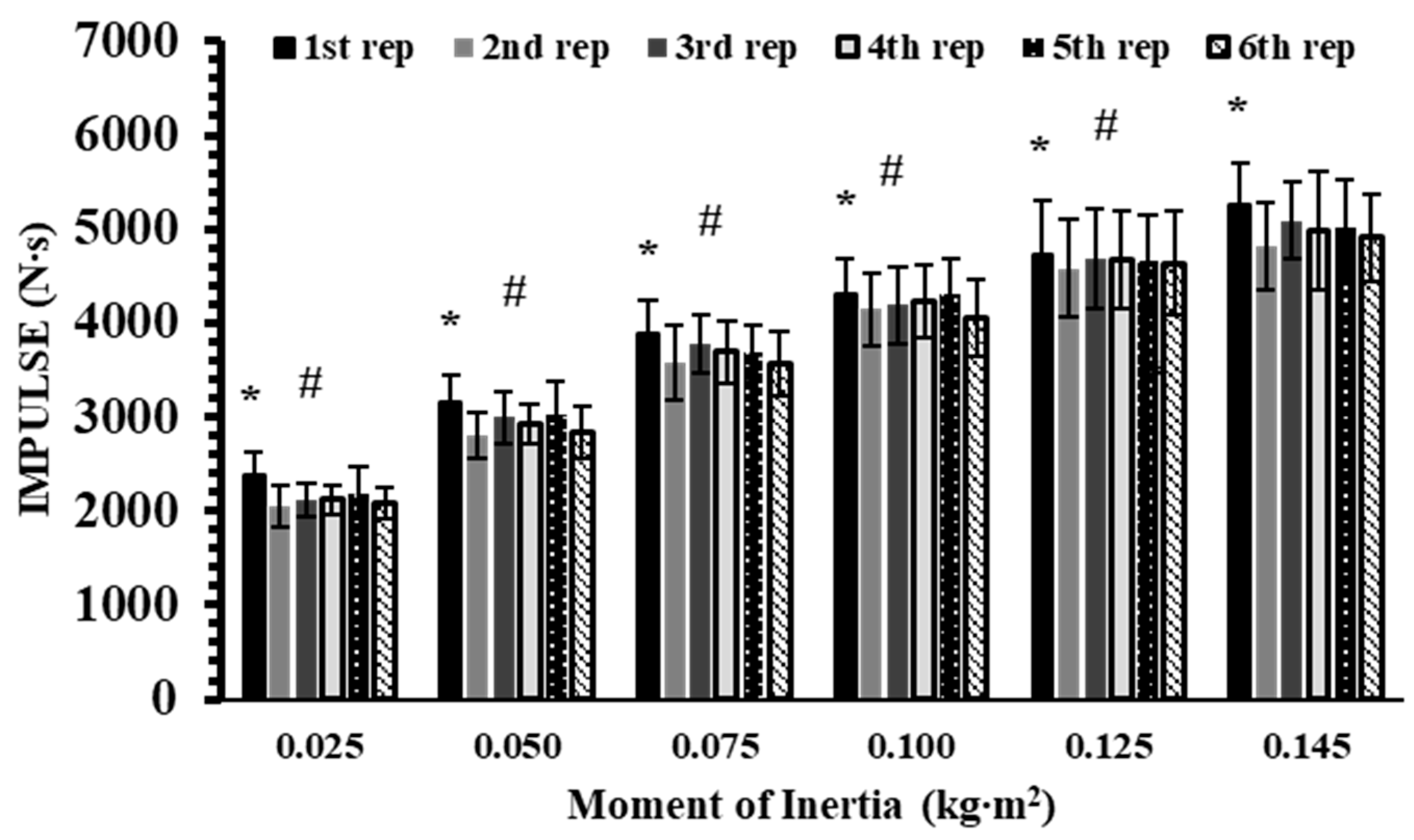
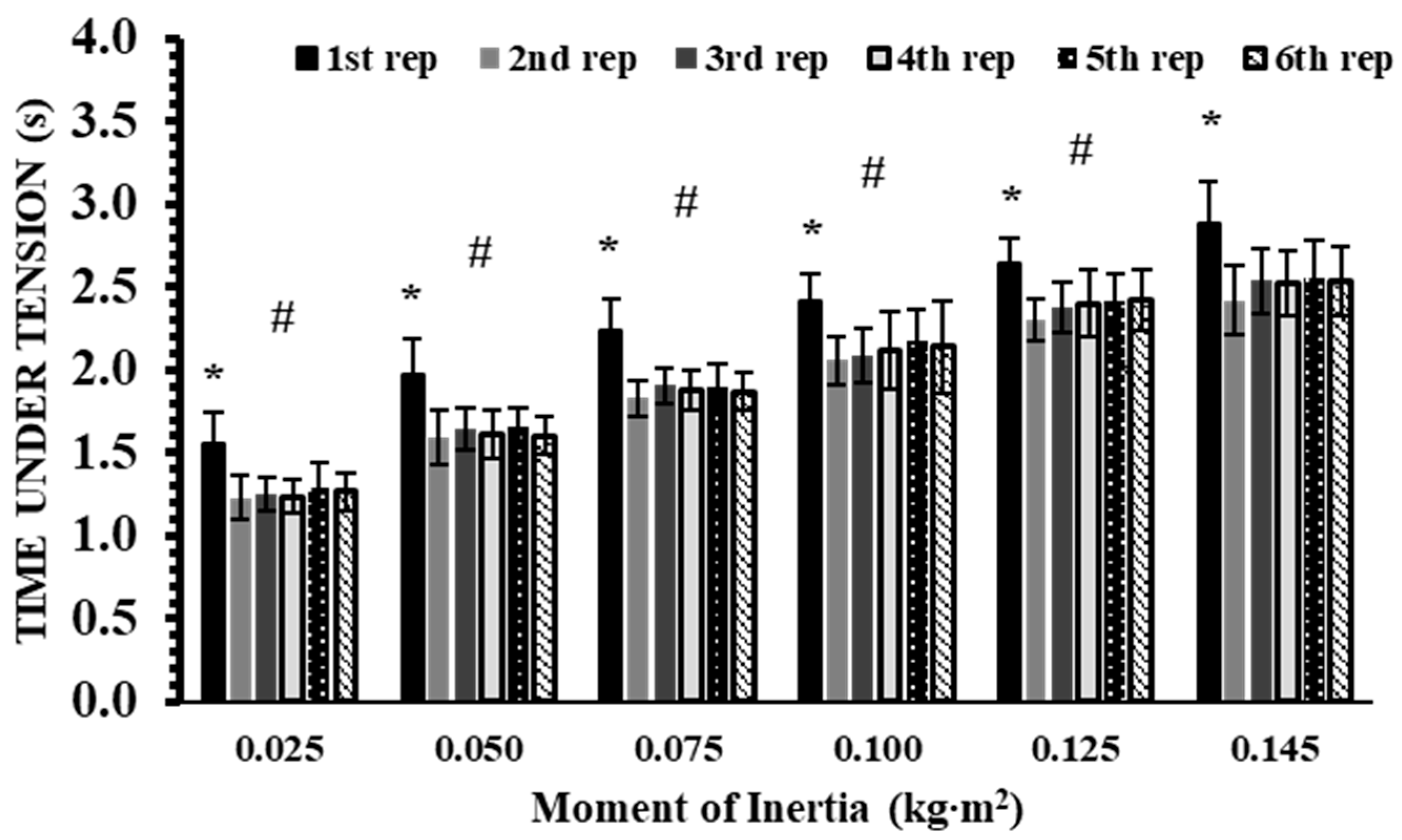

| Inertial Load (kg∙m2) | Total IMP (N∙s) (1–6 Reps) | TUT (s) (1–6 Reps) |
|---|---|---|
| 0.025 | 11,184 ± 4027 * | 7.82 ± 0.74 * |
| 0.050 | 17,744 ± 1419 * | 10.09 ± 0.75 * |
| 0.075 | 22,198 ± 1832 * | 11.62 ± 0.65 * |
| 0.100 | 25,222 ± 2102 * | 12.99 ± 0.99 * |
| 0.125 | 27,962 ± 3000 * | 14.57 ± 0.84 * |
| 0.145 | 30,080 ± 2617 | 15.47 ± 1.12 |
| Variable | Statistic | Mean Reps 1–6 |
|---|---|---|
| MV | SLOPE | −3.88 ± 0.64 |
| PEARSON r | −0.96 ± 0.03 | |
| R2 | 0.91 ± 0.05 | |
| Pearson’s r (Fisher’s Z-Transformed) | −1.98 ± 0.30 # | |
| PV | SLOPE | −5.54 ± 0.98 |
| PEARSON r | −0.95 ± 0.03 | |
| R2 | 0.91 ± 0.06 | |
| Pearson’s r (Fisher’s Z-Transformed) | −1.97 ± 0.33 # | |
| MECCV | SLOPE | −4.18 ± 0.96 |
| PEARSON r | −0.94 ± 0.05 | |
| R2 | 0.88 ± 0.09 | |
| Pearson’s r (Fisher’s Z-Transformed) | −1.85 ± 0.44 † | |
| IMP | SLOPE | 23477 ± 2678 |
| PEARSON r | 0.99 ± 0.01 | |
| R2 | 0.97 ± 0.02 | |
| Pearson’s r (Fisher’s Z-Transformed) | 2.55 ± 0.33 * | |
| TUT | SLOPE | 10.4 ± 1.6 |
| PEARSON r | 0.98 ± 0.01 | |
| R2 | 0.97 ± 0.02 | |
| Pearson’s r (Fisher’s Z-Transformed) | 2.59 ± 0.47 * | |
| MF | SLOPE | 2266 ± 1388 |
| PEARSON r | 0.78 ± 0.14 | |
| R2 | 0.62 ± 0.21 | |
| Pearson’s r (Fisher’s Z-Transformed) | 1.15 ± 0.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsoukos, A.; Bogdanis, G.C. The Value of the First Repetition: Force, Impulse, and Linear Velocity in Flywheel Deadlifts and Their Link to Maximal Free-Weight Strength. Sports 2025, 13, 345. https://doi.org/10.3390/sports13100345
Tsoukos A, Bogdanis GC. The Value of the First Repetition: Force, Impulse, and Linear Velocity in Flywheel Deadlifts and Their Link to Maximal Free-Weight Strength. Sports. 2025; 13(10):345. https://doi.org/10.3390/sports13100345
Chicago/Turabian StyleTsoukos, Athanasios, and Gregory C. Bogdanis. 2025. "The Value of the First Repetition: Force, Impulse, and Linear Velocity in Flywheel Deadlifts and Their Link to Maximal Free-Weight Strength" Sports 13, no. 10: 345. https://doi.org/10.3390/sports13100345
APA StyleTsoukos, A., & Bogdanis, G. C. (2025). The Value of the First Repetition: Force, Impulse, and Linear Velocity in Flywheel Deadlifts and Their Link to Maximal Free-Weight Strength. Sports, 13(10), 345. https://doi.org/10.3390/sports13100345








