The Concept of Optimal Dynamic Pedalling Rate and Its Application to Power Output and Fatigue in Track Cycling Sprinters—A Case Study
Abstract
:1. Introduction
1.1. Background
1.2. The Relationship between Force–Velocity and Power–Velocity in Track Cycling
1.3. The Force–Velocity Relationship and Fatigue
2. Methods
2.1. Test Design
2.2. Data Analysis
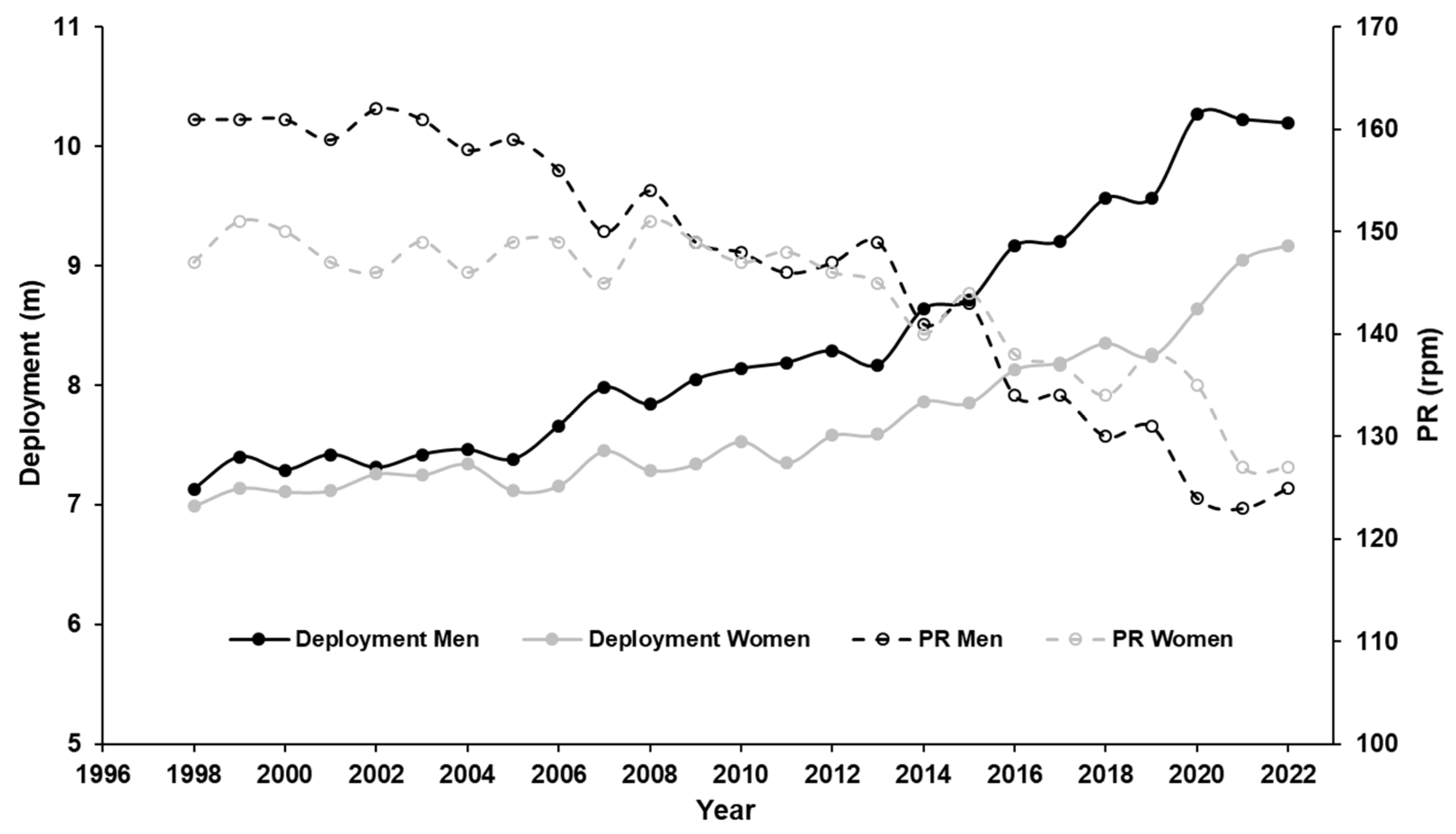
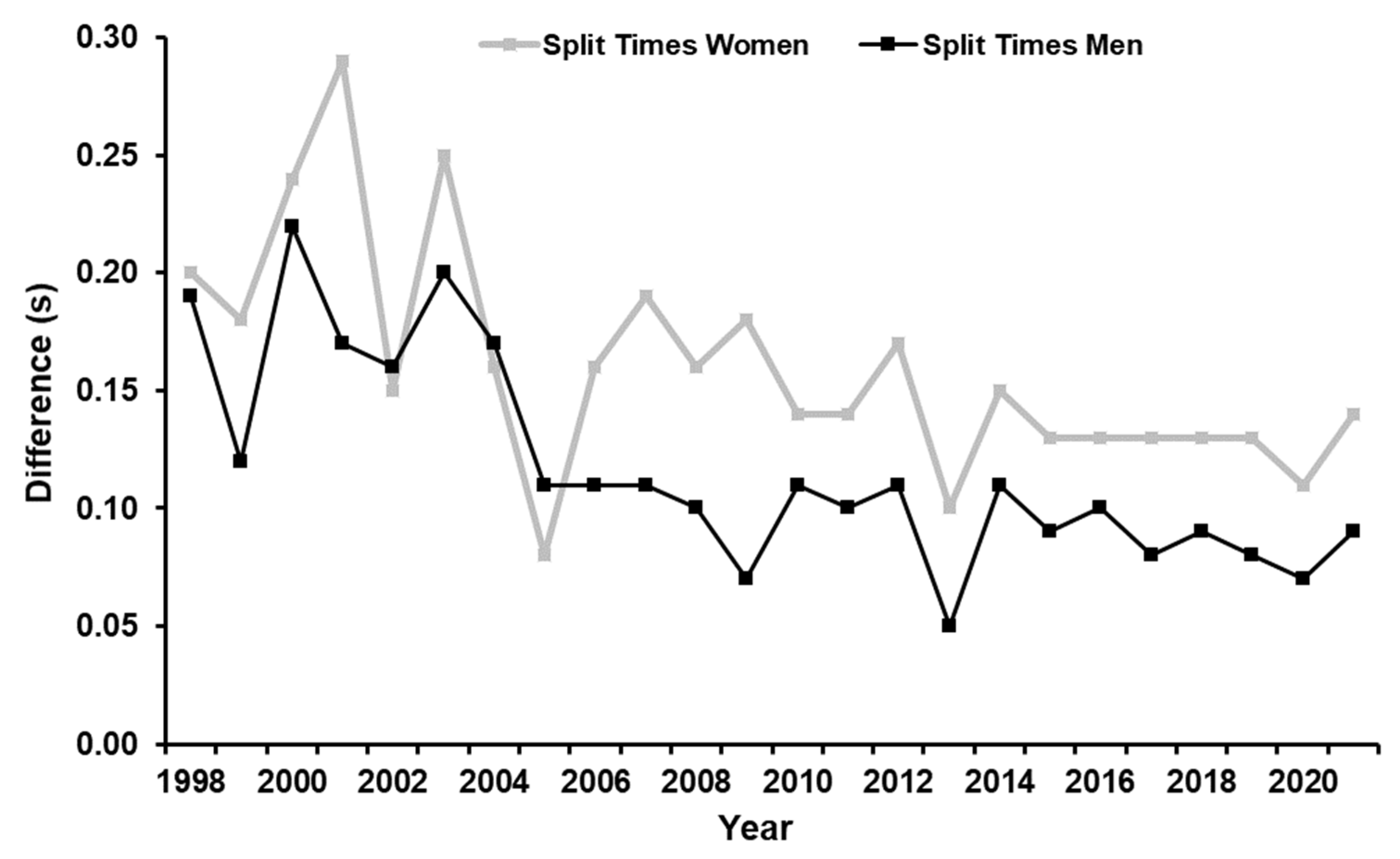
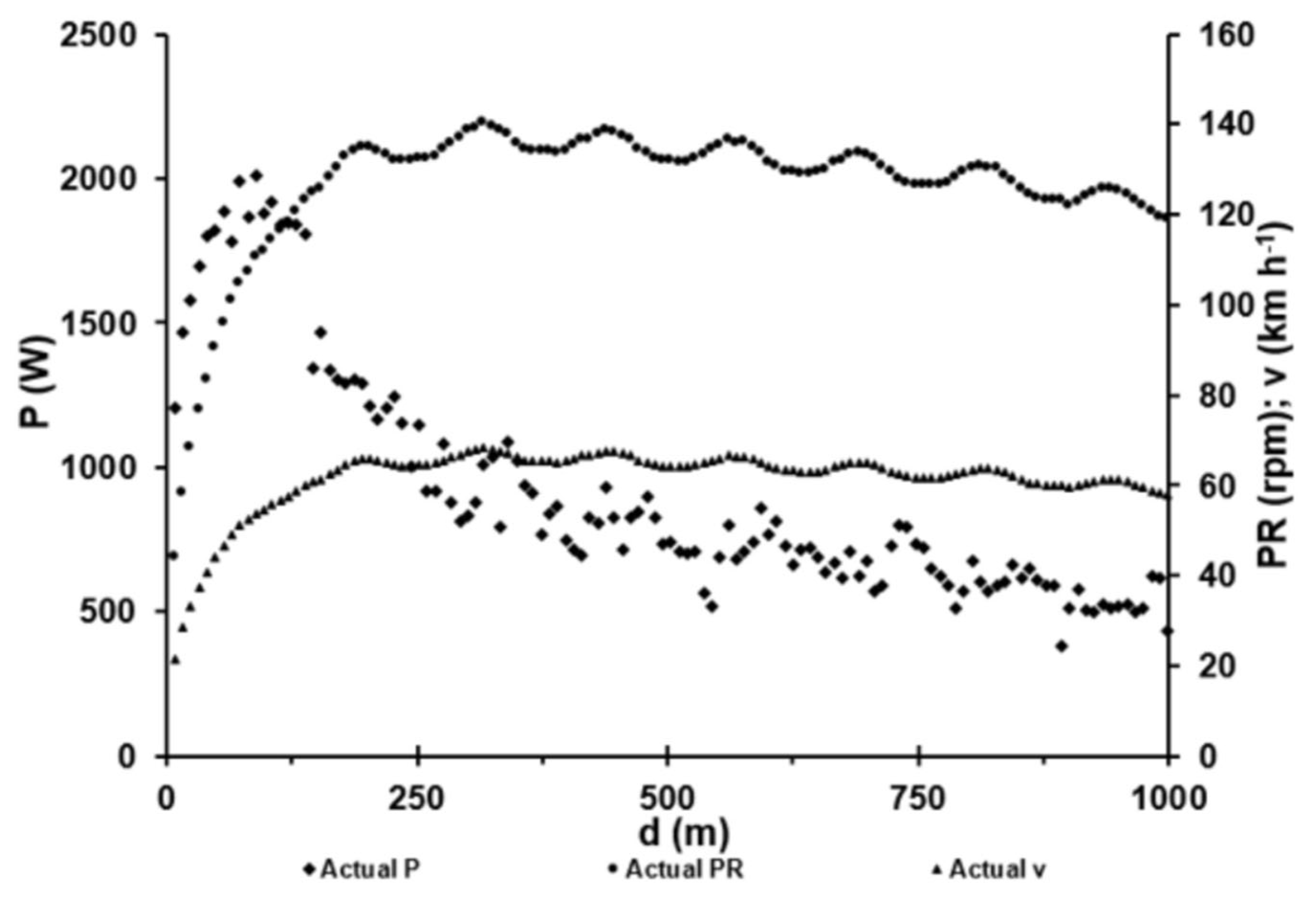
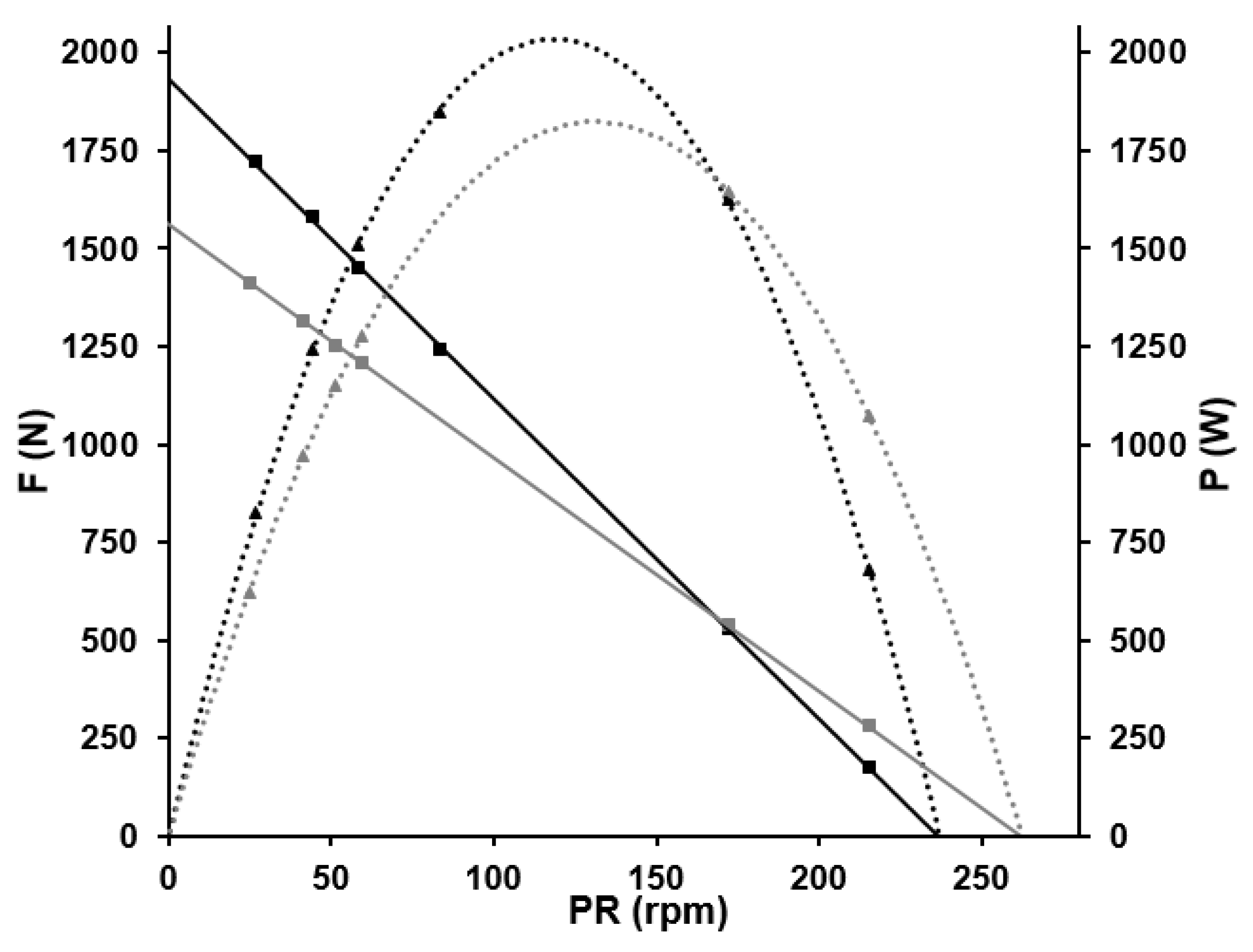
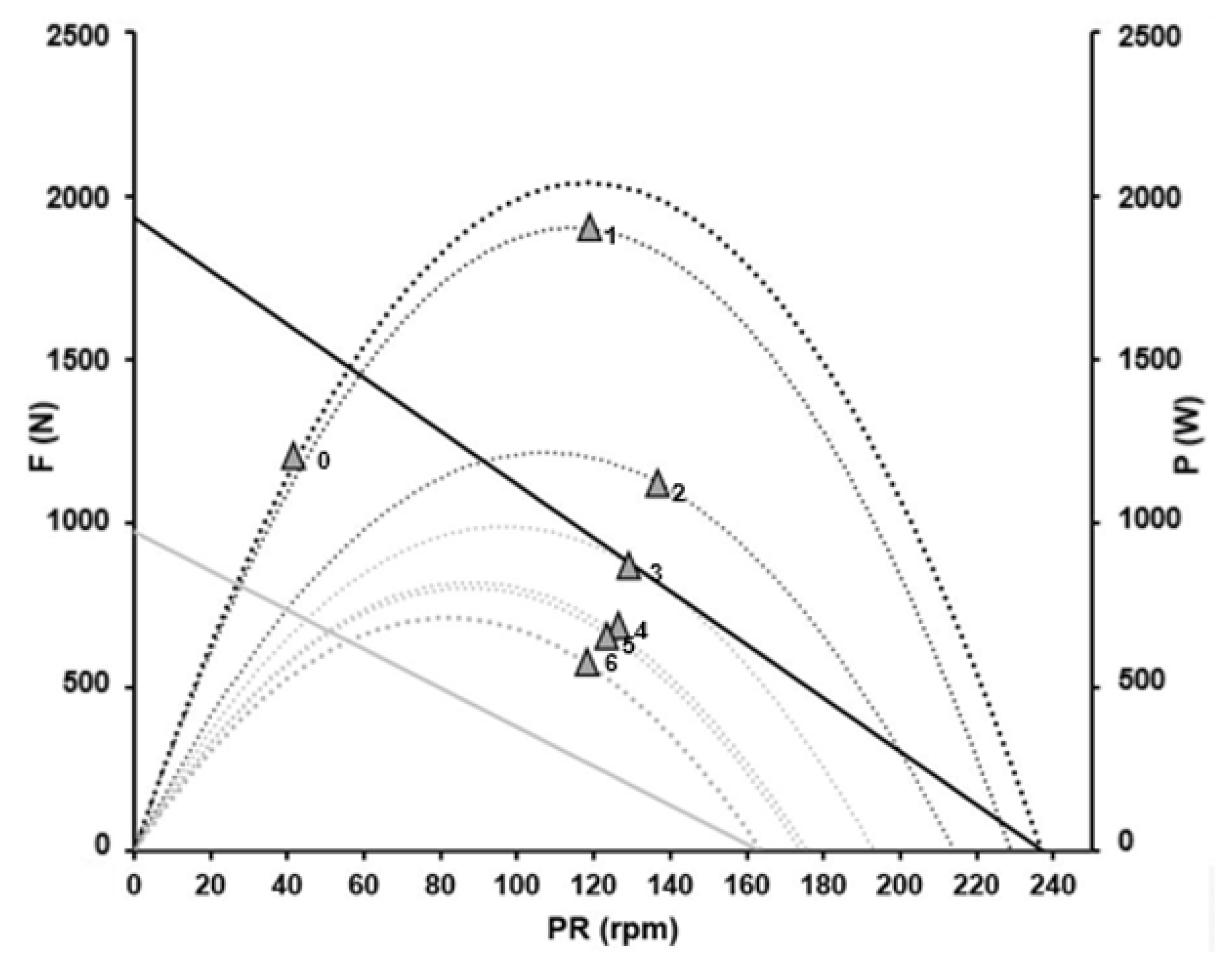
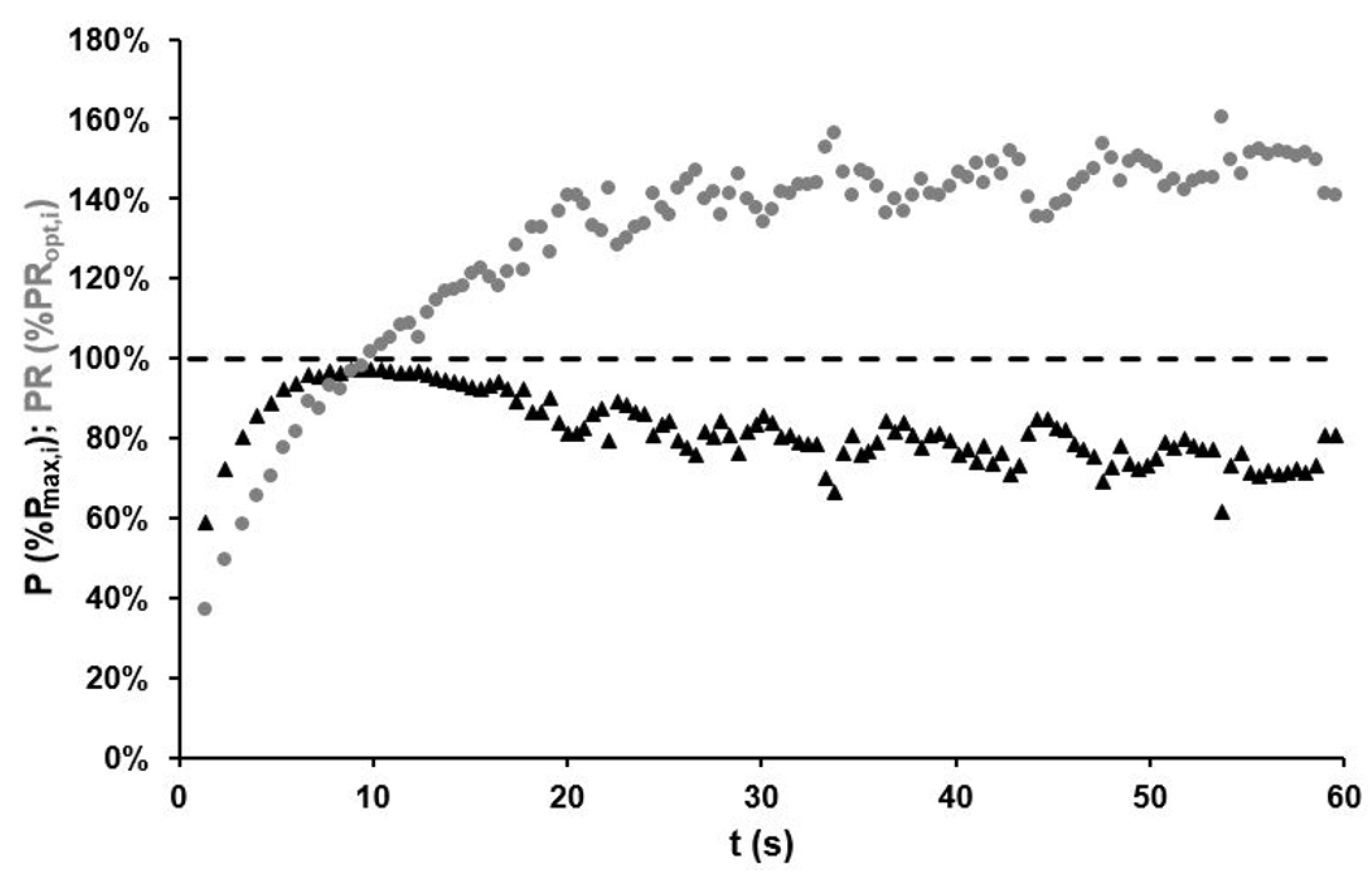
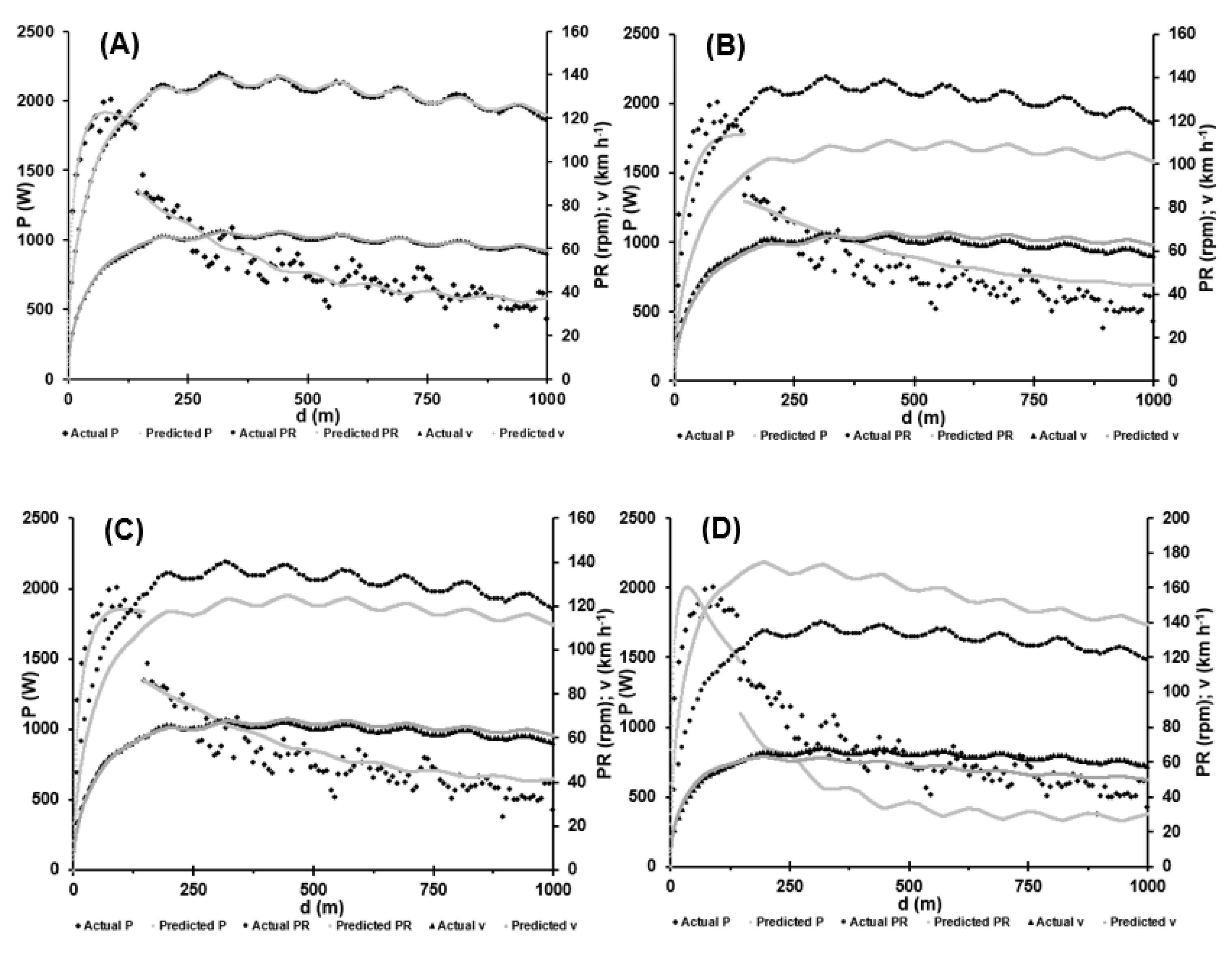
3. Results
4. Discussion
5. Practical Applications
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| a | Slope of the F/v profile |
| b | y-axis intercept of the F/v profile |
| bi | y-axis intercept of the F/v profile at crank revolution i |
| BFP | Body Fat Percentage |
| d | Distance |
| F/v | Force-velocity |
| F | Mean pedal force |
| Fmax | Maximal mean pedal force |
| Fmax,i | Maximal mean pedal force at crank revolution i |
| i | Number of crank revolutions; i = 1, 2, … |
| MHC | Myosin heavy chain |
| P | Power |
| Pmax | Maximum power output |
| Pmax,i | Maximal power output at crank revolution i |
| Pmean | Average power output |
| PR | Pedalling rate, cadence, frequency |
| PRmax | Maximal pedalling rate |
| PRopt | Optimal pedalling rate |
| PRopt,i | Optimal pedalling rate at crank revolution i |
| PRopt(t) | Optimal dynamic pedalling rate at timepoint t; time-dependent optimal pedalling rate |
| P/v | Power-velocity |
| rpm | Revolutions per minute |
| v | Velocity |
| vmax | Maximal velocity |
References
- Douglas, J.; Ross, A.; Martin, J.C. Maximal muscular power: Lessons from sprint cycling. Sport Med. Open 2021, 7, 48. [Google Scholar] [CrossRef] [PubMed]
- Dunst, A.K.; Grüneberger, R. A Novel Approach of Modelling and Predicting Track Cycling Sprint Performance. Appl. Sci. 2021, 11, 12098. [Google Scholar] [CrossRef]
- Dunst, A.K. Trends und Perspektiven im Radsport—Der Trend großer Übersetzungen und seine Konsequenz für das physiologische Anforderungsprofil im Bahnradsprint. Leistungssport 2021, 5, 34–37. [Google Scholar]
- Abbiss, C.R.; Peiffer, J.J.; Laursen, P. Optimal cadence selection during cycling. Int. J. Sport Med. 2009, 10, 1–15. [Google Scholar]
- Dorel, S.; Hautier, C.A.; Rambaud, O.; Rouffet, D.; Van Praagh, E.; Lacour, J.-R.; Bourdin, M. Torque and power-velocity relationships in cycling: Relevance to track sprint performance in world-class cyclists. Int. J. Sport Med. 2005, 26, 739–746. [Google Scholar] [CrossRef] [PubMed]
- Dunst, A.K.; Hesse, C.; Ueberschär, O.; Holmberg, H.C. Fatigue-Free Force-Velocity and Power-Velocity Profiles for Elite Track Sprint Cyclists: The Influence of Duration, Gear Ratio and Pedalling Rates. Sports 2022, 10, 130. [Google Scholar] [CrossRef] [PubMed]
- Hill, A. The Heat of Shortening and the Dynamic Constants of Muscle. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1938, 126, 136–195. [Google Scholar]
- Jaric, S. Force-velocity Relationship of Muscles Performing Multi-joint Maximum Performance Tasks. Int. J. Sport Med. 2015, 36, 699–704. [Google Scholar] [CrossRef]
- Schleichardt, A.; Badura, M.; Lehmann, F.; Ueberschär, O. Comparison of force-velocity profiles of the leg-extensors for elite athletes in the throwing events relating to gender, age and event. Sports Biomech. 2019, 20, 720–736. [Google Scholar] [CrossRef]
- Seck, D.; Vandewalle, H.; Decrops, N.; Monod, H. Maximal power and torque-velocity relationship on a cycle ergometer during the acceleration phase of a single all-out exercise. Eur. J. Appl. Physiol. 1995, 70, 161–168. [Google Scholar] [CrossRef]
- Hirntzy, F.; Belli, A.; Grappe, F.; Rouillon, J.-D. Optimal pedalling velocity characteristics during maximal and submaximal cycling in humans. Eur. J. Appl. Physiol. 1999, 79, 426–432. [Google Scholar] [CrossRef] [PubMed]
- Bertucci, W.; Taiar, R.; Grappe, F. Differences between sprint tests under laboratory and actual cycling conditions. J. Sports Med. Phys. Fit. 2005, 45, 277–283. [Google Scholar]
- Gadner, A.S.; Martin, J.C.; Martin, D.T.; Barras, M.; Jenkins, D.G. Maximal torque- and power-pedaling rate relationships for elite sprint cyclists in laboratory and field tests. Eur. J. Appl. Physiol. 2007, 101, 287–292. [Google Scholar] [CrossRef]
- Rylands, L.; Roberts, S.; Hurst, H. Variability in laboratory versus field testing of peak power, torque and time of peak power production amongst elite bicycle motocross cyclists. J. Strength Cond. 2015, 29, 2635–2640. [Google Scholar] [CrossRef]
- McCartney, N.; Heigenhauser, G.J.; Jones, N.L. Power output and fatigue of human muscle in maximal cycling exercise. J. Appl. Physiol. 1983, 55, 218–224. [Google Scholar] [CrossRef] [PubMed]
- Dunst, A.K.; Grüneberger, R.; Holmberg, H.C. Modeling optimal cadence as a function of time during maximal sprint exercises can improve performance by elite track cyclists. Appl. Sci. 2021, 11, 12105. [Google Scholar] [CrossRef]
- Sargeant, A.J. Human power output and muscle fatigue. Int. J. Sports Med. 1994, 15, 116–121. [Google Scholar] [CrossRef] [PubMed]
- Beelen, A.; Sargeant, A.J. Effect of fatigue on maximal power output at different contraction velocities in humans. J. Appl. Physiol. 1991, 71, 2332–2337. [Google Scholar] [CrossRef]
- Martin, J.C.; Davidson, C.J.; Pardyjak, E.R. Understanding Sprint-Cycling Performance: The Integration of Muscle Power, Resistance, and Modeling. Int. J. Sports Physiol. Perform. 2007, 2, 5–21. [Google Scholar] [CrossRef]
- Buttelli, O.; Seck, D.; Vandewalle, H.; Jouanin, J.C.; Monod, H. Effect of fatigue on maximal velocity and maximal torque during short exhausting cycling. Eur. J. Appl. Physiol. 1996, 73, 175–179. [Google Scholar] [CrossRef]
- Bogdanis, G.C.; Papaspyrou, A.; Theos, A.; Maridaki, M. Influence of resistive load on power output and fatigue during intermittent sprint cycling exercise in children. Eur. J. Appl. Physiol. 2007, 101, 313–320. [Google Scholar] [CrossRef] [PubMed]
- De Ruiter, C.J.; Jones, D.A.; Sargeant, A.J.; De Haan, A. The measurement of force/velocity relationships of fresh and fatigued human adductor pollicis muscle. Eur. J. Appl. Physiol. 1999, 80, 386–393. [Google Scholar] [CrossRef] [PubMed]
- De Ruiter, C.J.; Didden, W.J.M.; Jones, D.A.; De Haan, A. The force-velocity relationship of human adductor pollicis muscle during stretch and the effects of fatigue. J. Physiol. 2000, 526, 671–681. [Google Scholar] [CrossRef] [PubMed]
- Sargeant, A.J. Structural and functional determinants of human muscle power. Exp. Physiol. 2007, 92, 323–331. [Google Scholar] [CrossRef] [PubMed]
- Davidson, C.J.; Wagner, B.M.; Martin, J.C. Seated and standing maximal neuromuscular cycling power. Med. Sci. Sport Exerc. 2004, 36, S344. [Google Scholar]
- Davidson, C.J.; Horscroft, R.D.; McDaniel, J.T.; Tomas, A.; Hunter, E.L.; Grisham, J.D.; McNeil, J.; Gidley, L.; Carroll, C.; Thompson, F. The biomechanics of producing standing and seated maximal cycling power. Med. Sci. Sports Exerc. 2005, 37, S393. [Google Scholar]
- Reiser, R.F.I.; Maines, J.M.; Eisenmann, J.C.; Wilkinson, J.G. Standing and seated wingate protocols in human cycling. A comparison of standard parameters. Eur. J. Appl. Physiol. 2002, 88, 152–157. [Google Scholar] [CrossRef]
- Dwyer, D.B.; Molaro, C.; Rouffet, D.M. Force-velocity profiles of track cyclists differ between seated and non-seated positions. Sports Biomech. 2022, 1–12. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dunst, A.K.; Hesse, C.; Ueberschär, O. The Concept of Optimal Dynamic Pedalling Rate and Its Application to Power Output and Fatigue in Track Cycling Sprinters—A Case Study. Sports 2023, 11, 19. https://doi.org/10.3390/sports11010019
Dunst AK, Hesse C, Ueberschär O. The Concept of Optimal Dynamic Pedalling Rate and Its Application to Power Output and Fatigue in Track Cycling Sprinters—A Case Study. Sports. 2023; 11(1):19. https://doi.org/10.3390/sports11010019
Chicago/Turabian StyleDunst, Anna Katharina, Clemens Hesse, and Olaf Ueberschär. 2023. "The Concept of Optimal Dynamic Pedalling Rate and Its Application to Power Output and Fatigue in Track Cycling Sprinters—A Case Study" Sports 11, no. 1: 19. https://doi.org/10.3390/sports11010019
APA StyleDunst, A. K., Hesse, C., & Ueberschär, O. (2023). The Concept of Optimal Dynamic Pedalling Rate and Its Application to Power Output and Fatigue in Track Cycling Sprinters—A Case Study. Sports, 11(1), 19. https://doi.org/10.3390/sports11010019




