The Acute Effects of Heavy Sled Towing on Acceleration Performance and Sprint Mechanical and Kinematic Characteristics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Design
2.2. Participants
2.3. Procedures
2.4. Data Analysis
2.5. Statistical Analysis
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mero, A.; Komi, P.V.; Gregor, R.J. Biomechanics of sprint running. A review. Sports Med. 1992, 13, 376–392. [Google Scholar] [CrossRef] [PubMed]
- Hicks, D.S.; Schuster, J.G.; Samozino, P.; Morin, J.-B. Improving mechanical effectiveness during sprint acceleration: Practical recommendations and guidelines. Strength Cond. J. 2020, 42, 45–62. [Google Scholar] [CrossRef]
- Samozino, P.; Rabita, G.; Dorel, S.; Slawinski, J.; Peyrot, N.; Saez de Villarreal, E.; Morin, J.-B. A simple method for measuring power, force, velocity properties, and mechanical effectiveness in sprint running. Scand. J. Med. Sci. Sports 2016, 26, 648–658. [Google Scholar] [CrossRef] [PubMed]
- Morin, J.-B.; Edouard, P.; Samozino, P. Technical ability of force application as a determinant factor of sprint performance. Med. Sci. Sports Exerc. 2011, 43, 1680–1688. [Google Scholar] [CrossRef] [PubMed]
- Morin, J.-B.; Bourdin, M.; Edouard, P.; Peyrot, N.; Samozino, P.; Lacour, J.-R. Mechanical determinants of 100-m sprint running performance. Eur. J. Appl. Physiol. 2012, 112, 3921–3930. [Google Scholar] [CrossRef] [Green Version]
- Morin, J.-B.; Gimenez, P.; Edouard, P.; Arnal, P.; Jiménez-Reyes, P.; Samozino, P.; Brughelli, M.; Mendiguchia, J. Sprint acceleration mechanics: The major role of hamstrings in horizontal force production. Front. Physiol. 2015, 6, 404. [Google Scholar] [CrossRef]
- Morin, J.-B.; Samozino, P. Interpreting power-force-velocity profiles for individualized and specific training. Int. J. Sports Physiol. Perform. 2016, 11, 267–272. [Google Scholar] [CrossRef]
- Morin, J.-B.; Capelo-Ramirez, F.; Rodriguez-Pérez, M.A.; Cross, M.R.; Jimenez-Reyes, P. Individual adaptation kinetics following heavy resisted sprint training. J. Strength Cond. Res. 2020, 13, 1. [Google Scholar] [CrossRef]
- Winwood, P.W.; Posthumus, L.R.; Cronin, J.B.; Keogh, J.W.L. The acute potentiating effects of heavy sled pulls on sprint performance. J. Strength Cond. Res. 2016, 30, 1248–1254. [Google Scholar] [CrossRef] [Green Version]
- Lockie, R.G.; Murphy, A.J.; Schultz, A.B.; Knight, T.J.; Janse de Jonge, X.A.K. The effects of different speed training protocols on sprint acceleration kinematics and muscle strength and power in field sport athletes. J. Strength Cond. Res. 2012, 26, 1539–1550. [Google Scholar] [CrossRef] [Green Version]
- Chatzopoulos, D.E.; Michailidis, C.J.; Giannakos, A.K.; Alexiou, K.C.; Patikas, D.A.; Antonopoulos, C.B.; Kotzamanidis, C.M. Postactivation potentiation effects after heavy resistance exercise on running speed. J. Strength Cond. Res. 2007, 21, 1278–1281. [Google Scholar] [PubMed]
- Gourgoulis, V.; Aggeloussis, N.; Kasimatis, P.; Mavromatis, G.; Garas, A. Effect of a submaximal half-squats warm-up program on vertical jumping ability. J. Strength Cond. Res. 2003, 17, 342–344. [Google Scholar] [PubMed]
- Terzis, G.; Spengos, K.; Karampatsos, G.; Manta, P.; Georgiadis, G. Acute effect of drop jumping on throwing performance. J. Strength Cond. Res. 2009, 23, 2592–2597. [Google Scholar] [CrossRef] [PubMed]
- Turner, A.P.; Bellhouse, S.; Kilduff, L.P.; Russell, M. Postactivation potentiation of sprint acceleration performance using plyometric exercise. J. Strength Cond. Res. 2015, 29, 343–350. [Google Scholar] [CrossRef] [Green Version]
- Wilson, J.M.C.; Duncan, N.M.; Marin, P.J.; Brown, L.E.; Loenneke, J.P.; Wilson, S.M.; Jo, E.; Lowery, R.P.; Ugrinowitsch, C. Meta-analysis of postactivation potentiation and power: Effects of conditioning activity, volume, gender, rest periods, and training status. J. Strength Cond. Res. 2013, 27, 854–859. [Google Scholar] [CrossRef]
- Tillin, N.A.; Bishop, D. Factors modulating post-activation potentiation and its effect on performance of subsequent explosive activities. Sports Med. 2009, 39, 147–166. [Google Scholar] [CrossRef]
- Dinsdale, A.J.; Bissas, A. Eliciting postactivation potentiation with hang cleans depends on the recovery duration and the individual’s 1 repetition maximum strength. J. Strength Cond. Res. 2021, 35, 1817–1824. [Google Scholar] [CrossRef]
- Crewther, B.T.; Kilduff, L.P.; Cook, C.J.; Middleton, M.K.; Bunce, P.J.; Yang, G.-Z. The acute potentiating effects of back squats on athlete performance. J. Strength Cond. Res. 2011, 25, 3319–3325. [Google Scholar] [CrossRef]
- Cahill, M.J.; Cronin, J.B.; Oliver, J.L.P.; Clark, K.; Lloyd, R.S.; Cross, M.R. Sled pushing and pulling to enhance speed capability. Strength Cond. J. 2019, 41, 94–104. [Google Scholar] [CrossRef]
- Petrakos, G.; Morin, J.-B.; Egan, B. Resisted sled sprint training to improve sprint performance: A systematic review. Sports Med. 2016, 46, 381–400. [Google Scholar] [CrossRef]
- Pantoja, P.D.; Carvalho, A.R.; Ribas, L.R.; Peyré-Tartaruga, L.A. Effect of weighted sled towing on sprinting effectiveness, power and force-velocity relationship. PLoS ONE 2018, 13, e0204473. [Google Scholar] [CrossRef] [PubMed]
- Kawamori, N.; Newton, R.; Nosaka, K. Effects of weighted sled towing on ground reaction force during the acceleration phase of sprint running. J. Sports Sci. 2014, 32, 1139–1145. [Google Scholar] [CrossRef] [PubMed]
- Cross, M.R.; Brughelli, M.; Samozino, P.; Brown, S.R.; Morin, J.-B. Optimal loading for maximizing power during sled-resisted sprinting. Int. J. Sports Physiol. Perform. 2017, 12, 1069–1077. [Google Scholar] [CrossRef] [PubMed]
- Monaghan, D.J.; Cochrane, D.J. Can backward sled towing potentiate sprint performance? J. Strength Cond. Res. 2020, 34, 345–354. [Google Scholar] [CrossRef]
- Williams, J.J.; Herron, R.L.; Spradley, B.; Saracino, P. Postactivation potentiation effect of heavy sled towing on subsequent sprints. J. Strength Cond. Res. 2021, 35, 1229–1233. [Google Scholar] [CrossRef]
- Mangine, G.T.; Huet, K.; Williamson, C.; Bechke, E.; Serafini, P.; Bender, D.; Hudy, J.; Townsend, J. A resisted sprint improves rate of force development during a 20-m sprint in athletes. J. Strength Cond. Res. 2018, 32, 1531–1537. [Google Scholar] [CrossRef]
- Jarvis, P.; Turner, A.; Chavda, S.; Bishop, C. The acute effects of heavy sled towing on subsequent sprint acceleration performance. J. Trainol. 2017, 6, 18–25. [Google Scholar] [CrossRef] [Green Version]
- Van Den Tillaar, R.; Von Heimburg, E. Comparison of different sprint training sessions with assisted and resisted running: Effects on performance and kinematics in 20-m sprints. Hum. Mov. 2017, 18, 21–29. [Google Scholar] [CrossRef]
- Whelan, N.; OʼRegan, C.; Harrison, A.J. Resisted sprints do not acutely enhance sprinting performance. J. Strength Cond. Res. 2014, 28, 1858–1866. [Google Scholar] [CrossRef]
- Seitz, L.B.; Mina, M.A.; Haff, G.G. A sled push stimulus potentiates subsequent 20-m sprint performance. J. Sci. Med. Sport 2017, 20, 781–785. [Google Scholar] [CrossRef]
- Cronin, J.; Hansen, K.; Kawamori, N.; McNair, P. Effects of weighted vests and sled towing on sprint kinematics. Sports Biomech. 2008, 7, 160–172. [Google Scholar] [CrossRef] [PubMed]
- Cross, M.R.; Lahti, J.; Brown, S.R.; Chedati, M.; Jimenez-Reyes, P.; Samozino, P.; Eriksrud, O.; Morin, J.-B. Training at maximal power in resisted sprinting: Optimal load determination methodology and pilot results in team sport athletes. PLoS ONE 2018, 13, e0195477. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- de Salles, B.; Simao, R.; Miranda, F.; da Silva Novaes, J.; Lemos, A.; Willardson, J. Rest interval between sets in strength training. Sports Med. 2009, 39, 765–777. [Google Scholar] [CrossRef]
- Romero-Franco, N.; Jiménez-Reyes, P.; Castaño-Zambudio, A.; Capelo-Ramírez, F.; Rodríguez-Juan, J.J.; González-Hernández, J.; Toscano-Bendala, F.J.; Cuadrado-Peñafiel, V.; Balsalobre-Fernández, C. Sprint performance and mechanical outputs computed with an iPhone app: Comparison with existing reference methods. Eur. J. Sport Sci. 2017, 17, 386–392. [Google Scholar] [CrossRef] [PubMed]
- Economou, T.; Stavridis, I.; Zisi, M.; Fragkoulis, E.; Olanemi-Agilara, G.; Paradisis, G. Sprint mechanical and kinematic characteristics of national female track and field champions and lower-level competitors. J. Phys. Educ. Sport 2021, 21, 3227–3235. [Google Scholar]
- Chow, J.W. A panning videographic technique to obtain selected kinematic characteristics of the strides in sprint hurdling. J. Appl. Biomech. 1993, 9, 149–159. [Google Scholar] [CrossRef]
- Cohen, J. Statistical power analysis. Curr. Dir. Psychol. Sci. 1992, 1, 98–101. [Google Scholar] [CrossRef]
- Seitz, L.B.; Haff, G.G. Factors modulating post-activation potentiation of jump, sprint, throw, and upper-body ballistic performances: A systematic review with meta-analysis. Sports Med. 2016, 46, 231–240. [Google Scholar] [CrossRef]
- Hodgson, M.; Docherty, D.; Robbins, D. Post-activation potentiation: Underlying physiology and implications for motor performance. Sports Med. 2005, 35, 585–595. [Google Scholar] [CrossRef]
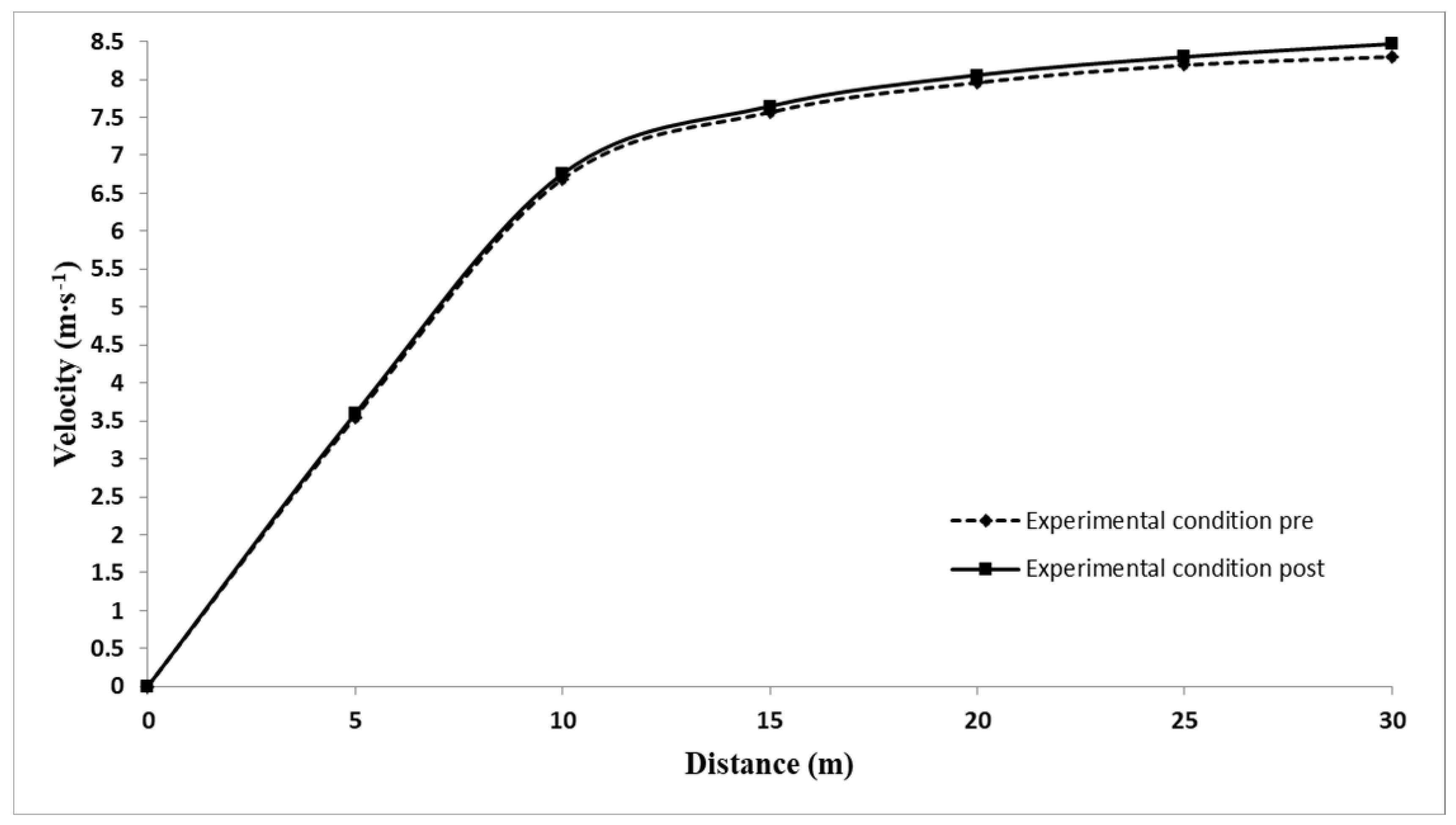
| Experimental Condition | Velocity (m/s) | Step Length (m) | Step Rate (Hz) | Contact Time (s) | Flight Time (s) | |
|---|---|---|---|---|---|---|
| 0–5 m | Pre | 3.55 ± 0.26 | 1.15 ± 0.08 | 3.11 ± 0.36 | 0.175 ± 0.018 | 0.079 ± 0.010 |
| Post | 3.59 ± 0.24 | 1.14 ± 0.07 | 3.15 ± 0.34 | 0.180 ± 0.023 | 0.077 ± 0.011 | |
| ES (95% CI) | 0.38 (−0.22–0.96) | −0.06 (−0.63–0.50) | 0.35 (−0.25–0.92) | 0.38 (−0.22–0.96) | −0.30 (−0.87–0.29) | |
| 5–10 m | Pre | 6.69 ± 0.48 | 1.57 ± 0.08 | 4.28 ± 0.31 | 0.143 ± 0.013 | 0.101 ± 0.009 |
| Post | 6.75 ± 0.53 * | 1.57 ± 0.08 | 4.30 ± 0.34 | 0.146 ± 0.015 | 0.102 ± 0.010 | |
| ES (95% CI) | 0.71 (0.58–1.33) | 0.18 (−0.40–0.75) | 0.21 (−0.37–0.77) | 0.45 (−0.16–1.03) | 0.09 (−0.48–0.66) | |
| 10–15 m | Pre | 7.57 ± 0.61 | 1.76 ± 0.09 | 4.31 ± 0.30 | 0.133 ± 0.012 | 0.108 ± 0.006 |
| Post | 7.64 ± 0.66 * | 1.77 ± 0.09 | 4.33 ± 0.30 | 0.133 ± 0.013 | 0.108 ± 0.007 | |
| ES (95% CI) | 0.98 (0.27–1.65) | 0.19 (−0.39–0.75) | 0.18 (−0.39–0.75) | 0.07 (−0.50–0.64) | −0.03 (−0.59–0.54) | |
| 15–20 m | Pre | 7.96 ± 0.72 | 1.87 ± 0.10 | 4.27 ± 0.28 | 0.126 ± 0.012 | 0.112 ± 0.006 |
| Post | 8.05 ± 0.77 * | 1.87 ± 0.10 | 4.30 ± 0.34 | 0.126 ± 0.013 | 0.113 ± 0.006 | |
| ES (95% CI) | 1.06 (0.33–1.76) | 0.17 (−0.41–0.73) | 0.19 (−0.38–0.76) | −0.17 (−0.74–0.40) | 0.18 (−0.40–0.74) | |
| 20–25 m | Pre | 8.19 ± 0.79 | 1.93 ± 0.11 | 4.25 ± 0.29 | 0.121 ± 0.012 | 0.117 ± 0.006 |
| Post | 8.29 ± 0.85 * | 1.94 ± 0.12 | 4.27 ± 0.25 | 0.121 ± 0.013 | 0.117 ± 0.005 | |
| ES (95% CI) | 0.83 (0.16–1.48) | 0.30 (−0.29–0.81) | 0.24 (−0.34–0.81) | 0.03 (−0.54–0.60) | −0.02 (−0.55–0.58) | |
| 25–30 m | Pre | 8.37 ± 0.87 | 1.98 ± 0.12 | 4.20 ± 0.30 | 0.120 ± 0.011 | 0.122 ± 0.007 |
| Post | 8.46 ± 0.92 * | 2.00 ± 0.11 | 4.21 ± 0.29 | 0.120 ± 0.014 | 0.122 ± 0.006 | |
| ES (95% CI) | 0.84 (0.16–1.49) | 0.43 (−0.18–1.01) | 0.11 (−0.46–0.67) | −0.15 (−0.72–0.42) | −0.11 (−0.67–0.46) | |
| Control Condition | Velocity (s) | Step Length (m) | Step Rate (Hz) | Contact Time (s) | Flight Time (s) | |
|---|---|---|---|---|---|---|
| 0–5 m | Pre | 3.55 ± 0.20 | 1.16 ± 0.08 | 3.08 ± 0.30 | 0.175 ± 0.022 | 0.082 ± 0.010 |
| Post | 3.56 ± 0.24 | 1.15 ± 0.09 | 3.12 ± 0.35 | 0.175 ± 0.019 | 0.081 ± 0.011 | |
| ES (95% CI) | 0.09 (−0.48–0.65) | 0.17 (−0.73–0.41) | 0.26 (−0.32–0.83) | −0.10 (−0.47–0.67) | −0.20 (−0.77–0.38) | |
| 5–10 m | Pre | 6.75 ± 0.50 | 1.58 ± 0.09 | 4.27 ± 0.32 | 0.144 ± 0.013 | 0.101 ± 0.011 |
| Post | 6.71 ± 0.49 | 1.58 ± 0.09 | 4.25 ± 0.31 | 0.144 ± 0.013 | 0.103 ± 0.011 | |
| ES (95% CI) | −0.31 (−0.88–0.28) | 0.02 (−0.55–0.58) | −0.23 (−0.80–0.35) | 0.09 (−0.48–0.65) | 0.30 (−0.29–0.87) | |
| 10–15 m | Pre | 7.65 ± 0.64 | 1.77 ± 0.10 | 4.32 ± 0.27 | 0.132 ± 0.011 | 0.107 ± 0.007 |
| Post | 7.61 ± 0.61 | 1.77 ± 0.09 | 4.29 ± 0.29 | 0.131 ± 0.012 | 0.110 ± 0.007 | |
| ES (95% CI) | −0.28 (−0.86–0.30) | 0.11 (−0.47–0.67) | −0.55 (−1.15–0.69) | −0.13 (−0.70–0.44) | 0.59 (−0.04–1.11) | |
| 15–20 m | Pre | 8.04 ± 0.73 | 1.88 ± 0.11 | 4.27 ± 0.27 | 0.125 ± 0.011 | 0.113 ± 0.005 |
| Post | 8.01 ± 0.73 | 1.88 ± 0.12 | 4.25 ± 0.28 | 0.126 ± 0.012 | 0.114 ± 0.007 | |
| ES (95% CI) | −0.22 (−0.79–0.28) | 0.08 (−0.49–0.65) | −0.19 (−0.75–0.39) | 0.10 (−0.47–0.66) | 0.25 (−0.33–0.82) | |
| 20–25 m | Pre | 8.26 ± 0.79 | 1.95 ± 0.11 | 4.24 ± 0.27 | 0.123 ± 0.011 | 0.117 ± 0.005 |
| Post | 8.23 ± 0.79 | 1.94 ± 0.11 | 4.24 ± 0.27 | 0.121 ± 0.012 | 0.118 ± 0.006 | |
| ES (95% CI) | −0.34 (−0.91–0.25) | −0.20 (−0.77–0.37) | 0.02 (−0.59–0.55) | −0.46 (−1.05–0.14) | 0.03 (−0.54–0.59) | |
| 25–30 m | Pre | 8.42 ± 0.83 | 2.00 ± 0.10 | 4.20 ± 0.26 | 0.119 ± 0.014 | 0.122 ± 0.006 |
| Post | 8.39 ± 0.84 | 2.01 ± 0.13 | 4.17 ± 0.29 | 0.120 ± 0.011 | 0.122 ± 0.007 | |
| ES (95% CI) | −0.32 (−0.89–0.27) | 0.05 (−0.52–0.62) | −0.39 (−0.97–0.21) | 0.23 (−0.35–0.80) | 0.24 (−0.34–0.81) | |
| Mechanical Variables | Experimental Condition | Control Condition | ||||
|---|---|---|---|---|---|---|
| Pre | Post | ES (95%CI) | Pre | Post | ES (95%CI) | |
| F0 (N·kg−1) | 7.51 ± 0.63 | 7.60 ± 0.66 | 0.16 (−0.41–0.73) | 7.72 ± 0.84 | 7.61 ± 0.60 | −0.19 (−0.76–0.38) |
| v0 (m·s−1) | 9.02 ± 1.11 | 9.13 ± 1.15 | 0.43 (−0.17–1.01) | 9.07 ± 1.03 | 9.03 ± 1.05 | −0.30 (−0.87–0.29) |
| Pmax (W·kg−1) | 17.02 ± 3.01 | 17.47 ± 3.46 | 0.47 (−0.14–1.06) | 17.62 ± 3.51 | 17.30 ± 3.15 | −0.25 (−0.82–0.33) |
| SFv (N·s−1/m·kg) | −0.84 ± 0.09 | −0.84 ± 0.07 | 0.29 (−0.54–0.59) | −0.86 ± 0.09 | −0.85 ± 0.06 | 0.13 (−0.44–0.70) |
| RFmax (%) | 44.4 ± 3.0 | 44.9 ± 3.6 | 0.43 (−0.17–1.01) | 45.1 ± 3.6 | 44.8 ± 3.2 | −0.23 (−0.80–0.35) |
| DRF (%·s·m) | −7.8 ± 0.9 | −7.8 ± 0.7 | 0.09 (−0.48–0.65) | −7.9 ± 0.9 | −7.8 ± 0.7 | 0.15 (−0.42–0.72) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zisi, M.; Stavridis, I.; Agilara, G.-O.; Economou, T.; Paradisis, G. The Acute Effects of Heavy Sled Towing on Acceleration Performance and Sprint Mechanical and Kinematic Characteristics. Sports 2022, 10, 77. https://doi.org/10.3390/sports10050077
Zisi M, Stavridis I, Agilara G-O, Economou T, Paradisis G. The Acute Effects of Heavy Sled Towing on Acceleration Performance and Sprint Mechanical and Kinematic Characteristics. Sports. 2022; 10(5):77. https://doi.org/10.3390/sports10050077
Chicago/Turabian StyleZisi, Maria, Ioannis Stavridis, Georgia-Olanemi Agilara, Theodosia Economou, and Giorgos Paradisis. 2022. "The Acute Effects of Heavy Sled Towing on Acceleration Performance and Sprint Mechanical and Kinematic Characteristics" Sports 10, no. 5: 77. https://doi.org/10.3390/sports10050077
APA StyleZisi, M., Stavridis, I., Agilara, G.-O., Economou, T., & Paradisis, G. (2022). The Acute Effects of Heavy Sled Towing on Acceleration Performance and Sprint Mechanical and Kinematic Characteristics. Sports, 10(5), 77. https://doi.org/10.3390/sports10050077







