Test–Retest Reliability and Sensitivity of Common Strength and Power Tests over a Period of 9 Weeks
Abstract
1. Introduction
2. Materials and Methods
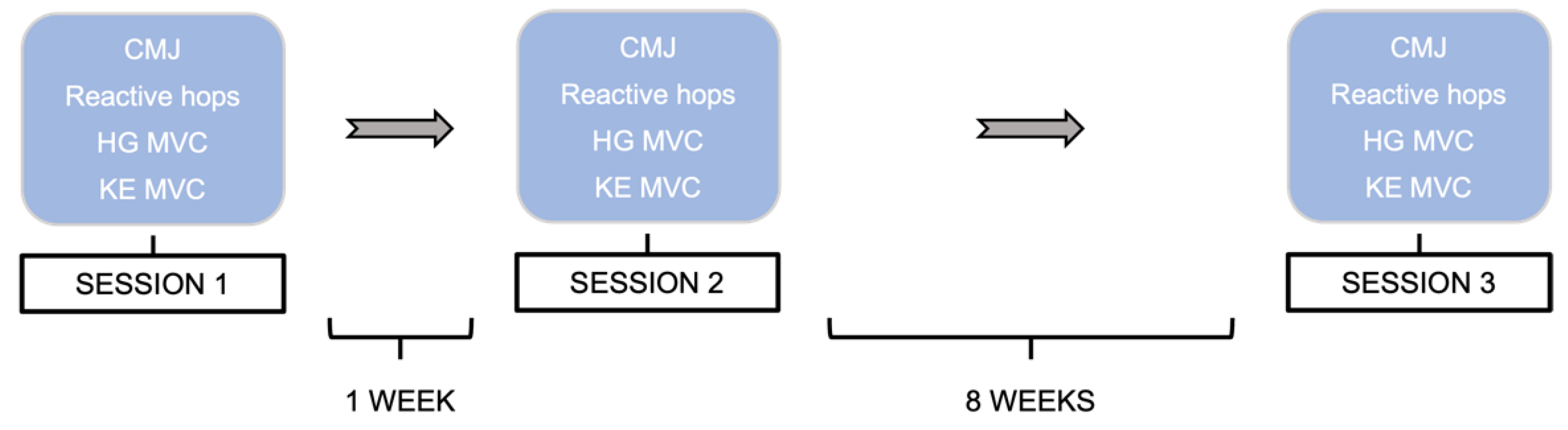
2.1. Study Design
2.2. Subjects
2.3. Isometric Leg Strength
2.4. Handgrip Strength
2.5. Countermovement Jumps
2.6. Reactive Hops
2.7. Statistics
3. Results
4. Discussion
4.1. Isometric Leg Strength
4.2. Handgrip Strength
4.3. Countermovement Jumps
4.4. Reactive Hops
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stevens, C.; Dascombe, B. The Reliability and Validity of Protocols for the Assessment of Endurance Sports Performance: An Updated Review. Meas. Phys. Educ. Exerc. Sci. 2015, 19, 177–185. [Google Scholar] [CrossRef]
- Hopkins, W.G. Measures of Reliability in Sports Medicine and Science. Sports Med. 2000, 30, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Bruton, A.; Conway, J.H.; Holgate, S.T. Reliability: What is it, and How Is it Measured? Physiotherapy 2000, 86, 94–99. [Google Scholar] [CrossRef]
- Atkinson, G.; Nevill, A.M. Statistical Methods for Assessing Measurement Error (Reliability) in Variables Relevant to Sports Medicine. Sports Med. 1998, 26, 217–238. [Google Scholar] [CrossRef] [PubMed]
- Baumgartner, T.A. Norm-Referenced Measurement: Reliability; Safrit, M.J., Wood, T.M., Eds.; Human Kinetics Books: Champaign, IL, USA, 1989; pp. 45–72. [Google Scholar]
- Currell, K.; Jeukendrup, A.E. Validity, Reliability and Sensitivity of Measures of Sporting Performance. Sports Med. 2008, 38, 297–316. [Google Scholar] [CrossRef]
- Markovic, G.; Dizdar, D.; Jukic, I.; Cardinale, M. Reliability and Factorial Validity of Squat and Countermovement Jump Tests. J. Strength Cond. Res. 2004, 18, 551–555. [Google Scholar] [CrossRef]
- Carlock, J.M.; Smith, S.L.; Hartman, M.J.; Morris, R.T.; Ciroslan, D.A.; Pierce, K.C.; Newton, R.U.; Harman, E.A.; Sands, W.A.; Stone, M.H. The Relationship between Vertical Jump Power Estimates and Weightlifting Ability: A Field-Test Approach. J. Strength Cond. Res. 2004, 18, 534–539. [Google Scholar] [CrossRef]
- Rodríguez-Rosell, D.; Mora-Custodio, R.; Franco-Márquez, F.; Yáñez-García, J.M.; González-Badillo, J.J. Traditional vs. Sport-Specific Vertical Jump Tests: Reliability, Validity, and Relationship with the Legs Strength and Sprint Performance in Adult and Teen Soccer and Basketball Players. J. Strength Cond. Res. 2017, 31, 196–206. [Google Scholar] [CrossRef]
- Gathercole, R.J.; Sporer, B.C.; Stellingwerff, T.; Sleivert, G.G. Comparison of the Capacity of Different Jump and Sprint Field Tests to Detect Neuromuscular Fatigue. J. Strength Cond. Res. 2015, 29, 2522–2531. [Google Scholar] [CrossRef]
- Wisløff, U.; Castagna, C.; Helgerud, J.; Jones, R.; Hoff, J. Strong Correlation of Maximal Squat Strength with Sprint Performance and Vertical Jump Height in Elite Soccer Players. Br. J. Sports Med. 2004, 38, 285–288. [Google Scholar] [CrossRef]
- Welsh, T.T.; Alemany, J.A.; Montain, S.J.; Frykman, P.N.; Tuckow, A.P.; Young, A.J.; Nindl, B.C. Effects of Intensified Military Field Training on Jumping Performance. Int. J. Sports Med. 2008, 29, 45–52. [Google Scholar] [CrossRef]
- Maloney, S.J.; Fletcher, I.M. Lower Limb Stiffness Testing in Athletic Performance: A Critical Review. Sports Biomech. 2021, 20, 109–130. [Google Scholar] [CrossRef]
- Butler, R.J.; Crowell, H.P.; Davis, I.M. Lower Extremity Stiffness: Implications for Performance and Injury. Clin. Biomech. 2003, 18, 511–517. [Google Scholar] [CrossRef]
- Bret, C.; Rahmani, A.; Dufour, A.B.; Messonnier, L.; Lacour, J.R. Leg Strength and Stiffness as Ability Factors in 100 m Sprint Running. J. Sports Med. Phys. Fit. 2002, 42, 274–281. [Google Scholar]
- Hobara, H.; Inoue, K.; Gomi, K.; Sakamoto, M.; Muraoka, T.; Iso, S.; Kanosue, K. Continuous Change in Spring-Mass Characteristics During a 400 m Sprint. J. Sci. Med. Sport 2010, 13, 256–261. [Google Scholar] [CrossRef]
- Chelly, S.M.; Denis, C. Leg Power and Hopping Stiffness: Relationship with Sprint Running Performance. Med. Sci. Sports Exerc. 2001, 33, 326–333. [Google Scholar] [CrossRef]
- Hobara, H.; Kimura, K.; Omuro, K.; Gomi, K.; Muraoka, T.; Iso, S.; Kanosue, K. Determinants of Difference in Leg Stiffness Between Endurance- and Power-Trained Athletes. J. Biomech. 2008, 41, 506–514. [Google Scholar] [CrossRef]
- Seyfarth, A.; Friedrichs, A.; Wank, V.; Blickhan, R. Dynamics of the Long Jump. J. Biomech. 1999, 32, 1259–1267. [Google Scholar] [CrossRef]
- Bohannon, R.W.; Magasi, S.R.; Bubela, D.J.; Wang, Y.-C.; Gershon, R.C. Grip and Knee Extension Muscle Strength Reflect a Common Construct among Adults. Muscle Nerve 2012, 46, 555–558. [Google Scholar] [CrossRef]
- Potteiger, J.A. ACSM’s Introduction to Exercise Science, 4th ed.; Wolters Kluwer Health: Philadelphia, PA, USA, 2022. [Google Scholar]
- Bohannon, R.W. Grip Strength: An Indispensable Biomarker for Older Adults. Clin. Interv. Aging 2019, 14, 1681–1691. [Google Scholar] [CrossRef]
- Arteaga, R.; Dorado, C.; Chavarren, J.; Calbet, J.A. Reliability of Jumping Performance in Active Men and Women under Different Stretch Loading Conditions. J. Sports Med. Phys. Fit. 2000, 40, 26–34. [Google Scholar]
- Bohannon, R.W.; Schaubert, K.L. Test–Retest Reliability of Grip-Strength Measures Obtained over a 12-Week Interval from Community-Dwelling Elders. Hand Ther. 2005, 18, 426–427. [Google Scholar] [CrossRef] [PubMed]
- Choukou, M.A.; Laffaye, G.; Taiar, R. Reliability and Validity of an Accelerometric System for Assessing Vertical Jumping Performance. Biol. Sport 2014, 31, 55–62. [Google Scholar] [CrossRef] [PubMed]
- Comyns, T.M.; Flanagan, E.P.; Fleming, S.; Fitzgerald, E.; Harper, D.J. Interday Reliability and Usefulness of a Reactive Strength Index Derived from 2 Maximal Rebound Jump Tests. Int. J. Sports Physiol. Perform. 2019, 14, 1200–1204. [Google Scholar] [CrossRef] [PubMed]
- Diggin, D.; Anderson, R.; Harrison, A.J. An Examination of the True Reliability of Lower Limb Stiffness Measures during Overground Hopping. J. Appl. Biomech. 2016, 32, 278–286. [Google Scholar] [CrossRef] [PubMed]
- Dirnberger, J.; Wiesinger, H.-P.; Kösters, A.; Müller, E. Reproducibility for Isometric and Isokinetic Maximum Knee Flexion and Extension Measurements Using the IsoMed 2000-Dynamometer. Isokinet. Exerc. Sci. 2012, 20, 149–153. [Google Scholar] [CrossRef]
- Heishman, A.D.; Daub, B.D.; Miller, R.M.; Freitas, E.D.S.; Frantz, B.A.; Bemben, M.G. Countermovement Jump Reliability Performed With and Without an Arm Swing in NCAA Division 1 Intercollegiate Basketball Players. J. Strength Cond. Res. 2020, 34, 546–558. [Google Scholar] [CrossRef]
- Hogrel, J.-Y. Grip strength Measured by High Precision Dynamometry in Healthy Subjects from 5 to 80 years. BMC Musculoskelet. Disord. 2015, 16, 139. [Google Scholar] [CrossRef]
- Lorimer, A.V.; Keogh, J.W.L.; Hume, P.A. Using Stiffness to Assess Injury Risk: Comparison of Methods for Quantifying Stiffness and their Reliability in Triathletes. PeerJ 2018, 6, e5845. [Google Scholar] [CrossRef]
- Moir, G.; Shastri, P.; Connaboy, C. Intersession Reliability of Vertical Jump Height in Women and Men. J. Strength Cond. Res. 2008, 22, 1779–1784. [Google Scholar] [CrossRef]
- Veilleux, L.N.; Rauch, F. Reproducibility of Jumping Mechanography in Healthy Children and Adults. J. Musculoskelet. Neuronal Interact. 2010, 10, 256–266. [Google Scholar]
- Thomas, C.; Dos’Santos, T.; Comfort, P.; Jones, P.A. Between-Session Reliability of Common Strength- and Power-Related Measures in Adolescent Athletes. Sports 2017, 5, 15. [Google Scholar] [CrossRef]
- Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef]
- Nakagawa, S.; Schielzeth, H. Repeatability for Gaussian and non-Gaussian Data: A Practical Guide for Biologists. Biol. Rev. 2010, 85, 935–956. [Google Scholar] [CrossRef]
- Weir, J.P. Quantifying Test-Retest Reliability Using the Intraclass Correlation Coefficient and the SEM. J. Strength Cond. Res. 2005, 19, 231–240. [Google Scholar] [CrossRef]
- Hopkins, W.G. How to Interpret Changes in an Athletic Performance Test. Sportscience 2004, 8, 1–7. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; Version 1.4.1717; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Kassambara, A. Rstatix: Pipe-Friendly Framework for Basic Statistical Tests, R Package Version 0.7.0. 2021. Available online: https://cran.r-project.org/web/packages/rstatix/rstatix.pdf (accessed on 2 June 2022).
- Chang, C.; Chang, G.C.; Leeper, T.J.; Becker, J. Rio: A Swiss-Army Knife for Data File I/O, R Package Version 0.5.29. 2021. Available online: https://rdrr.io/cran/rio/ (accessed on 2 June 2022).
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Fox, J.; Weisberg, S. An R Companion to Applied Regression, 3rd ed.; Sage: Thousand Oaks, CA, USA, 2019. [Google Scholar]
- Gamer, M.; Lemon, J.; Puspendra Singh, I.F. Irr: Various Coefficients of Interrater Reliability and Agreement, R Package Version 0.84.1. 2019. Available online: https://cran.r-project.org/web/packages/irr/index.html (accessed on 2 June 2022).
- Chamorro, C.; Armijo-Olivo, S.; De la Fuente, C.; Fuentes, J.; Javier Chirosa, L. Absolute Reliability and Concurrent Validity of Hand Held Dynamometry and Isokinetic Dynamometry in the Hip, Knee and Ankle Joint: Systematic Review and Meta-analysis. Open Med. (Wars) 2017, 12, 359–375. [Google Scholar] [CrossRef]
- Roberts, H.C.; Denison, H.J.; Martin, H.J.; Patel, H.P.; Syddall, H.; Cooper, C.; Sayer, A.A. A Review of the Measurement of Grip Strength in Clinical and Epidemiological Studies: Towards a Standardised Approach. Age Ageing 2011, 40, 423–429. [Google Scholar] [CrossRef]
- Slinde, F.; Suber, C.; Suber, L.; Edwén, C.E.; Svantesson, U. Test-Retest Reliability of Three Different Countermovement Jumping Tests. J. Strength Cond. Res. 2008, 22, 640–644. [Google Scholar] [CrossRef]
- Lloyd, R.S.; Oliver, J.L.; Hughes, M.G.; Williams, C.A. Reliability and Validity of Field-Based Measures of Leg Stiffness and Reactive Strength Index in Youths. J. Sports Sci. 2009, 27, 1565–1573. [Google Scholar] [CrossRef]
- Dalleau, G.; Belli, A.; Viale, F.; Lacour, J.R.; Bourdin, M. A Simple Method for Field Measurements of Leg Stiffness in Hopping. Int. J. Sports Med. 2004, 25, 170–176. [Google Scholar] [CrossRef] [PubMed]
- McMahon, T.A.; Cheng, G.C. The Mechanics of Running: How Does Stiffness Couple with Speed? J. Biomech. 1990, 23, 65–78. [Google Scholar] [CrossRef]
- Flanagan, E.P.; Comyns, T.M. The Use of Contact Time and the Reactive Strength Index to Optimize Fast Stretch-Shortening Cycle Training. J. Strength Cond. Res. 2008, 30, 32–38. [Google Scholar] [CrossRef]
- Schmidtbleicher, D. Training for Power Events. In The Encyclopedia of Sports Medicine: Strength and Power in Sport, 1st ed.; Komi, P., Ed.; Blackwell: Oxford, UK, 1992; Volume 3, pp. 169–179. [Google Scholar]
- Flanagan, E.P.; Ebben, W.P.; Jensen, R.L. Reliability of the Reactive Strength Index and Time to Stabilization During Depth Jumps. J. Strength Cond. Res. 2008, 22, 1677–1682. [Google Scholar] [CrossRef]
- Tenelsen, F.; Brueckner, D.; Muehlbauer, T.; Hagen, M. Validity and Reliability of an Electronic Contact Mat for Drop Jump Assessment in Physically Active Adults. Sports 2019, 7, 114. [Google Scholar] [CrossRef]
- Byrne, D.J.; Browne, D.T.; Byrne, P.J.; Richardson, N. Interday Reliability of the Reactive Strength Index and Optimal Drop Height. J. Strength Cond. Res. 2017, 31, 721–726. [Google Scholar] [CrossRef]

| Gender | Total | ||
|---|---|---|---|
| Female | Male | ||
| n | 7 | 10 | 17 |
| Age [years] | 23.1 ± 1.1 | 24.9 ± 2.6 | 24.2 ± 2.2 |
| Height [cm] | 1.65 ± 0.1 | 1.82 ± 0.1 | 1.75 ± 0.1 |
| Weight [kg] | 57.9 ± 7.1 | 76.1 ± 13.1 | 68.6 ± 14.2 |
| BMI [kg/m2] | 21.2 ± 1.7 | 22.8 ± 2.8 | 22.1 ± 2.5 |
| S1 | S2 | S3 | All Sessions | S1–S2 | S1–S3 | S2–S3 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean (±SD) | ICC (95% CI) | CV% | ICC (95% CI) | CV% | ICC (95% CI) | CV% | ICC (95% CI) | CV% | |||
| Knee extension MVC (Nm) | |||||||||||
| Avg | 256.2 (±90) | 252.9 (±95) | 244.6 (±87) | 0.988 (0.973–0.995) | 6.2 | 0.988 (0.970–0.996) | 5.1 | 0.976 (0.929–0.992) | 6.7 | 0.981 (0.949–0.993) | 5.3 |
| Hv | 262.2 (±90) | 258.8 (±98) | 253.6 (±92) | 0.971 (0.937–0.989) | 6.1 | 0.975 (0.937–0.991) | 4.9 | 0.964 (0.904–0.987) | 6.3 | 0.972 (0.925–0.990) | 5.4 |
| Handgrip MVC (kg) | |||||||||||
| Avg | 45.5 (±12) | 45.9 (±12) | 46.5 (±13) | 0.990 (0.977–0.996) | 3.9 | 0.995 (0.987–0.998) | 2.2 | 0.979 (0.942–0.992) | 3.7 | 0.980 (0.947–0.993) | 4.4 |
| Hv | 47.7 (±12) | 47.9 (±12) | 48.4 (±14) | 0.978 (0.952–0.991) | 3.4 | 0.991 (0.977–0.997) | 2.2 | 0.975 (0.933–0.991) | 3.1 | 0.969 (0.917–0.988) | 3.9 |
| S1 | S2 | S3 | All Sessions | S1–S2 | S1–S3 | S2–S3 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean (±SD) | ICC (95% CI) | CV% | ICC (95% CI) | CV% | ICC (95% CI) | CV% | ICC (95% CI) | CV% | |||
| Jump height (cm) | |||||||||||
| Avg | 44.2 (±11) | 44.0 (±10) | 44.7 (±10) | 0.994 (0.986−0.998) | 3.1 | 0.990 (0.974−0.996) | 2.6 | 0.989 (0.970−0.996) | 3.0 | 0.991 (0.974−0.997) | 2.6 |
| Hv | 45.6 (±11) | 45.9 (±10) | 46.3 (11) | 0.973 (0.942−0.989) | 3.3 | 0.980 (0.947−0.992) | 2.4 | 0.968 (0.917−0.988) | 3.3 | 0.968 (0.916−0.988) | 3.2 |
| Peak power (W/kg) | |||||||||||
| Avg | 46.7 (±10) | 45.9 (±10) | 46.7 (±10) | 0.994 (0.986−0.997) | 2.8 | 0.991 (0.969−0.997) | 2.2 | 0.991 (0.975−0.997) | 2.6 | 0.988 (0.966−0.996) | 2.7 |
| Hv | 48.0 (±11) | 47.4 (±10) | 47.8 (±10) | 0.965 (0.923−0.986) | 3.2 | 0.962 (0.904−0.986) | 2.8 | 0.976 (0.935−0.991) | 2.6 | 0.955 (0.882−0.984) | 3.2 |
| All Sessions | S1–S2 | S1–S3 | S2–S3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SEm (SEm%) | SWC | MD (MD%) | SEm (SEm%) | SWC | MD (MD%) | SEm (SEm%) | SWC | MD (MD%) | SEm (SEm%) | SWC | MD (MD%) | |
| Knee extension MVC (Nm) | ||||||||||||
| Avg | 9.6 (3.8%) | 17.7 | 26.7 (10.6%) | 9.8 (3.8%) | 18.2 | 27.0 (10.6%) | 13.4 (5.4%) | 17.4 | 37.2 (14.8%) | 12.2 (4.9%) | 17.9 | 33.7 (13.6%) |
| Hv | 15.6 (6%) | 18.3 | 43.1 (16.7%) | 14.5 (5.6%) | 18.5 | 40.3 (15.5%) | 17.0 (6.6%) | 18.0 | 47.0 (18.2%) | 15.8 (6.2%) | 18.7 | 43.8 (17.1%) |
| Handgrip MVC (kg) | ||||||||||||
| Avg | 1.2 (2.7%) | 2.4 | 3.4 (7.4%) | 0.8 (1.7%) | 2.3 | 2.2 (4.8%) | 1.8 (3.9%) | 2.5 | 5.0 (10.8%) | 1.7 (3.7%) | 2.5 | 4.8 (10.4%) |
| Hv | 1.8 (3.8%) | 2.5 | 5.1 (10.7%) | 1.1 (2.4%) | 2.4 | 3.1 (6.6%) | 2.0 (4.3%) | 2.6 | 5.7 (11.8%) | 2.2 (4.7%) | 2.5 | 6.2 (12.9%) |
| All Sessions | S1–S2 | S1–S3 | S2–S3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SEm (SEm%) | SWC | MD (MD%) | SEm (SEm%) | SWC | MD (MD%) | SEm (SEm%) | SWC | MD (MD%) | SEm (SEm%) | SWC | MD (MD%) | |
| Jump height (cm) | ||||||||||||
| Avg | 0.8 (1.8%) | 2.0 | 2.2 (5.1%) | 1.0 (2.3%) | 2.1 | 2.9 (6.5%) | 1.1 (2.5%) | 2.1 | 3.0 (6.8%) | 1.0 (2.2%) | 2.0 | 2.7 (6.1%) |
| Hv | 1.7 (2.7%) | 2.1 | 4.7 (10.3%) | 1.5 (3.2%) | 2.1 | 4.1 (8.9%) | 1.9 (4.2%) | 2.1 | 5.3 (11.5%) | 1.8 (4%) | 2.1 | 5.1 (11%) |
| Peak power (W/kg) | ||||||||||||
| Avg | 0.8 (1.7%) | 1.9 | 2.1 (4.5%) | 0.9 (2%) | 2.0 | 2.6 (5.6%) | 0.9 (2%) | 1.9 | 2.6 (5.5%) | 1.0 (2.2%) | 1.9 | 2.9 (6.2%) |
| Hv | 1.9 (3.9%) | 2.0 | 5.2 (10.8%) | 2.0 (4.1%) | 2.0 | 5.4 (11.4%) | 1.6 (3.3%) | 2.0 | 4.3 (9.1%) | 2.0 (4.3%) | 1.9 | 5.7 (11.9%) |
| S1 | S2 | S3 | All Sessions | S1–S2 | S1–S3 | S2–S3 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean (±SD) | ICC (95% CI) | CV% | ICC (95% CI) | CV% | ICC (95% CI) | CV% | ICC (95% CI) | CV% | |||
| Peak force (kN) | |||||||||||
| Avg | 3.48 (±1) | 3.58 (±1) | 3.81 (±1) #, & | 0.975 (0.925–0.991) | 7.1 | 0.972 (0.926–0.989) | 5.7 | 0.949 (0.629–0.986) | 7.8 | 0.965 (0.830–0.989) | 5.6 |
| Hv | 3.69 (±1) | 3.74 (±1) | 3.95 (±1) #, & | 0.942 (0.859–0.978) | 6.4 | 0.94 (0.848–0.977) | 5.6 | 0.926 (0.703–0.976) | 6.7 | 0.956 (0.748–0.987) | 4.9 |
| Average contact time (s) | |||||||||||
| Avg | 0.182 (±0.02) | 0.171 (±0.02) | 0.180 (±0.02) | 0.526 (−0.031–0.811) | 8.5 | 0.659 (0.090–0.872) | 6.0 | 0.32 (−1.014–0.760) | 8.9 | 0.256 (−0.909–0.723) | 7.9 |
| Lv | 0.168 (±0.02) | 0.165 (±0.02) | 0.169 (±0.02) | 0.536 (0.250–0.776) | 6.2 | 0.667 (0.316–0.859) | 4.5 | 0.511 (0.039–0.792) | 5.7 | 0.457 (−0.006–0.761) | 6.4 |
| All Sessions | S1–S2 | S1–S3 | S2–S3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SEm (SEm%) | SWC | MD (MD%) | SEm (SEm%) | SWC | MD (MD%) | SEm (SEm%) | SWC | MD (MD%) | SEm (SEm%) | SWC | MD (MD%) | |
| Peak force (kN) | ||||||||||||
| Avg | 0.16 (4.5%) | 0.20 | 0.45 (12.5%) | 0.17 (4.8%) | 0.20 | 0.47 (13.4%) | 0.23 (6.4%) | 0.21 | 0.65 (17.8%) | 0.19 (5.1%) | 0.20 | 0.53 (14.3%) |
| Hv | 0.25 (6.7%) | 0.21 | 0.70 (18.4%) | 0.26 (6.9%) | 0.21 | 0.71 (19.2%) | 0.30 (7.7%) | 0.22 | 0.82 (21.4%) | 0.21 (5.6%) | 0.20 | 0.59 (15.4%) |
| Average contact time (s) | ||||||||||||
| Avg | 0.015 (8.6%) | 0.004 | 0.042 (23.8%) | 0.012 (6.9%) | 0.004 | 0.034 (19.1%) | 0.019 (10.8%) | 0.005 | 0.054 (29.9%) | 0.019 (10.7%) | 0.004 | 0.052 (29.8%) |
| Lv | 0.012 (7.0%) | 0.003 | 0.032 (19.3%) | 0.009 (5.6%) | 0.003 | 0.026 (15.6%) | 0.012 (7%) | 0.003 | 0.033 (19.4%) | 0.013 (8.1%) | 0.004 | 0.037 (22.4%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Venegas-Carro, M.; Kramer, A.; Moreno-Villanueva, M.; Gruber, M. Test–Retest Reliability and Sensitivity of Common Strength and Power Tests over a Period of 9 Weeks. Sports 2022, 10, 171. https://doi.org/10.3390/sports10110171
Venegas-Carro M, Kramer A, Moreno-Villanueva M, Gruber M. Test–Retest Reliability and Sensitivity of Common Strength and Power Tests over a Period of 9 Weeks. Sports. 2022; 10(11):171. https://doi.org/10.3390/sports10110171
Chicago/Turabian StyleVenegas-Carro, Maria, Andreas Kramer, Maria Moreno-Villanueva, and Markus Gruber. 2022. "Test–Retest Reliability and Sensitivity of Common Strength and Power Tests over a Period of 9 Weeks" Sports 10, no. 11: 171. https://doi.org/10.3390/sports10110171
APA StyleVenegas-Carro, M., Kramer, A., Moreno-Villanueva, M., & Gruber, M. (2022). Test–Retest Reliability and Sensitivity of Common Strength and Power Tests over a Period of 9 Weeks. Sports, 10(11), 171. https://doi.org/10.3390/sports10110171








