Abstract
The lone star (Amblyomma americanum), black-legged (Ixodes scapularis) and American dog ticks (Dermacentor variabilis) are species of great public health importance as they are competent vectors of several notable pathogens. While the regional distributions of these species are well characterized, more localized distribution estimates are sparse. We used records of field collected ticks and an ensemble modeling approach to predict habitat suitability for each of these species in Florida. Environmental variables capturing climatic extremes were common contributors to habitat suitability. Most frequently, annual precipitation (Bio12), mean temperature of the driest quarter (Bio9), minimum temperature of the coldest month (Bio6), and mean Normalized Difference Vegetation Index (NDVI) were included in the final models for each species. Agreement between the modeling algorithms used in this study was high and indicated the distribution of suitable habitat for all three species was reduced at lower latitudes. These findings are important for raising awareness of the potential for tick-borne pathogens in Florida.
Keywords:
Ixodid ticks; distribution; geography; modeling; ensemble; niche; Lone star; Black-legged; American dog 1. Introduction
In Florida, cases of locally acquired tick-borne illnesses are reported yearly [1]. Officially recognized, locally acquired cases are sporadic, which may reflect variation in the types of human activities that influence exposure or transmission risk and/or variation in the distribution of vector species. Distribution estimates are often restricted to county level averages when detailed spatial information is unavailable or when the focus is on large geographic extents. While this approach can often leverage available data, it can mask important nuances in the distribution of exposure risk. In this paper, we address the latter aspect of vector-borne disease risk and this necessitates examining vector distributions at resolutions fine enough to associate human behaviors with the local environments. This requires discerning patterns at a spatial resolution representing the sub-county scales.
One of the major methodological challenges in characterizing tick vector distributions is that there are many statistical and pattern matching approaches to estimate the distribution of the vector [2]. All these approaches rely on identifying suitable habitat for a species based on associations between observed presence/abundance and environmental characteristics of those locations [3]. However, each modeling approach uses method-specific parameters and assumptions that may entrain unrecognized predictive biases unrelated to the biology of the species being modeled [4]. One solution to reduce the unrecognized biases is to use ensembles of different modeling algorithms with the presumption that their overall patterns will reduce the potential predictive bias produced by any single model [5,6]. Ensemble outputs highlight areas of agreement across predictions and are believed to indicate greater confidence in the suitability of those locations for the target (tick) species [5].
Many previous efforts of ensemble models for tick species’ distributions have been done at regional scales and relied on limited sets of environmental (primarily climatic) data [7,8,9,10,11]. Here, we use an ensemble prediction from five common modeling algorithms to estimate the geographic distributions of suitable habitat for the lone star (Amblyomma americanum), black-legged (Ixodes scapularis), and American dog ticks (Dermacentor variabilis), three species of public health importance in Florida. These models are developed at a resolution of one hectare, to provide a more detailed scale for case investigation, or intervention.
Nationally, the incidence of tick-borne diseases is increasing and represents an overwhelming majority of vector-borne infections in the U.S. each year [12]. Reports of these diseases have outpaced other vector-borne illness by a factor of 9:1 between 2004 to 2013 [12]. Lone star, American dog, and black-legged ticks are known to transmit several of the most frequently reported pathogens causing disease in humans. The black-legged tick is the primary vector for Lyme disease pathogens (Borrelia spp.) in the Eastern United States, as well as a vector for Anaplasma phagocytophilum, Ehrlichiosis causing agents, and the parasite Babesia microti [13,14,15,16,17]. Cases of Lyme disease account for nearly 70% of all nationally notifiable vector-borne diseases in the U.S. [12]. High abundance, voracious and nonspecific biting habits, and known or suspected competence for transmission of Ehrlichia chaffeensis and E. ewingii, Francisella tularensis, and the agent of southern tick-associated rash illness (STARI) make the lone star tick a species of significant public health concern [18,19,20,21,22,23,24,25,26,27]. The American dog tick is an important vector of both human and animal pathogens. This species is known to transmit Rickettsia rickettsii (Rocky Mountain spotted fever—RMSF), Francisella tularensis, and other notable pathogens [28,29].
In this study we used five modeling algorithms: Generalized linear models (logistic regression), boosted regression trees, random forests, multivariate adaptive regression splines, and maximum entropy to estimate the distribution of lone star, black-legged, and American dog ticks. The five modeling algorithms used in this study have been used in various ecological applications to estimate the geographic distributions of numerous vagile and non-vagile species, including ticks [11,30,31]. Common species distribution modeling (SDM) algorithms generally fall into one of two categories: Statistical approaches, which rely on underlying assumptions about the distributions of data values or models; and machine learning approaches, which instead group the data into distinct, homogeneous groupings (classification) without assuming an a priori distribution [32].
Traditional statistical approaches stem from regression methods and include generalized linear models (GLMs), and their extensions, such as generalized additive models (GAMs) and multivariate adaptive regression splines (MARS). Logistic regression (GLM with a logit link function) is a common statistical method to model binary responses such as presence/absence data. The method is well established and easily interpretable. The response variable from logistic regression is a probability that the outcome is the value of interest that is conditional on the weighted linear combination of predictor variables [33]. MARS can be thought of as piecewise regression in which the data are fit using a defined number of linear splines. This method is particularly useful if a species’ response to the environment is presumed to be non-monotonic [34].
Machine learning (ML) approaches, including classification methods, are ‘data-driven’. Unlike statistical approaches, which assume an initial data model (e.g., linear or logistic response), and specific distribution functions, ML attempts to learn the relationship by finding dominant patterns in the data [35]. Classification methods use a series of branching decisions regarding the predictor variables to partition the response variable into homogeneous groups (terminal nodes or leaves). These decision trees can then be used as a stand-alone classifier or in conjunction with other methods to build more robust predictions. One such approach to develop more robust classifiers is a method called random forests [35]. This approach uses a collection of classification trees, each trained on a random subset of the data. Each tree uses the predictor variables from a given data point to ‘vote’ for the most popular class for that input [35].
Boosted regression trees (BRTs) bridge the traditional statistical techniques such as GLMs and ML. Instead of relying on a ‘popular vote’ to determine the output class (as in RF), regression trees fit a mean response for observations within each leaf. For the logistic regression trees, the response is modeled via a logit function [36]. BRT combines the regression tree models with a method called boosting, which builds a collection of the individual trees in linear combination. As with RF and other classification, regression, or decision tree models, BRTs attempt to produce homogeneous subsets of the response variable by partitioning the multivariate predictor space [36].
Maximum entropy (MaxEnt) modeling also began as a general-purpose ML tool to make predictions from incomplete information [37]. This method attempts to estimate a target probability distribution of occurrence conditional on environmental variables by finding the distribution of maximum entropy subject to constraints defined by the target sample [37]. These constraints consist of five feature types that reflect the relationship between the probability distribution and environmental variables: linear, quadratic, product, threshold, and binary. It has since been shown to be mathematically equivalent to logistic regression under certain circumstances [10,37,38].
Application of these methods to species occurrence data and raster-based predictors allows us to generate high resolution estimations of geographic distributions based on environmental suitability for these species. These predictions can help increase understanding of vector distributions and target areas at risk of vector-borne pathogens. However, we have relatively little basis for understanding the differences in predicted vector distributions (and hence our projections of the human populations at risk) caused by using different modeling approaches and determining if one approach may heuristically outperform the others. In this study, we use an ensemble modeling approach to compare the performance of various models using a common set of environmental predictor data and geographically identical survey data sets of tick species occurrences. An examination of the geographic extents of suitable area conserved across models provides a starting point for evaluating the utility of these different modeling approaches.
2. Materials and Methods
2.1. Tick Distribution Data
We used georeferenced records from three years of tick collections performed from late 2015 through 2018 containing observations of adult Amblyomma americanum, Dermacentor variabilis, or Ixodes scapularis [39,40]. The initial dataset included 1956 surveys of presence or absence for each of the three species. Spatially, the dataset contained multiple transects spread across 41 sites in mainland Florida. Within each site, pairs of transects were run in the primary local biotopes (2–10 transects, depending on the size and heterogeneity of land cover at each site). In aggregate, sampling of the major biotopes was performed proportional to the state-wide land class coverages. Temporally, these transects were repeated regularly throughout the study period (repeated surveys of each transect). Collection efforts occurred year-round to ensure all sites were sampled with the same intensity regardless of when individual species’ peak seasonal activity occurred [39,40]. The methods for collection are described in further detail elsewhere [39,40]. The repeated sampling of multiple biotopes within sites produced a total of 1956 presence or absence records for the dataset.
As many of the environmental data layers were in raster format, a one-hectare vector grid matching the extent and resolution of the environmental predictors was generated. The geographic coordinates for the midpoints of the 1956 survey records was overlain on the vector grid. All surveys within individual cells were merged to a single record and if adult ticks were found during any of those surveys, that species was considered ‘present’ in that cell, otherwise it was declared absent. Thus, ‘absence’ cells never yielded adult ticks for an individual species throughout the entire study, while grid cells containing one or more occurrence records were considered ‘presence’ locations. In some cases, the same transect was linked to multiple grid cells during different surveys, primarily due to slight modifications in the position of the transect as a result of changes in the local environment such as prolonged flooding, burning, and other factors impacting accessibility of a transect location. In these cases, records were aggregated in the grid cell within which they occurred, rather than to the grid cell containing previous records of the same transect. The coordinates for the geometric centers of presence or absence cells was extracted and used to delineate the location of each record, resulting in a dataset of 560 points for subsequent modeling (Table 1).

Table 1.
Number of presence/absence observations used for modeling each species. The total number (n = 560) and geographic location of observations is conserved for each species, with only observed occurrence (presence) varying.
2.2. Selection of Environmental Predictors
Environmental predictors used in our species distribution models consisted of 36 characteristics describing the climatic and habitat conditions in the study area. Habitat variables included three descriptions of Normalized Difference Vegetation Index (NDVI; minimum, mean, and maximum), land cover, elevation, soil and geomorphologic characteristics, and distance from water features. The climatic characteristics considered were 19 measures of temperature and precipitation variability.
Variables describing NDVI, elevation, soil, and geomorphologic characteristics were derived from MODIS NDVI 16-day composites, ASTER Global DEM, STATSGO soils database and national hydrography datasets, respectively [41,42,43,44]. The land cover classification was derived from the Florida Cooperative Land Cover database, which includes statewide classifications of all major land cover types at a native resolution of 10 m [45]. The database represents a hierarchical classification. The primary state-level land cover types were aggregated using a majority rule to the coarsest level as one of five primary types: Forest, which included pine and hardwoods; shrub, which encompassed shrub and brush lands; grasslands; wetlands; and a final, general category including all other land types such as water bodies, urban areas, and seasonal agriculture. All environmental predictors were resampled using bilinear interpolation for continuous variables and majority rule for categorical variables and cropped to the same extent and 1 ha resolution.
The climatic variables consisted of 19 bioclimatic variables calculated from gridded daily temperature and precipitation estimates from Daymet [46]. The climatic variables follow the same naming conventions and are calculated following the methodology of Hijmans et al. (2005) as implemented in the ‘biovars’ function in the dismo R package [47,48]. The bioclimatic variables were calculated at the native 1 km2 resolution of the gridded daily estimates.
2.3. Distribution Models
Initial variable screening was performed before construction and selection of our distribution models to reduce the potential for collinearity. Reduction of the potential variable set was guided by the procedures outlined in Springer et al. (2015). First, Pearson, Spearman, and Kendall correlation coefficients were calculated amongst all environmental predictors. Univariate GAMs were constructed to assess initial significant relationships between each predictor and the dependent variable. Predictors were ranked by the deviance explained of the dependent variable. Deviance explained is a GAM parameter analogous to R-squared used GLMs and represents the amount of variation in the dependent variable that is explained by the given predictor [11]. To produce the final set of variables for consideration in the distribution models, the variable with the highest deviance explained from the univariate GAM was selected for inclusion. All additional variables were selected in descending order by deviance explained and whether all pairwise correlations with previously selected variables was below a ±0.7 threshold [49].
We used five different modeling algorithms: (1) general linear models (logistic regression—LR) [33], (2) boosted regression trees (BRTs) [36], (3) random forests (RF) [35], (4) multivariate adaptive regression splines (MARS) [34], and (5) maximum entropy (MaxEnt) [37], to estimate the distribution of each species. Each of these methods are generally considered to perform well using presence/absence or presence/background data [4,11]. It should be noted that MaxEnt is generally run as a ‘presence-only’ model, with background data drawn randomly from the study area, although it can be supplied with spatially biased pseudo-absences [50,51]. Here, MaxEnt was supplied with the same (‘true’) absence data as the other algorithms in place of the random background draw.
Each model algorithm was run through an iterative procedure to select the best model from the set of environmental predictors and was optimized using performance metrics specific to each method. The optimized GLM was selected by performing an exhaustive search of first order interactions in the model space. Competing models were compared using the small sample size corrected Akaike’s Information Criterion (AICc) and the final model was selected by minimizing this value [52,53]. The BRT model was optimized by varying tree complexity, learning rate, and ‘bag fraction’ to select a model minimizing mean deviance with at least 1000 trees according to Elith et al. (2008). The random forest model was optimized by varying the number of considered variables, node size, and sample size to minimize out-of-bag (OOB) error [36]. The MARS model selection procedure utilized an internal 10-fold cross validation procedure to select the appropriate variables and number of knots [34,54]. As with the GLM model, we only considered first-order interactions in the MARS model. The optimized model was selected to maximize the GRSq, which is a cross validated estimate of the predictive power of the model [54]. The MaxEnt model was selected by varying the betamultiplier with a contribution threshold of five percent and maximum correlation threshold between variables of 0.9. Optimization of these parameters allows for a certain amount of uncertainty to be introduced into the model and limits the inclusion of extraneous variables (low contribution) and collinearity. The optimal model was selected to maximize the Area Under the Curve (AUC) of internally withheld test data [55].
Validation of the final models was performed using 10-fold cross validation to assess the agreement between observed and predicted values. The dataset used to select the optimized model was divided into 10 folds. Each model was trained by withholding one fold of the data and running the model with the remaining folds. The withheld fold was used to test the predictive accuracy of each run. This procedure was repeated ten times so that each fold was withheld and used for testing. All models were validated using the same folds for consistency across methods.
2.4. Spatial Predictions
Estimated habitat suitability for each species was determined by applying the optimized algorithms to a set of raster variables. The output is a probability surface for the entire mainland portion of the state, representing the probability that the conditions in a given raster cell are suitable for each species. These probability surfaces were reclassified as suitable or unsuitable based on a specified threshold criterion for prediction accuracy (sensitivity = specificity). This threshold criterion was selected as a tradeoff between predicting true positives and true negatives. The ensemble prediction of the distribution of suitable habitat for each species is the agreement between models and was assessed by summing the binary suitability estimates for each method. Thus, suitability was based on a consensus score ranging from 0–5 ranking how many of the algorithms indicated a given location was suitable or not. We also retained the continuous probability estimates for each optimized model to visualize single model variation from the ensemble prediction.
3. Results
3.1. Predictor Variables
The correlation matrices and the GAM variable screening procedure reduced the set of 36 potential environmental covariates to 17 variables for A. americanum, 17 for I. scapularis, and 18 for D. variabilis. Several variables were important in models for all species, although there was some variation in the deviance they explained and their rank (Table 2). Variables capturing the extremes in climate patterns were frequently included for consideration, as were one or more measures of vegetation health or greenness. Average temperatures during the driest quarter, total precipitation, and precipitation during the wettest and driest months were considered for all three species. Mean NDVI was also considered for all species. Elevation, distance to water bodies and curvature, a geomorphological characteristic describing low-lying areas where water may pool transiently, were also considered for all species. Consideration of these variables are consistent with previous studies of tick distributions, which have selected variables either a priori or through similar selection procedures [7,8,9,10,11].

Table 2.
Deviance explained by considered variables and rank via univariate generalized additive models (GAM) for each species. NDVI is the Normalized Difference Vegetation Index, a proxy for vegetation health.
The final variables included in each model are listed in Table 3. Selection of final models for each species indicated that several variables were conserved across algorithms. Most frequently, annual precipitation (Bio12), mean temperature of the driest quarter (Bio9), minimum temperature of the coldest month (Bio6), and mean NDVI were included in the final models for each species. The conservation of these variables across algorithms and species is indicative of the similar ecological niches occupied by these ticks.

Table 3.
Variables included in final models for each species. The machine learning algorithms consider all variables initially, and unimportant variables are pruned back. As a result, all considered variables are listed for these models, though the contribution of some variables is quite small.
All the modeling algorithms performed comparably well for a given species. The cut off threshold for delineating presence from absence ranged from 0.06–0.3 which is on par with the thresholds for delineating presence used by James et al. (2015) and Kessler et al. (2018). The cross-validated AUC scores for A. americanum were all between 0.89 and 0.92. The AUC scores for I. scapularis and D. variabilis were slightly lower, with ranges of 0.83–0.90 and 0.76–0.83, respectively (Table 4). We found that all the algorithms displayed reduced performance when the imbalance between response classes (presence vs. absence) increased, which is likely a result of the smaller ‘presence’ sample sizes for I. scapularis and D. variabilis. For each of the species BRT, RF, and Logistic performed slightly better than MARS or MaxEnt.

Table 4.
Performance metrics associated with each of the five modeling algorithms for each species. AUC ranges correspond to the upper and lower bounds of a 95% CI calculated from across the 10-fold cross validation.
3.2. Spatial Predictions
The distributions of suitable habitat produced from the ensemble predictions for each species showed similar corridors of high model agreement through the center of the Florida peninsula (Figure 1, Figure 2 and Figure 3). Each ensemble map identified a contiguous area of suitability in North Central Florida, with generally reduced suitability in the southern portions of the state. In the South Central region of the state, the Lake Whales Ridge is identifiable in ensemble predictions for Amblyomma americanum and Ixodes scapularis as either unsuitable or suitable, respectively. The southwestern coast, however, from Naples south into Everglades National Park shows an area of predicted suitability that is conserved across models and species. The panhandle of the state is similarly less suitable for each of the species except for a disjunct region in the heavily forested northwestern corner of the state. The ensemble predictions for A. americanum and I. scapularis show high consensus across algorithms with more area deemed suitable by three or more algorithms. The prediction for D. variabilis showed greater discordance, with a greater area having only one or two algorithms agreeing on suitability; lower agreement for this species may be a result of the small sample size used for building the models. For all species, the MARS algorithms predicted the least amount of area as suitable habitat, and with the highest mean suitability scores. This could be a sign of overfitting in the model.
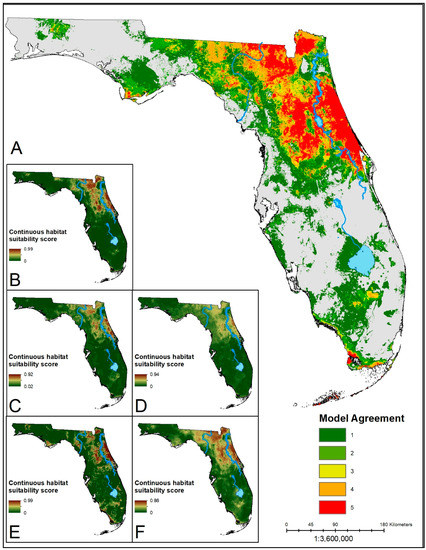
Figure 1.
(A) Ensemble prediction of suitable habitat for A. americanum. Hotter colors indicate higher agreement in the number of models predicting suitability of an area. (B–F) Continuous suitability scores for the five modeling algorithms: LR, BRT, RF, MARS, MaxEnt, respectively. A core region in the north-central region of the state shows consensus across all five algorithms. Suitable areas in the southern part of the state are sparser, with lower model agreement.
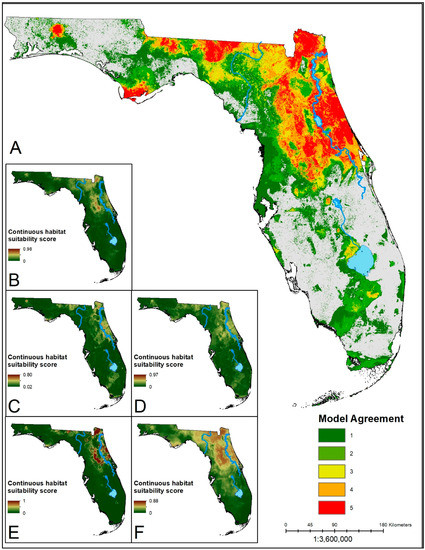
Figure 2.
(A) Ensemble prediction of suitable habitat for I. scapularis. Hotter colors indicate higher agreement on habitat suitability across models for a given area. (B–F) Continuous suitability scores for the five modeling algorithms: LR, BRT, RF, MARS, MaxEnt, respectively. Much of the northeastern part of the state is deemed suitable by the majority of the models. Southern areas of predicted suitability show lower consensus.
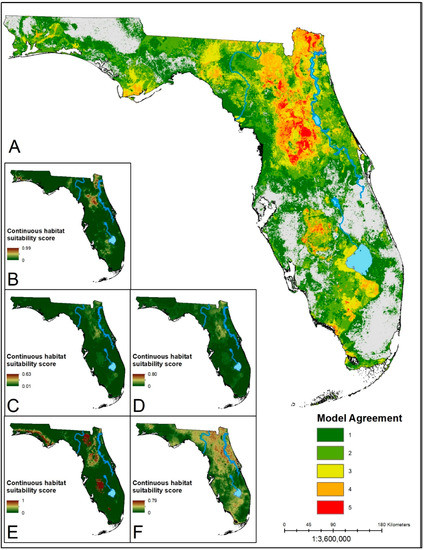
Figure 3.
(A) Ensemble prediction of suitable habitat for D. variabilis. Hotter colors indicate higher agreement in habitat suitability. (B–F) Continuous suitability scores for the five modeling algorithms: LR, BRT, RF, MARS, MaxEnt, respectively. Overall there is lower consensus on suitable habitat across the state. However, there is greater model agreement in the southern part of the state for this species than for black-legged or lone star ticks.
4. Discussion
The estimated distributions for the medically important tick species presented in this study show strikingly similar patterns. Much of northern Florida is considered suitable by the majority of—or all of—the modeling algorithms used, while suitability decreases at lower latitudes. The deviance explained, which is a measure of how well the model explains the relationship between dependent and independent variables, by any single predictor was very low for all species, with the greatest deviance explained being mean temperature of the coldest quarter (0.253), mean temperature of the wettest quarter (0.20), and mean diurnal range (0.137) for A. americanum, I. scapularis, and D. variabilis, respectively. This is indicative that a plethora of conditions influence suitability for these species and distributions are not driven by a predominant single factor. We found that while consensus among algorithms was high (as indicated by large regions of suitable habitat receiving a score of ≥3 in the consensus projections), each algorithm produced some variation in predicted suitable area. The use of an ensemble approach provides a degree of certainty that the estimated distribution reflects that of the species and is not simply a result of the choice of modeling algorithm.
However, it is important to remember that the consensus score of ensemble predictions are simple sums, so they could be disproportionately influenced by conservative SDM algorithms [5]. For example, in a study of invasive fish species in the United States, Marmion et al. (2009) found that MaxEnt produced estimated distributions with the smallest geographic area that did not extend much beyond existing presence records (although the model’s training AUC values were the highest of all models in their ensembles). As a result, the ensemble maps largely reflected the distributional estimates from their MaxEnt models. In our study, AUC values for each of the three species were quite close, indicating that the predictive performance of each algorithm was similar. However, MaxEnt consistently produced the lowest AUC values while producing the predictions of suitable area with the largest geographic extents for each species. This produces much of the low model agreement areas (green) in our predictions. Conversely, the MARS algorithm produced higher AUC values but was most conservative in its estimations of suitable area, which highlights one of the main criticisms of ensemble approaches; while MARS and other algorithms predict suitable conditions in the same areas, the extent of the MARS predictions limits the areas where highest model agreement is possible. Ultimately, the accuracy of the various models for these tick distributions in Florida will need to be determined by validation surveys in previously unsampled regions of the state. These studies are currently underway and will be completed following the annual activity periods of the adult ticks for each species.
In this study we limited our observations to occurrence records of adult specimens collected via flagging, which resembles casual human exposure more than other sampling techniques such as chemical attractants/traps or collections from sentinel species. Collections from free-ranging wildlife may be a more sensitive representation of tick burden on the landscape but make high resolution spatial and temporal predictions difficult because hosts may range widely through multiple habitat types, and ticks may be attached to hosts for multiple days [56]. Additionally, some tick species that have preferences for wildlife species rarely attach to humans. A primary utility of these records, however, involved validating (or refuting) the SDMs. Previous publications using other survey methods, including collections from wildlife, indicated the occurrence of lone star, black-legged, and American dog ticks across northern Florida, which supports the distributional estimates presented here [57,58,59]. However, records in the literature also note the presence of these species from regions in south Florida, although these historic records are sparse [57,60]. Although we rarely found questing ticks in southern Florida, several of the SDMs indicated suitable conditions broadly throughout the region. These regions might represent some of the best evaluations of alternative SDMs within the ensemble suite as they provide the clearest distinction in predictions. Sites where the five models either all predicted occurrence or absence provide little discriminating power concerning which modeling approach might be “best”. It is unclear if the north–south trend in suitability represents a true lack of suitable habitat in this region [61,62]. The meridional trend in A. americanum abundance [57] closely corresponds to the three primary ecoregions in Florida, implicating variable ecological conditions in the observed distributional patterns. Conversely, the predicted occurrences of tick species further south for some of the models, especially the general agreement among models in the furthest southwestern regions of the state, suggest there may be local foci of infestations that deserve further evaluation.
Previous studies modeling the distributions of these species across the United States and North America have captured similar general trends, although the resolution for these studies is spatially and temporally coarser (resolved to the county level for all available times). Our observed patterns in distribution for A. americanum are supported by the county-level analysis of the contiguous United States generated by Springer et al. [61], which observed reduced agreement for the suitability of southern (and southeastern especially) Florida. Hahn et al. (2016) observed reduced model agreement for south Florida in predictions for I. scapularis suitability. Similarly, the predicted distribution of suitable habitat for D. variabilis was supported by previous studies showing much of the state as suitable for the species, although the southeastern regions are less so [9,10]. The distribution estimate by James et al. (2015) additionally captured the area of higher suitability along the gulf coast of the panhandle for D. variabilis.
A practical application of high resolution ensemble models involves case investigations in regions where tick-borne pathogens are or might be emerging. Reported cases of locally acquired tick-borne infections in Florida are relatively rare compared to numbers in the Northeast and Upper mid-western United States. Additionally, they tend to be geographically scattered, making investigations challenging and expensive. The disparate occurrence of cases may reflect variation in the types of human activities that influence risk and/or variation in the distribution of vector species or pathogen. The ensemble models, if validated, could allow local and state health officials to target surveillance and other intervention strategies while minimizing marginal costs of staff, equipment and supplies.
Historic under-sampling of ticks in many counties in Florida likely produces poorly characterized distributions and estimates of human risk of exposure. The spatial predictions of questing Ixodid ticks in Florida produced by this research contributes to a better understanding of exposure risk to ticks and their pathogens by providing an initial indication of risky landscapes and may inform control measures by county, state, and federal agencies. Understanding the distributions for pathogen vectors, at high spatial resolutions, can be an important first step to identifying and targeting areas at risk for vector-borne diseases. If the maps are determined to be spatially accurate and temporally stable, they could also help diagnostically by ruling out certain species-associated pathogens based on geographic activity of the patient. This is evident in the consistently high negative predictive values for ruling out species distributions. The heterogeneous distributions of the three tick species covered by this study should help guide future work on evaluating human exposure risk to these vectors and their pathogens in Florida. We found numerous temperature and precipitation variables were important in predicting the distribution of adult lone star, black-legged, and American dog ticks in the state and the variables were conserved across model algorithms and species. Additional models informed by tick densities, pathogen prevalence, or disease incidence may better improve estimates of exposure risk to tick-borne diseases, as these approaches address important aspects of transmission not addressed by habitat suitability alone [63,64].
5. Conclusions
Broad patterns of environmental suitability for the three species modeled are similar. This finding speaks to the similarity in niches occupied by these species. The ecology of all three species is largely driven by similar responses to climatic conditions such as temperature and moisture availability. The northern and north central regions of the state consist of a large contiguous tract of suitable area that diminishes at southern latitudes.
The fine-grained distributions of suitable habitat for medically-important tick species in Florida are more heterogeneous than previous studies would suggest. Individually, each modeling algorithm produced estimates with closely similar accuracies and geographic distributions of suitability. By using an ensemble of multiple algorithms, we developed consensus predictions which highlighted suitable areas conserved across models. The high degree of consensus among algorithm predictions suggests that although each approach produces some noise, no single algorithm vastly outperformed the others. Each algorithm’s prediction should be considered individually, however, as high accuracy measures could be due to overfitting and produce low generalizability. As a result, reliance on any single algorithm carries a degree of uncertainty in its prediction. Validation surveys are required to test these predictions. When used in conjunction with additional behavioral or exposure factors to estimate risk of exposure to ticks or tick-borne pathogens, fine resolution habitat suitability models may be a useful tool for identifying areas of tick presence.
Author Contributions
Conceptualization, G.E.G.; Data curation, W.H.K. and C.G.; Formal analysis, W.H.K.; Funding acquisition, G.E.G.; Investigation, W.H.K., C.G. and G.E.G.; Methodology, W.H.K., C.G. and G.E.G.; Supervision, G.E.G.; Validation, W.H.K., C.G. and G.E.G.; Writing—original draft, W.H.K.; Writing—review & editing, C.G. and G.E.G.
Funding
This research was supported by CDC grant 1U01CK000510-01: Southeastern Regional Center of Excellence in Vector-Borne Diseases: the Gateway Program and the Emerging Pathogens Institute, at the University of Florida and the College of Liberal Arts and Sciences, as part of the University of Florida Preeminence Initiative. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the Centers for Disease Control and Prevention.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Health, F.D.O. Reportable Diseases Frequency Report; Florida Deparment of Health: Tallahassee, FL, USA, 2017. [Google Scholar]
- Guisan, A.; Zimmermann, N.E. Predictive habitat distribution models in ecology. Ecol. Model. 2000, 135, 147–186. [Google Scholar] [CrossRef]
- Blackburn, J.K. Integrating geographic information systems and ecological niche modeling into disease ecology: A case study of bacillus anthracis in the United States and Mexico. In Emerging and Endemic Pathogens: Advances in Surveillance, Detection, and Identificiation; O’Connell, K.P., Skowronski, E.W., Sulakvelidze, A., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 59–88. [Google Scholar]
- Elith, J.; Graham, C.H. Do they? How do they? Why do they differ? On finding reasons for differing performances of species distribution models. Ecography 2009, 32, 66–77. [Google Scholar] [CrossRef]
- Marmion, M.; Parviainen, M.; Luoto, M.; Heikkinen, R.K.; Thuiller, W. Evaluation of consensus methods in predictive species distribution modelling. Divers. Distrib. 2009, 15, 59–69. [Google Scholar] [CrossRef]
- Araujo, M.B.; New, M. Ensemble forecasting of species distributions. Trends Ecol. Evol. 2007, 22, 42–47. [Google Scholar] [CrossRef] [PubMed]
- Brownstein, J.S.; Holford, T.R.; Fish, D. A climate-based model predicts the spatial distribution of the lyme disease vector ixodes scapularis in the United States. Environ. Health Perspect. 2003, 111, 1152–1157. [Google Scholar] [CrossRef] [PubMed]
- Hahn, M.B.; Jarnevich, C.S.; Monaghan, A.J.; Eisen, R.J. Modeling the geographic distribution of ixodes scapularis and ixodes pacificus (acari: Ixodidae) in the contiguous United States. J. Med. Entomol 2016, 53, 1176–1191. [Google Scholar] [CrossRef]
- James, A.M.; Burdett, C.; McCool, M.J.; Fox, A.; Riggs, P. The geographic distribution and ecological preferences of the american dog tick, dermacentor variabilis (say), in the USA. Med. Vet. Entomol 2015, 29, 178–188. [Google Scholar] [CrossRef] [PubMed]
- Minigan, J.N.; Hager, H.A.; Peregrine, A.S.; Newman, J.A. Current and potential future distribution of the american dog tick (dermacentor variabilis, say) in North America. Ticks Tick Borne Dis. 2018, 9, 354–362. [Google Scholar] [CrossRef]
- Springer, Y.P.; Jarnevich, C.S.; Barnett, D.T.; Monaghan, A.J.; Eisen, R.J. Modeling the present and future geographic distribution of the lone star tick, amblyomma americanum (ixodida: Ixodidae), in the continental United States. Am. J. Trop. Med. Hyg. 2015, 93, 875–890. [Google Scholar] [CrossRef]
- Beard, C.B.E.R.J.; Barker, C.M.; Garofalo, J.F.; Hahn, M.; Hayden, M.; Monaghan, A.J.; Ogden, N.H.; Schramm, P.J. The Impacts of Climate Change on Human Health in the United States: A Scientific Assessment; USA Global Change Research Program: Washington, DC, USA, 2016; pp. 129–156. [Google Scholar]
- Telford, S.R., 3rd; Dawson, J.E.; Katavolos, P.; Warner, C.K.; Kolbert, C.P.; Persing, D.H. Perpetuation of the agent of human granulocytic ehrlichiosis in a deer tick-rodent cycle. Proc. Natl. Acad. Sci. USA 1996, 93, 6209–6214. [Google Scholar] [CrossRef]
- Spielman, A. Human babesiosis on nantucket island: Transmission by nymphal ixodes ticks. Am. J. Trop. Med. Hyg. 1976, 25, 784–787. [Google Scholar] [CrossRef] [PubMed]
- Johnson, D.K.; Schiffman, E.K.; Davis, J.P.; Neitzel, D.F.; Sloan, L.M.; Nicholson, W.L.; Fritsche, T.R.; Steward, C.R.; Ray, J.A.; Miller, T.K.; et al. Human infection with ehrlichia muris-like pathogen, United States, 2007–2013. Emerg. Infect. Dis. 2015, 21, 1794–1799. [Google Scholar] [CrossRef] [PubMed]
- Pritt, B.S.; Sloan, L.M.; Johnson, D.K.; Munderloh, U.G.; Paskewitz, S.M.; McElroy, K.M.; McFadden, J.D.; Binnicker, M.J.; Neitzel, D.F.; Liu, G.; et al. Emergence of a new pathogenic ehrlichia species, wisconsin and minnesota, 2009. N. Engl. J. Med. 2011, 365, 422–429. [Google Scholar] [CrossRef] [PubMed]
- Lane, R.S.; Piesman, J.; Burgdorfer, W. Lyme borreliosis: Relation of its causative agent to its vectors and hosts in North American and Europe. Annu. Rev. Entomol. 1991, 36, 587–609. [Google Scholar] [CrossRef] [PubMed]
- Hopla, C.E. Experimental studies on tick transmission of tularemia organisms. Am. J. Hyg. 1953, 58, 101–118. [Google Scholar] [PubMed]
- Hopla, C.E. The multiplication of tularemia organisms in the lone star tick. Am. J. Hyg. 1955, 61, 371–380. [Google Scholar] [PubMed]
- Anderson, B.E.; Greene, C.E.; Jones, D.C.; Dawson, J.E. Ehrlichia ewingii sp. Nov., the etiologic agent of canine granulocytic ehrlichiosis. Int. J. Syst. Bacteriol. 1992, 42, 299–302. [Google Scholar] [CrossRef] [PubMed]
- Anderson, B.E.; Sims, K.G.; Olson, J.G.; Childs, J.E.; Piesman, J.F.; Happ, C.M.; Maupin, G.O.; Johnson, B.J. Amblyomma americanum: A potential vector of human ehrlichiosis. Am. J. Trop. Med. Hyg. 1993, 49, 239–244. [Google Scholar] [CrossRef] [PubMed]
- Ledin, K.E.; Zeidner, N.S.; Ribeiro, J.M.; Biggerstaff, B.J.; Dolan, M.C.; Dietrich, G.; Vredevoe, L.; Piesman, J. Borreliacidal activity of saliva of the tick amblyomma americanum. Med. Vet. Entomol. 2005, 19, 90–95. [Google Scholar] [CrossRef]
- Masters, E.J.; Grigery, C.N.; Masters, R.W. Stari, or masters disease: Lone star tick-vectored lyme-like illness. Infect. Dis. Clin. N. Am. 2008, 22, 361–376. [Google Scholar] [CrossRef]
- Goddard, J.; Varela-Stokes, A.S. Role of the lone star tick, amblyomma americanum (L.), in human and animal diseases. Vet. Parasitol. 2009, 160, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Childs, J.E.; Paddock, C.D. The ascendancy of amblyomma americanum as a vector of pathogens affecting humans in the United States. Annu. Rev. Entomol. 2003, 48, 307–337. [Google Scholar] [CrossRef] [PubMed]
- Felz, M.W.; Durden, L.A.; Oliver, J.H., Jr. Ticks parasitizing humans in Georgia and South Carolina. J. Parasitol. 1996, 82, 505–508. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, P.M.; Brunet, L.R.; Spielman, A.; Telford, S.R., 3rd. Risk of lyme disease: Perceptions of residents of a lone star tick-infested community. Bull. World Health Organ. 2001, 79, 916–925. [Google Scholar] [PubMed]
- Philip, C.B.; Jellison, W.L. The american dog tick, dermacentor variabilis, as a host of bacterium tularense. Public Health Rep. 1934, 49, 7. [Google Scholar] [CrossRef]
- Azad, A.F.; Beard, C.B. Rickettsial pathogens and their arthropod vectors. Emerg. Infect. Dis. 1998, 4, 179–186. [Google Scholar] [CrossRef]
- Thomaes, A.; Kervyn, T.; Maes, D. Applying species distribution modelling for the conservation of the threatened saproxylic stag beetle (lucanus cervus). Biol. Conserv. 2008, 141, 1400–1410. [Google Scholar] [CrossRef]
- Stohlgren, T.J.; Ma, P.; Kumar, S.; Rocca, M.; Morisette, J.T.; Jarnevich, C.S.; Benson, N. Ensemble habitat mapping of invasive plant species. Risk Anal. 2010, 30, 224–235. [Google Scholar] [CrossRef] [PubMed]
- Miller, J. Species distribution modeling. Geogr. Compass 2010, 4, 490–509. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S. Applied Logistic Regression; John Wiley & Sons: New York, NY, USA, 1989. [Google Scholar]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–141. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef] [PubMed]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum entropy modeling of species geographic distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar] [CrossRef]
- Mount, J. The Equivalence of Logistic Regression and Maximum Entropy Models. Available online: http://www.win-vector.com/dfiles/LogisticRegressionMaxEnt.pdf (accessed on 18 May 2019).
- Kessler, W.H.; Blackburn, J.K.; Sayler, K.A.; Glass, G.E. Estimating the geographic distribution of host-seeking adult amblyomma americanum (acari: Ixodidae) in Florida. J. Med. Entomol. 2018, 56, 55–64. [Google Scholar] [CrossRef] [PubMed]
- Glass, G.E.; Ganser, C.; Kessler, W.H. Standardized ixodid tick surveys in mainland Florida. Insects 2019. Manuscript in Preparation. [Google Scholar]
- Spruce, J.P.; Gasser, G.E.; Hargrove, W.W. Modis Ndvi Data, Smoothed and Gap-Filled, for the Conterminous Us: 2000–2015; ORNL Distributed Active Archive Center: Oak Ridge, TN, USA, 2016. [Google Scholar]
- NASA/METI/AIST/Japan Spacesystems, and U.S./Japan ASTER Science Team; Aster Global Digital Elevation Model; NASA EOSDIS Land Processes DAAC. 2009. Available online: https://lpdaac.usgs.gov/products/astgtmv002/#citation (accessed on 18 May 2019).
- U.S. Soil Survey Staff. General Soil Map (statsgo2); Natural Resources Conservation Service, Ed.; United States Department of Agriculture: Washington, DC, USA, 2008. [Google Scholar]
- Geological Survey. National Hydrography Dataset; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2004. [Google Scholar]
- Kawula, R.; Redner, J. Florida Cooperative Land Cover v3.2, 3.2 ed.; Florida Fish and Wildlife Conservation, Ed.; Florida Fish and Wildlife: Tallahassee, FL, USA, 2016. [Google Scholar]
- Thornton, P.E.; Thornton, M.M.; Mayer, B.W.; Wei, Y.; Devarakonda, R.; Vose, R.S.; Cook, R.B. Daymet: Daily Surface Weather Data on a 1-km Grid for North America, 3rd ed.; ORNL DAAC: Oak Ridge, TN, USA, 2018. [Google Scholar]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Phillips, S.J.; Leathwick, J.R.; Elith, J. Package Dismo-Species Distribution Modeling (v 1.0-12). Circles 2017, 9, 1–68. [Google Scholar]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Guillera-Arroita, G.; Lahoz-Monfort, J.J.; Elith, J.; O’Hara, R.B. Maxent is not a presence-absence method: A comment on thibaud et al. Methods Ecol. Evol. 2014, 5, 1192–1197. [Google Scholar] [CrossRef]
- Phillips, S.J.; Dudik, M.; Elith, J.; Graham, C.H.; Lehmann, A.; Leathwick, J.; Ferrier, S. Sample selection bias and presence-only distribution models: Implications for background and pseudo-absence data. Ecol. Appl. 2009, 19, 181–197. [Google Scholar] [CrossRef]
- Buckland, S.T.; Burnham, K.P.; Augustin, N.H. Model selection: An integral part of inference. Biometrics 1997, 53, 603–618. [Google Scholar] [CrossRef]
- Calcagno, V.; de Mazancourt, C. Glmulti: An r package for easy automated model selection with (generalized) linear models. J. Stat. Softw. 2010, 34, 1–29. [Google Scholar] [CrossRef]
- Milborrow, S.; Hastie, T.; Tibshirani, R. Derived from mda:mars by T. Hastie and R. Tibshirani. Earth: Multivariate adaptive regression splines. R Package. 2011. Available online: http://www.milbo.org/doc/earth-notes.pdf (accessed on 18 May 2019).
- Jueterbock, A.; Smolina, I.; Coyer, J.A.; Hoarau, G. The fate of the arctic seaweed fucus distichus under climate change: An ecological niche modeling approach. Ecol. Evol 2016, 6, 1712–1724. [Google Scholar] [CrossRef] [PubMed]
- Ginsberg, H.S.; Ewing, C.P. Comparison of flagging, walking, trapping, and collecting from hosts as sampling methods for northern deer ticks, ixodes dammini, and lone-star ticks, amblyomma americanum (acari:Ixodidae). Exp. Appl. Acarol. 1989, 7, 313–322. [Google Scholar] [CrossRef] [PubMed]
- Allan, S.A.; Simmons, L.A.; Burridge, M.J. Ixodid ticks on white-tailed deer and feral swine in Florida. J. Vector Ecol. 2001, 26, 93–102. [Google Scholar] [PubMed]
- Burroughs, J.E.; Thomasson, J.A.; Marsella, R.; Greiner, E.C.; Allan, S.A. Ticks associated with domestic dogs and cats in Florida, USA. Exp. Appl. Acarol. 2016, 69, 87–95. [Google Scholar] [CrossRef] [PubMed]
- Durden, L.A.; Hu, R.; Oliver, J.H., Jr.; Cilek, J.E. Rodent ectoparasites from two locations in northwestern Florida. J. Vector Ecol. 2000, 25, 222–228. [Google Scholar] [PubMed]
- Durden, L.A.; Klompen, J.S.; Keirans, J.E. Parasitic arthropods of sympatric opossums, cotton rats, and cotton mice from merritt island, Florida. J. Parasitol. 1993, 79, 283–286. [Google Scholar] [CrossRef]
- Diuk-Wasser, M.A.; Gatewood, A.G.; Cortinas, M.R.; Yaremych-Hamer, S.; Tsao, J.; Kitron, U.; Hickling, G.; Brownstein, J.S.; Walker, E.; Piesman, J.; et al. Spatiotemporal patterns of host-seeking ixodes scapularis nymphs (acari: Ixodidae) in the United States. J. Med. Entomol. 2006, 43, 166–176. [Google Scholar] [CrossRef]
- Springer, Y.P.; Eisen, L.; Beati, L.; James, A.M.; Eisen, R.J. Spatial distribution of counties in the continental United States with records of occurrence ofamblyomma americanum(ixodida: Ixodidae). J. Med. Entomol. 2014, 51, 342–351. [Google Scholar] [CrossRef]
- Diuk-Wasser, M.A.; Hoen, A.G.; Cislo, P.; Brinkerhoff, R.; Hamer, S.A.; Rowland, M.; Cortinas, R.; Vourc’h, G.; Melton, F.; Hickling, G.J.; et al. Human risk of infection with borrelia burgdorferi, the lyme disease agent, in eastern United States. Am. J. Trop. Med. Hyg. 2012, 86, 320–327. [Google Scholar] [CrossRef] [PubMed]
- Diuk-Wasser, M.A.; Vourc’h, G.; Cislo, P.; Hoen, A.G.; Melton, F.; Hamer, S.A.; Rowland, M.; Cortinas, R.; Hickling, G.J.; Tsao, J.I.; et al. Field and climate-based model for predicting the density of host-seeking nymphalixodes scapularis, an important vector of tick-borne disease agents in the eastern United States. Glob. Ecol. Biogeogr. 2010, 19, 501–514. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).