Significance of Slippage and Electric Field in Mucociliary Transport of Biomagnetic Fluid
Abstract
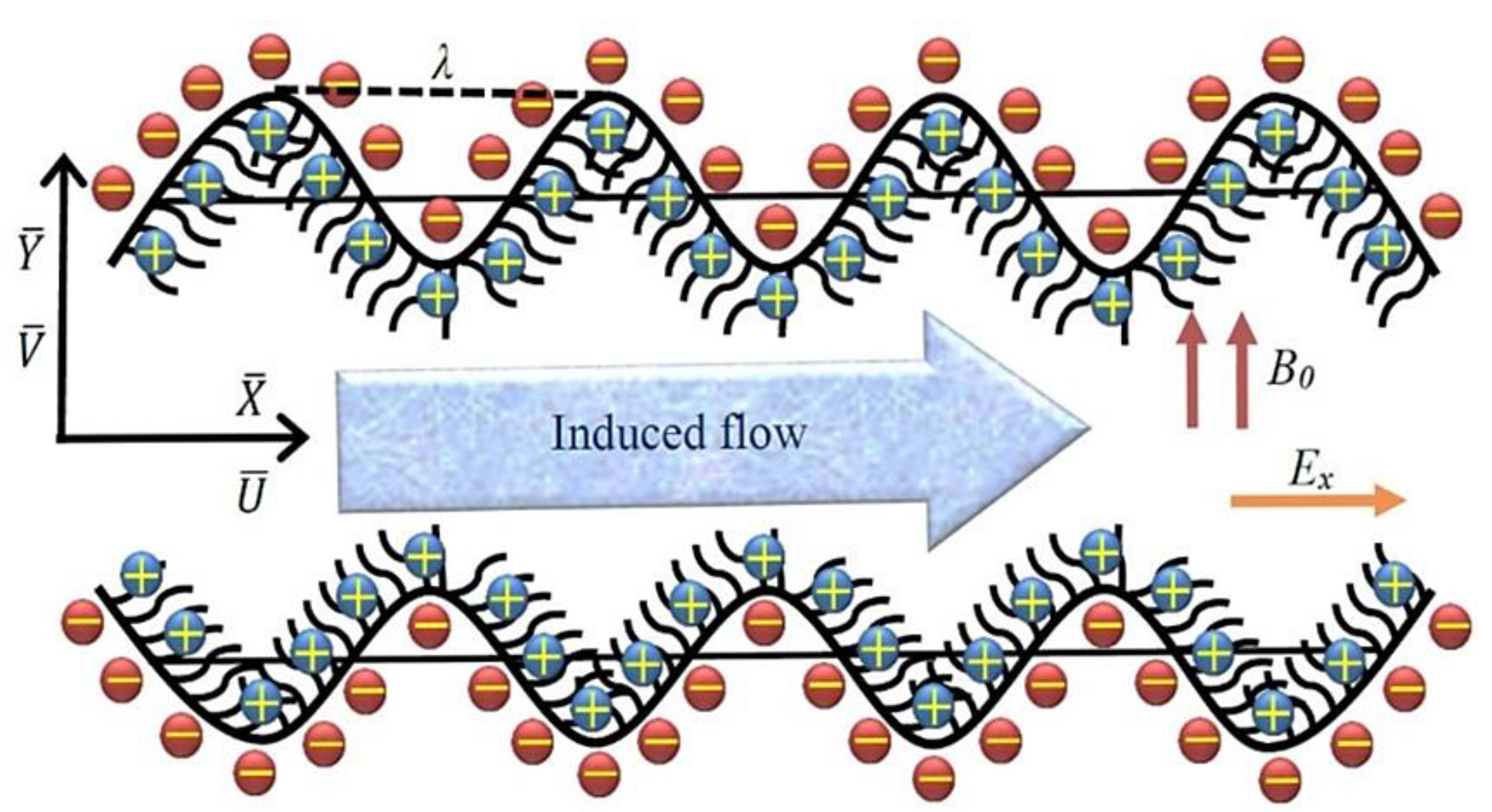
1. Introduction
2. Mathematical Formulation
3. Solution
3.1. Zeroth-Order System
3.2. First-Order System
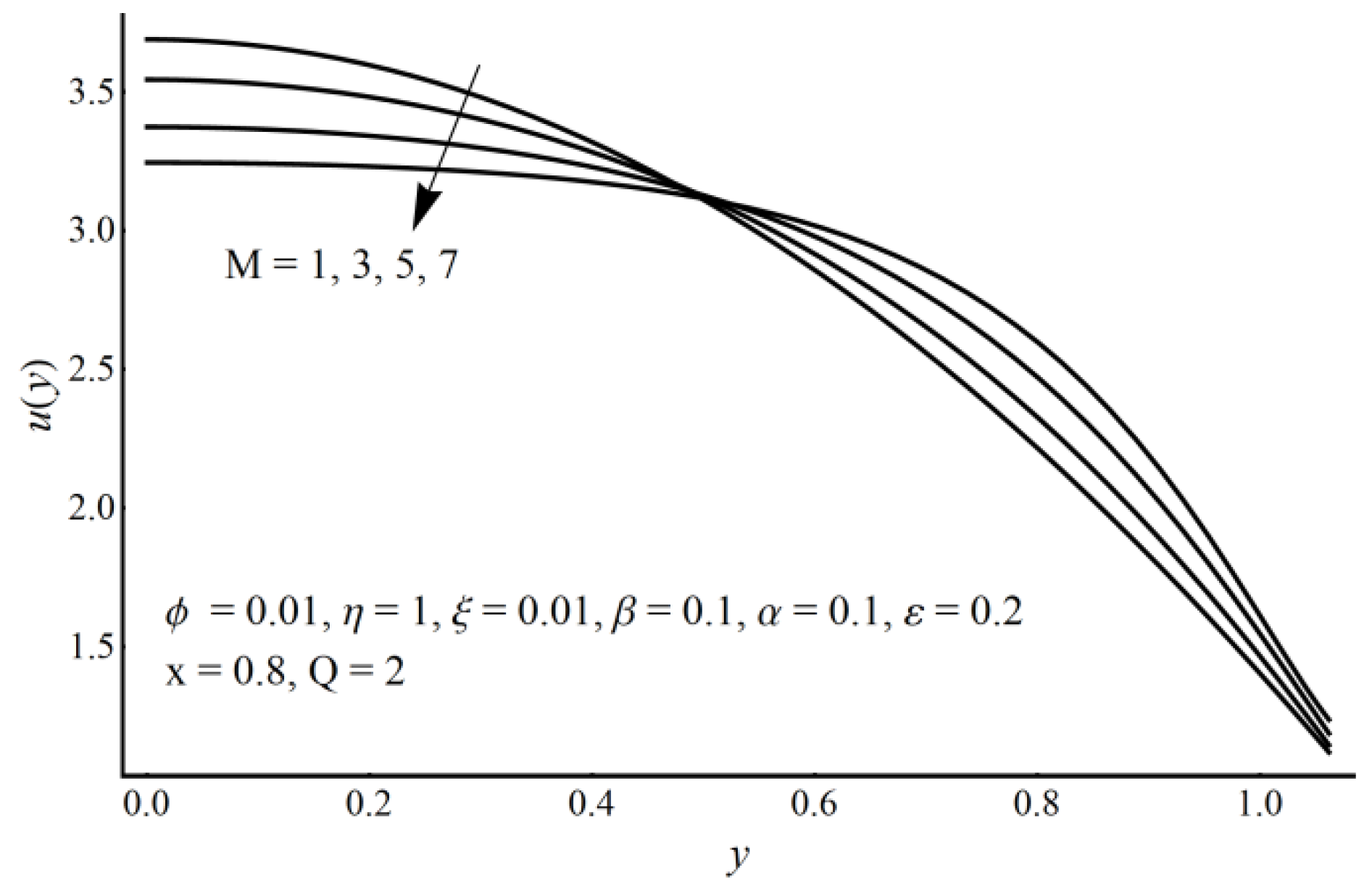
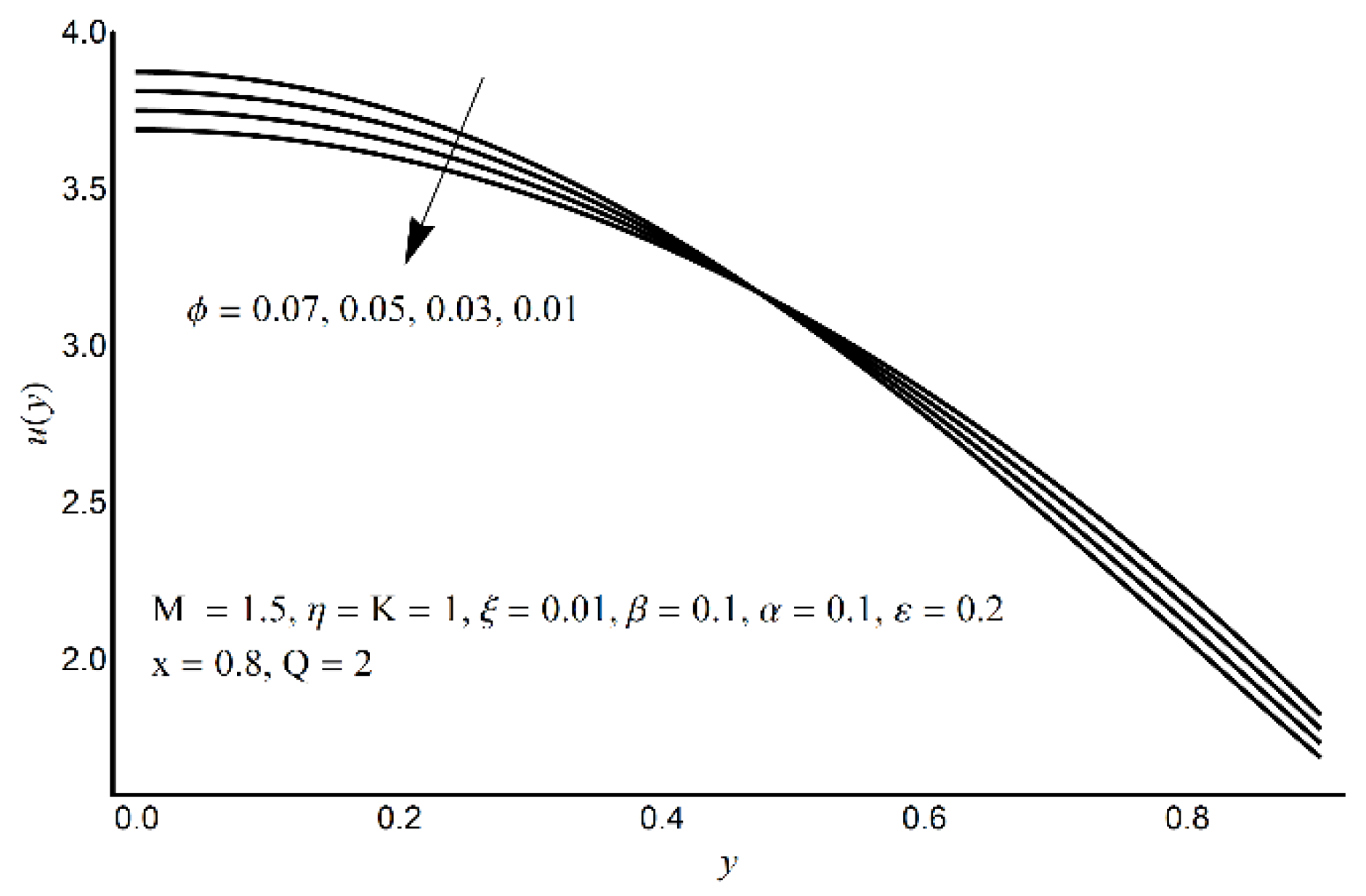
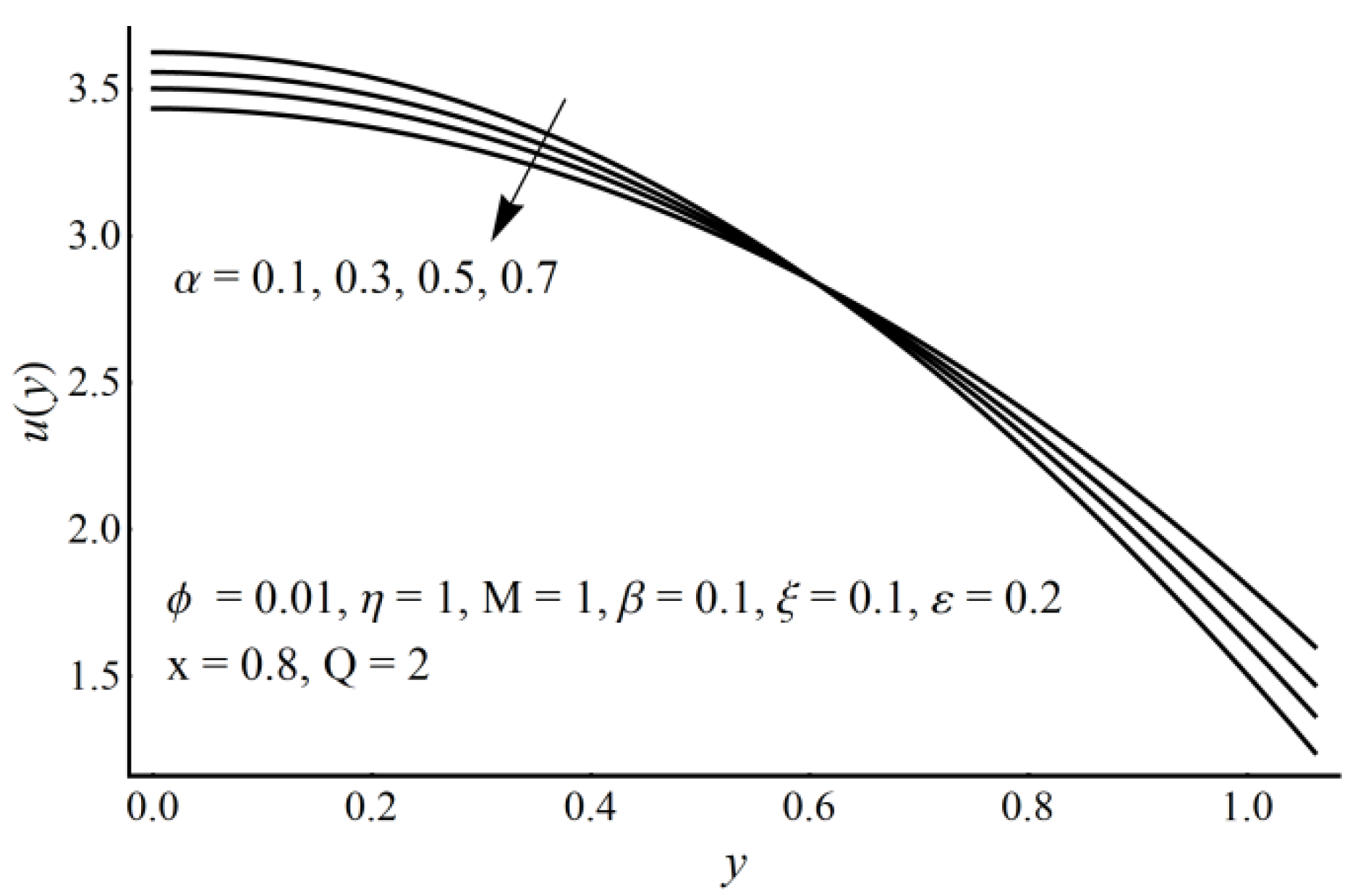
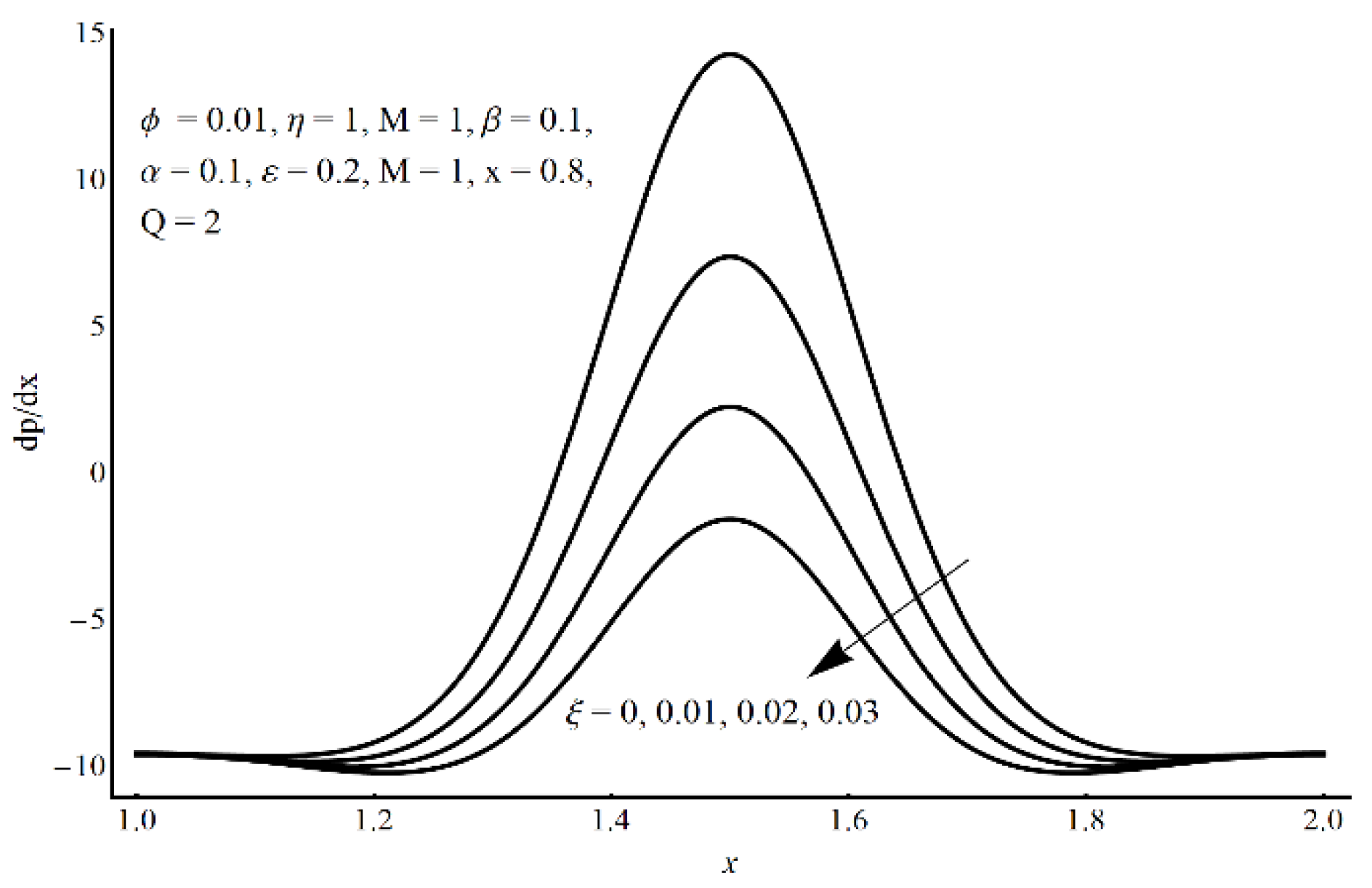
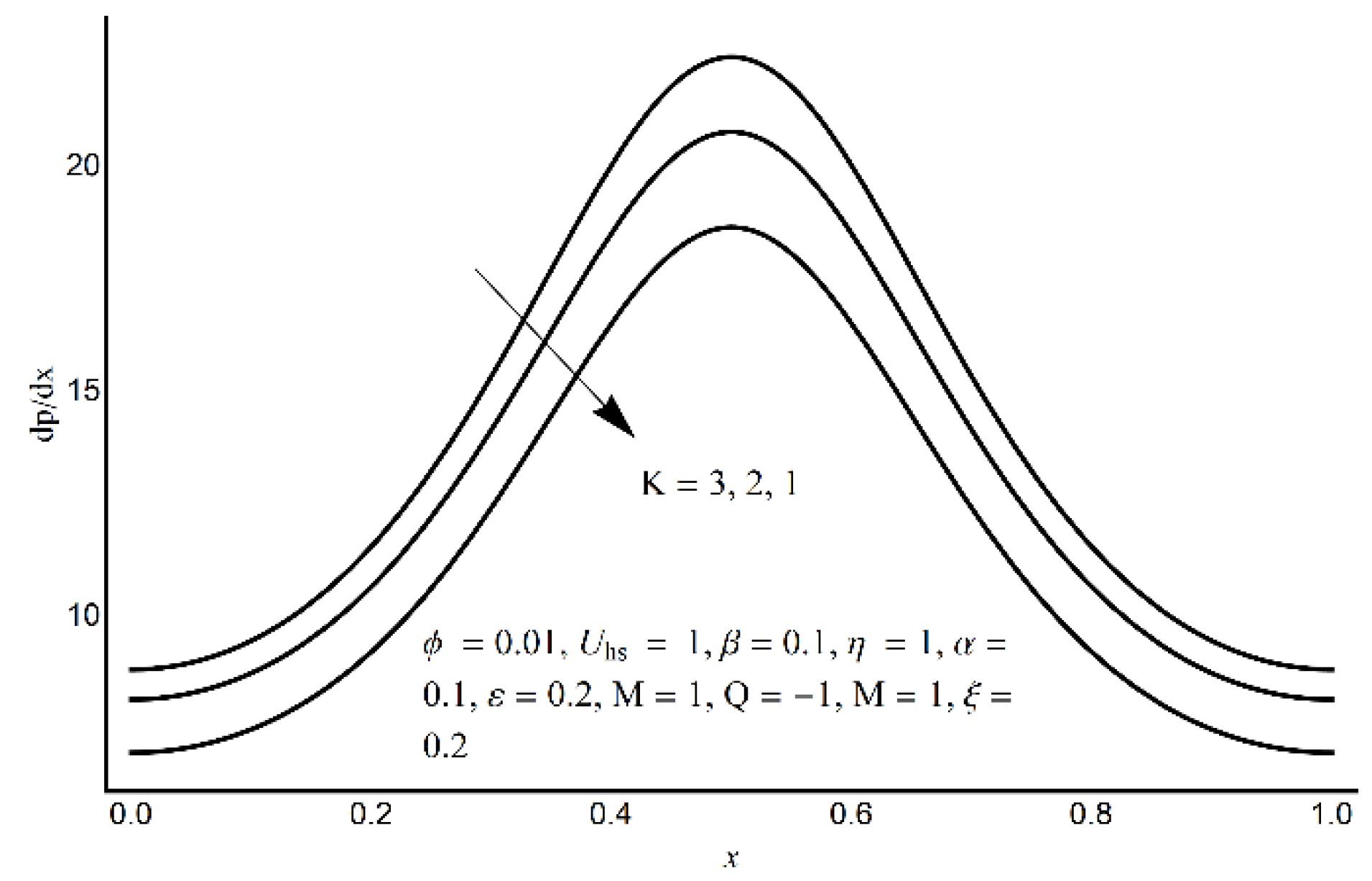
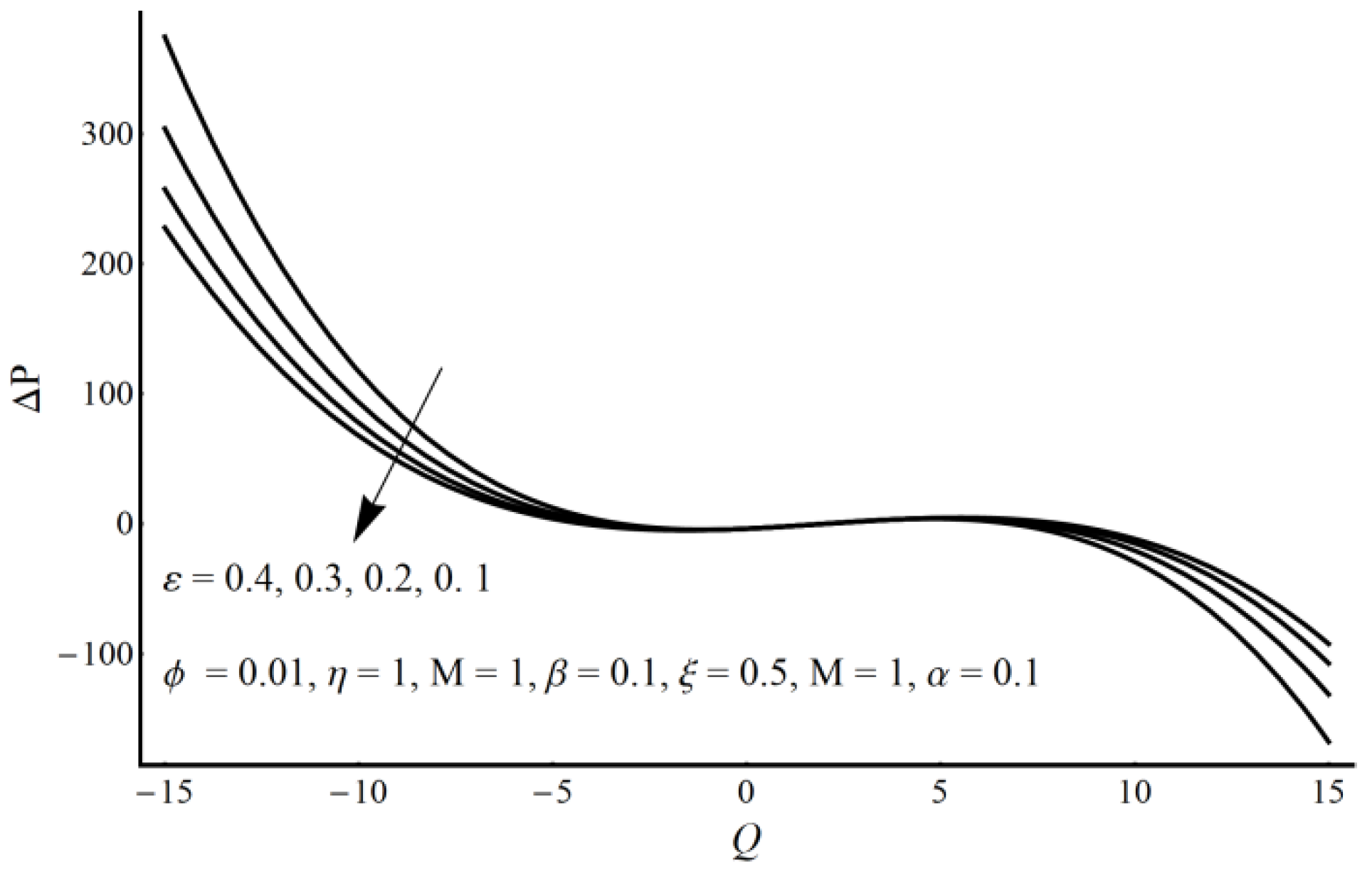
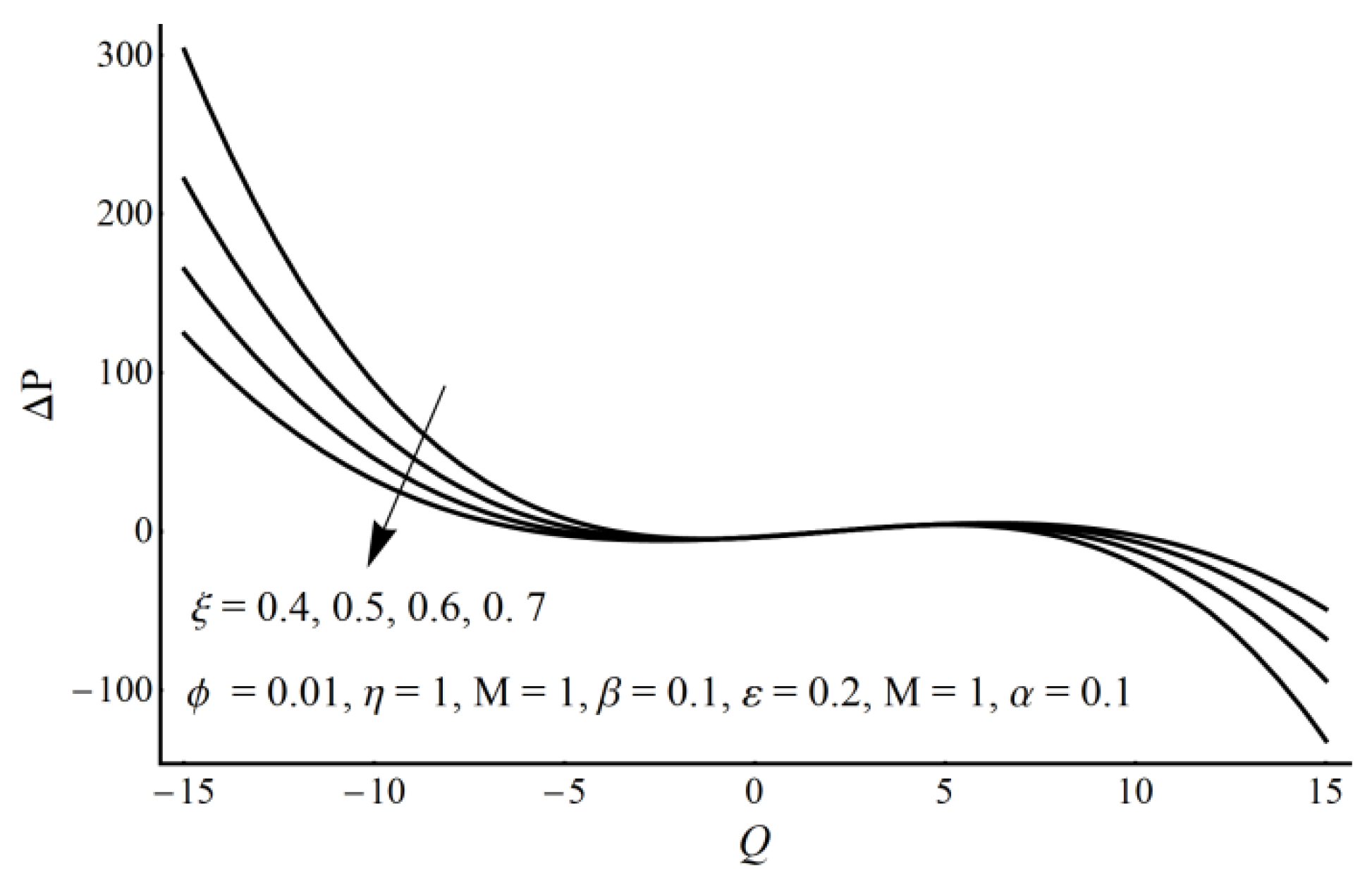
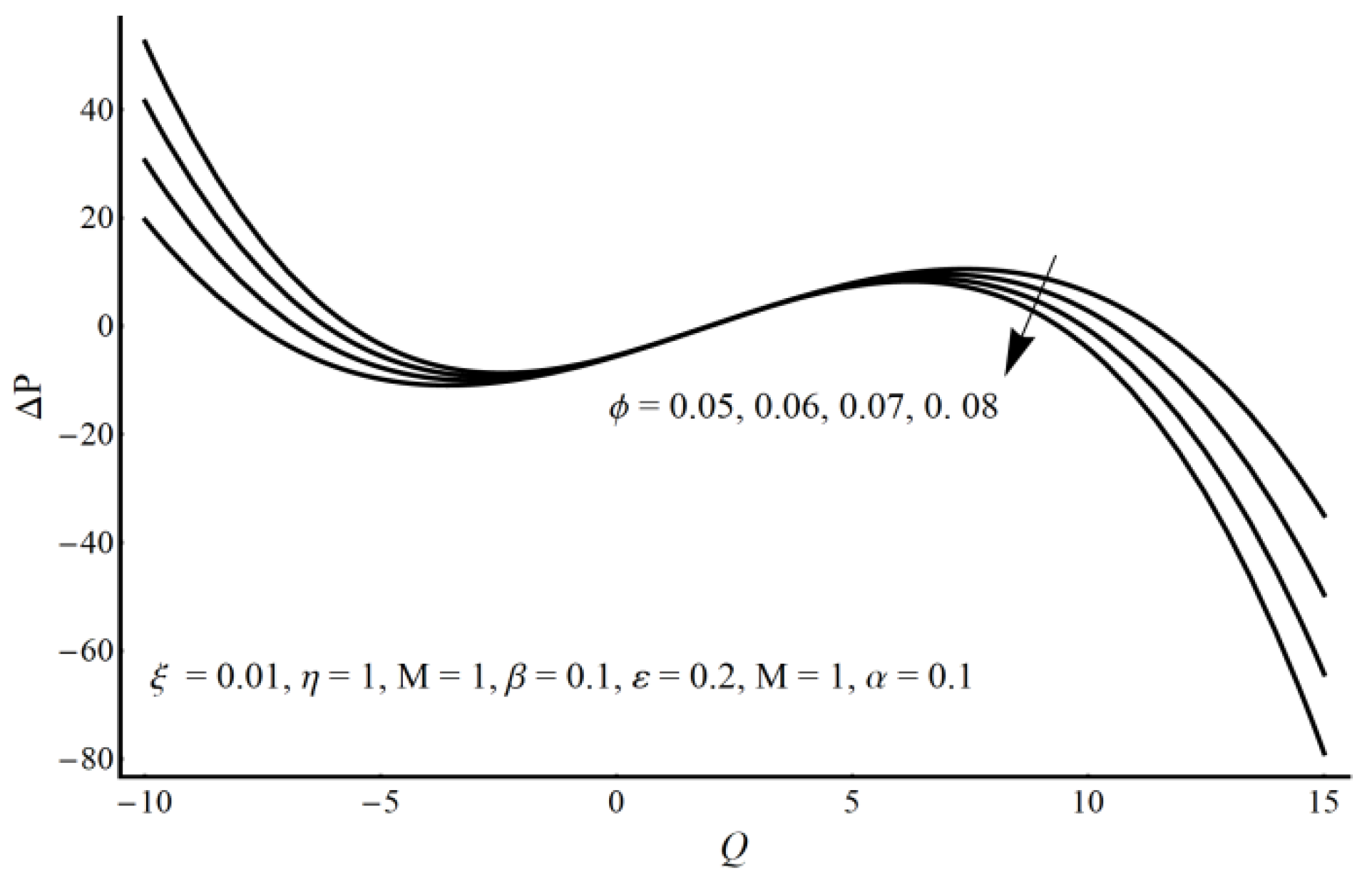
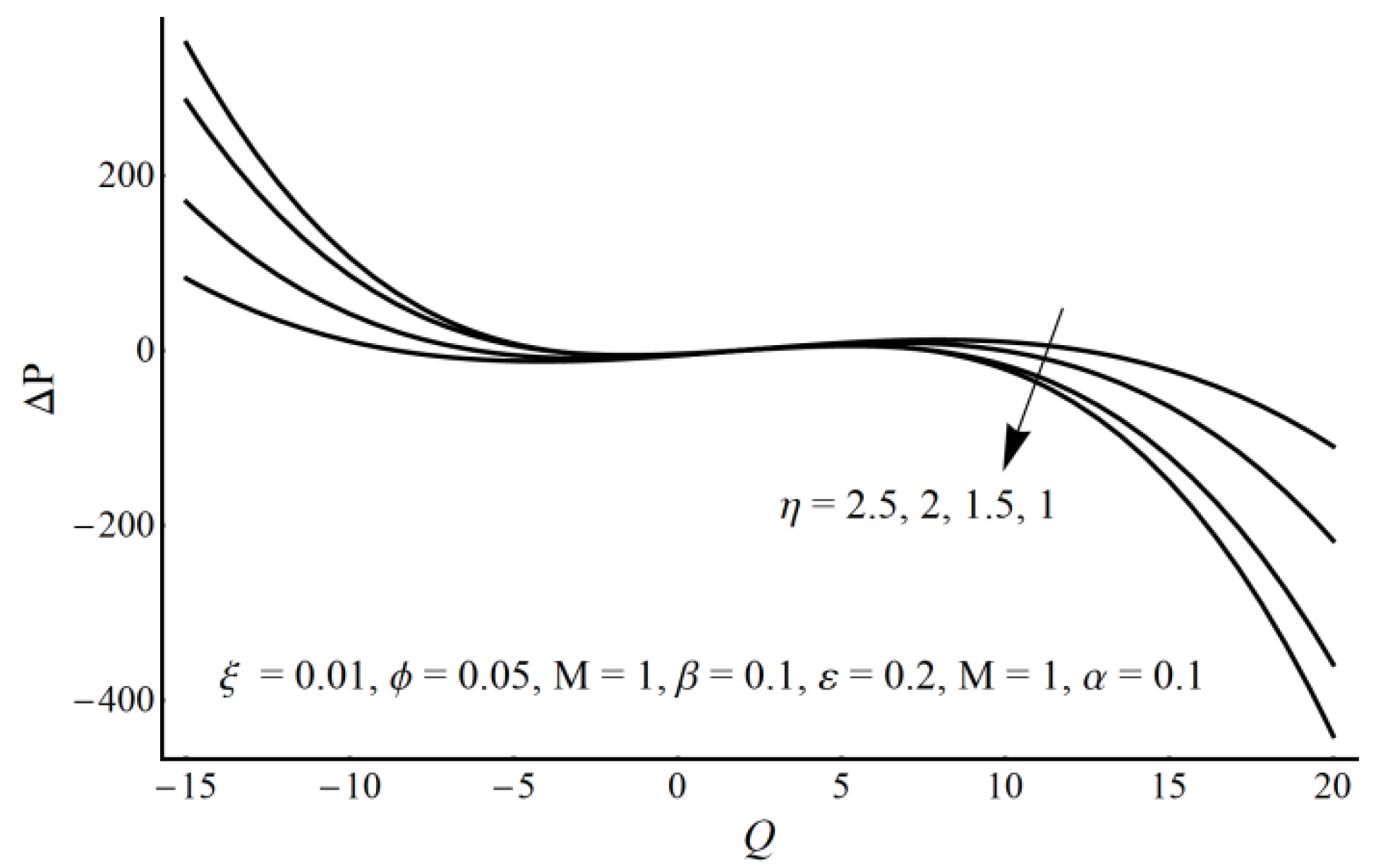
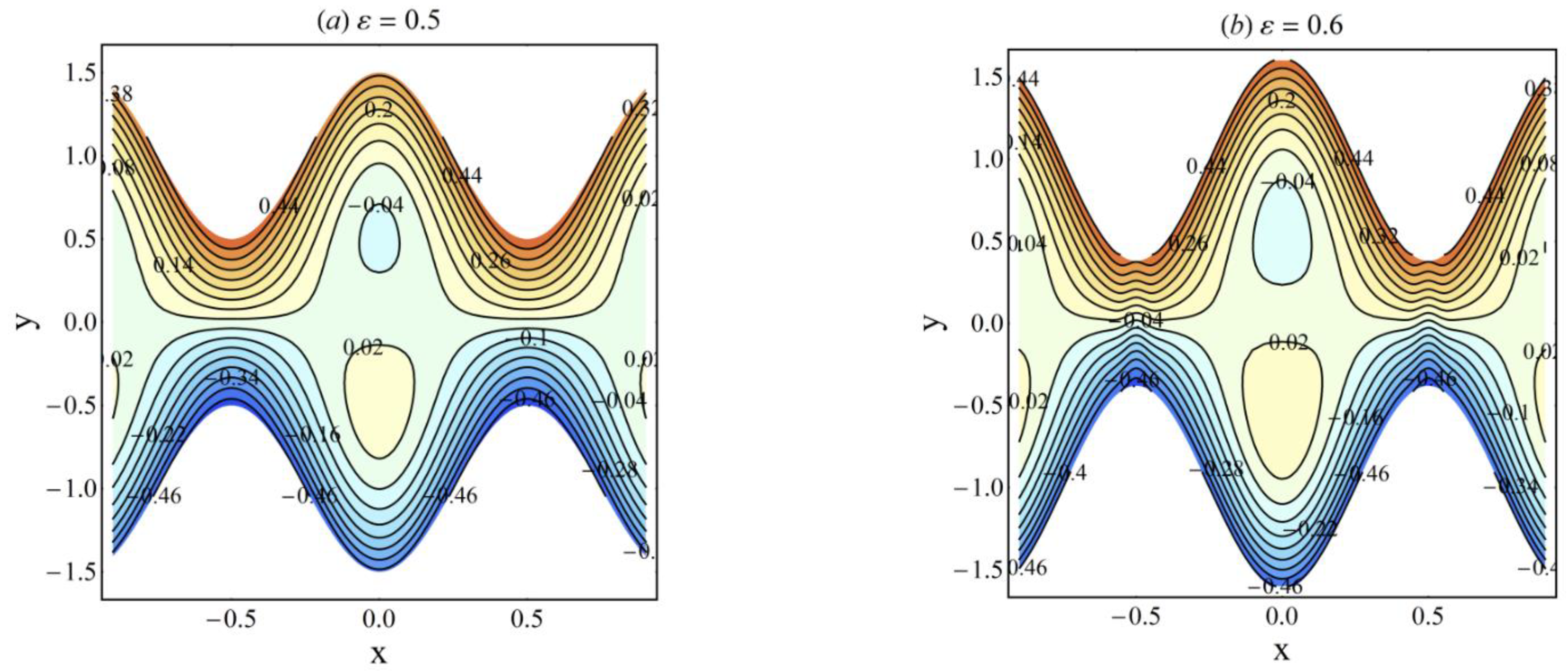
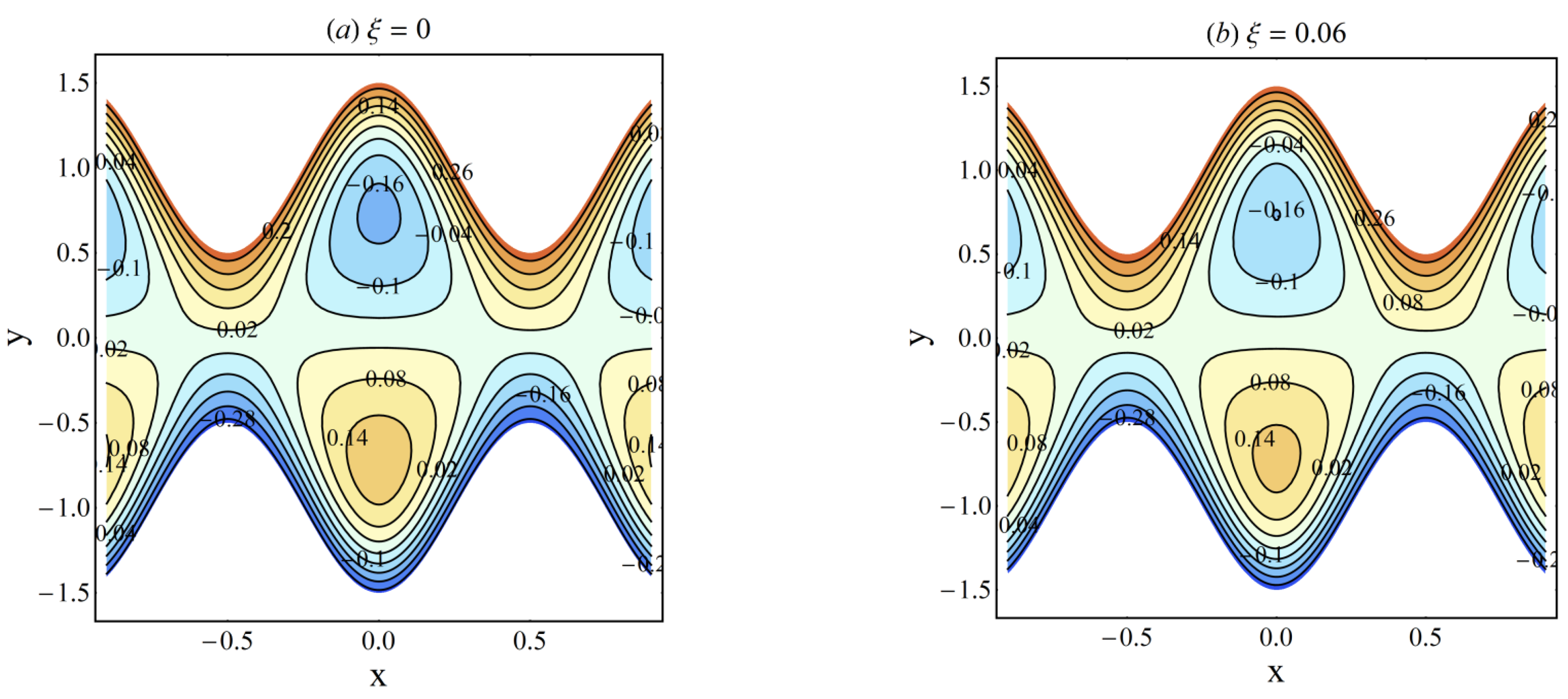
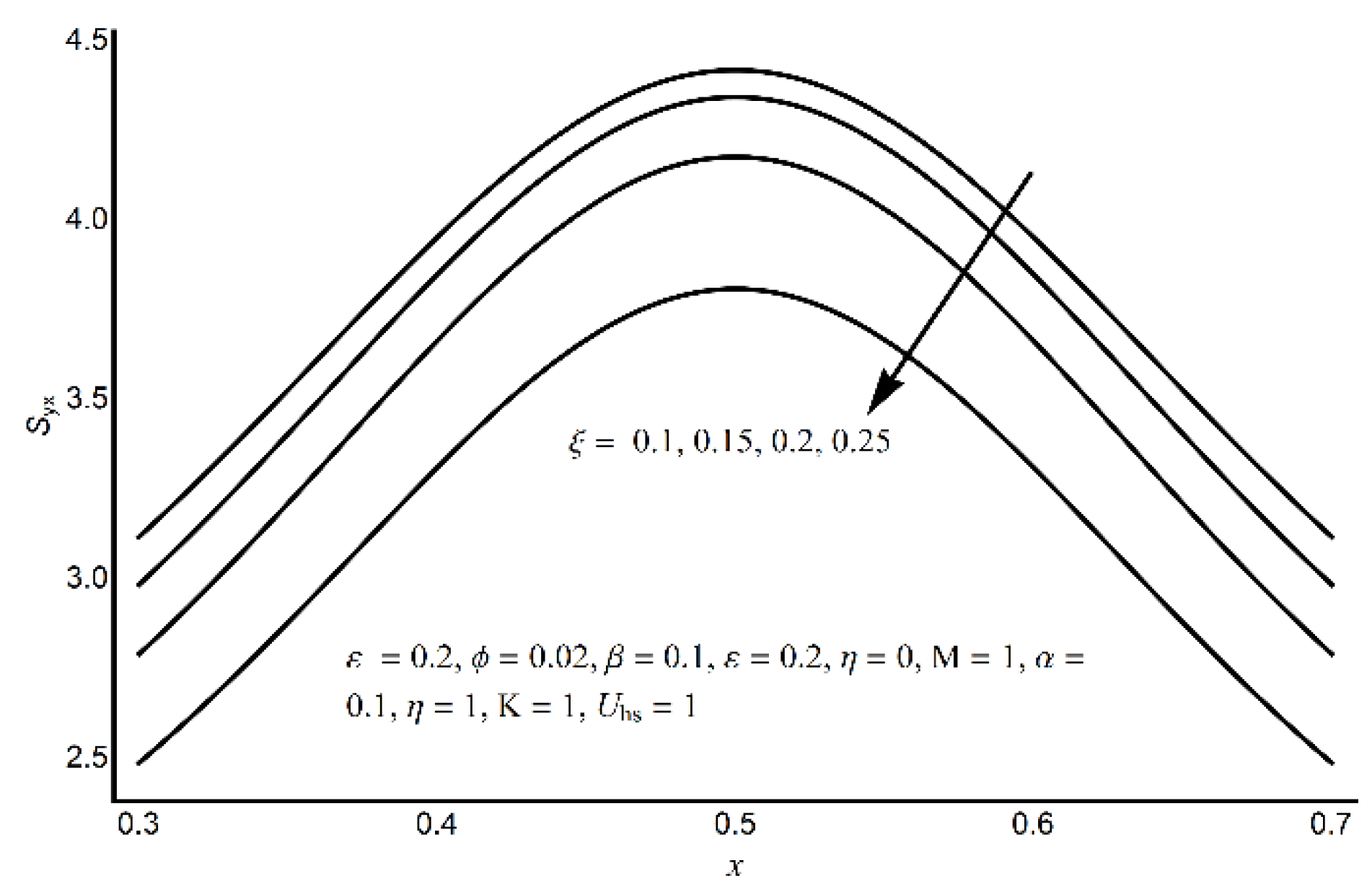
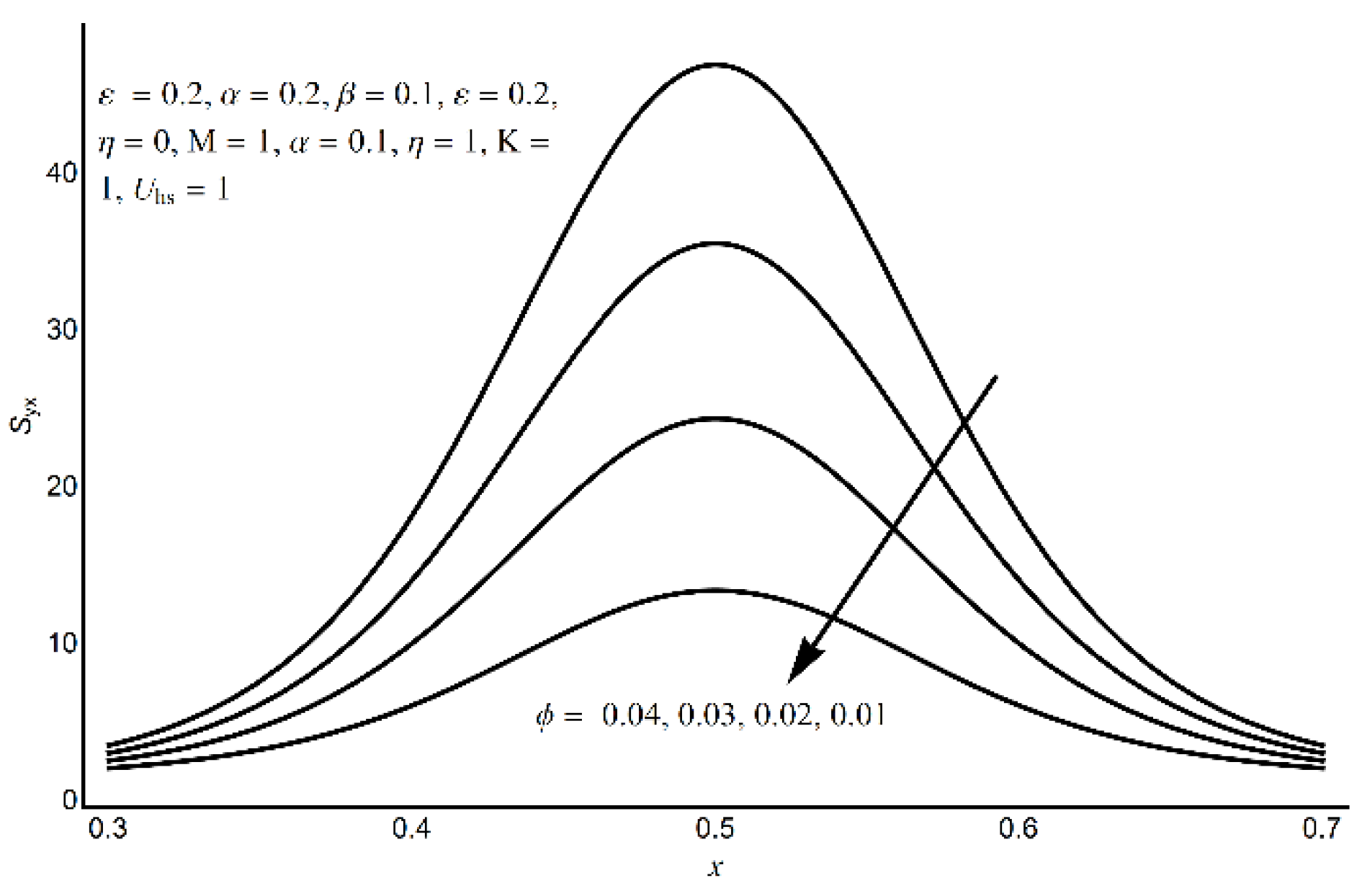
4. Results and Discussion
5. Conclusions
- For large values of Hartmann number, cilia length, electro-osmotic and eccentricity parameter, axial velocity decreases at the channel center and increases near the ciliated wall region.
- The Helmholtz–Smoluchowski velocity supports the fluid augmentation if applied in the direction of flow stream.
- In the core region, a considerable elevation in the pressure gradient is obtained for the small values of the slippage parameter and the large values of cilia length and eccentricity parameters.
- A more elevated pressure gradient is seen (for large values of electro-osmotic parameter) in the contracted channel zone than in the wider part of the channel.
- A pressure rise per wavelength is an increasing function of cilia length and perturbation parameter in the pumping region and shows the opposite behavior in the augmented pumping region.
- The pressure rise is an increasing function of the velocity slip parameter and Prandtl fluid parameter (η) in the augmented pumping region and a decreasing function in the pumping region.
- Shear stress at the ciliated wall surface increases when large values of the cilia length and small velocity slip parameters are considered.
- Shear stress becomes stronger for higher values of the eccentricity of cilia.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Knowles, M.R.; Boucher, R.C. Mucus clearance as a primary innate defense mechanism for mammalian airways. J. Clin. Investig. 2002, 109, 571–577. [Google Scholar] [CrossRef]
- Bustamante-Marin, X.M.; Ostrowski, L.E. Cilia and mucociliary clearance. Cold Spring Harb. Perspect. Biol. 2017, 4, a028241. [Google Scholar] [CrossRef] [PubMed]
- Pablo, J.L.; DeCaen, P.G.; Clapham, D.E. Progress in ciliary ion channel physiology. J. Gen. Physiol. 2016, 1, 37–41. [Google Scholar] [CrossRef]
- Eddy, C.A.; Pauerstein, C.J. Anatomy and physiology of the fallopian tube. Clin. Obstet. Gynecol. 1980, 4, 1177–1193. [Google Scholar] [CrossRef] [PubMed]
- Ghazal, S.; Makarov, J.K.; de Jonge, C.J. Egg transport and fertilization. Glob. Libr. Women’s Med. 2014, 2014. [Google Scholar] [CrossRef]
- Lehti, M.S.; Sironen, A. Formation and function of sperm tail structures in association with sperm motility defects. Biol. Reprod. 2017, 97, 522–536. [Google Scholar] [CrossRef]
- Wheway, G.; Nazlamova, L.; Hancock, J.T. Signaling through the Primary Cilium. Front. Cell Dev. Biol. 2018, 6, 8. [Google Scholar] [CrossRef] [PubMed]
- Brennen, C. Oscillating-boundary layer theory for ciliary propulsion. J. Fluid Mech. 1974, 65, 799–824. [Google Scholar] [CrossRef]
- Qiu, T.; Lee, T.; Mark, A.G.; Morozov, K.I.; Münster, R.; Mierka, O.; Turek, S.; Leshansky, A.M.; Fischer, P. Swimming by reciprocal motion at low Reynolds number. Nat. Commun. 2014, 5, 1–8. [Google Scholar] [CrossRef]
- Eytan, O.; Elad, D. Analysis of intra-uterine fluid motion induced by uterine contractions. Bull. Math. Biol. 1999, 61, 221–238. [Google Scholar] [CrossRef] [PubMed]
- Farooq, A.A.; Tripathi, D.; Elnaqeeb, T. Tripathi and Elnaqeeb, On the propulsion of micropolar fluid inside a channel due to ciliary induced metachronal wave. Appl. Math. Comput. 2019, 347, 225–235. [Google Scholar]
- Farooq, A.A.; Siddiqui, A.M. Mathematical model for the ciliary-induced transport of seminal liquids through the ductuli efferentes. Int. J. Biomath. 2017, 10, 1750031. [Google Scholar] [CrossRef]
- Ponalagusamy, R. Mathematical analysis of flow of non-Newtonian fluid due to metachronal beating of cilia in a tube and its physiological applications. Appl. Math. Comput. 2018, 337, 545–561. [Google Scholar] [CrossRef]
- Ezzat, M.; Djahanbakhch, O.; Arian, S.; Carr, B.R. Tubal transport of gametes and embryos: A review of physiology and pathophysiology. J. Assist. Reprod. Genet. 2014, 10, 1337–1347. [Google Scholar] [CrossRef]
- Stud, K.; Sephon, G.S.; Mishra, R.K. Pumping action on blood flow by a magnetic field. Bull. Math. Biol. 1977, 39, 385–390. [Google Scholar]
- Kothandapani, M.; Srinivas, S. Peristaltic transport of a Jeffrey fluid under the effect of magnetic field in an asymmetric channel. Int. J. Nonlinear Mech. 2008, 43, 915. [Google Scholar] [CrossRef]
- Maqbool, K.; Shaheen, S.; Mann, A.B. Exact solution of cilia induced flow of a Jeffrey fluid in an inclined tube. Springerplus 2016, 5, 1379. [Google Scholar] [CrossRef]
- Hayat, T.; Saleem, N.; Mesloub, S.; Ali, N. Magnetohydrodynamic Flow of a Carreau Fluid in a Channel with Different Wave Forms. Z. Nat. A 2011, 66, 215–222. [Google Scholar]
- Ramesh, K.; Tripathi, D.; Beg, O.A. Cilia-assisted hydromagnetic pumping of biorheological couple stress fluids. J. Propuls. Power 2019, 8, 221–233. [Google Scholar] [CrossRef]
- Sehra; Haq, S.; Shah, S.I.A.; Nisar, K.S.; Jan, S.U.; Khan, I. Convection heat mass transfer and MHD flow over a vertical plate with chemical reaction, arbitrary shear stress and exponential heating. Sci. Rep. 2021, 11, 4265. [Google Scholar] [CrossRef]
- Saleem, N.; Munawar, S. A mathematical analysis of MHD blood flow of Erying-Powell fluid through a constricted artery. Int. J. Biomath. 2016, 9, 1650017. [Google Scholar] [CrossRef]
- Akram, S.; Afzal, F.; Imran, M. Influence of metachronal wave on hyperbolic tangent fluid model with inclined magnetic field. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950139. [Google Scholar] [CrossRef]
- Burgreen, D.; Nakache, F.R. Electrokinetic flow in ultrafine capillary slits. J. Phys. Chem. 1964, 68, 1084–1091. [Google Scholar] [CrossRef]
- Yang, C.; Li, D. Electrokinetic Effects on Pressure-Driven Liquid Flows in Rectangular Microchannels. J. Colloid Interface Sci. 1997, 194, 95–107. [Google Scholar] [CrossRef] [PubMed]
- Chaube, M.K.; Yadav, A.; Tripathi, D. Electroosmotic flow of biorheological micropolar fluids through microfluidic channels. Korea-Aust. Rheol. J. 2018, 30, 89–98. [Google Scholar] [CrossRef]
- Akram, S.; Zafar, M.; Nadeem, S. Peristaltic transport of a Jeffrey fluid with double-diffusive convection in nanofluids in the presence of inclined magnetic field. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1850181. [Google Scholar] [CrossRef]
- Jayavel, P.; Jhorar, R.; Tripathi, D. Electroosmotic flow of pseudoplastic nanoliquids via peristaltic pumping. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 61. [Google Scholar] [CrossRef]
- Hang, H.U.; Pop, I.; Sun, Q. Fluid flow driven along microchannel by its upper stretching wall with electrokinetic effects. Appl. Math. Mech. Engl. Ed. 2018, 39, 395–408. [Google Scholar]
- Tripathi, D.; Yadav, A.; Bég, O.; Kumar, R. Study of microvascular non-Newtonian blood flow modulated by electroosmosis. Microvasc. Res. 2017, 117, 28–36. [Google Scholar] [CrossRef]
- Akram, J.; Akbar, N.; Maraj, E.N. A comparative study on the role of nanoparticle dispersion in electroosmosis regulated peristaltic flow of water. Alex. Eng. J. 2020, 59, 943–956. [Google Scholar] [CrossRef]
- Foster, W.M. Mucociliary Transport and Cough in Humans. Pulm. Pharmacol. Ther. 2002, 15, 277–282. [Google Scholar] [CrossRef]
- Taherali, F.; Varum, F.; Basit, A.W. A slippery slope: On the origin, role and physiology of mucus. Adv. Drug Deliv. Rev. 2018, 124, 16–33. [Google Scholar] [CrossRef]
- Baltz, J.M.; Williams, P.O.; Cone, R.A. Dense fibers protect mammalian sperm against damage. Biol. Reprod. 1990, 43, 485–491. [Google Scholar] [CrossRef]
- Tripathi, D.; Beg, O.A.; Curiel-Sosa, J.L. Homotopy semi-numerical simulation of peristaltic flow of generalised Oldroyd-B fluids with slip effects. Comput. Biomech. Biomed. Eng. 2014, 17, 433–442. [Google Scholar] [CrossRef]
- Makinde, O.D.; Reddy, M.G.; Reddy, K.V. Effects of thermal radiation on MHD peristaltic motion of walters-B fluid with heat source and slip conditions. J. Appl. Fluid Mech. 2017, 10, 1105–1112. [Google Scholar] [CrossRef]
- Hayat, T.; Saleem, N.; Hendi, A.A. Slip and Heat Transfer Effects on Peristaltic Motion of a Carreau Fluid in an Asymmetric Channel. Z. Nat. A 2010, 65, 1121–1127. [Google Scholar] [CrossRef]
- Hayat, T.; Saleem, N.; Hendi, A.A. A Mathematical Model for Studying the Slip Effect on Peristaltic Motion with Heat and Mass Transfer. Chin. Phys. Lett. 2011, 28, 034702. [Google Scholar] [CrossRef]
- Chaube, M.K.; Tripathi, D.; Beg, O.A.; Sharma, S.; Pandey, V.S. Peristaltic creeping flow of power law physiological fluids through a nonuniform channel with slip effect. Appl. Bionics Biomech. 2015, 2015, 152802. [Google Scholar] [CrossRef]
- Munawar, S.; Saleem, N. Entropy Analysis of an MHD Synthetic Cilia Assisted Transport in a Microchannel Enclosure with Velocity and Thermal Slippage Effects. Coatings 2020, 10, 414. [Google Scholar] [CrossRef]
- Ijaz, S.; Saleem, N.; Munawar, S. Slip effect on the magnetohydrodynamics channel flow in the presence of the across mass transfer phenomenon. J. Appl. Mech. Tech. Phys. 2017, 58, 54–62. [Google Scholar] [CrossRef]
- Ramesh, K. Effects of slip and convective conditions on the peristaltic flow of couple stress fluid in an asymmetric channel through porous medium. Comput. Meth. Prog. Biomed. 2016, 135, 1–14. [Google Scholar] [CrossRef]
- Saleem, N.; Munawar, S. Entropy analysis in cilia driven pumping flow of hyperbolic tangent fluid with magnetic field effects. Fluid Dyn. Res. 2020, 52, 025503. [Google Scholar] [CrossRef]
- Patel, M.; Timol, M.G. The stress strain relationship for viscousinelastic non-Newtonian fluids. Int. J. Appl. Math. Mech. 2010, 6, 79–93. [Google Scholar]
- Alsaedi, A.; Batool, N.; Yasmin, H.; Hayat, T. Convective Heat Transfer Analysis on Prandtl Fluid Model with Peristalsis. Appl. Bionics Biomech. 2013, 10, 197–208. [Google Scholar] [CrossRef]

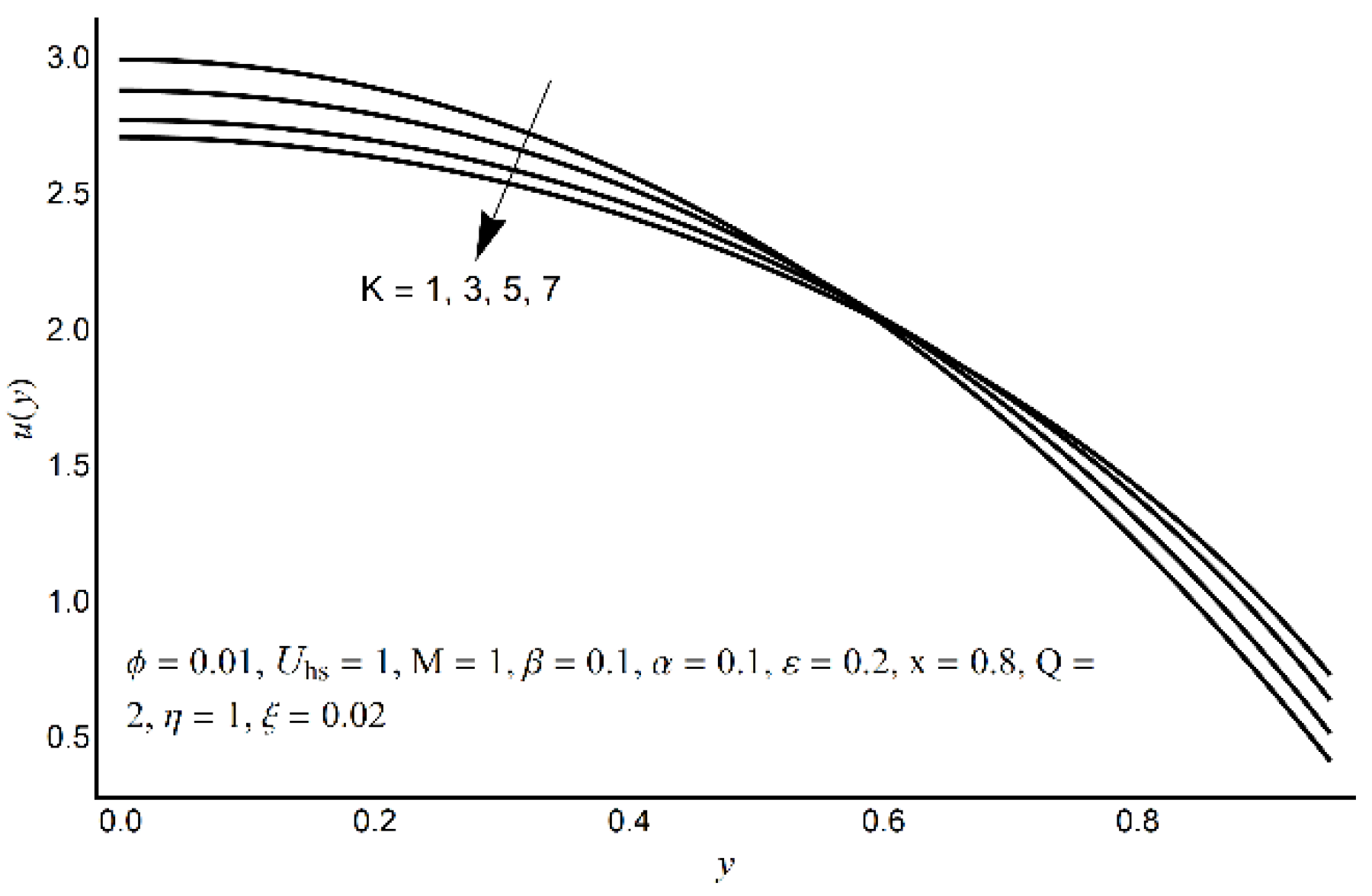
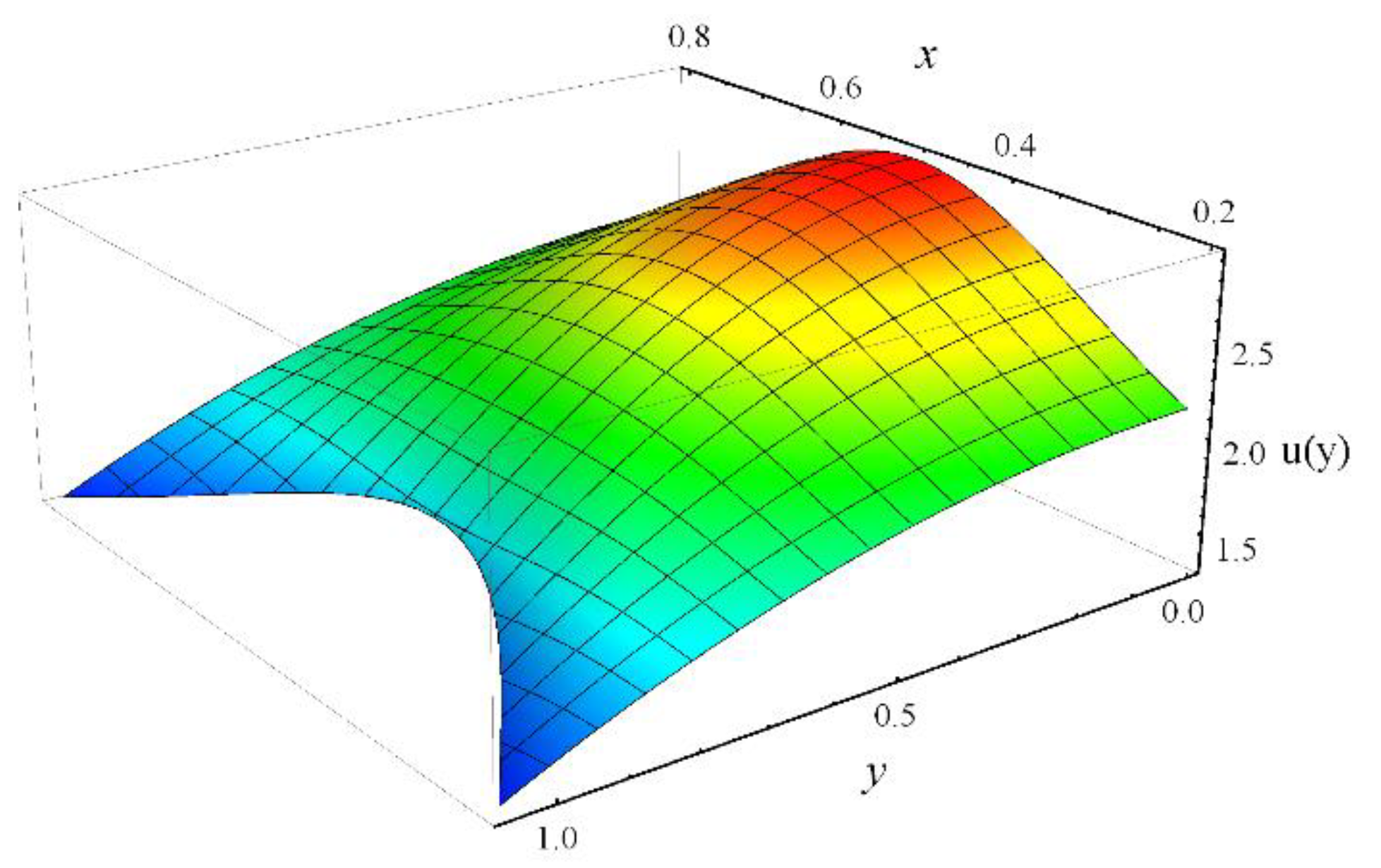
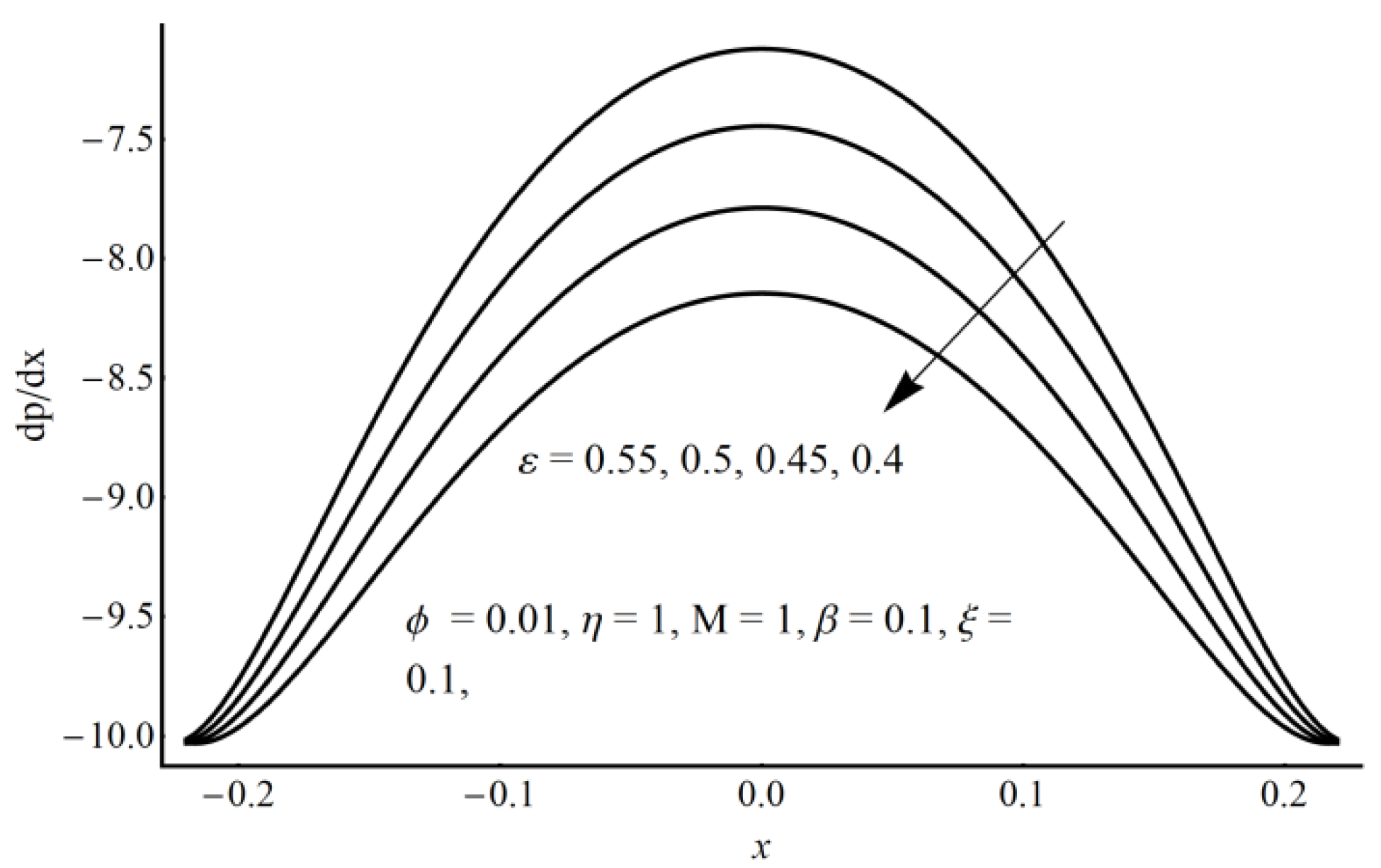
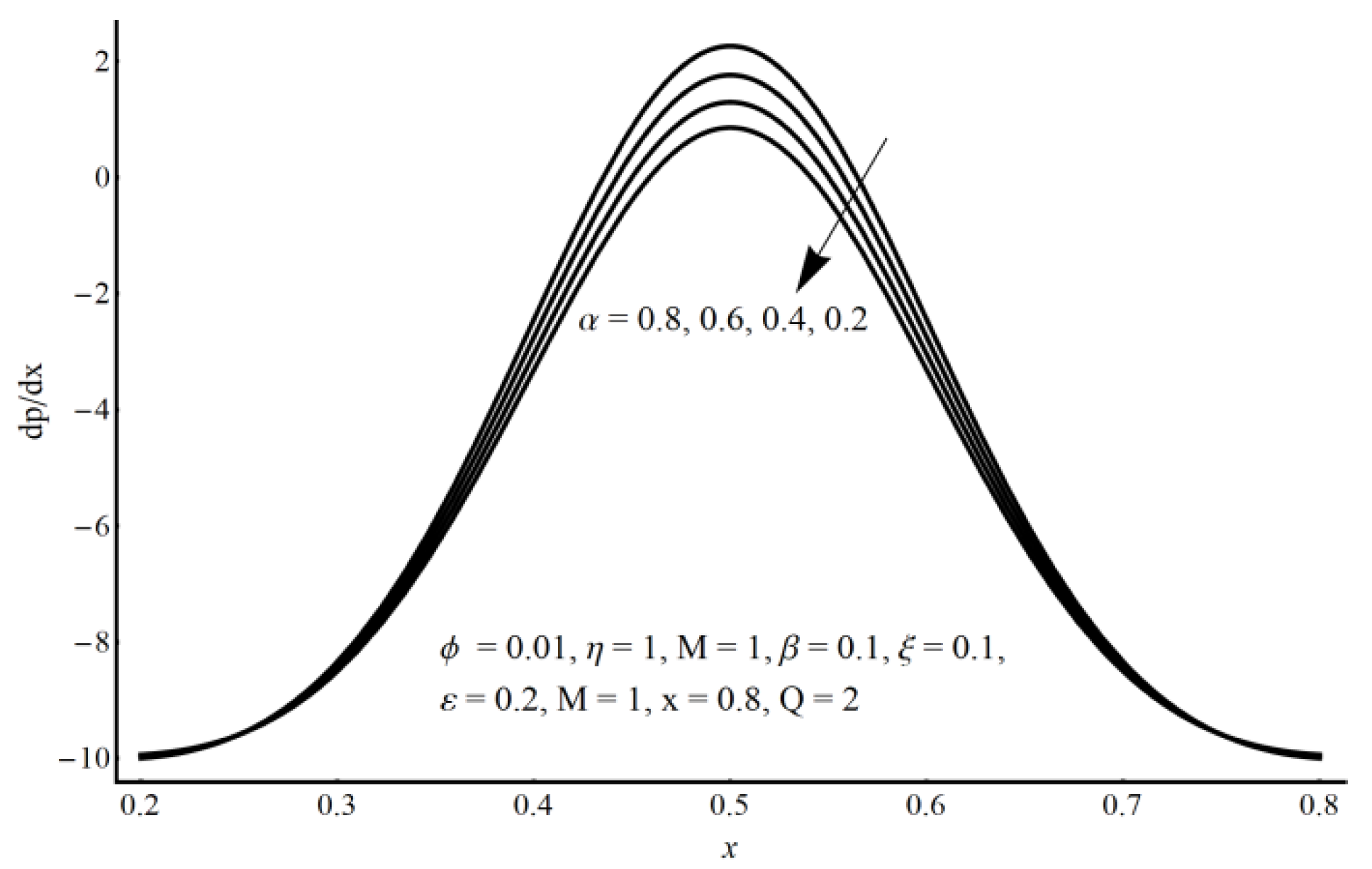




| M | Ψ″(h) (Analytic) | Ψ″(h) (Numerical) |
|---|---|---|
| 0.5 | −11.5061 | −11.5171 |
| 1 | −11.7651 | −11.7837 |
| 1.5 | −12.2013 | −12.2129 |
| 2 | −12.7451 | −12.7830 |
| 2.5 | −13.3785 | −13.4664 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munawar, S. Significance of Slippage and Electric Field in Mucociliary Transport of Biomagnetic Fluid. Lubricants 2021, 9, 48. https://doi.org/10.3390/lubricants9050048
Munawar S. Significance of Slippage and Electric Field in Mucociliary Transport of Biomagnetic Fluid. Lubricants. 2021; 9(5):48. https://doi.org/10.3390/lubricants9050048
Chicago/Turabian StyleMunawar, Sufian. 2021. "Significance of Slippage and Electric Field in Mucociliary Transport of Biomagnetic Fluid" Lubricants 9, no. 5: 48. https://doi.org/10.3390/lubricants9050048
APA StyleMunawar, S. (2021). Significance of Slippage and Electric Field in Mucociliary Transport of Biomagnetic Fluid. Lubricants, 9(5), 48. https://doi.org/10.3390/lubricants9050048




