Elastohydrodynamic Lubrication

Abstract

The development of EHL theory from its tentative beginnings is outlined, with an account of how Ertel explained its relation to Hertz contact theory. The problems caused by the failure of the early numerical analysts to understand that the film thickness depends on only two variables are emphasised, and answers of the form $H=F(P,S)$ given. Early methods of measuring the film thickness are described, but these became archaic with the development of optical EHL. The behaviour of surface roughness as it passes through the high pressure region and suffers elastic deformation is described, and the implication for the traditional $\mathsf{\Lambda }$-ratio noted. In contrast, the understanding of traction is far from satisfactory. The oil in the high pressure region must become non-Newtonian: the early explanation that the viscosity reduction is the effect of temperature proved inadequate. There must be some form of shear thinning (perhaps according to the Eyring theory), but also a limiting shear stress under which the lubricant shears as an elastic solid. It seems that detailed, and difficult, measurements of the high pressure, high shear-rate behaviour of individual oils are needed before traction curves can be predicted.

1. Introduction

Gear engineers have of course long known that when gears are removed from service after long use, the teeth, despite having been wiped (for of course only at the pitch point do they roll!) across each other for millions of passes, still show the original grinding marks. There must have been an oil film protecting the surface and preventing contact. However, classical lubrication theory when applied to very localised contacts, such as those between gear teeth, predicts film thicknesses way below the surface roughness. However, the classical theory satisfactorily explains the behaviour of thrust and journal bearings, predicting film thicknesses adequately greater than the surface roughness of the components. Why the difference?

Classical lubrication theory naturally assumes that a lubricating oil is a Newtonian fluid with a fixed viscosity, and that the bearings are elastic solids, which might bend under oil pressure or thermally, but could never deform locally. Surely that must be the case??

1.1. Classical Theory

Early investigations studied the simple two-dimensional problem: that is, where the lubricant flow is in one direction, and so should be governed by the one-dimensional Reynolds equation [1], in its simple integrated form $\frac{dp}{dx}=6\eta u_1\frac{h-h^{\ast }}{h^3}$, where $p$ is the pressure, $\eta$ the viscosity and $u_1$ the speed of the moving surface. $h^{\ast }$ arises as an integration constant, but then is recognisable as the film thickness at the location of the pressure maximum. While in a thrust pad or a journal bearing normally only one of the two bearing surfaces will be moving, in gear contacts invariably both teeth are moving. Until we look at friction and heat production only the sum, or average, of the two speeds matters. The average (or “rolling”) speed $\overline{u}\equiv (1/2)(u_1+u_2)$ will be used throughout this paper: accordingly the Reynolds equation must be written $\frac{dp}{dx}=12\eta \overline{u}\frac{h-h^{\ast }}{h^3}$. We note that $h^{\ast }$ then has an additional significance, for $\overline{u} h^{\ast }$ is the lubricant flow rate through the bearing.

Figure 1 (drawn for an inlet shape we shall meet later) shows the flow pattern in the inlet: the moving surfaces carry in more lubricant than can pass through the gap, and the surplus must be rejected and pushed back; and of course it is this surplus oil supply which causes the pressure build-up.

In a concentrated “contact” between a circular roller (radius $R$) and a plane, it is easy to show that locally the gap is approximately $h=h_0+x^2/2R$ (the parabolic approximation) [2]: the pressure is then readily found (analytically) to be as in Figure 2; the variations depending on the value of the ratio $h^{\ast }/h_0$.

The two curves of interest are the one through the origin ($h^{*}/h_0 =4/3$), which continues as the reflection of the curve from $-\infty$ to 0 and becomes zero again at $+\infty$, (known as the Sommerfeld solution), and the one becoming zero at the pressure minimum ($h^{*}/h_0 =1.2257$), the Reynolds solution. The Sommerfeld solution is useless here, for the symmetry means that no load is carried: the Reynolds solution supports a load (per unit width) of $W^{\prime }=4.895 \eta \overline{u}R/h_0$ (the “half-Sommerfeld” solution—ignoring the negative pressures—supports a load $W^{\prime }=4 \eta UR/h_0$; but violates flow continuity); in other words, the minimum film thickness $h_0$ will be $4.895 \eta \overline{u}R/W^{\prime }$ (the coefficient can be shown to be 6/H*). As an example of applying this to a gear tooth contact, take two steel teeth with relative radius of curvature $R=0.02 \mathrm{m}$ with a tooth load $W^{\prime }=5\times {10}^5 \mathrm{N}/\mathrm{m}$. If this were a Hertzian line contact with no lubricant, the maximum Hertz pressure, given by $p_0=\sqrt{\{W^{\prime }{E}^{\ast }/\pi R\}}$, with $E^{\ast }=115 {\mathrm{GN}/\mathrm{m}}^2$ would be an acceptable $0.96 {\mathrm{GN}/\mathrm{m}}^2$. However, with a speed $\overline{u}=2 \mathrm{m}/\mathrm{s}$ and oil of viscosity $\eta =0.07 {\mathrm{Ns}/\mathrm{m}}^2$, we find a film thickness of 0.03 µm, less than a realistic surface finish.

1.2. Digression: Factors of 2: Sums and Averages

We noted above that the Reynolds equation could be written using either the average speed $\overline{u}$ (or $U$), or the sum speed $u_{\Sigma }$, usually without warning. Either may be referred to as the “entraining“ speed, and so provide an opportunity of an error of a factor 2!

In the above Hertz calculation, we used the standard notation in Contact Mechanics [3] for the contact modulus $\frac{1}{E^{\ast }}\equiv \frac{1-{\nu }_1^2}{E_1}+\frac{1-{\nu }_2^2}{E_2}$, derived from the fundamental Boussinesq result that a point load $P$ on an elastic half space gives a displacement $w(r)=\frac{P·(1-{\nu }^2)}{\pi E r}$, so that the separation between two solids from the mutual effect of a force is the sum of two such terms. The combination $E / (1-{\nu }^2)$ is the plane strain modulus, conventionally denoted by $E^{\prime }$. A valuable consequence is that a solution of a contact problem between a rigid surface and an elastic solid, expressed in terms of $E^{\prime }$, can immediately be converted into the solution for two elastic solids by simply replacing $E^{\prime }$ by $E^{\ast }$. Unfortunately, in EHL [4] the basic elastic quantity is defined by $\frac{1}{E^{\prime }}\equiv \frac{1}{2}\left[\frac{1-{\nu }_1^2}{E_1}+\frac{1-{\nu }_2^2}{E_2}\right]$, a confusing double use of the symbol $E^{\prime }$. Thus, the maximum pressure in a Hertzian line contact with a rigid indenter will be $p_0=\sqrt{W^{\prime }{E}^{\prime }/\pi R}$ in contact mechanics, but $p_0=\sqrt{W^{\prime }{E}^{\prime }/2\pi R}$ in EHL!

We note with some surprise that although the local gap between two parallel rollers of radii $R_1$ and $R_2$ is $z=\frac{x^2}{2R_1}+\frac{x^2}{2R_2}$, giving $h=h_0+\frac{x^2}{2R_1}+\frac{x^2}{2R_2}$ in a concentrated contact with a minimum gap $h_0$, no-one seems to use the average curvature $\frac{1}{2}\left[\frac{1}{R_1}+\frac{1}{R_2}\right]$; happily, all define the effective radius of curvature by $\frac{1}{R}\equiv \frac{1}{R_1}+\frac{1}{R_2}$ and write $h=h_0+\frac{x^2}{2R}$. (However, be careful: for the contact between two crossed rollers of radii $R_1$ and $R_2$, consult Johnson [3].

2. First Attempts

In the solution above, the lubricating oil is, of course, taken to be a Newtonian fluid with a fixed viscosity. We all know that the viscosity of oil decreases seriously with temperature, and this must be considered in the design of ordinary bearings: any effect of pressures, of the order of a few MN/m² is (correctly) ignored. However, as noted above, in a dry gear contact there would be pressures of order 1 GN/m²; what would such a pressure due to the oil viscosity? There is good evidence that the Barus equation $\eta ={\eta }_0\exp (\alpha p)$ is at least a reasonable approximation [4] (chapter 4), with a pressure–viscosity index (for a typical mineral oil at 30 °C, but decreasing as the temperature rises) of $\alpha =20\times {10}^{-9}$ m²/N, so at 1 GN/m² the viscosity would increase by a factor of $e^{20}=5\times {10}^8$!

The Martin analysis [2] can easily be repeated using this viscosity law: the Reynolds equation becomes $\frac{dp}{dx}=12{\eta }_0{e}^{\alpha p }U\frac{h-h^{\ast }}{h^3}$ or $e^{-\alpha p }\frac{dp}{dx}=12{\eta }_{0}U\frac{h-h^{\ast }}{h^3}$, and the solution of the equation $\frac{dq}{dx}=12{\eta }_{0}U\frac{h-h^{\ast }}{h^3}$ is shown in Figure 1. Let $e^{-\alpha p }\frac{dp}{dx}=\frac{dq}{dx}$, and choose $q=0$ when $p=0$; then $q={\displaystyle {\int }_0^p{e}^{-\alpha p}dp}=(1/\alpha )·\left[1-e^{-\alpha p}\right]$. Thus, $p=-(1/\alpha )\ln (1-\alpha q)$, so that the q-plot is readily converted into a p-plot as in Figure 3.

The solid (“isoviscous”) curve is taken from Figure 2; the others are found from the $q\iff p$ equation. The pressures are substantially increased, and if the greatest pressure in the isoviscous solution ($q_{\max }=2.1509·\frac{ \eta U\sqrt{R}}{h_o^{3/2}}$) reaches 1/α, the real pressure becomes infinite. The minimum film thickness will then be $h_0={[2.1509\alpha {\eta }_{0}U\sqrt{R}]}^{2/3}=1.6663 {(\alpha {\eta }_{0}U)}^{2/3}{R}^{1/3}$ (Gatcombe [5]), while $h^{\ast }=2.04246 {(\alpha {\eta }_{0}U)}^{2/3}{R}^{1/3}$, and this is in fact quite close to what we now know to be correct. However, the very high pressures are local, and although the load is increased from the isoviscous load, it is only by a factor of 2.3 (i.e., $W^{\prime }=(2.3\times 4.985) {\eta }_0^{}UR/h_0$), so this seems unable to explain high load behaviour (if only Blok, while integrating the logarithmic pressures, had taken them seriously, and wondered what the response of the material to an infinite pressure spike would be, we might have had a Dutch EHL theory in 1952) [6].

Kapitza’s Solution

It is convenient here to divert temporarily from the discussion of line contacts to include another rigid contact solution. The three-dimensional Reynolds equation for flow in the x-direction is $\frac{\partial }{\partial x}\frac{h^3}{12\eta }\frac{\partial p}{\partial x}+\frac{\partial }{\partial y}\frac{h^3}{12\eta }\frac{\partial p}{\partial y}=U\frac{\partial h}{\partial x}$.

For a point contact the film thickness is approximately $h=h_0+x^2/2R_x+y^2/2R_y$. Kapitza [7] noticed that $p(x,y)=Cx/h^2$ is a solution of the Reynolds equation, provided that $C=-4\eta U/(1+2R_x/3R_y)$. Thus, for a sphere ($R_x=R_y$) we have $C=-(12/5) \eta U$, while for a roller ($R_y=\infty$) we get $C=-4\eta U$: and we recognise that $p(x)=-4\eta U x/h^2$ is just the Sommerfeld solution for line contact that we noted before. The maximum pressure is of course on the centreline $y=0$, at $x=\sqrt{(2/3) h_0{R}_x}$; [$h=(4/3)h_0$] and equals $p_{\max }=\frac{\eta U\sqrt{R_x}}{1+2R_x/3R_y}\frac{3\sqrt{3}}{2\sqrt{2}}{h}_0^{-3/2}$.

A convenient film thickness parameter is the ratio $h / [{(\alpha {\eta }_0 U)}^{2/3}{R}_x{}^{1/3}]$, which is denoted by $H_K$ commemorating Kapitza [7] (why Kapitza? For noting the simple hydrodynamic solution $p=K x/h^2$, but particularly for providing the first point contact solution). With this notation, the Gatcombe solution [5] becomes $H_K^{ \ast }=2.042$.

It can be seen that the maximum pressure along the centreline of a circular contact is reduced from that of a band contact by the factor ${(1+2R_{x}3R_y)}^{-1}$, and this is obviously attributable to “side-leakage”; not all the fluid which enters the inlet continues through the contact. Of course the exact factor is specific to the Kapitza analysis, but the same factor is a useful general guide.

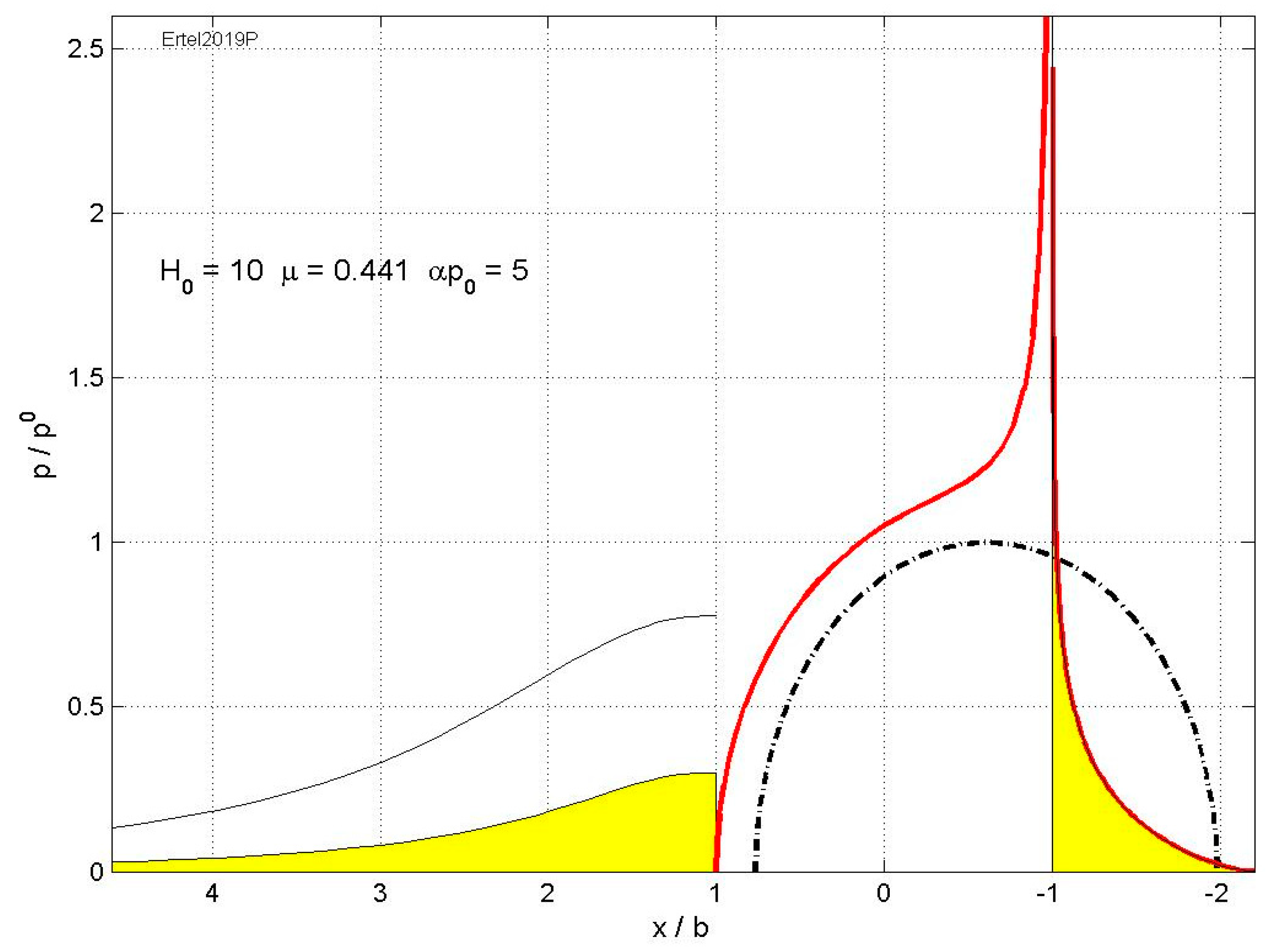
3. The “Grubin” Theory and Its Extension

It should be emphasised that the “Grubin” theory is not by Grubin [8], but by Ertel [9]. However, Ertel defected from the USSR, so in the political climate of the time neither his name nor his work could be mentioned. Grubin, the head of the department on which Ertel had done the work, correctly decided that the theory was too important not to be published.

Ertel saw that under the loads occurring in gear contacts, the metal parts must deform elastically to much the same way as in a Hertzian contact. In addition, indeed, at the pressure levels needed, the oil viscosity would be so enormous that the product $\eta ·(h-h^{\ast })$ in the Reynolds equation could only remain of an acceptable magnitude if $(h-h^{\ast })$ is vanishingly small: the oil must flow along a substantial parallel channel of width $h\approx h^{\ast }$—the geometry of a Hertzian contact, but with the surfaces separated by a constant film thickness. It must be in the inlet to this parallel channel that the oil pressure builds up to Hertzian levels.

The shape of the gap at the edge of a Hertz contact is well known: for a band contact of width $2b$ between two rollers with relative radius of curvature $R$, the gap is $z=(b^2/4R) a (x/b)$ where the shape function is $a (\xi )\equiv 2[ \left|\xi \right|\sqrt{{\xi }^2-1} -{\cosh }^{-1}\left|\xi \right| ]$. So we need to integrate the Reynolds equation from $x=-\infty$ to $x=-b$ along a channel of width $h=h^{\ast }+ (b^2/4R) a (x/b)$. It is convenient to do this for a constant viscosity oil and then convert the reduced pressures $q(x)$ so found into real pressures using the transformation $p=-(1/\alpha )\ln (1-\alpha q)$ introduced above. Then, by equating the reduced pressure $q(-b)$ at the end of the inlet to $1/\alpha$, we obtain a film thickness formula; the corresponding load is taken to be the Hertz load for this contact. Thus, for a Hertz load $W^{\prime }$ we have $b^2=\frac{8R{W}^{\prime }}{\pi E^{\prime }}$ and $\frac{1}{\alpha }=12{\eta }_{0}U{\displaystyle {\int }_{-\infty }^{-b}\frac{h-h^{\ast }}{h^3} }dx=12{\eta }_{0}U{\displaystyle {\int }_{-\infty }^{-1} \frac{(b^2/4R) a(\xi )}{{[h^{\ast }+(b^2/4R) a(\xi )]}^3} }bd\xi$.

Defining $H_0\equiv \frac{4R{h}^{\ast }}{b^2}$, we can write the equation as $G\equiv \frac{b^3}{8\alpha {\eta }_{0}U R^2}=24{\displaystyle {\int }_{-\infty }^{-1} \frac{a(\xi )}{{[H_0+a(\xi )]}^3}}d\xi \equiv f(H_0)$.

Ertel evaluated the integral numerically for a few values of $H_0$ (presumably laboriously by hand, so some inaccuracy is excusable) and made a log-log plot of $G(H_0)$ which he fitted by a power law. However, in fact the curve is not straight, the slope changing from −3/2 to −4/3 as $H_0$ increases, and it is better to consider $H_0·G^{2/3}\equiv \frac{h^{\ast }}{{(\alpha {\eta }_{o}U)}^{2/3}{R}^{1/3}}$, (which is the Kapitza film thickness parameter $H_K^{\ast }$), and plot it against $G$ (see Figure 4).

Also shown in Figure 4 is a solution to the problem by Crook [10], which avoids numerical integration by using the asymptotic approximation for the entrance to a Hertzian contact: $h\approx (b^{2}3R)(2^{3/2}){(x/b-1)}^{3/2}$. The integration can then be done analytically, giving $H_K=2.084 G^{-1/12}$. This gives reasonable answers for $G>1$, but is misleading for $G<1$ where numerical integration of the exact entry shape shows $H_K$ becoming constant. Cameron suggested replacing Crook’s use of the asymptotic equation for the inlet gap by a curve-fit $h\approx (b^2/2R)·(2.114 {(x/b-1)}^{1/55}$ (no extra work is involved). The agreement with Ertel is improved—but again only for $G>1$.

Ertel went on to consider the exit to the parallel region. To get the pressure back down from its high values, a negative pressure gradient is required, which from the Reynolds equation requires the film thickness to be less than the value $h^{\ast }$: there must be an exit constriction. Ertel argued that this implies a pressure spike (I believe this to be the first occurrence of the concept, predating Petrusevich’s encounter with it in his numerical solution), but this is explained more completely by Greenwood’s extension of the theory [11].

Extension to Ertel’s Theory

The Hertzian geometry provides no opportunity for the pressure to return to zero. However, suppose the Hertzian flat is moved forward [11] from its position on the centre-line of the rollers? The result is as shown in Figure 5.

A Hertzian flat centred on the original point of closest approach requires the standard Hertzian pressure distribution $p(x)=(E^{\prime }/4R)\sqrt{b^2-x^2}$. However, a flat moved forward a distance $d$, as shown in Figure 5 ($\mu \equiv d/b$), can be obtained by applying a pressure distribution $p(x+d)=\frac{E^{\prime }}{4R}\left[\sqrt{b^2-x^2}+d {\left(\frac{b+x}{b-x}\right)}^{1/2}\right]$.

Figure 6 shows examples of these pressures. When $\mu \equiv d/b$ is small, the pressure closely follows the Hertz curve, except for a narrow pressure spike at the end of the flat: then as $\mu$ increases the resemblance to Hertz disappears and the spike dominates (it should be noted that it is always a square root singularity).

Both the deformed shapes and the pressure distributions of Figure 5 and Figure 6 strongly resemble those found by the numerical solutions to be described later.

The inlet shape resulting from these pressures is known from contact mechanics, so just as for the Ertel analysis above, the Reynolds equation is integrated (for a constant viscosity), then interpreting the result as the reduced pressure $q=(1-\exp (\alpha p))/\alpha$) instead of $p$, and setting its terminal value (at the beginning of the flat) equal to $1/\alpha$ gives a film thickness equation, which now depends on both the contact width $2b$ and the shift d.

To find $d/b$, a second integration over the exit constriction is performed, terminating at the point where the film thickness returns to $h^{\ast }$: then matching the two integrals gives $d$. Then just as for the Ertel solution we could plot $G^{2/3}{H}_0\equiv \frac{h^{\ast }}{{(\alpha {\eta }_{o}U)}^{2/3}{R}^{1/3}}$, $G\equiv \frac{b^3}{8\alpha {\eta }_{0}U R^2}$ against (the relation between contact width and Hertz pressure is modified; now, $p_0/E^{\ast }=(b/2R) \sqrt{(1+2\mu )}$).

The figure shows that the Ertel extension, while explaining and locating the pressure spike, does not greatly alter the predicted film thickness: indeed, for $H_K<1.8$ ($G>1$), it is hardly changed; and even for $G<0.01$, where there is a 10% reduction in film thickness, the prime feature of $H_K$ becoming almost a constant (i.e., the film thickness varying as the two-thirds power of the speed,$h\propto U^{2/3}$) is unchanged.

Please note that now G has two (slightly) different meanings. The factor b is always the half-width of the flat, so in the extended theory it is no longer the Hertzian half-width b, and its relation to $p_0$ has changed from $b=4R{p}_0/E^{\prime }$, to $b=4R{p}_0/E^{\prime }\sqrt{1+2\mu }$ for the half-width of the off-centre flat.

Of course, none of this is a real solution of the EHL problem. Figure 6 shows only the pressure distributions found from elastic theory: it does not show the hydrodynamic pressures, particularly not the inlet pressures with their own, separate, pressure spike at the end of the inlet. The offence may be reduced by modifying Ertel’s condition that the reduced pressure $q\to 1/\alpha$; we may require it to tend to a lower value so that the hydrodynamic pressure tends to, for example $0.4p_0$ as used in Figure 7.

The outlet pressure distribution neatly continues the elastic spike, so offends less, and we get a plausible approximation of a complete pressure distribution (though now for a specific $\alpha p_0$, and with a slightly reduced value of G when $\alpha p_0$ is small (as here)). However, both contributions must increase the surface deformation, and so invalidate the integration by which they were found!

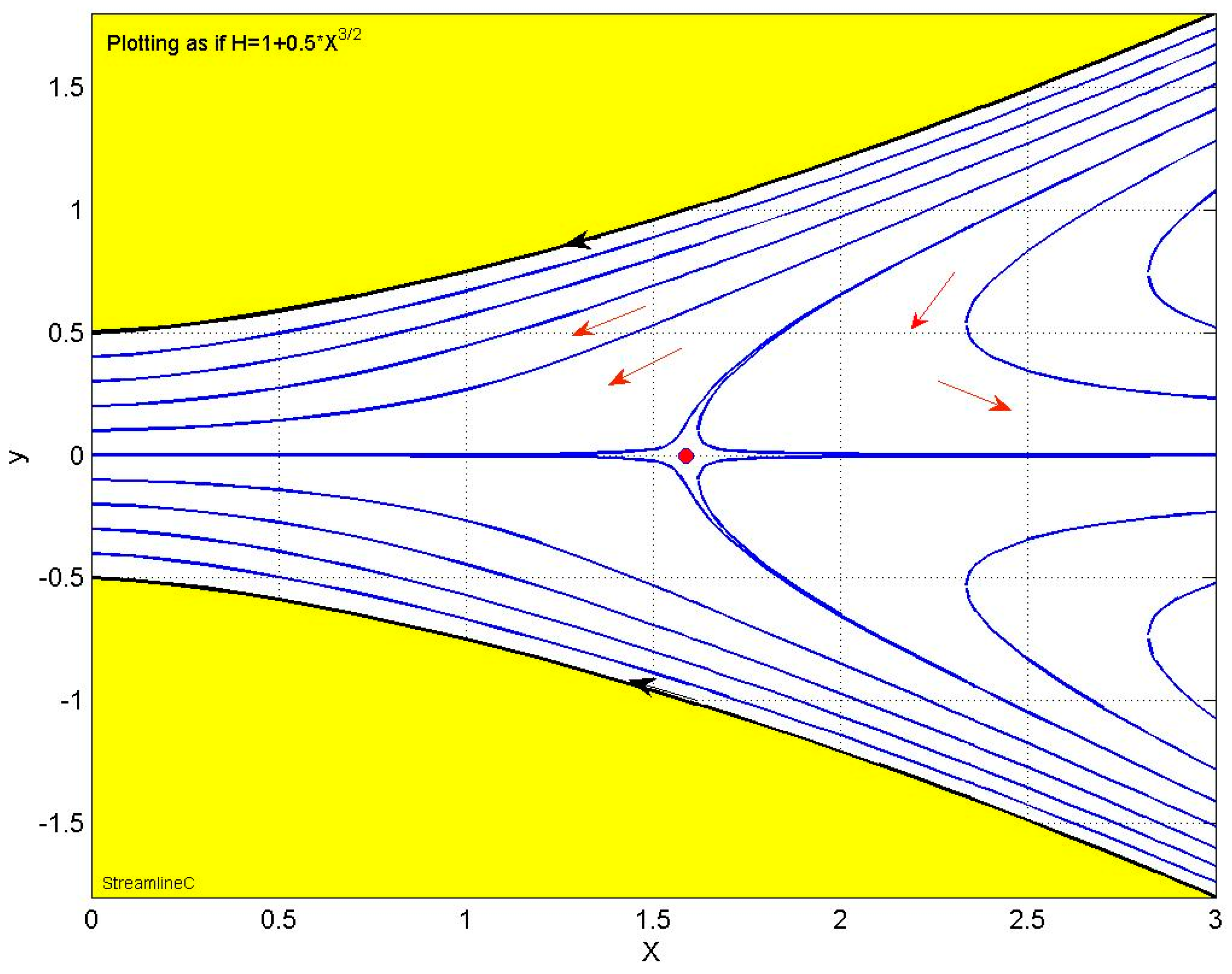
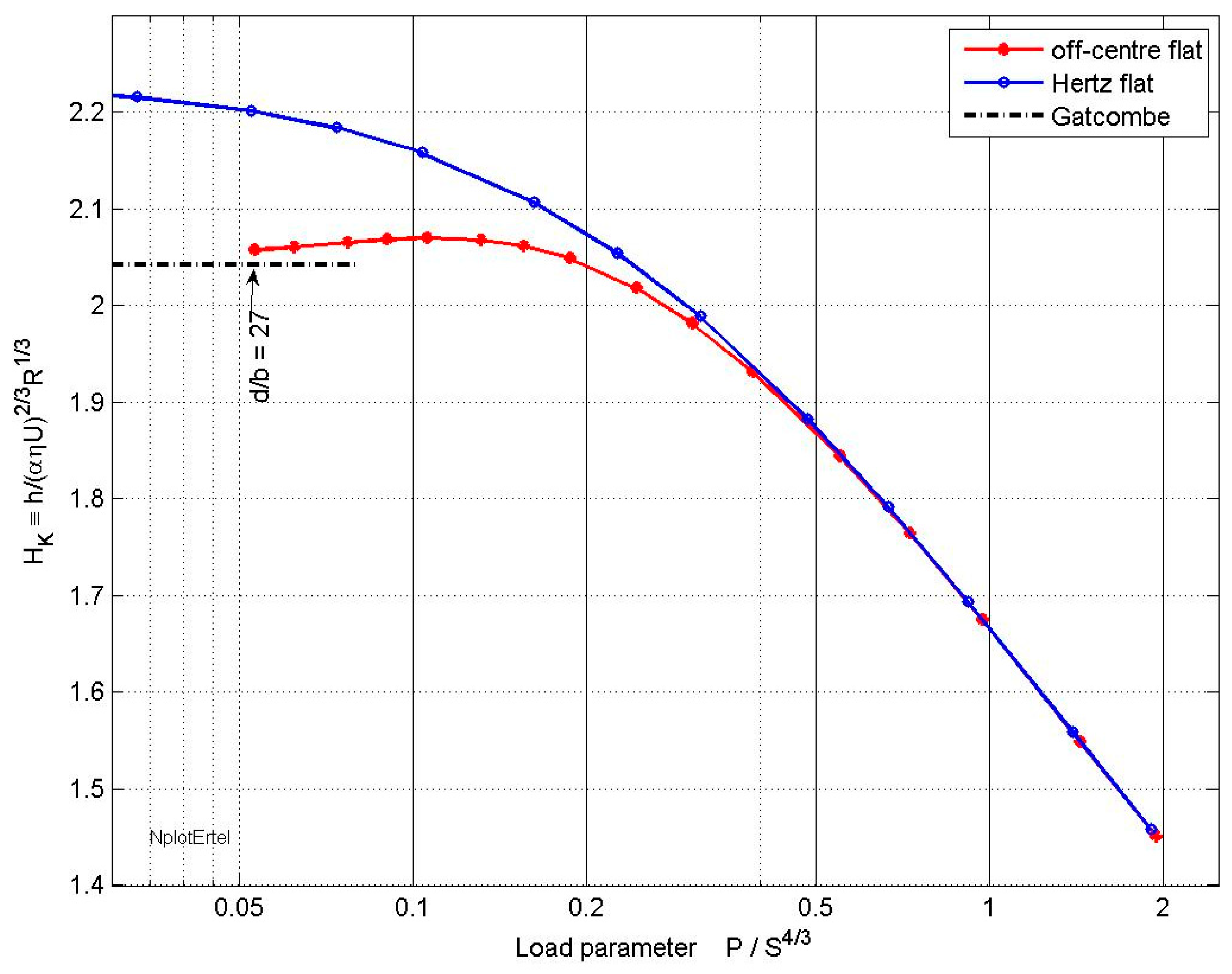
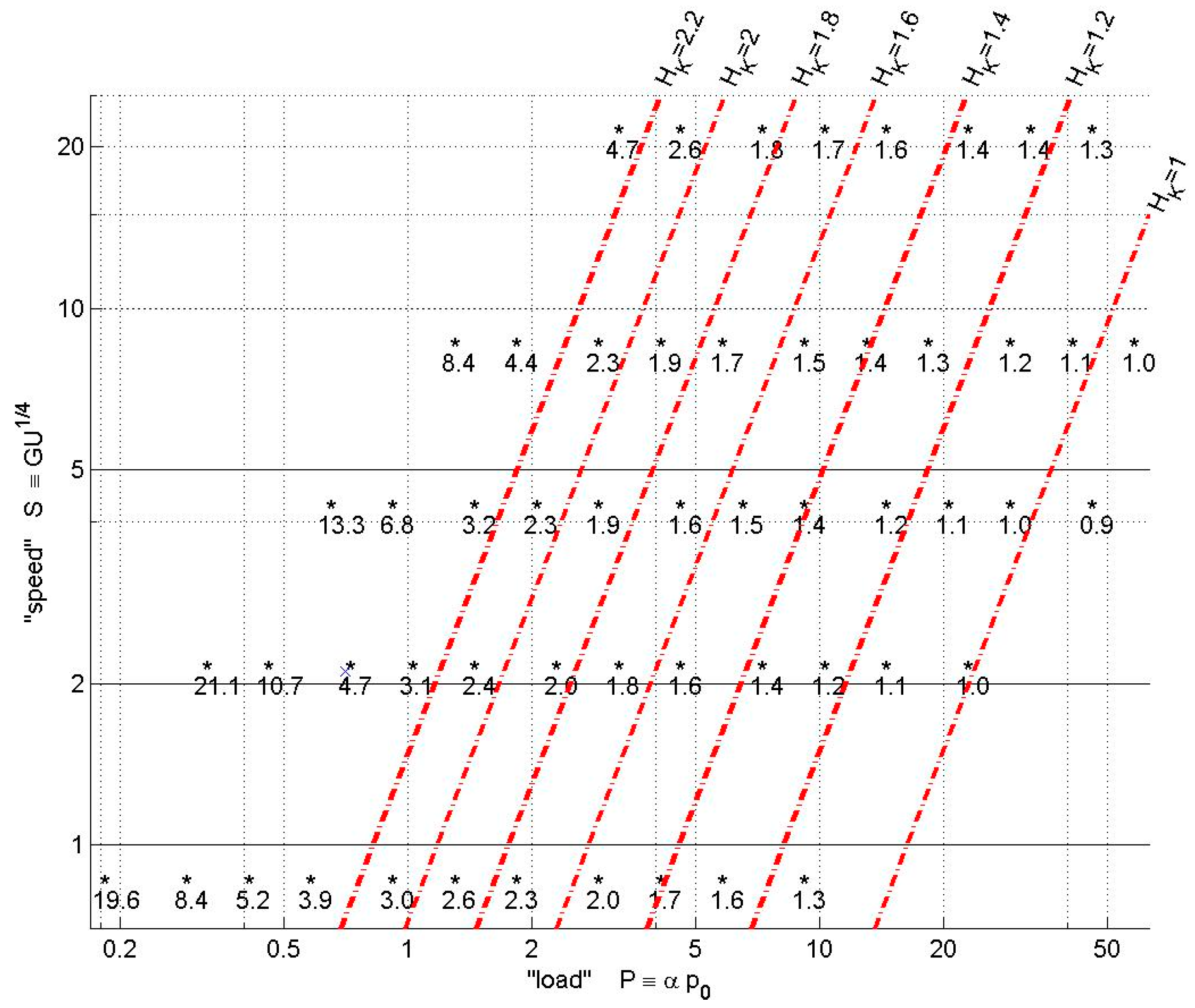
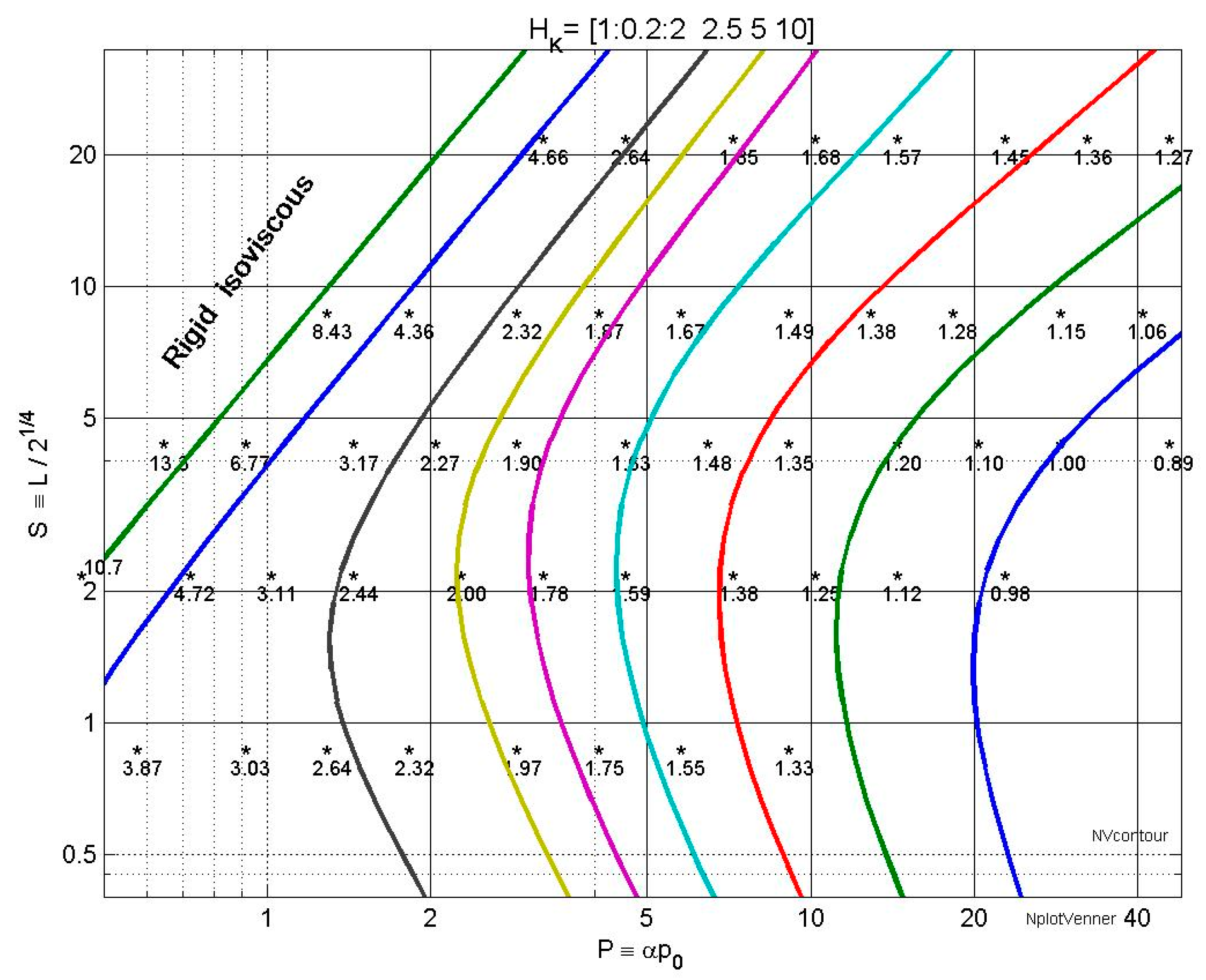
4. Numerical Solutions and Non-Dimensional Groups

The need for a full solution using hydrodynamic pressures to produce the film shape needed to generate those pressures was clear: a simultaneous solution of the Reynolds equation and the film shape, including the elastic deflection, is needed. The equations (for the line contact problem and assuming the Barus law governs the viscosity are [4,12]:

$\frac{dp}{dx}=12{\eta }_0{e}^{\alpha p} \overline{u}\frac{h-h^{\ast }}{h^3}$ where $h^{\ast }\equiv h (b)$ and $p(b)=0$.

$h (x)=h_0+\frac{x^2}{2R}+u(x)-u(0)$ (for the 2D problem, the deflection has an unknown datum)

$u(x)=\frac{4}{\pi E^{\prime }}{\displaystyle {\int }_{-\infty }^{b}p(x^{\prime })\ln (|x-x^{\prime }|) d{x}^{\prime }}$$w^{\prime }={\displaystyle {\int }_{-\infty }^{b}p(x^{\prime }) d{x}^{\prime }}$.

The first difficulty is the number of parameters involved in the problem: there are seven physical variables [${\eta }_0, \alpha , \stackrel{\rightharpoonup }{u}, R, h_0, E^{\prime }, w^{\prime }$], so a solution $h=F(U,R,{\eta }_{ 0},w^{\prime },E^{\prime },\alpha )$ is needed. (Either the film thickness $h_0$ at $x=0$, or the load per unit width $w^{\prime }$ will be known.)

Dimensional analysis helps, and leads to $h/R=F(\alpha E^{\prime } , {\eta }_0\overline{u}/E^{\prime }R, W^{\prime }/E^{\prime }R)$, where the three independent variables are the Dowson and Higginson parameters $G_D\equiv \alpha E^{\prime }, U_D\equiv {\eta }_0\overline{u}/E^{\prime }R$ and $W_D\equiv w^{\prime }/E^{\prime }R$. The first published numerical solutions all used this form, with unfortunate consequences, for the only way to report the answers was a grand curve-fitting exercise to obtain $h/R=C· {(G_D)}^m{( U_D)}^n {(W_D)}^p$. Much of the early literature is concerned with researchers [13] comparing their values for the three indices. This was despite Blok and his colleagues pointing out that by “optimal similarity analysis” it can be shown that only two independent variables are needed, so that film thicknesses can be plotted on a map and curve-fitting avoided [14]. One wonders if this was so long ignored because of the intimidating name [15]! For of course dimensional analysis is a valuable tool for the experimenter but quite unnecessary for a theoretician when all the equations are available (and so of course have dimensional analysis built in!); instead, just scale the equations and see how many (few!) governing parameters are needed. (Appendix A shows the procedure.)

The final two independent variable formats arrived at by Blok and his colleagues were the Moes variables $H_M=F(M,L)$ where $H_M\equiv h\sqrt{E^{\prime }/\eta { }_0{U}_{\mathsf{\Sigma }} R}$, $M\equiv w^{\prime }/\sqrt{({\eta }_0{U}_{\mathsf{\Sigma }}{E}^{\prime }R) }$, and $L\equiv \alpha E^{\prime } {\left({\eta }_0 U_{\mathsf{\Sigma }}/E^{\prime } R\right)}^{1/4}$ (using $U_{\mathsf{\Sigma }}\equiv 2U$!). These groups may of course be combined in many different ways, though a very desirable measure of the load is the Hertz pressure $p_0$; for if the answers for line contacts and point contacts are to be compared (using the same point contact parameter $W_D\equiv W/E^{\prime }{R}_x^2$ for all elliptical point contacts with varying a/b, using a fixed W is highly misleading) we cannot use the load per unit width $w^{\prime }$ for one but the load W itself for the other. This suggests the combination $\alpha p_0$ (for line contacts, $\alpha p_0\approx M^{1/2}L$). When the pressure distribution is roughly Hertzian, $\alpha p_0$ is a useful indicator of the viscosity enhancement, but for low loads (see Gatcombe’s solution!) it is merely a convenient load parameter (for line contacts $P\equiv \alpha p_0$ is found as $\alpha \sqrt{w^{\prime } E^{\prime }/2\pi R}$, for circular point contacts, $\alpha p_0$ must be found as $(\alpha /\pi ){(3W {E^{\prime }}^2/2R^2)}^{1/3}$. For elliptical contacts, approximate answers can be found by replacing R by $\sqrt{R_1{R}_2}$).

The Dowson and Higginson groups have the great virtue of having speed and load as separate, independent variables, which suits the experimenter; the Blok/Moes group $M$ is less suitable, so more appropriate partners are $S\equiv \alpha E^{\prime } {\left(\frac{{\eta }_0\overline{u}}{E^{\prime }R}\right)}^{1/4}$ ($S\equiv 2^{-1/4}·L$) and $P\equiv \alpha p_0$. Finally, the film thickness parameter should vary no more than necessary (charts using the parameter $W^{\prime } h/{\eta }_{}UR$ (to avoid using $E^{\prime }$ or $\alpha$) cover a range of 1 to 500), and it has become clear that the Kapitza combination $h / {(\alpha {\eta }_{0}U)}^{2/3}{R}^{1/3}$ ($H_K\propto H_M/ L^{2/3}$) is ideal. So the simplest form is $H_K=F(P, S)$ with $H_K\equiv H_M/{(L/2)}^{2/3}=2^{1/2}·H_M/S^{2/3}$. The fact that the problem requires only two independent variables means that the indices in a three-group equation cannot be independent; writing $h/R=C {(\alpha E^{\prime })}^k{({\eta }_{0}U/E^{\prime } R)}^n{(W^{\prime }/E^{\prime } R)}^m$, the indices must satisfy $2n+m-k/2=1$. Thus, the original Dowson and Higginson equation [7] (chapter 7) with $k=0.6, n=0.7, m=-0.13$ has $2n+m-k/2=0.97$ and is impossible (uncorrected in the second edition of Elastohydrodynamic Lubrication (1977), sixteen years after the first edition). In the end, the results were reviewed, and the exponent $k$ reduced to 0.54, to give (from ESDU (line contacts) 1985) $h_{\min }/R=2.65 G_D{}^{0.54}{U}_D{}^{0.70}{W}_D{}^{-0.13}$ or in full $h_{\min }=2.65 {\alpha }^{0.54}{({\eta }_{0}U)}^{0.70}{R}^{0.43}{W^{\prime }}^{-0.13}{E^{\prime }}^{-0.03}$ (Note how slight is the dependence on $E^{\prime }$, and indeed, in the original equation the exponent is positive: ${E^{\prime }}^{+ 0.03}$). The corrected form can be written $H_K=2.65 {(G_D{U}_D^{1/4})}^{0.13}{(G_D{W}_D^{1/2})}^{-0.26}$ or substituting $G_D{W}_{{}_D}^{1/2}=\sqrt{2\pi } P$, as $H_K=2.09 {(S)}^{0.13}{(P)}^{-0.26}$; note the dependence is on the combination $(S/P^2)$ (There is a direct correspondence between the Dowson and Higginson load and speed variables and the preferred ones; thus, for line contacts $P=(G/\sqrt{2\pi }) W_D^{1/2}$, $S=G{U}_D^{1/4}$; then $H_K={(G{U}_D)}^{-2/3}{H}_D$).

(Even later Pan and Hamrock [16] offered {for ${(H_D)}_{\min }$} $k=0.568, n=0.694, m=-0.128$ with a checksum 0.976 instead of 1; fitting their data in a two-variable form leads to $k=0.562, n=0.695, m=-0.153$, with no loss of accuracy.) The results of the Ertel analysis can also of course be written in terms of $S$ and $P$. For the Ertel solution, $G=8P^3/S^4$ or $P/S^{4/3}=0.5 G^{1/3}$, while for the extended solution, $P/S^{4/3}=0.5 G^{1/3}·{(1+2\mu )}^{1/2}$.

The plot is similar to Figure 6, now replacing the abscissa G by $0.5 G^{1/3}·{(1+2\mu )}^{1/2}$. For $P/S^{4/3}>0.4$ ($d/b<0.2$) the two models predict the same film thicknesses.

It is of interest to consider the limiting behaviour of the off-centre flat model as $d/b\to \infty$, that is, as the length of the flat tends to zero. Then the deformation becomes very local, and the body effectively a rigid body for which the Gatcombe (like Kapitza, but with the correct Reynolds exit condition) analysis applies. This gives $H_K^{*}=2.0425$, and as Figure 8 shows, this is a plausible asymptote to the answers found.

4.1. Regimes of Lubrication

Attempts have been made in the past to identify different “regimes” [17], moving from the classical Rigid-Isoviscous (RI) to Rigid-Piezoviscous (RP) and Elastic-Isoviscous (EI) before reaching the full Elastic-Piezoviscous (EP) regime. (Piezoviscous being a convenient shorthand for “viscosity increasing with pressure”.) One method of determining the boundaries is to locate where the curve-fits obtained for the different regimes become equal; this becomes problematic if the curve-fits are inaccurate. (One chart found in this way located an EP region for which its curve-fit equation was based almost entirely on calculated film thicknesses at points which then proved to lie outside the region! (see [18]).) When maps giving numerical values of the film thickness for substantial ranges of load and speed were not available, such that power law curve-fits had to be employed, it was vital to identify where they were valid, and so to identify the regions noted above, and use the power law for that region. However, now consulting the ESDU charts [19] is easier and more reliable.

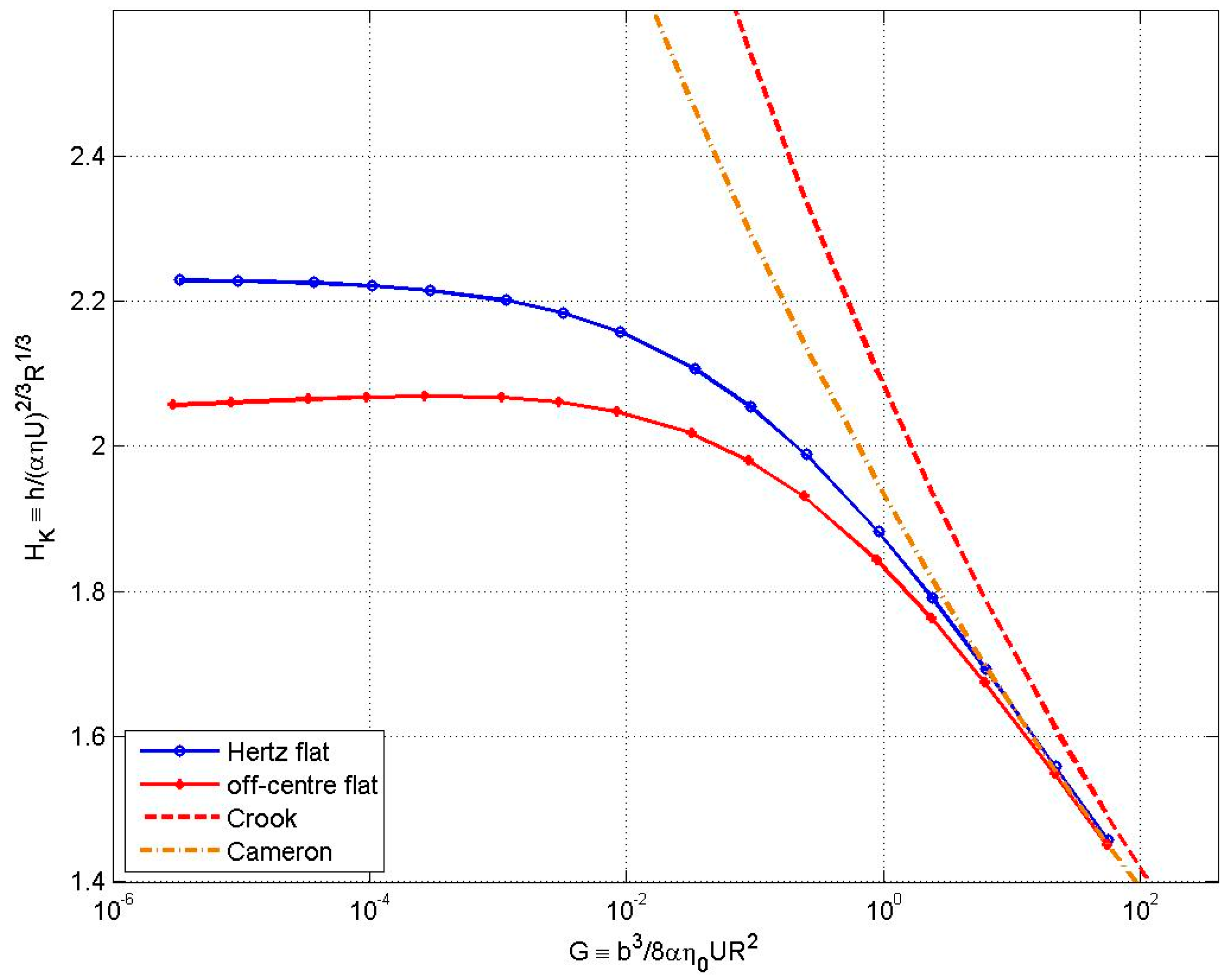
4.2. Line Contacts

“Once more detailed (and probably more accurate) values of the film thickness in line contacts became available (Venner [20], it is possible to investigate how accurate are the power law curve fits. Figure 9 compares the Dowson & Higginson power law discussed above with Venner’s calculated values.”

The two certain features in Figure 9 are that the film thickness decreases when the load increases, and that it increases when the speed increases. Clearly there is general agreement between the two sets of values in the area where the Dowson contours $H_K<2.2$ have been drawn; note in particular the Venner points near the Dowson $H_K=1.4$ contour. In contrast, the contours of both Ertel and extended Ertel solutions will be straight lines of slope 3/4; very different from the slope 2 of the Dowson contours. However, see Figure 10, showing the interpolated contours of the Venner values! The $H_K=2.2$ contour is already failing to match the increase of the Venner results, showing that at lighter loads or higher speeds, the film thicknesses are considerably above the $H_K\approx 1 \mathrm{to} 2$ range of the right side. The Kapitza parameter is no longer the best film-thickness parameter, and we are approaching the rigid-isoviscous region where the classical (Martin) equation $h_0=4.895 \eta \overline{u}R/W^{\prime }$ holds. Indeed, rewriting the Martin equation in the present terms it becomes $H_K=1.56 S^{4/3}/P^2$. The condition for this to be double the “universal” Kapitza prediction $H_K^{\min }=1.5$ is the line $S\approx 1.6P^{3/2}$, and this is perhaps a better boundary to the EHL region than the Dowson contour. To the right of the $H_K=2$ contour, or better the line $S\approx 1.6P^{3/2}$, the film thicknesses all more or less agree, but no more. The Dowson contours have the best overall slope, but this is just an average between the slightly negative slopes at low speeds and the positive ($\approx 1$) slopes on the upper right; there is certainly no suggestion that the points lie along straight lines. The Ertel 3/4 slopes become more plausible in the upper right-hand corner.

When contours are drawn from the Venner [20] data, they are very far from straight, and clearly a power law curve fit, which necessarily assumes straight contours, simply cannot reproduce the answers accurately. There is a strong resemblance to the contours given by the ESDU (point contact) item [19]. Note how the gentle spacing of the contours in the $1<H_K<2$ dramatically changes with the $H_K=5,10$ contours: the move into the rigid isoviscous region is clear.

More generally, we see that only such a plot enables the differences between sets of solutions to be seen: in contrast, a loglog plot of theoretical $h/R$ against measured $h/R$, covering a range from 10⁻⁶ to 10⁻³ is dominated by the speed dependence, and indeed, one published example, although showing results differing by factors up to 2, “[can be taken as showing] that the equation can be used with some confidence”. Of course, often this may be good enough!

4.3. Circular Point Contacts

Numerical analysis of EHL point contacts inevitably lagged behind the solution for line contacts, but advances in computing power and (perhaps more importantly) in computing techniques mean that film thickness values, and indeed, film thickness maps, are now available. Not surprisingly, the dependence of film thickness on load and speed is similar, and the differences can to some extent be explained as being due to “side leakage”; not all the oil drawn into the inlet needs to be passed downstream through the “Hertz” region, though this leakage is impeded by the side constrictions which develop (and may house the point of minimum film thickness). Figure 11 provides a direct comparison with Figure 10, although it is for the (more confidently determined) central film thickness.

We see the same feature of a large region on the right where the film thickness varies gently from $H_K=1$ to $H_K=2$, bordered on the upper left by the region where $H_K$ rises violently. This of course merely confirms the unsuitability of our film thickness parameter for this region. The actual film thickness behaves much as predicted by Kapitza’s initial isoviscous analysis $h/R\propto {({\eta }_0\overline{u}R/W)}^2$, so very steeply using our variables.

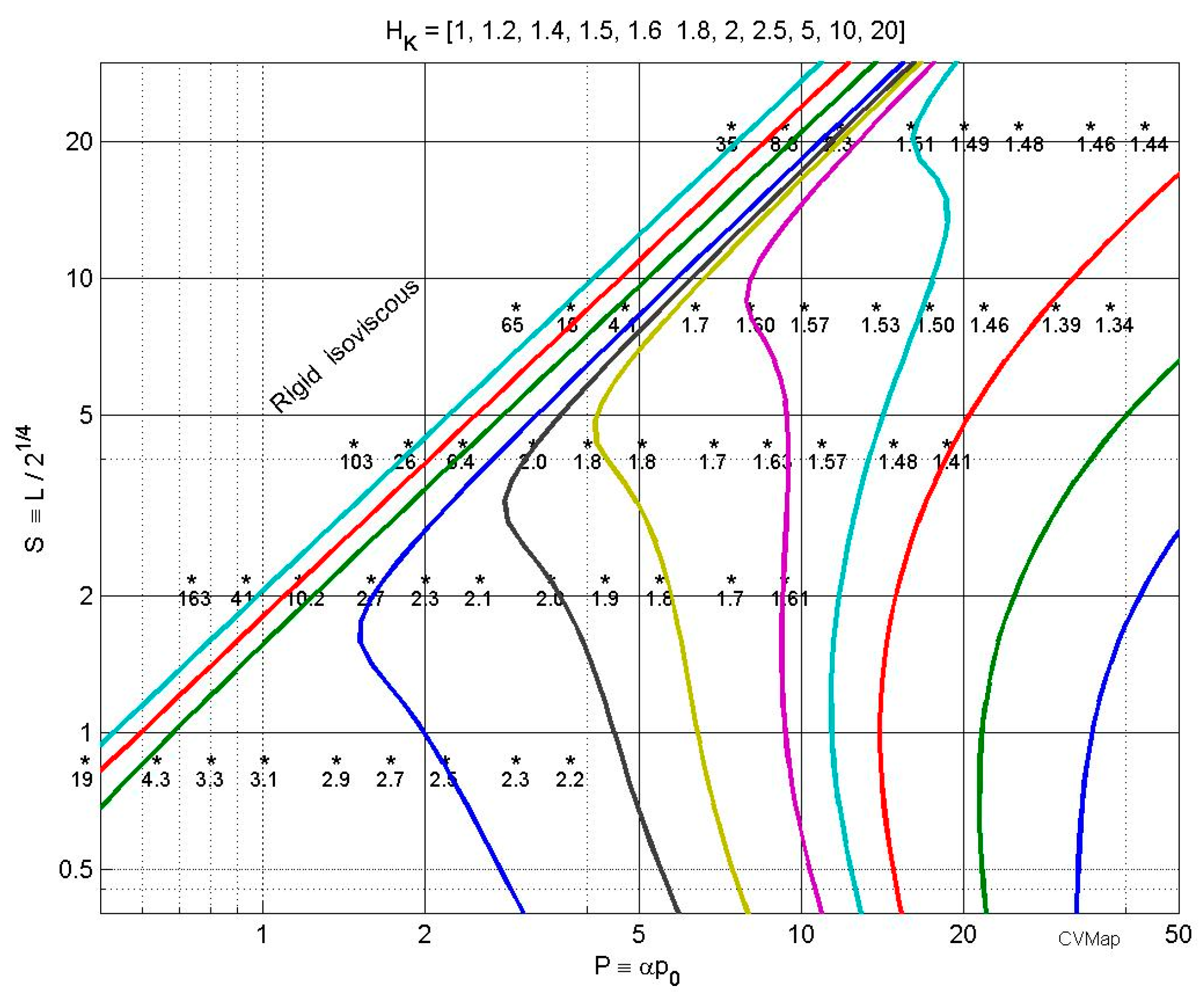
4.4. Elliptical Point Contacts and Side-Leakage

The study of circular point contacts is very convenient both theoretically and experimentally, but contacts in ball bearings are often elliptical. A film thickness equation drawn from Hamrock and Dowson [21] is often used: $H_D=2.69R_x{U}_D{}^{0.67}{G}_D{}^{0.53}{W}_D^{-0.067}(1-0.61e^{-0.73\epsilon })$.

Here the usual Dowson and Higginson variables (now $W_D\equiv W/E^{\prime }{R}_x^2$, where $R_x$ is the radius of curvature in the entraining (the minor “b”) direction) are supplemented by an approximate ellipticity factor $\epsilon =1.03{(R_y/R_x)}^{0.64}$ (i.e., $\epsilon \approx a/b$). This is based on 25 values for $k=6$ for varying $U_D, W_D$, supplemented by 10 values for varying $k$ (from 1 to 8) at $U_D=1.68\times {10}^{-12}, W_D=0.1106\times {10}^{-6}$. Hamrock & Dowson (H&D) [21] report that the curve fit value for a circular contact is 9.4% low, but remarkably Lubrecht et al. [22] report good general agreement with their calculations.

However, of course $W_D=0.1106\times {10}^{-6}$ represents a very different Hertz pressure for a circular contact ($\alpha p_0=5.73$) than it does for a highly elliptical ($k=8, \alpha p_0=1.55$—almost a line!) contact: and we know that film thickness decreases when the Hertz pressure is increased. This raises the question, how much of the film thickness reduction below the line-contact value is side leakage, and how much is the effect of “load”, i.e., of Hertz pressure?

To test this, we calculate the Hertz pressure for Hamrock’s 10 points for varying $k$, and for the 10 points for $k=6$ for the same speed, and compared the film thicknesses. Figure 12 shows the result.

The $k=6$ points are for varying load ($W_D$), but would have negligible side leakage [($1-0.61\exp (-0.73k))=0.992$]; the $k\ne 6$ are for a single $W_D$. Clearly there is no side leakage (and some inaccurate computing!); this merely shows that the film thickness decreases when the Hertz pressure increases. Note the general agreement with a curve fit for all 34 points $H_K\approx 2.62 ·S^{0.078}{P}^{-0.234}$, which is simpler then the H&D equation, and a (slightly) better fit to their values, with a maximum deviation of 6% compared with their “less than 10%” (i.e., 9.7%!).

It is of course well-known that in point contacts, side-lobes develop within the Hertzian area, already for near-circular contacts, but very much more for slender contacts (ones with entrainment along the major axis). For these the minimum film thickness will be much lower that the minimum along the centre-line, although compressibility can sometimes offset this, and give a central film thickness less than the “minimum”. The side lobes will certainly impede side flow, but this is within the “flat”, and so acts after the film thickness has already been determined in the inlet. So it is not clear why the side flow factor ${(1+2R_{x}3R_y)}^{-1}$ predicted by the Kapitza analysis seems to be absent.

The recognition that for “wide” contacts ($k\equiv a/b>1$) increasing $k$ while keeping $W_D$ fixed will reduce the film thickness by increasing the Hertz pressure, and make it harder to identify any effect of side-leakage was late to appear. Perhaps the first statement was by Wheeler et al. [23] 2016, who wrote:

“Yet, Chittenden et al. varied the ellipticity ratio while keeping constant the dimensionless parameters (U, G, and W as defined by Hamrock and Dowson). Consequently, the actual load was varied in a large range together with the ellipticity, and the influence of the latter on film thickness could not be highlighted in itself.”

Yet, they then calculated film thicknesses for fixed speeds and loads (u_e = 0.5 m/s, 2 m/s, 10 m/s and w = 120 N, 800 N, 2500 N.), maintaining fixed Hertz pressure by varying $R_x$ as $k$ varied, so replacing the confusion between P and k by confusion between S and k. It is not clear how their (no doubt correct) conclusion that the greatest value of $h_c$ is when $k\approx 2/3$ could be used.

A direct demonstration of the absence of side leakage (for $k>1$) is provided by the calculated film thickness values reported in [22]. These are for $R_y/R_x=$ 1, 2, 5, 10…100, with the loads being adjusted to keep the Hertz pressure constant. Two combinations were studied: [P = 7.9; S = 5.15] and [P = 15.8, S = 10.30]. For each set, the film thicknesses were almost constant, with perhaps slightly lower values for $R_y/R_x=$ 1, 2 (see

Table 1. H_k calculated by LVC [22] for varying R_y/R_x but fixed speed and Hertz pressure.

Ry/Rx	1	2	5	10	20	50	100	Mean
P = 7.9; S = 5.15	1.631	1.690	1.711	1.664	1.662	1.659	1.657	1.668
P = 15.8; S = 10.3	1.471	1.536	1.561	1.553	1.553	1.545	1.540	1.537

).

It seems that when the Hertz pressure is constant, the ellipticity has no effect on the film thickness. For wide contacts ($k>1$) there is no evidence of side-leakage.

Perhaps a more important contribution from Wheeler et al. [24] is their investigation of the accuracy of six different published curve-fit equations for the central film thickness of elliptical contacts. They calculated the film thickness for some dozen combinations, and compared the answers with their own. They conclude that for circular, and “wide” (k = 2.92) elliptical contacts, all the equations overestimate the central film thickness, although for circular contacts the best (Chittenden et al. [CDDT] [25]) are only 2% high. (Hamrock and Dowson (HD) [21] averages 9% high). For the k = 2.92 contacts they find CDDT averages 11%, HD 14%: the best being a recent (2015) set from Mostofi and Khonsari [26] at 5%.

For slender contacts (k = 0.34) the errors are larger. The only equation found (CDDT [27]) gives answers (for $h_{cen}$) which are too low, by between 10% and 30%. (Perhaps more seriously, their answers for $h_{\min }$ are too high by between 20% and 200%, but it will be clear to the reader that because of shear thinning the author distrusts all Newtonian $h_{\min }$ calculations.)

It should, of course, be remembered that it may be the Wheeler et al. values that are inaccurate. In addition, in fairness to the authors whose equations are studied, note that Wheeler et al. use a different pressure-viscosity law (“an improved Yasutomi correlation”) and a different compressibility law (the Murnaghan equation), so there may be no errors: simply results for a different fluid (see discussion of Sperka et al. 2018 below).

5. Experimental

Direct confirmation of these film thickness predictions was made using disc machines, initially from oil flow measurements [28], then more comprehensive measurements were made by shining X-rays through the oil gap [29], or by measuring the capacitance between the discs [10], which gives an average film thickness, or monitoring the varying capacitance between evaporated strips on the discs, which, at least qualitatively, confirms the predicted shape with its exit constriction [30]. General satisfaction with the agreement between experimental values, numerical solutions, and Ertel’s theory was perhaps partly due to the use of a film thickness parameter with a range of 100, where as noted above, a factor 2 discrepancy seemed minor. Comparison of the exponents in power law curve-fits again showed only “general agreement”. However, the important point, then, was that the oil-film existed!

Extending the capacitance techniques to point contacts is unsatisfactory because of the stray capacitances (much more serious in three dimensions), but fortunately this technique became unnecessary with the introduction of optical interference methods—essentially the use of Newton’s rings.

5.1. Optical EHL

Newton’s rings depend on the path difference between light reflected at the glass/air interface and that reflected at the air/steel interface, but it is essential that the amplitudes of the two beams are comparable. For a glass/air interface, the two refractive indices are substantially different and there is a strong reflected beam, but oil and glass have similar refractive indices, giving a weak reflected beam and consequently poor fringes. To overcome this, a thin, semi-transparent reflecting layer must be deposited on the glass (or preferably synthetic sapphire, with a higher elastic modulus). Much of the development of the techniques was in the Imperial College Lubrication Laboratory [31], but optical EHL rigs are now common, almost invariably for contact between a ball and a rotating disc.

The fringes show a central area recognisable as the “Hertz” contact, but within this a central band which is almost flat, but terminating in an exit constriction with a reduced film thickness much as predicted for a line contact, but in addition there are side lobes with usually, but not invariably, a very much reduced film thickness. Advances in computing techniques and computer speeds have enabled matching contour maps to be found numerically.

We note a minor inconvenience of optical EHL: the contours are unlabelled! To some extent this is circumvented by using white light, for the contours are separated by an integer multiple of the wavelength, resulting in recognisable differences between the appearance of the first few contours; but the main technique is simply to increase the running speed gently, keeping careful count as the contours change. There is also the need to rely on the Lorenz-Lorentz relation between the refractive index and density to predict the refractive index at the relevant pressures. A third inconvenience may offend the practical engineer: one surface must be transparent, so steel/steel contacts cannot be studied. That the elastic modulus of sapphire discs is not too far below that of steel is some defence.

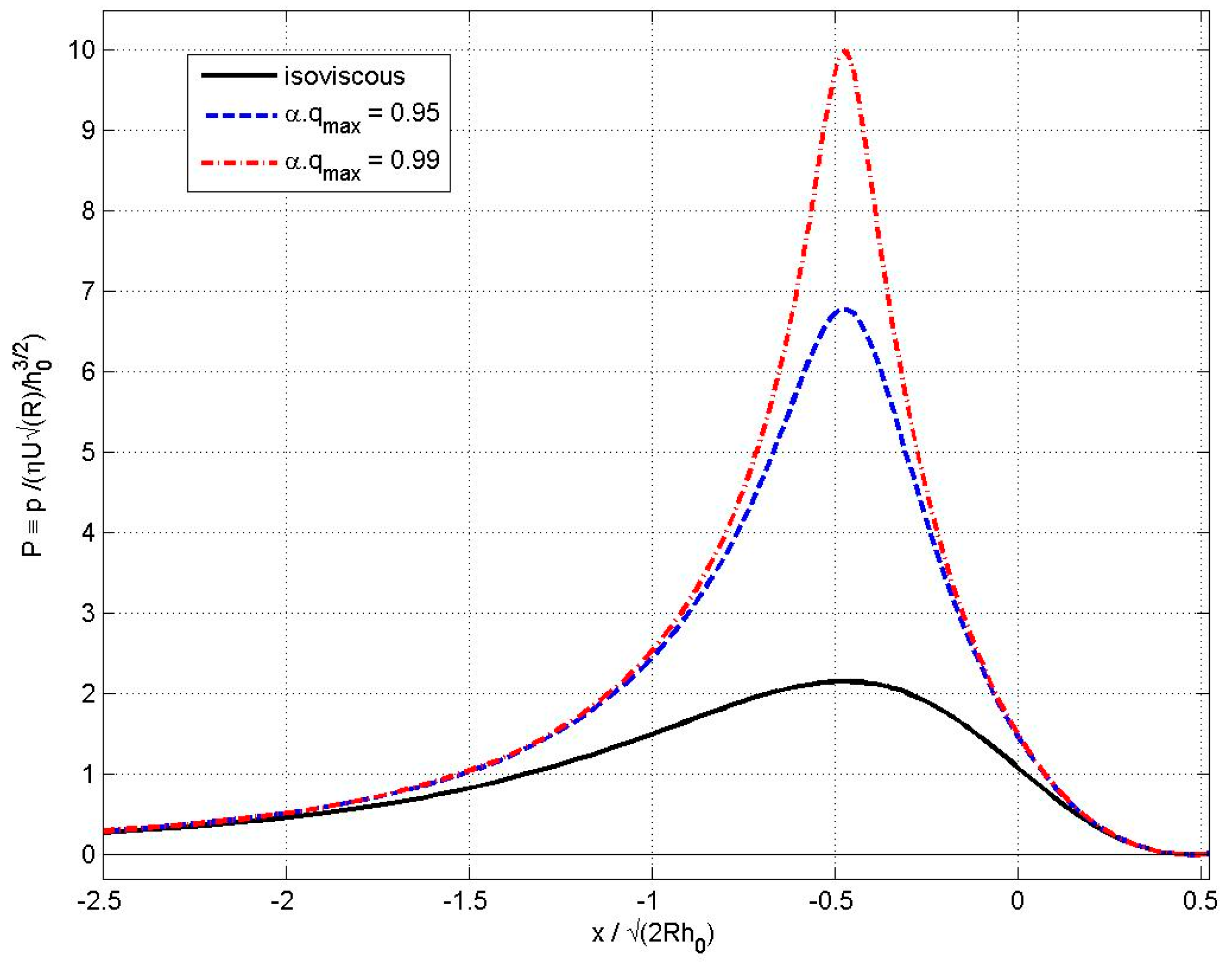
5.2. Pressure Spikes and Minimum Film Thickness

The visual impact of optical EHL is no reason to forget the discoveries of experiments on rollers using sensitive pressure and capacitance transducers bonded to one of the rollers. Hamilton and S.L. Moore [32] believed they had constructed a pressure transducer capable of resolving the predicted pressure spikes: but found only much smaller spikes (the first pressure spikes ever observed); their simultaneous film shape measurements found $h_{\min }$ to be much closer to $h^{\ast }$ than predicted. The exit constriction was correspondingly longer than calculated. Hirst & A.J.Moore [33] pointed out that even in pure rolling, the Reynolds equation implies shear stresses reaching $(h/2)(dp/dx)$; they argued that the critical shear stress found in their traction measurements (typically 10 MN/m²) was below the shear stress required to generate the pressure spike (which needed 10 MN/m² on the leading edge of the predicted pressure spike but 100 MN/m² behind it!). They concluded that because of the modest pressures in the inlet where the central film thickness is determined (it is the lubricant flow rate $\rho h^{\ast }$ which is determined in the inlet), the values found by analysis using a Newtonian fluid should be acceptable, but that to predict the minimum film thickness (or the size of the pressure spike) a non-Newtonian model must be used. Despite this, much effort, both numerical and analytical, has been put into studying the height (or finiteness) of the pressure spike.

Even more have attempts to predict the minimum film thickness using a Newtonian fluid. There is some agreement that for point contacts the correct way to find the minimum film thickness is through a detailed study of the ratio $h_{\min }/h_{cen}$ (minimum to central film thickness). Sperka et al. [34] investigated the ratio for circular contacts for an extensive range of values of L and M, and offered a curve-fit to their calculated results $h_{cen}/h_{\min }=1+0.1{\alpha }_f{}^{0.128}{M}^{0.38}-\sqrt{M }.\left[({\alpha }_f^{0.2}\ln (L)-3)/22.7{]}^2\right]$.

The term ${\alpha }_f$ needs some explanation. When the Barus viscosity law $\eta ={\eta }_0\exp (\alpha p)$ is replaced by a more complicated law such as the Roelands law, then in effect the constant α becomes a variable. Blok long ago suggested that to make calculated results from different viscosity laws comparable, an equivalent pressure/viscosity index must be used, and he proposed a quantity ${\alpha }^{\ast }$ defined by ${({\alpha }^{\ast })}^{-1}=I(\infty )\equiv {\displaystyle {\int }_0^{\infty }\frac{{\eta }_0}{\eta (p)}}dp$, and it is usually this quantity, not ${\alpha }_0$, which is used in $G_D=\alpha E^{\prime }, P=\alpha p_0$ etc. Bair et al. [35] argued that since the film thickness is determined by the pressures in the inlet, Blok’s upper limit is too high, and the integration should only be to $3/{\alpha }^{\ast }$ replacing Blok’s $I(\infty )$ by $I(3/{\alpha }^{\ast })\equiv {\displaystyle {\int }_0^{3/{\alpha }^{\ast }}\frac{{\eta }_0}{\eta (p)}dp}$. However, if the example of Blok’s definition ${\alpha }^{\ast }\equiv 1/I(\infty )$ were followed and ${\alpha }_f$ defined as $1/I(3/{\alpha }^{\ast })$, then for a Barus fluid (where ${\alpha }^{\ast }=\alpha$), we should have the unsatisfactory result ${\alpha }_f=\alpha /(1-e^{-3}).$ To avoid this, Bair defines ${\alpha }_f\equiv (1-e^{-3})/I(3/{\alpha }^{\ast })$. ${\alpha }_f$ is proposed as the new universal pressure/viscosity index.

Thus, for the three fluids considered in [34], with ${\alpha }_0=11, 22, 33$ GPa⁻¹ the Roelands law used gives ${\alpha }_f=8.7, 20.6, 32.7$ GPa⁻¹, and it is these three numbers, with no units, which are to be inserted into the equation. More accurately, what is inserted into the equation is the ratio (${\alpha }_f/I$) where $I$ is the dimensioned quantity 1 GPa⁻¹; units have been introduced into the non-dimensional equation. To put this differently, the ratio of film thicknesses depends on the length of a bar of platinum in a cellar in Paris! Now of course the authors’ method works: but what can the calculated film thickness ratio really depend on? An immediate possibility is on the ratio ${\alpha }_{rat}\equiv {\alpha }_{film}/{\alpha }_0$, and happily we find that ${(“{\alpha }_f”)}^{0.2}\approx 2{\alpha }_{rat}$, so the equation can be rewritten $h_{cen}/h_{\min }=1+0.1 {(2{\alpha }_{rat})}^{0.625}{M}^{0.38}-\sqrt{M }·\left[(2{\alpha }_{rar})·\ln (L)-3)/22.7{]}^2\right]$.

We find that this equation is just as good a fit to the data tabulated by the authors as the original. (The power in the second term has been adjusted from 5 × 0.128 to (slightly) improve the fit (actually slightly better: [2.86%, 3.52%, 3.75%] instead of [3.02%, 3.76%, 3.71%]).)

Figure 13 shows how the film thickness ratio varies with load and speed for the authors’ case (3); ${\alpha }_0=33 {\mathrm{GPa}}^{-1}$. It differs from the authors’ figure only in the choice of axes, though that brings out that very extensive ranges of L and M do not cover what might be thought a useful (P, L) area.

Please note that the classical belief that the minimum is 20% to 30% less than the central value (contours 1.2 to 1.4) holds only in a very limited region. The white area is because the data in [34] is limited to M ≤ 1000, and the plot may already have been extrapolated too far: surely the film thickness ratio cannot increase further? The curved contours near the origin hint that they might return into the white area, so the ratio may well decrease there.

Sperka et al. [34] carried out optical film thickness experiments to accompany the numerical work. The agreement between the two is only moderate except for case (3) (that shown in the figure), for which 2.2% accuracy was found. However, undoubtedly film thickness ratios up to 2.6 are measured: so perhaps some lubricants may show Newtonian behaviour.

5.3. Effects of Sliding and Oil Properties

When the two surfaces move at different speeds, as of course gears do except at the pitch point, the shearing of the oil produces heat. This produces a temperature rise in the oil as well as raising the temperature of the bearing/gear surfaces, both of which reduce the oil viscosity. It should be clear from the above that the film thickness is determined by the behaviour in the inlet, so the direct effect on the film thickness is small, but temperatures in the parallel channel will be higher. Calculations suggest that the only effect on the central film thickness will be due to the resulting change in ${\eta }_0$ (and perhaps in $\alpha$), and that the film thickness should be calculated using the oil properties at the inlet temperature, estimated as best one can! (Experimentally, a thermocouple dragging on the surface helps.)

The oil is also heated to some extent in the inlet, even in a rolling contact, since the reduction in the gap height in the inlet is itself a form of shearing: but this effect is only serious at very high speeds. A good estimate of the reduction factor is given by the equation $f={(1+0.46X)}^{-0.45}$, where $X\equiv ({\overline{u}}^2/K)\left|-d{\eta }_0/d\theta \right|$, $K$ being the thermal conductivity of the oil, itself dependent on temperature and pressure [36].

As noted above, lubricating oils are shear-thinning (we shall see later in the discussion of traction that the problem of non-Newtonian behaviour is much worse in the high pressure region). This does not usually affect the central film thickness, except that the viscosity increase in mineral oils due to polymer additives may disappear completely under EHL conditions.

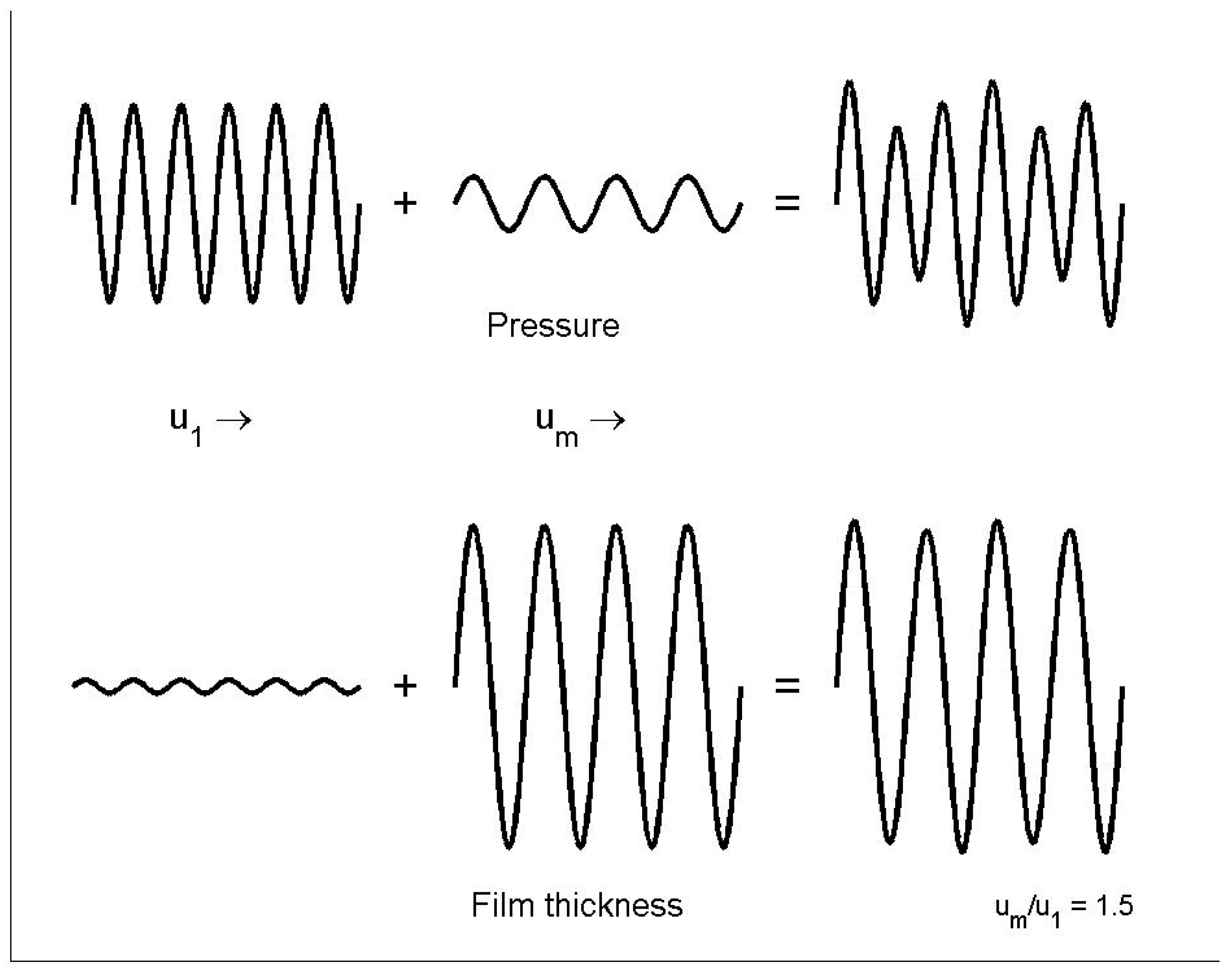
6. Surface Roughness

The desire to know the film thickness was of course to ensure that it exceeded the surface roughness, and traditionally the “lambda ratio” $\mathsf{\Lambda }=h_{\min }/R_q$ has been studied, where $h_{\min }$ is the predicted minimum film thickness for smooth surfaces and $R_q$ is the centre-line average (cla) roughness. Values of $\mathsf{\Lambda }\ge 3$ were recommended, but were often found to be unachievable and not necessary, and lower values ($\mathsf{\Lambda }~1-2$) were allowed, with warnings about reliability and to avoid substantial sliding speeds. However, of course $\mathsf{\Lambda }<1$—(a film thickness less than the roughness!) is absurd—and yet successful operation is usually achieved. So what is wrong with the lambda ratio concept?

Some effort has been put into finding and solving a modified Reynolds equation applicable to rough surface lubrication, but always regarding the roughness as given. However, when computing techniques advanced to the point when it became possible to solve the EHL problem of sliding over a single, stationary, rough surface, surprising results were found [37]. (All deformation was assumed to be elastic, and heating effects were ignored.) The roughness was largely eliminated, to give almost a uniform gap with the predicted smooth surface film thickness $h^{\ast }$ (and little sign of an exit constriction). Optical EHL experiments gave general support to the numerical findings [38]. In contrast, the pressures resembled a grossly magnified surface roughness profile, superimposed on the Hertz pressure distribution. Thus, the problem was transformed from worrying about scuffing failure to worrying whether the violent pressure fluctuations could lead to a fatigue failure.

To understand this behaviour, we must return to the Ertel argument that at the high pressures of an EHL contact, the viscosity is so high that the Poiseuille term in the Reynolds equation can be neglected, so the line contact Reynolds equation becomes simply $h=h^{\ast }$; because the fluid flow rate is constant along the channel, the film thickness must also be constant, even if the surface is rough! There must be additional pressure fluctuations to provide the necessary elastic deformation.

To allow a simple treatment [39,40], we consider a sinusoidal roughness $z(x)=z_1 \sin (2\pi x/\lambda )$ on the stationary surface: then the elastic deflection $u(x)$ must equal the roughness $z_1 \sin (2\pi x/\lambda )$. To find the pressures needed to do this, we use the answer for the pressures needed to flatten an infinite wavy surface, where it is well-known that a pressure $p_1 \sin (2\pi x/\lambda )$ gives a deformation $u(x)=(2\lambda p_1/\pi E^{\prime }) \sin (2\pi x/\lambda )$, so immediately $p_1 =(\pi E^{\prime }/2\lambda ) z_1$, and this is a good approximation to the answers obtained in full numerical analyses.

However, this is not the complete story. The Reynolds equation is not properly a statement about the volume flow rate but about the mass flow rate, and should be $\frac{\partial }{\partial x}\frac{\rho h^3}{12\eta }\frac{\partial p}{\partial x}+\frac{\partial }{\partial y}\frac{\rho h^3}{12\eta }\frac{\partial p}{\partial y}=U\frac{\partial (\rho h)}{\partial x}$, and for EHL pressures we can no longer treat the density $\rho$ as a constant. Then with Ertel’s observation that the Poiseuille terms can be neglected, the equation reduces to a simple $U\frac{\partial (\rho h)}{\partial x}=0$; it is the product $\rho h$ which is constant, not the film thickness itself.

If the density obeys the law usually assumed in EHL studies, $\rho /{\rho }_0=(1+\gamma p)/(1+\beta p)$, then the bulk compressibility of the fluid $B\equiv \rho (dp/d\rho )$ will be $B\equiv \overline{p}/C$ where $C=1/(1+\beta \overline{p}) - 1/(1+\gamma \overline{p})$. Then for small pressure variations the density variations can be taken as $\rho /\overline{\rho }\approx 1+C(p-\overline{p})/\overline{p}$ (with the usual values $\gamma =2.266\times {10}^{-9}, \beta =1.683\times {10}^{-9}{m}^2/N$, we get $C=0.0665$ when $\overline{p}=1 GN/m^2$).

Consider now a smooth geometry with a film thickness $\overline{h}$ and a uniform pressure $\stackrel{\rightharpoonup }{p}$ (which could be the mean Hertz pressure {$\pi p_0/4$ in line contact}). We assume the additional pressures to be small (although we shall find they are not!), so that if the pressure fluctuations are also sinusoidal $(p-\overline{p})=p_1\sin (kx)$, then so will be the density variations: $\rho /\overline{\rho }\approx 1+C(p_1\sin kx)/\overline{p}$.

Then $\rho h=\overline{\rho } \overline{h}$ gives $\frac{\rho }{\overline{\rho }}= \frac{\overline{h}}{h}$; and $h=\overline{h}-z+\mathrm{v}$ so $\frac{\overline{h}}{h}\approx 1 + \frac{z}{\overline{h}}-\frac{\mathrm{v}}{\overline{h}}$. Thus, $1+C p_1\sin (2\pi x/\lambda )/\overline{p}=1+(z_1/\overline{h})\sin (2\pi x/\lambda )-(2\lambda p_1/\pi E^{\prime } \overline{h})\sin (2\pi x/\lambda )$ or $C(p_1/\overline{p}) + (2\lambda p_1/\pi E^{\prime } \overline{h})=(z_1/\overline{h})$.

Thus, $\frac{p_1}{\overline{p}}=\frac{1}{C+A}\frac{z_1}{\overline{h}}$ where $A\equiv \frac{2\lambda \overline{p}}{\pi \overline{h}{E}^{\prime }}$, relating the amplitude of the pressure fluctuations to the amplitude of the roughness ripples, and perhaps more impressively, $\frac{h-\overline{h}}{z_1}=\frac{C}{C+A}$. Since $\frac{C}{A}\equiv \left(\frac{1}{1+\beta \overline{p}}-\frac{1}{1+\gamma \overline{p}}\right)·\frac{\pi E^{\prime }}{2\overline{p}}\frac{\overline{h}}{\lambda }=24\frac{\overline{h}}{\lambda }$ for $\overline{p}=1 GN/m^2$, and decreases if $\overline{p}$ increases, we conclude that the compressibility contribution is usually small compared to the elastic contribution, except for very short wavelengths. Thus, compressibility does prevent the complete reduction of the roughness, but leaves the prediction of the amplitude of the pressures largely unchanged.

We note (applying the results far beyond the validity of the analysis!) that if $z_1=\overline{h}$ when we naively expect solid contact at the roughness maxima, no problems would arise.

The analysis above can easily be extended to a roughness of any form, or to a bump or dent, by representing the roughness by a Fourier series and using superposition (for elastic theory is linear and we have linearised the compressibility). Good agreement is obtained for small amplitude features [40], but when the pressure variation is so large that pressures approaching (or below!) zero are predicted, the agreement becomes poor.

However, this proves to be only the beginning of the story. Hooke [41] derived more complete equations for the attenuated roughness, which for line contact become: $\frac{h-\overline{h}}{z_1}=\frac{1-i\stackrel{⌢}{C}Q}{1-iQ-i\stackrel{⌢}{C}Q}$, where $\stackrel{⌢}{C}\equiv \pi E^{\prime }h/(2\lambda B)$ (and so equals $C/A$); and $Q=\frac{12}{{\pi }^2}\frac{\eta u_s}{h}\frac{1}{\stackrel{\rightharpoonup }{E}}\frac{{\lambda }^2}{h^2}$, where $u_s$ is the sliding speed. (The complex form accounts for the phase change needed when reconstructing the result for a general roughness from its Fourier components.). If $Q\to \infty$ this reduces to $\frac{h-\overline{h}}{z_1}=\frac{\stackrel{⌢}{C}}{1+\stackrel{⌢}{C}}$, which is just the earlier result [39]. In addition, for a Newtonian fluid, $Q$ is indeed enormous. However, note the factor $\eta u_s/h$, which is the shear stress. With the enhanced viscosity ${\eta }_0\exp (\alpha p)$ this is usually orders of magnitude greater than the yield stress of steel: the oil cannot be a Newtonian fluid under these conditions, but must be shear-thinning. This will be discussed at length under “Friction”; here we note only that Hooke [42] showed that the shear stress could be replaced by a limiting value ${\tau }_0$, independent of speed, and representing either the “Eyring stress” or a limiting shear stress. Then $Q$ becomes $Q=\frac{6}{{\pi }^2}\frac{{\tau }_0}{\stackrel{\rightharpoonup }{E}}\frac{{\lambda }^2}{h^2}$ and is finite, so the full form of the attenuation equation must be used. In addition, by some very impressive optical EHL experiments, Sperka et al. [43] found good agreement with the theory.

6.1. Moving Roughness

If the roughness is on a moving surface, the response becomes more complicated, and indeed, when the first numerical solution for sliding with a moving dent appeared, the results are very hard to believe [44,45]. For the (attenuated) dent and the associated pressure fluctuation became completely separated! The problem is no longer one of steady motion, and the relevant (line contact) Reynolds equation becomes $\frac{\partial }{\partial x}\frac{\rho h^3}{12\eta }\frac{\partial p}{\partial x}=\overline{u}\frac{\partial (\rho h)}{\partial x}+\frac{\partial (\rho h)}{\partial t}$ or, again dropping the Poiseuille term, $\overline{u}\frac{\partial (\rho h)}{\partial x}+\frac{\partial (\rho h)}{\partial t}=0$. This is a simple transport equation, with a solution $\rho h=f(x-\overline{u}t)$, as well as the simple solution $\rho h=\mathrm{const}$. This is often called the “particular integral”, and is indeed the solution we just found for stationary roughness, except that now it (the pressures and the displacements) moves through the contact with the speed of the surface carrying the roughness. In effect, the moving roughness (speed $u_1$) is replaced by a moving pressure pulse (speed $u_1$). However, any solution of the form $\rho h=f(x-\overline{u}t)$ (the “complementary solution”) can be added [46].

Numerical solutions showing typical behaviour are shown in [44]. To understand this, we need to think about the inlet, and unfortunately, we know rather little about it. However, it is clear that each ridge of the surface roughness; however much attenuated, is going to deliver a varying amount of fluid to the parallel gap, and that this must be accommodated. A sine wave entering the inlet moving at speed $u_1$ must deliver fluid at a frequency $u_1/\lambda$, but it must be carried down the channel at a speed $\overline{u}$, so the pumped fluid must have a wavelength ${\lambda }^{\prime }\equiv \overline{u}/(u_1/\lambda )=\lambda (\overline{u}/u_1)$. Some success in predicting its amplitude has been achieved [47], but currently it seems safer to rely on numerical solutions [48], which suggest the fluid flow can be represented by an attenuated roughness with amplitude given by $z_2/z_1={(1+0.125\overline{\nabla }+0.04{\overline{\nabla }}^2)}^{-1}$ where $\overline{\nabla }\equiv (\lambda /b)({(2\pi )}^{3/4}{P}^{3/2}/L^2\sqrt{u_1/\overline{u}} )$ (recall $L=2^{1/4}S$). The surface amplitudes given by this Lubrecht-Venner equation are just the elastic deflections due to the varying pressures, so directly the amplitude of the pressure (it might be more fundamental to regard the action of the input as pumping a fluctuating volume of lubricant into the channel, where it must be accommodated just as for the removal of the actual roughness by a combination of compression and deformation. If we knew the pumped mass flow $<\rho h> \equiv r\sin (2\pi (x-u_{1}t)/\lambda )$, the amplitude of the necessary pressure variations would then be $\frac{p_2}{\overline{p}}=\frac{1}{C+A^{″}}\frac{r}{\overline{\rho } \overline{h}}·$) is $p_2=z_2 {[2{\lambda }^{\prime }/\pi E^{\prime }]}^{-1}$, or $\frac{p_2}{\overline{p}}=\frac{1}{A^{″}}\frac{z_2}{\overline{h}}·$ where $A$ is now based on the new wavelength ${\lambda }^{\prime }\equiv \lambda (\overline{u}/u_1)$ and so becomes $A^{″}\equiv \frac{2\overline{p}}{\pi \overline{h}{E}^{\prime }}·\frac{\lambda \overline{u}}{u_1}$.

In Figure 14, the left-hand pair represents the Particular Integral, which moves at the speed $u_1$ of the rough surface: below, the film thickness (much smaller than the roughness because of the elastic deformation) and above, the large pressure variations needed. The centre pair is the C.F., which moves at the mean speed $u_m=1.5u_1$ ($u_2=2u_1$). Below is the attenuated initial roughness (attn $\times 0.3$) and above, the relatively small pressures needed to produce it. The right hand pair shows the combination; both curves vary because of the differing speeds, but because of the relative magnitudes, the film thickness appears to move at $u_m$ (and be long wavelength), while the pressure variations move with the rough surface at $u_1$.

This is relatively easy to understand. However, using Fourier analysis, a discrete feature such as a bump or a dent can be represented by a set of waves, again with the same two speeds. This can lead to the pressures triggered by the feature reaching the end of the channel and disappearing, while the feature, still in the channel, travels along with “no” effect (for both surfaces moving, but the rough one the slower, so $u_m>u_1$). However, if the rough surface is faster, then $u_m<u_1$ and the feature may exit the channel, leaving behind an “inexplicable” pressure pulse!

However, it is not clear how much of the above is real and not just “computer games”! For we shall see when we consider traction that we cannot assume the fluid in the “Hertzian” channel to be a Newtonian fluid, with the enormous viscosity we have been assuming to explain the film thickness, for then the friction would become impossibly high. Studies of waviness using one form of fluid behaviour, an Eyring fluid (see below), show that while the pressure predictions remain, the roughness is no longer removed. However experiments [45] using optical EHL (with a mineral “bright stock” oil) do indeed seem to support the theory (But, of course they cannot confirm the detachment of dent from pressure; only the film shape is available); later experiments [49,50] show agreement with a theory modified for a non-Newtonian fluid [42]. Corresponding experiments examining the “complementary function”, by choosing a feature and speeds to separate the CF from the PI [49] also show agreement with theory, but it is not clear which of many versions of the theory, especially of the modification for a point contact, should be preferred.

6.2. The Λ Ratio

There remains the vital question of how much of the roughness on a real gear tooth can be removed elastically. My belief (but is it just a hope?) is that most of the long wavelength components can be removed, and usually these contribute the majority of the “roughness amplitude” (the cla roughness). So a Λ-ratio less than 1 is not necessarily disastrous.

Perhaps the feature that comes out most clearly from investigations of the critical Λ-ratio is the lack of attention to the nature of surface roughness. It is absurd to associate contact with rms roughness; what possible connection with contact do the valleys have? Back in 1933 Abbott and Firestone knew better, when they invented the Abbott curve, and divided it into peak, medial and valley zones. Contact occurs at high peaks—wear occurs at high peaks—but the main contribution to rms roughness is from the medial roughness (divide the total height range into the top 10%, the middle 80% and the bottom 10%; then the surface area in the middle section is the medial roughness). Hansen et al. [51], by relocation profilometry, showed clearly where contact and wear has taken place, and will not take place again; the minimal change to the rms roughness is self-evident. Not surprisingly, they report successful operation with a Λ-ratio of 0.33.

Other assessments are perhaps more realistic. The conclusion reached by Cann et al. [52] “the Λ criterion [is] at low values inapt, leading, perhaps, to an overly conservative or widely optimistic view of the level of lubrication” after they decide that the film-thickness prediction $h$ is untrustworthy because of non-Newtonian effects (especially with grease), and starvation, and that the roughness $\sigma$ is irrelevant because the roughness is composed of a spectrum of amplitudes, all contributing to the cla (or rms), but not all present in the high pressure region. Jacobson [53] reinforces the worries about the effect of starvation on the film thickness: but also emphasises that surfaces will often run-in to a well-lubricated state, but that sometimes they do not!

Despite problems over whether in general the Λ-ratio does or does not indicate contact, attempts have been made to link contact with friction. Clarke et al. [54], using electrical contact resistance as an indicator of contact, plot a delightful pair of graphs, the first showing how there is negligible contact for $\mathsf{\Lambda }\ge 1$, but a dramatic fall to full contact (actually to zero contact resistance) as the rolling speed is reduced and $\mathsf{\Lambda }$ falls to 0.5. The second shows the measured friction, falling slightly as $\mathsf{\Lambda }$ increases from 0.5, with no signs of any distinction between the values for $\mathsf{\Lambda }\ge 1$ (full film?) and those for $\mathsf{\Lambda }$ between 0.5 and 1 (partial contact?). Zapletal et al. [55] show the relative contact area (based on optical EHL measurements) rising from zero for $\mathsf{\Lambda }<0.7$, but friction rising steadily from the full-film value for $\mathsf{\Lambda }<3$. So it appears that roughness can increase friction without contact occurring! (Both studies are for a ball on a plane. We note wryly that while [54] uses the Chittenden et al. film thickness equation, based on point contact film thickness calculations for many geometries including circular contacts, [55] uses the earlier Hamrock and Dowson equation, based almost entirely on elliptical contact solutions ($a/b=6$) and on a single solution for a circular contact, and it differs by 4% from the curve fit. However, such a change is not important.)

7. Friction

It is not clear how much notice need be taken of film thicknesses, whether calculated or measured: engineers built and used gears very happily when lubrication theory predicted film thicknesses far below the known surface roughness; and while it is perhaps satisfactory to know that gear lubrication is possible, it is no great surprise. Of course, an approximate value is needed, for the shear stress is the ratio of the sliding velocity to the film thickness. It does not depend, as most authors seem to believe, on the slide/roll ratio. This may be unfair, for the film thickness depends approximately on the two-thirds power of the rolling speed, so $\frac{\left|u_2-u_1\right|}{h}\cong \frac{\left|u_2-u_1\right|}{\left|u_2+u_1\right|}$, roughly!

7.1. Thermal Effects

More important is the prediction of friction, and now that we have EHL theory and an exponential viscosity increase, this is a problem. For we now know that we essentially have a long parallel channel containing oil with an enormous viscosity [$\eta ={\eta }_0\exp (\alpha p_0)$], suggesting a friction force $(2b)\eta U_s/h$, where $U_s$ is the sliding speed $U_s\equiv \left|u_1-u_2\right|$, and this is impossibly large. However, this energy dissipation increases the oil temperature, and so decreases the viscosity. Crook [56] showed that although for thrust or journal bearings the heat is carried away by the hot oil leaving the bearing (and where of course the oil temperature rise is often a design parameter), under EHL conditions the heat flow is across the film to the bearing surfaces, and the heat is then convected away by the moving parts.

Crook [57] derived a simple implicit equation for the temperature rise across the film:

$U_s=\sqrt{{\displaystyle {\int }_{{\theta }_1}^{{\theta }_c}\frac{2K}{\eta (\theta )}}d\theta }+\sqrt{{\displaystyle {\int }_{{\theta }_2}^{{\theta }_c}\frac{2K}{\eta (\theta )}}d\theta }$ where ${\theta }_1, {\theta }_2$ are the temperatures of the surfaces, and ${\theta }_c$ is the maximum oil temperature and $K$ the thermal conductivity of the oil, and derived a corresponding equation for the shear stress. Here we shall take the two surface temperatures to be the same, so Crook’s equations become $U_s=2 {\left\{{\displaystyle {\int }_{{\theta }_1}^{{\theta }_c}\frac{2K}{\eta (\theta )}}d\theta \right\}}^{1/2}$ and $\tau ·h=2{\displaystyle {\int }_{{\theta }_1}^{{\theta }_c}2K} {\left\{{\displaystyle {\int }_{\theta }^{{\theta }_c}\frac{2K}{\eta (\theta )}}d\theta \right\}}^{-1/2}d\theta$.

If we assume the oil thermal conductivity to be constant and the viscosity to obey $\eta ={\eta }_1\exp (-\gamma \theta )$, so that ${\eta }_1$ is the viscosity at the temperature of the surfaces, still increased by the pressure term $\exp (\alpha p)$], we obtain $U_s=2\sqrt{\frac{2K}{\gamma {\eta }_1}} X$ and $\tau ·h=2\sqrt{\frac{2K{\eta }_1}{\gamma }}\frac{{\sinh }^{-1}X}{\sqrt{1+X^2}}$ where $\gamma ({\theta }_c-{\theta }_1)=\ln (1+X^2)$. Figure 15 shows the resulting traction.

It must be emphasised that this graph is very much a half-truth. As well as the simplification of assuming the two surfaces to be at equal temperatures, the temperatures have been taken as fixed. In practice they will not be equal, and will be higher when the sliding speeds and thus the heat generation increase: at high sliding speeds the curve will be misleadingly high. However, it does illustrate the important point that one must not refer to the oil film temperature: the markers give the difference between the maximum oil temperature (in this case mid-film) and the oil temperature at the surface. With a typical coefficient $\gamma =0.02$ as assumed by Crook, there is already, at the curve maximum, a 50 °C temperature difference within (across!) the oil!

However, of course a disc machine does not measure shear stress, but only traction, and this shear stress prediction is for a particular combination of pressure and surface temperatures. To predict the traction, the shear stress must be integrated along the contact, taking account of the pressure variation (including the pressure spike!). However, the surface temperatures (${\theta }_1$ and ${\theta }_2$) must also be calculated by the usual methods of flash temperature calculation for sliding contacts. The general results are unchanged: the expected proportionality between sliding speed and shear stress holds only for low sliding speeds. The shear stress and the traction reach a maximum, and then fall as the sliding speed is increased further. For moderate pressures and rolling speeds the final predictions agree qualitatively with experiment [57,58].

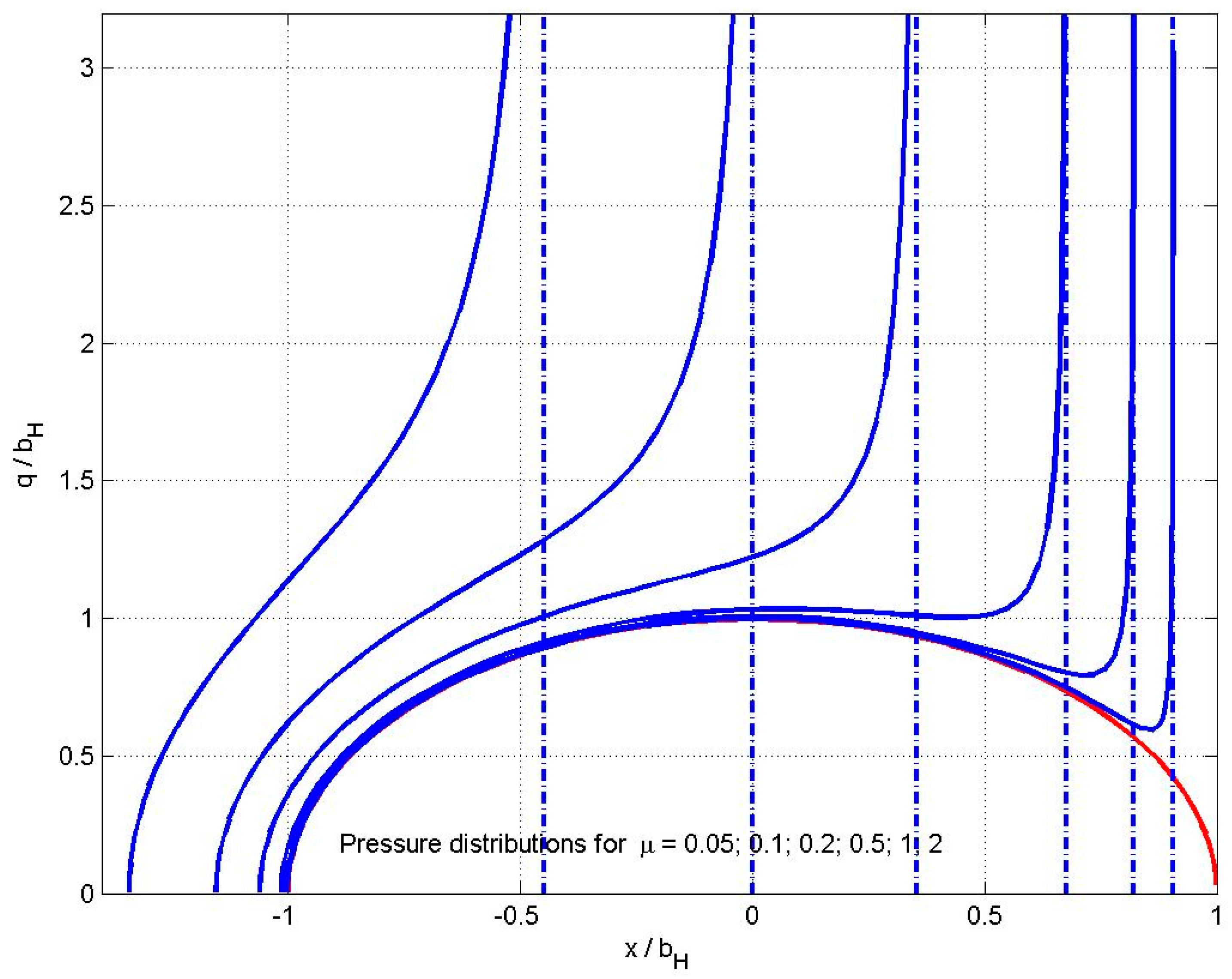
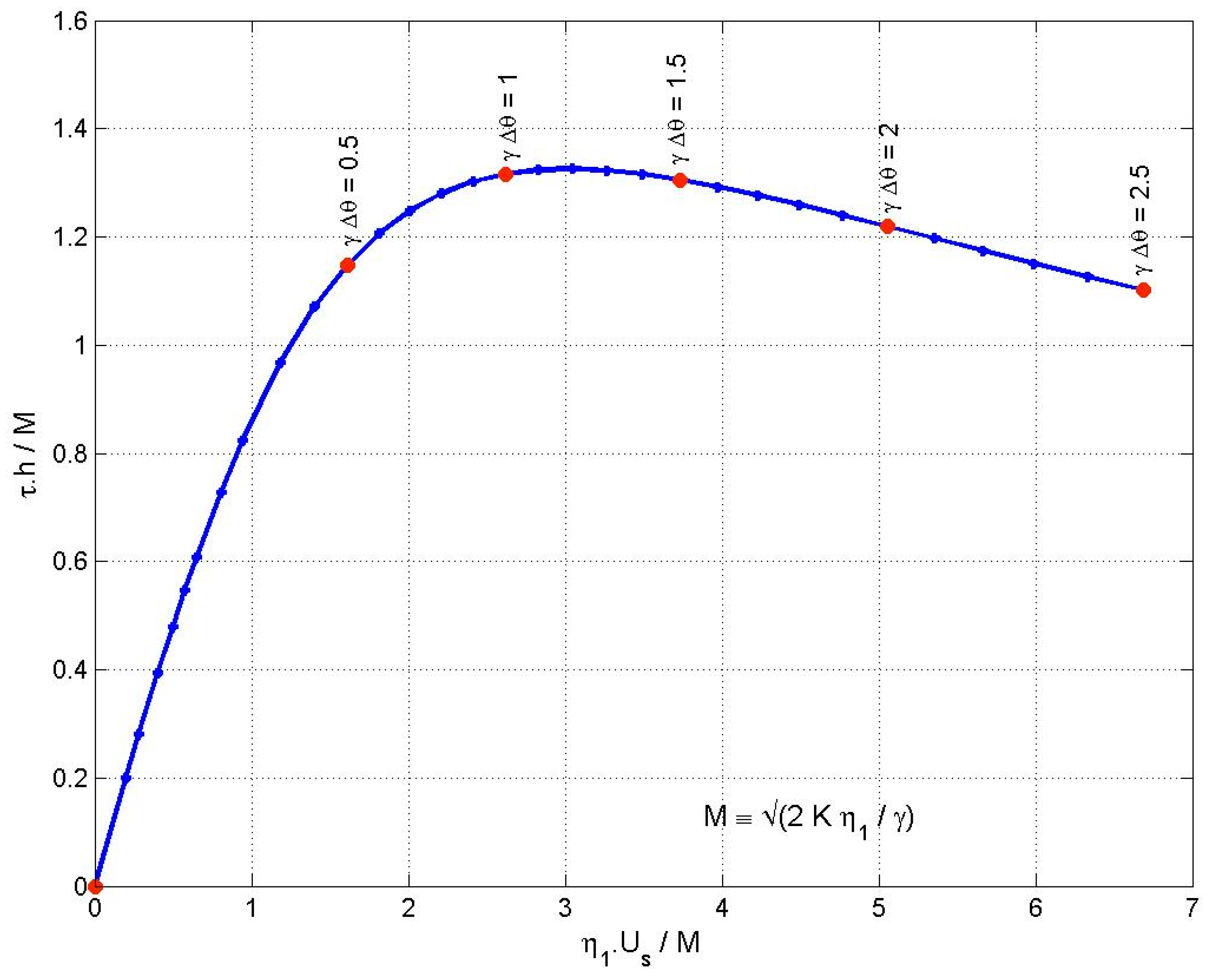
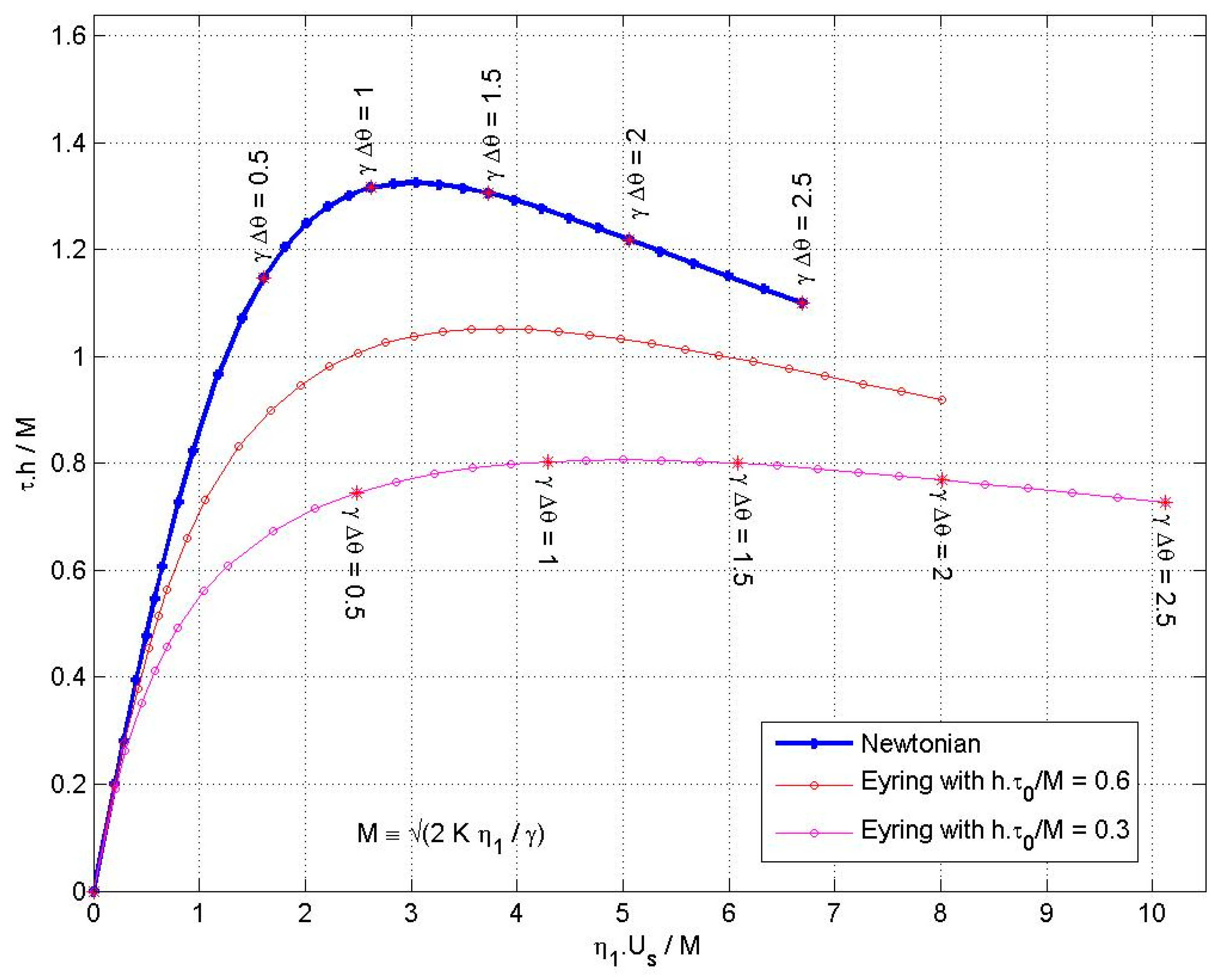
7.2. Non-Newtonian Behaviour

For thinner films (higher pressures and lower rolling speeds) the predicted traction is too high, and the maximum occurs at lower sliding speeds than predicted: the oil must be showing some form of non-Newtonian behaviour!

One explanation is that the oil is an “Eyring fluid” with a shear-stress/shear-strain behaviour predicted by the Eyring thermal activation energy theory of fluid flow. According to this, the strain rate $\dot{\gamma }$ obeys a relation $(\eta \dot{\gamma })={\tau }_0\sinh (\tau /{\tau }_0)$, where $\eta$ and ${\tau }_0$ are related to molecular properties. Eyring’s theory predicts the exponential increase of $\eta$ with pressure, and an exponential decrease with (1/T). It seems clear that in the physical chemistry world the predicted hyperbolic sine was not taken seriously; that $\tau /{\tau }_0$ was assumed to be small so that $\sinh (\tau /{\tau }_0)\approx \tau /{\tau }_0$, and this was an explanation of Newtonian behaviour. In contrast, in EHL the Eyring theory is treated seriously, and the full $\eta \dot{\gamma }={\tau }_0\sinh (\tau /{\tau }_0)$ is used, typically with ${\tau }_0=4 {\mathrm{MN}/\mathrm{m}}^2$, but probably increasing with pressure.

When Crook’s thermal analysis is repeated using the Eyring relation [59], the results are $U_s=2 \sqrt{\frac{{\tau }^{\ast }}{\tau }} {\left\{{\displaystyle {\int }_{{\theta }_1}^{{\theta }_c}\frac{2K}{\eta (\theta )}}d\theta \right\}}^{1/2}$ and $h·\tau =2 \sqrt{\frac{\tau }{{\tau }^{\ast }}}{\displaystyle {\int }_{{\theta }_1}^{{\theta }_c}2K} {\left\{{\displaystyle {\int }_{\theta }^{{\theta }_c}\frac{2K}{\eta (\theta )}}d\theta \right\}}^{-1/2}d\theta$, where ${\tau }^{\ast }\equiv {\tau }_0\sinh (\tau /{\tau }_0)$; these reduce to the equations for a Newtonian fluid when $\tau /{\tau }_0$ is small, so that ${\tau }^{\ast }\approx \tau$. We write these as $U_s= \sqrt{\frac{{\tau }^{\ast }}{\tau }} F({\theta }_c)$ and $h·\tau = \sqrt{\frac{\tau }{{\tau }^{\ast }}}G({\theta }_c)$. To compare Eyring and Newtonian behaviour, we assume the same $\eta (\theta )$ law for both fluids, and denote the shear stress and the corresponding sliding speed of the solution for a Newtonian fluid by ${\tau }_N$ and $V_s$, so that $V_s= F({\theta }_c)$ and $h·{\tau }_N= G({\theta }_c)$. Then $U_s/V_s= \sqrt{\frac{{\tau }^{\ast }}{\tau }}$ and $\tau /{\tau }_N= \sqrt{\frac{\tau }{{\tau }^{\ast }}}\equiv \sqrt{\frac{\tau /{\tau }_0}{\sinh (\tau /{\tau }_0)}}$. The last equation may be solved iteratively to obtain $\tau /{\tau }_0$ as a function of $\tau /{\tau }_N$, and hence to get $\tau /{\tau }_N$ as a function of ${\tau }_N/{\tau }_0$. Thus, we can scale the Newtonian ${\tau }_N(V_s)$ to obtain the Eyring curve $\tau (U_s)$ by shifting each point to the right by the factor $\tau /{\tau }_N$, and downwards by the factor ${\tau }_N/\tau$ (Figure 16). Please note that while the Newtonian curve is linear almost to $\gamma \Delta \theta =0.5$, the Eyring curve is non-linear well before this (the parameter $h{\tau }_0/M$ used here is the reciprocal of the parameter $\chi$ of the original Johnson and Greenwood paper. Μ is not related to the Moes parameter mentioned earlier).

The reduced shear stresses due to the Eyring behaviour shown above (and much larger reductions can occur) raise the question of whether both methods of reducing the shear stresses must be considered?

An isothermal Eyring analysis for a parallel channel is easily done [60]: the equilibrium condition gives the shear stress across the film as $\tau ={\tau }_1+z·P^{\prime })$ where $P^{\prime }$ is used for the pressure gradient $dp/dx$, and substituting in the Eyring equation gives $\frac{\partial u}{\partial z}=\frac{{\tau }_0}{\eta }\sinh (\frac{{\tau }_1+z·P^{\prime }}{{\tau }_0})$. Integrating and substituting in the boundary conditions on speed leads to $u_2-u_1=\frac{{\tau }_0^2}{\eta P}\left[\cosh \left\{\frac{{\tau }_1+h{P}^{\prime }/2}{{\tau }_0}\right\}-\cosh \left\{\frac{{\tau }_1-h{P}^{\prime }/2}{{\tau }_0}\right\}\right]=\frac{2{\tau }_0^2}{\eta P}\left[\sinh \left\{\frac{{\tau }_1}{{\tau }_0}\right\}\sinh \left\{\frac{h{P}^{\prime }}{2{\tau }_0}\right\}\right]$ from which ${\tau }_1={\tau }_0·\mathrm{arcsinh}\left\{\frac{\eta (u_2-u_1)}{h {\tau }_0}·{\Phi }^{-1}(\{h·\left|P^{\prime }\right|/2{\tau }_0\})\right\}$ where ${\Phi }^{-1}(V)\equiv V/\sinh (V)$.

The rapid increase of sinh(V) with $V$ suggests the possibility of a greatly reduced effective shear rate, but in fact the pressure gradient $dp/dx$ will be of the order $p_0/b$, so the term will be of the order $(h/b)(p_0/{\tau }_0)$. The second factor will be large, typically 500 (2 GN/m²/4 MN/m²), but the first factor will be small (0.2 mm/0.5 µm) giving $V\approx 1$ and $\Phi \approx 1$, so a reasonable approximation is simply ${\tau }_1={\tau }_0·\mathrm{arcsinh}\left\{\frac{\eta (u_2-u_1)}{h {\tau }_0}\right\}$ (especially near the maximum pressure location, where it matters most). Thus, the shear stress steadily increases with sliding speed; the traction decrease found experimentally by Crook, with a maximum found to be too high and at too high a sliding speed in Johnson’s experiments, does not occur. To account for it, both shear-thinning and temperature rise must be allowed for.

Please note that the shear stress on the moving surfaces is not ${\tau }_1$: just as for a Newtonian fluid it is $(h/2)(dp/dx)\pm {\tau }_1$, depending on which surface is the faster. However, with $h$ constant and the pressure effectively zero at each end of the channel, so that ${\displaystyle {\int }_{-b}^b(dp/dx) dx=0}$, only ${\tau }_1$ contributes to the traction.

As noted above, the shear stress curve is merely the first step towards predicting the traction curve, for that requires the integration over the contact area, taking into account the pressure and temperature variations. To some extent an approximate traction curve can be obtained using the shear stress curve for the mean pressure and estimated surface temperatures: and this basis has led experimenters to believe that oil behaviour is even more complex, with in addition to the non-linear relation between shear stress and strain, also a limiting shear stress (and of course steels have a limiting shear stress, so why not oils?). Although earlier it was believed that these were alternatives, favoured by different groups, it now seems that both a shear-thinning mechanism and a limiting shear stress are needed. Even this is not all; under some conditions it seems the oil has an elastic modulus and so gives a viscoelastic response.

Thus, the prediction of the friction force requires many choices.

(1)

It is generally agreed that the Barus equation for the pressure dependence $(\exp \{\alpha p\})$ of the oil viscosity is inadequate. The initial exponential increase is not continued, and this is described by the Roelands (2-parameter) equation [61]. This correctly describes the viscosity up to 0.4 GN/m² and is adequate for (central) film thickness predictions. However, the region where the traction is developed has much higher pressures, and direct measurements up to 1.4 GN/m² in a falling ball viscometer show an upturn in the log(viscosity) curve, so that the Roelands viscosities are then too low, and the Yasutomi equation [62] should be used.

(2)

An equation for the dependence of the viscosity on temperature is needed to allow for the surface temperature rise. The simple $\eta \propto \exp (-\gamma \theta )$ is unjustified at high pressures, and values from the full Roelands equation (which then becomes a four-parameter equation) may be better. However, it is claimed that experimental values require the use of the full Yasutomi equation (which then has eight parameters). A full thermal analysis of the whole configuration to find the surface temperatures is needed.

(3)

Unless the neglect of temperature variations within the oil film is justified, an acceptable equation for the variation of the oil thermal conductivity with pressure and temperature is needed.

(4)

Which non-Newtonian model should be used, and what are its parameters? Are the Eyring stress ${\tau }_0$ (or the limiting shear stress) constants, or do they depend on temperature and pressure?

All the above must then be combined with a full numerical EHL analysis to determine the film thickness and the complete pressure distribution.

What are actually available are full isothermal analyses, using the Roelands equation for the viscosity and the Eyring shear stress model (Jacod [63]). A curve fit over all the manifold cases studied led to a beautifully simple master curve. Oddly, this is published in a form reminiscent of Hooke’s famous publication of “ut tension, sic vis” as an anagram, and it was 10 years later before one of the authors published the solution [64]: that the friction depends on the simple combination ${\tau }_c\equiv 2 \{\eta (p_0)·u_s/h \} / {\tau }_0)$, where $u_s$ is the sliding speed $\left|(u_2-u_1)\right|$ (I malign them: they use the product of the rolling speed and the slide/roll ratio, not the sliding speed), so that this is just (twice) the ratio of the Newtonian shear stress at the pressure maximum to the Eyring stress ${\tau }_0$—the combination already introduced above! Then the master curve is $\mu =({\tau }_0/p_0) {\sinh }^{-1}({\tau }_c/5)$. This is shown to be a good fit to most of the numerical examples, except for slow sliding speeds, where it is suggested that an additional contribution comes from rolling friction, and may generally be neglected. More importantly, experimental measurements were found to lie on the master curve, although in fitting them, the estimates of ${\tau }_0$ from the experimental traction curves (by the original authors) were used. We might note that the factor 5 is of little importance, for because of the factor $\eta (p_0)$, the values of ${\tau }_c$ are enormous, and ${\sinh }^{-1}({\tau }_c/5)~\ln (2·{\tau }_c/5)=\ln ({\tau }_c)-0.9$; the shift $(-0.9)$ is insignificant compared with perhaps $\ln ({10}^{10})=23$.

However, the master curve shows the traction steadily increasing with shear rate: there is no indication of the maximum reported by the experimenters (either a thermal effect or due to reaching a limiting shear stress), or of the subsequent decreasing branch of the curve (surely thermal?). A later publication presents a master curve for a limiting shear stress fluid [65]—this is $\frac{1}{\mu }=\frac{p_0}{{\tau }_0}\left[1+\frac{(4/3) }{{\sinh }^{-1}({\tau }_c^{\ast }/5)} \right]$—but now ${\tau }_c^{\ast }$ is calculated not using $\eta (p_0)$ as ${\tau }_c$, but from the viscosity at a modified (lower) pressure $p^{\ast }$. Experimental results are given, agreeing and showing the traction curve beginning to flatten out. However, in contrast, results from Habchi et al. [66] show a picture more resembling Figure 16, although their calculations include a different form of shear-thinning (see below) and a limiting shear stress as well as thermal effects. Both experiments and calculations (for a steel ball sliding on a steel disc at 2 m/s, p₀ = 0.85 GN/m²) show the friction rising rapidly before levelling out at $\mu \approx 0.07$ (when $u_s\approx 0.2\mathrm{m}/\mathrm{s}$), then the experiment and the full solution show a gentle decrease to $\mu \approx 0.06$ at $u_s\approx 4 \mathrm{m}/\mathrm{s}$. They also present an isothermal solution, and this gives a continuing gentle rise to $\mu \approx 0.075$. However, the authors emphasise the need to use the exact (independently measured) true thermal properties (thermal conductivity and specific heat) of the oil, varying with temperature and pressure, instead of constant values. They emphasise the importance of using real values of viscosity variation throughout the contact rather than using the Roelands equation to describe its dependence on pressure and temperature. They cast doubt on the Crook thermal analysis, arguing that heat convection along the channel is significant, and also assert that heat generated from fluid compression where the pressure is rising, and absorbed during decompression when the pressure falls, must be taken into account. Perhaps the most recent (2019) contribution [67] shows experimental and calculated traction curves for squalane, again using measured fluid properties. There is reasonable agreement, again with a maximum friction coefficient (0.05 at p₀ = 1 MN/m² or 0.07 at p₀ = 2 MN/m²), followed by a gentle decrease.

Both the two last cited contributions [66,67] use yet another shear-thinning law, referred to as the “Carreau equation”. The Carreau equation $\eta ={\eta }_{\infty }+({\eta }_0-{\eta }_{\infty }){(1+{(\lambda \dot{\gamma })}^a)}^{(n-1)/a}$ (but in a general tensor form) is widely used to describe rheology in chemical engineering. Liu et al. [67] do indeed use this, in its basic form with $a=2$ and omitting the term ${\eta }_{ \infty }$, so that no “second Newtonian regime” is included (but is believed to be needed with polymer-thickened oils). With $n<1$ this does describe shear-thinning (they take n = 0.463). In contrast, the equation used by Habchi et al. [66] is $\eta (\tau )=\eta (0).{[1+{(\tau /G)}^a]}^{(1-1/n)/a}$ (with, for Shell T9, G = 7 MN/m², a = 5, n = 0.35.), with the shear stress τ replacing the shear rate $\dot{\gamma }$ as the independent variable, does not seem to be a Carreau equation, but with three fitting constants certainly provides a convenient framework for fitting experimental data.

For comparison, note that the Eyring equation may be written $\eta (\tau )=\eta (0).[(\tau /{\tau }_0) / \sinh (\tau /{\tau }_0)]$, the Eyring stress ${\tau }_0$ replacing $G$: the two equations differ only qualitatively, and the solution procedures will be the same.

However, can it really be true that unless oil companies supply oil accompanied by a complete set of parameters, traction cannot be predicted? (Habchi et al. [66] detailed 18 oil parameters, presumably all oil-specific, plus 4 material parameters). Traction coefficients all seem to reach maxima in the band 0.05 to 0.1, after a linear range at low sliding speeds, and followed by a gentle decrease as the sliding speed increases. Can a simple guide not be derived? Habchi et al. [68] make perhaps the first step at establishing what must be included by eliminating in turn the various factors; in contrast Liu et al. [67] obtain acceptable predictions by simply assuming a Hertzian pressure distribution. Is there hope?

8. Conclusions

EHL theory is now able to predict film thicknesses in heavily loaded contacts, and to explain how these can happen. For this, the classical idea of a lubricating oil as Newtonian fluid, but with its viscosity strongly pressure dependent (to accompany the known temperature dependence) is all that is needed. There remains some doubt as to whether the famous, and embarrassing, pressure spikes are real, and correspondingly the predicted minimum film thicknesses may be somewhat pessimistic.

Surface roughness is seen to be a less immediate threat than traditionally believed, as its amplitude as it passes through the high pressure region will be greatly reduced by elastic deformation: but the associated pressure ripples may “assist” fatigue failure.

In the end, it seems that at present no useful guide to traction for the practising engineer is available. Claims in the literature that traction curves can only be predicted by using full detailed information obtained by direct, independent tests to obtain the detailed variation of oil properties must, one hopes, be pessimistic. Certainly, traction initially rises with sliding speed before levelling off: almost certainly it then falls as the sliding speed increases further. However, the details of this behaviour—the actual values and the pressures and speeds at which they occur—vary between individual oils, and at this point no general advice is available.