Dynamic Performances of Foil Bearing Supporting a Jeffcot Flexible Rotor System Using FEM
Abstract
1. Introduction
1.1. Garett’s Technology
1.2. Mohawk Innovative Technology Incorporated (MITI) Technology
- In-depth research on the tribological phenomena related to stopping and starting [15]; dry friction that occurs during these phases is the main cause of deterioration of the bearings. The state of the surfaces and the materials in contact have a decisive influence in the phenomena involved;
- -
- Isothermal operating regime;
- -
- The fluid, which is air, is thermodynamically assimilated to a perfect gas;
- -
- Coulomb friction between the different solid parts is neglected.
2. The Basic Equations
2.1. Reynolds Equation
2.2. Equation of the Film Geometry in the Case of a Foil Bearing
2.3. Expression of the Radial Deformation U
- e: is the eccentricity such as
- : bearing radial clearance,
- : the circumferential coordinate measured from the axis .
3. Resolution of Compressible Reynolds Equation under Transient Conditions
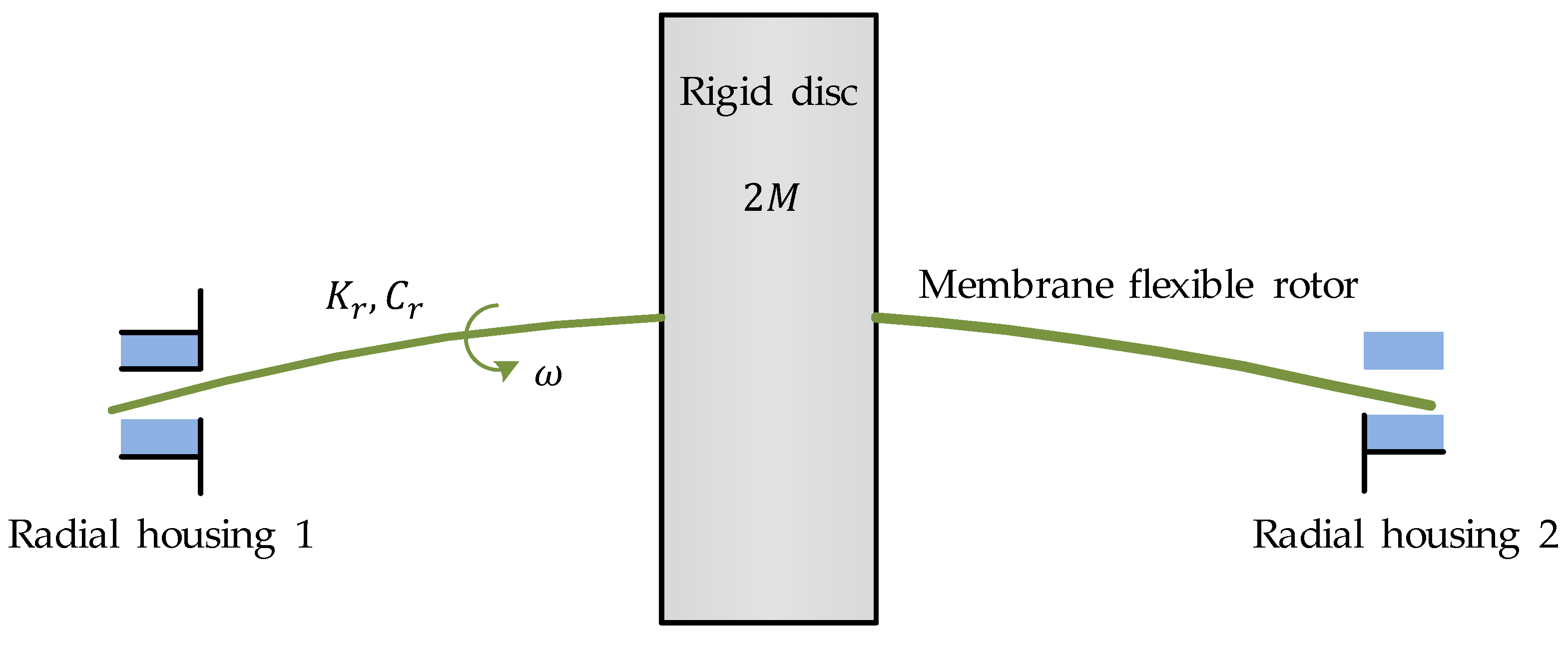
4. Equations of Rotor Motion
Balance of External Forces
- weight of the rotor;
- external dynamic forces;
- aerodynamic forces generated in the air film.
5. Parametric Studies
Data
6. Results and Discussion
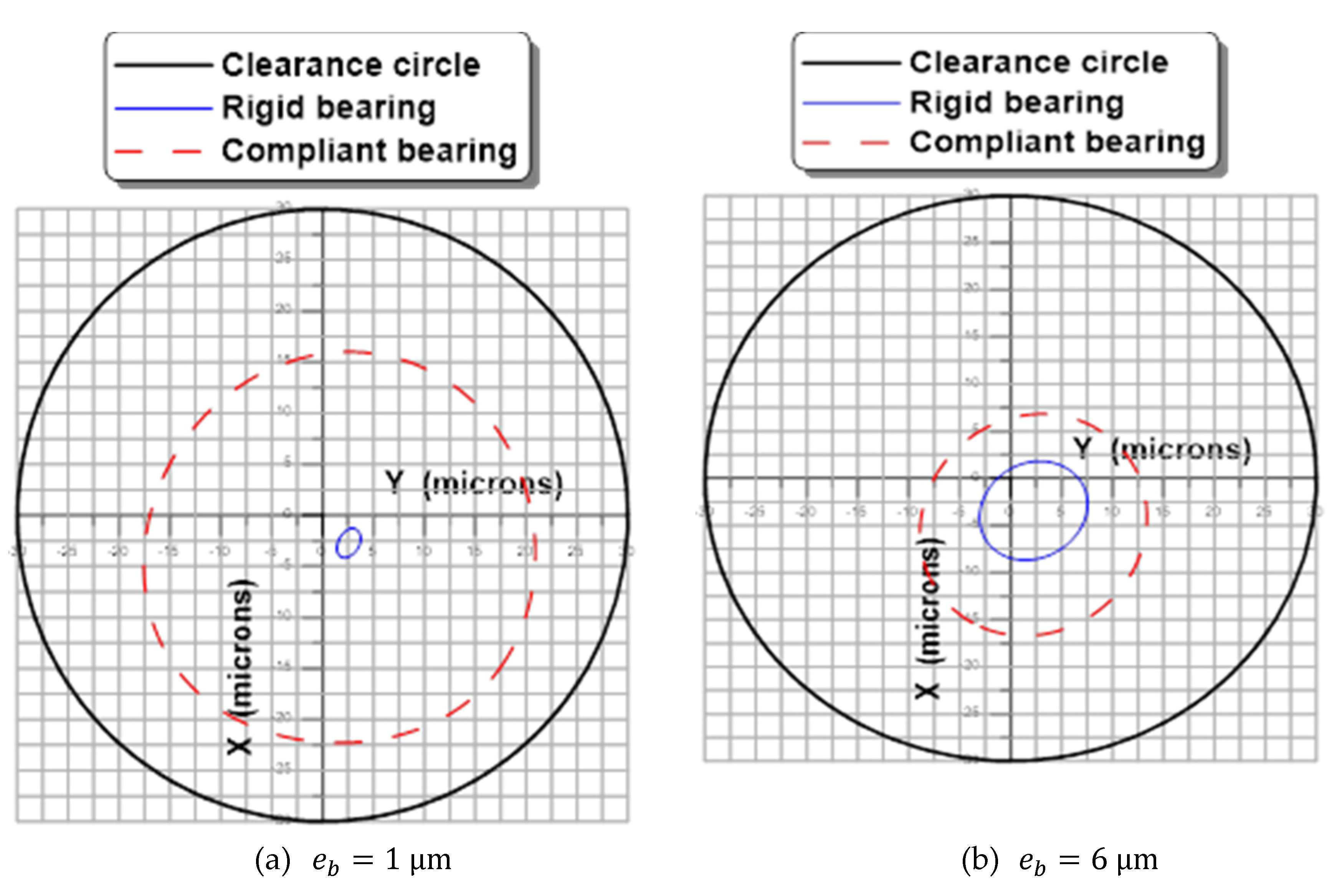
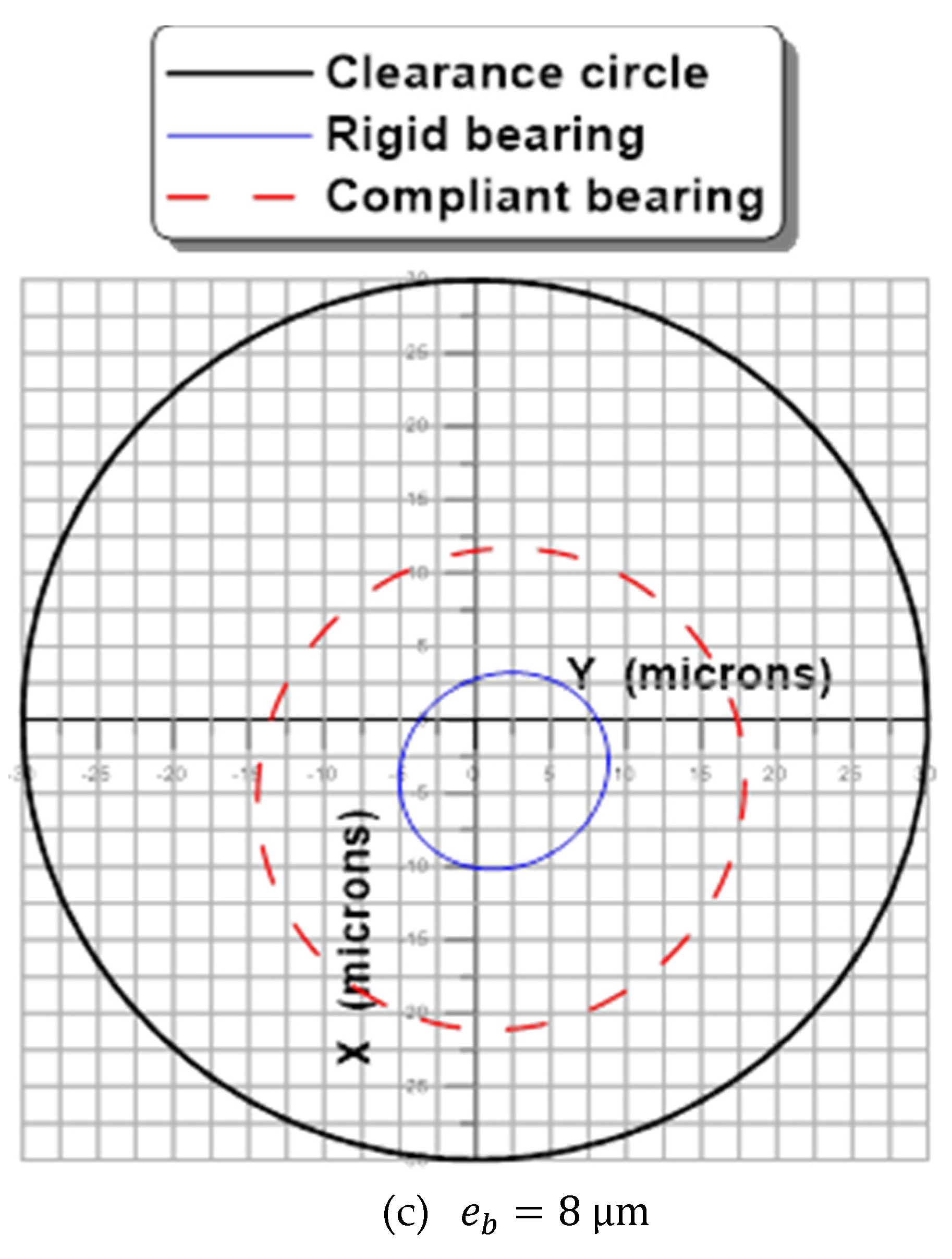
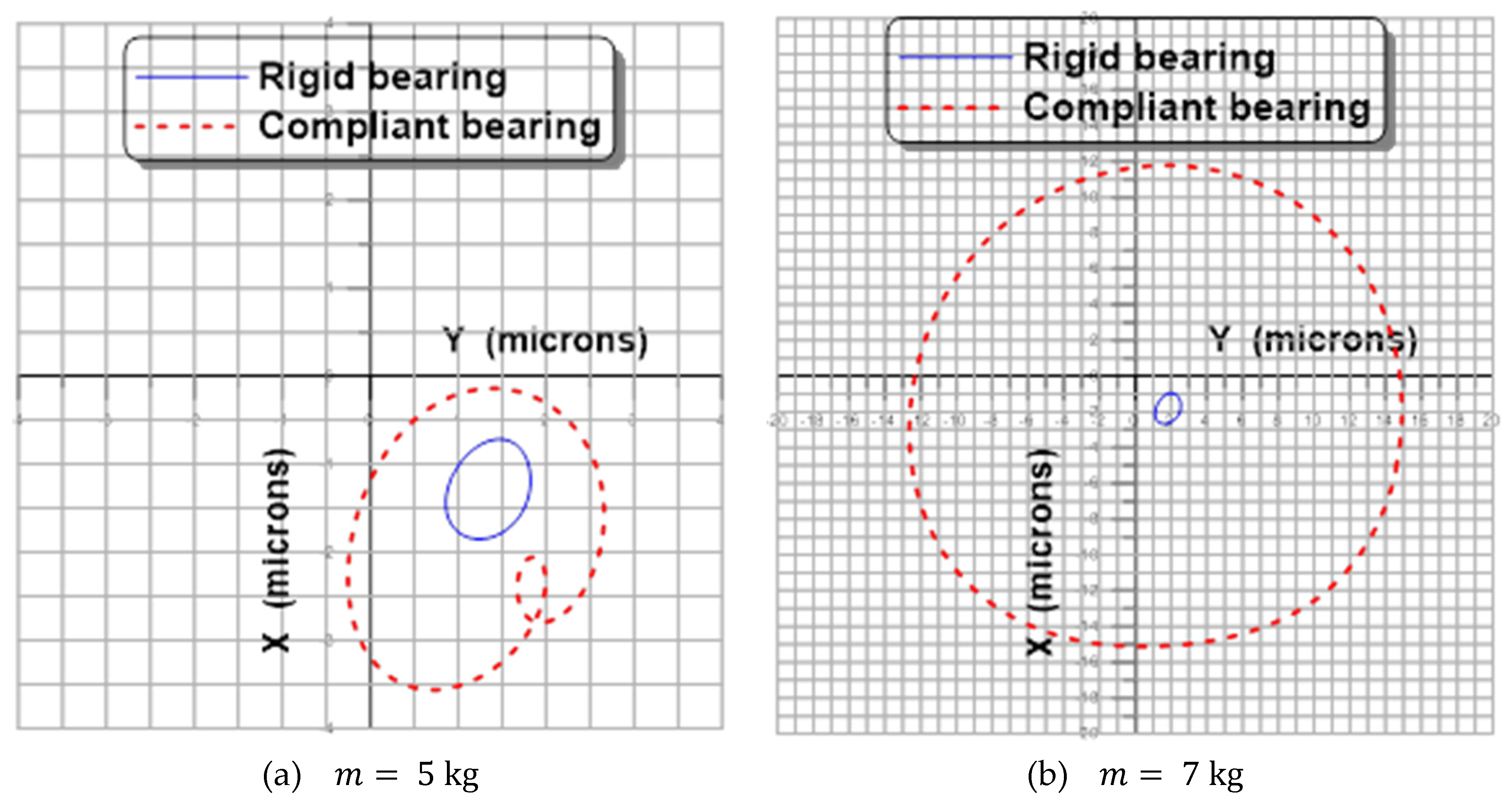
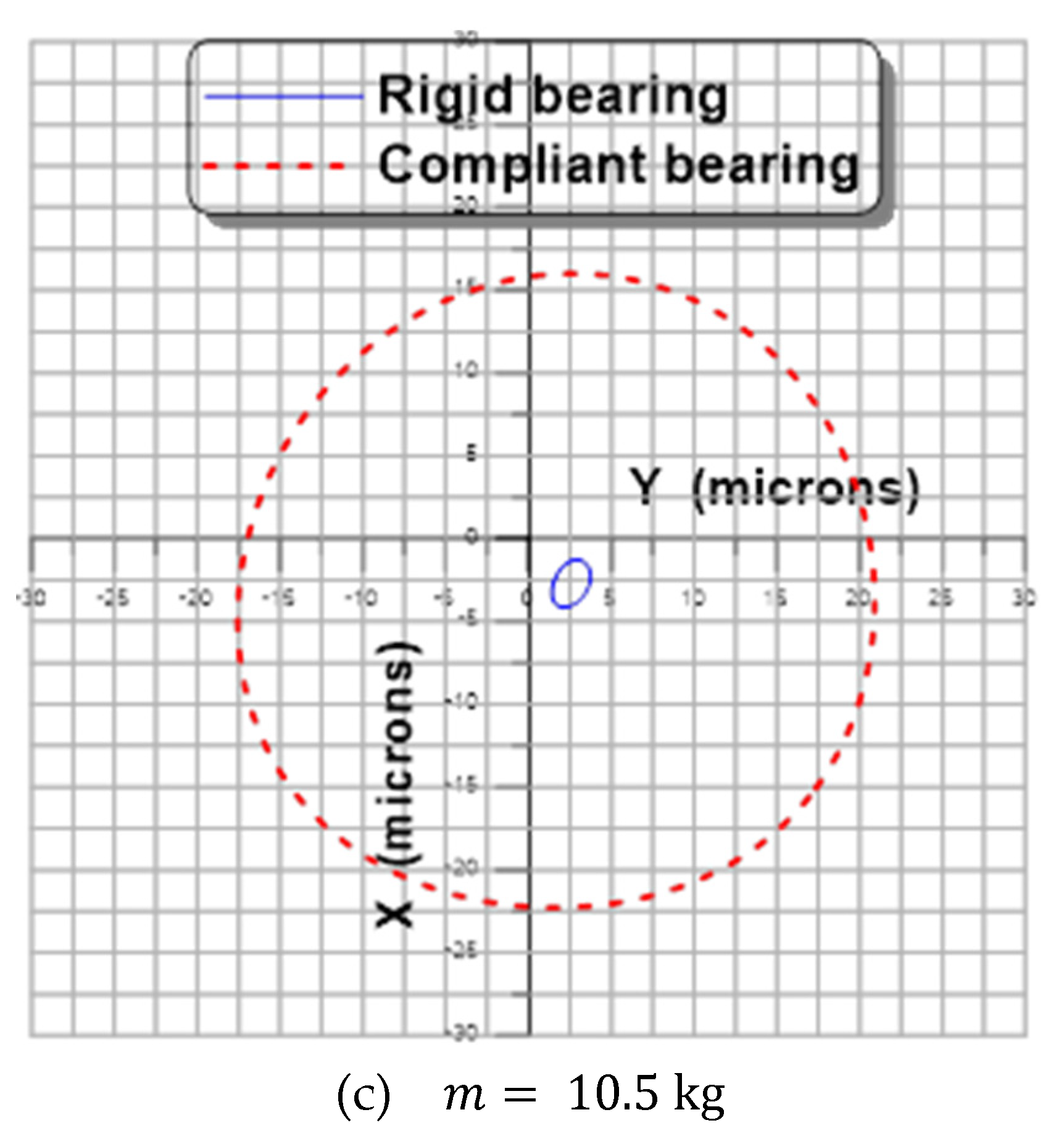
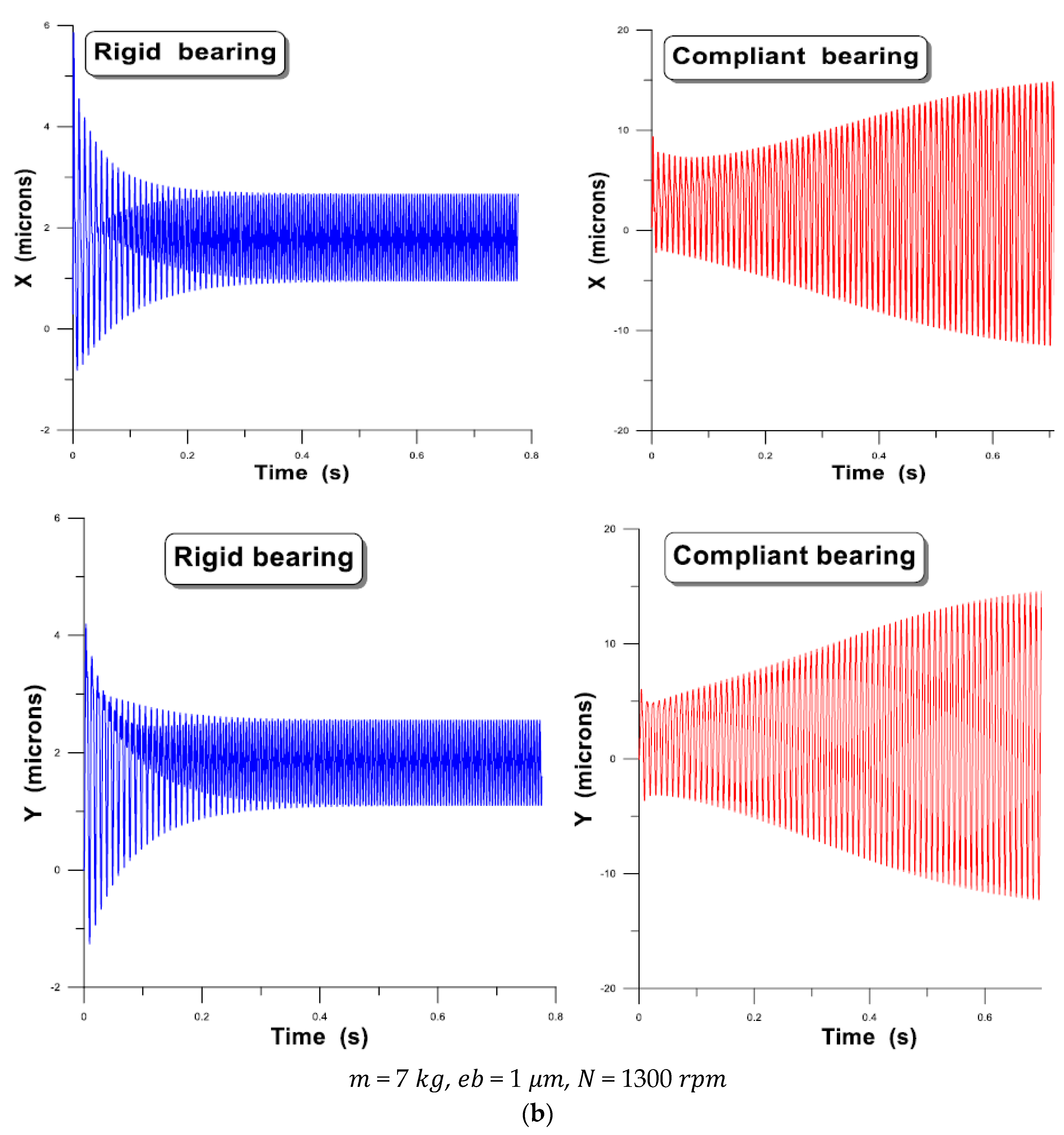
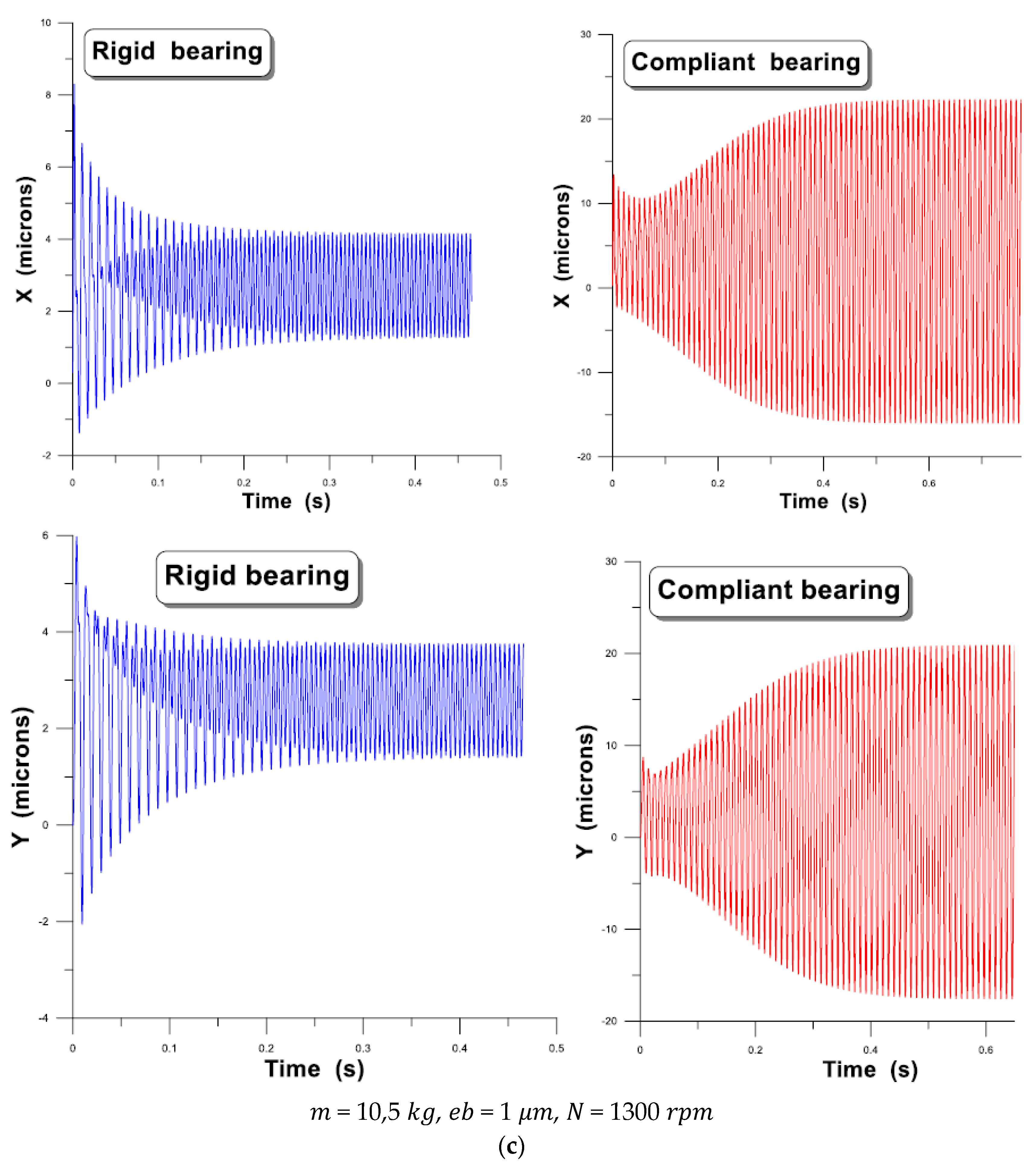
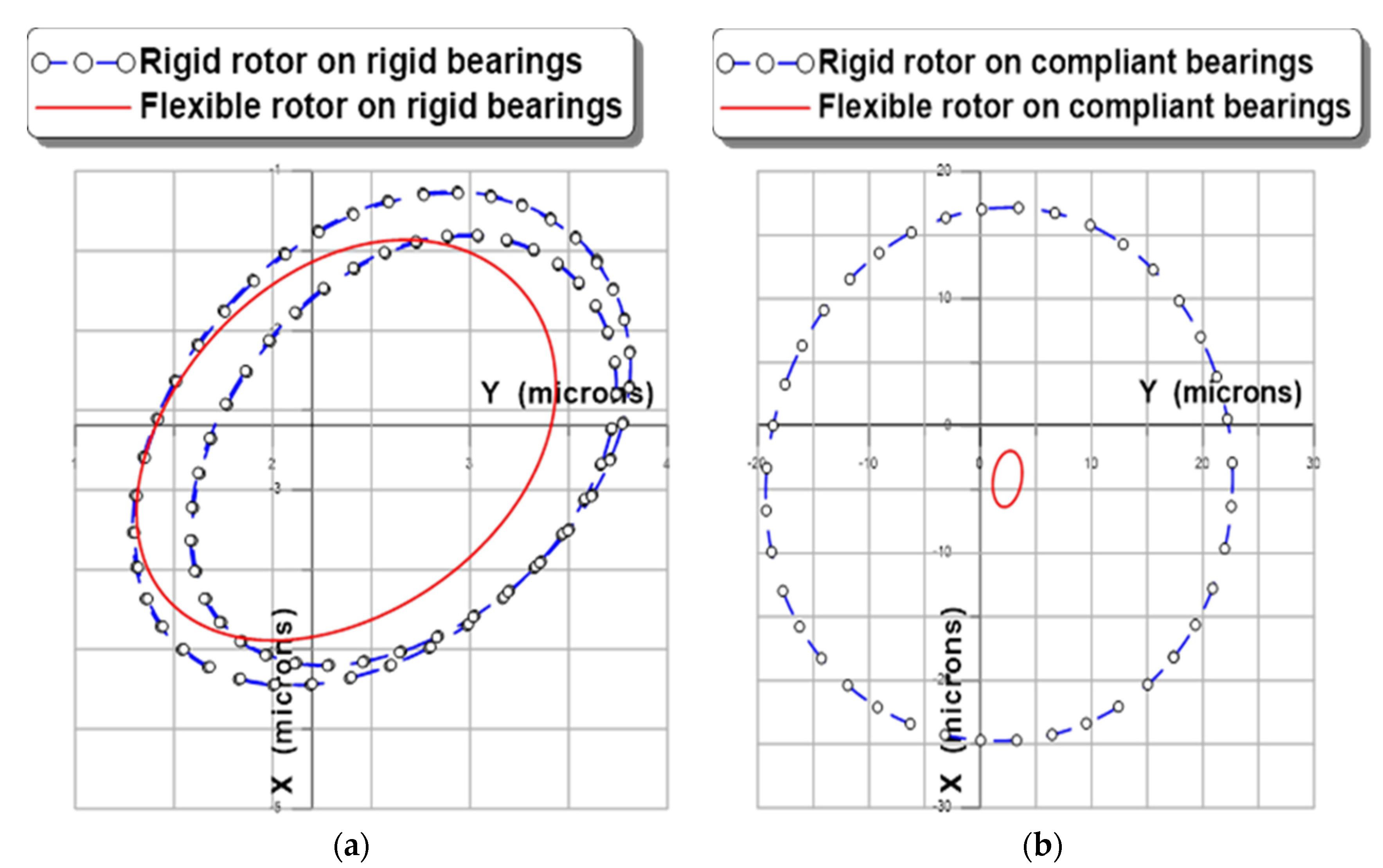
Effects of Rotor Flexibility
- The compliance of the sheets plays a negative role in the stability of the rotor-bearing system, especially for the high rotational speeds of the rotor.
- The size of the orbit increases with the unbalance eccentricity.
- Increasing the rotor mass reduces the size of the orbit.
- The flexibility of the rotor attenuates the vibration amplitudes.
7. Conclusions
- -
- Higher radial clearance;
- -
- Different equilibrium position;
- -
- Non-linear rotor trajectories;
- -
- Higher orbital magnitude.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Notation
| Unbalance eccentricity, | |
| Film thickness, m | |
| Dimensionless film thickness, | |
| Bump stiffness, | |
| Bearing lenght, | |
| Rotor mass assigned to the bearing, | |
| Rotor mass, | |
| Aerodynamic pressure, | |
| Dimensionless aerodynamic pressure, | |
| Atmospheric pressure, | |
| Bearing radius, | |
| Perfect gas constant, | |
| Bump thickness, | |
| Static load, | |
| Shaft center coordinates, | |
| Shaft center speed components | |
| Bearing axial coordinate, | |
| Dimensionless bearing axial coordinate, | |
| Greek symbols: | |
| α | Compliance coefficient |
| γ | Excitation frequency, γ = ν⁄ω |
| Λ | Dimensionless compressibility number, Λ = (6μω)〖R/C)〗^2/p_a |
| ε | Eccentricity ratio, ε = e/C |
| θ | Bearing angular coordinate, rad |
| ν | Bump Poisson coefficient |
| μ | Dynamic viscosity, Pa.s |
| Lubricant density, | |
| ω | Rotational speed, =2πN⁄60, rad/s |
| Attitude angle, | |
References
- Dykas, B.; Howard, S. Journal design considerations for turbomachine shafts supported on foil air bearings. Tribol. Trans. 2004, 47, 508–516. [Google Scholar] [CrossRef]
- Howard, S.; Dellacorte, C.; Valco, M.; Prahl, J.; Heshmat, H. Dynamic stiffness and damping characteristics of a high-temperature air foil journal bearing. Tribol. Trans. 2001, 44, 657–663. [Google Scholar] [CrossRef]
- Maraiy, S.Y.; Crosby, W.A.; EL-Gamal, H.A. Thermohydrodynamic analysis of airfoil bearing based on bump foil structure. Alexandria Eng. J. 2016, 55, 2473–2483. [Google Scholar] [CrossRef][Green Version]
- Feng, K.; Guan, H.Q.; Zhao, Z.L.; Liu, T.L. Active bump-type foil bearing with controllable mechanical preloads. Tribol. Int. 2018, 120, 187–202. [Google Scholar] [CrossRef]
- Li, C.; Du, J.; Zhu, J.; Yao, Y. Effects of structural parameters on the load carrying capacity of the multi-leaf gas foil journal bearing based on contact mechanics. Tribol. Int. 2019, 131, 318–331. [Google Scholar] [CrossRef]
- Tkacz, E.; Kozanecki, Z.; Kozanecka, D. Numerical methods for theoretical analysis of foil bearing dynamics. Mech. Res. Comm. 2017, 82, 9–13. [Google Scholar] [CrossRef]
- Bonello, P.; Bin Hassan, M.F. An experimental and theoretical analysis of a foil-air bearing rotor system. J. Sound Vibration 2018, 413, 395–420. [Google Scholar] [CrossRef]
- Guo, Z.; Peng, L.; Feng, K.; Liu, W. Measurement and prediction of nonlinear dynamics of a gas foil bearing supported rigid rotor system. Measurement 2018, 121, 205–217. [Google Scholar] [CrossRef]
- Barzem, L.; Bou-Said, B.; Rocchi, J.; Grau, G. Aero-elastic bearing effects on rotor dynamics: A numerical analysis. Lubr. Sci. 2013. [Google Scholar] [CrossRef]
- Suriano, F.J.; Dayton, R.D.; Woessner, F.G. Test Experience with Turbine-End Foil Bearing Equipped Gas Turbine Engines. In Proceedings of the ASME 1983 International Gas Turbine Conference and Exhibit, Phoenix, AZ, USA, 27–31 March 1983. [Google Scholar]
- Heshmat, H.; Ku, C.P.R. Compliant foil bearing structural stiffness analysis: Part I—theoretical model including strip and variable bump foil geometry. ASME J. Tribol. 1992, 114, 647–657. [Google Scholar]
- Heshmat, H.; Walowit, J.A.; Pinkus, O. Analysis of gas-lubricated foil journal bearings. J. Lubr. Tech. 1983, 105, 647–655. [Google Scholar] [CrossRef]
- Kim, T.H.; San Andrés, L. Heavily Loaded Gas Foil Bearings: A Model Anchored to Test Data. In Proceedings of the ASME Turbo Expo 2005: Power for Land, Sea, and Air, Reno, NV, USA, 6–9 June 2005. [Google Scholar]
- Bouchehit, B.; Bou-Saïd, B.; Garcia, M. Static and Dynamic Performances of Refrigerant-Lubricated Bearings. Tribol. Int. 2016, 96, 326–348. [Google Scholar] [CrossRef]
- Iordanoff, I.; Bou-Saïd, B.; Meziane, A.; Berthier, Y. Effect of internal friction in the dynamic behavior of aerodynamic foil bearings. Tribol. Inter. 2008, 41, 387–395. [Google Scholar]
- Bou-Saïd, B.; Iordanoff, I.; Grau, G. On non-linear rotor dynamic effects of aerodynamic bearings with simple flexible rotors. J. Eng. Gas Turb. Power 2007, 130, 012503. [Google Scholar] [CrossRef]
- Carpino, M.; Talmage, G. A fully coupled element formulation for elasticity supported foil journal bearings. Tribol. Trans. 2003, 46, 560–565. [Google Scholar] [CrossRef]
- Le Lez, S.; Arghir, M.; Frene, J. A New Bump-Type Foil Bearing Structure Analytical Model. J. Eng. Gas Turb. Power 2007, 129, 1047–1057. [Google Scholar] [CrossRef]
- Kim, T.H.; San Andrés, L. Analysis of Gas Foil Bearings with Piecewise Linear Elastic Supports. In Proceedings of the WTC 2005, Washington, DC, USA, 12–16 September 2005. [Google Scholar]
- Constantinescu, V. Basic relationships in turbulent lubrification and their extension to include thermal effects. J. Lubr. Tech. 1973, 95, 147–154. [Google Scholar] [CrossRef]
- Barzem, L. Analyse théorique et experimentale de la dynamique de rotor sur paliers à feuilles lubrifié par l’air. Ph.D. Thesis, INSA Lyon, Villeurbanne, France, 2011. [Google Scholar]
- Dhatt, G.; Touzot, J.L. Ouvrage Modélisation des structures par éléments finis; Hermès–Lavoisier–Eyrolles: Paris, France, 1992; Volume 3. [Google Scholar]
- Zienkiewicz, O. The Finite Element Method, 3rd ed.; McGraw-Hill Book Company (UK) Limited: Maidenhead, UK, 1977. [Google Scholar]
- Lalanne, M.; Ferraris, G.; Der Hapagopian, J. Rotordynamics Prediction in Engineering; Wiley: Hoboken, NJ, USA, 1990. [Google Scholar]
- Zhang, J.; Kang, W.; Lin, Y. Numerical method and bifurcation analysis of Jeffcott rotor system supported in gas journal bearings. J. Comput. Nonlinear Dyn. ASME 2009, 4, 011007. [Google Scholar] [CrossRef]
- Klit, J. Calculation of the dynamic coefficients of a journal bearing, using a variationnal approach. J. Tribol. 1996, 108, 421–425. [Google Scholar] [CrossRef]
- Liester, T.; Seemann, W.; Bou-Saïd, B. Passive Vibration Control by Frictional Energy Dissipation in Refrigerant-Lubricated Gas Foil Bearing Rotor Systems. Proc. Appl. Math. Mech. 2018, 18. [Google Scholar] [CrossRef]

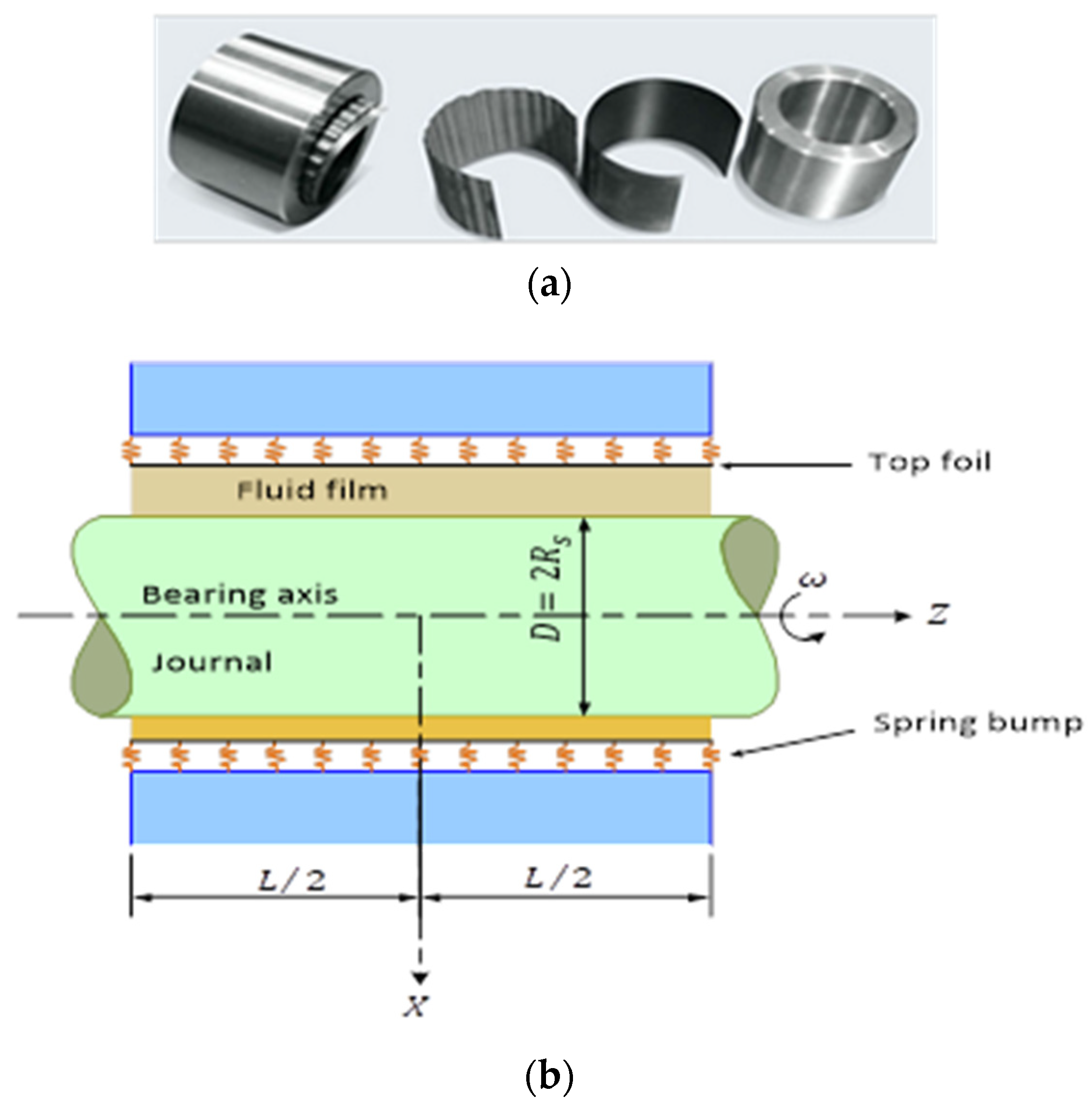
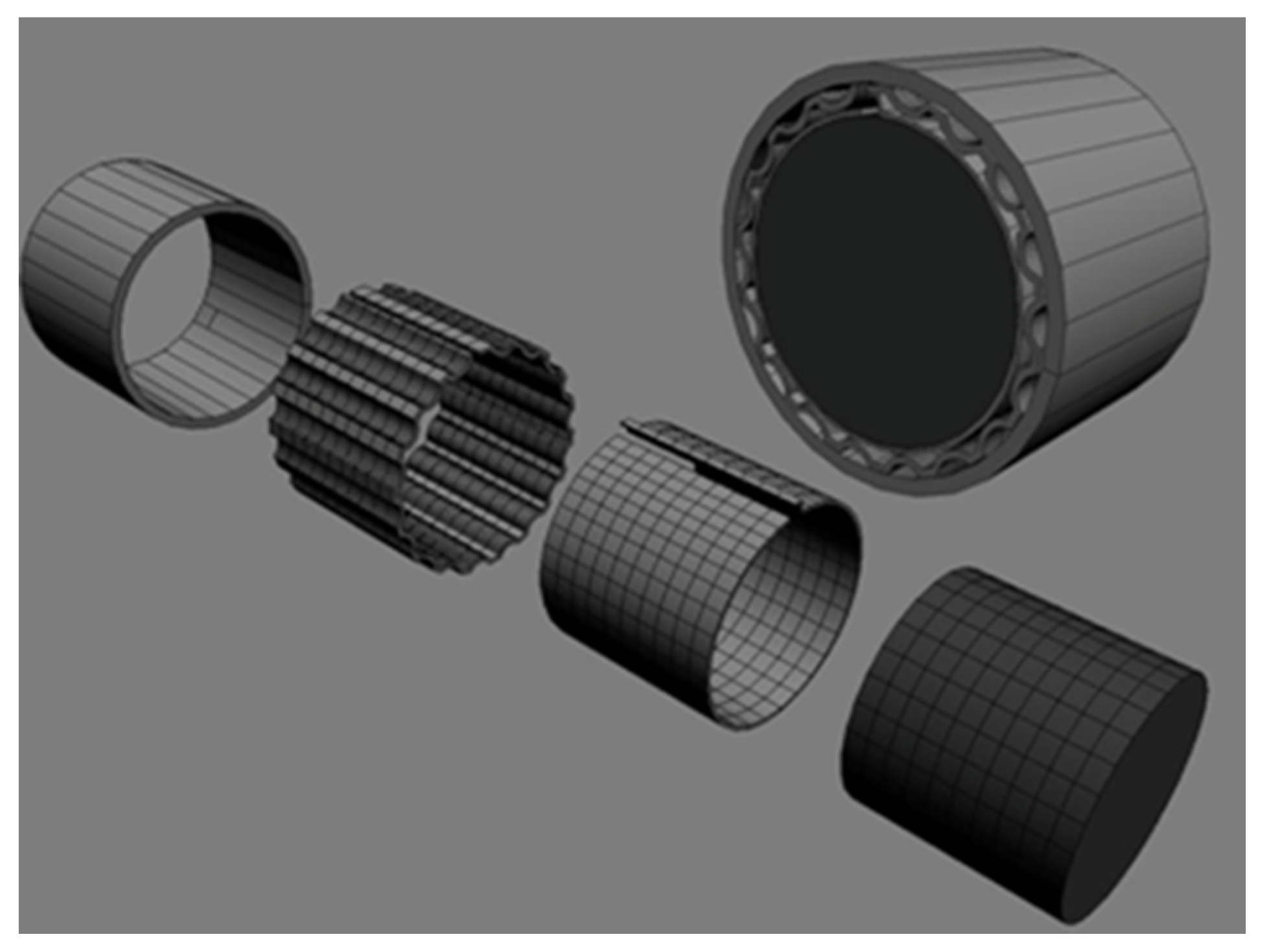
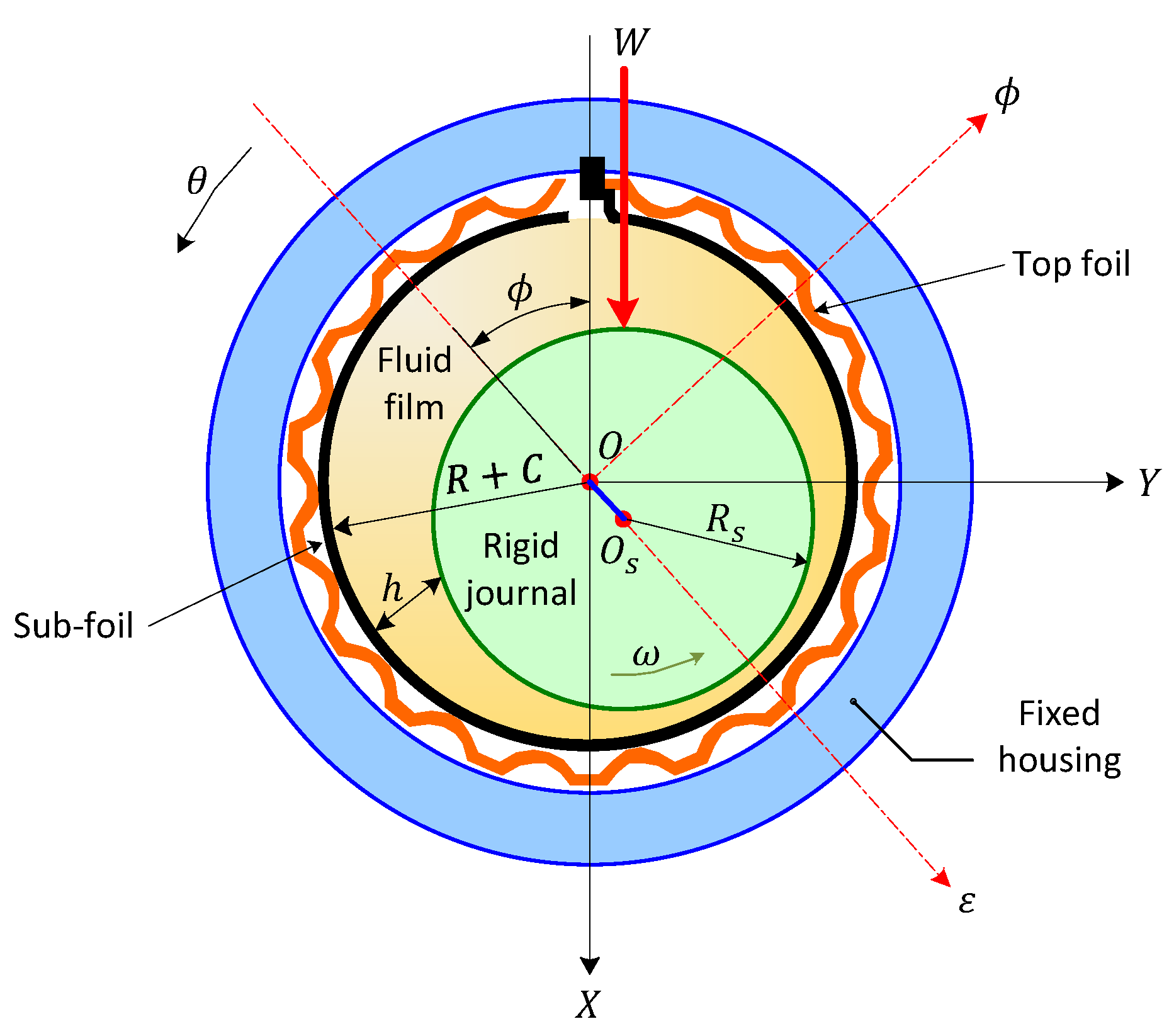

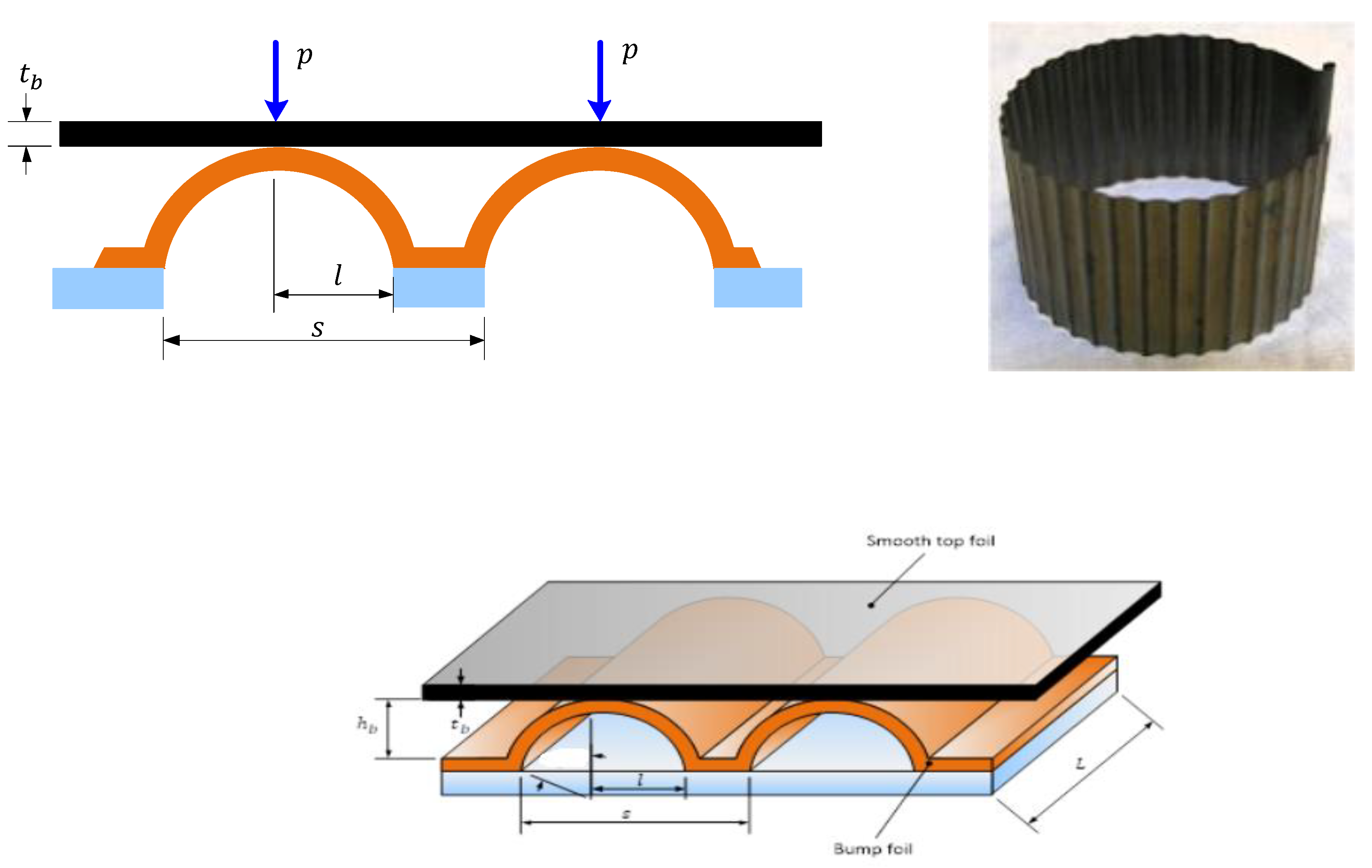



| Parameter | Symbol | Value | Unit (SI) |
|---|---|---|---|
| Radius | 50 × 10−3 | ||
| Lenght | 110 × 10−3 | ||
| Radial clearance | 30 × 10−6 | ||
| Bump foil thickness | 0.1016 × 10−3 | ||
| Bump pitch | 4.572 × 10−3 | ||
| Bump length | 3.556 × 10−3 | ||
| Young modulus | ∞ (rigid) 207 | ||
| Poisson ratio | 0:30 |
| Parameter | Symbol | Value | Unit (SI) |
|---|---|---|---|
| Rotor mass assigned to bearing | 10.5 | ||
| Rotational speed | 12,300 | ||
| Atmospheric pressure | 1.013 × 105 | ||
| Unbalance eccentricity | 0 | ||
| Rotor stiffness assigned to bearing | 2.03 × 105 2.03 × 106 | ||
| Rotor damping assigned to bearing | 10103 |
| Parameter | Value |
|---|---|
| Element of approximation | Quadrilateral bilinear C° 4 nodes |
| Number of elements in circumferential and axial directions (half bearing) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bou-Saïd, B.; Lahmar, M.; Mouassa, A.; Bouchehit, B. Dynamic Performances of Foil Bearing Supporting a Jeffcot Flexible Rotor System Using FEM. Lubricants 2020, 8, 14. https://doi.org/10.3390/lubricants8020014
Bou-Saïd B, Lahmar M, Mouassa A, Bouchehit B. Dynamic Performances of Foil Bearing Supporting a Jeffcot Flexible Rotor System Using FEM. Lubricants. 2020; 8(2):14. https://doi.org/10.3390/lubricants8020014
Chicago/Turabian StyleBou-Saïd, Benyebka, Mustapha Lahmar, Ahcène Mouassa, and Bachir Bouchehit. 2020. "Dynamic Performances of Foil Bearing Supporting a Jeffcot Flexible Rotor System Using FEM" Lubricants 8, no. 2: 14. https://doi.org/10.3390/lubricants8020014
APA StyleBou-Saïd, B., Lahmar, M., Mouassa, A., & Bouchehit, B. (2020). Dynamic Performances of Foil Bearing Supporting a Jeffcot Flexible Rotor System Using FEM. Lubricants, 8(2), 14. https://doi.org/10.3390/lubricants8020014




