Abstract
The present study theoretically evaluates the stability potential of noncircular geometries when they are adopted in the outer bearing of floating ring bearings (FRB). A numerical study is carried out to evaluate the stability about the static equilibrium position of a balanced, symmetrical, rigid rotor, horizontally placed, and supported at both ends by identical FRBs. In the analysis, the outer bearing of these FRBs is alternatively shaped with common circular bore (CB), two lobe-wave bore (2LWB) or lemon bore (LB), assuming a linearization of the film forces. A minor part of the study consists of partially supporting the results of the above study by means of a nonlinear, transient analysis. Despite limiting to the theoretical aspect, dealt with under several simplifying hypotheses, the investigation highlights the influence of the examined non-circular geometries on the stability of the static equilibrium position, when these geometries are adopted for shaping the outer housing of the FRB. The paper shows that contrasting effects are obtained, depending on the chosen geometrical parameters. In the paper, the acronyms CB, 2LWB, and LB are used to indicate the FRB layouts respectively equipped with outer circular, wave, and lemon bearing.
1. Introduction
The present analysis theoretically investigates the effects of giving the outer bearing of a floating ring bearing (FRB) a non-circular geometry. The common FRB is a lubricated bearing that incorporates a thin bush or ring between the journal and the casing. This layout presents consequently an inner and an outer oil film, respectively delimited by the journal and the bush and by the bush and the casing. Besides floating, the bush is free to spin, so that the whole bearing practically doubles a simple sleeve bearing. The result is a device with remarkable capability to support ultra-high speed, high-temperature rotating machinery, owing to the significant damping accomplished by the two oil films operating in series. Reduced power loss and low costs are mainly the further key aspects that justify the wide recourse to such bearings, especially in the support of turbochargers. Instabilities are unavoidable effects of the rotor-support nonlinearities, to which the pronounced hydrodynamic concept of the FRB highly contributes. They are typically represented by subsynchronous, self-excited vibrations, which manifest in addition to the synchronous component excited by the rotor unbalance. Oil whirl and whip, bifurcations from one limit-cycle to a different one, with collapse of the limit-cycle itself or the possible evolution to a severe, total instability, are the ingredients of the dynamics of FRBs supported rotors [1,2]. The above remarks justify a bulk investigation carried out in decades, especially focused on the effects of the different parameters on the static and dynamic properties of the FRB [3,4,5,6,7,8], largely motivated by the need to guarantee higher specific power with lightweight assemblies and to overcome as far as possible the major drawbacks of non-linear instabilities. Shaw and Nussdorfer [3] mentioned the early use of such bearings in the connecting rods of the 1920–1930 Bristol aircraft engines. They analytically evaluated the ring to journal speed ratio, taking account of both the clearances ratio and the radii ratio, as well as the heat generated in the FRB in comparison to that obtained in an equivalent journal bearing. An experimental measurement of the whirl to rotating speed ratio of the ring was also carried out in their study. Ng and Orcutt [4] calculated the stiffness and damping coefficients of the FRB around the static equilibrium position through linearization of the film forces. Fractional-frequency whirling was observed in the experimental tests, whereas the whirl amplitude was controlled through the oil feeding pressure, the oil viscosity, and the outer clearance. Tanaka and Hori [5] calculated the stability charts for a simple rotor on FRBs, evaluating the effects of the different FRB parameters and rotor flexibility as well as proving the superior stability of the FRB with respect to the conventional journal bearing. A good agreement between experimental and theoretically predicted stability limits was also obtained in the investigation. Boyaci et al. [6] theoretically investigated the Hopf-bifurcation of a rigid, balanced rotor on FRBs. The π-film, short bearing model was adopted together with the linearization of the film forces around the static equilibrium position. The sub-critical or super-critical nature of the bifurcations, occurring under different operating conditions, was also characterized with recourse to non-linear analysis. Hatakenaka et al. [7] set up a Reynolds equation with a suitable cavitation model that could take into account the centrifugal force. This way the FRB-model showed how the increase of the cavitation zone with the journal speed could influence the stiffness cross-coupling coefficients and justify the reduction of the bush-to-shaft speed ratio. Chasalevris [8] set up an analytical model of the finite-length FRB. Comparison to the numerical approach with finite difference method confirmed the capability of the method to give accurate predictions at reduced computational cost, when adopted within rotordynamic algorithms. Yet, a significant part of the literature was specifically addressed to the study of realistic turbocharger (TC) models equipped with FRBs [1,2,9,10,11,12]. These analyses turn out to be relatively involved. In order to guarantee an adequate predictive level, the implemented theoretical tools had to consider the mass and unbalance distributions and temperature gradients, in addition to the different parameters that characterize the operation of the FRBs. Gunther and Chen [9] and Inagaki et al. [10] investigated the onset of translational and conical unstable whirling modes, respectively through finite element analysis and flexible multibody model, with further use of experimental tests. To save computational time, the short bearing approximation was often preferred to the finite-length characterization of the oil films [10,11]. Tian et al. [11] and Schweizer [1,12] carried out thorough nonlinear analyses by means of run-up and coast-down simulations, putting in evidence the influence of the unbalance distribution within the TC rotor and giving particular emphasis to the character of the whirling modes and the phenomenon of total instability. The dynamical behavior of TC rotor on semi floating ring bearings, which differ from FRBs because the locking of the bush rotation was also studied by Bonello [13] and San Andrés et al. [14]. The effect of adopting a non-circular geometry for the bearing clearance, in place of the common circular one, remained though practically neglected in the research literature about FRBs. This circumstance contrasts with the widespread and consolidated recourse to lemon, multi-lobe, and pressure-dam shapes in journal bearings, as a mean to guarantee higher stability of the lubricated pair with respect to the simple circular geometry. To the best author’s knowledge, only a few, recent papers have dealt with this topic. Eling et al. [15] theoretically analyzed a TC on FRBs with six-lobe-shaped bush. The study showed that, in spite of an increase in the friction losses due to the lobe geometry, a reduction in sub-synchronous vibrations, with respect to the use of common bush, could be obtained, as confirmed by experimental tests. Soni and Vakharia [16] investigated the steady-state characteristics of a FRB presenting an outer lemon bore. The theoretical analysis, which assumed a finite length bearing and solved the lubrication problem through the finite element method, made it possible to assess a better load capacity of the lobe geometry with respect to the reference circular one. Bernhauser et al. [17] presented a run-up analysis of a TC multibody model with FRBs similar to those adopted in [15]. Regarding the practical employment of TCs within combustion engines, the authors pointed out the importance of imbalance-excite and self-excited TC vibration as responsible of disturbing tonal noise during the engine operation. The study theoretically proved that an optimization of the TC dynamics, through reduction or suppression of the said vibrations, can be actually achieved by means of the assumed, uncommon geometry.
Previous studies carried out by the present author were focused on lubricated bearings equipped with non-circular casing, specifically shaped as a two-lobe wave bore. The highest degree of dissymmetry, in the class of multi-lobe geometries, showed by the 2LWB, makes it possible to test the effects of the casing orientation with respect to external loads presenting a fixed direction (e.g., gravity load). On the other hand, the wave amplitude represents a parameter apt to grade the preloading effect. The non-linear behavior of unbalanced rotors supported by these bearings, with special regard to the stability of periodic solution and bifurcations, was investigated in [18,19] with recourse to the continuation method. The theoretical outcomes from [18] showed that a suitable choice of the above geometric parameters is beneficial regarding the stability behavior of a rigid rotor on 2LWB. The present investigation shares with these past studies the consideration of a non-circular geometry, extending its use to an FRB, whose outer bearing, formed by the ring and the fixed casing, was made as a 2LWB or a lemon bearing (LB). Nevertheless, the dynamic aspects under examination limit here to the stability of the steady equilibrium point of a perfectly balanced rotor. The only bifurcation investigated in the following of the paper, by means of the classic linear stability analysis, is the Hopf-transition that gives rise to a limit cycle. How the said non-circular FRB geometry influences this dynamics, in comparison to the common circular geometry, represents the main topic of the paper. By way of example, a further inspection into the bifurcation scenario, with extension to a higher speed range, is carried out through the brute-force integration of the system’s equations. This numerical, non-linear approach completes the investigation by enabling the dynamics survey through observation of the journal and ring orbits, the evaluation of the minimum film thickness, and that of a suitable orbit-based index.
2. Rotor Model and Aspects of the Linear Stability Analysis
2.1. Bearing Geometries
A horizontal, rigid rotor is supported with FRB placed at both ends. Owing to assumed symmetry with respect to the rotor middle plane, the analysis is restricted to a half rotor supported by one end FRB. The floating ring is rotating with speed around its geometrical axis and whirling in a precession motion within the fixed housing. No misalignment of the ring nor of the journal is hypothesized. When the shape of the outer bore is non-circular, with difference to the CB, the ring rotates inside of a clearance whose radial dimension is not more constant. In the present analysis two different non-circular shapes are adopted:
(1) Two-lobe wave bore (2LWB): the outer clearance Clo,WB (the subscript “o” indicates the outer bearing) is expressed in dimensionless way and polar coordinates as
The wave amplitude B represents the degree of deviation from the circular shape, while the angle φ indicates the angular displacement of the outer bearing with respect to the horizontal axis of a fixed frame of reference whose origin is in the bore center (Figure 1a). A null B value corresponds to the CB case.
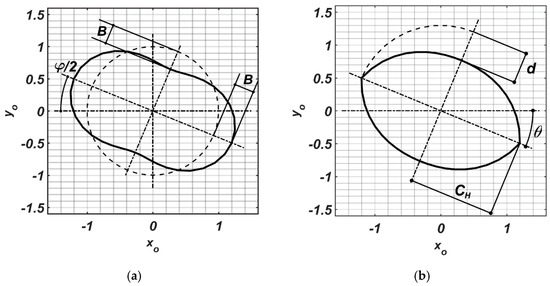
Figure 1.
Geometry of the 2LWB and LB clearances. B, d and CH are dimensionless quantities, obtained by division with the radius Co of the CB clearance (represented by the dashed circle with dimensionless unit radius in the left figure). In figure θ = φ/2 = φ/8. (a) 2LWB; (b) LB.
(2) Lemon bore (LB): the clearance in this well-known geometry [20,21,22] is enclosed between two shells, each one presenting a circumferential extension that is not a complete half-circle (Figure 1b). It can be expressed in polar coordinates as
In the above expression, the k index refers to the k shell. The whole lengths are generally made dimensionless by division with
. Differently, they are expressed here in the ratio to the dimension Co of the CB clearance, according to the plot in Figure 1b, where the orientation angle θ is also indicated. The ratio
represents the ellipticity of the profile. It is worth to remark that, differently to the CB and accordingly to the geometry in Figure 1b, the journal (i.e., the ring, in the present case) is impeded to cover the whole clearance, owing to its radial dimension and to the shape discontinuity of the clearance wall. It must be also noticed, in Figure 1, the absence of holes or grooves for the oil circulation, according to the assumed hypothesis of a bearing model with side inlet-outlet at ambient pressure.
In order to carry out a comparison between the two shapes shown in Figure 1, regarding their use in the outer bearing, their geometrical parameters are to be suitably assigned in order to establish some mutual equivalence and further reference to the CB case. In this regard, in addition to setting the same angular displacement through the relationship , it seems quite reasonable to assume, on the one hand, that the dimensional clearances respectively pertaining to the two profiles, i.e., and , have equal mean values
On the other hand, imposing equal maxima
or, alternatively, equal minima
is assumed to represents a plausible, further condition of equivalence. As a result, the ellipticity parameter and the dimensionless law of the LB clearance , which comply with the requirement of equal mean values and maxima (LBmx), are
whereas equating mean values and minima it is alternatively obtained (LBmn)
Figure 2a,b show the comparison of the two elliptical clearances LBmx and LBmn, respectively determined according to Equations (6) and (7).
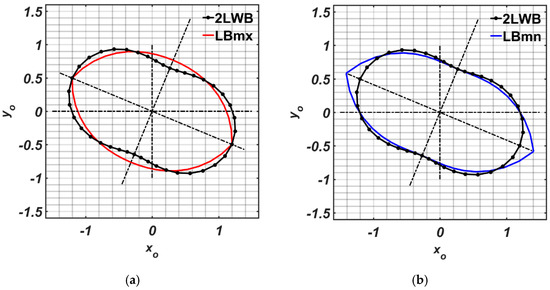
Figure 2.
Comparison between the 2LWB and the LB clearances (the differences have been expressly highlighted by assigning B = 0.3). (a) conditions of equal mean values and maxima (LBmx); (b) conditions of equal mean values and minima (LBmn).
2.2. Rotor-Bearing Model
After suitable manipulation, the equations of motion of the rotor-bearing system are eventually written in a dimensionless way
The significance of the symbols is given in the relative section. The inner film force components are evaluated, according to the isoviscous, laminar, π-film model, under the infinitely short-bearing approximation, (πSBA), through the analytical procedure reported in [23], suitably adapted to the inner bearing, where both the ring and the journal rotate with different speeds (Appendix A). The ratio
between these angular speeds has been expressed in approximate way [24], so as to be independent of the rotor speed
Expressions of the outer film force components, limiting to the CB layout, could be obtained similarly to the inner ones. A semi-analytical, more general procedure is instead adopted, which holds in the whole different geometries, i.e., CB, 2LWB, and LB. According to the SBA and the selected bearing geometry, the oil pressure is analytically obtained in the whole points of a grid with M circumferential rows × N axially oriented columns, suitably fixed to represent the outer film in discretized way. After discarding the negative values, in accord to the Gumbel cavitation model, a numerical integration over the same grid yields the oil force components (Appendix A).
2.3. Linear Stability Analysis
A linear stability analysis is carried out through the linearized equations written about stationary equilibrium points. With this aim, the bearing modulus
and the Sommerfeld number ratio Σ
are assumed to represent a distinctive operating set of the system parameters (i.e., main geometrical parameters, load, and dynamic viscosity of the lubricant). In particular,
is related to the modified Sommerfeld numbers and , which respectively characterize the current operating conditions within the inner and the outer film, by means of the relationships
Two intervals, respectively of and of s, are suitably assigned, so that at each , the rotor speed s is varied in . This way, different sets are fixed in turn by means of Equation (11). The static equilibrium point regarding each set is hence obtained by solving the system
Above equation system is obtained from Equation (8) by setting derivatives and unbalance equal to zero. It must be observed that the inner force can be evaluated here directly through the expression of obtained by adaptation of the plain bearing case [24] and reported in Appendix A. Once is obtained, the following linearized equations of motion hold in its neighborhood
The submatrices , , and are written through the stiffness and damping coefficients, as explained in Appendix B. Further manipulation of Equation (13) (Appendix B) yields the eigenvalues problem
Provided that the stationary equilibrium point is hyperbolic, the instability threshold is represented by conditions where some , representing a real eigenvalue or a pair of conjugate imaginary eigenvalues, turn out to have null real part.
2.4. Choice of the Parameter Values for the Analysis
Numerical simulation has been carried out for different operating conditions, fixed in turn by choosing the parameter values with suitable criterion, in order to limit the case study work. The values and 0 were assumed for the orientation angle , together with a wave amplitude B = 0.2. The last quantity, employed within Equations (6) and (7) for the LBmx and LBmn profiles, yields an ellipticity ratio respectively equal to 0.262 and 0.408. The LB-clearance ratio , with , represents a parameter that is frequently used too in literature and assumes values 1.36 and 1.69, respectively in the above two cases. The parameters , , , , and were given values as follows: ; ; = 1, 2; = 1.32, 1.5; = 0.025, 0.043, 0.075. Some of these values have been adopted in [5,6]. When the outer bearing is a 2LWB or an LB, and are respectively evaluated with reference to the outer radius of the ring, which is maintained comparing the different geometries, and to the clearance . A grid with M = 21 rows × N = 221 columns has been used to discretize the outer film.
3. Results
3.1. Steady-State Behavior: A Preliminary Comparison
Figure 3a,b illustrate the journal eccentricity ratio vs. the eccentricity ratio of the ring, respectively in two cases relative to CB and LB mount. The parameter values = 1.2, = 0.001, = 0.5, and = 0.7 and 1.3 have been adopted in order to carry out a comparison to the data from [16], also shown in figures. The CB data have been obtained here as well as in [16] as a limit case of the LB geometry. To the author’s knowledge and according to the short literature review given above in the introductory section, the bearing model dealt with in [16] is so far the only one presenting some similarity with the FRB adopted in the present study. Regarding the plots put in comparison in Figure 3a,b, it is worth pointing out the differences between the present LB model and that adopted in [16], where a finite different method-scheme and a finite bearing model with L/D = 1 have been used to characterize the steady-state performances of an FRB with outer LB. In the light of these remarks, the comparison may be assumed acceptable with exception of the LB layout and = 0.7.
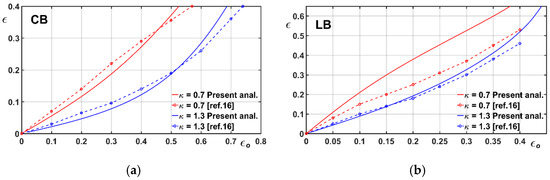
Figure 3.
Journal eccentricity ratio vs. the ring eccentricity ratio : comparison to results from [16]. (a) CB geometry. (b) LB geometry with = 0.5.
3.2. Linear Stability Analysis: The CB Case
Some check about the reliability of the semi-analytical procedure addressed to the linear stability analysis, as described in the above section, has been carried out with reference to the operation of a rotor on FRBs with outer CB. In this case, the stability responses obtained in both semi-analytical and analytical way (see for example [5,6]) have been put in comparison. Figure 4a shows the results (the analytical curves are reported in black) for three different values and the remaining parameters fixed as in [6]. The plots in figure show some differences in the outcomes of both procedures, particularly for the higher branches obtained with = 1.5 and 2. In this regard, the following remarks are worth to be considered. The analytical curves have been here obtained expressing the inner and outer fluid film forces as well as the inner and outer stiffness and damping coefficients in full analytical way, according to [5]. On the other hand, the stability borders obtained in semi-analytical way are calculated through a procedure that implies: the integration of the pressure distribution on a finite mesh; the account of cavitation through cut off of the negative values; the calculation of stiffness and damping coefficients by means of numerical derivatives. In both cases, the occurrence of pure imaginary eigenvalues, which is crucial for the determination of the instability threshold, has been carried out numerically. According to these aspects, the differences in the outcomes, as they appear in Figure 4a, receive some justification.
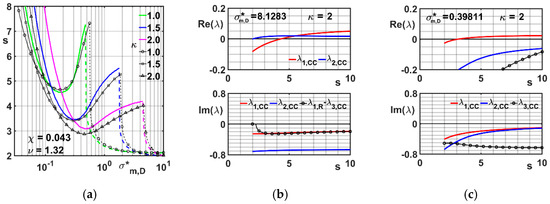
Figure 4.
Results for the CB layout. (a): Stability thresholds: numeric (in color) and analytic (in black). (b,c): partial portraits of the eigenvalues behavior vs. s for = 2 in the LSR, at = 8.13 (b) and the HSR, at = 0.398 (c).
In Figure 4a, it may be observed that each -case is represented by a curve with two distinct branches, so as to organize the whole area under exam in two regions, a left higher stability region (HSR) and a right lower stability region (LSR). The branch in the HSR, at lower values of the bearing modulus , represents stability loss very likely due to supercritical Hopf bifurcations, whereas the branch in the LSR, characterized by light-load conditions, would very likely represent instability originated by subcritical bifurcations [6]. These behaviors are due to the play of the eight eigenvalues at varying the rotor speed s. In this regard, it is worth remarking that: (1) the set of eigenvalues is generally made by real eigenvalues (REs) , p = 1, P, and complex conjugate eigenvalues (CCEs) , q = 1, Q; (2) the number of eigenvalues in each subset can change from s to s, on condition, in the present system, that P + 2 Q = 8. As an example, Figure 4b,c, which refer to the curve in Figure 4a numerically obtained for = 2, illustrate the conditions occurring at the onset of instability when = 8.13 and = 0.398, respectively. Both figures show the behavior of the real parts Re of the eigenvalues (upper diagrams) and that of the imaginary parts Im in the interval s = 2 ÷ 10 (for better clarity, only the non-positive Im have been plotted). Furthermore, owing to the different magnitudes of the eigenvalues parts, only partial data, i.e., those relevant to the Hopf bifurcations under analysis, have been reported. That being said, from Figure 4b it can be inferred that the loss of stability at = 8.13, occurs at s around 2, when the pair crosses the imaginary axis from the negative to the positive half-plane. It can be seen that, at the same speed, there are a second pair of CCEs and a RE , the latter one changing soon after, when s is about 2.2, into a further pair of CCEs. At the onset of instability, the absolute value of the imaginary part of the eigenvalues that determine the bifurcation, i.e., , is higher than that of . Differently in the HSR, when = 0.398, Figure 4c shows that the loss of stability, about s = 3, is due to the eigenvalue , which possesses the lowest absolute value of the imaginary part with respect to the further CCEs (two of which, i.e., and , are depicted in the upper and bottom diagrams of the figure). The above conditions, regarding the magnitude of the imaginary parts of the critical eigenvalues, have been observed in [6] to be frequently associated to sub-critical (Figure 4b) and super-critical (Figure 4c) bifurcations. Nevertheless, the same conditions cannot represent a criterion to decide whether the bifurcation is of the former or the latter type, nor in the present analysis are adopted the appropriate tools, like continuation or center manifold analysis, in order to solve the issue.
The change from LSR scenario to the HSR one manifests with a jump, as it can be inferred from the plots in Figure 4a and can be explained as follows, still making reference to Figure 4b,c, without providing further data for the sake of conciseness. According to the above remarks, the Hopf bifurcations in the LSR (Figure 4b) and in the HSR (Figure 4c) are due to different critical eigenvalues, i.e., and , respectively. As the value of the bearing modulus is decreased from 10 to 2 (compare Figure 4b,c), the remains over the zero axis (i.e., the pair is continuing to cross the imaginary axis). Differently diminishes gradually in value, till to abandon the zero axis and to position entirely beyond it. Owing to its slope, when separates from the zero axis and ceases to be critical (around ), there is a jump from the critical s value that is due to , say this end value, to the critical s value that is due to , say this initial value, placed upward in the interval. The difference - justifies the discontinuity in the observed threshold curve for = 2 in Figure 4a. Similar considerations hold for the remaining curves.
3.3. Linear Stability Analysis: The 2LWB and LB Cases
When the outer bearing is changed from the CB to the 2LWB or LB shapes, the dependence of the stability curves on the bearing orientation and the level of deviation from the circular shape (respectively represented in both types by the amplitude B and the ellipticity parameter ) turns out to be apparent. Figure 5a,b report the stability charts obtained adopting the 2LWB with B = 0.2, , = 1.32 and = 0.043; the clearance ratio was given the values of 1 and 2, respectively in both figures. The curves in each figure show similarities to the plots of Figure 4a and are mostly characterized by the presence of two distinct branches, corresponding to HSR and LSR. In each figure, the threshold curve obtained with the CB layout, operating under the same respective parameter values, has been added in order to allow comparison to the lobe solutions, so that a general increase in stability, gained by the non-circular geometry, may be observed. In fact, the threshold branches corresponding to the 2LWB are higher than in the CB case, with the only exception of the orientation. This effect is particularly remarkable in the HSR and even more when the clearance ratio is equal to 1, whereas the dotted-line branches in the LSR turn out to be very close each to the other. Also worth of notice is the broadening of the HSR, at the expense of the LSR, when is raised from 1 to 2. Yet, comparing in each figure the curves corresponding to different angles, it can be inferred that the apparent improvement of the stable behavior in the HSR is higher the less the slope with respect to the horizontal layout assigned through the angle. Nevertheless, the orientation angle yields a some contrasting stability response: (1) poor when = 1, i.e., worse than that of the CB mount, in a relatively broad interval of and, moreover, without a distinct separation between HSR and LSR; (2) generally better than the CB response when = 2, with a threshold even higher than in the whole comparing cases, in a restricted interval of the bearing modulus, placed just downstream the jump up to the higher branch.
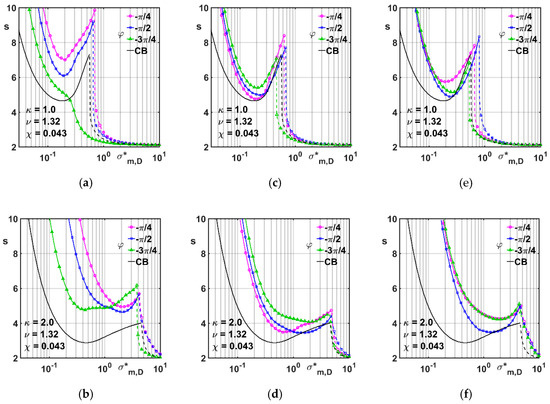
Figure 5.
Stability charts for CB and non-circular geometries, , = 1.32, = 0.043, = 1 (a,c,e), = 2 (b,d,f). (a,b): 2LWB; (c,d): LBmx; (e,f): LBmn.
Figure 5c–f illustrate the stability charts obtained replacing the 2LWB with an LBmx bearing (Figure 5c,d) or an LBmn one (Figure 5e,f). In order to ease the comparison between geometries, the whole set of Figure 5a–f is organized by rows, i.e., the figures on a same row are obtained with the same parameter values. In the whole cases, it can be seen that the LB curves (Figure 5c–f) are more gathered, with partial overlapping, and closer to the CB branches than in the 2LWB mount (compare Figure 5a,b). From comparison, it can also be inferred a general, moderate decrease of the stability thresholds gained by the lemon profiles, as well as the clear similarities to the respective 2LWB results (compare figures on a same row), mainly consisting in similar partitions of the diagram area in HSR and LSR. Some attention may be paid to examining the performances of the different angular orientations, with particular reference to the HSR. The positioning of the LB curves, almost generally above the CB ones, is still to indicate better stability with respect to the circular geometry. Nevertheless, the relative gathering of the branches denotes a weak influence of the angle in this set of values, even though some differences in the performance quality can be observed comparing the results pertaining to a same given value in the LBmx and LBmn geometries (compare, for instance, the branches with in Figure 5c,d respectively to those in Figure 5e,f).
A separate analysis is addressed just to the mentioned 2LWB case with and = 1, in order to throw light onto the characteristic continuity, i.e., without the typical jump from HSR to LSR or vice-versa, exhibited by the corresponding curve in Figure 5a. Figure 6a,b make it possible to assess that represents the critical eigenvalue both in the LSR and the HSR (compare Figure 5a). Owing to coalescences between the different eigenvalues, observed in the Re and Im diagrams at varying in its interval, maintains its position over the zero axis, so that the critical value of (i.e., the speed at which the pair crosses the imaginary axis) varies continuously without jumps and intervention of different eigenvalues. It is also worth noticing that changes its relative magnitude with respect to the other eigenvalues when passing from LSR to the HSR, as it can be inferred comparing the bottom diagrams in Figure 5a,b.
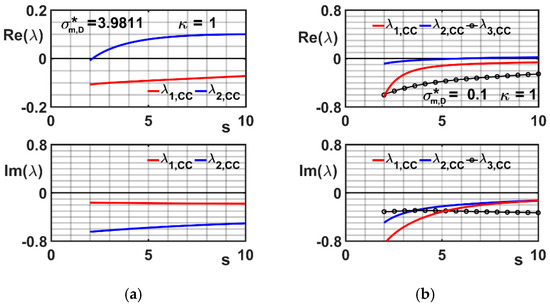
Figure 6.
Partial portraits of the eigenvalues behavior vs. s for = 2, at = 3.98 (a) and = 0.1 (b).
The effects of an increase in the radius ratio from 1.32 to 1.5 can be observed from Figure 7a–f. As in the previous set of figures, in each row it is possible to compare the 2LWB data (left) to the LBmx (center) and LBmn ones (right), obtained under the same parameter values. Observation and comparison of the plots in these figures make it possible to conclude that the above modification in the value keeps unchanged the characteristics already observed in Figure 5a–f, while determining an increased stability, as confirmed by the raising of the whole branches. On the other hand, it was observed that a moderate change in the value of the mass ratio yielded no sensible modification in the charts depicted in Figure 5a–f. Related results to support this remark were obtained assuming = 0.025 and 0.075 and are not presented here for the sake of brevity.
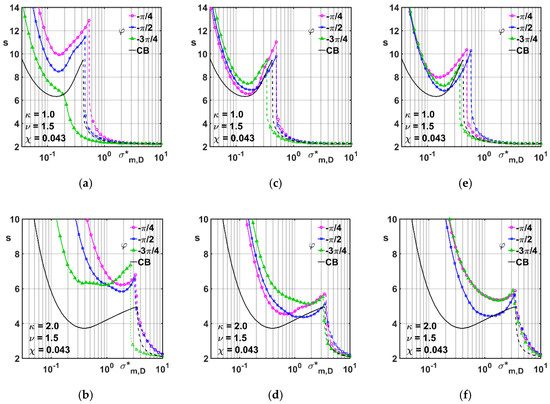
Figure 7.
Stability charts for CB and non-circular geometries, , = 1.5, = 0.043, = 1 (a,c,e), = 2 (b,d,f). (a,b): 2LWB; (c,d): LBmx; (e,f): LBmn.
The stability charts obtained with the same parameter values of Figure 5a–f, but adopting a further set of angular positions, i.e., , are reported in Figure 8a–c and Figure 9a–f. The values = 1 and = 2 were respectively adopted in the former and the latter set of figures. A general decay of stability, partly lessened at higher loads, is shared by the different curves, which show substantial similarities in the three, compared geometries. It is apparent that, whatever the noncircular bearing shape, when = 1 the threshold curves for and are positioned quite below the CB curve. Differently, some higher branches of the curves calculated with and overstep the CB stability border when is about less than 0.2. Similar behavior characterize the data for with restriction to the LBmx and LBmn profiles (Figure 8b,c). A further remark can be made about the shape of the curves, which are deprived of distinct separation between the HSR and LSR, with the only exception of the 2LWB and LBmx branches at .
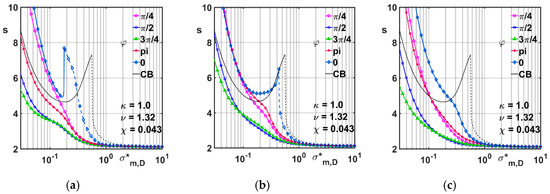
Figure 8.
Stability charts for CB and non-circular geometries, , = 1.32, = 0.043 and = 1. (a): 2LWB; (b): LBmx; (c): LBmn.
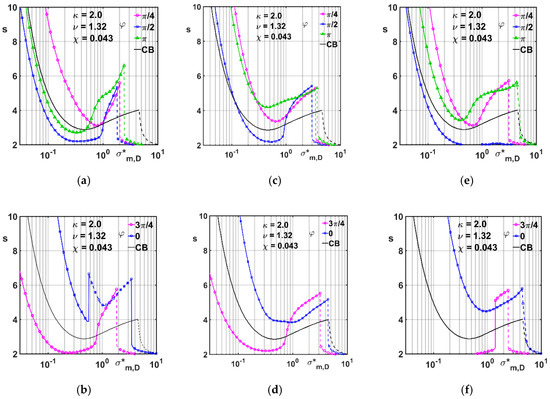
Figure 9.
Stability charts for CB and non-circular geometries, , = 1.32, = 0.043 and = 2. (a,b): 2LWB; (c,d): LBmx; (e,f): LBmn.
When = 2 (Figure 9a–f) a higher spread, with respect to the results of Figure 8a–c, is observed in the stability performances. Angular positions with and yield a remarkable lowering of the limit curves. This circumstance is particularly evident for the LBmn profile. Conversely, the best performance pertains to the orientation: this horizontal layout of the outer bearing, makes the stability borders in Figure 9b,d,f comparable to the higher branches depicted in Figure 5b,d,f, respectively. Even in this case, this outcome appears more evident when the LBmn shape is adopted. A further comment is to be addressed to the discontinuities exhibited in Figure 9b,f, which could represent, at first glance, numerical artifacts. Nevertheless, an inspection into the behavior of the critical eigenvalues clarifies the point. Figure 10a–e show the partial portraits of the eigenvalues obtained in the interval of rotor speed s, taken at different, close values of the bearing modulus. In particular, Figure 10a–c, relative to a sequence of values around 3.5, show how the critical eigenvalue is initially represented by (Figure 10a,b, top) and successively (Figure 10c, top) by . The passage from the one eigenvalue to the other takes place with a jump in the critical value s* of s, which justifies the right discontinuity in the curve of Figure 9b. Further downward, when is around 0.54 another jump takes place, as confirmed by the left discontinuity in the curve of Figure 9b. Differently from the previous case, the jump in the critical value s* from 6.7 c.a. to 4.2 c.a. when is due to the only eigenvalue, as confirmed by the behavior summarized in the top diagrams of Figure 10d,e.
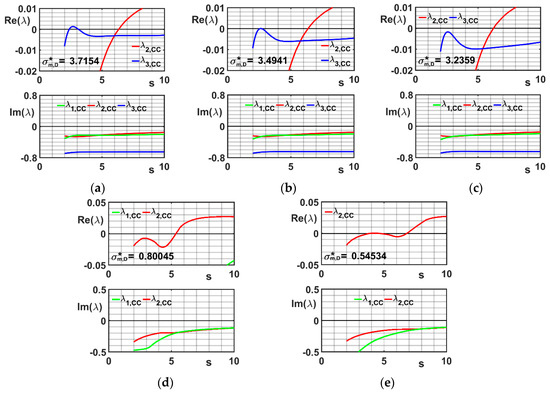
Figure 10.
Behavior of the eigenvalues (partial portraits) related to the curve in Figure 9b, taken at successive values of . (a–c): sequence involved in the right discontinuity about = 3.5; (d,e): sequence involved in the left discontinuity about = 0.54.
3.4. Non-Linear Analysis with Brute-Force Method
The above analysis of stability suffers from the limits due to the several simplifying hypotheses that have been assumed, among which the linearization of the fluid film forces is a distinctive feature. The brute-force approach, based on the numerical integration of the system’s ODE, represents a first, classic tool at disposal to get further insight into the dynamics under analysis [23], especially in the post-bifurcation scenario, before recurring to possible different methods, like continuation analysis or center manifolds analysis [6,18,19]. However, it is worth remarking that the brute-force method can cast light on the investigated dynamics, though restricting to the stable solutions and on condition to evaluate suitably the sensibility to initial conditions, so as to detect the presence of possibly coexisting solutions. Nevertheless, regarding the investigation carried out in the above section, this approach can effectively play a supporting role, mainly consisting in a survey of the bifurcation dynamics predicted through the linear stability analysis. Particularly, the stability loss can be verified by observing the positions occupied by the journal and ring centers within their respective clearances, as the speed is gradually increased in the low values range. In fact, when the bifurcation manifests, their equilibrium point-status is replaced by a motion condition as an effect of the onset of a limit cycle. Both the speed at which the transition sets in and the way the orbits’ size increase can be suitably appraised through the numerical simulation.
On these premises, two examples have been chosen from the case-studies presented in the above section, in order to show the use of the brute-force procedure in the present context. In each example, for a given set of , , , and values, the rotor speed is assigned in steps within a suitable interval. At each step, the numerical integration of Equation (8), written in the absence of unbalance, is carried out by means of an ode15s MATLAB routine, up to attaining a steady condition after that the initial transient is damped out. This procedure is repeated for different FRB layouts, whose responses are eventually compared in terms of journal and ring center orbits, minimum film thickness, and SI index. The last quantity is specifically related to the orbits. Besides contrasting the orbits obtained from a layout to the other at some chosen s values, the said index, defined as
where
and and are the x and y coordinates of the orbit points, makes it possible to evaluate approximatively the orbit dimensions along the examined interval of speed.
The two selected examples are characterized by the following sets of parameters:
Set (1) = 0.1, = 2, = 1.32, = 0.043, layouts: CB, 2WLB with rad (reference to Figure 5b and Figure 9b);
Set (2) = 0.22, = 1, = 1.32, = 0.043, layouts: CB, 2WLB with rad (reference to Figure 8a).
In the examples, intervals: 1.18 ÷ 15.4 (10 ÷ 130 krpm) or 1.18 ÷ 21.3 (10 ÷ 190 krpm) of the s rotor speed, in steps Δs = 0.355 (3 krpm), have been assumed.
Figure 11a,b depict the behavior of the SI index respectively for the above Set1 and Set2 conditions. Each curve in the diagrams starts at a speed value that is generally not coinciding with the exact critical one, but turns out to be placed just downstream of it, owing to the step resolution and the fact that the index assumes null values in the presence of equilibrium points. The SI behavior shown in the plots makes it possible to infer that:
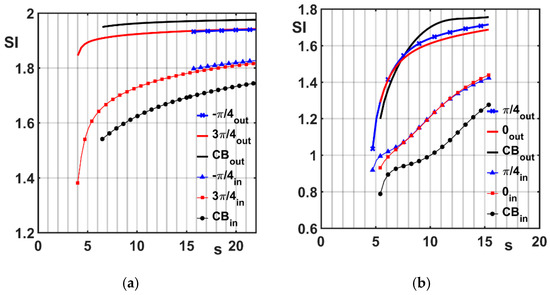
Figure 11.
Behavior of the SI index relative to the orbits of the journal and ring centers (respectively: ‘in’ and ‘out’ subscripts): examples for the CB and 2LWB layouts. (a) Set 1 conditions and layouts; (b) Set 2 conditions and layouts.
- -
- The orbits described by the ring center in the outer bearing are larger than those described by the journal center. In particular, the orbits of the ring center for the CB are generally larger than in the other layouts. An opposite outcome appears when comparing the orbits of the journal bearing, which are, for the circular geometry, smaller than in the 2LWB examples.
- -
- Under the Set 1 conditions, the bifurcation manifests at rotor speeds that are quite different each to the other (Figure 11a). The 2WLB, layout presents a critical speed about s = 15, remarkably higher than those that occur about s = 6 and s = 4, respectively for the CB and the 2WLB − cases. This outcome is quite congruent with the predictions that can be deduced from Figure 5b and Figure 9b for these three layouts.
- -
- Adopting the Set 2 (Figure 11b), the critical speeds obtained for the different FRBs are closer than in the Set 1 conditions. The lowest one, at about s = 4.5, is obtained when the outer bearing, i.e., the FRB housing, has a lobe profile with a slope. In the other two cases, represented by the CB and 2WLB − layouts, the transition to the limit cycle manifests at about s = 5. Comparison to Figure 8a makes it possible to assess a sufficient congruence between the data in these conditions too, despite the jump exhibited in the same figure by the threshold curve relative to the lobe bearing with slope.
An insight into the results presented in Figure 11a,b can be achieved through inspection of the trajectories described by the journal and ring centers at different speeds and depicted in Figure 12a,c,e, for conditions of Set 1, and in Figure 12b,d,f for the Set 2 ones. A first indication about the stability performances that pertain to the different layouts, is obtained by noticing the long-lasting permanence of the equilibrium point at speed increase, which manifests in some cases with respect to the other ones. This remark complies particularly with the behavior of the 2WLB − reported in Figure 12e. The wide orbits of the centers, detected for s = 16, contrast with the minute orbits obtained when s = 15. Differently, the other two geometries analyzed under the same Set 1 conditions (Figure 12a,c) turn out to exhibit big orbits well before, when s = 7.
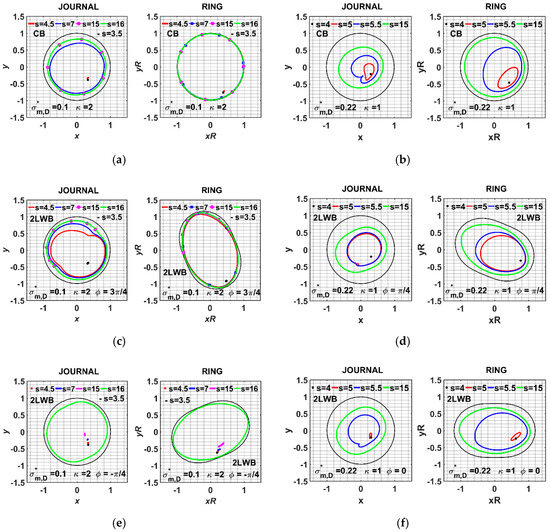
The data of Figure 12a,c,e also confirm that the trajectories of the ring center in the CB layout are on average closer to the housing wall with respect to the compared lobe geometries, as inferred from observation of the SI curves in Figure 11a. The opposite result, relative to the magnitude of the journal bearing orbits, which appears to be relatively lesser in the CB case than in the compared geometries, is also verified. Figure 12b,d,f depict the trajectories obtained when conditions are those of Set 2. The critical speed occurs for s values between 4 and 5 in the whole three bearing types. Yet, the transition to the precession motion appears slightly anticipated by the 2WLB − layout with respect to the CB and the 2WLB − ones. Furthermore, comparing the data obtained at s = 4 and 5 in Figure 12d,f to those relative to s = 3.5 and 4.5 in Figure 12c and s = 15 and 16 in Figure 12e, it can be said that the transition in the Set 2 cases manifests very likely some more gradually than in the Set 1 examples. Further observation of the data in Figure 12a–f makes it possible to notice the presence of higher harmonics that affect, at some degree, the journal orbits downstream of the stability loss, particularly under the Set 2 conditions.
The brief portrait given in the present section is completed here below with an observation of the minimum thickness behavior, as reported in Figure 13a,b. The whole curves in the plots present an initial branch that raises with the rotor angular velocity, from the initial s = 2 value up to the critical speed. This behavior is justified by the gradual centering of the steady equilibrium points within the bearing clearances, which evolves as far as the speed is increased. The difference in the loading conditions from Set 1 and Set 2 explains the different range of values pertaining to the curves reported in the lower part of Figure 13a,b and relative to the inner bearing. It is worth observing that the minimum thickness assumes practically the same values, whatever the FRB layout in the examples. The curves shows quite clearly the jump that is due to the stability loss, with indications that agree with those inferred from Figure 11 and Figure 12. The significant jumps that affect the minimum film thickness in the inner bearing under Set 1 are also worth of remark. This outcome appears to be reasonably explained in terms of the said equilibrium point-centering and load condition effects. The example represented by the 2WLB − case in Figure 13a is representative in this regard.
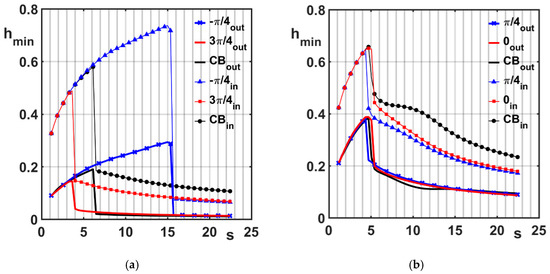
Figure 13.
Minimum film thickness within the inner and outer bearings. (a) Set 1 conditions and layouts. (b) Set 2 conditions and layouts.
4. Discussion and Conclusions
The paper presents a theoretical investigation that shows how the instability threshold of a perfectly balanced, horizontally placed, rigid rotor on FRBs is dependent on the shape of the FRB housing. With this aim, two geometries, respectively characterized by a two-lobe wave shape and a lemon one, have been considered in place of the circular profile commonly adopted for the outer plain bearing. The angular orientation and the preload level are distinctive parameters of these two unsymmetrical profiles. Shaping the bore of journal bearings by means of multi-lobe, dammed or stepped profiles is a well-known, low cost practice to gain a better rotor stability with respect to the basic circular geometry. Past research carried out by the author on this topic and the relative scarceness of studies about the specific use of noncircular geometries within FRBs motivated the present study, carried out with a linear approach. In this sense, and through the extension to different bearing layouts, it particularly follows in the wake of some previous works [5,6] focused on the behavior of the common FRB.
The results make it possible to assess the incidence of the noncircular shape and, particularly, of the angular orientation of the profile, on the stability response of the rotor system, with positive or negative effects that vary from case to case. In particular, the adoption of FRBs with outer 2LWB, makes it possible to obtain better stability performances with respect to the CB layout when negative values of the angle are employed. The highest instability thresholds are obtained with the negative angle that presents the lesser absolute value among the adopted ones, i.e., . Above this value, i.e., when is null or positive, the performance gradually worsens, with a sensible lowering of the curves occurring beyond . These remarks make it possible to infer that, regarding the analyzed type of stability loss, the response of the 2LWB layout is better than the CB one, on condition that the bearing is not too much inclined above the horizontal, with a peak in the counter-clockwise range of angular displacements. The worst responses are instead obtained with the and clockwise positions. These circumstances are likely in relation to the assumed vertical direction of the external load and the counter-clockwise, positive angular speed of the journal. The influence due to modifications of the radius and clearance ratios, in terms of extension and position of the HSR and LSR, are in line with those observed in the CB case, whereas varying the mass ratio in the range 0.025–0.075 yields no sensible changes.
When the LBmx and LBmn shapes are adopted in the outer FRB bearing, the stability charts appear rather similar to those obtained in the corresponding 2LWB cases. The influence of negative values is less pronounced than in the 2LWB layout, despite a general improvement of stability may be detected, with curves that appear more gathered and close to the CB ones adopted for reference. Nevertheless, the results of these specific inclinations show some differences with respect to those described about the 2LWB layout, particularly in the case of the LBmx profile. A higher degree of similarity may instead be assessed in the stability charts obtained for the 2LWB and the two LB layouts, from case to case, when positive values are assigned.
The inspection of the eigenvalues behavior has proved to be an effective tool in order to justify some specific features of the threshold curves. The recourse to brute-force integration, in a few examples related to the case-studies considered in the previous analysis, has given further insight into the examined dynamics. This part of the investigation has been carried out through observation of the journal and ring orbits and evaluation of the minimum film thickness, with further use of a suitable parameter correlated to the orbit dimensions.
The several, simplifying hypotheses in the analysis and, above all, the restriction to the Hopf bifurcation, which takes place from the steady state equilibrium of the perfectly balanced rigid rotor, mark the limits of the investigation. Nevertheless, the obtained results highlight significant effects of the non-circular geometry, as it has been assumed here within the FRB layout, which could reasonably encourage further research on the topic.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
Nomenclature
| Symbols | Description |
| dimensionless wave amplitude of the 2LWB | |
| clearance of the inner bearing [m] | |
| parameter of the LB bore [m] | |
| clearance of the outer bearing (CB bore, reference for the 2LWB and LB cases) [m] | |
| clearance of the outer bearing (2LWB bore) [m] | |
| clearance of the outer bearing (LB bore) [m] | |
| parameter of the LB bore [m] | |
| diameter of the inner bearing [m] | |
| : dimensionless force components of the inner fluid film | |
| : dimensionless force components of the outer fluid film | |
| , | force components of the inner fluid film [N] |
| , | force components of the outer fluid film [N] |
| g | gravity acceleration [m/s2] |
| h | dimensionless fluid film thickness of the inner bearing |
| L | axial length of the inner bearing [m] |
| m, | semi-mass of the rotor, mass of the ring [kg] |
| oil film pressure [N] | |
| : reference pressure in the internal oil film [N] | |
| : lemon-bearing ellipticity ratio | |
| : reference pressures in the outer oil film [N] | |
| R | radius of the inner bearing [m] |
| s | : dimensionless rotor speed |
| t | time [s] |
| W, | half-weight of the rotor, weight of the ring [N] |
| , | dimensionless coordinates of the journal (Oxy: right-hand reference with horizontal x-axis) |
| , | coordinates of the journal center [m] |
| , | , : dimensionless relative positions between journal and ring |
| z | dimensionless axial coordinate of the bearing |
| angular position of the film border (Appendix A) | |
| circumferential coordinate | |
| dimensionless pressure of the oil film | |
| : dimensionless axial coordinate | |
| : orientation angle of the LB profile (Figure 1b) | |
| : clearance ratio | |
| eigenvalue (Appendix B) | |
| : axial length ratio | |
| absolute viscosity of the lubricant in the inner bearing [Pa s] | |
| : viscosity ratio | |
| : Sommerfeld number in the inner oil film | |
| : Sommerfeld number in the outer oil film | |
| : bearing parameter | |
| : Sommerfeld number ratio | |
| : dimensionless time | |
| : radius ratio | |
| angular orientation of the noncircular outer bearing (Figure 1a) | |
| : mass ratio | |
| : lemon-bearing clearance ratio | |
| rotor angular speed [rad s−1] | |
| [rad s−1] | |
| : angular speed ratio | |
| : reference angular frequency [rad s−1] | |
| subscript for the quantities relative to the outer bearing | |
| subscript for the quantities relative to the ring | |
| dimensionless time derivative |
Appendix A
Appendix A.1. Inner Bearing
Dimensionless Reynolds Equation with SBA:
Pressure within the oil film:
Dimensionless expression of the force components of the inner oil film:
Sommerfeld number for the inner oil film:
is the number relative to the simple plain bearing.
Appendix A.2. Outer Bearing
Dimensionless Reynolds Equation with SBA:
Dimensionless oil film pressures:
The following equation expresses the components in dimensionless way
where
Appendix B
Main quantities adopted in Equation (13):
The matrices and can be deduced from ([5], Appendix A), with the remarks
, , , , , , .
The elements of and are numerically obtained by means of finite difference approximations of the partial derivatives of the outer film force around the equilibrium point.
With use of the following quantities
Equation (13) can be equivalently written
and furthermore
where
Let the solution of Equation (A13) be given as , so as to write
After premultiplication by it is obtained
and eventually
which represents the eigenvalue problem with .
References
- Schweizer, B. Total instability of turbocharger rotors—Physical explanation of the dynamic failure of rotors with full-floating ring bearings. J. Sound Vib. 2009, 328, 156–190. [Google Scholar] [CrossRef]
- Tian, L. Investigation into Nonlinear Dynamics of Rotor-Floating Ring Bearing Systems in Automotive Turbochargers. Ph.D. Thesis, University of Sussex, Brighton, UK, 2012. [Google Scholar]
- Shaw, M.C.; Nussdorfer, T.J. An Analysis of the Full-Floating Journal Bearing; NACA Report 866; National Advisory Committee for Aeronautics: Washington, DC, USA, 1947. [Google Scholar]
- Orcutt, F.K.; Ng, C.W. Steady-state and dynamic properties of the floating ring journal bearing. ASME J. Lubr. Tech. 1968, 90, 243–253. [Google Scholar] [CrossRef]
- Tanaka, M.; Hori, Y. Stability characteristics of floating bush bearings. ASME J. Lubr. Tech. 1972, 94, 248–256. [Google Scholar] [CrossRef]
- Boyaci, A.; Hetzler, H.; Seemann, W.; Proppe, C.; Wauer, J. Analytical bifurcation analysis of a rotor supported by floating ring bearings. Nonlinear Dyn. 2009, 57, 497–507. [Google Scholar] [CrossRef]
- Hatakenaka, K.; Tanaka, M.; Suzuki, K. A theoretical analysis of floating bush journal bearing with axial oil film rupture being considered. ASME J. Tribol. 2002, 124, 494–505. [Google Scholar] [CrossRef]
- Chasalevris, A. Finite length floating ring bearings: Operational characteristics using analytical methods. Tribol. Int. 2016, 94, 571–590. [Google Scholar] [CrossRef]
- Gunter, E.J.; Chen, W.J. Dynamic Analysis of a Turbocharger in Floating Bushing Bearings. In Proceedings of the ISCORMA-3, 3rd International Symposium on Stability Control of Rotating Machinery, Cleveland, OH, USA, 19–23 September 2005. [Google Scholar]
- Inagaki, M.; Kawamoto, A.; Abekura, T.; Suzuki, A.; Rübel, J.; Starke, J. Coupling Analysis of Dynamics and Oil Film Lubrication on Rotor—Floating Bush Bearing System. J. Syst. Des. Dyn. 2011, 5, 461–473. [Google Scholar] [CrossRef][Green Version]
- Tian, L.; Wang, W.J.; Peng, Z.J. Nonlinear effects of unbalance in the rotor-floating ring bearing system of turbochargers. Mech. Syst. Signal. Process. 2013, 34, 298–320. [Google Scholar] [CrossRef]
- Schweizer, B. Dynamics and stability of turbocharger rotors. Arch. Appl. Mech. 2010, 80, 1017–1043. [Google Scholar] [CrossRef]
- Bonello, P. Transient modal analysis of the non-linear dynamics of a turbocharger on floating ring bearings. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2009, 223, 79–93. [Google Scholar] [CrossRef]
- San Andrés, L.; Rivadeneira, J.C.; Chinta, M.; Gjika, K.; LaRue, G. Nonlinear Rotordynamics of Automotive Turbochargers: Prediction and Comparison to Test Data. ASME J. Eng. Gas Turbines Power 2007, 129, 488–493. [Google Scholar] [CrossRef]
- Eling, R.; van Ostayen, R.; Rixen, D. Multilobe Floating Ring Bearings for Automotive Turbochargers. In Proceedings of the 9th IFToMM International Conference on Rotor Dynamics, Milan, Italy, 22–25 September 2014; Mechanisms and Machine Science 21. Pennacchi, P., Ed.; Springer: Cham, Switzerland, 2015; pp. 821–833. [Google Scholar]
- Soni, S.; Vakharia, D.P. A steady-state performance analysis of a non-circular cylindrical floating ring journal bearing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 231, 41–56. [Google Scholar] [CrossRef]
- Bernhauser, L.; Heinisch, M.; Schörgenhumer, M.; Nader, M. The Effect of Non-Circular Bearing Shapes in Hydrodynamic Journal Bearings on the Vibration Behavior of Turbocharger Structures. Lubricants 2017, 5, 6. [Google Scholar] [CrossRef]
- Adiletta, G.; Mancusi, E.; Strano, S. Nonlinear behaviour analysis of a rotor on two-lobe wave journal bearings. Tribol. Int. 2011, 44, 42–54. [Google Scholar] [CrossRef]
- Adiletta, G. An insight into the dynamics of a rigid rotor on two-lobe wave squeeze film damper. Tribol. Int. 2017, 116, 69–83. [Google Scholar] [CrossRef]
- Pinkus, O. Analysis of elliptical bearings. Trans. ASME 1956, 78, 965–973. [Google Scholar]
- Ott, H.H.; Buchter, J.-E.; Frey, U. Wellenlage, Reibung und Öldurchsatz von Radial-Gleitlagern mit zwei zusammengeschobenen Kreisschalen (Zitronenspiellager). Schweiz. Bauztg. 1969, 87, 207–212. [Google Scholar]
- Myers, C.J. Bifurcation theory applied to oil whirl in plain cylindrical journal bearings. ASME J. Appl. Mech. 1984, 51, 244–250. [Google Scholar] [CrossRef]
- Capone, G. Descrizione analitica del campo di forze fluidodinamico nei cuscinetti cilindrici lubrificati. Energ. Elettr. 1991, 3, 105–110. [Google Scholar]
- Lang, O.R.; Steinhilper, W. Gleitlager: Berechnung und Konstruktion von Gleitlagern mit Konstanter und Zeitlich Veränderlicher Belastung, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1978; pp. 304–307. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).