The Impact of Lubricant Film Thickness and Ball Bearings Failures †
Abstract
1. Introduction
2. Empirical Equations for Life
3. Tribological Predictions of Life
4. First Parametric Study
5. Second Parametric Study
6. Conclusions
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Number of revolutions before 10% chance of failure | |
| SKF | Svenska Kullagerfabriken |
| RMS | Root Mean Square |
References
- Stachowiak, G.; Batchelor, A. Engineering Tribology, 4th ed.; Butterworth-Heinemann: Oxford, UK, 2005. [Google Scholar]
- Gohar, R. Elastohydrodynamics; World Scientific Publishing Company: Singapore, 2002. [Google Scholar]
- Ranger, A.; Ettles, C.; Cameron, A. The solution of the point contact elasto-hydrodynamic problem. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1975, 346, 227–244. [Google Scholar] [CrossRef]
- Blau, P. On the nature of running-in. Tribol. Int. 2005, 38, 1007–1012. [Google Scholar] [CrossRef]
- Hu, Y.; Li, N.; Tønder, K. A dynamic system model for lubricated sliding wear and running-in. J. Tribol. 1991, 113, 499–505. [Google Scholar] [CrossRef]
- Suzuki, M.; Ludema, K. The wear process during the “running-in” of steel in lubricated sliding. J. Tribol. 1987, 109, 587–591. [Google Scholar] [CrossRef]
- Endo, K.; Kotani, S. Observations of steel surfaces under lubricated wear. Wear 1973, 26, 239–251. [Google Scholar] [CrossRef]
- Nanbu, T.; Yasuda, Y.; Ushijima, K.; Watanabe, J.; Zhu, D. Increase of traction coefficient due to surface microtexture. Tribol. Lett. 2008, 29, 105–118. [Google Scholar] [CrossRef]
- Wong, P.; Huang, P.; Wang, W.; Zhang, Z. Effect of geometry change of rough point contact due to lubricated sliding wear on lubrication. Tribol. Lett. 1998, 5, 265–274. [Google Scholar] [CrossRef]
- Cann, P.; Spikes, H. In-contact IR spectroscopy of hydrocarbon lubricants. Tribol. Lett. 2005, 19, 289–297. [Google Scholar] [CrossRef]
- Jiang, P.; Li, X.M.; Guo, F.; Chen, J. Interferometry measurement of spin effect on sliding EHL. Tribol. Lett. 2009, 33, 161–168. [Google Scholar] [CrossRef]
- Reddyhoff, T.; Spikes, H.A.; Olver, A.V. Compression heating and cooling in elastohydrodynamic contacts. Tribol. Lett. 2009, 36, 69–80. [Google Scholar] [CrossRef]
- Timken Manual 10424, October 2016. Available online: https://www.timken.com/resources/timken-engineering-manual/ (accessed on 13 April 2019).
- Svenska Kullager Fabriken AB. SKF Bearing Calculator. 2017. Available online: http://webtools3.skf.com/BearingCalc/selectProduct.action (accessed on 23 April 2019).
- SKF Bearing Maintenance Handbook; SKF Group: Gothenburg, Sweden, 2011; ISBN 978-91-978966-4-1.
- Zaretsky, E.V. Rolling Bearing Life Prediction, Theory, and Application; NASA Technical Report. Available online: https://ntrs.nasa.gov/search.jsp?R=20160013905 (accessed on 10 September 2018).
- Zaretsky, E.V. A. Palmgren Revisited a Basis for Bearing Life Prediction; NASA Technical Memorandum; Lewis Research Center: Clevelend, OH, USA, 1997. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19970025228.pdf (accessed on 10 September 2018).
- Rolling Bearings: Dynamic Load Ratings and Rating Life; International Organization for Standardization (DIN): Berlin, Germany, 2007; Available online: https://www.iso.org/standard/38102.html (accessed on 10 September 2018).
- Greenwood, J.; Williamson, J. Contact of nominally flat surfaces. Proc. R. Soc. Lond. A 1966, 295, 300–319. [Google Scholar] [CrossRef]
- Bush, A.; Gibson, R.; Keogh, G. The limit of elastic deformation in the contact of rough surfaces. Mech. Res. Commun. 1976, 3, 169–174. [Google Scholar] [CrossRef]
- Carbone, G. A slightly corrected Greenwood and Williamson model predicts asymptotic linearity between contact area and load. J. Mech. Phys. Solids 2009, 57, 1093–1102. [Google Scholar] [CrossRef]
- McCool, J. Comparison of models for the contact of rough surfaces. Wear 1986, 107, 37–60. [Google Scholar] [CrossRef]
- Bush, A.; Gibson, R.; Thomas, T. The elastic contact of a rough surface. Wear 1975, 35, 87–111. [Google Scholar] [CrossRef]
- Persson, B. Contact mechanics for randomly rough surfaces. Surf. Sci. Rep. 2006, 61, 201–227. [Google Scholar] [CrossRef]
- Finkin, E. Applicability of Greenwood-Williamson theory to film covered surfaces. Wear 1970, 15, 291–293. [Google Scholar] [CrossRef]
- Cann, P.; Ioannides, E.; Jacobson, B.; Lubrecht, A. The lambda ratio—A critical Re-examination. Wear 1994, 175, 177–188. [Google Scholar] [CrossRef]
- Marko, M. Friction of Tungsten-based coatings of steel under sliding contact. Lubricants 2019, 7, 14. [Google Scholar] [CrossRef]
- Crook, A. The lubrication of rollers. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1958, 250, 387–409. [Google Scholar] [CrossRef]
- Archard, J. The temperature of rubbing surfaces. Wear 1958, 2, 438–455. [Google Scholar] [CrossRef]
- Jaeger, J. Moving sources of heat and the temperature at sliding contact. Proc. R. Soc. N. S. W. 1942, 76, 203–224. [Google Scholar]
- Blok, H. Theoretical study of temperature rise at surfaces of actual contact under oiliness conditions. Proc. Inst. Mech. Eng. Gen. Discuss. Lubr. 1937, 2, 222–235. [Google Scholar]
- Cameron, A.; Gohar, R. Theoretical and experimental studies of the oil film in lubricated point contact. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1966, 291, 520–536. [Google Scholar] [CrossRef]
- Hamrock, B.; Dowson, D. Isothermal Elastohydrodynamic Lubrication of Point Contacts, III Fully Flooded Results; NASA Tech. Note; National Aeronautics and Space Administration: Washington, DC, USA, 1976; p. D-8317.
- Hamrock, B.; Dowson, D. Isothermal Elastohydrodynamic Lubrication of Point Contacts, I Theoretical Formulation; NASA Tech. Note; National Aeronautics and Space Administration: Washington, DC, USA, 1975; p. D-8049.
- Hamrock, B.; Dowson, D. Isothermal Elastohydrodynamic Lubrication of Point Contacts, IV Starvation Results; NASA Tech. Note; National Aeronautics and Space Administration: Washington, DC, USA, 1976; p. D-8318.
- Dowson, D. Elastohydrodynamic and micro-elastohydrodynamic lubrication. Wear 1995, 190, 125–138. [Google Scholar] [CrossRef]
- Nam, J.; Ryou, H.; Cho, S. A numerical model of rotating bearings for thermo-mechanical coupled analysis. Proc. Int. Conf. Simul. Exp. Heat Transf. Appl. 2016, 106, 25–31. [Google Scholar] [CrossRef]
- Lugt, P.M.; Velichov, S.; Tripp, J.H. On the chaotic behavior of grease lubrication in rolling bearings. Tribol. Trans. 2009, 52, 581–590. [Google Scholar] [CrossRef]
- Van Zoelen, M.; Venner, C.; Lugt, P. Prediction of film thickness decay in starved elasto-hydrodynamically lubricated contacts using a thin layer flow model. J. Eng. Tribol. 2009, 223, 541–552. [Google Scholar] [CrossRef]
- Venner, C.H.; Popovici, G.; Lugt, P.M.; Organisciak, M. Film thickness modulations in starved elastohydrodynamically lubricated contacts induced by time varying lubricant supply. ASME J. Tribol. 2008, 130, 041501. [Google Scholar] [CrossRef]
- Venner, C.; van Zoelen, M.; Lugt, P. Thin layer flow and film decay modeling for grease lubricated rolling bearings. Tribol. Int. 2012, 47, 175–187. [Google Scholar] [CrossRef]
- Fillot, N.; Berro, H.; Vergne, P. From continuous to molecular scale in modelling elastohydrodynamic lubrication: Nanoscale surface slip effects on film thickness and friction. Tribol. Lett. 2011, 43, 257–266. [Google Scholar] [CrossRef]
- Guo, F.; Wong, P.L.; Geng, M.; Kaneta, M. Occurrence of wall slip in elastohydrodynamic lubrication contacts. Tribol. Lett. 2009, 34, 103–111. [Google Scholar] [CrossRef]
- Krupka, I.; Bair, S.; Kumar, P.; Svoboda, P.; Hartl, M. Mechanical degradation of the liquid in an operating EHL contact. Tribol. Lett. 2011, 41, 191–197. [Google Scholar] [CrossRef]
- Marko, M. The Tribological Effects of Lubricating Oil Containing Nanometer-Scale Diamond Particles. Ph.D. Thesis, Columbia University, New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Marko, M.; Kyle, J.P.; Wang, Y.S.; Terrell, E.J. Tribological investigations of the load, temperature, and time dependence of wear in sliding contact. PLOS ONE 2017, 12, e0175198. [Google Scholar] [CrossRef] [PubMed]
- Marko, M.D.; Kyle, J.P.; Branson, B.; Terrell, E.J. Tribological improvements of dispersed nano-diamond additives in lubricating mineral oil. J. Tribol. 2015, 137, 011802. [Google Scholar] [CrossRef]
- Marko, M.D.; Kyle, J.P.; Wang, Y.S.; Branson, B.; Terrell, E.J. Numerical and experimental tribological investigations of diamond nanoparticles. J. Tribol. 2016, 138, 032001. [Google Scholar] [CrossRef]
- Johnson, K. Contact Mechanics; Cambridge University Press: New York, NY, USA, 1987. [Google Scholar]
- Einstein, A. Neue Bestimmung der molekuldimensionen. Ann. Phys. 1906, 19, 289–306. [Google Scholar] [CrossRef]
- Pabst, W. Fundamental considerations on suspension rheology. Ceram. Silik. 2004, 48, 6–13. [Google Scholar]
- So, B.; Klaus, E. Viscosity-pressure correlation of liquids. ASLE Trans. 1980, 23, 409–421. [Google Scholar] [CrossRef]
- ASTM D341-09, Standard Practice for Viscosity-Temperature Charts for Liquid Petroleum Products; ASTM-International: West Conshohocken, PA, USA, 2009; Available online: www.astm.org (accessed on 21 January 2013).
- Cengel, Y. Heat Transfer, a Practical Approach, 2nd ed.; Mcgraw-Hill: Boston, MA, USA, 2002. [Google Scholar]
- Abdel-Aal, H. A remark on the flash temperature theory. Int. Commun. Heat Mass Transf. 1997, 24, 241–250. [Google Scholar] [CrossRef]
- Barber, J. Distribution of heat between sliding surfaces. J. Mech. Eng. Sci. 1967, 9, 351–354. [Google Scholar] [CrossRef]
- Blok, H. The flash temperature concept. Wear 1963, 6, 483–494. [Google Scholar] [CrossRef]
- Archard, J.; Rowntree, R. The temperature of rubbing bodies; Part 2, the distribution of temperatures. Wear 1988, 128, 1–17. [Google Scholar] [CrossRef]
- White, F. Fluid Mechanics, 5th ed.; McGraw-Hill: Boston, MA, USA, 2003. [Google Scholar]
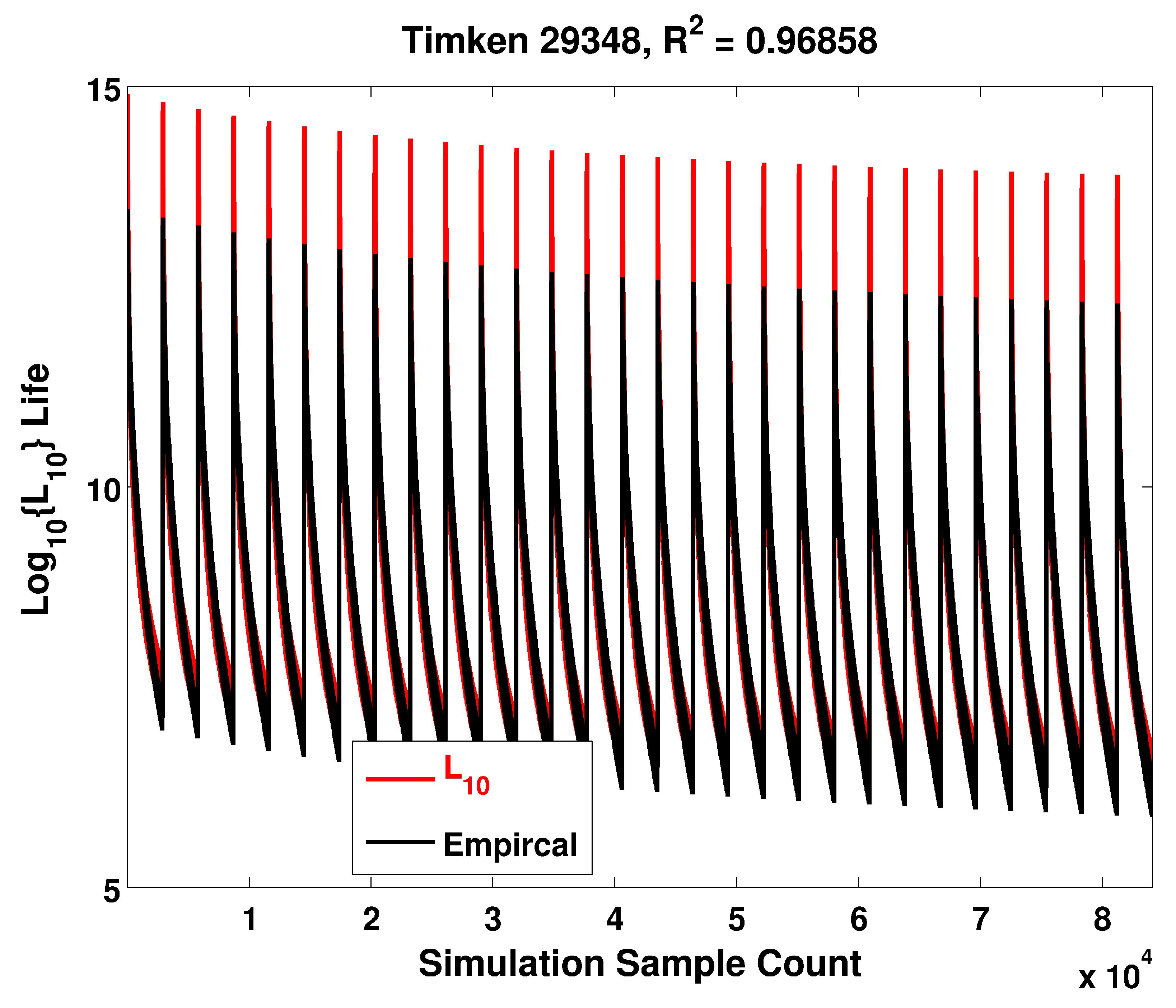
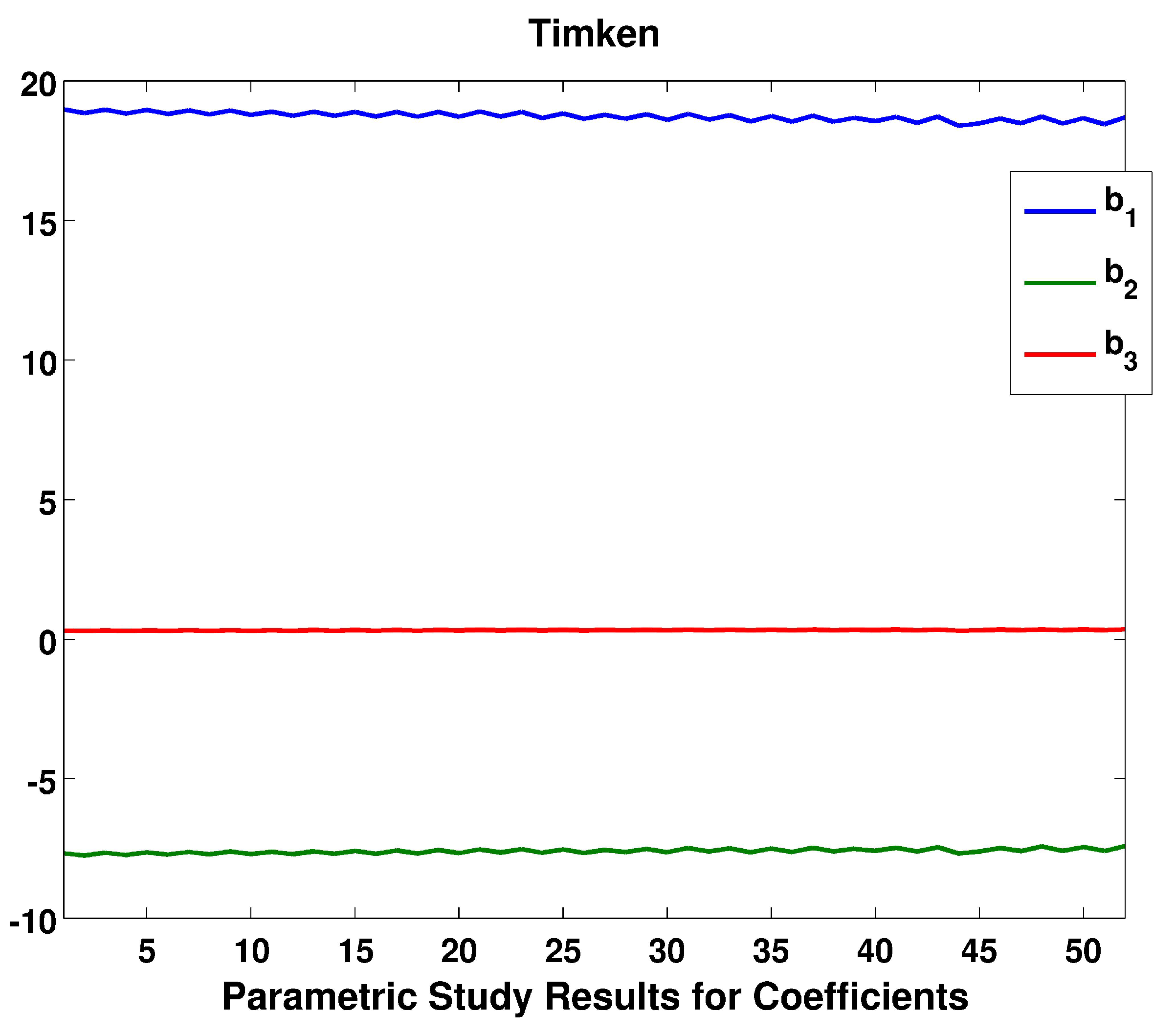
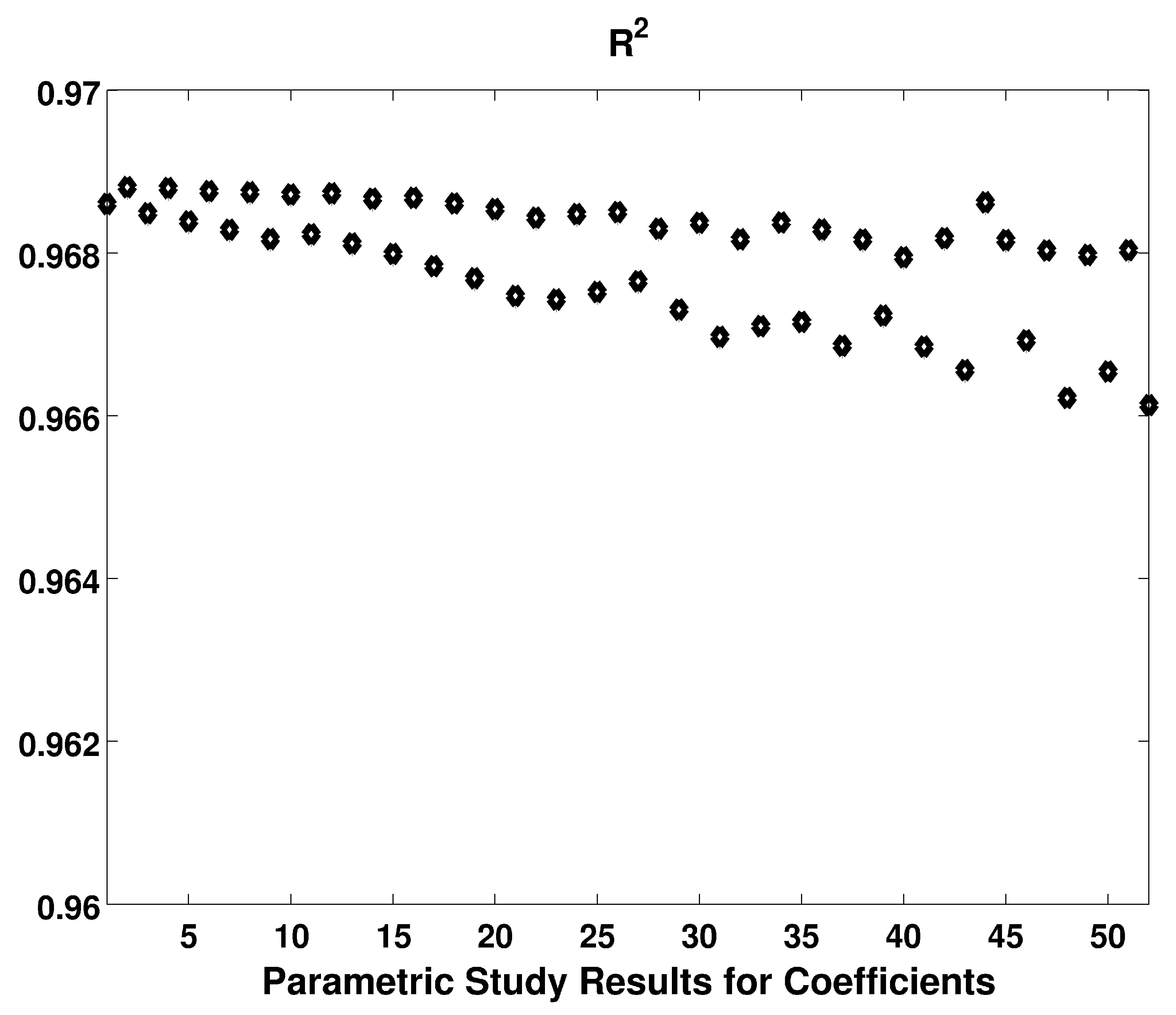
| Model | d (mm) | (kN) | (mm) | H (mm) | E (mm) | D (mm) | |
|---|---|---|---|---|---|---|---|
| 1 | 29418 | 90 | 820 | 98.9 | 148 | 137 | 190 |
| 2 | 29320 | 100 | 462 | 108.1 | 141 | 134 | 170 |
| 3 | 29420 | 100 | 1020 | 108.8 | 164 | 151 | 210 |
| 4 | 29322 | 110 | 604 | 118.6 | 157 | 149 | 190 |
| 5 | 29422 | 110 | 1200 | 120.3 | 180 | 167 | 230 |
| 6 | 29324 | 120 | 768 | 128.5 | 172 | 163 | 210 |
| 7 | 29424 | 120 | 1390 | 131.6 | 197 | 182 | 250 |
| 8 | 29326 | 130 | 852 | 140.3 | 186 | 177 | 225 |
| 9 | 29426 | 130 | 1600 | 142.4 | 213 | 197 | 270 |
| 10 | 29328 | 140 | 970 | 148.9 | 199 | 188 | 240 |
| 11 | 29428 | 140 | 1640 | 152.8 | 223 | 207 | 280 |
| 12 | 29330 | 150 | 993 | 159.5 | 209 | 198 | 250 |
| 13 | 29430 | 150 | 1860 | 163.5 | 238 | 222 | 300 |
| 14 | 29332 | 160 | 1190 | 170.5 | 225 | 213 | 270 |
| 15 | 29432 | 160 | 2100 | 175 | 255 | 237 | 320 |
| 16 | 29334 | 170 | 1230 | 179.2 | 235 | 223 | 280 |
| 17 | 29434 | 170 | 2380 | 184.8 | 270 | 251 | 340 |
| 18 | 29336 | 180 | 1430 | 190.7 | 251 | 238 | 300 |
| 19 | 29436 | 180 | 2660 | 197.6 | 286 | 267 | 360 |
| 20 | 29338 | 190 | 1620 | 202.2 | 268 | 253 | 320 |
| 21 | 29438 | 190 | 3040 | 205.5 | 303 | 281 | 380 |
| 22 | 29340 | 200 | 1880 | 213.3 | 284 | 269 | 340 |
| 23 | 29440 | 200 | 3210 | 217 | 317 | 295 | 400 |
| 24 | 29344 | 220 | 1950 | 231.6 | 303 | 288 | 360 |
| 25 | 29444 | 220 | 3350 | 237.8 | 339 | 317 | 420 |
| 26 | 29348 | 240 | 2040 | 251.9 | 323 | 308 | 380 |
| 27 | 29448 | 240 | 3410 | 259 | 360 | 338 | 440 |
| 28 | 29352 | 260 | 2580 | 275.7 | 356 | 340 | 420 |
| 29 | 29452 | 260 | 4160 | 279.2 | 391 | 367 | 480 |
| 30 | 29356 | 280 | 2580 | 296.8 | 376 | 360 | 440 |
| 31 | 29456 | 280 | 4920 | 300.6 | 423 | 397 | 520 |
| 32 | 29360 | 300 | 3150 | 315.6 | 407 | 388 | 480 |
| 33 | 29460 | 300 | 4990 | 321.1 | 443 | 418 | 540 |
| 34 | 29364 | 320 | 2830 | 333.3 | 427 | 407 | 500 |
| 35 | 29464 | 320 | 5155 | 320 | 469 | 444 | 580 |
| 36 | 29368 | 340 | 3120 | 365.8 | 463 | 443 | 540 |
| 37 | 29468 | 340 | 5922 | 340 | 500 | 473 | 620 |
| 38 | 29372 | 360 | 3632 | 360 | 476 | 457 | 560 |
| 39 | 29472 | 360 | 5440 | 360 | 528 | 498 | 640 |
| 40 | 29376 | 380 | 4295 | 380 | 507 | 486 | 600 |
| 41 | 29476 | 380 | 6493 | 380 | 546.1 | 518 | 670 |
| 42 | 29380 | 400 | 3850 | 400 | 534 | 510 | 620 |
| 43 | 29480 | 400 | 7333 | 400 | 577.1 | 547 | 710 |
| 44 | 29284 | 420 | 2682 | 420 | 513.1 | 498 | 580 |
| 45 | 29384 | 420 | 4040 | 420 | 561 | 537 | 650 |
| 46 | 29484 | 420 | 6780 | 420 | 608 | 576 | 730 |
| 47 | 29388 | 440 | 4530 | 440 | 585 | 561 | 680 |
| 48 | 29488 | 440 | 8606 | 440 | 635 | 602 | 780 |
| 49 | 29392 | 460 | 4820 | 460 | 614 | 589 | 710 |
| 50 | 29492 | 460 | 8120 | 460 | 666 | 631 | 800 |
| 51 | 29396 | 480 | 4820 | 480 | 635 | 610 | 730 |
| 52 | 29496 | 480 | 9320 | 480 | 700 | 662 | 850 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marko, M.D. The Impact of Lubricant Film Thickness and Ball Bearings Failures. Lubricants 2019, 7, 48. https://doi.org/10.3390/lubricants7060048
Marko MD. The Impact of Lubricant Film Thickness and Ball Bearings Failures. Lubricants. 2019; 7(6):48. https://doi.org/10.3390/lubricants7060048
Chicago/Turabian StyleMarko, Matthew David. 2019. "The Impact of Lubricant Film Thickness and Ball Bearings Failures" Lubricants 7, no. 6: 48. https://doi.org/10.3390/lubricants7060048
APA StyleMarko, M. D. (2019). The Impact of Lubricant Film Thickness and Ball Bearings Failures. Lubricants, 7(6), 48. https://doi.org/10.3390/lubricants7060048





