A CFD-Based Frequency Response Method Applied in the Determination of Dynamic Coefficients of Hydrodynamic Bearings. Part 1: Theory
Abstract
:1. Introduction
2. Scope of Work
- Alternative methods to separate the dynamic stiffness into added mass and static stiffness effects are investigated. The authors [20] previously demonstrated that temporal inertia effects as embodied in added mass coefficients are inherent within transient CFD simulations. It then becomes necessary to perturb the bearing at multiple frequencies in order to fit the static stiffness and added mass parameters. However, different techniques for fitting the dynamic stiffness will provide different estimates of the coefficients depending on assumed behavior of the coefficients. Details regarding the implementation and robustness of these techniques are explored herein.
- The proposed methodology is extended to hydrodynamic journal bearing geometries. These bearings are generally of more practical interest than simple slider bearings and an extension of the CFD-based frequency response method to determine the dynamic coefficients is a non-trivial task, warranting a thorough explanation. The dynamic coefficients predicted for short and long journal bearing geometries are compared directly with those obtained from the perturbed Reynolds equation.
3. Geometry
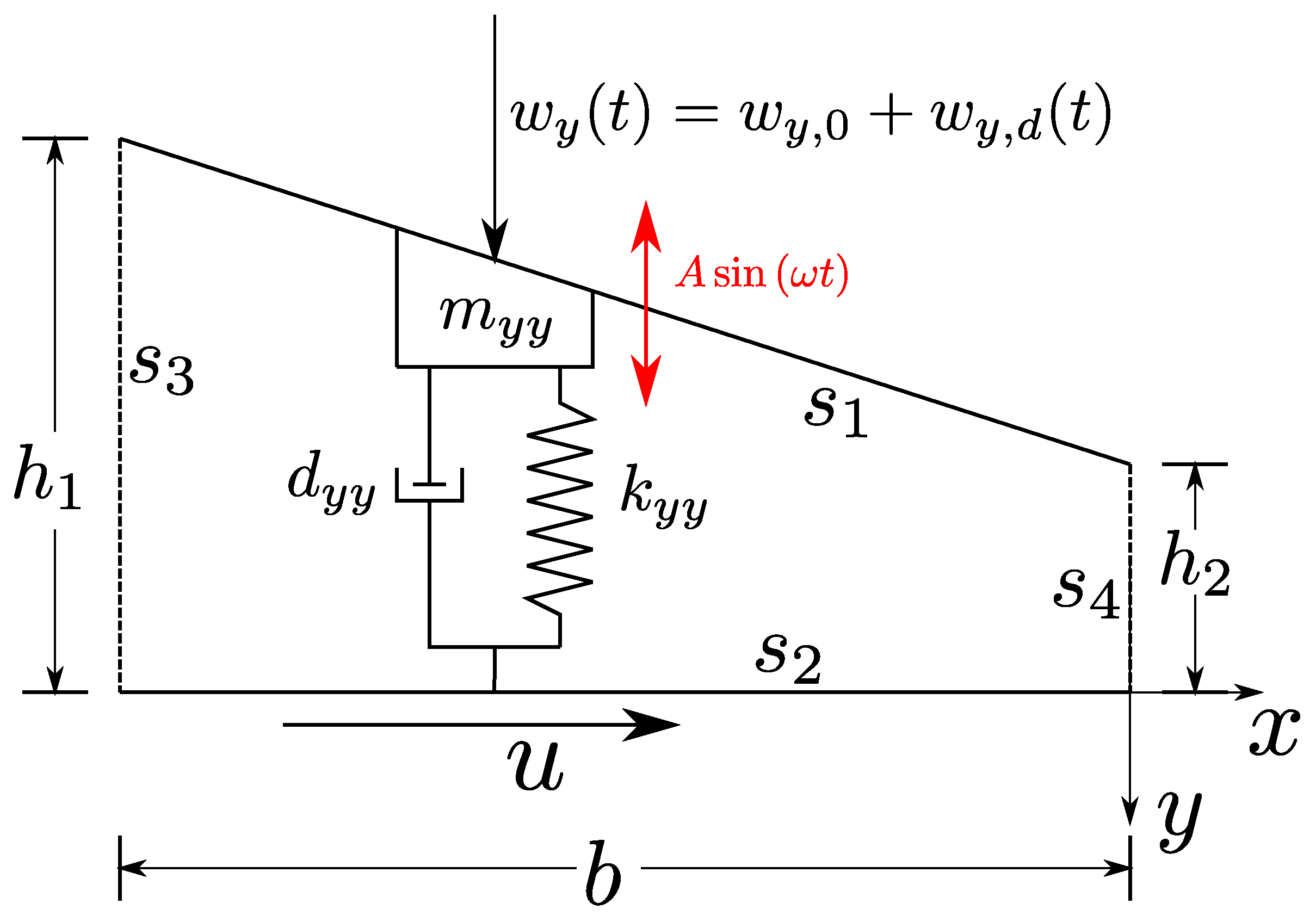
3.1. Linear Slider Bearing
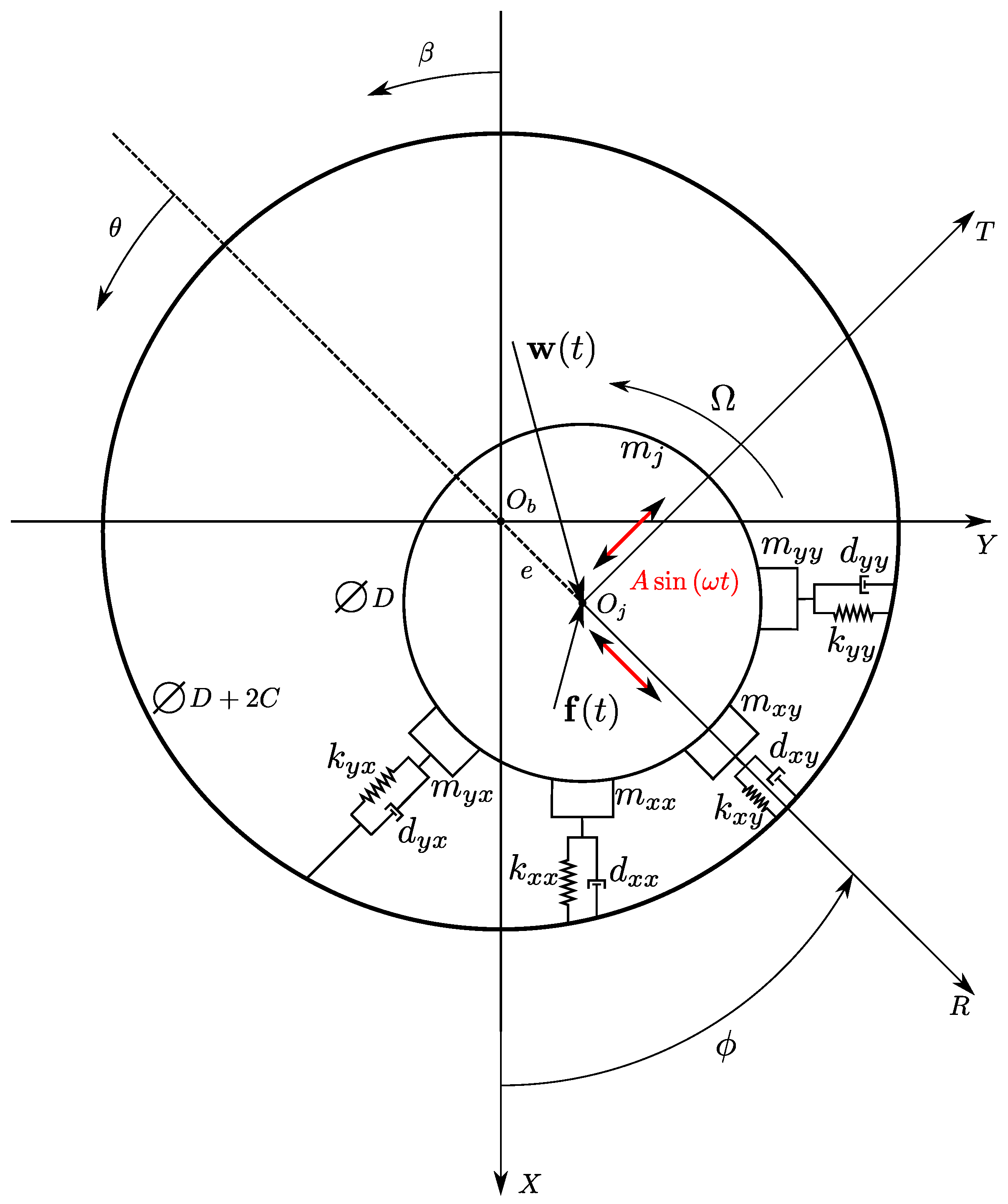
3.2. Journal Bearing
4. Mathematical Modeling
4.1. Dynamic Models
4.1.1. Linear Slider Bearing
4.1.2. Journal Bearing
4.2. Hydrodynamic Fluid Film
5. Numerical Model Setup
5.1. CFD Solver
5.2. Boundary Conditions
5.2.1. Linear Slider Bearing
5.2.2. Journal Bearing
5.3. Numerical Accuracy Quantification
5.3.1. Linear Slider Bearing
5.3.2. Journal Bearing
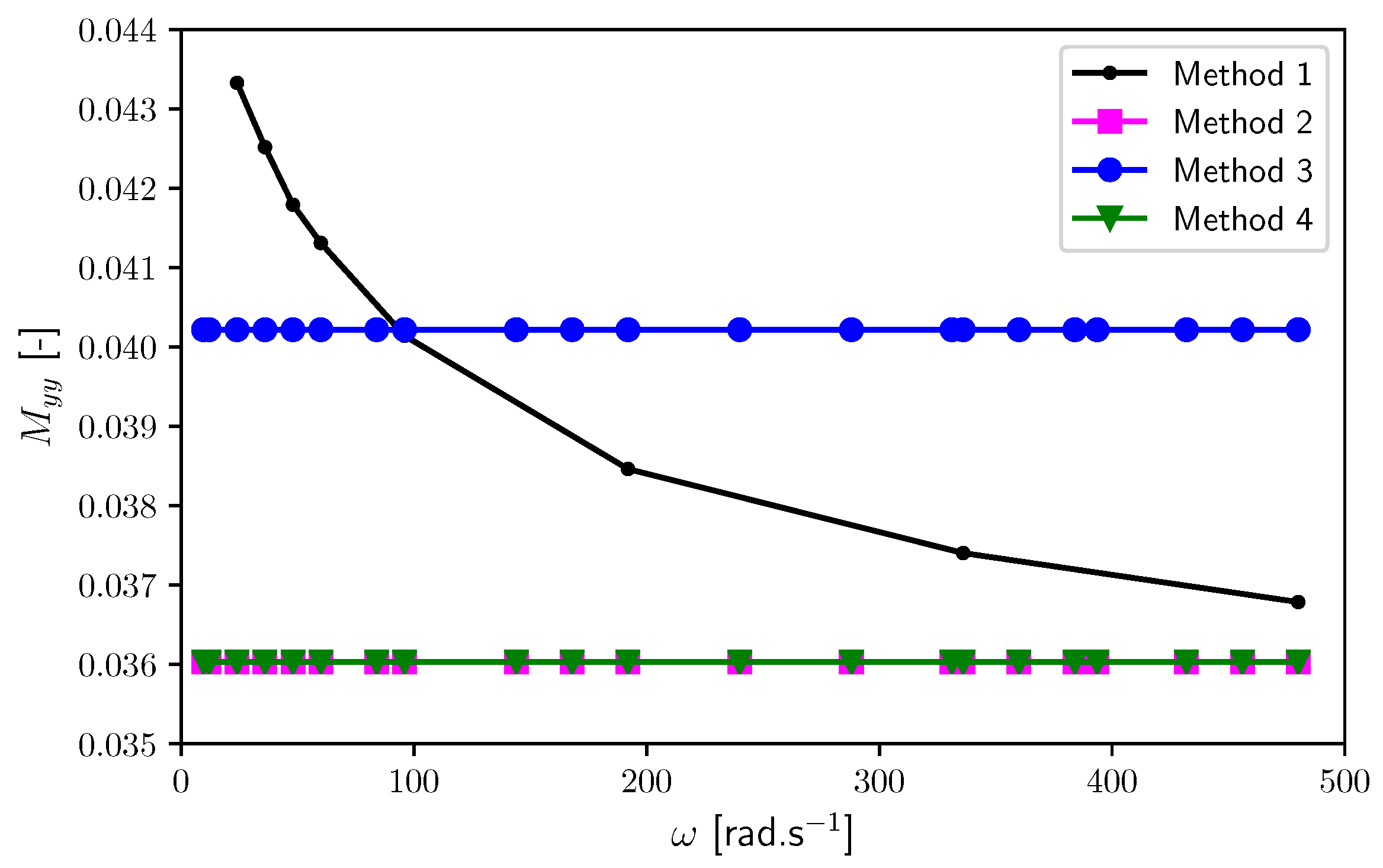
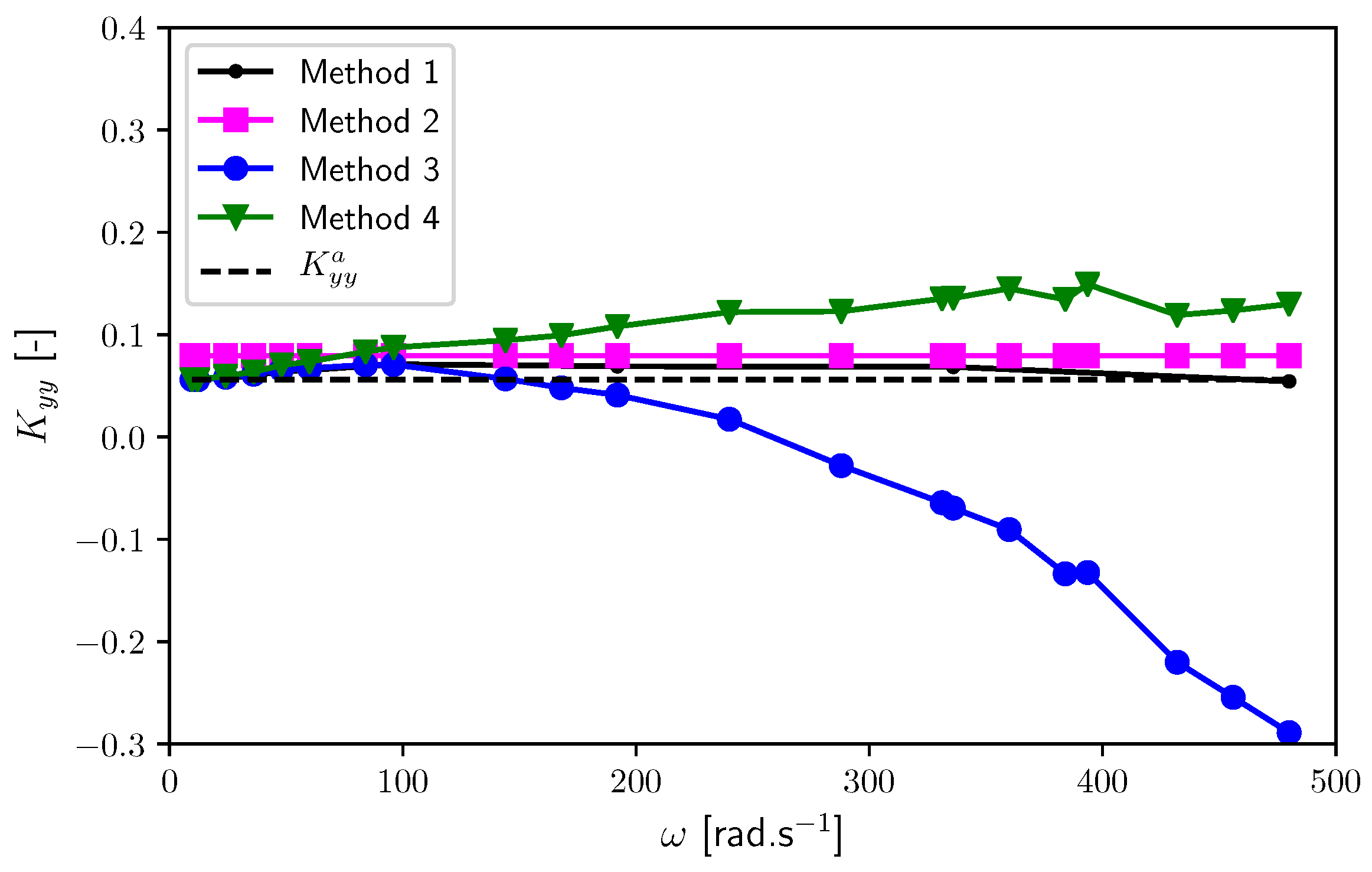
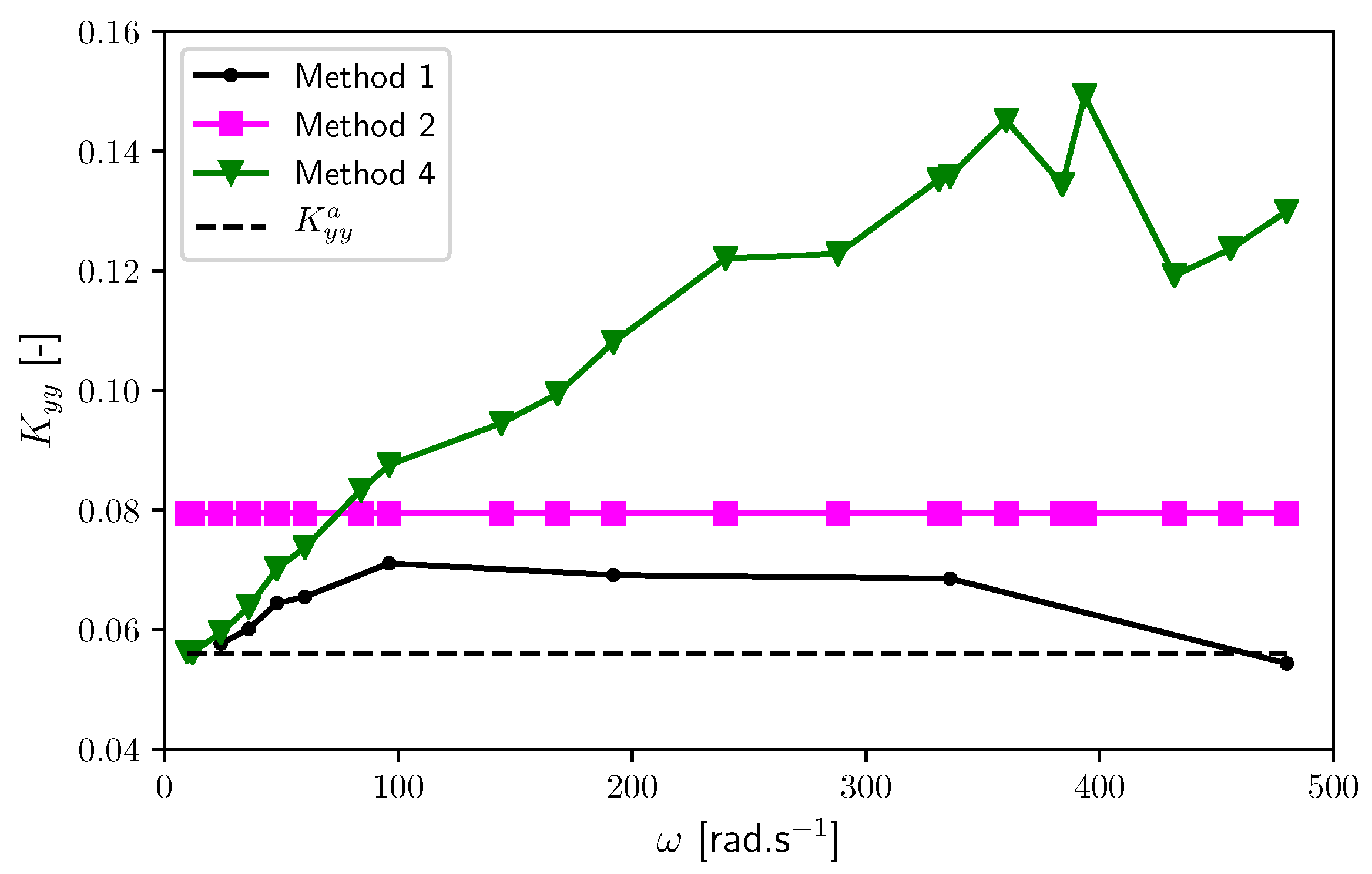
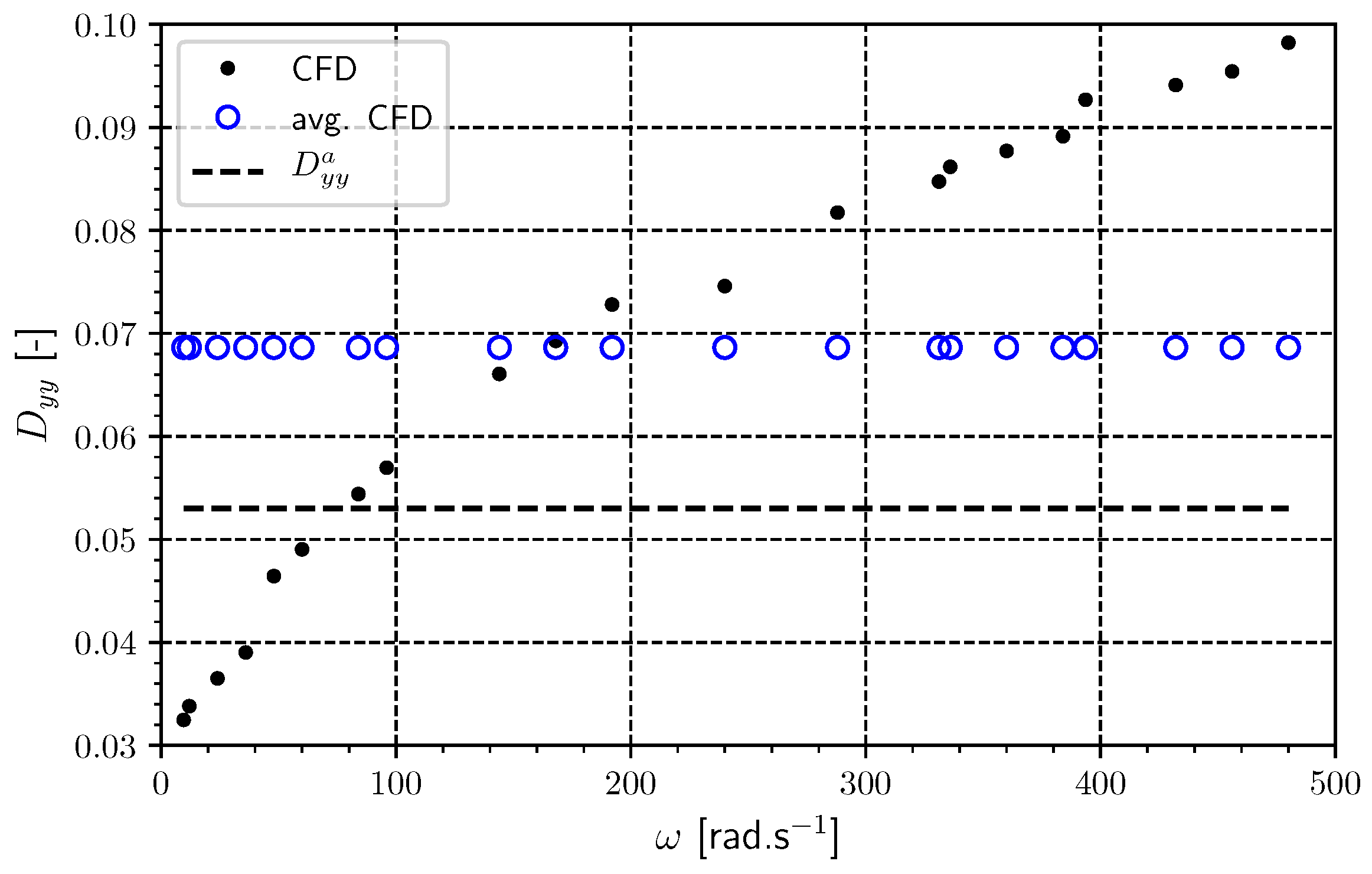
6. Results and Discussion
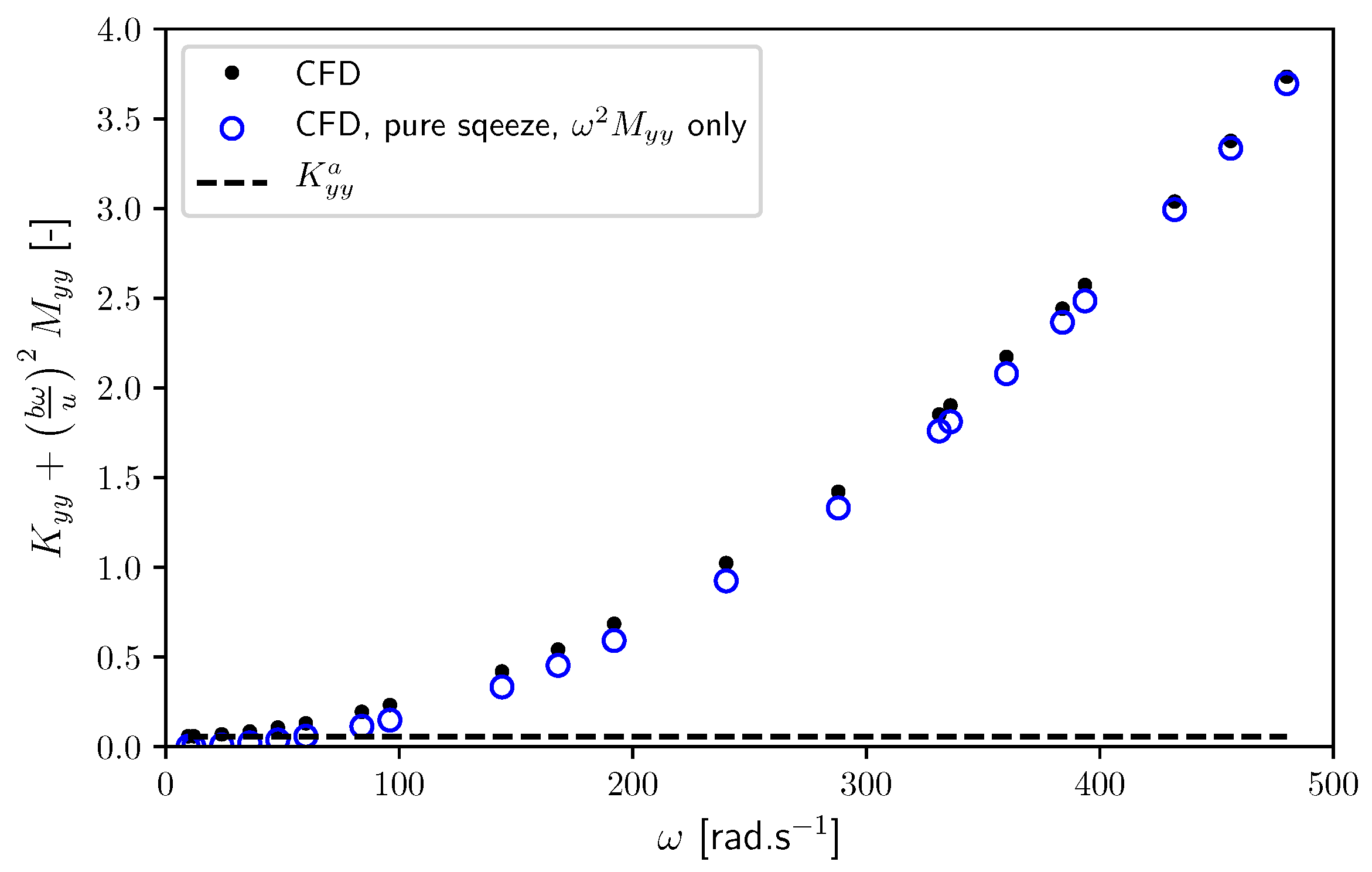
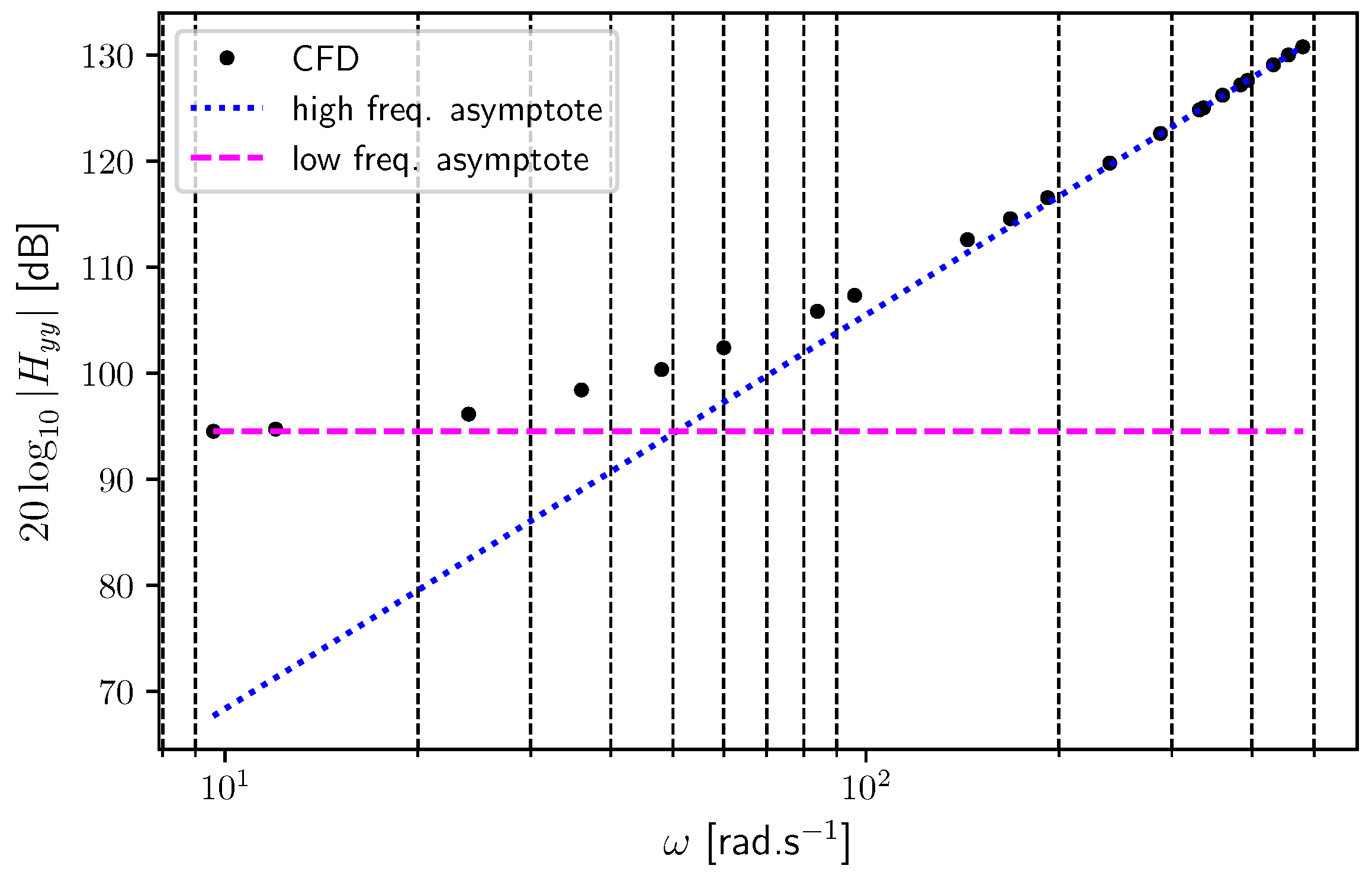
6.1. Linear Slider Bearing (Extremely Long)
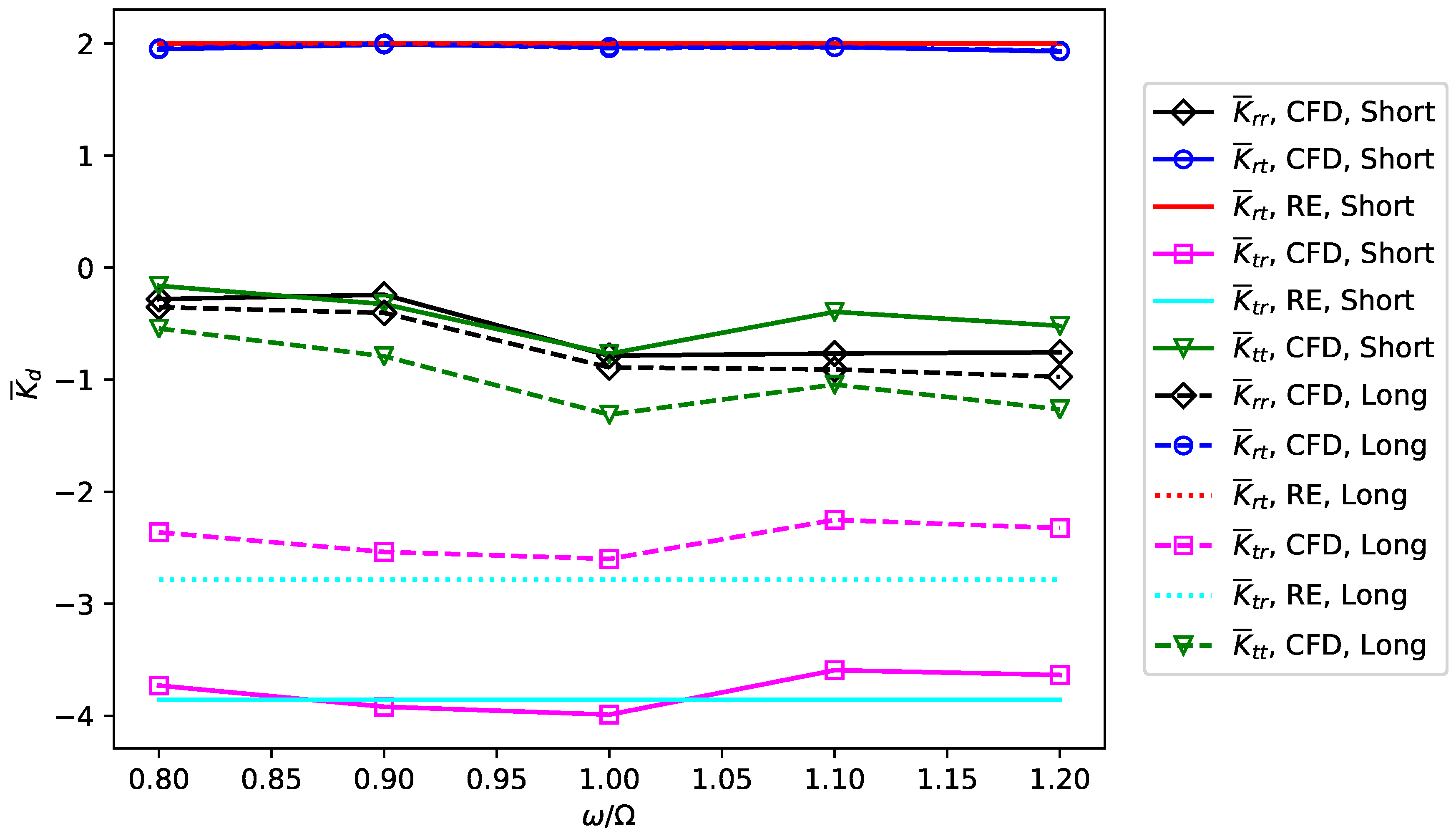
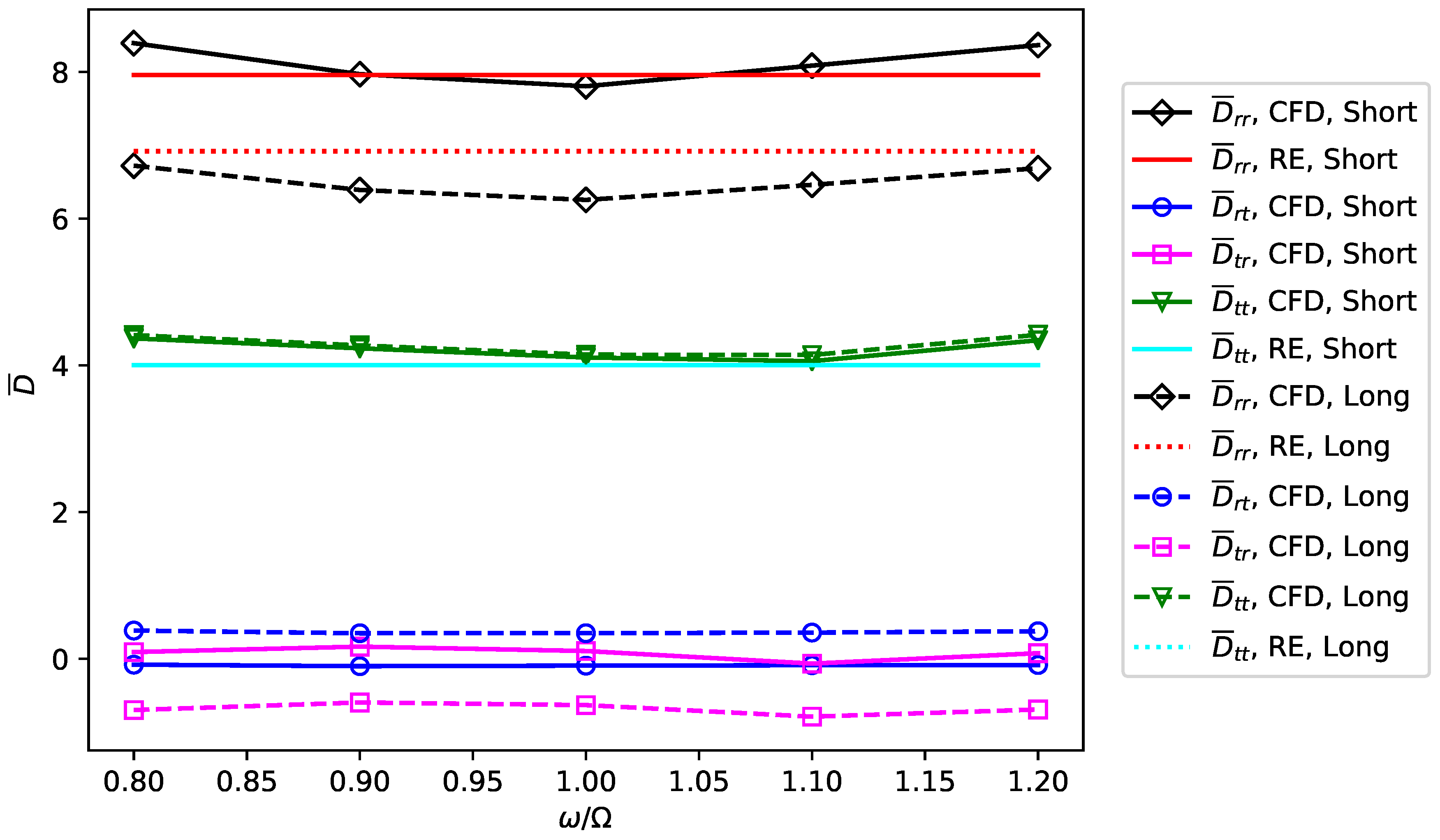
6.2. Journal Bearing
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| FRF | Frequency Response Function |
| RE | Reynolds Equation |
References
- Dimond, T.; Sheth, P.; Allaire, P.; He, M. Identification methods and test results for tilting pad and fixed geometry journal bearing dynamic coefficients—A review. Shock Vib. 2009, 16, 13–43. [Google Scholar] [CrossRef]
- Goodwin, M. Experimental techniques for bearing impedance measurement. J. Eng. Ind. 1991, 113, 335–342. [Google Scholar] [CrossRef]
- Tiwari, R.; Lees, A.; Friswell, M. Identification of speed-dependent bearing parameters. J. Sound Vib. 2002, 254, 967–986. [Google Scholar] [CrossRef]
- Someya, T. Journal Bearing Data Book; Springer: Berlin, Germany, 1989. [Google Scholar]
- Kanki, H.; Ozawa, Y.; Oda, T.; Kawakami, T. Study on the Dynamic Characteristics of a Water-lubricated Pump Bearing: 1st Report, Cylindrical Bearing under High Ambient Pressure. Bull. JSME 1986, 29, 1824–1829. [Google Scholar] [CrossRef]
- Diana, G.; Borgese, D.; Dufour, A. Experimental and Analytical Research on a Full Scale Turbine Journal Bearing. In Proceedings of the 2nd IMechE International Conference on Vibration in Rotating Machinery, Cambridge, UK, 2–4 September 1980; pp. 2–4. [Google Scholar]
- Xu, S. Experimental investigation of hybrid bearings. Tribol. Trans. 1994, 37, 285–292. [Google Scholar] [CrossRef]
- Ha, H.C.; Yang, S.H. Excitation frequency effects on the stiffness and damping coefficients of a five-pad tilting pad journal bearing. J. Tribol. 1999, 121, 517–522. [Google Scholar] [CrossRef]
- Ono, K. Dynamic characteristics of air-lubricated slider bearing for noncontact magnetic recording. J. Lubr. Technol. 1975, 97, 250–258. [Google Scholar] [CrossRef]
- Parsell, J.; Allaire, P.; Barrett, L. Frequency effects in tilting-pad journal bearing dynamic coefficients. ASLE Trans. 1983, 26, 222–227. [Google Scholar] [CrossRef]
- Franchek, N.; Childs, D. Experimental test results for four high-speed, high-pressure, orifice-compensated hybrid bearings. J. Tribol. 1994, 116, 147–153. [Google Scholar] [CrossRef]
- Bendat, J.; Piersol, A.G. Random Data: Measurement and Analysis Procedures; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Childs, D.; Hale, K. A test apparatus and facility to identify the rotordynamic coefficients of high-speed hydrostatic bearings. J. Tribol. 1994, 116, 337–343. [Google Scholar] [CrossRef]
- Al-Ghasem, A.; Childs, D. Rotordynamic Coefficients Measurements versus Predictions For a High Speed Flexure-Pivot Tilting-Pad Bearing (Load-Between-Pad Configuration). J. Eng. Gas Turbines Power 2005, 128, 896–906. [Google Scholar] [CrossRef]
- Delgado, A.; Vannini, G.; Ertas, B.; Drexel, M.; Naldi, L. Identification and prediction of force coefficients in a five-pad and four-pad tilting pad bearing for load-on-pad and load-between-pad configurations. J. Eng. Gas Turbines Power 2011, 133, 092503. [Google Scholar] [CrossRef]
- Rouvas, C.; Childs, D. A parameter identification method for the rotordynamic coefficients of a high Reynolds number hydrostatic bearing. J. Vib. Acoust. 1993, 115, 264–270. [Google Scholar] [CrossRef]
- Zhang, X.; Yin, Z.; Gao, G.; Li, Z. Determination of stiffness coefficients of hydrodynamic water-lubricated plain journal bearings. Tribol. Int. 2015, 85, 37–47. [Google Scholar] [CrossRef]
- Constantinescu, V.N.; Nica, A.; Pascovici, M.D.; Ceptureanu, G.; Nedelcu, S. Sliding Bearings; Allerton Press: New York, NY, USA, 1985. [Google Scholar]
- Tiwari, R.; Lees, A.W.; Friswell, M.I. Identification of dynamic bearing parameters: A review. Shock Vib. Digest 2004, 36, 99–124. [Google Scholar] [CrossRef]
- Snyder, T.; Braun, M. Comparison of Perturbed Reynolds Equation and CFD Models for the Prediction of Dynamic Coefficients of Sliding Bearings. Lubricants 2018, 6, 5. [Google Scholar] [CrossRef]
- Gent, A.N. Engineering with Rubber: How to Design Rubber Components; Carl Hanser Verlag GmbH Co KG: Munich, Germany, 2012. [Google Scholar]
- Laukiavich, C.A.; Braun, M.J.; Chandy, A.J. An Investigation into the Thermal Effects on a Hydrodynamic Bearing’s Clearance. Tribol. Trans. 2015, 58, 980–1001. [Google Scholar] [CrossRef]
- Leaded Commercial Bronze, UNS C31400. Available online: http://www.matweb.com/search/DataSheet.aspx?MatGUID=157ae24937a644aea8d06805b4b2eb80 (accessed on 5 January 2019).
- Horvat, F.; (Manager of Research and Development, Duramax Marine LLC). Personal communication, 2016.
- Szeri, A. Fluid Film Lubrication, 2nd ed.; Cambridge University Press: Cambridge, UK, 2011; p. 254. [Google Scholar]
- Huang, P. Numerical Calculation of Lubrication: Methods and Programs; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
- Stokes, G.G. On the Effect of the Internal Friction of Fluids on the Motion of Pendulums; Pitt Press: Cambridge, UK, 1851; Volume 9. [Google Scholar]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Issa, R. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Patankar, S.V.; Spalding, D.B. Numerical Predictions of Three-Dimensional Flows; Technical Report MED Rep. EF/TN/A/46; Imperial College: London, UK, 1972. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Braun, M.J. Tribology Lecture Notes; The University of Akron: Akron, OH, USA, 2018. [Google Scholar]
- Jones, E.; Oliphant, T.; Peterson, P. SciPy: Open source scientific tools for Python, 2001. Available online: http://www.scipy.org/ (accessed on 19 January 2019).
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: Berlin, Germany, 1978; pp. 105–116. [Google Scholar]
- Münch, C.; Ausoni, P.; Braun, O.; Farhat, M.; Avellan, F. Fluid–structure coupling for an oscillating hydrofoil. J. Fluids Struct. 2010, 26, 1018–1033. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering, 5th ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 2010. [Google Scholar]
- Qiu, Z.; Tieu, A. Experimental Study of Freely Alignable Journal Bearings—Part 2: Dynamic Characteristics. J. Tribol. 1996, 118, 503–508. [Google Scholar] [CrossRef]
- Voigt, A.J.; Iudiciani, P.; Nielsen, K.K.; Santos, I.F. CFD Applied for the Identification of Stiffness and Damping Properties for Smooth Annular Turbomachinery Seals in Multiphase Flow. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Korea, 13–17 June 2016; p. V07BT31A034. [Google Scholar]
- Taylor, S.J.; Anagnostou, A.; Kiss, T.; Terstyanszky, G.; Kacsuk, P.; Fantini, N.; Lakehal, D.; Costes, J. Enabling Cloud-based Computational Fluid Dynamics with a Platform-as-a-Service Solution. IEEE Trans. Ind. Inform. 2019, 15, 85–94. [Google Scholar] [CrossRef]
- Snyder, T.A.; Braun, M.J.; Pierson, K.C. Two-way coupled Reynolds and Rayleigh–Plesset equations for a fully transient, multiphysics cavitation model with pseudo-cavitation. Tribol. Int. 2016, 93, 429–445. [Google Scholar] [CrossRef]
| Parameter | Value | Unit |
|---|---|---|
| 533.4 | [m] | |
| 266.7 | [m] | |
| b | 39.22 | [mm] |
| u | 1.88 | [m·s] |
| A | 26.7 | [m] |
| 1.004 × 10 | [m·s] | |
| varied | [-] |
| Parameter | Value | Unit |
|---|---|---|
| C | 173 | [m] |
| D | 50.8 | [mm] |
| 0.25 or 3.0 | [-] | |
| 706.8 | [rpm] | |
| 0.5 | [-] | |
| A | 8.636 | [m] |
| 1.004 × 10 | [m·s] | |
| varied | [-] |
| Boundary | U | P | D |
|---|---|---|---|
| movingWallVelocity; value uniform (0 0 0); | zeroGradient; | oscillatingDisplacement; amplitude (0 2.667 0) omega varied; value uniform (0 0 0); | |
| fixedValue; value uniform (1.88 0 0); | zeroGradient; | fixedValue; value uniform (0 0 0); | |
| pressureInletOutletVelocity; value uniform (0 0 0); | fixedValue; value uniform 0; | slip; | |
| pressureInletOutletVelocity; value uniform (0 0 0); | fixedValue; value uniform 0; | slip. |
| Boundary | U | P | D |
|---|---|---|---|
| Journal | movingWallVelocity; value uniform (0 0 0); | zeroGradient; | oscillatingDisplacement; amplitude (0 2.667 0) omega varied; value uniform (0 0 0); |
| Bearing | rotatingWallVelocity; origin; axis (0 0 1); omega 74.016; value uniform (0 0 0); | zeroGradient; | fixedValue; value uniform (0 0 0); |
| Front | pressureInletOutletVelocity; value uniform (0 0 0); | fixedValue; value uniform 0; | slip; |
| Back | pressureInletOutletVelocity; value uniform (0 0 0); | fixedValue; value uniform 0; | slip. |
| Curve-Fit | FRF | |||
|---|---|---|---|---|
| 1470 (147 × 10) | ||||
| 3315 (221 × 15) | ||||
| 5880 (294 × 20) | ||||
| Curve-Fit | FRF | |||
|---|---|---|---|---|
| 100 | ||||
| 200 | ||||
| 300 | ||||
| Curve-Fit | FRF | |||
|---|---|---|---|---|
| 3 | ||||
| 5 | ||||
| 8 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Snyder, T.; Braun, M. A CFD-Based Frequency Response Method Applied in the Determination of Dynamic Coefficients of Hydrodynamic Bearings. Part 1: Theory. Lubricants 2019, 7, 23. https://doi.org/10.3390/lubricants7030023
Snyder T, Braun M. A CFD-Based Frequency Response Method Applied in the Determination of Dynamic Coefficients of Hydrodynamic Bearings. Part 1: Theory. Lubricants. 2019; 7(3):23. https://doi.org/10.3390/lubricants7030023
Chicago/Turabian StyleSnyder, Troy, and Minel Braun. 2019. "A CFD-Based Frequency Response Method Applied in the Determination of Dynamic Coefficients of Hydrodynamic Bearings. Part 1: Theory" Lubricants 7, no. 3: 23. https://doi.org/10.3390/lubricants7030023
APA StyleSnyder, T., & Braun, M. (2019). A CFD-Based Frequency Response Method Applied in the Determination of Dynamic Coefficients of Hydrodynamic Bearings. Part 1: Theory. Lubricants, 7(3), 23. https://doi.org/10.3390/lubricants7030023




