Squeeze Flow of Bingham Fluids through Reticulated, Compressed Foams
Abstract
:1. Introduction
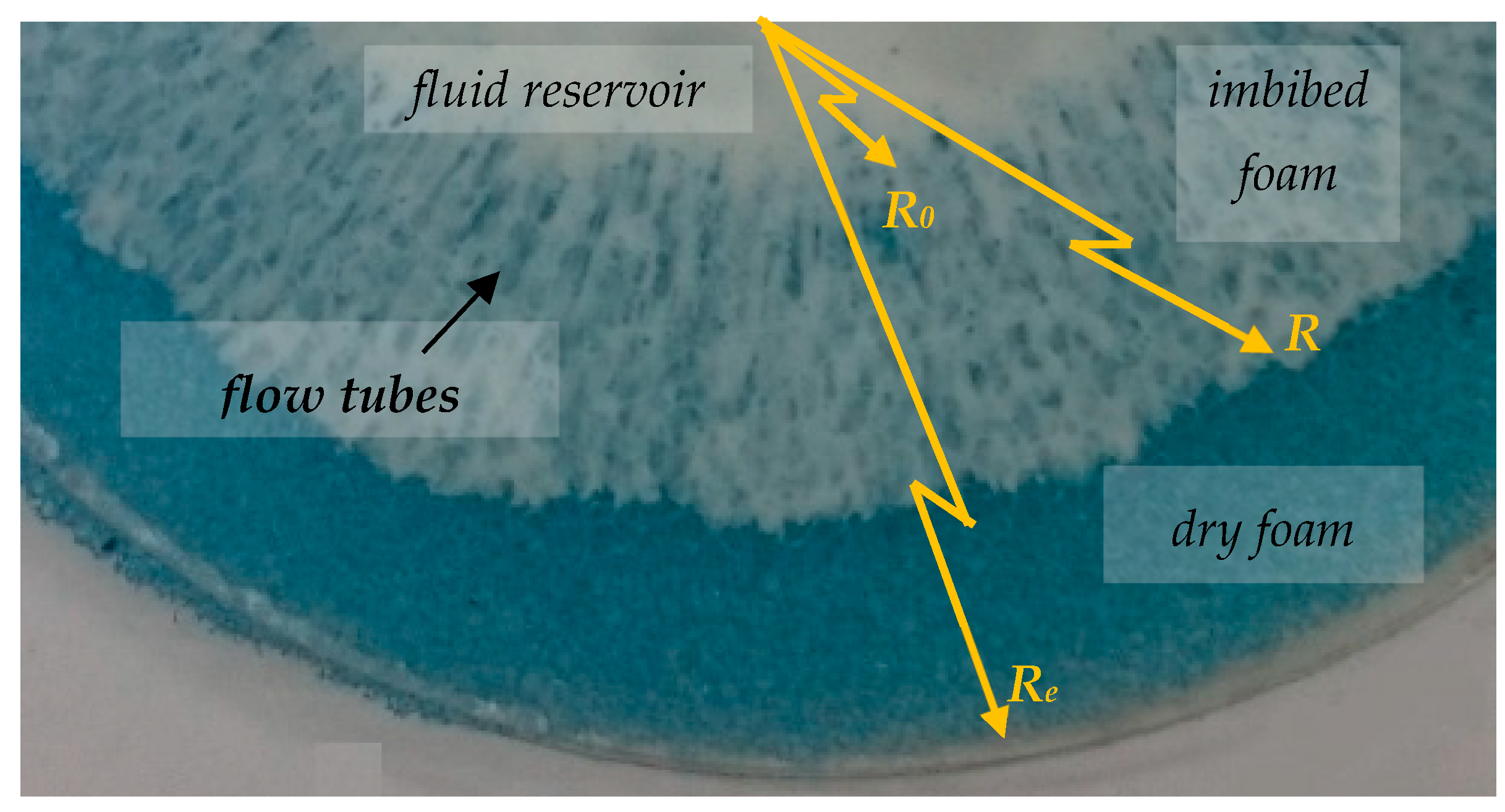
2. Experimental Evidence
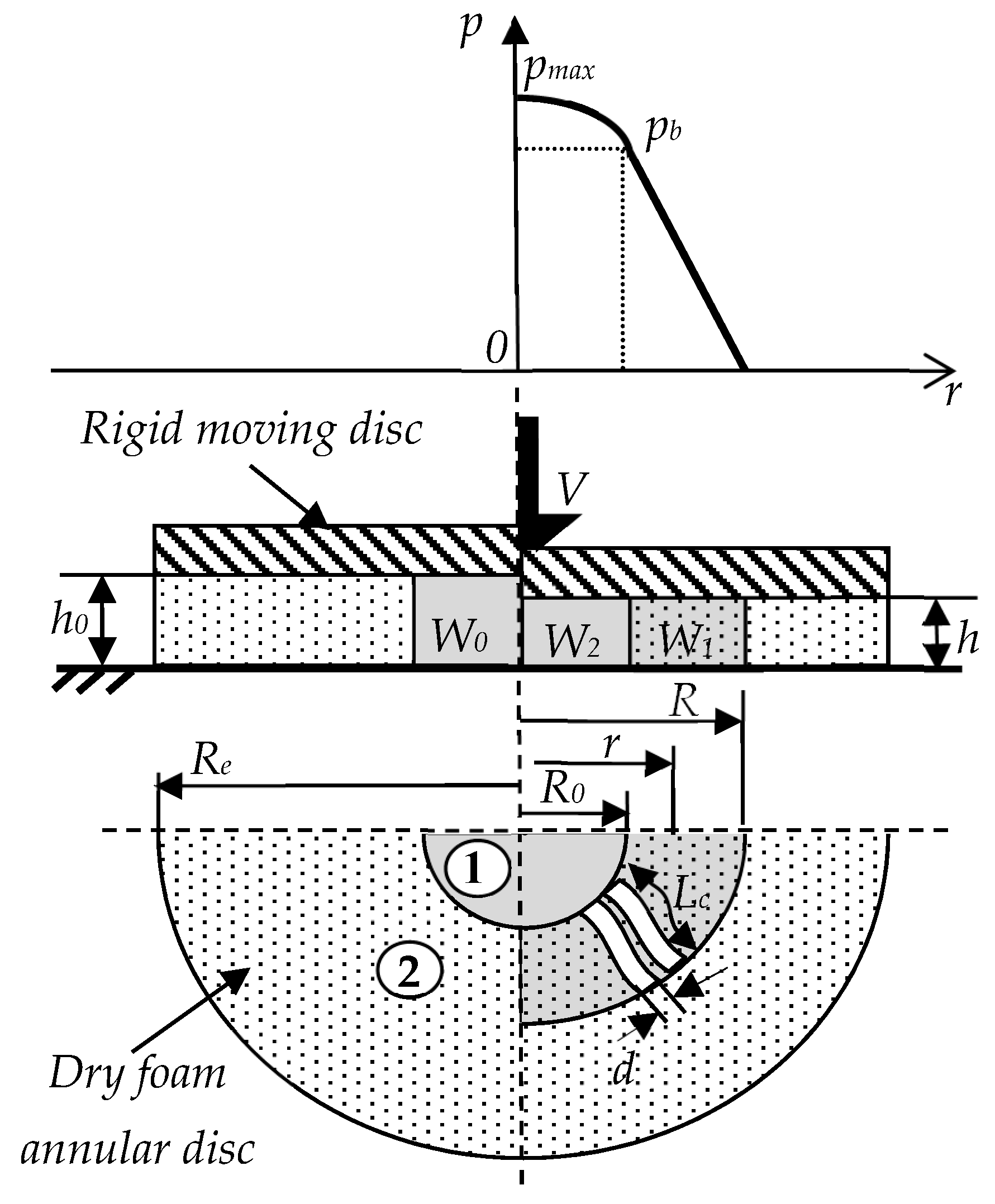
3. Analytical Model
3.1. Flow Model for Zone 1
3.2. Flow Model for Zone 2
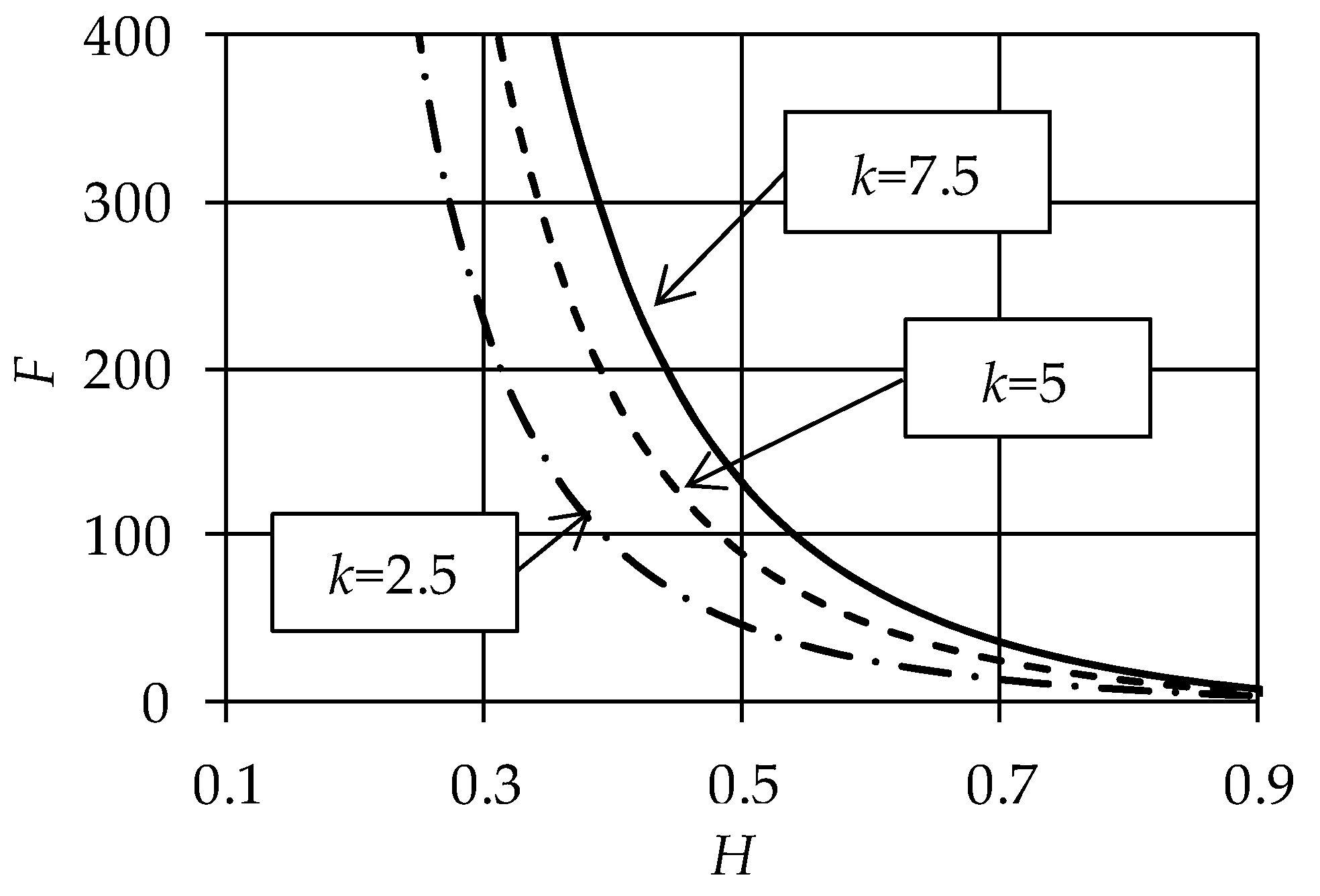
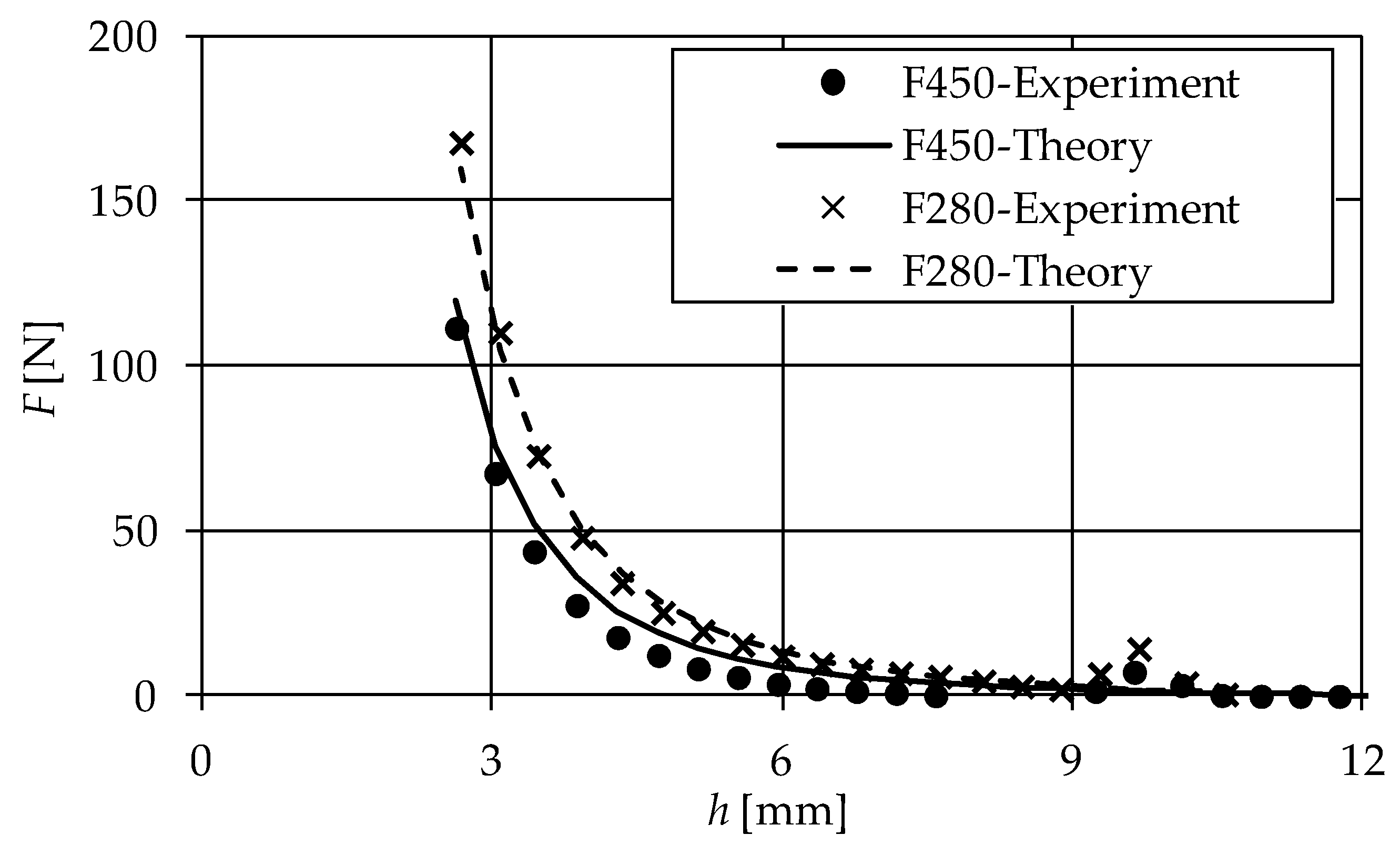
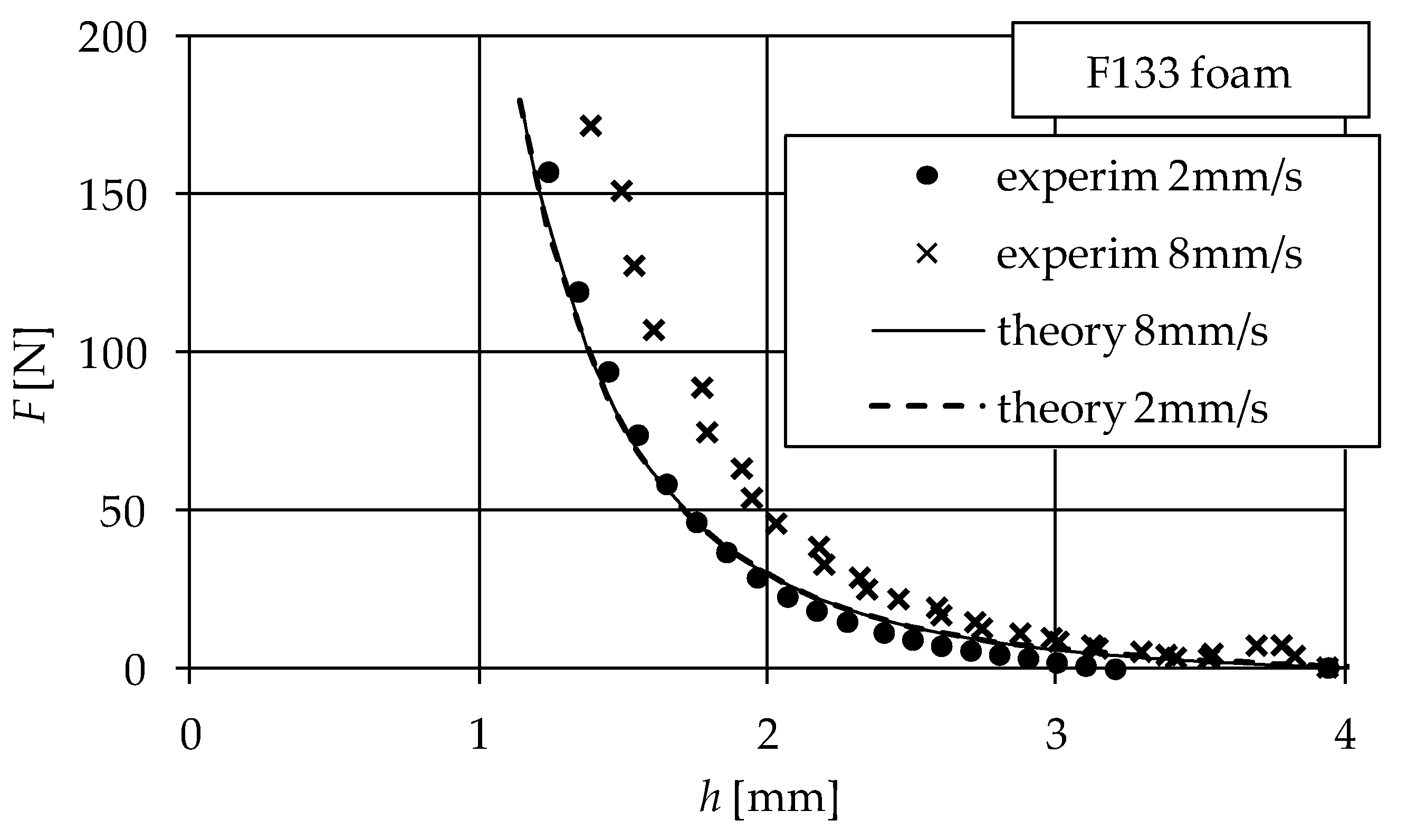
4. Model Validation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
List of Notations
| Latin Alphabet Notations | |
| Bn | Bingham number, |
| d | average diameter of flow tube/pore |
| F | total force |
| dimensionless force, | |
| h | porous layer thickness |
| H | dimensionless layer thickness, |
| lc | length of elementary flow path |
| k | size factor, |
| p | pressure |
| pb | pressure at the boundary of the reservoir |
| r | radial coordinate |
| R | radius of the front of the flow |
| Re | outer radius of the annular disc |
| dimensionless relative radius of the front of the flow, | |
| S | plasticity number, |
| T | tortuosity, |
| um | fluid average velocity |
| V | squeeze speed |
| W | volume of fluid |
| Greek Alphabet Notations | |
| α | flow tube cross section area |
| β | tube cross section perimeter |
| ε | porosity |
| η | dynamic viscosity |
| ρ | hydraulic radius |
| τ0 | threshold/yield stress |
| Subscripts | |
| 0 | initial (corresponding to undeformed layer) |
| 1 | corresponding to zone 1 |
| 2 | corresponding to zone 2 |
Appendix A
References
- Pascovici, M.D.; Cicone, T. Squeeze-film of unconformal, compliant and layered contacts. Tribol. Int. 2003, 36, 791–799. [Google Scholar] [CrossRef]
- Pascovici, M.D.; Russu, C.; Cicone, T. Squeeze film of conformal, layered, compliant and porous contacts. Acta Teh. Napoc. Ser. Appl. Math. Mech. 2004, 47, 425–430. [Google Scholar]
- Radu, M.; Cicone, T. Squeeze effects of an infinitely long, rigid cylinder on a highly compressible porous layer imbibed with liquid. UPB Sci. Bull. Ser. D 2014, 76, 91–102. [Google Scholar]
- Pascovici, M.D.; Popescu, C.S.; Marian, V. Impact of a rigid sphere on a highly compressible porous layer imbibed with a Newtonian liquid. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 789–795. [Google Scholar] [CrossRef]
- Radu, M.; Cicone, T. Experimental determination of the damping capacity of highly compressible porous materials imbibed with water. J. Balkan Tribol. Assoc. 2014, 22, 390–400. [Google Scholar]
- Pascovici, M.D.; Cicone, T.; Marian, V. Squeeze process under impact, in highly compressible porous layers imbibed with liquids. Tribol. Int. 2009, 42, 1433–1438. [Google Scholar] [CrossRef]
- Melciu, C.; Cicone, T.; Pascovici, M.D. Saturated porous layers squeezed between parallel disks in enclosed cells. IOP Conf. Ser. Mater. Sci. Eng. 2017, 174, 012031. [Google Scholar] [CrossRef] [Green Version]
- Cicone, T.; Pascovici, M.D.; Melciu, C.; Turtoi, P. Optimal porosity for impact squeeze of soft layers imbibed with liquids. Tribol. Int. 2019, 138, 140–149. [Google Scholar] [CrossRef]
- Wu, Q.; Andreopoulos, Y.; Xanthos, S.; Weinbaum, S. Dynamic compression of highly compressible porous media with application to snow compaction. J. Fluid Mech. 2005, 542, 281–304. [Google Scholar] [CrossRef]
- Crawford, R.; Nathan, R.; Wang, L.; Wu, Q. Experimental study on the lift generation inside a random synthetic porous layer under rapid compaction. Exp. Therm. Fluid Sci. 2012, 36, 205–216. [Google Scholar] [CrossRef]
- Nabhani, M.; Khlifi, M.; Bou-Said, B. A general model for porous medium flow in squeezing film situations. Lubr. Sci. 2010, 22, 27–52. [Google Scholar] [CrossRef]
- Gbehe, O.S.T.; Khlifi, M.; Nabhani, M.; Bou-Said, B. Investigation of couple stress effects on poroelastic squeeze film of parallel plates. Lubr. Sci. 2017, 29, 93–113. [Google Scholar] [CrossRef]
- Dowson, M.A.; McKinley, G.H.; Gibson, L.J. The Dynamic Compressive Response of Open-Cell Foam Impregnated with a Non-Newtonian Fluid. J. Appl. Mech. 2009, 76, 061011. [Google Scholar] [CrossRef]
- Dawson, M.A. Modeling the Dynamic Response of Low-Density, Reticulated, Elastomeric Foam Impregnated with Newtonian and Non-Newtonian Fluids. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2008. [Google Scholar]
- Vossen, B.G. Modeling the Application of Fluid Filled Foam in Motorcycle Helmets; Scientific Report; Eindhoven University of Technology: Eindhoven, The Netherlands, 2010. [Google Scholar]
- Chevalier, T.; Chevalier, C.; Clain, X.; Dupla, J.C.; Canou, J.; Rodts, S.; Coussot, P. Darcy’s law for yield stress fluid flowing through a porous medium. J. Non-Newton. Fluid Mech. 2013, 195, 57–66. [Google Scholar] [CrossRef]
- Pearson, J.R.A.; Tardy, P.M.J. Models for flow of non-Newtonian and complex fluids through porous media. J. Non-Newton. Fluid Mech. 2002, 102, 447–473. [Google Scholar] [CrossRef]
- Covey, G.H.; Stanmore, B.R. Use of the parallel-plate plastomer for the characterization of viscous fluids with a yield stress. J. Non-Newton. Fluid Mech. 1981, 8, 249–260. [Google Scholar] [CrossRef]
- Mitsoulis, E. Flows of viscoplastic materials: Models and computations. Rheol. Rev. 2007, 64, 135–178. [Google Scholar]
- Scheidegger, A.E. The Physics of Flow through Porous Media, 3rd ed.; University of Toronto Press: Toronto, ON, Canada, 1974. [Google Scholar]
- Delesse, M.A. Procede Mecanique Pour Determiner la Composition des Roches; Librarie de la Societe Geologique de France: Paris, France, 1866. [Google Scholar]
- Guyon, E.; Huliu, J.P.; Petit, L. Hydrodinamique Physique; EDP Sciences/CNRS Editions: Paris, France, 2001. [Google Scholar]
- Sun, Z.; Tang, X.; Cheng, G. Numerical simulation for tortuosity of porous media. Microporous Mesoporous Mater. 2013, 173, 37–42. [Google Scholar] [CrossRef]
- Salem, H.; Chilingarian, G. Influence of porosity and directional of flow on Tortuosity in unconsolidated porous media. Energy Sources 2000, 22, 207–213. [Google Scholar]
- Montillet, A.; Comiti, J.; Legrand, J. Determination of structural parameters of metallic foams from permeametry measurements. J. Mater. Sci. 1992, 27, 4460–4464. [Google Scholar] [CrossRef]
- Ortega, J.M. A porous media model for blood flow within reticulated foam. Chem. Eng. Sci. 2013, 99, 59–66. [Google Scholar] [CrossRef] [Green Version]


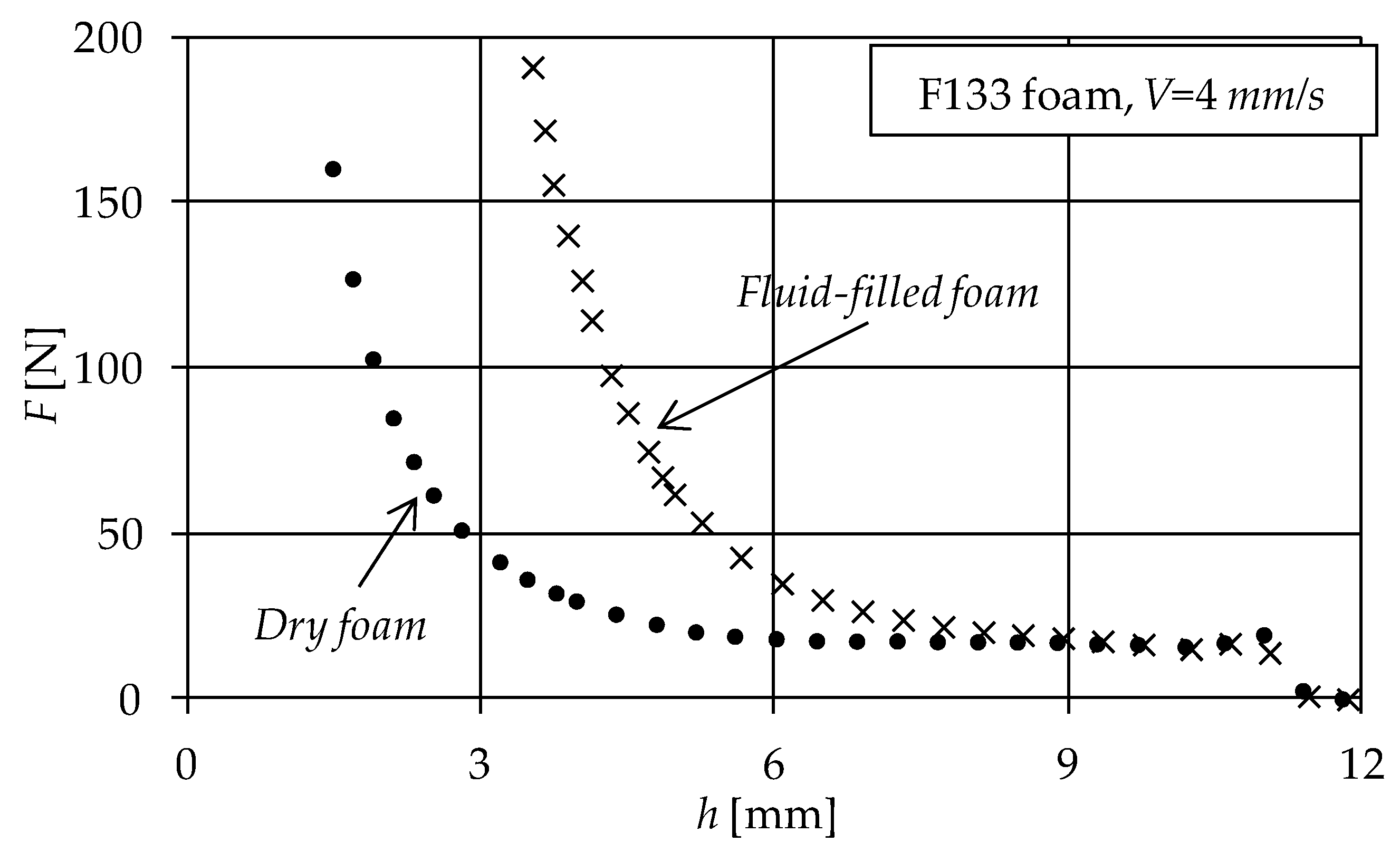
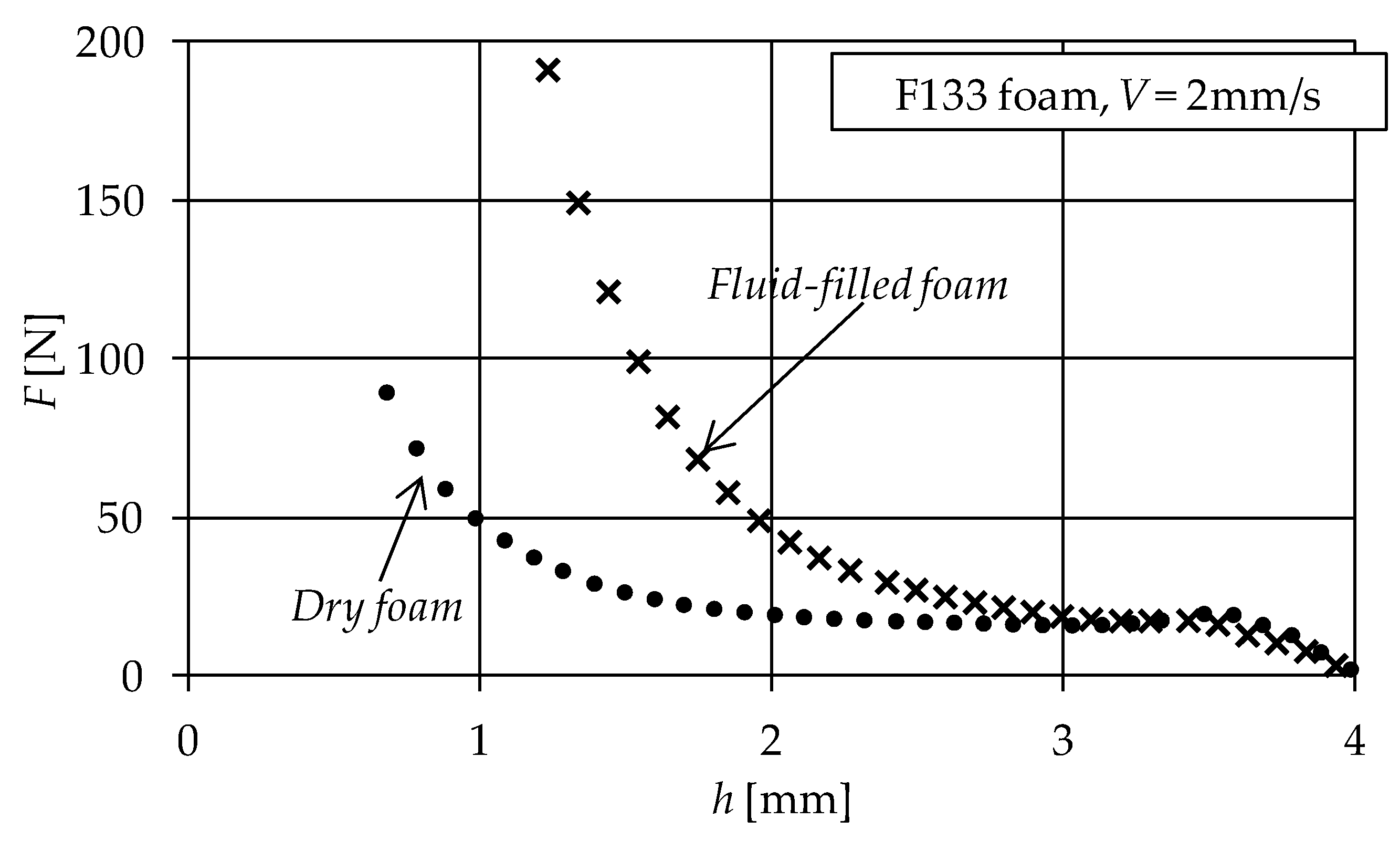
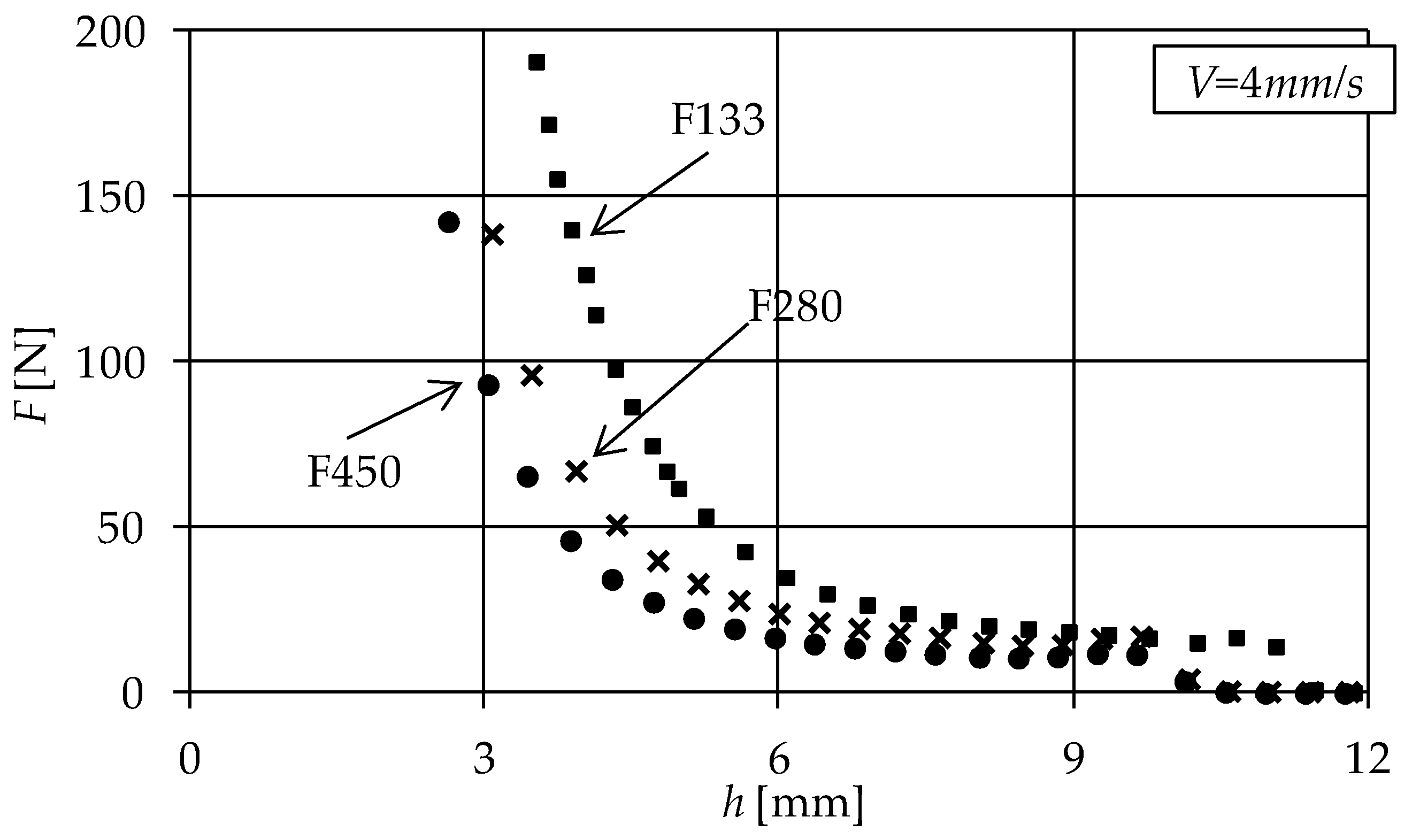
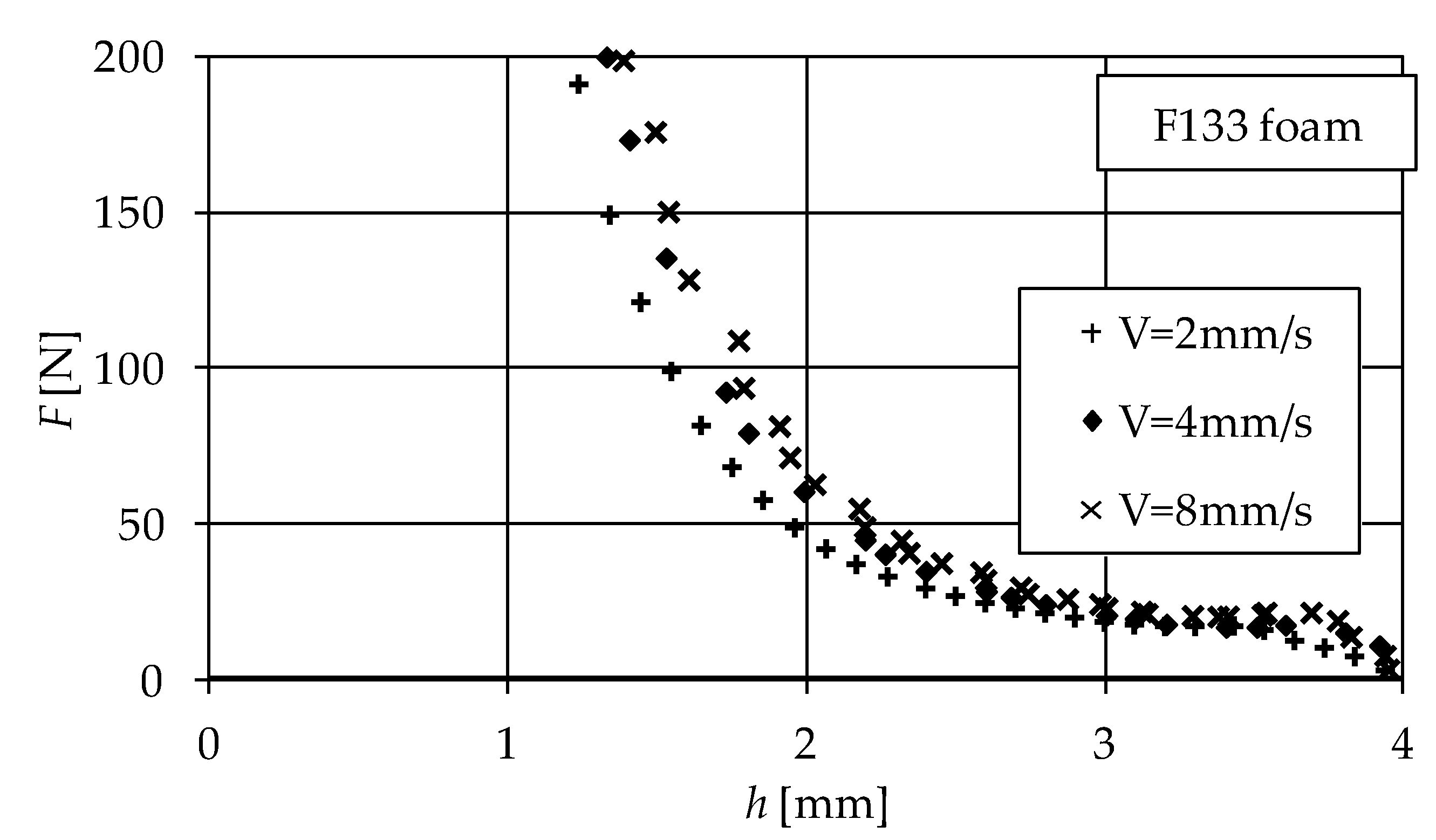
| Disc No. | Foam Symbol | Commercial Name | Pore size [mm] (1) | Initial Porosity, ε0 | Thickness h0 [mm] |
|---|---|---|---|---|---|
| 1 | F133 | FILTREN® TM 25133 | 1.06–1.66 | 0.976 | 12 |
| 2 | F280 | FILTREN® TM 25280 | 2.2–3.4 | 0.982 | 12 |
| 3 | F450 | FILTREN® TM 25450 | 3.4–5.6 | 0.997 | 12 |
| 4 | F133 | FILTREN® TM 25133 | 1.06–1.66 | 0.976 | 4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turtoi, P.; Pascovici, M.D.; Cicone, T. Squeeze Flow of Bingham Fluids through Reticulated, Compressed Foams. Lubricants 2019, 7, 86. https://doi.org/10.3390/lubricants7100086
Turtoi P, Pascovici MD, Cicone T. Squeeze Flow of Bingham Fluids through Reticulated, Compressed Foams. Lubricants. 2019; 7(10):86. https://doi.org/10.3390/lubricants7100086
Chicago/Turabian StyleTurtoi, Petrică, Mircea D. Pascovici, and Traian Cicone. 2019. "Squeeze Flow of Bingham Fluids through Reticulated, Compressed Foams" Lubricants 7, no. 10: 86. https://doi.org/10.3390/lubricants7100086
APA StyleTurtoi, P., Pascovici, M. D., & Cicone, T. (2019). Squeeze Flow of Bingham Fluids through Reticulated, Compressed Foams. Lubricants, 7(10), 86. https://doi.org/10.3390/lubricants7100086





