Abstract
To further improve efficiency in automotive engine systems, it is important to understand the generation of friction in its components. Accurate simulation and modeling of friction in machine components is, amongst other things, dependent on realistic lubricant rheology and lubricant properties, where especially the latter may change as the machine ages. Some results of research under laboratory conditions on the aging of engine commercial oils with different performance levels (mineral SAE 30, synthetic SAE10W-40, and bio-based) are presented in this paper. The key role of the action of pressure and temperature in engine oils’ aging is described. The paper includes the results of experiments over time in laboratory testing of a single cylinder motorbike. The aging of engine oil causes changes to its dynamic viscosity value. The aim of this work is to evaluate changes due to temperature and pressure in viscosity of engine oil over its lifetime and to perform uncertainty analysis of the measured values. The results are presented as the characteristics of viscosity and time in various temperatures and the shear rates/pressures. This paper also includes a Computational Fluid Dynamics (CFD) model, applying the experimental results in the piston ring tribology problem.
1. Introduction
Machines consist of moving parts, interacting with each other. Friction, which often produces heat, affects a system’s lifetime, creating additional stresses between the machine components and increasing the possibility of severe failures.
For several purposes [1,2], biofuels are at the forefront of research in many fields. Production of biofuels has already seen an incremental increase in production: Nowadays, the produced amounts are in the order of 1% of fuel, with the prediction to be 7% by 2030 [3]. Furthermore, and according to the new directive 2009/28/EC (RED—renewable energy directive) [4], prospective targets are to substitute 10% of common fuels for biofuels by 2020.
The necessity to improve the engine’s efficiency has been leading to reducing lubricants’ viscosity to minimize the losses in the hydrodynamic lubrication regime. However, this strategy has forced the piston ring/cylinder bore system to work more in the mixed and boundary lubrication regimes. In these last two lubrication regimes, the strategy adopted to reduce friction and consequently improve efficiency is the use of friction modifiers [5,6]. Oil viscosity reduction is the result of antiwear additives, such us zinc dialkyldithiophosphate (ZDDP). Therefore, the importance of tribofilm formation from friction modifiers and antiwear additives on tribo phenomena is continuously increasing. According to Spikes [6], the increasing importance of tribofilms on piston ring/cylinder bore system performance has been leading to a frequent use of tribotests in the effort to understand how tribofilms form from additives and behave on the control of friction and wear.
Nowadays, the automotive industry is trying to reduce CO2 emission levels and to improve engine efficiency. Cars, motor vehicles, and trucks are the main sources of CO2 emissions. Low engine speeds during the cold start-up period lead to some significant energy loss through friction in city driving [7]. This is convenient, according to the New European Driving Cycle, who say that a large portion (60–80%) of engine emissions occur during their cold start-up period. As a result, the majority of industrial groups are attempting to reduce mechanical energy loss and to find ways to improve the performance of tribocontacts. A significant portion of engine friction losses—in the order of 35–45%—are caused by the piston system. Engine oils designed with piston and ring-pack assembly have a crucial role in the reduction of friction, wear, and fuel consumption in internal combustion engines [8,9].
The piston ring component has the primary role in power transmission within the engine. Several tribometric studies have shown the crucial impact of ring-liner contact on engine friction and fuel efficiency. Furuhama and Sasaki [10] studied the lubrication performance of ring-liner contact to determine the variation in friction and minimum lubricant film. It was found that multigrade oils have a potential role in ring friction. Tian [11] reported the dynamic performance of the ring pack tribosystem regarding the wear of ring/liner conjunction and lubricant film variation. It was indicated that both the second ring-face worn profile and piston dynamic motion have a significant role in top ring tribological behavior. Zavos et al. [12], Rahmani et al. [13], and Morris et al. [14] presented remarkable results by including the effects of the ring-liner conjugating surfaces, thermal conditions, and in-cylinder pressure degradation. These authors demonstrated that the profiles of the ring-cylinder surfaces and the flow conditions may strongly influence the mechanisms of friction and minimum film thickness. Furthermore, the lubricant flow within the ring-liner interface is also more complex. Shahmohamadi et al. [15] provided Computational Fluid Dynamics (CFD) predictions, including the effect of the cavitation phenomenon on friction, film thickness, and ring temperature. They concluded a thermomixed lubrication model, showing that cavitation flow has a dominant role in load-carrying capacity under high engine speeds. Bewsher et al. [16] also observed that oil availability can create starvation in the contact due to the reverse flow and the lack of oil. They found that this effect may lead to increased friction and low lubricant films. With regard to the thin nature of the piston ring, analytical and experimental reports were also presented on ring tribology for different engine conditions. Numerical predictions and experimental measurements of the piston ring–liner mechanism were presented by Rahmani et al. [17], Baker et al. [18], and Zavos et al. [19]. It was found that the elastodynamics thin ring performance showed thinner lubricant films and higher friction values when hot engine conditions were expected.
As a result, current engine lubricants used in internal combustion engines (ICE) are responsible for reducing engine friction losses and contact wear. Therefore, the impact of engine oil viscosity and aging is of prime interest with regard to the motion of passenger cars [20]. Several methods were presented and discussed in the open literature to study the variation of lubricant viscosity and oil degradation over time. For instance, a novel lab-based artificial aging method for the evaluation of engine oils in biofueled automotives was studied by Besser et al. [21]. They found that oil formulations have a dominant effect on typical oil parameters, such as oxidation and aging procedure. Sikora and Miszczak [22] in their report included experimental results to investigate the change of viscosity and lubricity of engine oil used in two harbor tugs, called HEROS’, in Caterpillar CAT3516DITA engines at similar working hours. The used oil was a product of the Fuchs Oil Corporation, which meets the specifications of SAE 15W-40. They measured the viscosity on the Haake Mars III rheometer in the range of temperatures between 10 to 120 °C. These authors indicated that engine oil aging has a crucial impact on the lubrication and wear performance of journal bearings. Additionally, Dam et al. [23] investigated how the engine oil aging history in an engine affects its emission levels. A 12.7 L heavy-duty diesel engine was tested in an engine dynamometer test cell over 40 h using an engine oil with type of SAE 15W-40. They found that oil aging has a limited effect on gaseous and mass emissions and metal contents of exhaust.
The contribution of this paper is the combination of the experimental procedure and the implementation of the viscosity measurements in a CFD model in order to predict the tribological behavior into the piston ring-liner conjunction under aged oil conditions. In detail, the deterioration of the lubricants’ properties and behavior during service is a crucial problem, especially in the sector of transportation vehicles, and there is a significant effort to come up with an integrated approach. The CFD predictions reported here are the most popular and useful in engine tribology, in terms of friction and minimum film thickness. The results of experiments of a single-cylinder motorbike over time in laboratory setting are discussed. How the aging of engine oil causes a change in its dynamic viscosity value is also analytically presented. The aim of this work is firstly to evaluate the changes in viscosity, due to the aging of engine oils in the time of its exploitation, and to perform an uncertainty analysis of the measured values, and secondly, to examine the effects of the viscosity variation in the tribological performance of a piston ring. Aging is performed under real operating engine conditions. The tribological performance is simulated by a development of a CFD model applying the results in the piston ring tribology problem.
2. Experimental Details and Methods
2.1. Description of the Capillary Tube Viscometer
The viscosity measurement tests were performed using an EH105 capillary tube viscometer manufactured by DELTALAB (Carcassonne, France). The temperature range varied between 25 and 80 °C and the pressure was up to 2 MPa. The viscometer and some of its main parts are shown in Figure 1.

Figure 1.
Photograph of EH105 capillary tube viscometer.
The liquid to be studied is placed in the pressurized vessel (1) and fixed on the magnetic stirrer (15). Pressure is applied to the tube (3) at a value controlled by the control valve (11) and monitored by the mercury manometer (12). The capillary tube is inserted in the thermostatically controlled sleeve (2). This sleeve and the coil (5), inserted in the vessel, are supplied with water thermostatically controlled by the control system (8). The fluid flows into the capillary tube at the temperature indicated by the thermometer and then passes through the graduated pipette (14). The button (13) releases pressurized air to the graduate pipette. The vessel can be drained through the nozzle (6). By measuring the time taken to fill the graduated pipette, we calculated the viscosity of the fluid referring to the temperature.
The measurement of oils’ rheological properties is a challenging task. The ability to measure viscosity over a range of flow rates, and hence shear rates, pre-assumes rheometric capabilities. Cone, plate, and coaxial cylinder viscometers are more capable of providing measurements in higher shear rates. In this work, a capillary tube viscometer was used. The aged oil had firstly run in real conditions and then its viscosity was measured using this type of viscometer. The priority here was given to the SAE 10W40 synthetic oil, which is one of the most used lubricants in the automotive industry, and also the base synthetic oil for the engine under investigation, which was reported by Zavos et al. [19].
2.2. Method of Viscosity Measurement with EH105 Viscometer
The experimental procedure for the viscosity measurement of engine oils is described step by step in Figure 2. The dynamic viscosity (n) is defined as:
where R is the capillary tube radius, l is the capillary tube length, and is the gradient from the line defined, figuring the variation of Δp versus q.
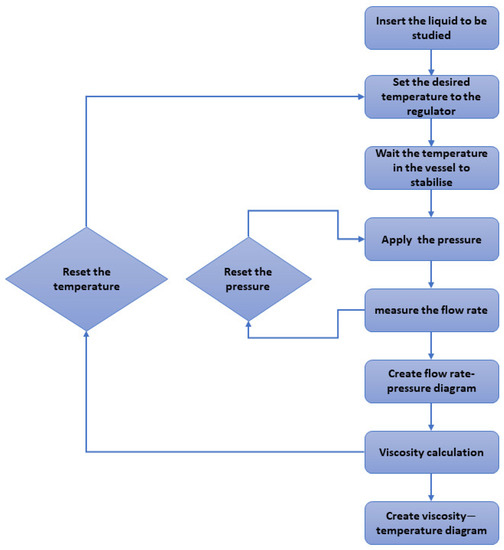
Figure 2.
The flow chart for the viscosity measurement of engine oils.
When a set of measurements were received for the flow rate, the values were plotted to the corresponding pressures. To make sure that the flow is definitely a Poiseuille flow, the experimental values must follow a straight-line equation.
2.3. Uncertainty Analysis of Viscosity Measurement
There are a lot of uncertainties related with the viscosity measurement devices, dealing with processes, the mathematical expressions, the measurements, and so on. In this work, the described capillary tube viscometer was used for viscosity measurements. Regarding the process followed by this particular device, the following parameters are necessary for the uncertainty analysis:
- Uncertainty in the measurement of pressure,
- Uncertainty in the measurement of flow rate,
- Uncertainty in the measurement of volume,
- Uncertainty in the measurement of time,
- Uncertainty from the radius of capillary tube,
- Uncertainty from the length of capillary tube,
As all above input quantities are independent, the combined standard uncertainty is given by:
where , , and are all the quantities that we took into consideration (). The uncertainty value regarding viscosity using the values of Table 1 is (n) = ±0. 010304 Pa s with confidence 95% for each case.

Table 1.
Uncertainty parameters and values.
The procedure of the uncertainty analysis is significant here in order to calculate through several measurements, with a higher accuracy, the viscosity values. All the tests were performed by an accredited device in a temperature controlled room, and the uncertainty quantities concern the device components.
2.4. CFD Quasi-Static Analysis of Piston Ring-Liner Conjunction
The numerical procedure reported here has been provided by Zavos and Nikolakopoulos [12]. A one-dimensional analysis is used. The CFD model considers fully flooded inlet conditions. The side leakage of the lubricant is not taken into account around the periphery of the ring. The solution of the developed pressure between the ring-liner tribo-pair is produced using the Navier-Stokes equations [24]. The set of equations is solved using the ANSYS Multiphysics code. Figure 3 shows the boundary flow conditions in the ring-liner conjunction. The ring reciprocates along the liner following the piston sliding velocity [25]:
where rcr is the crank-pin radius, ω is the rotational crankshaft speed, ϕ is the crank angle, and λCR is the control ratio. The ring twist is not accounted for. The in-cylinder pressure, pc, and the outlet pressure, pout (from crankcase), values are assumed as inputs, depending on the direction of the piston motion.
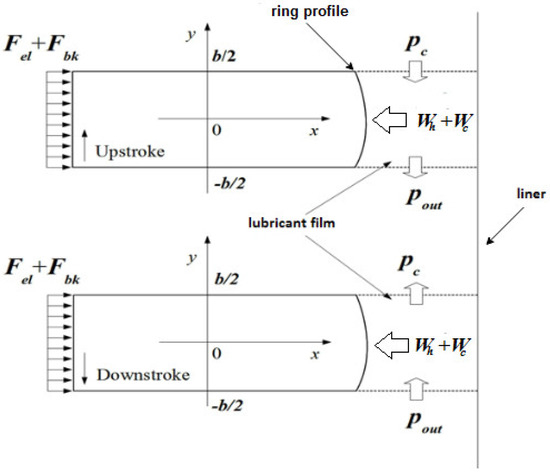
Figure 3.
Forces and boundary flow conditions on piston ring-liner contact.
To obtain the minimum lubricant film thickness at any crank angle, a film shape expression is needed as follows:
where is the minimum film thickness, is the parabolic ring profile , and is the localised contact pressure-induced deflection. In reality, the ring profile has a rough axial asymmetric shape as reported in References [13,19]. However, an idealized parabolic ring shape is used in this investigation. In addition, the cylinder liner also has a perfect circular shape. The current study focuses on engine synthetic oil aging, which is suitable for the piston ring tribology undertaken here. The effect of the ring contact profile and the cylinder’s bore geometry is not the scope of this analysis. The latter parameter has a limited effect in the ring-liner contact for this analysis. According to the authors of [12], this shows that localized ring deformation has a small effect on lubricant film distribution. More specifically, this factor has a critical impact when higher combustion pressures are expected.
Regarding in-plane ring behavior, two outward forces are applied between the piston and the back profile of the ring. The ring tension force is obtained as:
where the elastic pressure is taken as: , while the ring cross section is defined as: . Additionally, the back gas force is given as:
In the current analysis, the ring tension force FT and the gas force FG should be equal to the hydrodynamic reaction, Wh, due to the lubricant film in the ring-liner conjunction, and the load, due to asperities, Wc. At every crankshaft position, ring balance should take place according to the following expression:
Under mixed and hydrodynamic regimes of lubrication, the ring-liner conjunction is not covered by lubricant film only, but there is a part of the ring which suffers from the asperities. The hydrodynamic local capacity and the load carried by surface asperities are expressed as:
The load equilibrium is fulfilled when the relationship (10) is confirmed as:
When ring balance is not reached, then the minimum film thickness is recalculated through the iterative process. In this analysis, the value of the parameter χ is taken as: χ = 0.05.
To evaluate the load by the surface asperities, the Greenwood-Tripp contact model [26] is used. describes the root mean square (RMS) surface finish of the contact surfaces. E’ is the effective elastic modulus of the ring-liner system and A is the nominal contact area of the ring face-width. The terms and are also the roughness parameter and the asperity slope, respectively. Furthermore, the statistical function F5/2(λ) is expressed as a relation of the Stribeck oil film parameter [27]. The limits between various regimes of lubrication are used to indicate the changes at contact, and these regimes are depicted in the minimum film thickness curve.
In the piston ring-cylinder liner conjunction, the total friction is obtained as:
Under the hydrodynamic regime of lubrication, the viscous friction is given as:
where τ is the viscous shear stress of the lubricant film:
When the film ratio is , the load by surface asperities should be taken into account; therefore, the ring boundary friction can be described as [28]:
where the non-Newtonian Eyring shear stress and the boundary shear strength of the conjugating surfaces are MPa and ς = 0.17, respectively. A coefficient of friction with a value of 0.17 was used for the formed ferrous surface oxide layer, as reported by Teodorescu et al. [29]. The asperity contact area Ac is also defined as [26]:
where the statistical function F2(λ) is:
After grid sensitivity tests, 15 divisions are used along the lubricant film and 1000 divisions are considered along the ring face-width. The total number of cells is 15 × 103. The fluid region is meshed with finite volumes. The CFD procedure is specified by Zavos and Nikolakopoulos [12] in more detail. The current analysis assumes an isothermal mixed lubrication model, where the thermal gradient in the contact is negligible. Therefore, the lubricant density and viscosity were evaluated with the pressure variation according to Roelands [30], as follow:
where:
and the pressure–viscosity index is:
In the literature, there are a lot of pressure-viscosity models that were employed in the beginning of elasto-hydrodynamic line contact calculations. Barus [31] and Dowson et al. [32] are two well-known models. However, at high film pressures of the order of 1 GPa, encountered in many highly loaded elastohydrodynamic lubrication (EHL) contacts, the Barus equation is no longer applicable. The most popular one, in the open literature on EHL operations, is the Roelands pressure-viscosity equation. Bair [33] refused the accuracy of the Roelands equation by showing that it is incorrect from about 0.5 GPa or higher, depending on the fluid considered, and proposed alternatives. However, the popularity of the Roelands equation shows that many of the film thickness approximations on the ring-liner contact have been based on it showing good agreement with experiments.
The pressure viscosity coefficient, in general, depends on the lubricant at hand and on the pressure, temperature, and shear rate in the contact areas. It is a very important factor, especially for heavily loaded elasto-hydrodynamically lubricated contacts, which requires the value of the pressure-viscosity coefficient to be known. The estimation of this value will easily lead to errors in pressure distribution and film thickness, for example. The pressure viscosity coefficient is generally recognized as temperature dependent, according to the Barus equation, and is usually considered constants in a wide range of temperatures, according to Roelands equation [30,31]. Nevertheless, a number of works have been made to combine in one equation the effects of temperature and pressure upon viscosity. Various researchers also report that their equations are accurate for a certain type of fluids, but either not so accurate or unusable for other types, highlighting pressure viscosity coefficient dependency to viscosity.
The nominal lubricant properties are obtained from the capillary tube viscometer described in Section 2.1. For clarity, the overall methodology of the ring lubrication problem is summarized and shown in Figure 4. The final solution was attained when both pressure and ring balance criteria were obtained simultaneously, and after the analysis was moved to the new crank angle location.
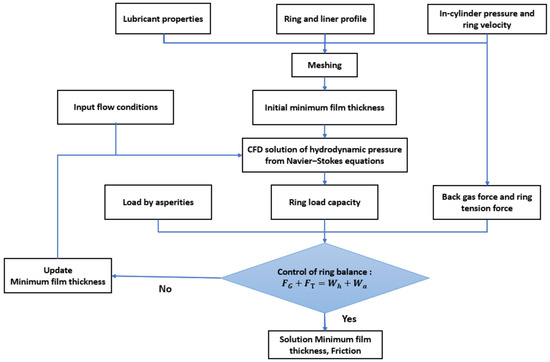
Figure 4.
Methodology of the Computational Fluid Dynamics (CFD) ring lubrication problem.
3. Results and Discussion
3.1. Validity of Viscosity Measurement
Before the viscosity procedure measurement, it was necessary to run a validation process first. The validation deals with both the whole process and equipment validity. In order to validate the viscometer and the measurement procedure, the viscosity of distilled water was first examined and measured in two different temperatures—at 25 °C in the first case and at 40 °C in the second. According to the procedure described in the flow chart of Figure 2, the flow rate of the capillary tube as a function of the applied pressure must be plotted in order to use Equation (1) for the calculation of dynamic viscosity. Therefore, two diagrams, Figure 5 and Figure 6, were obtained, one for each tested temperature. The straight line was created using the mean square least method. Furthermore, and using the data from the two previous figures, in Table 2, the experimental viscosity values are compared with the standard viscosity values of the distilled water. It is observed to be in very good agreement. Furthermore, the uncertainty concerning the viscosity measurements is also given in Table 2. The properties of the distilled water were obtained by Reference [34].
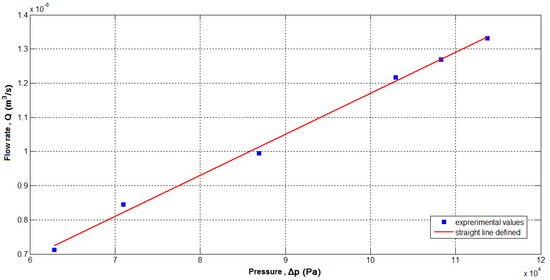
Figure 5.
Experimental results for distilled water at 25 °C.
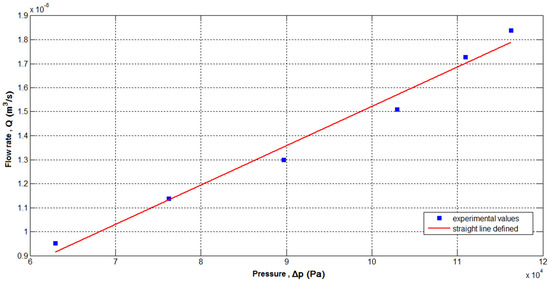
Figure 6.
Experimental results for distilled water at 40 °C.

Table 2.
Viscosity measurements and validation.
3.2. Viscosity Measurements for Commercial Engine Oils
In this study, three different engine lubricants used. SAE 30 oil, SAE 10W40 synthetic oil, and AWS-100 biolubricant were tested. The temperature in all cases varied between 20 and 75 °C, and the test pressure was set at 2 MPa. The basic properties of the lubricants are listed in Table 3. The biolubricant complies with DIN 51524 part 2 and 3, while the SAE-10W40 complies with API SL/CF, ACEA A3-02B, B4-04, B3-03.

Table 3.
The basic properties of the commercial engine oils used in the experiments.
The variation of the measured viscosity for the SAE 30, the environmentally based and the SAE 10W40 oils are presented in Figure 7, Figure 8 and Figure 9. Regarding the engine oil SAE 30 and the biolubricant AWS-100, the viscosity curves are illustrated only for the fresh conditions as a function of increasing temperature, while for the SAE 10W40 oil, the aged conditions are additionally provided.
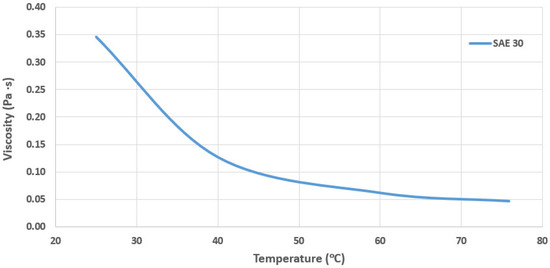
Figure 7.
Measured viscosity for fresh engine oil SAE 30.
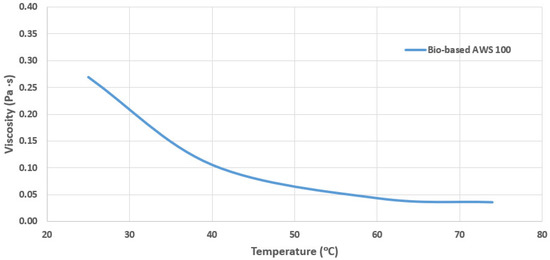
Figure 8.
Measured viscosity for fresh oil AWS-100.
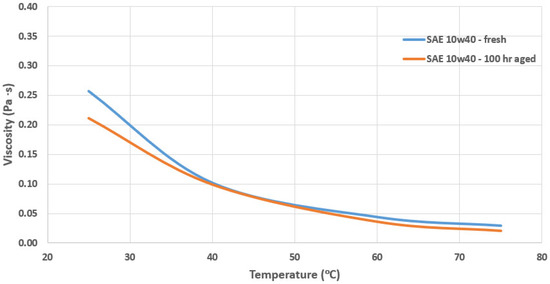
Figure 9.
Measured viscosity for fresh and aged synthetic oil SAE 10W40.
Figure 9 shows the viscosity variation of the synthetic oil SAE 10W40 after 100 engine working hours. We selected the SAE 10W40 synthetic oil, which is the base synthetic oil for the engine under investigation, reported in Reference [19]. The used engine was a four-stroke single cylinder motorbike engine. The corresponding engine speed was 1500 rpm without load. The basic specifications of the tested engine were fully provided by Zavos and Nikolakopoulos [19]. This viscosity variation due to temperature is quite significant, taking into consideration that it occurred in a period of 100 working hours. The mathematical equation, after the relevant approximation, which describes the two curves is given as [35]:
In Table 4, the coefficients regarding the approximation of the viscosity Equation (23) and the goodness of fit are listed. According to the squared error (SSE) and the R-square values, the approximate values are in very good agreement with the measurements.

Table 4.
The basic parameters of the viscosity mathematical expression.
Engine oils are used in engines by mixing with various additives. The role of the engine oils is to reduce friction between moving surfaces and to transfer the contaminants and remaining particles away from moving parts. However, oils are subjected to thermal and oxidative degradation during internal combustion engine operation, as they are exposed to high temperatures due to combustion and pressures due to bearings operation under air environment. Viscosity defines the performance and fatigue life of engines, and it plays an important role in determining the oxidative stability of engine oils. In this work, the synthetic oil SAE10W40 was aged in a single cylinder internal combustion engine, which means that it was exposed to high temperatures and pressures. The kinematic viscosity of the aged oil decreased, as it can be seen in Figure 9. This is expected [36] because high decomposition temperatures tend to break the hydrocarbons present in oil via the attack of oxygen via alkoxy and peroxy bond β-scission, which leads to a decrease in dynamic viscosity. However, viscosity in general may increase, mainly as a result of the formation of products with high molecular mass. On the other hand, oil viscosity may rise due to the penetration of diluents and contaminants into it or, in most cases, as a consequence of the shearing of long-chain hydrocarbon molecules of the oil base of a viscosity modifier. Indeed, in this work, in some cases, the viscosity of the aged oil decreased in comparison to that of fresh oil, due to contaminants in it. Despite this fact, we believe that exposure to high temperatures and pressures during aging time leads to hydrocarbon break and, consequently, to dynamic viscosity decrement against the presence of wear debris. Nevertheless, the corresponding chemistry of the aged oil should be further investigated through infrared spectroscopy. This is the next plan of this experimental study.
3.3. CFD Model Validation
It is important to investigate the accuracy of CFD predictions. In order to validate the results from the current computational model, the computed results were compared with the predictions by Shahmohammadi et al. [15]. The same data (geometrical characteristics, velocity, and pressure profile during the engine cycle) were used for the validation. In Figure 10, the CFD predictions regarding the minimum film thickness are presented and compared. The current CFD approach neglects the effect of cavitation; however, the minimum film thickness in the ring-liner conjunction is in very good agreement with other similar analyses. More specifically, deviation is approximately 11%.
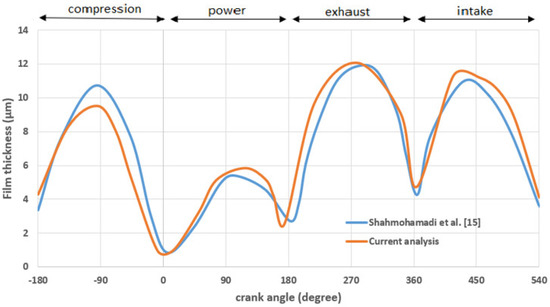
Figure 10.
Comparison of minimum film thickness between the current analysis (blue line) and published work [15].
3.4. The Effect of Synthetic Oil Aging on Piston Ring Tribology
A parabolic artificial ring profile was modelled. The simulated piston ring was a hard chrome-plated thin ring. The complete data of the piston assembly are presented in Table 5.

Table 5.
Piston assembly data of a single-cylinder motorbike engine.
The in-cylinder pressure measurements are taken at 50% throttle and presented in Figure 11. The position of the higher chamber pressure occurs at 20 degrees crank angle, after the Top Dead Center (TDC), in the power stroke. The corresponding gas pressures were used as input in the CFD analysis to determine ring friction and minimum film thickness. Additionally, regarding oil temperature, both cold and hot engine conditions were presented and compared. These operating conditions were chosen for the simulation of the low speed NEDC (New European Drive Cycle), which correspond to both cold and hot running tests [17].
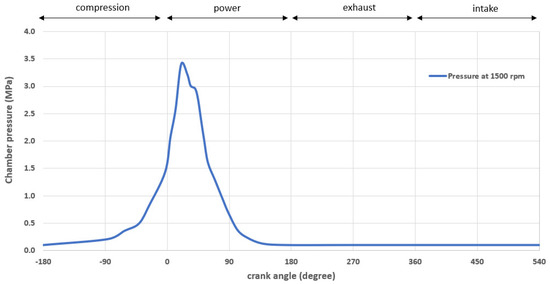
Figure 11.
Chamber pressure at 1500 rpm and 50% throttle.
In Figure 12, the computed minimum lubricant film data are shown and compared. The dashed lines indicate the regimes of lubrication from the boundary (λ < 1) to mixed regimes (1 ≤ λ < 4). Both lubricants show thin films at TDC reversal, where in-cylinder pressures are quite high. The minimum film thickness is observed at the instant of combustion. This occurs because there is a significant in-cylinder pressure load on the piston ring-liner contact, which follows the relationship between shear stress and pressure from the first term in Equation (15). However, when piston speed is increased, the ring profile promotes the fully hydrodynamic conditions during mid-stroke. These results are used to indicate the major contribution of the synthetic oil SAE 10W40 aging at cold running conditions. The lubricant temperature was 40 °C. It is evident that the difference between the two cases is almost negligible. Particularly, the measured lubricant viscosity for the aged synthetic oil SAE 10W40 falls in higher temperatures. This means that, until 40 °C, aging does not affect oil performance immediately.
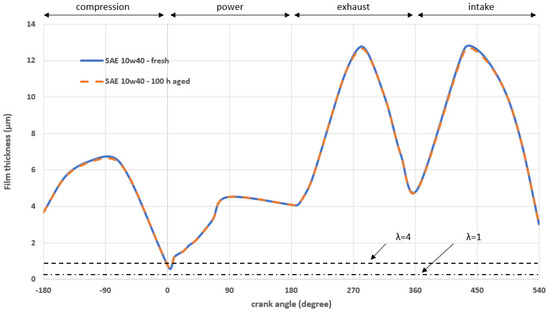
Figure 12.
Variations of minimum film thickness for fresh and aged synthetic engine oil SAE 10W40 at 40 °C.
Under cold controlled condition and low engine speed, the changes in the overall ring friction are shown in Figure 13. The maximum total ring friction occurs in the power stroke between the TDC point and the mid-stroke position. This is because of the mixed lubrication conditions, where the Poiseuille shear and the direct asperity interactions take place. In addition, the corresponding friction values are lower at the Top Dead Center and Bottom Dead Center in the exhaust and intake strokes, respectively. This particular behavior is the same for both fresh and aged oil. It can be explained because asperity friction is negligible due to low gas pressures and viscosity values. The above combination of engine conditions showed that lubricant viscosity temperature variations are a significant design factor, influencing frictional losses during the engine cycles.
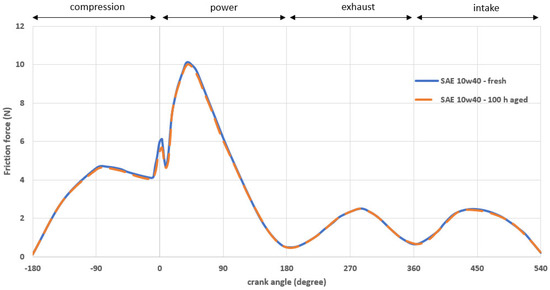
Figure 13.
Variations of total ring friction for fresh and aged synthetic engine oil SAE 10W40 at 40 °C.
In Figure 14, the computed minimum lubricant film data concerning the hot engine conditions are illustrated. The chosen oil temperature was assumed at 75 °C. As can be seen, the minimum film thickness has a significant reduction in the order of 13.5%. This behavior is clearly presented in Figure 9, at crank angle of 300 degrees (exhaust area), owing to lubricant’s viscosity variation.
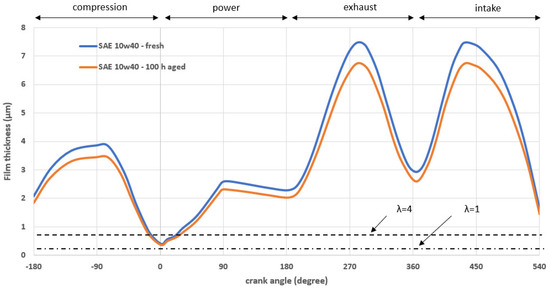
Figure 14.
Variations of minimum film thickness for fresh and aged synthetic engine oil SAE 10W40 at 75 °C.
It seems that higher oil temperatures can influence oil performance, and thus the tribology of the ring-liner contact. This is obvious from Figure 15. The red curve presents the behavior of the engine’s parabolic ring, when the aged synthetic oil is used. The low piston speed and the low viscosity of the aged oil can provide a maximum ring friction in the transition between the compression stroke to the power stroke (see the engine operational conditions in Figure 11), and particularly close at the higher combustion pressures region at crank angle of 5°. Boundary friction is predominant. This can be explained due to lower films in the TDC region (compression region of Figure 14). Therefore, it is important to note that the aforementioned behavior may result in continuously increased power loss ratio and wear around TDC. On the other hand, when piston speed is increased (for example, if the engine is in the power region), viscous friction is the dominant component and low, while asperity interactions in this case are negligible. Consequently, the improvement of frictional losses of this conjunction is a significant challenge.
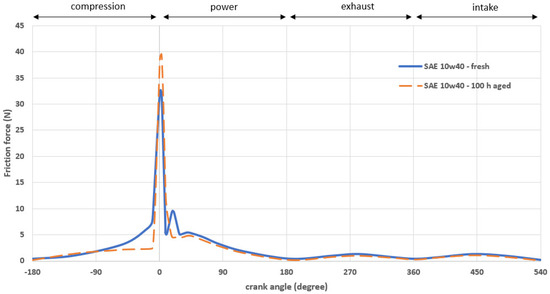
Figure 15.
Variations of total ring friction for fresh and aged synthetic engine oil SAE 10W40 at 75 °C.
All in all, this work deals with the effect of the viscosity variation of liquid lubricants, due to aging, on their lubrication performance, focused on the thickness of the oil film and the frictional forces expected to be developed. Both experimental and simulation results are presented. The main idea was to show, using experimental data and a suitable model, how crucial the variation of the lubricants’ properties is in an internal combustion engine. For further analysis, the aging of the SAE 30 and the AWS 100, as well as the test in all lubricants for higher pressures and different types of viscometers could be considered.
4. Conclusions
In this work, the performance of synthetic-based lubricant with viscosity in aged conditions in comparison to fresh oil was investigated, concerning piston ring applications. The results generally reveal that the aged (due to temperature) synthetic lubricant provides a different piston ring tribological behavior. The following conclusions can be drawn:
- The variation of the dynamic viscosity for the engine oil SAE10W40 is more than 19% at 25 °C and more than 28.5% at 75 °C.
- The minimum film thickness has insignificant variation through the crankshaft angles for the fresh and aged SAE10W40 oil at 40 °C, whereas very high variation appears as temperature increases. In practical terms, there is a significant reduction in the order of 13.5%, for example in 300 degrees, due to the lubricant’s viscosity temperature variations for 2 MPa test pressure at 75 °C.
- The variation of total ring friction is almost 7.8% at the TDC between fresh and aged oil. The smaller value concerns aged oil, due its slight viscosity variation at 40 °C. Instead, boundary friction is higher, 19.25% at 75 °C, for aged oil than for fresh oil. This means that aged oil significantly influences in engine friction losses and contact wear. The impact of oil aging on ring and liner wear is the next plan of this work.
Author Contributions
P.G.N. proofread the paper, performed the methodology in experiments, and in simulations analyzed the results and wrote the main body of the paper. S.M. performed the simulations and experiments and participated in the scientific discussions. A.Z. supported the interpretation and validation of the simulation results.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| A | nominal contact area |
| Ac | asperity contact area |
| b | ring face-width |
| dgap | ring end gap |
| E’ | equivalent (reduced) modulus of elasticity |
| Ering | Young’s modulus of elasticity of the ring |
| El | Young’s modulus of elasticity of the liner |
| F | applied ring load |
| ftot | total friction |
| ffl | viscous friction |
| fb | boundary friction |
| FG | combustion gas force |
| FT | ring tension force |
| F5/2, F2 | statistical functions |
| h | lubricant film thickness |
| hmin | minimum film thickness with time |
| hs | ring axial profile |
| Iring | second moment of ring area |
| ph | hydrodynamic pressure |
| pel | ring elastic pressure due to fitment |
| pbk | ring back gas pressure acting behind the inner ring rim |
| pc | combustion pressure |
| pout | outlet pressure at the ring conjunction |
| patm | ambient pressure |
| rcr | Crank-pin radius |
| ro | nominal bore radius |
| t | time |
| w | ring radial width |
| Wc | load share of asperities |
| Wh | load carried by the lubricant film |
| X | parameter for load balance criterion |
| Greek symbols | |
| a* | modified pressure–viscosity coefficient |
| δp | local contact deformation |
| ζ | surface density of asperity peaks |
| κ | average asperity tip radius |
| λ | Stribeck oil film parameter |
| λCR | control ratio |
| μ | lubricant dynamic viscosity |
| μο | ambient dynamic viscosity |
| ρ | lubricant density |
| ρο | lubricant density at atmospheric pressure and ambient temperature |
| σ | root mean square roughness value of examined tribo pair |
| ς | coefficient parameter of boundary shear strength |
| τ | viscous shear stress |
| το | Eyring shear stress of the lubricant film |
| υring | ring sliding velocity |
| ϕ | crank angle |
| χ | step for minimum film thickness loop |
| ω | rotational crankshaft speed |
| Abbreviations | |
| BDC | Bottom Dead Center |
| CFD | Computational Fluid Dynamics |
| NEDC | New European Drive Cycle |
| RS | Root Square |
| TDC | Top Dead Center |
References
- Boons, M.; Van Den Bulk, R.; King, T. The Impact of E85 Use on Lubricant Performance; SAE Technical Paper no. 2008-01-1763; SAE International: Warrendale, PA, USA, 2008. [Google Scholar]
- Tseng, M.; Lin, R.; Liu, F. Assessment on the Impact of the 3% Ethanol Gasoline Fuel Blend on Passenger Cars and Motorcycles in Taiwan; SAE Technical Paper no. 2008-32-0019; SAE International: Warrendale, PA, USA, 2008. [Google Scholar]
- Russo, D.; Dassisti, M.; Lawlor, V.; Olabi, A.G. State of the art of biofuels from pure plant oil. Renew. Sustain. Energy Rev. 2012, 16, 4056–4070. [Google Scholar] [CrossRef]
- World Energy Council. Global Transport Scenarios 2015; WEC: London, UK, 2011. [Google Scholar]
- Rudnick, L.S. Lubricant Additives–Chemistry and Applications, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Spikes, H. Friction Modifier Additives. Tribol. Lett. 2015, 60. [Google Scholar] [CrossRef]
- Zavos, A.; Nikolakopoulos, P.G. Measurement of friction and noise from piston assembly of a single-cylinder motorbike engine at realistic speeds. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017. [Google Scholar] [CrossRef]
- Rahnejat, H. Multi-Body Dynamics: Vehicles, Machines and Mechanisms; SAE/PEP (IMechE): Warrendale, PA, USA; London, UK, 1998. [Google Scholar]
- Tung, S.C.; McMillan, M.L. Automotive tribology overview of current advances and challenges for the future. Tribol. Int. 2004, 37, 517–536. [Google Scholar] [CrossRef]
- Furuhama, S.; Sasaki, S. Effect of oil properties on piston frictional forces. JSAE Rev. 1984, 15, 68–76. [Google Scholar]
- Tian, T. Dynamic behaviors of piston rings and their practical impact. Part 2: Oil transport, friction and wear of ring/liner interface and the effects of piston and ring dynamics. Proc. Inst. Mech. Eng. Part J 2002, 216, 229–248. [Google Scholar] [CrossRef]
- Zavos, A.; Nikolakopoulos, P. Thermo-mixed lubrication analysis of coated compression rings with worn cylinder profiles. Ind. Lubr. Tribol. 2017, 69, 15–29. [Google Scholar] [CrossRef]
- Ma, W.; Biboulet, N.; Lubrecht, A.A. Performance evolution of a worn piston ring. Tribol. Int. 2018, 126, 317–323. [Google Scholar] [CrossRef]
- Morris, N.; Mohammadpour, M.; Rahmani, R.; Johns-Rahnejat, P.M.; Rahnejat, H.; Dowson, D. Effect of cylinder deactivation on tribological performance of piston compression ring and connecting rod bearing. Tribol. Int. 2018, 120, 243–254. [Google Scholar] [CrossRef]
- Shahmohamadi, H.; Rahmani, R.; Rahnejat, H.; Garner, C.P.; King, P.D. Thermo-mixed hydrodynamics of piston compression ring conjunction. Tribol. Lett. 2013, 51, 323–340. [Google Scholar] [CrossRef]
- Bewsher, S.R.; Mohammadpour, M.; Rahnejat, H.; Offner, G.; Knaus, O. An investigation into the oil transport and starvation of piston ring pack. Proc. Inst. Mech. Eng. Part J 2018. [Google Scholar] [CrossRef]
- Rahmani, R.; Rahnejat, H.; Fitzsimons, B.; Dowson, D. The effect of cylinder liner operating temperature on frictional loss and engine emissions in piston ring conjunction. Appl. Energy 2017, 191, 568–581. [Google Scholar] [CrossRef]
- Baker, C.; Theodossiades, S.; Rahmani, R.; Rahnejat, H.; Fitzsimons, B. On the Transient Three-Dimensional Tribodynamics of Internal Combustion Engine Top Compression Ring. J. Eng. Gas Turbines Power 2017, 139, 062801. [Google Scholar] [CrossRef]
- Zavos, A.; Nikolakopoulos, P.G. Tribology of new thin compression ring of fired engine under controlled conditions—A combined experimental and numerical study. Tribol. Int. 2018, 128, 214–230. [Google Scholar] [CrossRef]
- Kaleli, H.; Yavasliol, I. Oil ageing-drain period in a petrol engine. Ind. Lubr. Tribol. 1997, 49, 120–126. [Google Scholar] [CrossRef]
- Besser, C.; Schneidhofer, C.; Dörr, N.; Novotny-Farkas, F.; Allmaier, G. Investigation of long-term engine oil performance using lab-based artificial ageing illustrated by the impact of ethanol as fuel component. Tribol. Int. 2012, 46, 174–182. [Google Scholar] [CrossRef]
- Sikora, G.; Miszczak, A. The Influence of Oil Ageing on the Change of Viscosity and Lubricity of Engine Oil. Solid State Phenom. 2013, 199, 182–187. [Google Scholar] [CrossRef]
- Dam, M.; Nuszkowski, J.; Thompson, G.J. Effects of Oil Aging on Laboratory Measurement of Emissions from a Legacy Heavy-Duty Diesel Engine; SAE Technical Paper No. 2011-01-1163; SAE Technical: Warrendale, PA, USA, 2011. [Google Scholar]
- White, F.M. Viscous Fluid Flow, 2nd ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Gohar, R.; Rahnejat, H. Fundamentals of Tribology; Imperial College Press: London, UK, 2008. [Google Scholar]
- Greenwood, J.A.; Tripp, J.H. The contact of two nominally flat rough surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Pirro, D.M.; Wessol, A.A. Lubrication Fundamentals; Marcel Dekker Inc.: New York, NY, USA; Basel, Switzerland, 2001. [Google Scholar]
- Yang, P.; Cui, J.; Jin, Z.M.; Dowson, D. Transient Elastohydrodynamic Analysis of Elliptical Contacts. Part 2: Thermal and Newtonian Lubricant Solution. J. Eng. Tribol. 2005, 219, 187–200. [Google Scholar]
- Teodorescu, M.; Kushwaha, M.; Rahnejat, H.; Rothberg, S.J. Multi-Physics Analysis of Valve Train Systems: From System Level to Microscale Interactions. J. Multibody Dyn. 2007, 221, 349–361. [Google Scholar] [CrossRef]
- Roelands, C.J.A. Correlational Aspects of the Viscosity-Temperature-Pressure Relationship of Lubricating Oils. Ph.D. Thesis, Technische Hogeschool te Delt, Delft, The Netherlands, 1966. [Google Scholar]
- Barus, C. Isothermals, isopiestics and isometrics relative to viscosity. Am. J. Sci. 1893, 45, 87–96. [Google Scholar] [CrossRef]
- Dowson, D.; Higginson, G.R. Elastohydrodynamic Lubrication, 1st ed.; Pergamon: Oxford, UK, 1966; p. 235. [Google Scholar]
- Bair, S. High Pressure Rheology for Quantitative Elastohydrodynamics; Elsevier: Amsterdam, The Netherlands, 2007; p. 240. [Google Scholar]
- Properties of Distilled Water. Available online: http://www.efunda.com/materials/common_matl/show_liquid.cfm?MatlName=WaterDistilled4C (accessed on 20 July 2018).
- Stachowiak, G.W.; Batchelor, A.W. Engineering Tribology; University of Western Australia: Perth, Australia, 2001. [Google Scholar]
- Tripathi, A.K.; Vinu, R. Characterization of Thermal Stability of Synthetic and Semi-Synthetic Engine Oils. Lubricants 2015, 3, 54–79. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).