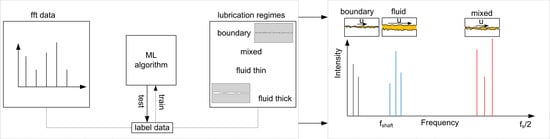
Lubrication Regime Classification of Hydrodynamic Journal Bearings by Machine Learning Using Torque Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
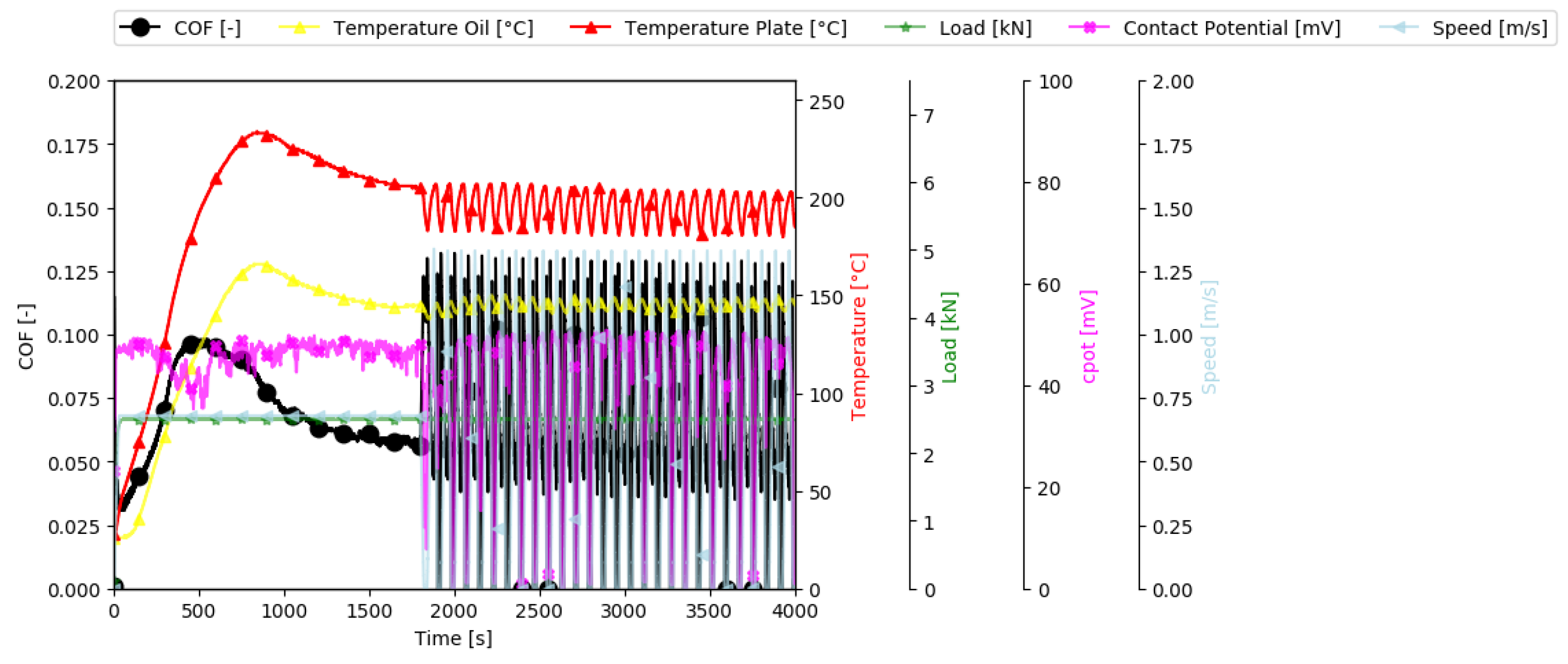
2.2. Testing Procedure
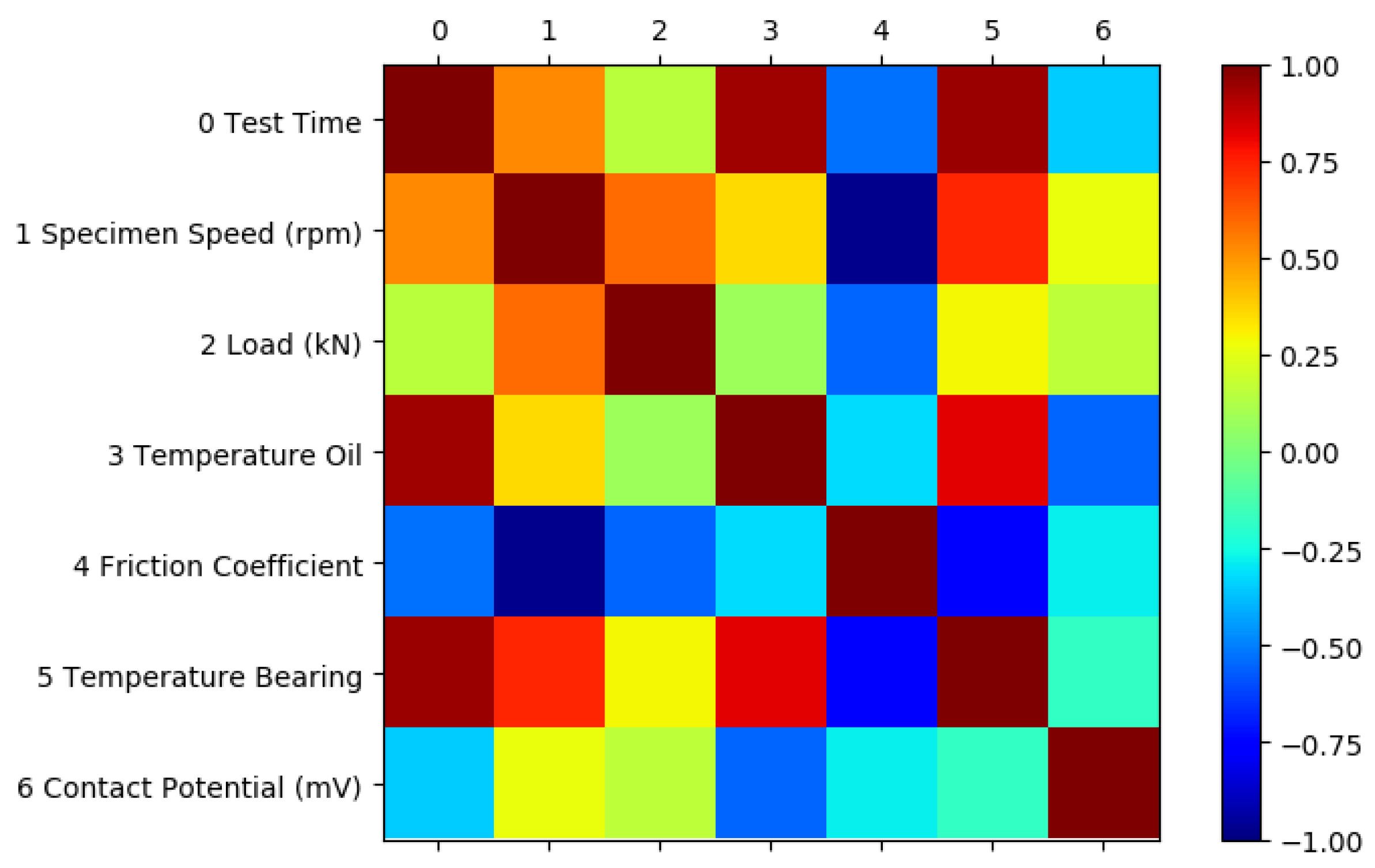
2.3. Data Processing
2.4. Machine Learning Methods
- Perform fft transform of torque high-speed data signals.
- Manually label each fft record to a lubrication regime.
- Shuffle all records to eliminate order influence.
- Scale data to improve convergence and accuracy of algorithms.
- Split the data into a training and a test set taking into account stratification.
- Train the model with a batch gradient descent algorithm.
- Evaluate performance on training and test set based on accuracy.
2.4.1. Logistic Regression
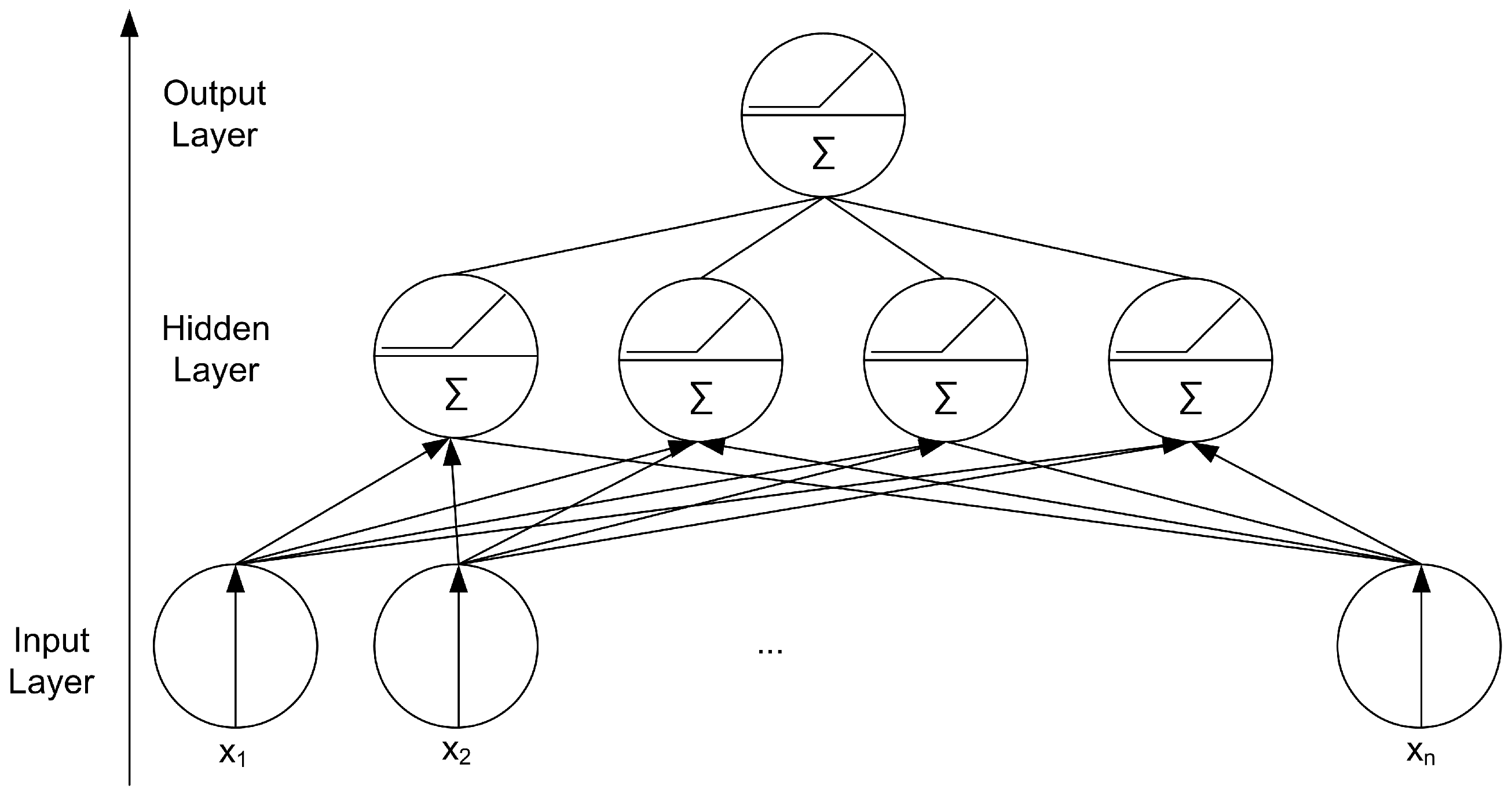
2.4.2. Deep Neural Networks (DNNs)
3. Results
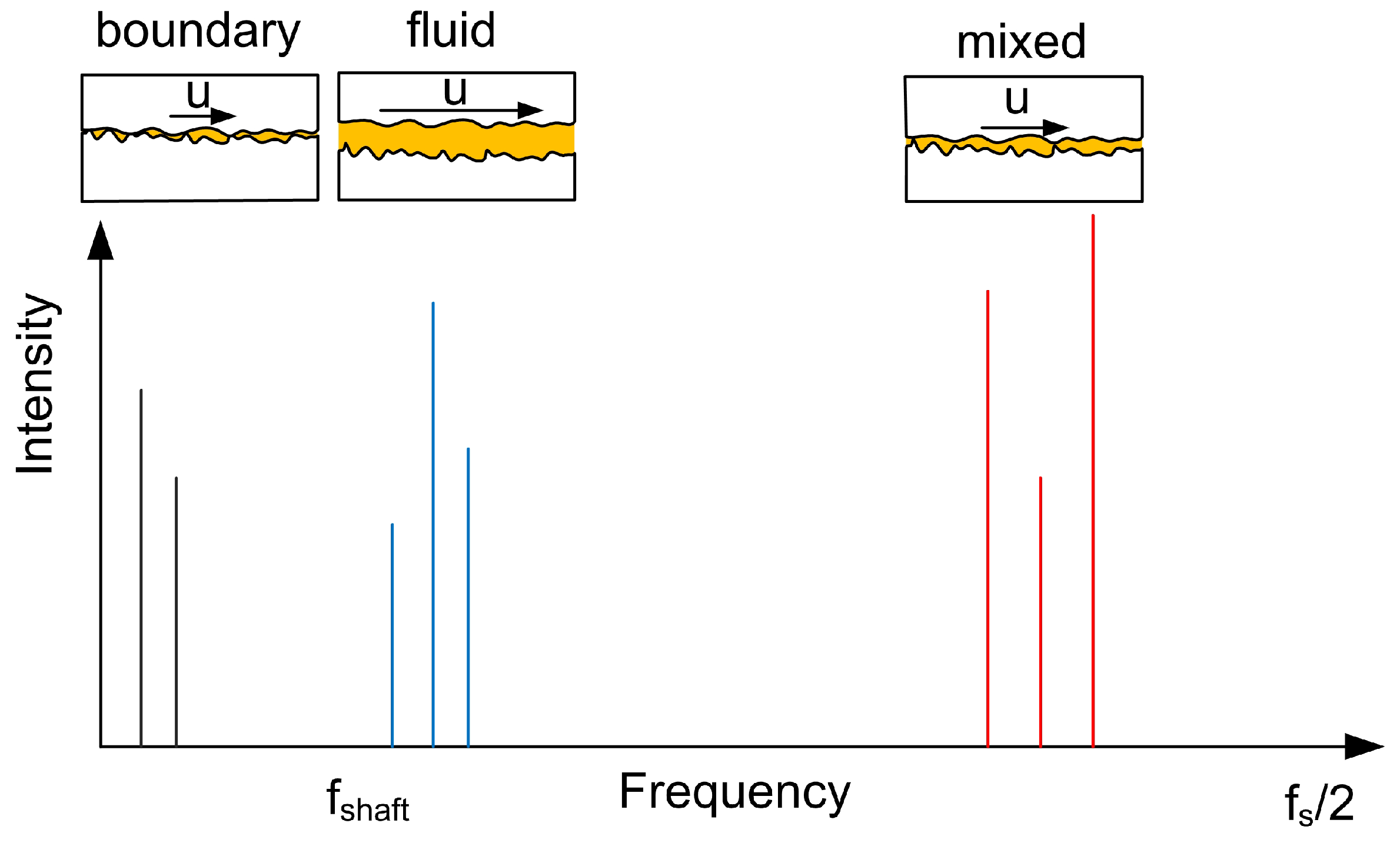
3.1. High-Speed Data Results
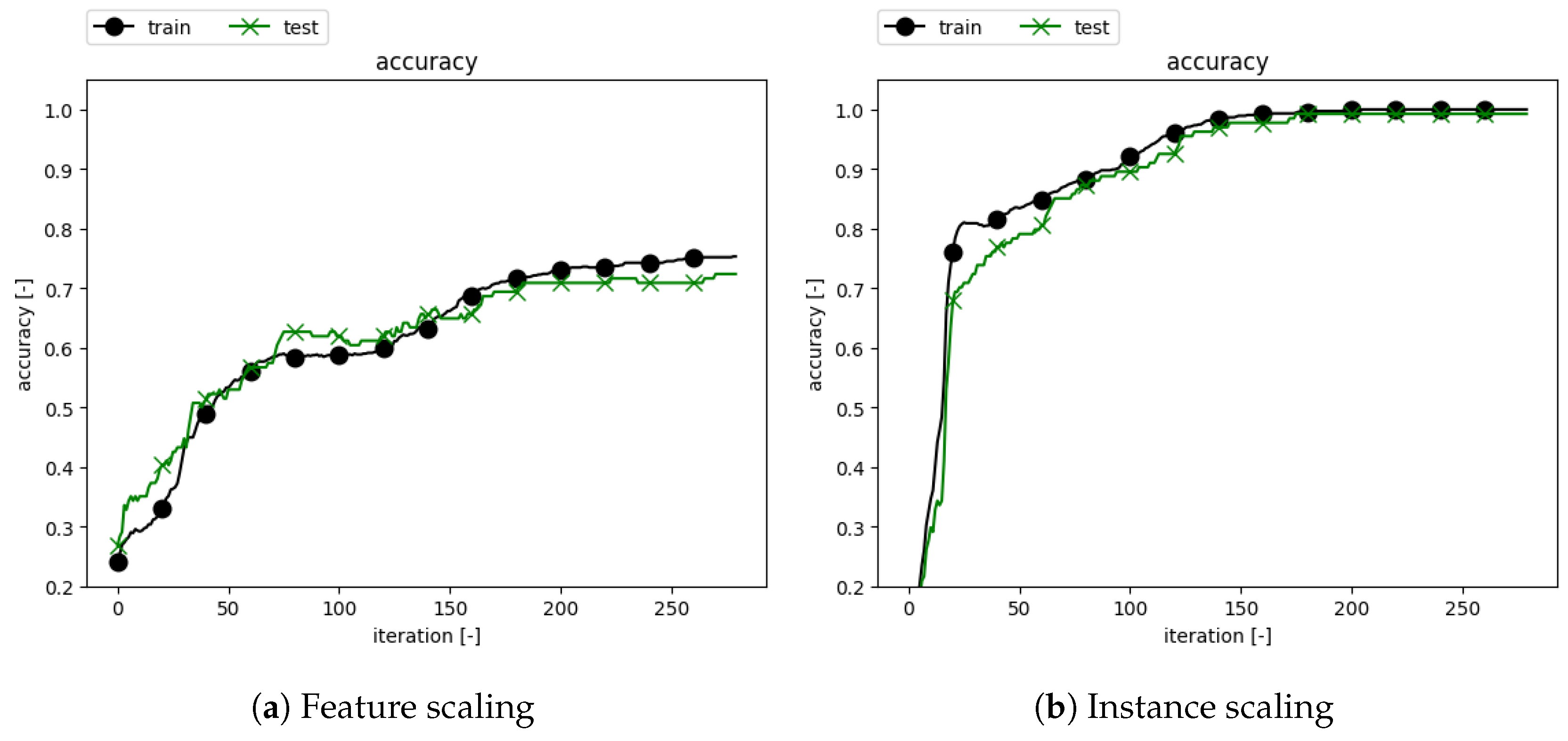
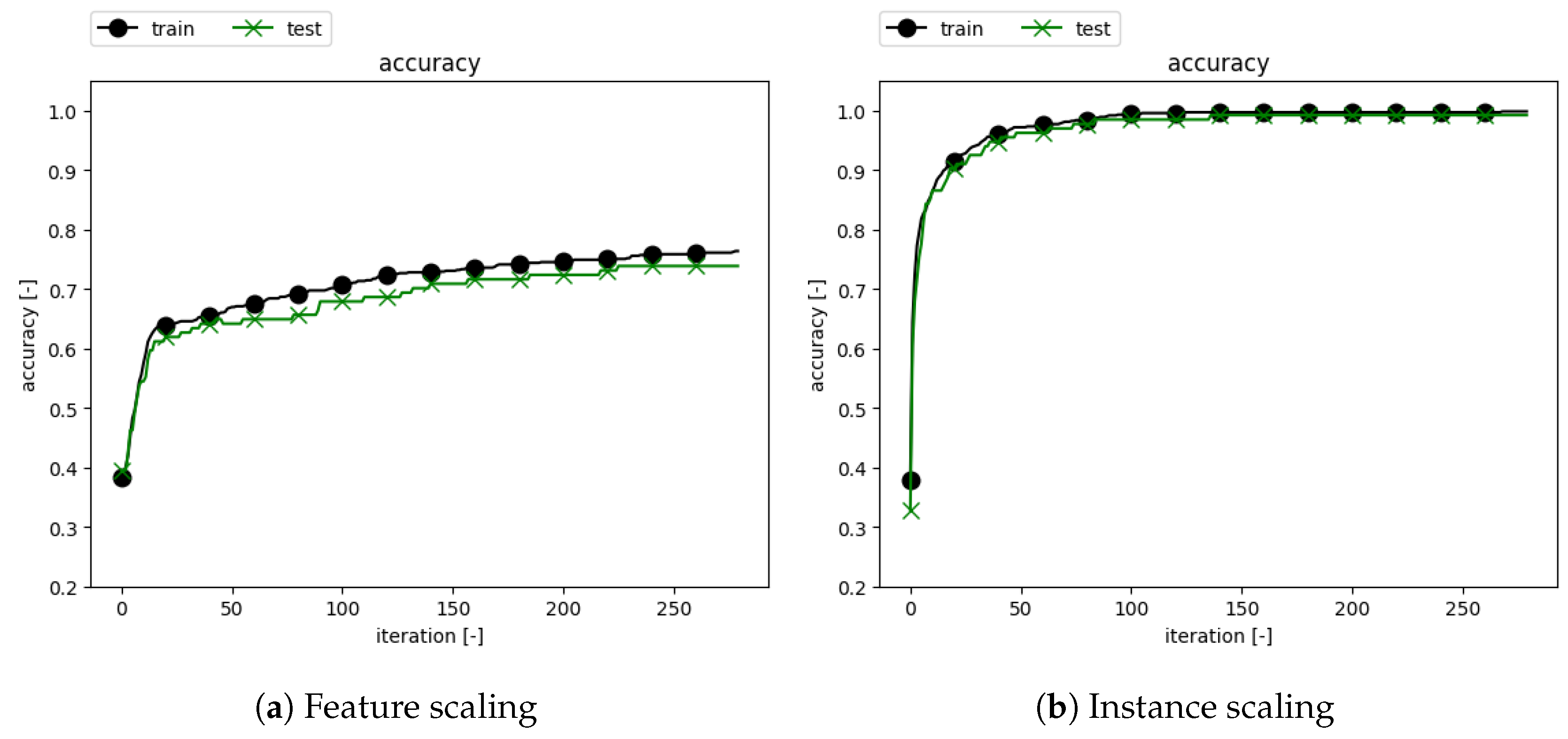
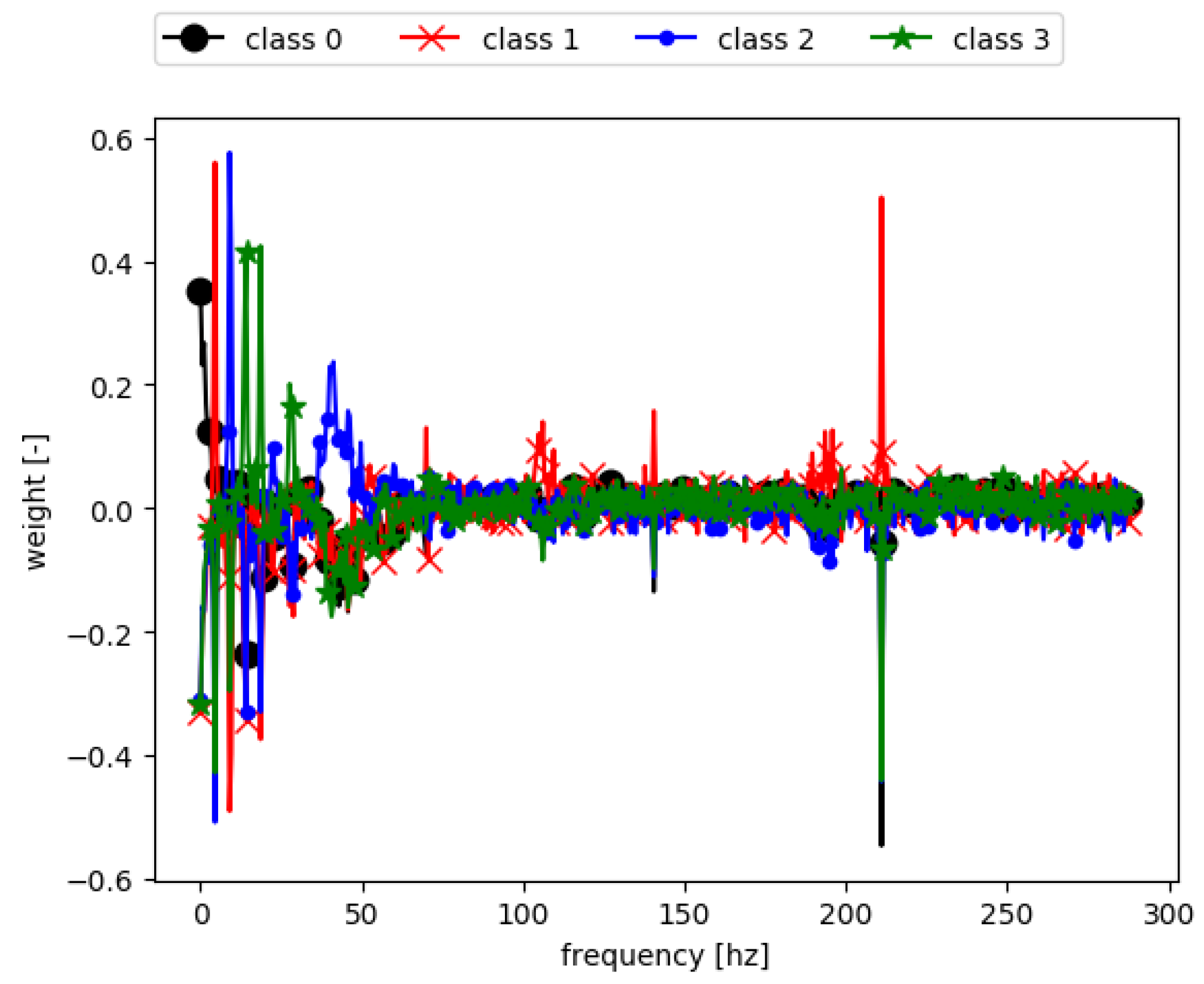
3.2. Classification Results
4. Discussion
5. Conclusions
- Neural networks perform well on the classification task, reaching accuracies of up to 99.25%.
- A shallow neural networks performs equally well on the problem and reaches high accuracies after fewer iterations compared to a deep neural network.
- A linear classification model, namely logistic regression, also delivers the same quality of results compared to neural networks.
- Feature scaling, which is often used in data analysis, is not suitable for the task of fft classification, since characteristic peaks might disappear due to the process.
- Each lubrication regime yields characteristic frequencies, which could be linked to different phenomena, such as specimen waviness, imperfections, or test-rig influences.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DNN | Deep neural network |
| AE | Acoustic emission |
| WT | Wavelet transform |
| fft | Fast Fourier transform |
| STFT | Short time Fourier transform |
| ReLU | Rectified Linear Unit |
| OvR | one-vs-rest |
| mean | mean value |
| std | standard deviation |
| E(X) | Expected value of X |
| Angular position | |
| Initial angular position | |
| Angular speed | |
| Component of time signal | |
| Component of fft | |
| m | Number of instances |
| n | Number of features |
| Input matrix | |
| Target vector | |
| Target prediction | |
| Logistic function | |
| Instance vector | |
| Weight vector | |
| Cost function | |
| Learning rate | |
| Mean | |
| Standard deviation | |
| Correlation coefficient of X, Y |
References
- Van Basshuysen, R.; Schäfer, F. Handbuch Verbrennungsmotor: Grundlagen, Komponenten, Systeme, Perspektiven; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Aufischer, R.; Hager, G.; Hamdard, K.; Offenbecher, M. Bearing Technology Combinations for Low Friction Cranktrains. MTZ Ind. 2016, 6, 56–63. [Google Scholar] [CrossRef]
- Becker, E.P. Trends in tribological materials and engine technology. Tribol. Int. 2004, 37, 569–575. [Google Scholar] [CrossRef]
- Grün, F.; Gódor, I.; Eichlseder, W. Fundamentals of optimizing aluminium-based journal bearing materials. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2009, 223, 777–785. [Google Scholar] [CrossRef]
- Yang, W.; Tavner, P.J.; Crabtree, C.J.; Feng, Y.; Qiu, Y. Wind turbine condition monitoring: Technical and commercial challenges. Wind Energy 2014, 17, 673–693. [Google Scholar] [CrossRef]
- McFadden, P.; Smith, J. Model for the vibration produced by a single point defect in a rolling element bearing. J. Sound Vib. 1984, 96, 69–82. [Google Scholar] [CrossRef]
- Brie, D. Modelling of the spalled rolling element bearing vibration signal: An overview and some new results. Mech. Syst. Signal Process. 2000, 14, 353–369. [Google Scholar] [CrossRef]
- Slavič, J.; Brković, A.; Boltežar, M. Typical bearing-fault rating using force measurements: Application to real data. J. Vib. Control 2011, 17, 2164–2174. [Google Scholar] [CrossRef]
- Tandon, N.; Nakra, B.C. Comparison of vibration and acoustic measurement techniques for the condition monitoring of rolling element bearings. Tribol. Int. 1992, 25, 205–212. [Google Scholar] [CrossRef]
- Castejón, C.; Lara, O.; García-Prada, J. Automated diagnosis of rolling bearings using MRA and neural networks. Mech. Syst. Signal Process. 2010, 24, 289–299. [Google Scholar] [CrossRef]
- Boness, R.; McBride, S.; Sobczyk, M. Wear studies using acoustic emission techniques. Tribol. Int. 1990, 23, 291–295. [Google Scholar] [CrossRef]
- Baccar, D.; Söffker, D. Wear detection by means of wavelet-based acoustic emission analysis. Mech. Syst. Signal Process. 2015, 60, 198–207. [Google Scholar] [CrossRef]
- Moshkovich, A.; Perfilyev, V.; Lapsker, I.; Feldman, Y.; Rapoport, L. Study of the transition from EHL to BL regions under friction of Ag and Ni. I. Analysis of acoustic emission. Tribol. Int. 2017, 113, 189–196. [Google Scholar] [CrossRef]
- Rastegaev, I.; Merson, D.; Danyuk, A.; Afanasyev, M.; Vinogradov, A. Using acoustic emission signal categorization for reconstruction of wear development timeline in tribosystems: Case studies and application examples. Wear 2018, 410, 83–92. [Google Scholar] [CrossRef]
- Bergmann, P.; Grün, F.; Summer, F.; Gódor, I.; Stadler, G. Expansion of the metrological visualization capability by the implementation of acoustic emission analysis. Adv. Tribol. 2017, 2017, 3718924. [Google Scholar] [CrossRef]
- Mcfadden, P.; Toozhy, M. Application of synchronous averaging to vibration monitoring of rolling element bearings. Mech. Syst. Signal Process. 2000, 14, 891–906. [Google Scholar] [CrossRef]
- Christian, K.; Mureithi, N.; Lakis, A.; Thomas, M. On the Use of Time Synchronous Averaging, Independent Component Analysis and Support Vector Machines for Bearing. In Proceedings of the First International Conference on Industrial Risk Engineering, Montreal, QC, Canada, 17–19 December 2007; pp. 610–624. [Google Scholar]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Sadegh, H.; Mehdi, A.N.; Mehdi, A. Classification of acoustic emission signals generated from journal bearing at different lubrication conditions based on wavelet analysis in combination with artificial neural network and genetic algorithm. Tribol. Int. 2016, 95, 426–434. [Google Scholar] [CrossRef]
- Jung, J.H.; Jeon, B.C.; Youn, B.D.; Kim, M.; Kim, D.; Kim, Y. Omnidirectional regeneration (ODR) of proximity sensor signals for robust diagnosis of journal bearing systems. Mech. Syst. Signal Process. 2017, 90, 189–207. [Google Scholar] [CrossRef]
- Aghdam, A.; Khonsari, M. Prediction of wear in grease-lubricated oscillatory journal bearings via energy-based approach. Wear 2014, 318, 188–201. [Google Scholar] [CrossRef]
- Summer, F.; Bergmann, P.; Grün, F. Damage Equivalent Test Methodologies as Design Elements for Journal Bearing Systems. Lubricants 2017, 5, 47. [Google Scholar] [CrossRef]
- Moder, J.; Grün, F.; Summer, F.; Gasperlmair, T.; Andritschky, M. Effect of temperature on wear and tribofilm formation in highly loaded DLC-steel line contacts. Tribol. Int. 2018, 123, 120–129. [Google Scholar] [CrossRef]
- Grün, F.; Krampl, H.; Schiffer, J.; Moder, J.; Gódor, I.; Offenbecher, M. Tribometric Development Tools for Journal Bearings—A novel test adapter. In Proceedings of the World Tribology Congress 2013, Torino, Italy, 8–13 September 2013. [Google Scholar]
- Cooley, J.W.; Tukey, J.W. An algorithm for the machine calculation of complex Fourier series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Géron, A. Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems, 1st ed.; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2017. [Google Scholar]
- Bartel, D. Simulation von Tribosystemen; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Moder, J.; Grün, F.; Gódor, I. A modelling framework for the simulation of lubricated and dry line contacts. Tribol. Int. 2018, 120, 34–46. [Google Scholar] [CrossRef]
- Bergmann, P.; Grün, F.; Gódor, I.; Stadler, G.; Maier-Kiener, V. On the modelling of mixed lubrication of conformal contacts. Tribol. Int. 2018, 125, 220–236. [Google Scholar] [CrossRef]
- Tensorflow. Available online: https://www.tensorflow.org/api_docs/ (accessed on 8 October 2018).
- Scikit Learn. Available online: http://scikit-learn.org/stable/documentation.html (accessed on 8 October 2018).



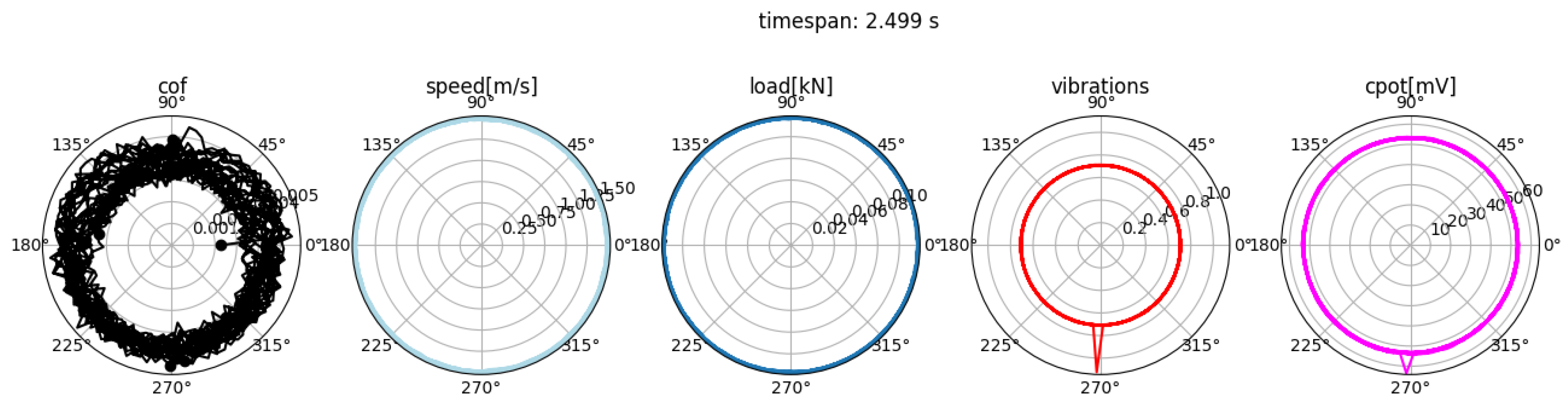


| ID | Material Combination | Load | Maximum Speed | Oil Temperature |
|---|---|---|---|---|
| 1 | Aluminium-Steel | 0.7 MPa | 17 hz | 65 °C |
| 2 | Lead-Steel | 0.7 MPa | 17 hz | 65 °C |
| 3 | Polymer-Steel | 0.7 MPa; 2 MPa | 17 hz | 65 °C |
| 4 | DLC-Steel | 26.65 MPa | 15 hz | 145 °C |
| DNN | Scaling | Accuracy |
|---|---|---|
| Hidden 6 | None | 52.96% |
| Hidden 1 | None | 54.47% |
| Hidden 6 | Feature | 72.39% |
| Hidden 1 | Feature | 73.88% |
| Hidden 6 | Instance | 99.25% |
| Hidden 1 | Instance | 99.25% |
| Scaling | Accuracy |
|---|---|
| None | 73.03% |
| Feature | 92.13% |
| Instance | 99.25% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moder, J.; Bergmann, P.; Grün, F. Lubrication Regime Classification of Hydrodynamic Journal Bearings by Machine Learning Using Torque Data. Lubricants 2018, 6, 108. https://doi.org/10.3390/lubricants6040108
Moder J, Bergmann P, Grün F. Lubrication Regime Classification of Hydrodynamic Journal Bearings by Machine Learning Using Torque Data. Lubricants. 2018; 6(4):108. https://doi.org/10.3390/lubricants6040108
Chicago/Turabian StyleModer, Jakob, Philipp Bergmann, and Florian Grün. 2018. "Lubrication Regime Classification of Hydrodynamic Journal Bearings by Machine Learning Using Torque Data" Lubricants 6, no. 4: 108. https://doi.org/10.3390/lubricants6040108
APA StyleModer, J., Bergmann, P., & Grün, F. (2018). Lubrication Regime Classification of Hydrodynamic Journal Bearings by Machine Learning Using Torque Data. Lubricants, 6(4), 108. https://doi.org/10.3390/lubricants6040108