Analytical Formula for the Ratio of Central to Minimum Film Thickness in a Circular EHL Contact

Abstract

Prediction of minimum film thickness is often used in practice for calculation of film parameter to design machine operation in full film regime. It was reported several times that majority of prediction formulas cannot match experimental data in terms of minimum film thickness. These standard prediction formulas give almost constant ratio between central and minimum film thickness while numerical calculations show ratio which spans from 1 to more than 3 depending on M and L parameters. In this paper, an analytical formula of this ratio is presented for lubricants with various pressure–viscosity coefficients. The analytical formula is compared with optical interferometry measurements and differences are discussed. It allows better prediction, compared to standard formulas, of minimum film thickness for wide range of M and L parameters.

1. Introduction

Prediction of film thickness represents an important step necessary for up-to-date design of lubricated concentrated contact. Analytical prediction formula can provide simple and rapid estimate of film thickness in elastohydrodynamically lubricated (EHL) contact. Minimum film thickness is used for calculation of film parameter to judge if machine will operate in full or mixed lubrication regime.

Since the pioneering work of Hamrock–Dowson in 1977 [1], numerous prediction formulas have been published in the literature [2,3,4,5,6]. An overview of the prediction formulas can be found in References [7,8,9]. A common approach is to make full numerical simulations of a contact for some range of conditions and solve regression analysis of film thickness results on operating conditions. These regressions were proven to be surprisingly accurate (considering the time of original formulation), if conditions of contact inlet are isothermal Newtonian. This is especially true for central film thickness, but generally not the case of minimum film thickness [10,11,12,13,14].

Several authors have showed that the ratio between central and minimum film thickness vary significantly with operating parameters [5,15,16,17]. Moreover, trend of the ratio is not monotonous depending on L parameter, i.e., reaching a local maximum at some value of L parameter. Classic prediction formula defined as a power function of operating conditions cannot represent such phenomenon. For better minimum film thickness formula, it is necessary to search for analytical form that can describe the ratio between central and minimum film thickness. Recently, a parameterization for the ratio of central to minimum film thickness was found for slender contacts (contact size in entrainment direction is much larger than in perpendicular direction) [18].

In this paper, the ratio between central film thickness and minimum film thickness is studied depending on M and L dimensionless parameters. New analytical formula allowing rapid prediction of minimum film thickness in circular point contact is suggested based on numerical simulations. The new formula is compared to ratio that come from Hamrock–Dowson equations and optical interferometry measurements.

2. Material and Methods

2.1. Numerical Calculations

An isothermal Newtonian numerical solution of elastohydrodynamically lubricated (EHL) point contact is assumed. Mathematical model consists of Reynolds equation

$$\frac{\partial }{\partial x}\left(\frac{{\mathsf{\rho }\mathrm{h}}^3}{12\mathsf{\eta }}\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{{\mathsf{\rho }\mathrm{h}}^3}{12\mathsf{\eta }}\frac{\partial p}{\partial y}\right)-\mathrm{u}\frac{\partial \left(\mathsf{\rho }\mathrm{h}\right)}{\partial x}=0$$

(1)

with boundary conditions p(x_a, y) = p(x_b, y) = p(x, y_a) = p(x, y_b) = 0 and the cavitation condition p(x, y) ≥ 0, film thickness equation

$$h\left(x,y\right)=h_0+\frac{x^2}{2R_x}+\frac{y^2}{2R_y}+\frac{2}{\mathsf{\pi }{E}_r}{\iint }_{-\infty }^{\infty }\frac{p\left(x^{\prime },y^{\prime }\right)d{x}^{\prime }d{y}^{\prime }}{\sqrt{{\left(x-x^{\prime }\right)}^2+{\left(y-y^{\prime }\right)}^2}}$$

(2)

and force balance equation

$$F={\iint }_{-\infty }^{\infty }p\left(x,y\right)dxdy$$

(3)

Roelands pressure–viscosity and Dowson–Higginson pressure–density relations have been considered

$$\mathsf{\eta }\left(p\right)={\mathsf{\eta }}_0\exp \left[\left(\ln {\mathsf{\eta }}_0+9.67\right)\left({\left(1+\raisebox{1ex}{$p$}\!\left/ \!\raisebox{-1ex}{$0.196·{10}^9$}\right.\right)}^Z-1\right)\right]$$

(4)

$$Z=\frac{{\mathsf{\alpha }}_0·0.196·{10}^9}{\ln {\mathsf{\eta }}_0+9.67}$$

(5)

$$\mathsf{\rho }\left(p\right)={\mathsf{\rho }}_0\frac{5.9·{10}^8+1.34p}{5.9·{10}^8+p}$$

(6)

The mathematical model in Equations (1)–(3) was solved by the multilevel multi-integration technique [19]. Second order discretization was assumed. Several mashes with number of grid points from 129 × 129 to 1025 × 1025 were used and differences between results were monitored to ensure results free of significant grid effect.

Pressure–viscosity response is important for film forming capability of a contact, which is described well by reciprocal asymptomatic isoviscous pressure coefficient α* or film pressure–viscosity coefficient α_film which is proportional to the α* evaluated up to maximum inlet zone pressure [20]. This pressure is, according to Bair et al. [20], considered to be equal to 3/α*.

$${\mathsf{\alpha }}^{*}={\left[{\int }_0^{\mathrm{p}}\frac{{\mathsf{\eta }}_{0}dp}{\mathsf{\eta }\left(p\right)}\right]}^{-1}$$

(7)

$${\mathsf{\alpha }}_{\mathrm{film}}={\mathsf{\alpha }}^{*}\left[1-\exp \left(-3\right)\right]$$

(8)

The α_film pressure–viscosity parameter is used in the present analytical model of central to minimum film thickness ratio.

2.2. Film Thickness Measurement

Film thickness measurements were done on a custom developed ball-on-disk optical tribometer (Brno University of Technology, Brno, Czech republic) [12]. This device measures film thickness in an elastohydrodynamic contact between steel ball and glass (sapphire) disk based on optical interferometry principle. Interferograms are formed between light beams reflected from a ball surface and bottom side of the glass (sapphire) disk coated by thin layer of chromium to ensure high interference contrast. Interferograms are evaluated by Thin film colorimetric interferometry. The measurement method uses robust calibration procedure which establishes film thickness/color calibration from monochromatic and chromatic interferogram of a static contact. The calibration procedure and method are described in References [21,22]. The present configuration is without spacer layer which enables evaluation of film thickness in a range of 0–800 nm with resolution better than 1 nm.

Film thickness was measured for steel on glass and steel on sapphire configurations with reference fluid tri (2-ethylhexyl) trimellitate (TOTM, Sigma–Aldrich, Darmstadt, Germany) as a lubricant. Rheological properties of this fluid were measured in [23]. Basic rheology parameters for test temperature are in

Table 1. Lubricant parameters.

	TOTM
Test temperature	30 ± 0.5 °C
Ambient viscosity	0.1517 Pa·s
Initial pressure–viscosity coefficient α0	23.9 GPa−1
Pressure–viscosity coefficient α*	21.5 GPa−1
Film pressure–viscosity coefficient αfilm	20.9 GPa−1

. Temperature was measured in contact inlet by thermocouple calibrated to more accurate thermistor sensor. Properties of contact bodies are in

Table 2. Properties of contact bodies.

	Steel	Glass	Sapphire
Radius of curvature	12.7 mm	∞	∞
Young modulus	206 GPa	81 GPa	405 GPa
Poisson’s ratio	0.3	0.209	0.25

.

3. Results and Discussion

A series of EHL contacts with parameters listed in

Table 3. Range of numerically simulated conditions.

M	L	α0	α*	αfilm
2, 5, 10, 20, 50, 100, 200, 500, 750, 1000	1, 2, 5, 7, 10, 15, 20, 25, 30	11, 22, 33 GPa−1	8.2, 20.3, 32.6 GPa−1	8.7, 20.6, 32.7 GPa−1

were numerically simulated. A convergence better than 10⁻⁴ was required. The ratio of central to minimum film thickness h_c/h_min was evaluated. Contact simulations were done on square grids with different number of points in a range from 129 × 129 to 1025 × 1025. A difference between results on coarse and finer meshes were evaluated and accepted only when data were with relative difference < 1% for M < 750 and < 3% for M ≥ 750 to ensure they were free of mesh density influence. All calculated data of ratios are listed in the

Table A1. Ratios of central film thickness to minimum film thickness in a point contact for α_film = 8.7 GPa⁻¹.

		M
		2	5	10	20	50	100	200	500	750	1000
L	1		1.24	1.35	1.36	1.48	1.61	1.79	2.08	2.23	2.35
	2		1.24	1.34	1.38	1.53	1.70	1.90	2.24	2.41	2.55
	5		1.23	1.31	1.40	1.59	1.78	2.01	2.41	2.63	2.77
	7		1.23	1.30	1.40	1.60	1.79	2.03	2.43	2.64	2.81
	10		1.23	1.29	1.40	1.59	1.78	2.02	2.42	2.63	2.80
	15	1.14	1.21	1.28	1.38	1.56	1.74	1.97	2.36	2.57	2.74
	20	1.13	1.19	1.26	1.36	1.53	1.70	1.92	2.30	2.50	2.65
	25	1.12	1.18	1.25	1.34	1.50	1.66	1.87	2.23	2.43	2.58
	30	1.10	1.17	1.24	1.32	1.48	1.63	1.83	2.17	2.36	2.50

,

Table A2. Ratios of central film thickness to minimum film thickness in a point contact for α_film = 20.6 GPa⁻¹.

		M
		2	5	10	20	50	100	200	500	750	1000
L	1		1.25	1.37	1.39	1.52	1.67	1.87	2.20	2.38	2.50
	2		1.25	1.37	1.42	1.61	1.81	2.04	2.43	2.64	2.78
	5		1.28	1.36	1.49	1.71	1.93	2.18	2.62	2.85	3.02
	7		1.30	1.37	1.49	1.71	1.92	2.17	2.60	2.82	3.00
	10		1.29	1.36	1.47	1.67	1.86	2.10	2.51	2.73	2.90
	15	1.19	1.25	1.32	1.42	1.59	1.77	1.98	2.37	2.58	2.73
	20	1.16	1.22	1.29	1.38	1.53	1.69	1.90	2.25	2.45	2.61
	25	1.14	1.20	1.26	1.34	1.49	1.64	1.83	2.17	2.36	2.51
	30		1.18	1.24	1.31	1.45	1.59	1.78	2.10	2.28	2.42

and

Table A3. Ratios of central film thickness to minimum film thickness in a point contact for α_film = 32.7 GPa⁻¹.

		M
		2	5	10	20	50	100	200	500	750	1000
L	1		1.25	1.37	1.40	1.54	1.70	1.90	2.25	2.44
	2		1.26	1.38	1.44	1.65	1.86	2.11	2.52	2.75
	5		1.30	1.39	1.53	1.77	1.99	2.27	2.72	2.96
	7		1.33	1.40	1.53	1.76	1.97	2.23	2.67	2.89	3.09
	10		1.32	1.39	1.51	1.70	1.90	2.13	2.54	2.77	2.95
	15	1.21	1.27	1.34	1.44	1.61	1.78	1.99	2.37	2.57	2.73
	20	1.18	1.24	1.33	1.41	1.54	1.70	1.90	2.24	2.44	2.59
	25				1.35	1.51	1.64	1.83	2.15	2.37

.

Film thickness ratios were compared to published results in [17,18]. The average difference (

Table 4. Comparison of present h_c/h_min results to published ones.

	Comparison 1	Comparison 2	Comparison 3
Published result	Venner [18]	Venner [18]	Chevalier [17]
Present result	numerical results	analytical model	analytical model
Average difference	4.4%	4.3%	3.5%

) is 4.4% and 3.5%, respectively. Because it was found in present results that film thickness ratio depends on pressure–viscosity coefficient, besides M and L parameters, certain part of the deviations can come from differences in this coefficient. The values of pressure–viscosity, for which the film thickness ratios were obtained, are not clear in the literature sources.

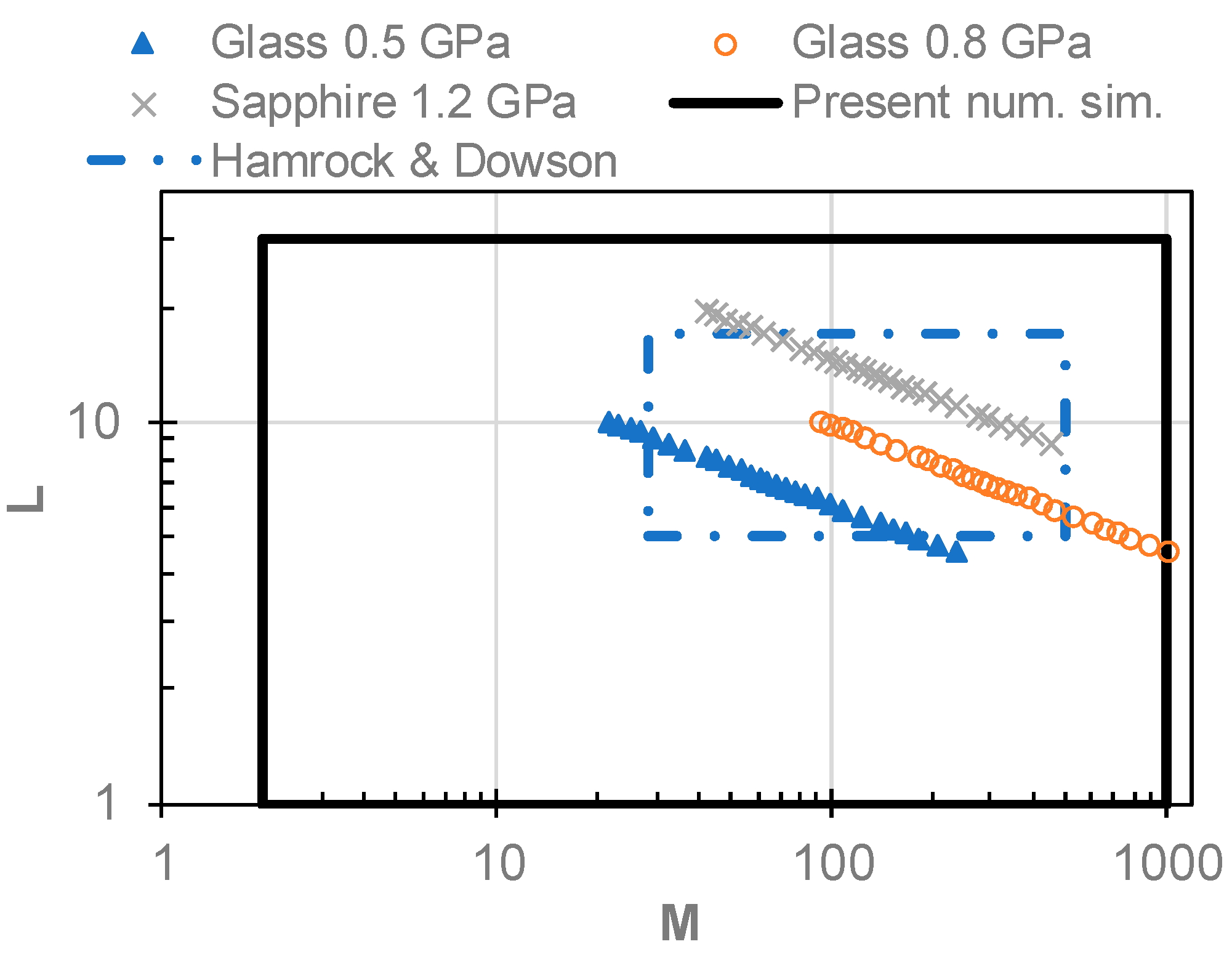
Figure 1 shows a domain of current simulations, operating points of experiments and domain of parameters on which Hamrock–Dowson film thickness equations were established. These equations are one of the most employed in EHL field, therefore, it was chosen for comparison. According to [1], the central and minimum film thickness can be predicted by

$$h_{\mathrm{c}}=2.69R_x{U}^{0.67}{G}^{0.53}{W}^{-0.067}\left[1-0.61{\mathrm{e}}^{-0.73\mathrm{k}}\right]$$

(9)

$$h_{\min }=3.63R_x{U}^{0.68}{G}^{0.49}{W}^{-0.073}\left[1-e^{-0.68k}\right]$$

(10)

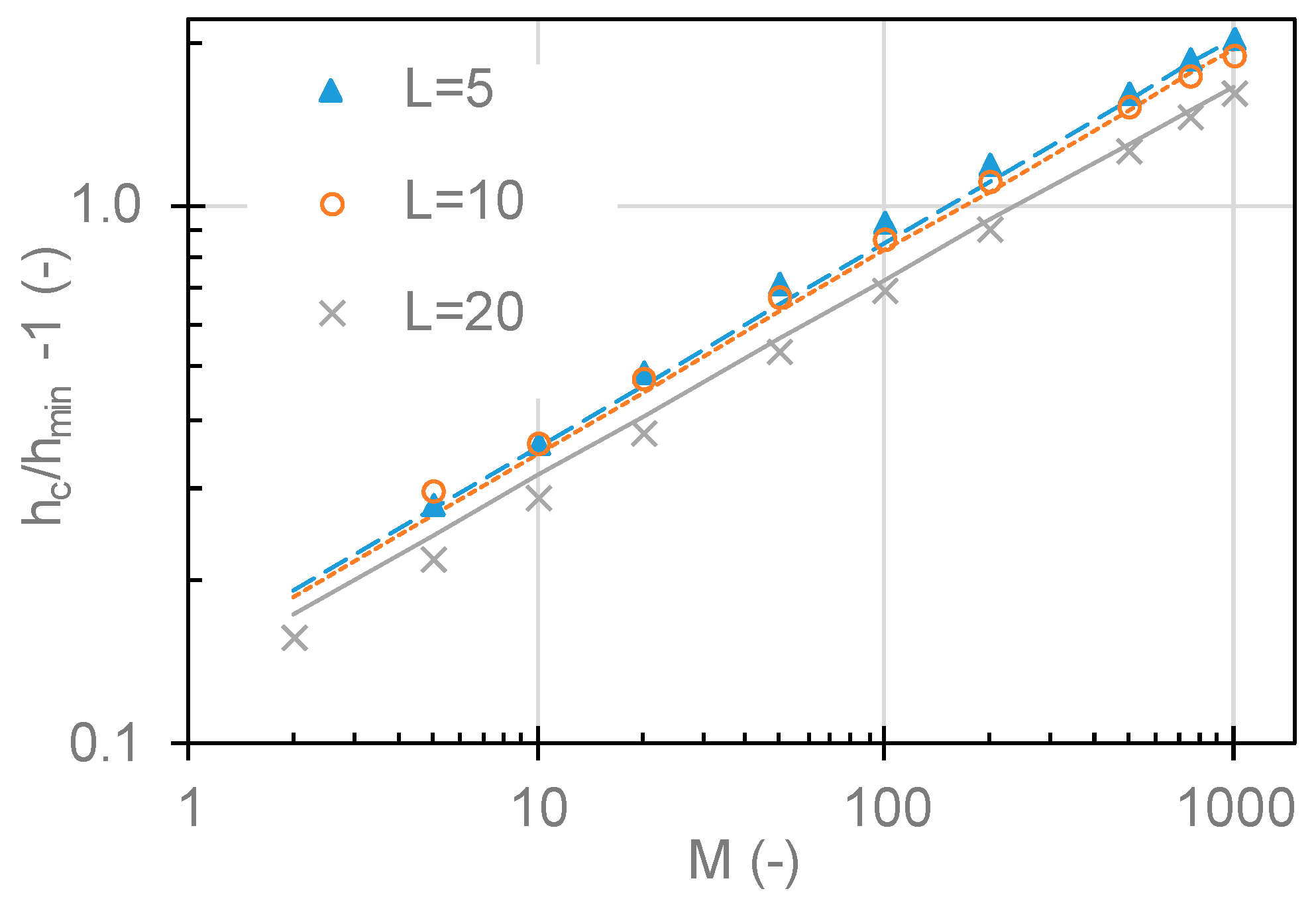
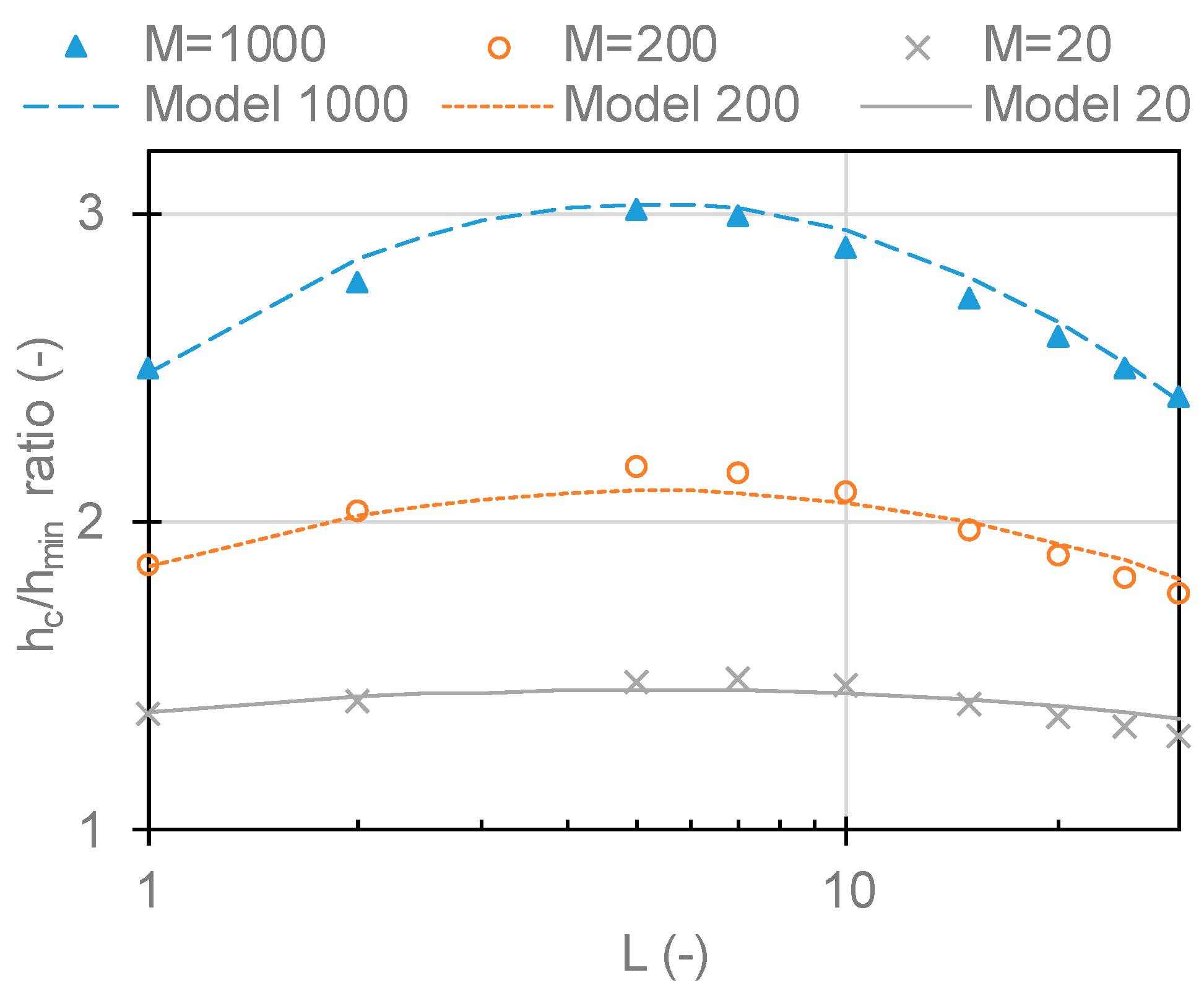
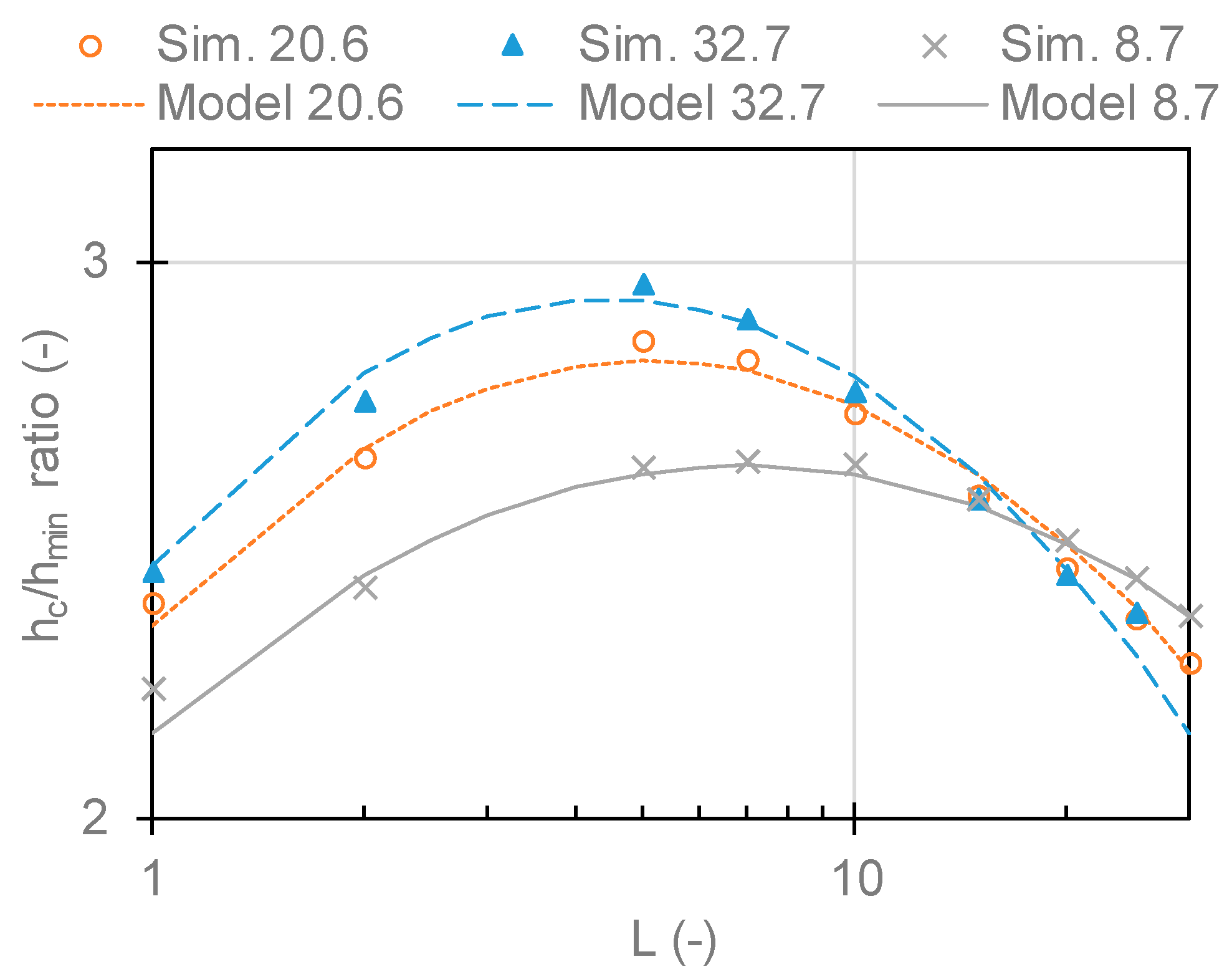
Figure 2 shows a dependency of film thickness ratio h_c/h_min−1 on M parameter for three fixed L values. Figure 3 presents a dependency of film thickness ratio h_c/h_min on L parameter for three fixed M values. Both plots are for α_film = 20.6 GPa⁻¹. The dependency of the film thickness ratio monotonically rises on M while there is a local maximum in dependency on parameter L. This local maximum is around L = 5 and seems to slightly change with increasing M parameter. The ratio approaches 1 for low L and M values.

Since axes in Figure 2 are in log scale, the points follow power trend with parameter M. When x axis in Figure 3 is transformed to log scale, the points follow close to quadratic trend. Therefore, the complete dataset was fitted to Equation (11), where a, b, c and d are fitting constants.

$$\raisebox{1ex}{$h_{\mathrm{c}}$}\!\left/ \!\raisebox{-1ex}{$h_{\min }$}\right.=1+a·M^{\mathrm{b}}-\sqrt{M}{\left[c·\ln \left(L\right)-d\right]}^2$$

(11)

The effect of different reduced radii of curvature, elastic properties or lubricant ambient viscosity on the ratio was checked by numerical simulations and no effect was found; therefore, the results are considered independent of chosen geometry and elasticity. On the other hand, it was found that film thickness ratio is sensitive to pressure–viscosity coefficient; simulations were done for three values (Table 3) in a range from 8.7 to 32.7 GPa⁻¹. It corresponds to the pressure–viscosity coefficient according definition in Equation (8) published by Bair [23]. It was shown that it is able precisely capture relation of viscosity on pressure necessary for film thickness formation in EHL contacts. 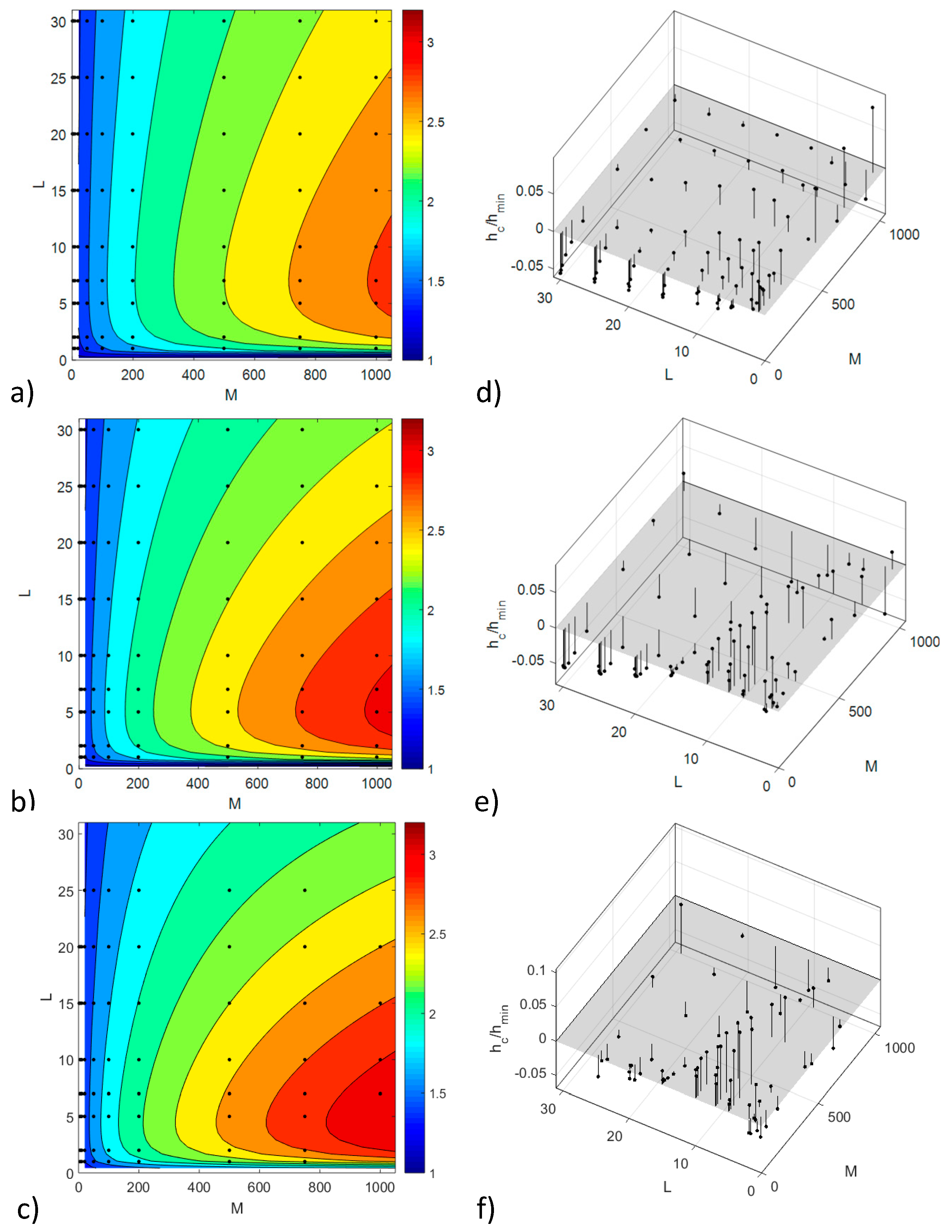According Table 3, the values of α_film are not far from α* coefficient. The analytical model fitted to the results is shown in Figure 4 in a form of contour plot on the left side and residuals from fitting in the right plots. Final form of analytical model of film thickness ratio which depends on M and L parameters and α_film pressure–viscosity coefficient is given by Equation (12). Quality parameters of the fits shown in Figure 4 are listed in

Table 5. Parameters of fitting goodness.

αfilm	8.7 GPa−1	20.6 GPa−1	32.7 GPa−1
Root mean square error (RMSE)	0.031	0.038	0.039
RMSE in %	1.7%	2.0%	2.1%

; root mean square of the error is 0.03–0.04 which represents about 2% of average film thickness ratio. Equation (12) was plotted as a model in Figure 2, Figure 3, Figure 4 and Figure 5.

$$\raisebox{1ex}{$h_{\mathrm{c}}$}\!\left/ \!\raisebox{-1ex}{$h_{\min }$}\right.=1+0.1·{{\alpha }_{\mathrm{film}}}^{0.128}·M^{0.38}-\sqrt{M}{\left[\frac{{{\alpha }_{\mathrm{film}}}^{0.2}·\ln \left(L\right)-3}{22.7}\right]}^2$$

(12)

where α_film is in GPa⁻¹. The equation is repeated together with list of assumptions and conditions for which it was obtained in Appendix B.

According Equation (12) and Figure 2, the pressure–viscosity coefficient modifies constant in power trend on M parameter, but the power slope remains the same. In terms of dependency on L parameter, the pressure–viscosity coefficient shifts the position of maximum peak, as it is shown in Figure 5.

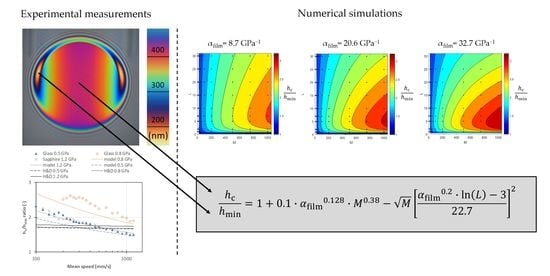
Next to the simulations, a film thickness was measured at three levels of Hertzian pressure. It was a contact of steel against glass for 26 and 112 N giving Hertzian pressure of 0.493 and 0.799 GPa, respectively, and a contact of steel with sapphire loaded by 63 N giving 1.186 GPa. Central film thickness was evaluated and corrected for refractive index change with pressure, as in [10], while minimum film thickness was left without correction since the place of minimum is expected to be in the area of low pressure. A range of speeds from 100 to 1200 mm/s was measured and h_c/h_min ratio was calculated.

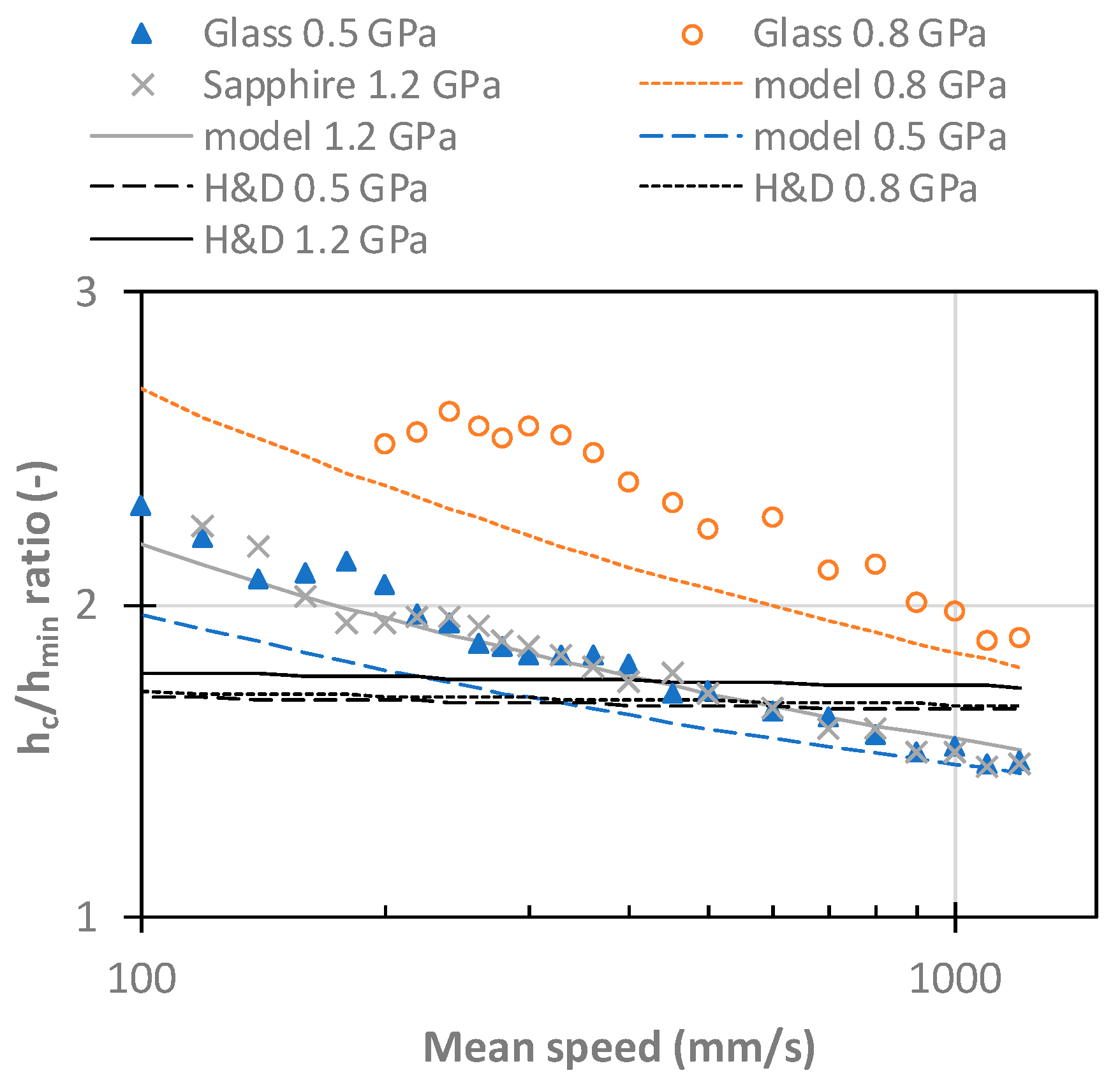
In Figure 6, there is a comparison of measured ratios with predictions given by present model (Equation (12)) and prediction according Hamrock–Dowson formulas (Equations (9) and (10)). The Hamrock–Dowson formulas gives almost constant h_c/h_min ratio which is close to measured value only for 0.5 and 1.2 GPa and small range of speed around 500 mm/s. Present model gives good prediction of trends in all cases. Quantitatively, there is very good agreement for 1.2 GPa and not as good agreement for 0.5 and 0.8 GPa. Average differences between measurement and predictions are listed in

Table 6. Average difference of measurement and h_c/h_min ratio estimation by Hamrock–Dowson (H&D) and present analytical formula.

	Case 1	Case 2	Case 3
Measurement pressure	0.5 GPa	0.8 GPa	1.2 GPa
H&D formulas (Equations (9) and (10))	12.9%	36.5%	9.7%
Present formula (Equation (12))	8.8%	10.6%	2.2%

. It shows that present formula predicts the ratio within 11%, while Hamrock–Dowson is off by up to 37%.

Ratios calculated from measured data having uncertainties can produce a large error when thin films are studied. Therefore, conditions with h_min film thickness above 60 nm and h_c film thickness above 140 nm were considered. Measurements were repeated three times for each pressure; ratios were evaluated independently and averaged. Average standard deviation of measured ratios is 0.028 which corresponds to 1.3%. Measurement has another error which comes from the fact that minimum film thickness is evaluated as a global minimum in a contact. Every ball has a certain roughness (3 nm RMS in present measurement); therefore, the evaluated h_min is practically always picked on a peak of roughness. As a result, measured minimum film thickness tends to be systematically evaluated as lower than the true value. Typical in-contact RMS value of roughness was 0.6 nm, therefore, distance of mid plane to highest peaks was about 1.8 nm which makes average impact on film thickness ratio 0.03, i.e., much less then observed difference.

As shown in Figure 3 and Figure 5, present model (Equation (12)) cannot fully capture the highest values of simulated ratios. The highest fit residuals are between L parameter 5 and 7 where experimental conditions of 0.5 and 0.8 GPa are localized (see Figure 1). Nevertheless, these local residuals of the fit are up to 0.08, thus they cannot fully explain differences in measurements.

In present study, Roelands model for pressure–viscosity relationship and Dowson–Higginson relation of density dependency on pressure were used. These models have limitations. Various lubricants can behave differently, especially under high pressure. Nevertheless, it is commonly expected that low pressure rheology is important for film forming capabilities. Furthermore, real lubricant compressibility influences central film thickness, which affects the film thickness ratio.

4. Conclusions

The ratio between central and minimum film thickness in a circular EHL contact varies between 1 and 3.16 for considered range of conditions. This trend cannot be captured by widely used prediction formulas employing (monotonous) power function, since dependency on L parameter has a local extreme at L = exp(3/α_film^0.2). Isothermal Newtonian numerical simulations were used to compute the film thickness ratio for wide range of M and L parameters and three pressure–viscosity coefficients. A new analytical formula for fitting of the ratio is presented. Final regression of numerical simulations has root mean square error of 0.036, i.e., 1.9%. A comparison with measurement showed good trend agreement and quantitatively smaller difference than Hamrock–Dowson formulas. This new formula together with published formula for central film thickness can be used for minimum thickness prediction.