Abstract
Hydrodynamic journal bearings are subjected to progressively rough loading conditions leading to an increased share of operation in mixed and boundary lubrication. This results in increased frictional losses, additional wear and a higher chance of failure, which calls for the understanding of wear processes and the necessity of a numerical assessment. We conducted wear investigations of journal bearings by making use of a close-to-component test setting, and the progress of wear could be linked to the introduced frictional energy and in combination with a comprehensive surface analysis tribological effects could be resolved in detail. Achieved wear coefficients were implemented in a novelly developed numerical framework, which allows for the dynamic numerical evaluation of operation in the fluid and mixed lubrication regime and simultaneously occurring wear processes. By comparing numerical and experimental results, we evaluated the numerical framework’s capability to conduct holistic simulations including aspects like dynamically changing operation conditions, fluid and mixed lubrication as well as wear.
1. Introduction
Hydrodynamic journal bearings are machine elements, which allow for a relative movement and the transmission of forces of two relatively moved parts and are used in numerous applications, e.g., automotive industry, shipping or energy production. Such bearings are lubricated and designed to be operated in the fluid lubrication regime in which the load is carried by the hydrodynamic pressure and the surfaces of bearing shell and shaft are completely separated. However, during a hydrodynamic journal bearing’s life time the separating fluid film can not always be maintained and hence this machine element suffers from operation in the boundary and mixed lubrication regime [1,2]. These regimes are characterized by the coexistence of hydrodynamic and asperity contact pressure where the latter is generally responsible for increased frictional losses, wear and a higher chance of failure. On the one hand, these circumstances demand a continuous further development of the tribological partners shaft and journal bearing material as well as the lubricant by experimental investigations [2,3,4,5,6,7,8,9]. On the other hand, the prediction of wear based on numerical investigations becomes increasingly important especially in the course of the design process and the evaluation of life expectancy [10,11].
Concerning the aspect of numerical wear evaluation in tribological systems, conducted literature study reveals the adaptive mesh approach as the most common choice with respect to the numerical method [12,13,14,15,16]. Based on a wear measure, which is in most cases the wear height, surface mesh nodes of the contacting surfaces are moved. This and tentative necessary re-meshing is performed by external scripts, which are used in addition to the simulation software. Several authors [12,13,14,15,16,17] use the wear model according to Archard and Hirst [18] to calculate the extent of wear. Furthermore energetic approaches are reported [19]. Studied literature reveals that predominantly unlubricated contacts were the object of investigations in this regard. The evaluation of wear under lubricated conditions and operation in mixed lubrication was for example investigated by Sander et al. [20]. The authors demonstrated the adoption of the journal bearing surface under edge loading during the running in process. A further approach of modelling wear in the mixed lubrication regime is reported by Reichert et al. [15]. In regard to mixed lubrication, Beheshti and Khonsari [21] focused on an elastohydrodynamic lubrication (EHL) line contact and presented an engineering approach for the prediction of wear under steady-state operation in the mixed lubrication regime by making use of the load-sharing concept and a modified Archard’s wear law. Besides steady-state operation, journal bearings are also subjected to varying operation conditions, e.g., instabilities and starting and stopping [22]. The consideration of the dynamic state of operation is an important aspect within the numerical evaluation of journal bearings. In this regard, Haneef et al. [23] presented a method to simulate wear of journal bearings in internal combustion engines by an integration of wear and vibration analysis of all three lubrication regimes. The numerical analysis was conducted on a 2D model of a journal bearing based on a MATLAB/SIMULINK environment.
In the current work, COMSOL Multiphysics® 5.2a (Comsol Multiphysics GmbH, Göttingen, Germany), which allows numerical investigations of wear processes under dynamically varying operation conditions, was chosen for the development of the numerical framework. One key factor within the numerical wear assessment is the derivation of suitable wear coefficients. For that purpose, a method that aims at allowing tests with high reference to application load cases while providing meaningful wear coefficients is presented. Close-to-component wear tests are the foundation of this approach and give deep insights into the tribological behaviour of the investigated system. Furthermore, they allow the deduction of utilizable wear coefficients.
The primary aim of this work represents the experimental assessment of wear of a representative journal bearing contact and a comprehensive evaluation of the underlying wear process in order to provide a sophisticated base for the subsequent numerical assessment. Therefore, wear investigations on conventional industrial journal bearings are presented under two different load cases.
The secondary aim concerns the development of a numerical framework for the assessment of the tribological behaviour in the fluid, boundary and mixed lubrication regime and wear. The evaluation of the numerical framework’s capability to simulate the dynamic change of lubrication state in connection with wear and its informative value are of interest and will be discussed within the course of the present work.
2. Materials and Methods
Experimental testing involved wear investigations of journal bearings under constant and start–stop loading conditions. The tests were conducted by the use of a Bearing Segment Test Adapter (BSTA) in combination with a rotary tribometer TE92 from Phoenix Tribology (Basingstoke, UK). This setting has been a reliable testing facility throughout recent years allowing detailed investigations of friction and wear processes of a simplified journal bearing contact while granting a close link to industrial applications [5,24,25]. The investigated journal bearing specimens depict a multilayer structure of which the wear process of the top sliding layer, which consists of a PbSn based material is of interest. Preceding methodology tests were conducted in order to evaluate suitable test parameters, which are described subsequently.
2.1. Test Setting
The setting mainly comprises of a motor, the driving shaft (1) and the BSTA (see Figure 1). The motor is mounted on top of the tribometer’s frame and provides the required power. Rotational speed and torque are introduced into the tribological system via the driving shaft. The BSTA is pivot mounted on a crosshead, which is guided vertically via two pillars and comprises of a loading unit (2) and an oil bath (3). The latter contains the lubricant and ensures a fully oil-immersed contact between shaft and journal bearing specimens. Via heating elements, which are placed below the oil bath, the system can be heated. The loading unit pushes the two 120 journal bearing specimens (4) against the rotating shaft specimen (5), which is directly mounted onto the driving shaft. The thereby resulting frictional torque can be measured by a load unit, which prevents the rotational movement of the BSTA. Under consideration of the adapter’s geometry and the applied normal force , respectively, the normal load the coefficient of friction (COF) can be calculated. The measurement of the system’s temperature T1 indicates the overall thermal condition of the system. Additionally, the contact close temperature T2 is measured at the back of one of the journal bearing specimens and gives deeper insights into the thermal conditions of the contact. For a detailed resolution of the state of operation, a contact resistance measurement is installed. Provided the specimens are conductive, the measured voltage, the Contact Potential (CP), yields if the system operates in the boundary, mixed or fluid lubrication regime. While a complete separation of both surfaces represents a resistance, which results in a measurable voltage of maximum 50 mV, a reduced fluid film thickness or asperity contact represents a reduced resistance, which leads to a drop of the CP. Additionally to the standard acquisition rate of 1 Hz, the COF, and CP can be acquired in a high speed data acquisition mode (HSDA) with a sampling frequency of 1 kHz allowing the detailed resolution of quickly occurring tribological processes. The bearing shell exhibits a diameter of 48.6 mm. A relative bearing clearance of 1.3‰ was chosen.
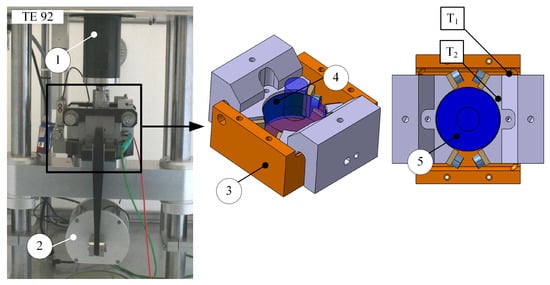
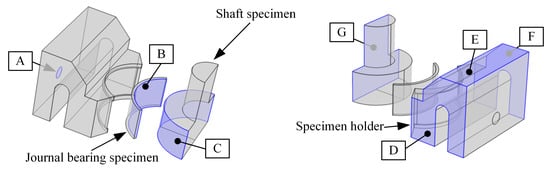
Figure 1.
(Left): test setting including a rotary tribometer TE92 in combination with a Bearing Segment Test Adapter (BSTA). (Right): CAD models of the test cell. (1) driving shaft, (2) loading unit, (3) oil bath, (4) journal bearing specimen, (5) shaft specimen.
2.2. Test Strategies
The subsequently presented test strategies aim at visualizing the wear behaviour of the tribological contact under investigation. For this task, two test strategies were developed based on two principle possible load cases deduced from industrial applications. This is, on the one hand, the start–stop and, on the other hand, the constant test strategy. The initial conditions during the running in phase A1 of the start–stop test strategy, which lasts for 900 s, are set to a sliding speed of 0.38 m/s, see Figure 2a. Tests are started at room temperature and throughout this initial phase external heating remains disabled. The applied load, which is kept constant throughout the entire test at 1.67 MPa, sets the journal bearing system into a regime of mild mixed lubrication to allow for an alignment of the contacting surfaces in order to reach an energy optimized state and to avoid early unpredicted seizure effects due to local intense bondings. Within the subsequent heating phase B1, the standing still system is heated to the desired test temperature of 120 C within 900 s. The last phase C1 of the test program includes the conductance of start–stop cycles. Within a time range of 5 s, the system is accelerated from 0 m/s to the maximum sliding speed of 1.26 m/s. The deceleration phase lasts for 3 s in order to reduce the test duration. To allow for an efficient conductance of tests and subsequent evaluation, the strategy was structured with the help of a loop, which is run through an arbitrary number of cycles to create varying time spans and provide varying intensities for the elucidation of the wear behaviour.
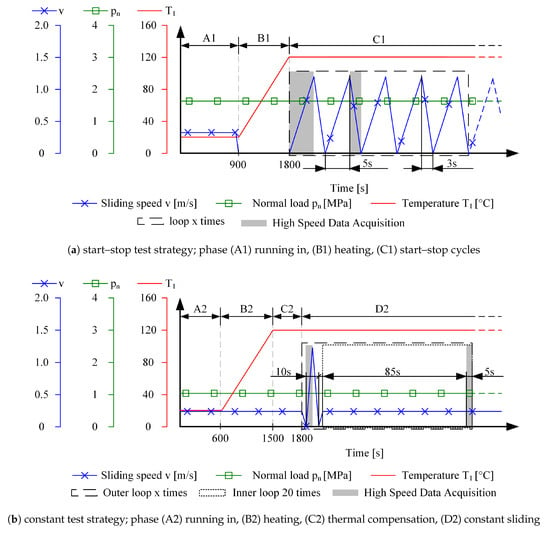
Figure 2.
Test programs for start–stop (a) and constant (b) testing.
Within one loop cycle, five start–stop cycles are conducted of which the first rising and the second dropping speed ramp is recorded in HSDA in addition to the standard acquisition mode due to the short ramp duration. The data acquired within these two cycles are considered to be representative for the remaining number of cycles within this loop run and multiplied accordingly in order to evaluate the total resulting frictional energy within this loop cycle.
The constant test program depicts a running in phase A2, which lasts for 600 s (see Figure 2b). The load is constantly held at 1.06 MPa. The sliding speed is set to 0.23 m/s to provoke constant operation in the mixed lubrication regime. The heating phase B2 remains the same as described for the start–stop test strategy. To balance thermal inertia effects, a compensation phase C2 of 300 s duration is attached to the heating phase. Thereafter, the constant test strategy involves two cascaded loops, which are introduced in order to allow for an effective conductance of tests and subsequent evaluation of measured data. The outer loop is conducted in a variable amount and comprises of a start–stop cycle prior to the inner loop, which is conducted 20 times. The preceding start–stop cycle of a duration of 10 s was introduced in order to evaluate the current state of operation by allowing the creation of a Stribeck curve based on the introduced start–stop cycle. The rising speed ramp of the start–stop cycle is recorded in HSDA. The resulting frictional energy is considered identical for the evaluated rising ramp and the subsequent falling speed ramp. The inner loop represents the actual load case. Comparable to the previously described start–stop strategy, a reduced time span of 5 s of the constant phase is acquired in HSDA mode and considered representative for the preceding period of 85 s.
2.3. Test Evaluation
The performance of the system under investigation with respect to friction and wear was evaluated based on the input variables T1, and v as well as the measurement variables COF, T2, CP and the worn volume . The journal bearing specimens were weighted before and after testing. Under consideration of the top layer’s density the wear volume was calculated. The weighing was conducted with a laboratory scale Sartorius CP225D-OCE (Sartorius Corporation, New York, NY, USA), which exhibits a minimum resolution of 0.01 mg. The subsequently explained used wear model represents an energetic approach, which demands the calculation of the arisen frictional energy . Since wear induced by solid contact is provoked and of interest within this study, operation conditions in the absence of asperity contact need to be excluded from the chronological energetic summation. As explained in Section 2.1 the CP serves as an indicator of the state of lubrication. Hence, this measurement variable is used to ensure that solely operation in the presence of asperity contact, i.e., operation with a reduced CP, contributes to the summation of the wear relevant (see Equation (1)). Herein, the CP is used as an weighting factor, which yields a total energetic increase of the resulting under 100% asperity contact and 0 contribution when the system is operated in the fluid lubrication regime, indicated by a measurement of the maximum contact potential . In between these two extremes, a linear behaviour is assumed:
2.4. Test Materials
The used lubricant was Shell Rimula 10 W (Shell Deutschland Oil GmbH, Hamburg, Germany). The tested shaft material was a 34CrNiMo6 steel, which represents a widely used characteristic crank shaft steel. The multilayer journal bearing structure consisted of a steel back, a bronze lining layer including Pb phases and a Pb-Sn based sliding material on top (see Figure 3, respectively, and Table 1 for the corresponding energy dispersive X-ray spectroscopy (EDX) analysis). The lining layer is composed of a copper matrix and lead phases, which is separated from the top sliding material by a Ni-layer in order to prevent diffusion processes. The light microscopic depiction on the left-hand side of Figure 3 exhibits dark and light gray coloured areas of the sliding material. The dark gray areas are oxidized, which is indicated by the high portion of O of the EDX measurement positions C and D. The sliding material is composed of a lead matrix (position F) with distributed Sn phases (position G) of a large extent and SnCu hard phases (position E and H) of smaller size. The initial layer thickness is 17 µm.

Figure 3.
(Left): light microscopic depiction of the investigated material composed of a Cu-Pb lining material, a Ni-layer in between and the Pb-Sn top sliding layer; (Right): material contrast of the marked section including EDX measurement positions.

Table 1.
EDX analysis corresponding to Figure 3 (EDX values obtained at 10 kV and given in at %).
2.5. Simulation
For the numerical wear evaluation, the commercial software COMSOL Multiphysics® 5.2a which allows the simulation of multi-physical problems based on the finite element method (FEM) was used. The contact of interest represents an EHL problem with focus on operation in the mixed lubrication regime accompanied by wear. The following section includes a description of the underlying theory and used equations. Furthermore, the numerical model and procedure are described.
2.5.1. Governing Equations
The mathematical framework concerning the description of the hydrodynamic processes in a thin lubrication gap h as it is present in journal bearings and the test setting under investigation was laid by Reynolds [26]. Reynolds’ formulation holds for a fluid film thickness, which exceeds the combined roughness of both surfaces significantly. However, when the ratio comes within the range of 3, the surface roughness increasingly alters the fluid flow, which consequently violates a basic assumptions within Reynolds’ mathematical description, viz., the assumption of smooth surfaces. Patir and Cheng [27,28] resolved this problem by introducing the averaged Reynolds equation, which allows the consideration of the fluid flow altering effects of rough surfaces by the use of pressure and shear flow factors and (see Equation (2)). The valid implementation of this equation into COMSOL was subject of the author’s former work and is described in detail in [29]. Furthermore, Reference [29] includes details concerning the subsequently described theory and the description of the detailed approach concerning surface evaluation, calculation of flow factors and contact models, which were also used for the current work:
Patir and Cheng provided empirical equations for the pressure and shear flow factors, which depend on h, and the orientation parameter of the combined surface roughness [30]. is the correlation length at which a profile’s autocorrelation function is reduced to 0.5. The respective flow factors were calculated according to the theory by Patir and Cheng, implemented into the simulation software and used for the numerical investigations.
Generally, the rheological behaviour of a lubricant is dependent on temperature and pressure [31]. In most cases, both the density and dynamic viscosity decrease with with increasing temperature and increase with increasing pressure [32,33]. However, for the current study, the lubricant’s behaviour is chosen independent of pressure since the contact under investigation experiences low loads, which lead to hydrodynamic pressures whose scale is sufficiently small to allow the neglect of the pressure effect. On the other hand, the thermal effect is significant why the temperature dependency of and is considered. For that purpose, the global oil temperature is derived from the contact close temperature T2, which is measured at the bearing back close to the high-load area of the bearing. This approach does not take into account the local temperatures of the lubricant but includes the thermal effects by considering the representative global lubricant temperature as was also shown by e.g., Allmaier et al. [34].
Besides the dependency on temperature and pressure, lubricants are also dependent on the shear-rate [33,35,36,37]. This especially holds for conventional multi-grade oils. However, for a single-grade oil, as used within this study, the rheological behaviour can be considered as Newtonian for the predominant operating conditions [38,39]. Therefore, and as a simplification measure, the shear-rate dependency of the lubricant was neglected within the current study. In the diverging part of the lubrication gap, the resulting cavitation is considered by applying the half-Sommerfeld condition [40]. The asperity contact pressure was calculated based on the theory according to Greenwood and Williamson [41], who investigated the contact between a rough and a nominally smooth surface. This idea can be also applied for two rough surfaces, as was shown by McCool [42]. The asperity contact pressure as a function of the normalized fluid film thickness is given by Equation (3). The parameters and were calculated by using statistical methods [43]:
where
The fluid film thickness h depends on the initial film thickness h0, the deformation of the bearing and the shaft and the wear height :
Wear as a consequence of asperity contact interactions in the mixed lubrication regime is calculated according to Archard [18], which represents a widely used approach for the estimation of the wear volume for both mild and severe forms of wear. The wear law relates the wear volume and the sliding distance s, the applied normal load , the flow pressure of the softer material , and the constant K, which describes the probability of the production of a wear particle:
Equation (5) can be transformed into Equation (6) by division with the nominal area A and a subsequent derivative according to the time. The material related parameters K and are combined to C, which is referred to as wear intensity. This relation goes back to Preston [44] who prior to Archard suggested the correlation of the time dependent change of the wear height with the asperity contact pressure , the sliding velocity v and the empirical wear intensity C:
The wear intensity C represents the relation of worn volume to the arisen frictional energy due to solid asperity contact and hence represents the link between experimental results and the developed numerical framework. The structural behaviour under the assumption of a linear elastic material behaviour is considered by including the equation of motion, the strain–displacement equation and the constitutive equation (see Equations (7)–(9) in the numerical analysis):
2.5.2. Model Description
The governing equations of the presented physical relations concerning elastic structural and hydrodynamic behaviour are provided by COMSOL by interfaces, which are applied on the desired boundaries and bodies and allow for the definition of boundary and initial conditions. Furthermore, COMSOL provides an interface for an implementation of ordinary differential equations, which enables the use of the wear law according to Equation (6) and a fully coupled simulation of hydrodynamic pressure formation, change of lubrication gap geometry resulting from elastic deformation and wear and the occurrence of asperity contact pressure in dependency of the lubrication gap height. Within the simulation, the core parts of the BSTA under utilization of symmetry are considered, as depicted in Figure 4. The external force is applied on boundary A. The journal bearing surface, boundary B, is the surface where the averaged Reynolds equation, the equation for the asperity contact pressure as well as the wear equation are solved. The resultant hydrodynamic and asperity contact pressure are applied on boundary B as well as on boundary C in order to satisfy the equilibrium condition. In return, the resulting deformation is considered for the calculation of the fluid film gap height h. The exchange of the respective quantities between different domains is conducted by coupling operators, which map an expression respectively a variable, defined on an arbitrary source, to any destination geometry. Necessary interpolation due to variation of dimension or mesh is automatically conducted by COMSOL. The applied boundary conditions on boundary D, E and F represent the guiding function of the surrounding structure, which is realized by the application of roller boundary conditions, which restrict deformation in the boundary’s normal direction. Boundary G indicates the plane of symmetry.
2.5.3. Mesh
The mesh, which is the same for the calculation of all physics, is created with the aid of COMSOL. A tetrahedral mesh of sufficient size is chosen for the model including the shaft specimen, the journal bearing specimen and the specimen holder. For the global mesh, a maximum element size of 6.7 mm and a minimum element size of 1.21 mm is chosen. The maximum element growth rate is set to 1.5. A curvature factor of 0.6 is set and a resolution factor of 0.5 for narrow regions is chosen. The density of the bearing surface, surface B, is additionally increased in order to resolve the quantities on this surface more accurately. Thirty-five elements are chosen in a circumferential direction of the bearing’s surface and 15 elements along the width of the bearing. The mesh of the specimen holder and journal bearing are depicted in Figure 5. In total, 110,807 degrees of freedom (DOFs) arise within this model, which split into 102,306 for the mechanical model, 2201 for the description of the hydrodynamic pressure and 6300 for the wear height.
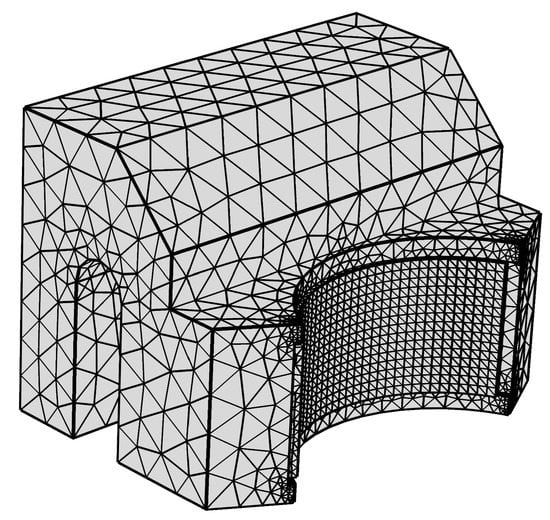
Figure 5.
Meshed specimen holder and journal bearing specimen.
2.5.4. Numerical Procedure
The simulation task at hand consists of the fluid flow in a thin film, governed by the averaged Reynolds equation, structural mechanics and the evaluation of wear. The dependent variables are the hydrodynamic pressure phyd, the displacement field u and the wear height . The respective equations are assembled in one system matrix, which is solved in a fully coupled approach by linearisation with the Newton–Raphson method and a MUMPS (Multifrontal Massevily Parallel sparse direct Solver). The solution of the unknowns is approximated by second order shape functions. A solution is assumed converged when the relative tolerance between two consecutive Newton iterations is smaller than a maximum value of . The absolute tolerance is set to . The flow chart depicted in Figure 6 visualizes the solution procedure comprising of two studies. The purpose of the first study is to establish stable numerical and operational conditions. The system is set into a stationary state of operation in the fluid lubrication regime by assigning a sufficiently high sliding speed. This avoids the occurrence of asperity contact pressure and wear which leads to faster convergence. To further increase convergence, the BSTA is initially fully supported by a spring foundation with a spring constant and the load is applied incrementally by scaling the load with the parameter . By a stepwise increase of from 0 to 1, the system is incrementally loaded while the spring support is reduced with each step. In this manner, a stationary state of operation in the fluid lubrication regime can be established with a high degree of convergence in order to speed up simulation. The outcome of study 1 is then used as the initial solution of study 2. Within this study, the subsequent process is controlled chronologically and includes a reduction of speed to bring the system into the appropriate starting state. From this time on, the loading parameters follow the chronological run of the test programs described in Section 2.2. The choice of a time step’s length is left to COMSOL. Numerical results are saved every second during the interspersed start–stop cycles and every 100 s during constant sliding conditions.
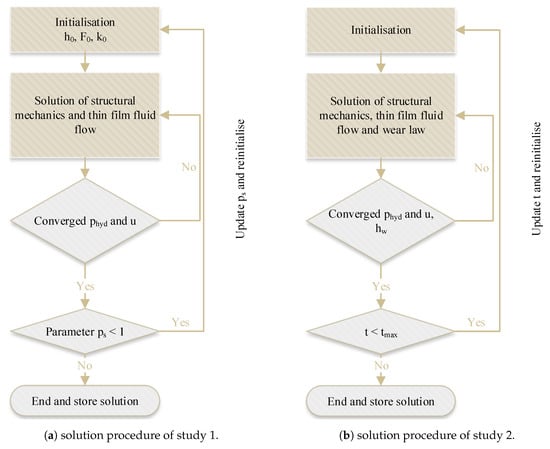
Figure 6.
Solution procedure.
3. Results and Discussion
The following section includes the presentation and discussion of the tribological test and wear results in correlation with surface analysis. Afterwards, the numerical results are presented and evaluated by comparison with experimental findings in regard to their validity and significance.
3.1. Tribological Results
In total, 54 tests were conducted of which 38 were used for further evaluation. The rest was neglected due to insufficient contact patterns. The tests were stopped after different time spans in order to evaluate the behaviour of the specimens’ state of wear. The following section deals with the presentation and interpretation of two representative tests. In addition, the reproducibility of the used test methodology is of interest.
3.1.1. Start–Stop
Figure 7 depicts a representative start–stop test run of maximum test duration. The chronological depiction of the results compresses the measured COF of the individual start–stop cycles, which result in a behaviour according to Stribeck’s finding when resolved sufficiently, to single peaks. Due to the fast changing tribological processes within each cycle, the standard acquisition rate is insufficient to resolve the tribological processes in detail. Hence, the presented data in Figure 7 represent rather a mean value of the coefficient of friction during each start–stop cycle. For a detailed resolution of the tribological processes within a start–stop cycle, data of the HSDA mode are used, as depicted in Figure 8. However, the chronological presentation of the tribological test results provides a good overview of the overall behaviour of the investigated system and allows a convenient presentation as conducted below.
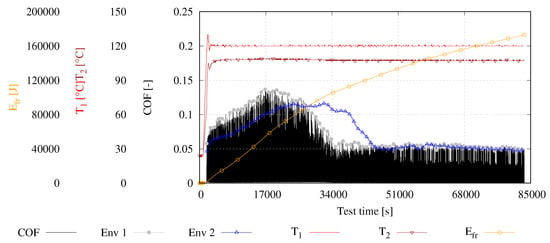
Figure 7.
Representative graph of a start–stop test with maximum test duration. In addition, the envelopes (Env. 1 and Env. 2) of the friction values of the presented and its repetition test are presented in order to evaluate the test settings’ reproducibility.
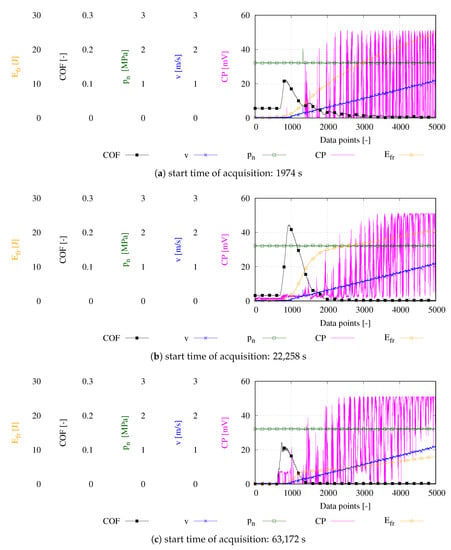
Figure 8.
Selected high speed data results of the presented representative start–stop test in Figure 7.
The initial running in phase is negligible concerning the overall wear development due to its short duration and insignificant contribution to the energetic effort. The factual progress of wear starts with the beginning of the start–stop cycles after the heating phase. At an elevated temperature, the coefficient of friction yields an initial value of 0.06. With increasing number of cycles, the COF steadily increases until 17,000 s. From this point on, the COF decreases towards its minimum at 34,000 s. Within the following test phase, the system yields steady low friction. The change in the frictional behaviour can be correlated to the processes within the sliding material as well as wear processes, which will be described in Section 3.3 in combination with the presentation of the surface analysis. Throughout the entire test period, the system operates under stable thermal conditions indicated by the steady runs of temperatures T1 and T2. In accordance with the frictional behaviour, the resulting friction energy behaves. While the gain in energy depicts a steep inclination for the initial cycles, the amount of added energy decreases with continuation of the test, which finally results in a change from a progressive run to a digressive run during the final test phase.
For the purpose of reproducibility evaluation, selected tests were repeated. The individual peaks of the COF represent an unfeasible evaluation parameter. Hence, the envelope (Env.) of the entire number of cycles was calculated (see Env. 1). Accordingly, the envelope of a repeated test is also depicted (see Env. 2). The thermal conditions were identical and the run of behaved in accordance with the resulting frictional losses. Both measurement parameters were excluded from the depiction in order to increase clarity. Env. 2 shows lower frictional losses at the beginning of the test but an enlarged area of elevated frictional losses until 50,000 s, whereas Env. 1 already depicts decreased frictional losses at 34,000 s. From 50,000 s on, both runs coincide. The aim of the conducted investigations is the evaluation of wear processes by investigating the correlation between and . The friction energy of the presented test amounts to 173,150 J and a wear volume of 9.97 mm3, whereas the repetition test results in 173,955 J and 9.58 mm3. The deviations of both measurement parameters appear acceptable. In combination with the previously described phenomenological reproducibility, which was observed in a comparable manner during all conducted tests, a satisfying reproducibility can be stated.
Figure 7 depicts three start–stop ramps in HSDA of the representative previously described test in order to depict the ongoing tribological processes in deeper detail. The acquisition was started at 1974 s, 22,258 s and 63,172 s. Figure 8a depicts the tribological behaviour during start cycles acquired during the initial start–stop phase of the test in HSDA. Initially, the COF exhibits a constant value resulting from the pre loading torque of the standing still system. Prior to the actual rotation, the motor incrementally provides increasing torque, which ultimately forces the system into motion. Consequently, the frictional torque and COF rise. With the onset of motion, a maximum boundary coefficient of friction COF0 of 0.12 is measured. With increasing sliding speed v, friction drops according to a conventional Stribeck curve since the hydrodynamic pressure increasingly contributes to the load carrying capacity and reduces asperity interactions. However, the load is predominantly carried by solid contact until the initial significant rise of the CP indicates the starting separation of both surfaces after 1500 acquired data points. One can observe oscillations of the COF which decrease steadily with increasing sliding speed. Hence, the vibrations result from the contact situation, which occur at a specific rotation angle. However, with increasing speed, the share of CP around its maximum increases, which suggests an increasing separation of both surfaces. However, the surfaces can not be separated totally at this early stage of test even at the maximum test speed. The run of the friction energy sets on simultaneously to the start of the shaft rotation. With increasing sliding speed, the energy depicts a digressive run due to the reducing intensity of solid contact, which is indicated by the increasing CP. In accordance with the results presented in Figure 7, the measured friction losses during the starting ramp at a test time of 22,258 s depicted in Figure 8b show an elevated level in the boundary and mixed lubrication regime until 2000 acquired data points. The operation in mixed lubrication during the preceding start–stop cycles lead to optimized aligned surfaces, which reduces the oscillations significantly and allows for a total lift off of the two surfaces indicated by the high level of CP and the low COF in the second half of the acquired data. During this span of acquisition, the CP does not drop but shows predominantly values at its possible maximum indicating operation in the fluid lubrication regime. The frictional energy depicts an intense increase during operation in the boundary and mixed lubrication regime. From the transition point at approximately 2000 data points on the run, a strikingly lower inclination is depicted since both surfaces are mostly completely separated and only local contact events result in relevant contact states which increase the frictional energy due to solid contact. The last start–stop cycle depicts a maximum boundary COF of 0.1 which again represents a decreased value (see Figure 8c). The wear that occured pushed the transition point towards lower sliding speeds, resulting in an early transition into operation in the fluid lubrication regime. Hence, the frictional losses correlated to asperity contact represent the lowest contribution of the presented data.
3.1.2. Constant
Figure 9 depicts a representative run of a conducted constant test. Generally, the constant tests ran for a significantly longer period of time to achieve the same extent of wear. The periods of constant operation are interrupted by the interspersed start–stop cycles. After the running in phase, the introduced sliding motion results in a COF below 0.02. The frictional losses reduce subsequently followed by a rise of the COF until its overall maximum value of 0.04. This principle behaviour of an initially rising COF with a subsequent reduction of friction followed by a stabilized run in operation with low frictional losses coincides with the previous start–stop test results. During the time of increasing frictional losses around 30,000 s, the contact close temperature T2 rises, which indicates the increased heat emergence resulting from intense friction processes. Thereafter, the system recovers and the COF as well as T2 decrease which leads to the establishment of stable thermal conditions. The constant operation in mixed lubrication forces an ongoing alignment of the contacting surfaces resulting in a steady decrease of the COF until the duration of 150,000 s at which a sudden rise of the COF occurs. Simultaneously, T2 rises as well while the overall thermal condition indicated by T1 remains unaltered. Since the input parameters as well as the remaining measurement parameters do not show a significant change in their behaviour, the reason for the change in friction can be explained by a change in the contact situation due to the ongoing wear processes. A change in the contact situation in this regard may be attributed to a formation of new contact zones on the one hand. Parts which were in contact prior to this stepwise increase of friction became worn out and surface regions which were not in contact before coming into contact due to the change in geometry. These regions are unworn or not run in yet and hence depict a higher COF when they come into contact. Since this sudden rise occurs at an advanced period of time, a possibility could also be a newly established contact between shaft and a significant extent of the laid bare Ni-layer, which exhibits significantly different tribological properties in comparison to the overlay. The subsequent presentation of high speed data sheds more light on this. From this sudden increase on, the system depicts a comparable behaviour to the preceding period of time. With increasing test duration, the COF decreases steadily indicating the steady alignment of the newly contacting surfaces.
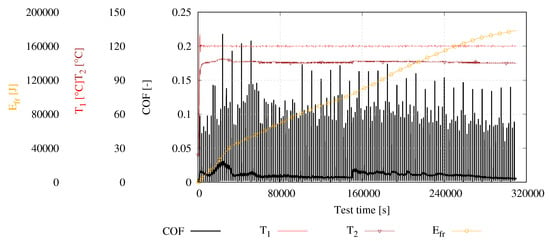
Figure 9.
Representative graph of a constant test with maximum test duration.
Figure 10a depicts the acquired high speed data during a time span of high frictional losses at 30,338 s. Comparable to the presented high speed data of the start–stop test program, one can observe oscillations resulting from changing local contact conditions dependent on the angular position of the shaft specimen. The system operates in stable conditions and the rotational variations remain constant. The CP yields predominantly values below its maximum leading to a steady increase of . Per one rotation, the COF depicts a steady increase until the the first local maximum is reached. Thereafter, the advancing rotation establishes contact conditions, which lead to a reduced COF. Afterwards, the frictional losses rise again towards its overall maximum before the initial starting position is reached again.
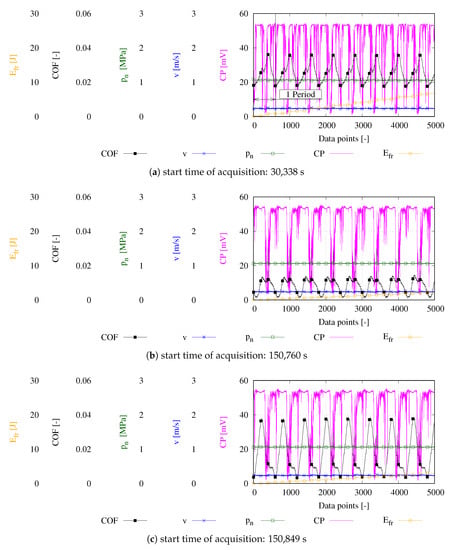
Figure 10.
Selected high speed data results of the presented representative constant test in Figure 9.
Figure 10b depicts the acquired high speed data starting at 150,760 s, which represents the time of acquisition right before the rapid increase of COF depicted in Figure 9. The frictional losses have decreased due to a constant alignment of surfaces. Nevertheless, operation with a considerable share of asperity contact occur indicated by the drop of the CP, which leads to a steady increase of the frictional energy. Since the frictional losses are reduced due to the aligned surfaces, the resulting is in general reduced in comparison to the acquired high speed data presented in Figure 10c. Concerning the previously mentioned forming of the two peaks per rotation, one can observe that especially the second peak is now reduced while the first remained rather unaffected from operation. Since the frictional losses correlate with the actual position of the shaft, this behaviour suggests the local intense wear of material at the position where the second friction peak occurs while the position where the first peak occurs experienced less alignment. The presented high speed data in Figure 10c depict the data directly acquired after the stepwise increase of the COF and visualize the increased friction losses. Presented data confirm the earlier stated assumption that local conditions are responsible for the change in friction. Of the two characteristic friction peaks, the first is more pronounced while the second vanished. Hence, the position which experienced reduced wear so far is in contact and the contact with the predominantly unworn or less worn surface results in increased frictional losses. Accordingly, the behaves and yields an increased inclination.
3.2. Wear Results
Figure 11 depicts the resulting wear volume dependent on the evaluated frictional energy. Both test strategies fall within a common scatter, which speaks for the universal applicability of the CP based evaluation method. This result appears coherent to the authors since, for a given wear volume, the expended energy must remain the same independent of the type of loading as long as the wear mechanism remains the same. This is taken care of due to the almost identical operation conditions apart from the sliding speed. The wear behaviour of the investigated tribological system can be split into two regimes. Regime 1 represents wear of the top sliding material whereupon regime 2 represents wear of combined mixed lubrication contact of the top sliding material and the subjacent lining material or Ni-layer. Regime 1 exhibits a mean wear intensity C of m3/J. In regime 2 not only the top sliding material but also the subjacent lining material contribute to the wear behaviour. Since the Cu-matrix of the lining material exhibits a higher hardness than the sliding layer, an increased energetic input is necessary to provoke the same amount of wear. This results in the reduced wear intensity of m3/J.
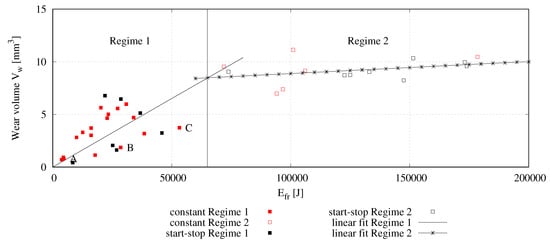
Figure 11.
Wear volume in dependency of . While in regime 1 the top sliding layer wears out, the combined contact of sliding layer and subjacent bronze matrix result in a reduced wear intensity. Tests A–C were utilized for the evaluation of the contact behaviour. Experimental data of test C is utilized for a comparison with numerical results.
3.3. Surface Analysis
An impression of the overall wear process of the top sliding material is given in Figure 12. The asperity peaks of the initially rough surface (outermost parts in Figure 12a) level out due to solid contact with the shaft specimen. This results in a polished shiny smooth surface as depicted in Figure 12a. With advancing wear, the top sliding layer runs through a material transformation, which results in the occurrence of dark zones within the contact pattern. A respective specimen of elevated wear within regime 1 is depicted in Figure 12b. In the last stage of the investigated wear range, the top sliding layer has been completely worn in parts which leads to the emergence of the subjacent lining material (see Figure 12c).

Figure 12.
Wear evolution: (a) polished intact top layer; (b) material transformation (dark areas) due to intense wear; (c) the completely worn off top sliding layer exposes the subjacent lining material.
Metallographic sections were prepared of representative test specimens and analysed by using a light microscope Olympus SZX12 (Olympus Austria GmbH, Vienna, Austria). In addition, a Zeiss MA15 scanning electron microscope (SEM) (Carl Zeiss NTS GmbH, Oberkochen, Germany), aided by energy dispersive X-ray spectroscopy (EDX) allows for detailed surface analysis. The specimens were cleaned with Isopropanol in advance. The acceleration voltage for the SEM analysis was chosen as a constant 10 kV. Figure 13a depicts the light microscopic images of the chronological wear progress. The corresponding topography and material contrast images are depicted in Figure 13b,c, respectively. The EDX analysis of the marked positions in Figure 13c are presented in Table 2 given in atomic percent (at %). Under tribological loading, the initial state transforms into state 1. The large Sn-phases, see position I in the material contrast depiction, are decomposed and form in combination with Cu of the top sliding layer’s matrix hard phases which gather at the surface and protect the softer subjacent sliding material. The hard phases appear light in the light microscopy as presented in the overall depiction of the contact pattern in Figure 12a, which shows a smoothed shiny surface in the area where solid contact occurred. With enduring tribological loading, the protecting hard phases wears off leaving the subjacent matrix in contact (see state 2). The Pb-based matrix appears dark in the light microscopic image. This state of wear can also be observed in Figure 12b, which depicts a significant share of surface which is dark. This part of the surface does not provide SnCu hard phases to protect the subjacent matrix. In combination with the presented tribological results, the increasing COF during the initial test phase can hence be correlated to the described formation of protecting CuSn hard phases, which lead to increased frictional losses. When the protecting top hard phase layer wears off, the COF sinks again proportional to the share of residual Pb-based matrix, which contributes to the solid contact. During the onward process of wear, the topmost sliding layer does not change in material combination but gets constantly worn off. Additionally, areas which are completely worn off and show contact with the subjacent Cu-based lining material contribute to the process of wear. This results in low friction losses and a wear curve of decreased inclination.
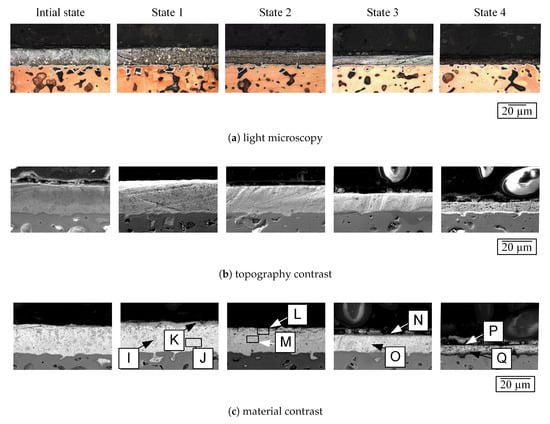
Figure 13.
Chronological run of the sliding layer’s process of wear.

Table 2.
EDX analysis corresponding to Figure 13 (EDX values obtained at 10 kV and given in at %).
In addition to the material related processes induced by solid contact wear and the effect on the tribological performance, the topographic pattern of the surface evolves under the influence of wear. The topographic state is an important aspect with regard to the statistical contact model which was used for the numerical analysis. Hence, the surfaces of specimens at initial state and at the end of three conducted tests were investigated to study the topographic evolution of the journal bearing’s surface under the impact of wear. The surface analysis was conducted with Alicona’s InfiniteFocus G4 (Alicona Imaging GmbH, Raaba, Austria). The microscope’s measurement principle is based on Focus-Variation. A section of 0.5 × 0.5 mm was scanned with a 100×-magnification. A horizontal and vertical resolution of 1.2 µm and 20 nm, respectively, was chosen. The provided measurement and evaluation software IF-MeasureSuite 5.1 × 64 (Alicona Imaging GmbH, Raaba, Austria) was utilized to remove the overall form of the recorded 3D data by applying a second order polynomial filter.
Figure 14 depicts the surface of a shaft specimen after a conducted test, the initial state of a journal bearing specimen and the journal bearing surface after three conducted tests with varying test time. The wear of the shaft specimens is assumed to be negligible in comparison to the change regarding the journal bearing specimens. For the evaluation of the effect of wear on the topography of the journal bearing specimens, tests A, B and C were chosen, which endured an input of of 4678 J, 28,581 J and 53,199 J. While the initial state exhibits a surface with a range of roughness heights between µm and 2.5 µm, solid contact leads to a decrease of the surface roughness of the tests A–C. Test A still depicts a recognizable roughness pattern which is in the range of the roughness of the shaft. The continuous contact with the shaft, however, leads to an intense smoothing of the surface roughness in the case of tests B and C, which do not allow a distinct differentiation of the state of surface between these two tests.
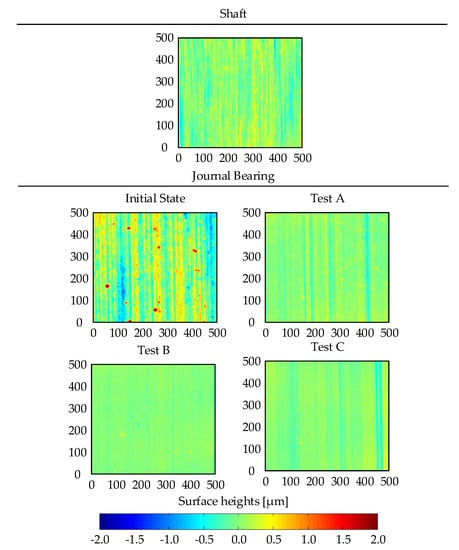
Figure 14.
Surface topography of a representative shaft specimen, a journal bearing specimen in the initial state and surface at an advances state of wear: Test A 4678 J, Test B 28,581 J, and Test C 53,199 J.
Based on the evaluated surfaces, the asperity contact pressure was calculated according to Equation (3) yielding the asperity contact pressure dependent on the normalized separation H (see Figure 15). As already indicated by the visual impression of the surfaces, the contact behaviour calculated based on the initial surface state indicates contact at the largest surface separations due to the high roughness of the journal bearing surface. The asperity interaction during testing and the evolution of wear reduced the roughness significantly and led to contact behaviour in a narrow range for the surfaces of the run tests. With a higher energy input, the function of the asperity contact pressure increasingly shifts to lower separations, which can be directly related to the smoothing of the surface roughness .
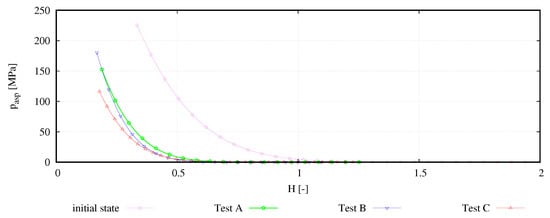
Figure 15.
Asperity contact pressure as a function of the normalized fluid film thickness H.
3.4. Numerical Evaluation
For the numerical evaluation, Test C including the chronological test sequence, the choice of wear intensity and contact model was chosen which represents the conducted test with maximum of regime 1. Test C was a constant test, which consisted of 10 cycles of the outer loop and lasted for 20,400 s. Figure 16a depicts the measured COF and the two measured temperatures of the conducted test. During the running in phase, the temperatures as well as the COF depict a constant behaviour indicating the absence of intense running in processes. With the onset of heating, the decreasing viscosity results in an insufficient load carrying capacity of the hydrodynamic fluid film, which leads to increased asperity interactions and increased frictional losses. In the subsequent period of time, the heating regulation establishes constant thermal conditions. After reaching the maximum COF, the frictional losses decrease subsequently. Over the entire test, slight variations of the frictional losses can be observed, which is accompanied by a correspondent behaviour of the contact close temperature. Analogous to the previous findings, the variations can be led back to the local characteristics of the contact situation. Within the second to last constant phase, the COF starts to sink and the system starts to transform into operation of combined contact of sliding layer and subjacent bronze matrix accompanied by lower frictional losses, which was confirmed by optical survey of the specimens.
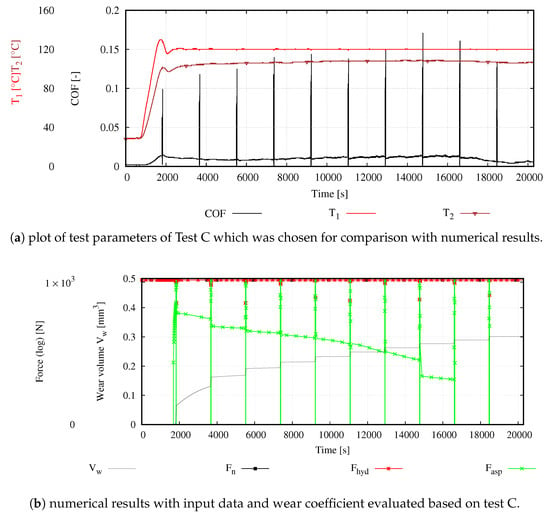
Figure 16.
Depiction of conducted test C (a) and the numerical representation (b).
For the evaluation of the numerical results, the chronological run of the external force , the hydrodynamic force , the force resulting from the asperity contact pressure and the volume of wear are presented in Figure 16b. Since the contribution of the to the force equilibrium is of minor magnitude throughout the constant phases, a logarithmic scale is necessary to allow for the evaluation of the force equilibrium. The numerical representation of test C depicts a complete absence of solid contact during the entire running in phase. is balanced by solely. This was expected since the implemented contact model represents the surface state at the end of the test at which the surface roughness has already been reduced significantly. The experimental heating of the subsequent phase was considered in the numerical analysis by a steady decrease of and according to the rheological behaviour of the used lubricant. Due to the consequently decreasing hydrodynamic load carrying capacity, the asperity contact pressure ultimately becomes effective, which leads to an increase of the . At the end of the heating phase, the external load is carried for the most part by . In accordance with the onset of , the wear volume increases. Within the subsequent constant phase, the system is permanently operated in mixed lubrication indicated by the continuous presence of the . Operation in the mixed lubrication regime results in continuous wear of the journal bearing surface, which leads to increasingly better aligned surfaces. This supports the hydrodynamic pressure build up and results in a steady decrease of the asperity contact force’s contribution to the force equilibrium. This is a typical process observed while running in. The interspersed start–stop cycles force intense mixed lubrication conditions, which explains the striking inclination of the wear volume during these phases. With increasing wear volume and alignment, decreases steadily and, as a consequence, the gain of wear decreases as well. During the last two constant phases, asperity contact is completely absent. Hence, the wear volume remains unaltered due to a constant operation in the fluid lubrication regime. This is in good agreement with the observed experimental results, which show a reduction of the COF and T2 during these phases. This visualizes the transition of operation to a state of operation with reduced energy output.
Figure 17 depicts the chronological run of the wear evolution as visual impression, which allows a qualitative comparison of the numerically and experimental achieved contact patterns presented in Figure 12. The contact pattern of the conducted tests exhibit a larger extent than the numerical results. This is strongly affected by the choice of contact model, which can be considered conservative in the actual case. Additionally, the thermal expansion of the structure, which was neglected in the current work, could also affect the contact pattern. In connection with the wear intensity, these three aspects contribute significantly to the difference in the resulting wear whereby the final wear volume in the case of the numerical evaluation sums up to 0.33 mm3, whereas the experimentally achieved wear volume comes to 3.73 mm3. The comparison between numerical and experimental results yields a significant difference. In the authors’ view, this can be mainly attributed to the used contact model and wear coefficient. As stated previously, the used contact model represents a run in state of the surface. This leads to a general underestimation of asperity contact and consequently wear throughout the entire simulation sequence. However, from the methodological perspective, nothing essentially new could be brought to the fore apart from a change in the absolute wear extent by including a different asperity contact behaviour. Regarding the wear coefficient, special attention must be paid to the correlation function in the course of the CP dependent weighting of the frictional energy. In the actual work, a linear correlation was chosen, which appears to weight the correlation between frictional energy and wear volume insufficiently. By implementing a different weighting function, this relation and hence the wear coefficient can be altered. This measure would certainly affect the significance of the numerical results the most. A respective function needs to be developed accordingly to test results and demands an in-depth analysis of experimental results. This task will be the subject of future investigations.
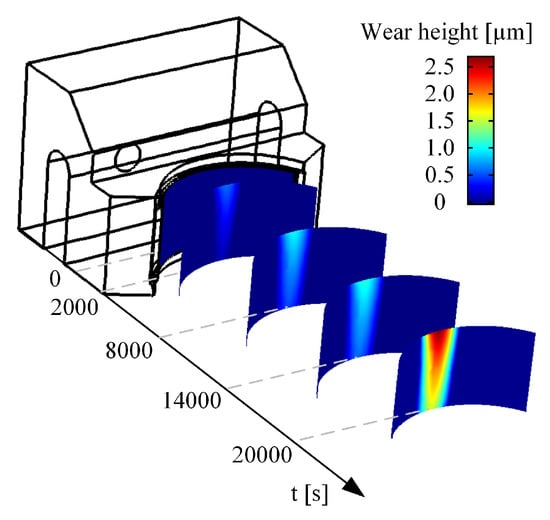
Figure 17.
Chronological evolution of the wear pattern.
4. Conclusions
- The used test methodology in combination with the comprehensive surface analysis chain is capable of resolving the wear process of journal bearing specimens. With the help of this methodology, the process of wear and its effect on the tribological behaviour could be resolved in deep detail. By the use of the CP, the identification of different states of lubrication was enabled, which subsequently allowed a weighting of asperity contact intensity. In the following, this approach allowed for a coherent wear evaluation. For both test strategies which included two different types of loading conditions, the CP supported evaluation method provided a common scatter and correlated the same share of energy input for a resulting wear volume for both strategies, which points out the universal applicability of this method.
- The developed numerical framework represents the first approach concerning wear simulation in tribological contacts with COMSOL, which allows the simulation of operation in fluid and mixed lubrication and a simultaneous wear evaluation. The calculation can be conducted effectively and yields phenomenological comparable results to experimental data. However, a significant deviation in absolute numbers is evident. This can be mainly attributed to the used contact model and the evaluated wear intensity. As presented, a conservative contact model representing a run in state of surface was chosen. This leads to a general underestimation of asperity contact and, consequently, wear. The use of a contact model representing the initial surface state would increase the amount of wear but would not bring deeper insights. Hence, for a better estimation of wear, an additional feature which allows the consideration of a varying contact intensity dependent on the states of surface and wear is sought for the upcoming investigations, which will certainly increase the capability of wear prediction in absolute numbers.
- Special attention must also be given to the correlation function of the CP weighting. In the actual work, a linear correlation was chosen. The use of a different weighting function, which needs to be developed in agreement with test results, could certainly increase the significance of the numerical results.
Author Contributions
Conceptualization, P.B., F.G. and I.G.; Methodology, P.B., F.G. and I.G.; Software, P.B.; Validation, P.B., F.G., F.S. and I.G.; Formal Analysis, P.B.; Investigation, P.B. and F.S.; Resources, F.G.; Data Curation, P.B.; Writing—Original Draft Preparation, P.B.; Writing—Review and Editing, P.B., F.G., F.S. and I.G.; Visualization, P.B. and F.S.; Supervision, F.G.; Project Administration, P.B.; Funding Acquisition, F.G.
Funding
This research was funded by the Austrian Federal Government (COMET Funding Programme).
Acknowledgments
Financial support by the Austrian Federal Government (in particular from Bundesministerium für Verkehr, Innovation und Technologie and Bundesministerium für Wissenschaft, Forschung und Wirtschaft) represented by Österreichische Forschungsförderungsgesellschaft mbH and the Styrian and the Tyrolean Provincial Government, represented by Steirische Wirtschaftsförderungsgesellschaft mbH and Standortagentur Tirol, within the framework of the COMET Funding Programme is gratefully acknowledged. The authors like to express their thanks to Miba Gleitlager GmbH for the support and provided specimens.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BSTA | Bearing segment test adapter |
| HSDA | High speed data acquisition mode |
| EDX | Energy dispersive X-ray spectroscopy |
| FEM | Finite element method |
| MUMPS | Multiftrontal massevily parallel sparse direct solver |
| SEM | Scanning electron microscope |
| EHL | Elastohydrodynamic lubrication |
| DOF | Degrees of freedom |
| CAD | Computer-aided design |
Nomenclature
| mean summit radius, µm | |
| mechanical strain, - | |
| lubricant viscosity, mPas | |
| summit density, m−2 | |
| orientation parameter, - | |
| Poisson’s ratio of surface material 1 and 2, - | |
| summit interface, µm | |
| standardized summit interface, - | |
| shear flow factor, - | |
| pressure flow factor, - | |
| lubricant density, kg/m3 | |
| standard deviation of surface heights (surface roughnes), µm | |
| standard deviation of summits heights, µm | |
| mechanical stress, MPa | |
| normalized summit height, - | |
| summit height measured from the mean summit plane, µm | |
| C | wear intensity, J/m3 |
| COF | coeffcient of friction, - |
| COF0 | maximum boundary coefficient of friction, - |
| CP | contact potential, mV |
| DOF | degree of freedom, - |
| E’ | combined Young’s modulus, GPa |
| E1,2 | Young’s modulus of surface material 1 and 2, GPa |
| Efr | frictional energy, J |
| F | loads within structual mechanics, N |
| Fasp | force resutling from asperity contact pressure, N |
| Fhyd | hydrodynamic force, N |
| Fn | normal force, N |
| H | normalized surface separation, - |
| h | fluid film gap height, m |
| h0 | initial lubrication gap height, m |
| h2 | wear height, m |
| K | empirical wear constant (Archard’s wear law), - |
| k | spring constant, N/m |
| pasp | asperity contact pressure, MPa |
| phyd | hydrodynamic pressure, MPa |
| pm | flow pressure of softer material in contact, MPa |
| pn | normal load, MPa |
| ps | scaling parameter, - |
| s | sliding distance, m |
| T1 | system temperature, C |
| T2 | contact close temperature, C |
| U1,2 | velocity of surface 1 and 2, m/s |
| ub,s | deformation of bearing and shaft, m |
| v | sliding speed, m/s |
| Vw | wear volume, m3 |
References
- Rozeanu, L.; Kennedy, F.E. Wear of hydrodynamic journal bearings. In Tribology Series; Dalmaz, G., Lubrecht, A.A., Dowson, D., Priest, M., Eds.; Elsevier: New York, NY, USA, 2001; Volume 39, pp. 161–166. [Google Scholar]
- Grün, F.; Gódor, I.; Gärtner, W.; Eichlseder, W. Tribological performance of thin overlays for journal bearings. Tribol. Int. 2011, 44, 1271–1280. [Google Scholar] [CrossRef]
- Grün, F.; Gódor, I.; Eichlseder, W. Test methods to characterise differently designed tribomaterials. Tribotest 2008, 14, 159–176. [Google Scholar] [CrossRef]
- Grün, F.; Summer, F.; Pondicherry, K.S.; Gódor, I.; Offenbecher, M.; Lainé, E. Tribological functionality of aluminium sliding materials with hard phases under lubricated conditions. Wear 2013, 298–299, 127–134. [Google Scholar] [CrossRef]
- Summer, F.; Grün, F.; Schiffer, J.; Gódor, I.; Papadimitriou, I. Tribological study of crankshaft bearing systems: Comparison of forged steel and cast iron counterparts under start–stop operation. Wear 2015, 338, 232–241. [Google Scholar] [CrossRef]
- Summer, F.; Grün, F.; Offenbecher, M.; Taylor, S.; Lainé, E. Tribology of journal bearings: Start stop operation as life-time factor. Tribol. Schmier. 2017, 64, 46–56. [Google Scholar]
- Farfán-Cabrera, L.I.; Gallardo-Hernández, E.A. Wear evaluation of journal bearings using an adapted micro-scale abrasion tester. Wear 2017, 376–377, 1841–1848. [Google Scholar] [CrossRef]
- Gebretsadik, D.W.; Hardell, J.; Prakash, B. Friction and wear characteristics of different Pb-free bearing materials in mixed and boundary lubrication regimes. Wear 2015, 340–341, 63–72. [Google Scholar] [CrossRef]
- Gebretsadik, D.W.; Hardell, J.; Prakash, B. Tribological performance of tin-based overlay plated engine bearing materials. Tribol. Int. 2015, 92, 281–289. [Google Scholar] [CrossRef]
- Taylor, C. Automobile engine tribology—Design considerations for efficiency and durability. Wear 1998, 221, 1–8. [Google Scholar] [CrossRef]
- Priest, M.; Taylor, C. Automobile engine tribology—Approaching the surface. Wear 2000, 241, 193–203. [Google Scholar] [CrossRef]
- Albers, A.; Reichert, S. On the influence of surface roughness on the wear behavior in the running-in phase in mixed-lubricated contacts with the finite element method. Wear 2017, 376–377, 1185–1193. [Google Scholar] [CrossRef]
- Põdra, P.; Andersson, S. Simulating sliding wear with finite element method. Tribol. Int. 1999, 32, 71–81. [Google Scholar] [CrossRef]
- Arjmandi, M.; Ramezani, M.; Giordano, M.; Schmid, S. Finite element modelling of sliding wear in three-dimensional woven textiles. Tribol. Int. 2017, 115, 452–460. [Google Scholar] [CrossRef]
- Reichert, S.; Lorentz, B.; Heldmaier, S.; Albers, A. Wear simulation in non-lubricated and mixed lubricated contacts taking into account the microscale roughness. Tribol. Int. 2016, 100, 272–279. [Google Scholar] [CrossRef]
- Khader, I.; Renz, A.; Kailer, A. A wear model for silicon nitride in dry sliding contact against a nickel-base alloy. Wear 2017, 376–377, 352–362. [Google Scholar] [CrossRef]
- Chun, S.M.; Khonsari, M.M. Wear simulation for the journal bearings operating under aligned shaft and steady load during start-up and coast-down conditions. Tribol. Int. 2016, 97, 440–466. [Google Scholar] [CrossRef]
- Archard, J.; Hirst, W. The wear of metals under unlubricated conditions. Proc. R. Soc. Lond. A 1956, 236, 397–410. [Google Scholar] [CrossRef]
- Aghdam, A.; Khonsari, M. Prediction of wear in grease-lubricated oscillatory journal bearings via energy-based approach. Wear 2014, 318, 188–201. [Google Scholar] [CrossRef]
- Sander, D.E.; Allmaier, H.; Priebsch, H.; Reich, F.; Witt, M.; Skiadas, A.; Knaus, O. Edge loading and running-in wear in dynamically loaded journal bearings. Tribol. Int. 2015, 92, 395–403. [Google Scholar] [CrossRef]
- Beheshti, A.; Khonsari, M.M. An engineering approach for the prediction of wear in mixed lubricated contacts. Wear 2013, 308, 121–131. [Google Scholar] [CrossRef]
- Mokhtar, M.O.A.; Howarth, R.B.; Davies, P.B. The Behavior of Plain Hydrodynamic Journal Bearings during Starting and Stopping. ASLE Trans. 1977, 20, 183–190. [Google Scholar] [CrossRef]
- Haneef, M.; Randall, R.; Smith, W.; Peng, Z. Vibration and wear prediction analysis of IC engine bearings by numerical simulation. Wear 2017, 384–385, 15–27. [Google Scholar] [CrossRef]
- Bergmann, P.; Grün, F.; Summer, F.; Gódor, I.; Stadler, G. Expansion of the Metrological Visualization Capability by the Implementation of Acoustic Emission Analysis. Adv. Tribol. 2017, 2017, 17. [Google Scholar] [CrossRef]
- Summer, F.; Bergmann, P.; Grün, F. Damage Equivalent Test Methodologies as Design Elements for Journal Bearing Systems. Lubricants 2017, 5, 47. [Google Scholar] [CrossRef]
- Reynolds, O. On the Theory of Lubrication and Its Application to Mr. Beauchamp Tower’s Experiments, Including an Experimental Determination of the Viscosity of Olive Oil. Philos. Trans. R. Soc. Lond. 1886, 177, 157–234. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of Average Flow Model to Lubrication Between Rough Sliding Surfaces. J. Lubr. Technol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Bergmann, P.; Grün, F.; Gódor, I.; Stadler, G.; Maier-Kiener, V. On the modelling of mixed lubrication of conformal contacts. Tribol. Int. 2018, 125, 220–236. [Google Scholar] [CrossRef]
- Peklenik, J. New Developments in Surface Characterization and Measurements by Means of Random Process Analysis. Proc. Inst. Mech. Eng. 1967, 182, 108–126. [Google Scholar] [CrossRef]
- Cameron, A. Principles of Lubrication; Longman Publishing Group: Harlow, UK, 1986. [Google Scholar]
- Committee, A.I.H. ASM Handbook; ASM International: Almere, The Netherland, 1992; Volume 18. [Google Scholar]
- Dowson, D.; Higginson, G. Elasto-Hydrodynamic Lubrication; International Series On Materials Science and Technology; Pergamon Press: Oxford, UK, 1977. [Google Scholar]
- Allmaier, H.; Priestner, C.; Six, C.; Priebsch, H.H.; Forstner, C.; Novotny-Farkas, F. Predicting friction reliably and accurately in journal bearings—A systematic validation of simulation results with experimental measurements. Tribol. Int. 2011, 44, 1151–1160. [Google Scholar] [CrossRef]
- Gohar, R. Elastohydrodynamics; Computing in Engineering; Imperial College Press: London, UK, 2001. [Google Scholar]
- Spikes, H.A. Sixty years of EHL. Lubr. Sci. 2006, 18, 265–291. [Google Scholar] [CrossRef]
- Spikes, H.A. Basics of EHL for practical application. Lubr. Sci. 2015, 27, 45–67. [Google Scholar] [CrossRef]
- Sander, D.E.; Allmaier, H.; Priebsch, H.H.; Reich, F.M.; Witt, M.; Füllenbach, T.; Skiadas, A.; Brouwer, L.; Schwarze, H. Impact of high pressure and shear thinning on journal bearing friction. Tribol. Int. 2015, 81, 29–37. [Google Scholar] [CrossRef]
- Walters, K. The Importance and Measurement of Lubricant Rheology. In Thinning Films and Tribological Interfaces; Dowson, D., Priest, M., Taylor, C., Ehret, P., Childs, T., Dalmaz, G., Lubrecht, A., Berthier, Y., Flamand, L., Georges, J.M., Eds.; Tribology Series; Elsevier: New York, NY, USA, 2000; Volume 38, pp. 487–499. [Google Scholar] [CrossRef]
- Hamrock, B.; Schmid, S.; Jacobson, B. Fundamentals of Fluid Film Lubrication; Mechanical Engineering Fundamentals of Fluid Film Lubrication; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. A 1966, 295, 300–319. [Google Scholar] [CrossRef]
- McCool, J.I. Comparison of models for the contact of rough surfaces. Wear 1986, 107, 37–60. [Google Scholar] [CrossRef]
- Kalin, M.; Pogačnik, A.; Etsion, I.; Raeymaekers, B. Comparing surface topography parameters of rough surfaces obtained with spectral moments and deterministic methods. Tribol. Int. 2016, 93, 137–141. [Google Scholar] [CrossRef]
- Preston, F.W. The Theory and Design of Plate Glass Polishing Machines. J. Soc. Glass Technol. 1927, 11, 214. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).