Dynamical Simulations of a Flexible Rotor in Cylindrical Uncavitated and Cavitated Lubricated Journal Bearings
Abstract
1. Introduction
2. Materials and Methods
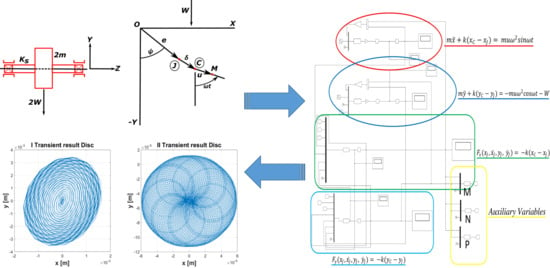
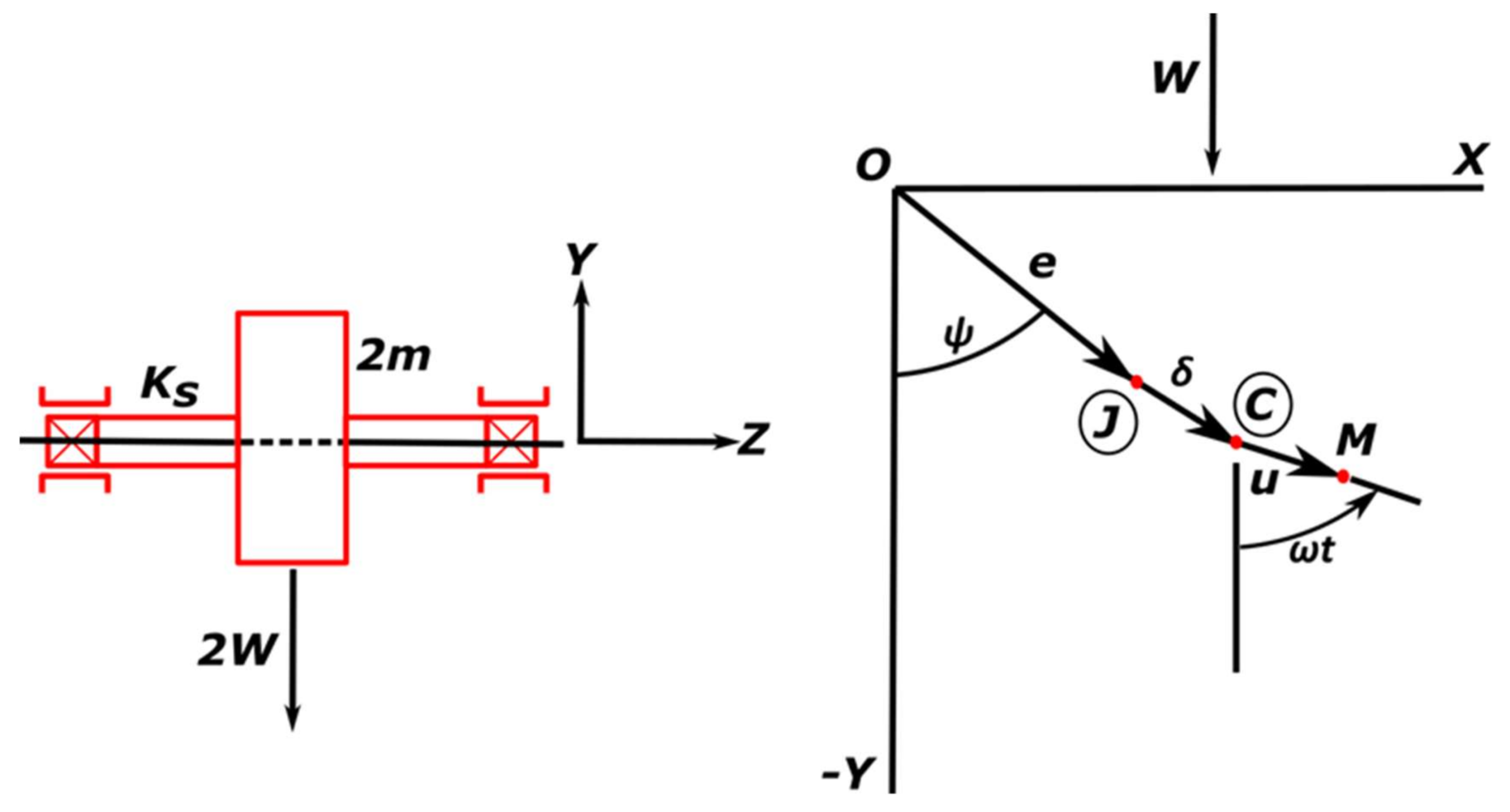
2.1. The System
- the system is completely symmetrical with respect to the disc
- the motion of the disk is plane.
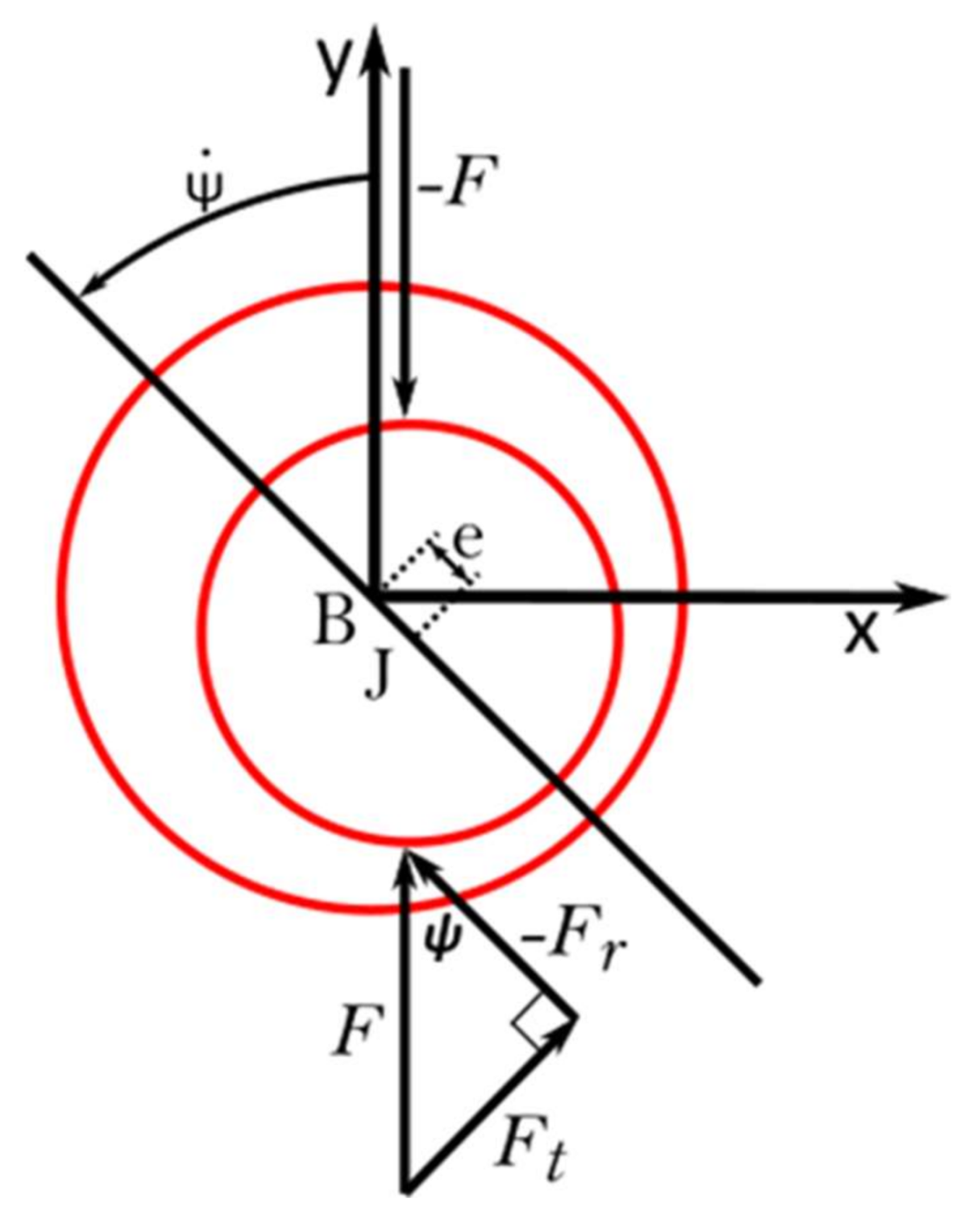
2.2. Journal Bearings
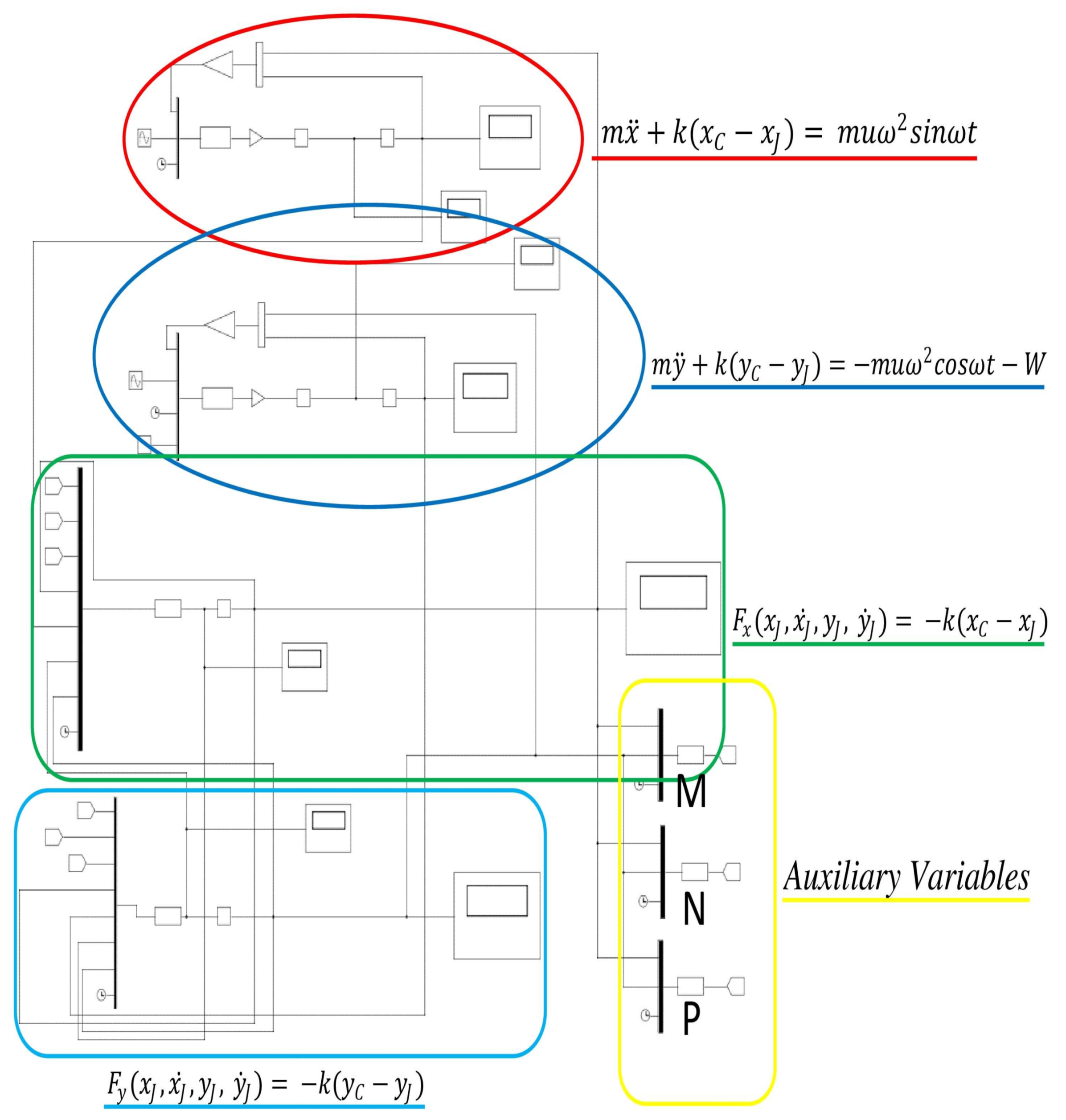
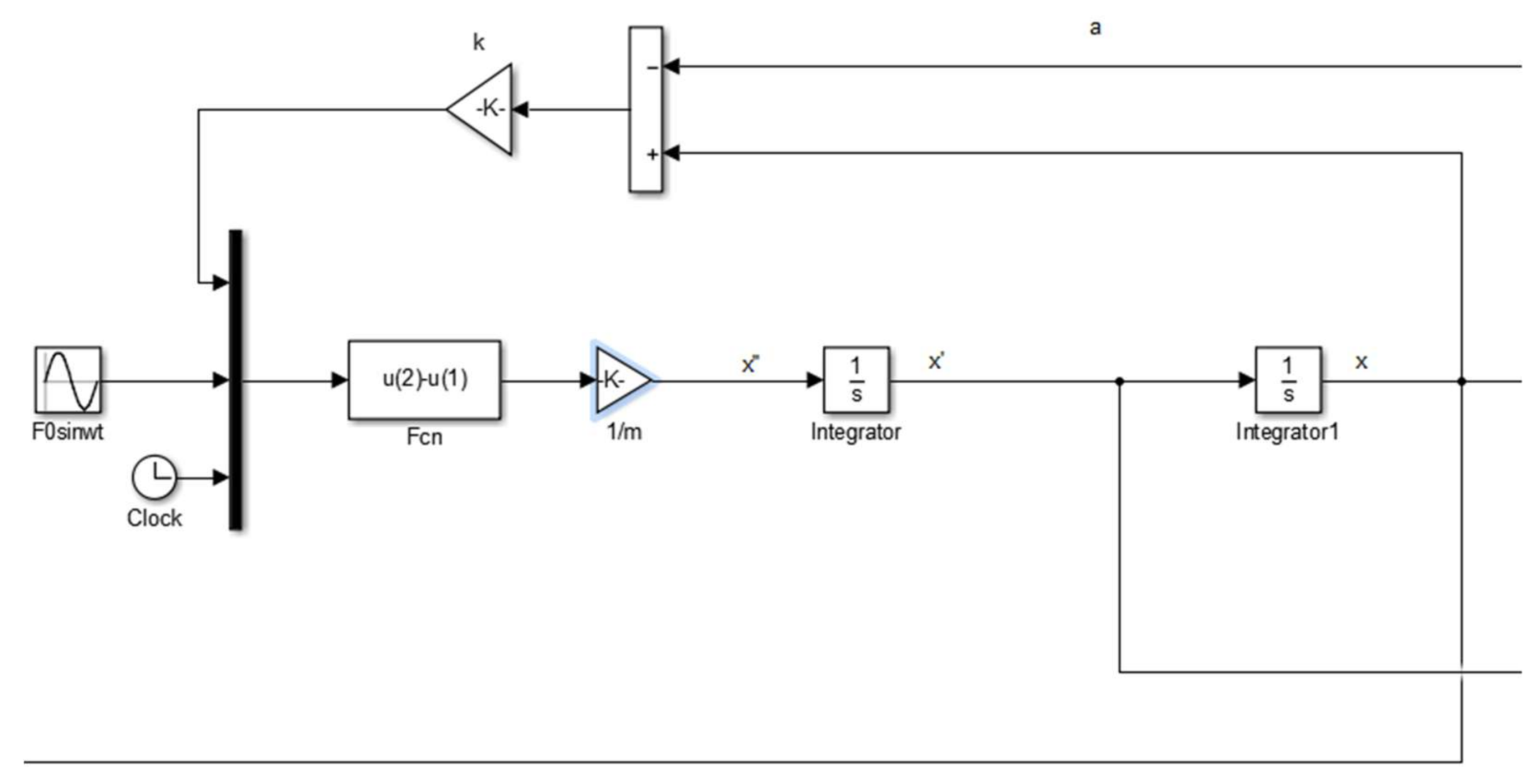
2.3. Equations of Motion
- force of inertia
- spring force (k is the flexural stiffness of the shaft)
- centrifugal force of inertia
- static load (due to the rotor weight).
- nonlinear fluid film force
- spring force.
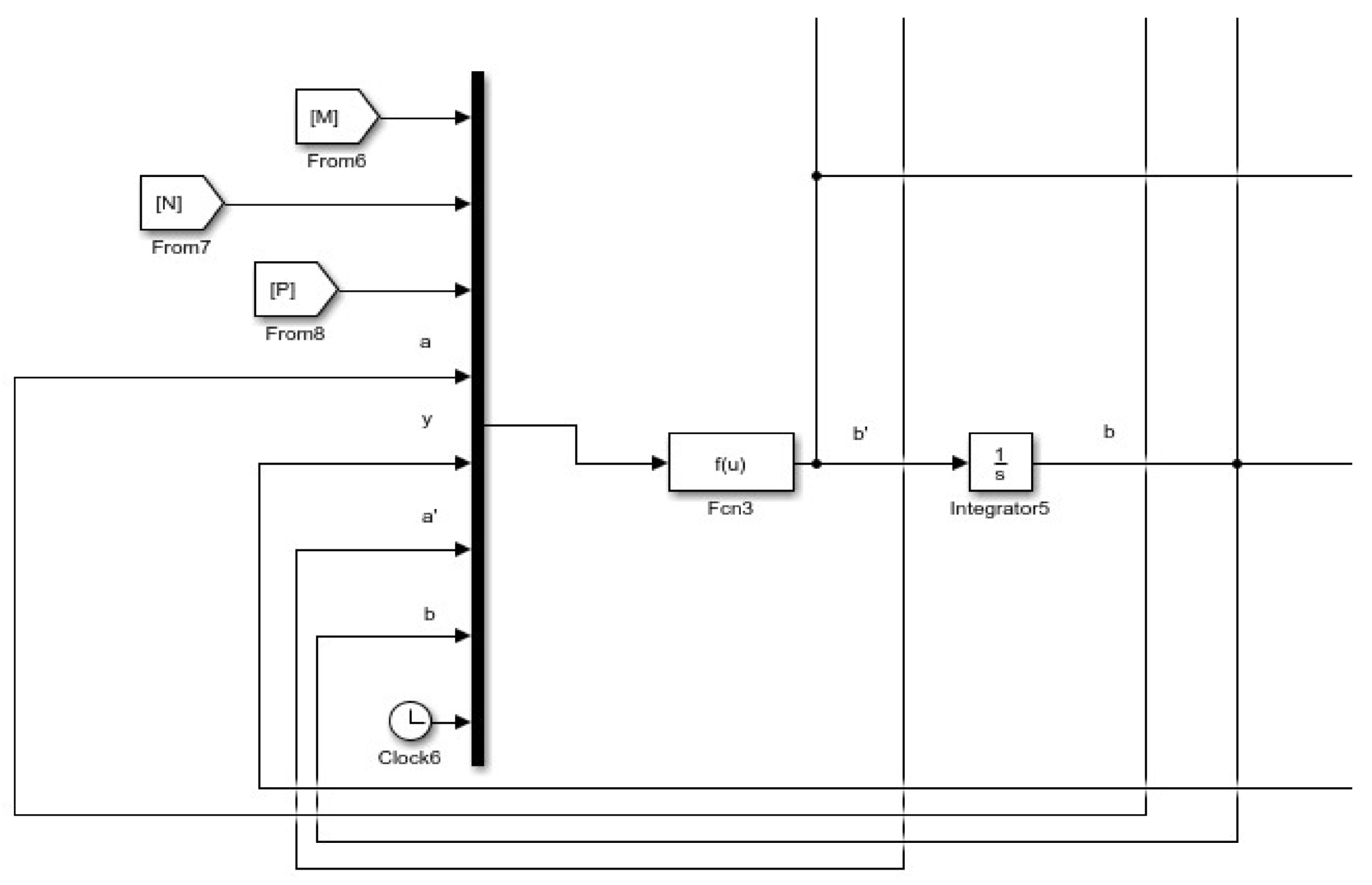
2.4. Numerical Integration of the Equations of Motion
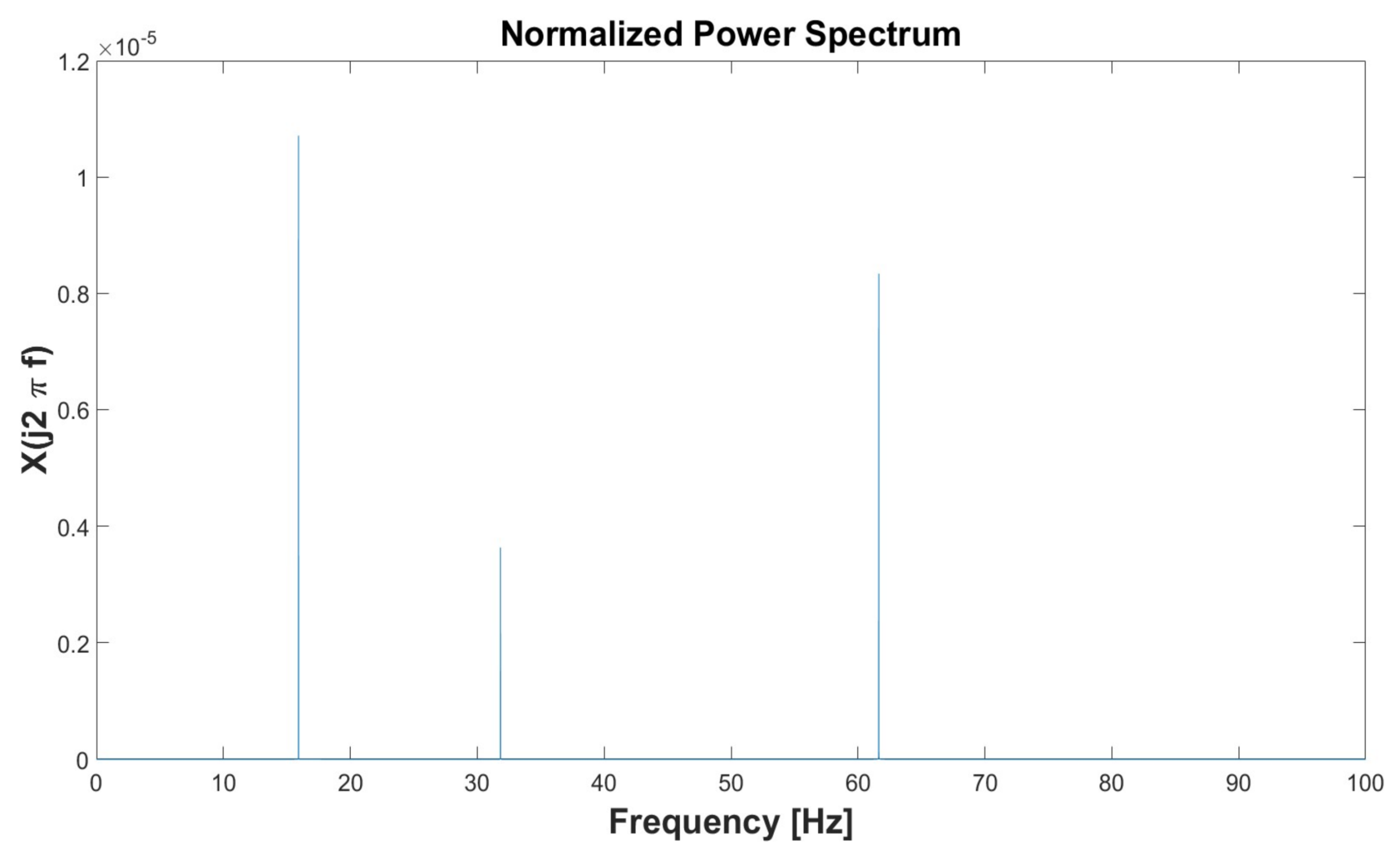
3. Results and Discussions
3.1. Simulation 1
3.2. Simulation 2
3.3. Simulation 3
3.4. Simulation 4
3.5. Simulation 5
4. Conclusions
Author Contributions
Conflicts of Interest
Nomenclature
| 2m | disc mass |
| Ks | shaft bending stiffness |
| 2W | static load |
| O | bearing centre |
| J | journal centre |
| C | disc geometric centre |
| M | disc centre of gravity |
| u | disc static imbalance |
| R | journal radius |
| r | disc radius |
| L | bearing length |
| c | radial bearing clearance |
| e | eccentricity |
| eccentricity ratio | |
| δ | shaft deflection |
| ω | disc angular velocity |
| μ | lubricant viscosity |
| ω | angular velocity of the journal (constant) |
| attitude angle | |
| k | flexural stiffness of the shaft |
| angular velocity of the line of centres (journal whirling) | |
| (xc,yc) | disc centre coordinates |
| (xj,yj) | journal centre coordinates |
References
- Friswell, M.I.; Penny, J.E.T.; Garvey, S.D.; Lees, A.W. Dynamics of Rotating Machines; Cambridge University Press: Cambridge, UK, 2010; ISBN 9780511780509. [Google Scholar]
- Lund, J.W. Review of the Concept of Dynamic Coefficients for Fluid Film Journal Bearings. J. Tribol. 1987, 109, 37. [Google Scholar] [CrossRef]
- Muszynska, A. Stability of whirl and whip in rotor/bearing systems. J. Sound Vib. 1988, 127, 49–64. [Google Scholar] [CrossRef]
- D’Agostino, V.; Guida, D.; Ruggiero, A.; Senatore, A. An analytical study of the fluid film force in finite-length journal bearings. Part I. Lubr. Sci. 2001, 13, 329–340. [Google Scholar] [CrossRef]
- Poritsky, H. Contribution to the theory of oil whip. Trans. ASME 1953, 75, 1153–1161. [Google Scholar]
- Huang, T.-W.; Weng, C.-T. Dynamic characteristics of finite-width journal bearings with micropolar fluids. Wear 1990, 141, 23–33. [Google Scholar] [CrossRef]
- Bansal, P.; Chattopadhayay, A.K.; Agrawal, V.P. Linear Stability Analysis of Hydrodynamic Journal Bearings with a Flexible Liner and Micropolar Lubrication. Tribol. Trans. 2015, 58, 316–326. [Google Scholar] [CrossRef]
- Naduvinamani, N.B.; Hiremath, P.S.; Gurubasavaraj, G. Static and dynamic behaviour of squeeze-film lubrication of narrow porous journal bearings with coupled stress fluid. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2001, 215, 45–62. [Google Scholar] [CrossRef]
- Naduvinamani, N.B.; Marali, G.B. Dynamic Reynolds equation for micropolar fluids and the analysis of plane inclined slider bearings with squeezing effect. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2007, 221, 823–829. [Google Scholar] [CrossRef]
- Das, S.; Guha, S.K.; Chattopadhyay, A.K. Linear stability analysis of hydrodynamic journal bearings under micropolar lubrication. Tribol. Int. 2005, 38, 500–507. [Google Scholar] [CrossRef]
- Harika, E.; Bouyer, J.; Fillon, M.; Hélène, M. Measurements of lubrication characteristics of a tilting pad thrust bearing disturbed by a water-contaminated lubricant. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2013, 227, 16–25. [Google Scholar] [CrossRef]
- Vania, A.; Pennacchi, P.; Chatterton, S. Dynamic Effects Caused by the Non-Linear Behavior of Oil-Film Journal Bearings in Rotating Machines. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition (Volume 7: Structures and Dynamics, Parts A and B), Copenhagen, Denmark, 11–15 June 2012; ASME: New York, NY, USA, 2012; p. 657. [Google Scholar]
- Harika, E.; Bouyer, J.; Fillon, M.; Hélène, M. Effects of Water Contamination of Lubricants on Hydrodynamic Lubrication: Rheological and Thermal Modeling. J. Tribol. 2013, 135, 41707. [Google Scholar] [CrossRef]
- Sukumaran Nair, V.P.; Prabhakaran Nair, K. Finite element analysis of elastohydrodynamic circular journal bearing with micropolar lubricants. Finite Elem. Anal. Des. 2004, 41, 75–89. [Google Scholar] [CrossRef]
- Lin, T.-R. Hydrodynamic lubrication of journal bearings including micropolar lubricants and three-dimensional irregularities. Wear 1996, 192, 21–28. [Google Scholar] [CrossRef]
- Prabhakaran Nair, K.; Sukumaran Nair, V.P.; Jayadas, N.H. Static and dynamic analysis of elastohydrodynamic elliptical journal bearing with micropolar lubricant. Tribol. Int. 2007, 40, 297–305. [Google Scholar] [CrossRef]
- Pennacchi, P.; Vania, A.; Chatterton, S. Nonlinear effects caused by coupling misalignment in rotors equipped with journal bearings. Mech. Syst. Signal Process. 2012, 30, 306–322. [Google Scholar] [CrossRef]
- Lund, J.W.; Sternlicht, B. Rotor-Bearing Dynamics with Emphasis on Attenuation. J. Basic Eng. 1962, 84, 491. [Google Scholar] [CrossRef]
- Pinkus, O. The Reynolds Centennial: A Brief History of the Theory of Hydrodynamic Lubrication. J. Tribol. 1987, 109, 2. [Google Scholar] [CrossRef]
- Szeri, A.Z. Some Extensions of the Lubrication Theory of Osborne. J. Tribol. 1987, 109, 21–36. [Google Scholar] [CrossRef]
- Nitzschke, S.; Woschke, E.; Daniel, C.; Strackeljan, J. Einfluss der masseerhaltenden Kavitation auf gleitgelagerte Rotoren unter instationärer Belastung. In Proceedings of the SIRM 2013-10, Internationale Tagung Schwingungen in Rotierenden Maschinen, Berlin, Germany, 25–27 February 2013; p. ID-210. [Google Scholar]
- Ruggiero, A.; Gómez, E.; D’Amato, R. Approximate closed-form solution of the synovial fluid film force in the human ankle joint with non-Newtonian lubricant. Tribol. Int. 2013, 57, 156–161. [Google Scholar] [CrossRef]
- Ruggiero, A.; Hloch, S.; Kozak, D.; Valasek, P. Analytical fluid film force calculation in the case of short bearing with a fully developed turbulent flow. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 395–401. [Google Scholar] [CrossRef]
- Van der Pol, B.; Van der Mark, J. The heartbeat considered as a relaxation oscillation, and an electrical model of the heart. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1928, 6, 763–775. [Google Scholar] [CrossRef]
- Thompson, J.M.T.; Stewart, H.B. Nonlinear Dynamics and Chaos; Wiley: Hoboken, NJ, USA, 2002; ISBN 0471876453. [Google Scholar]
- Vance, J.M. Rotordynamics of Turbomachinery; Wiley: Hoboken, NJ, USA, 1988; ISBN 0471802581. [Google Scholar]
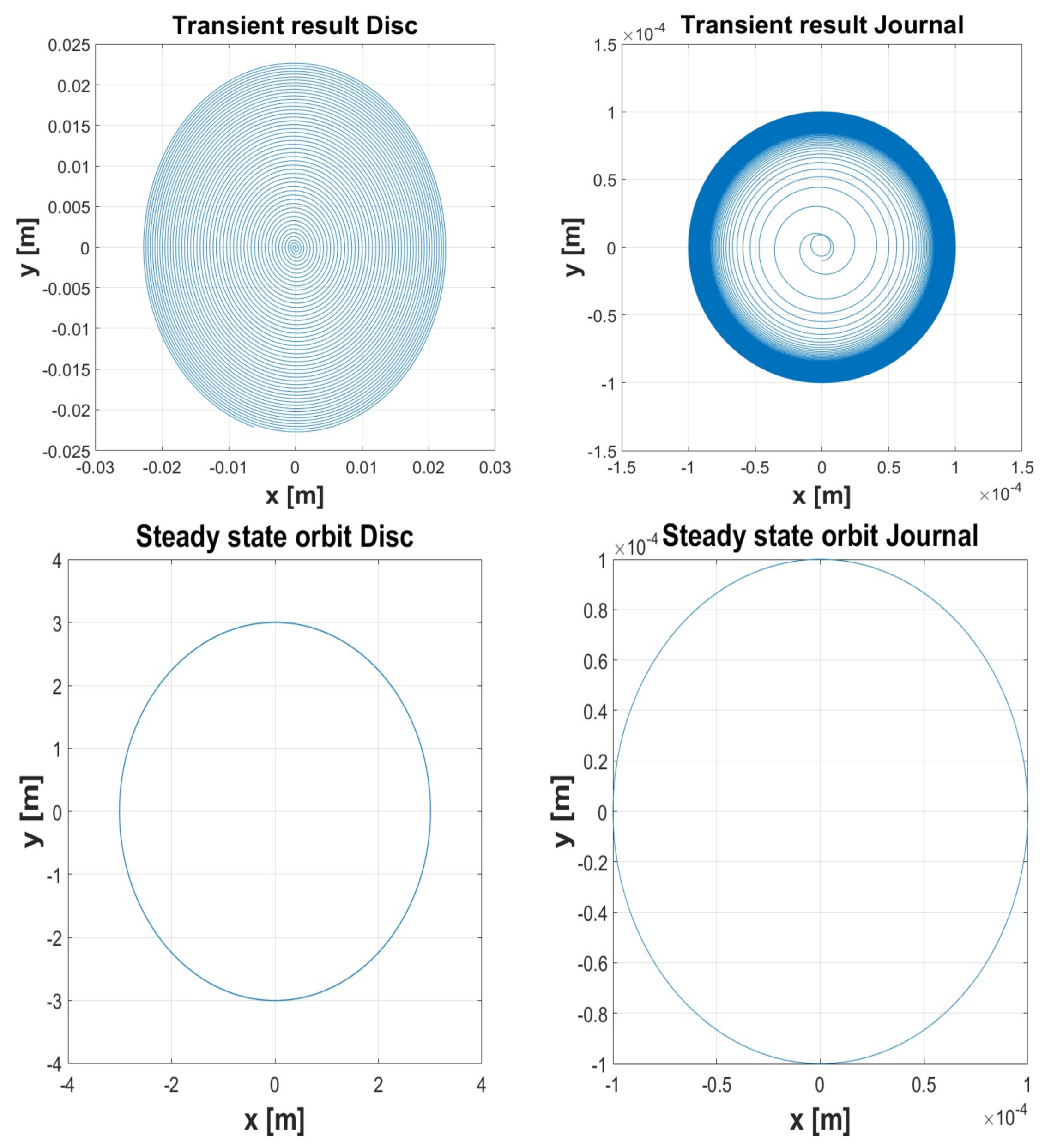
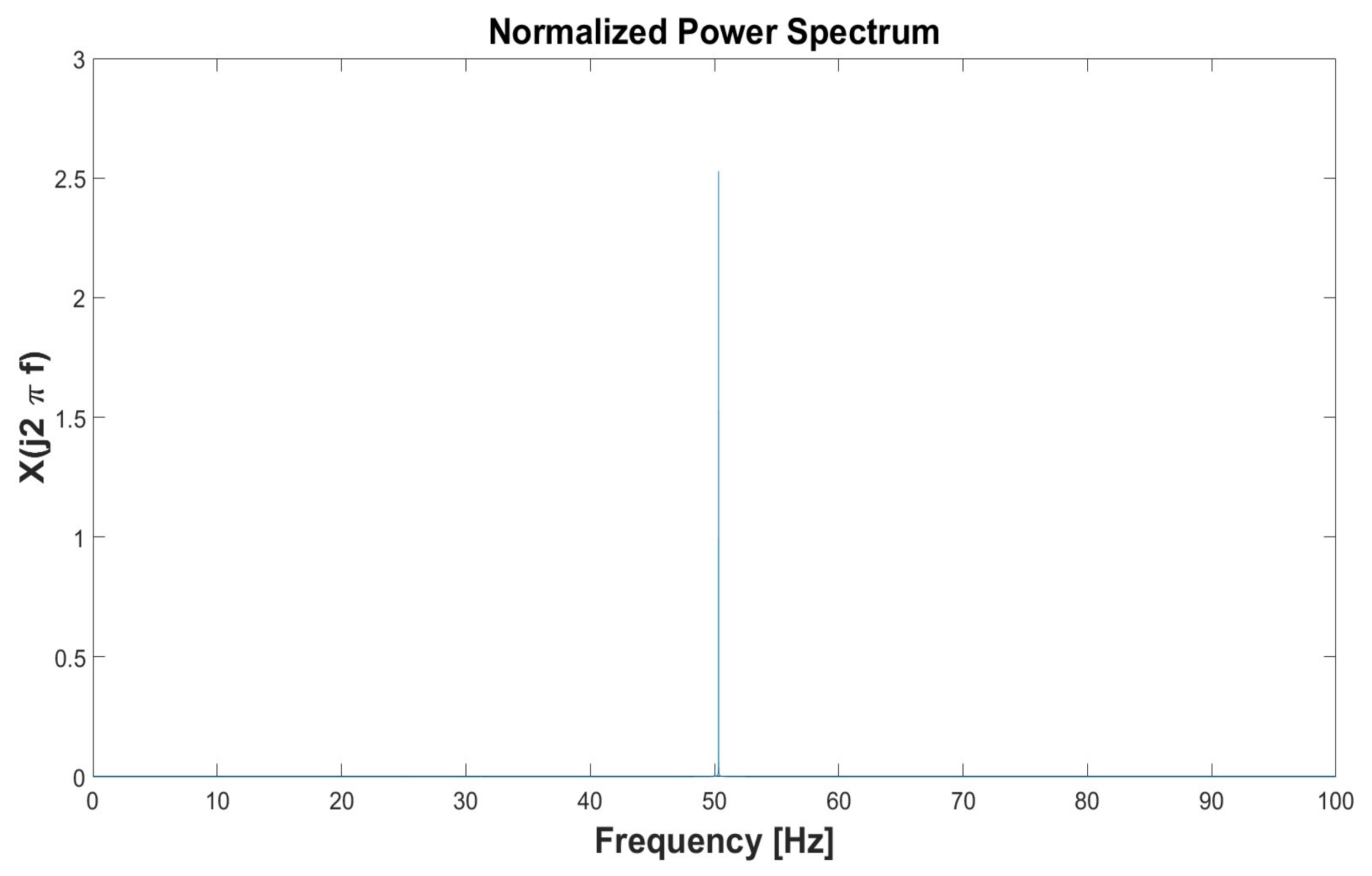
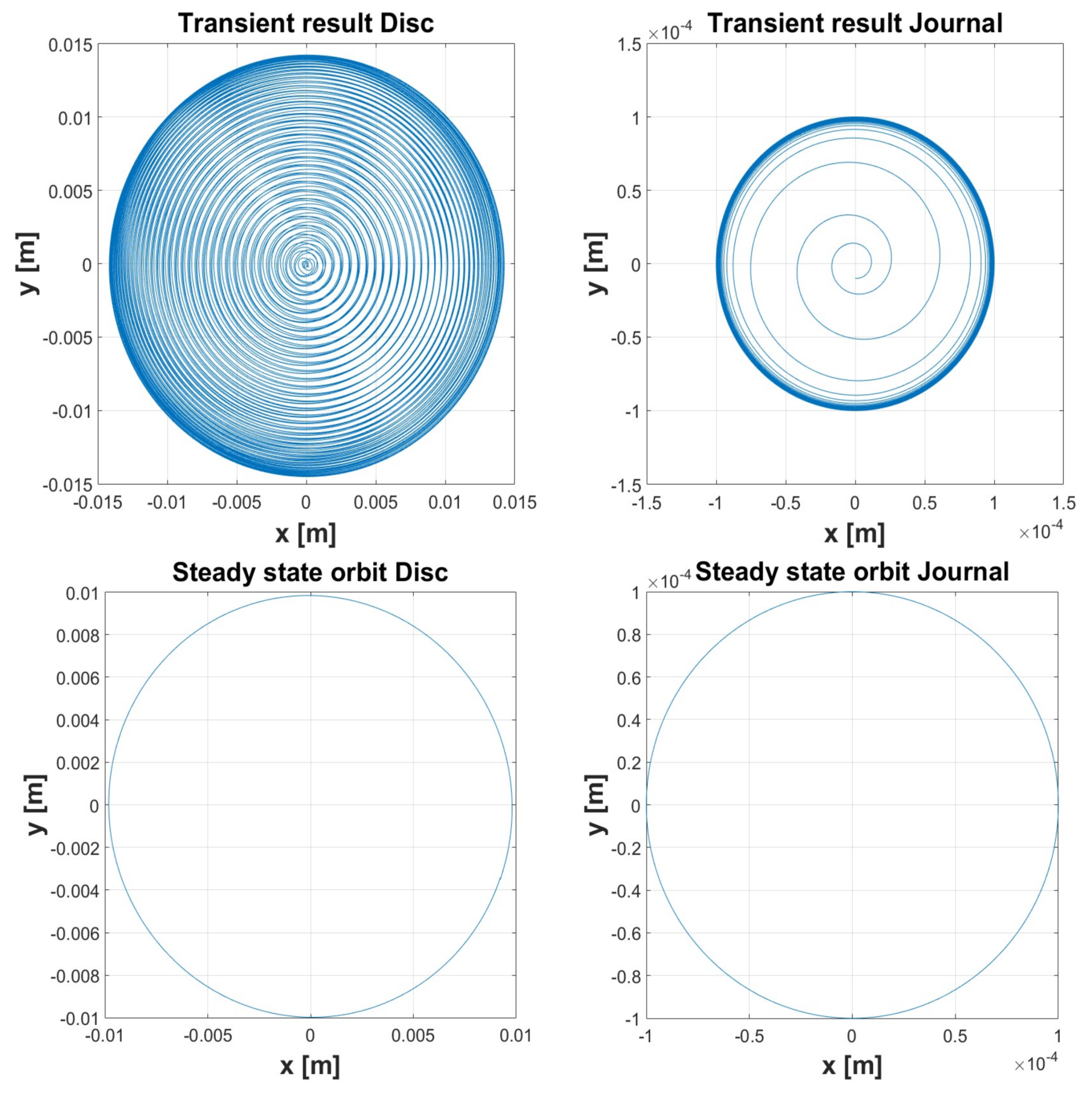
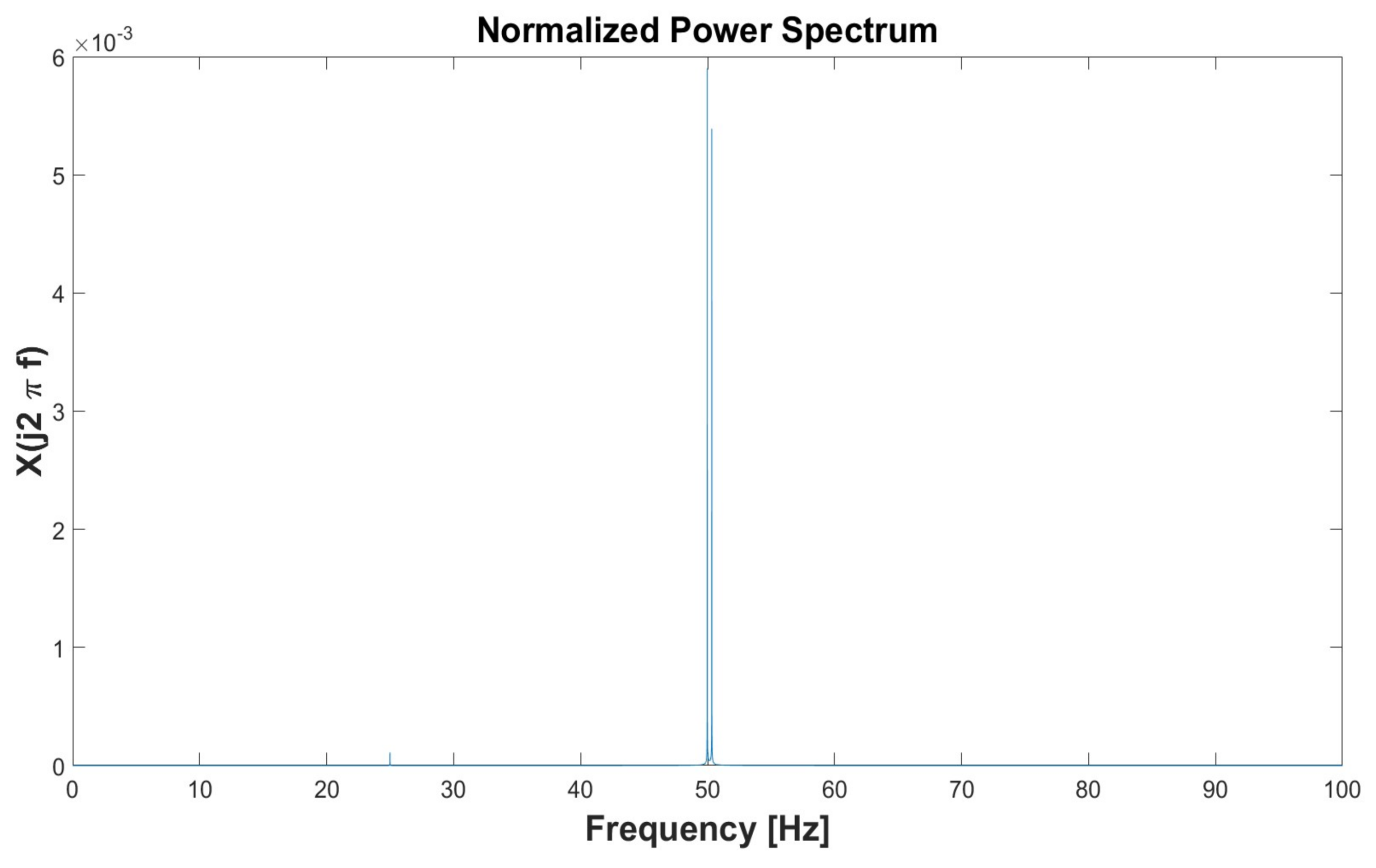
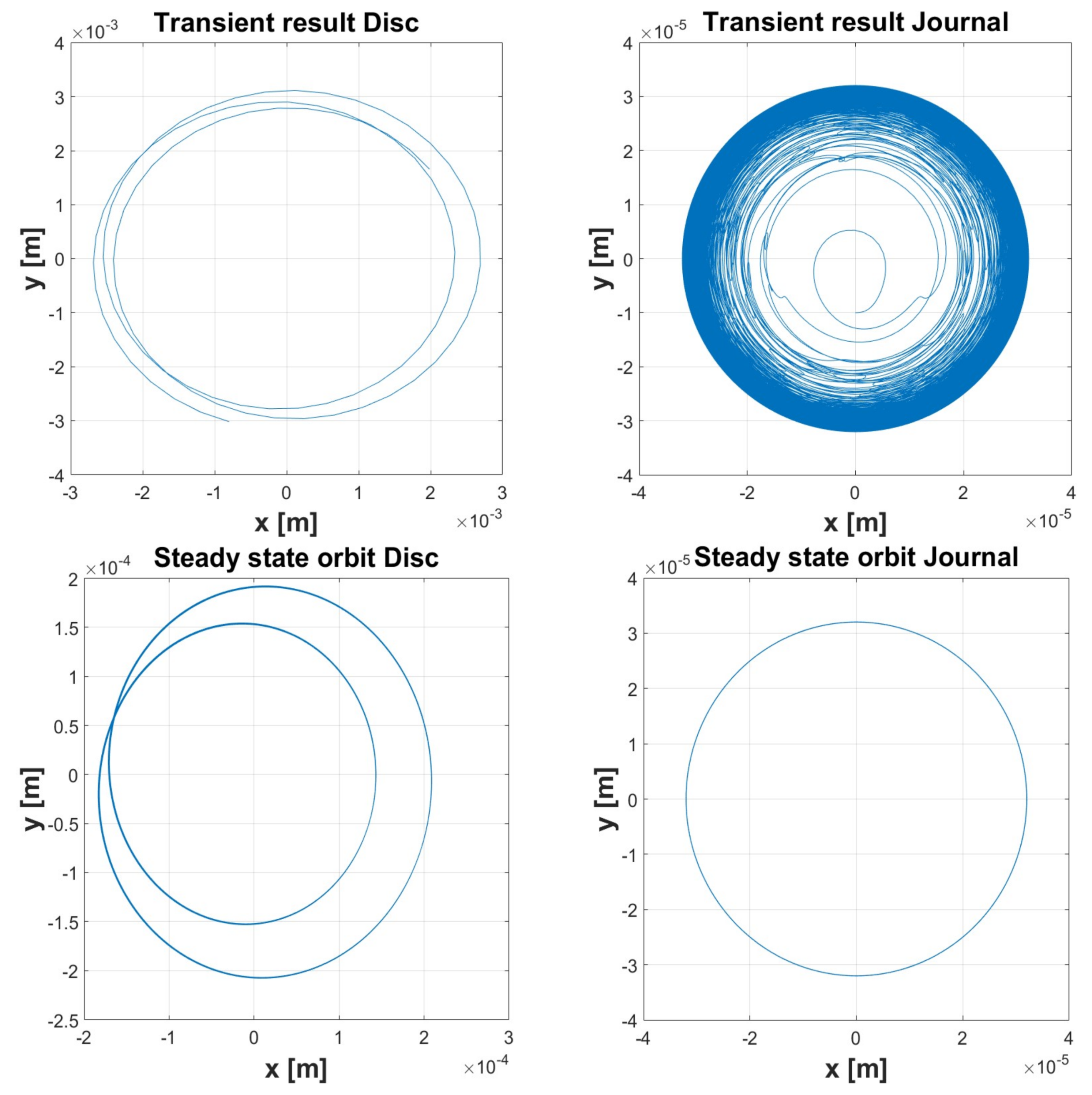

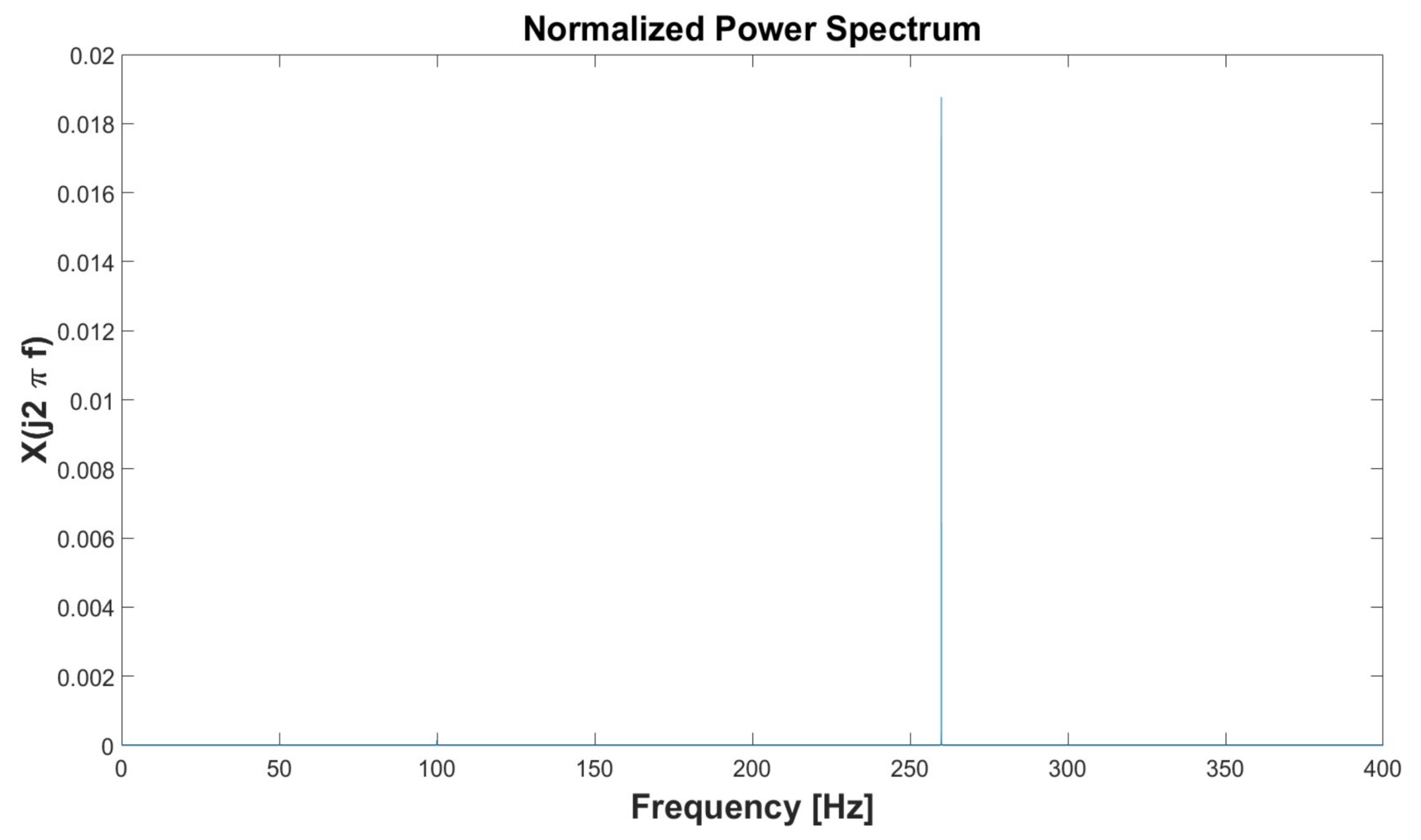
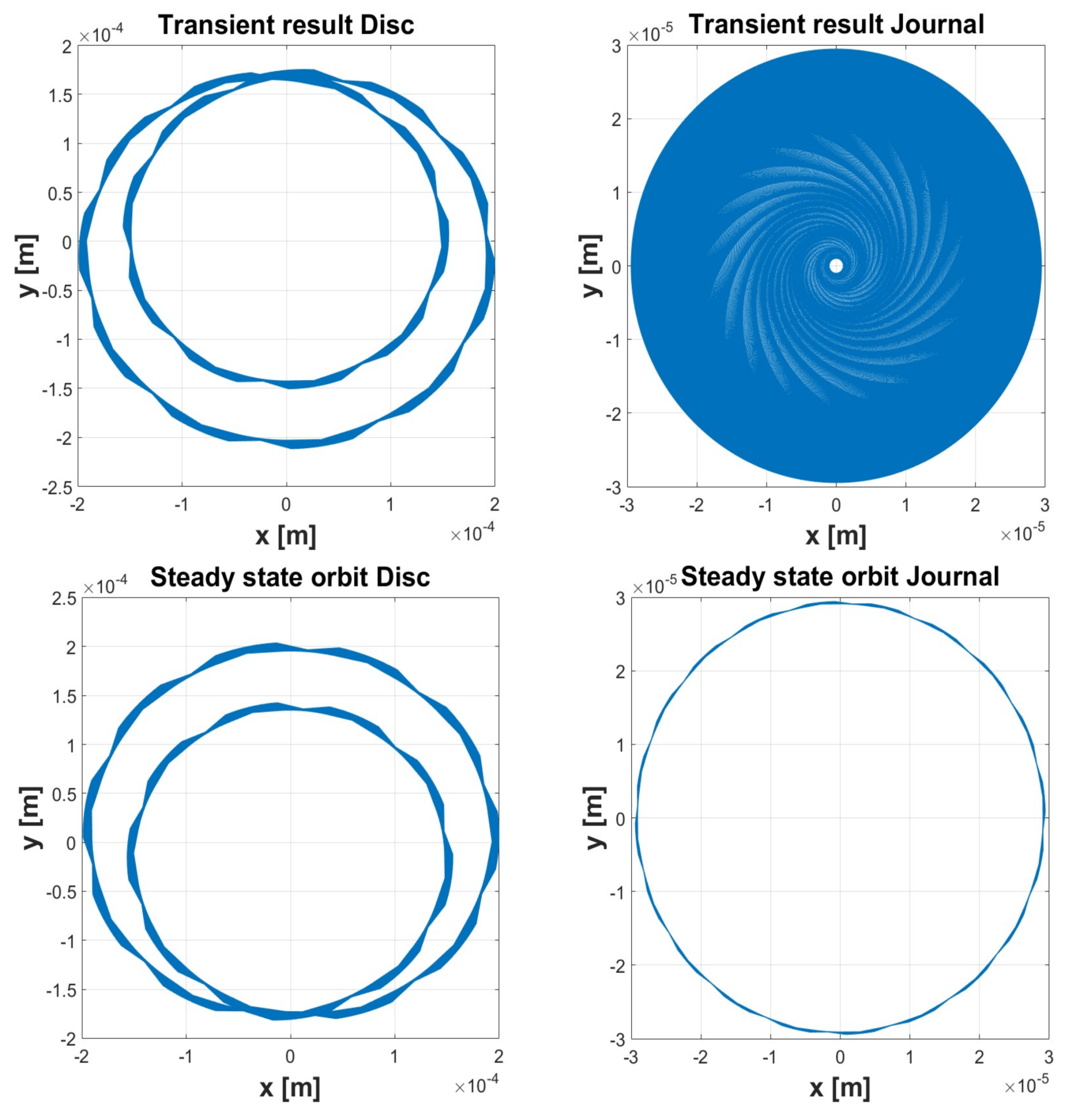
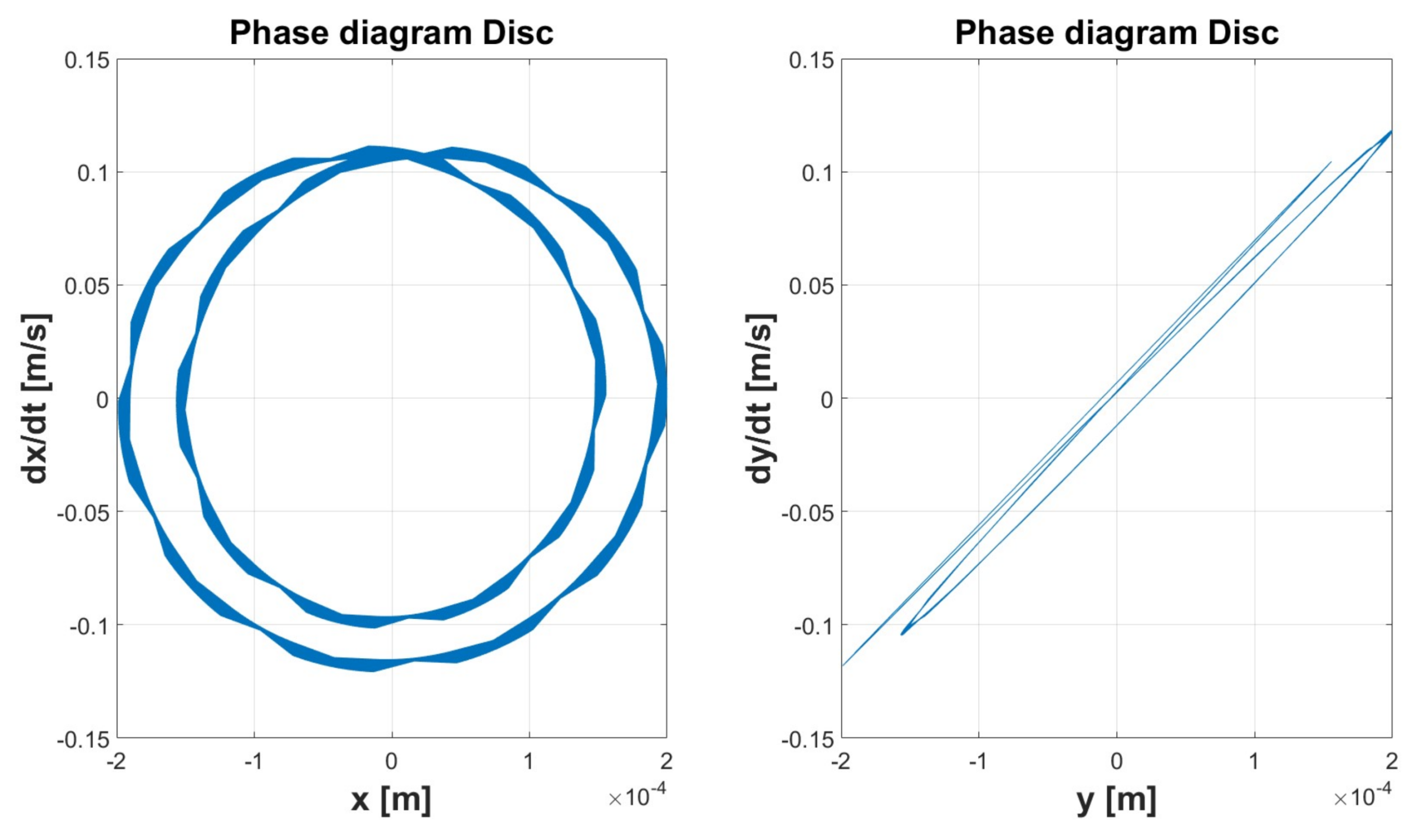
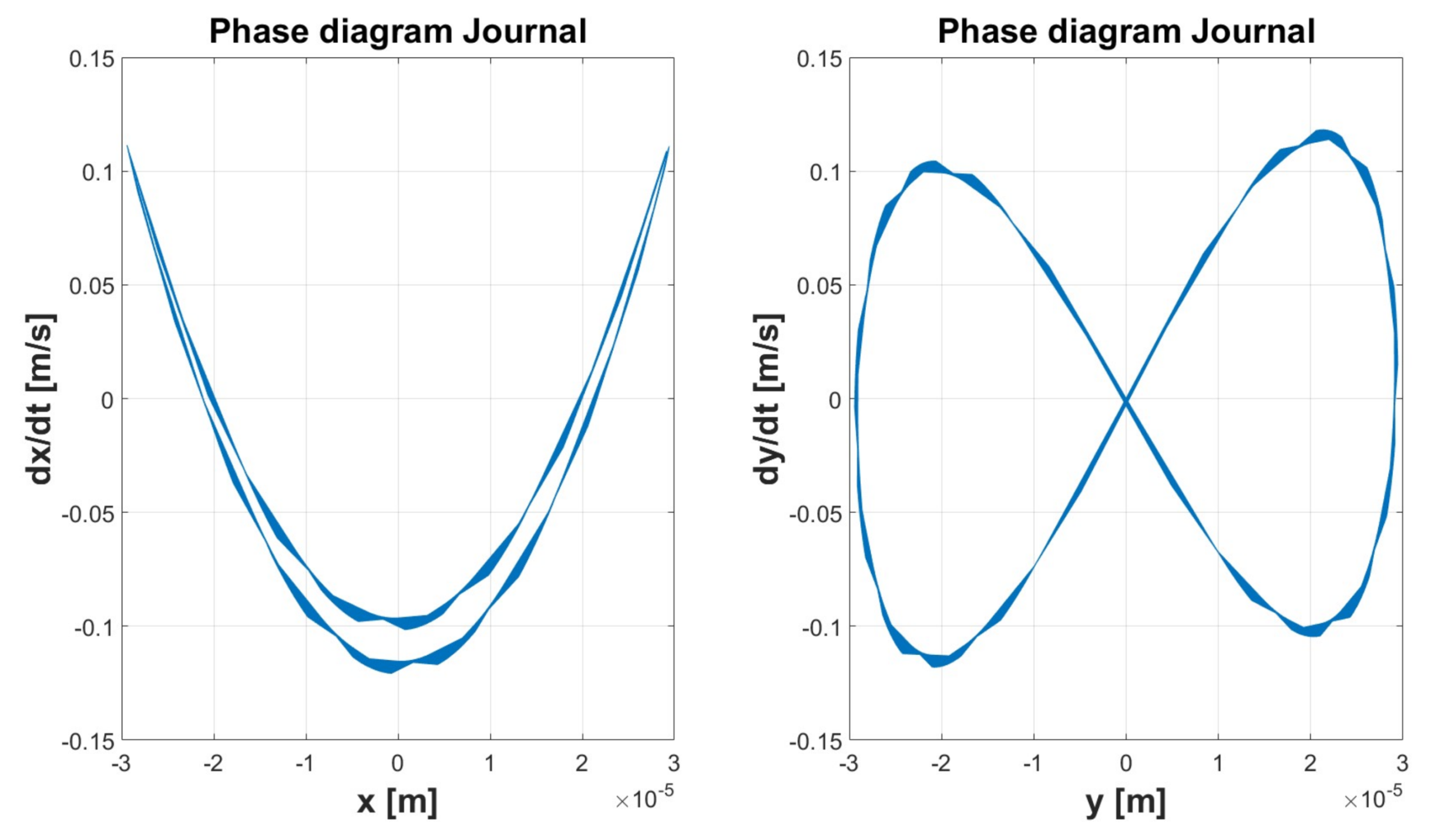

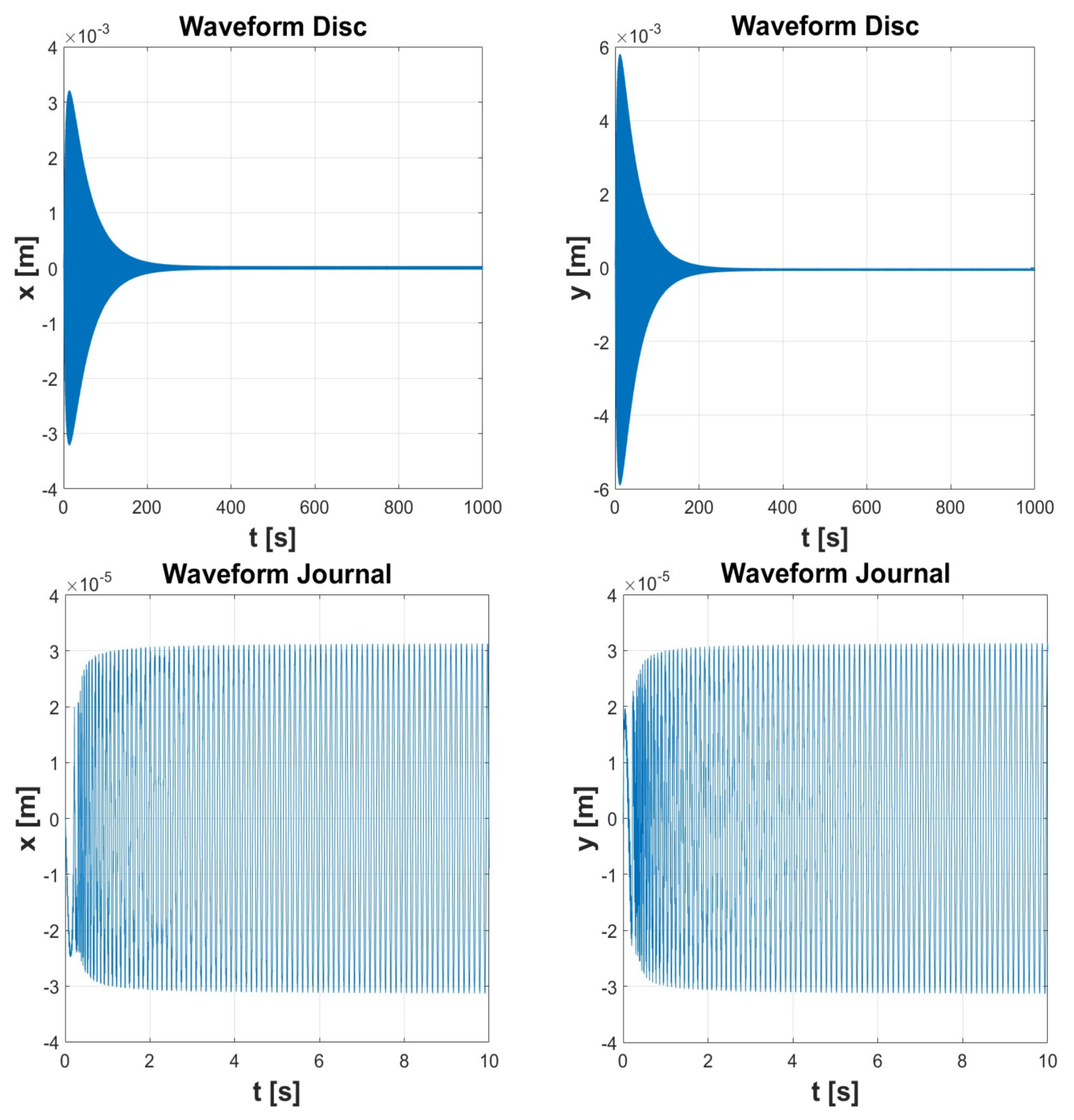
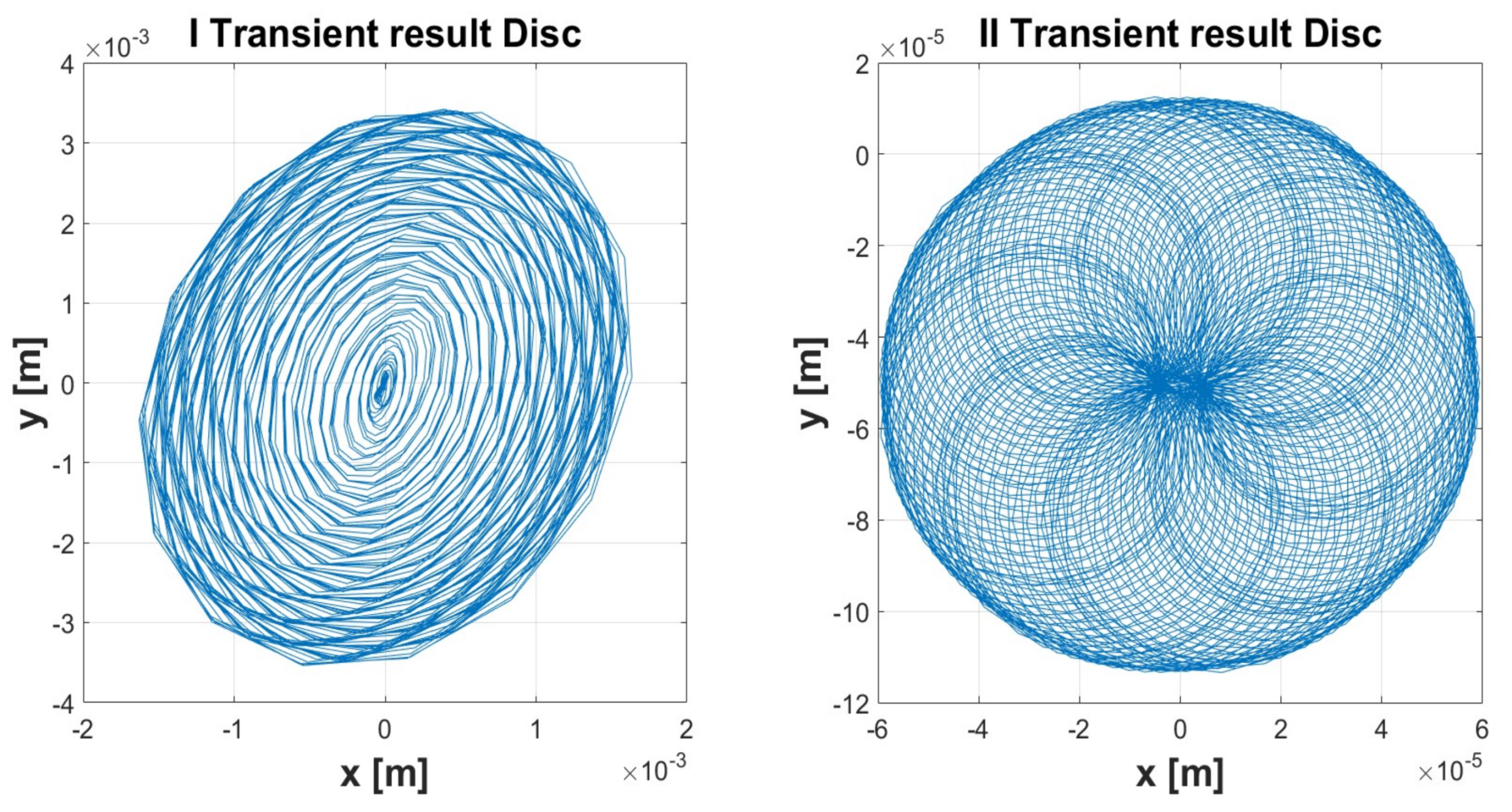
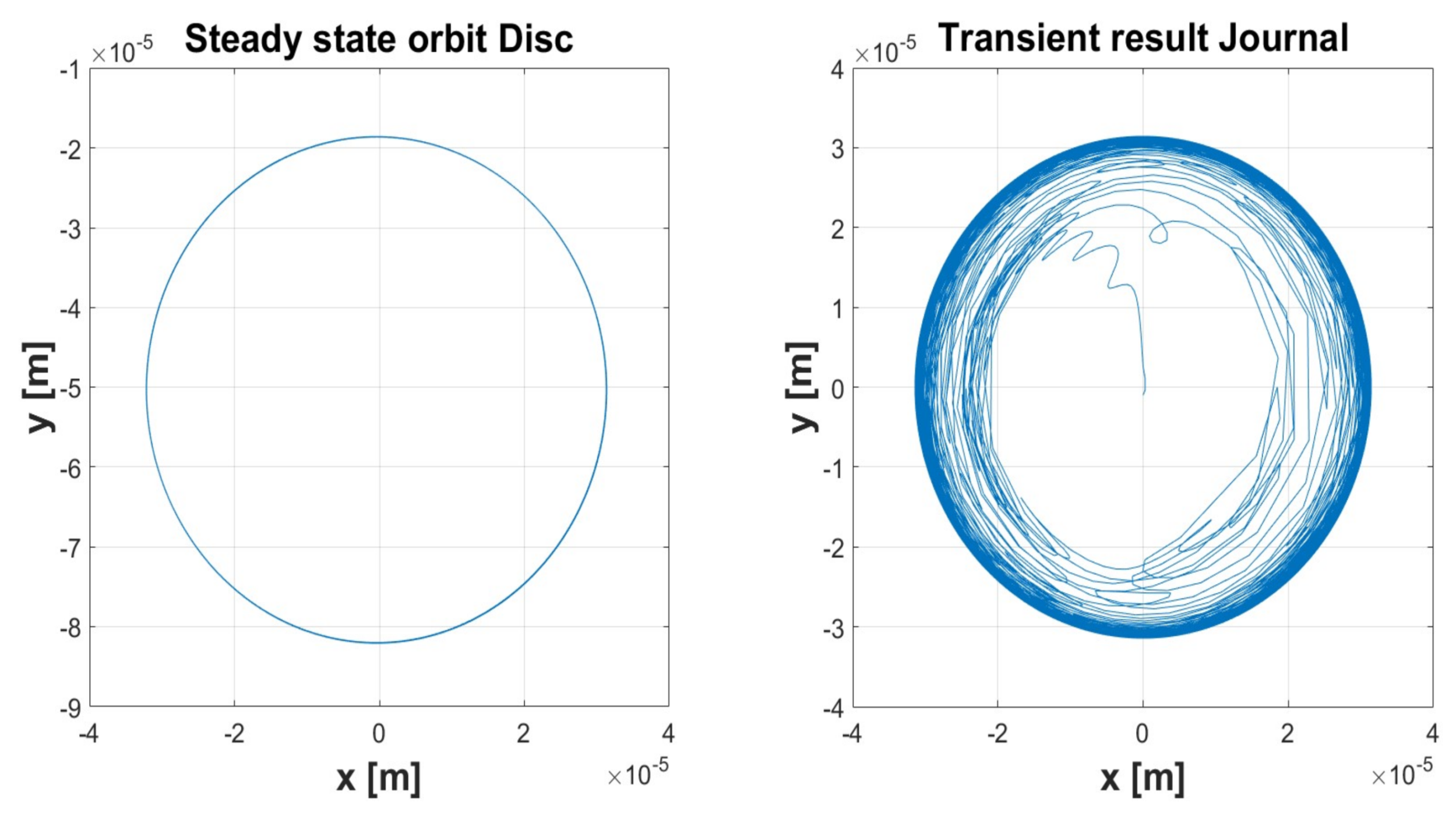
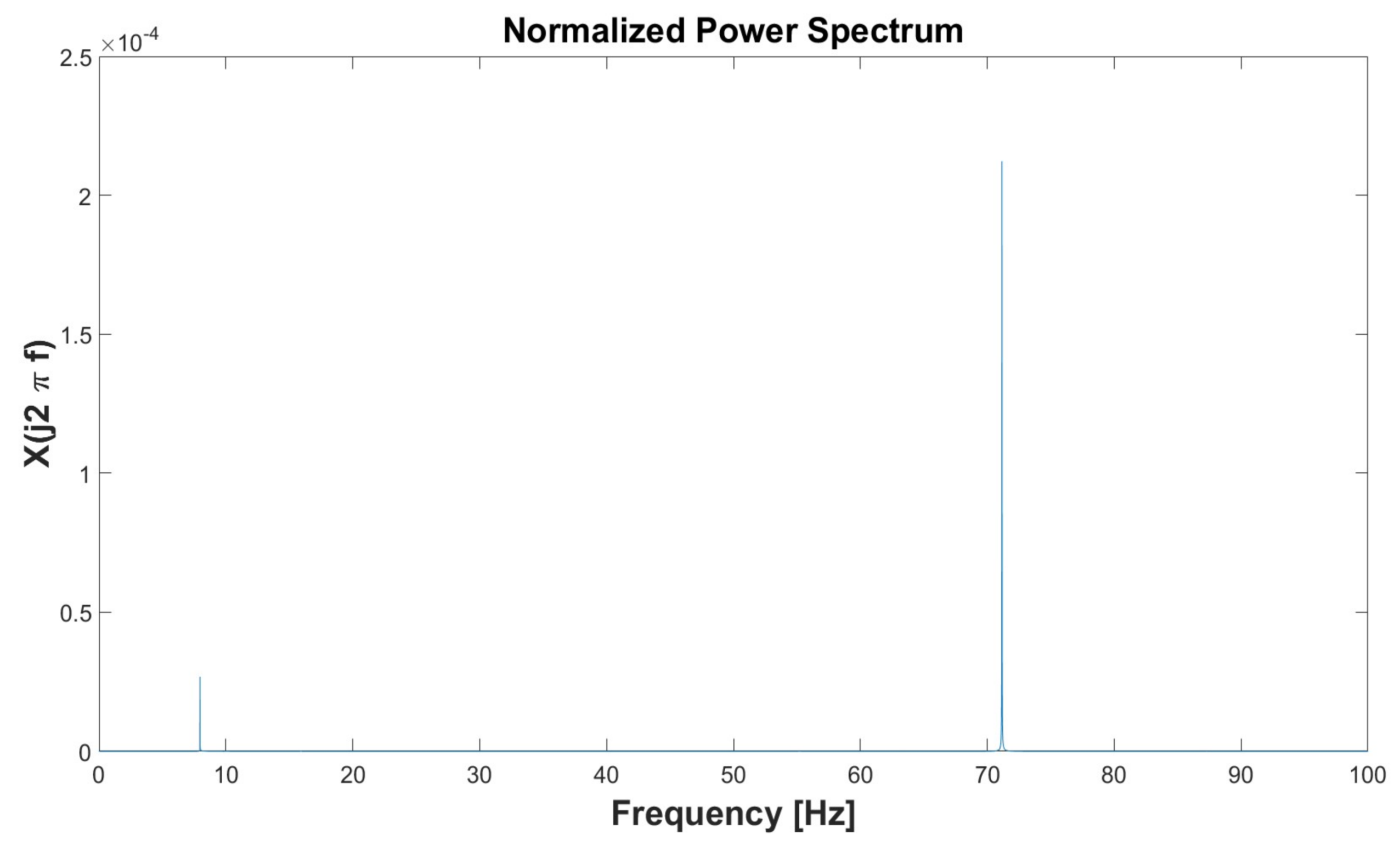
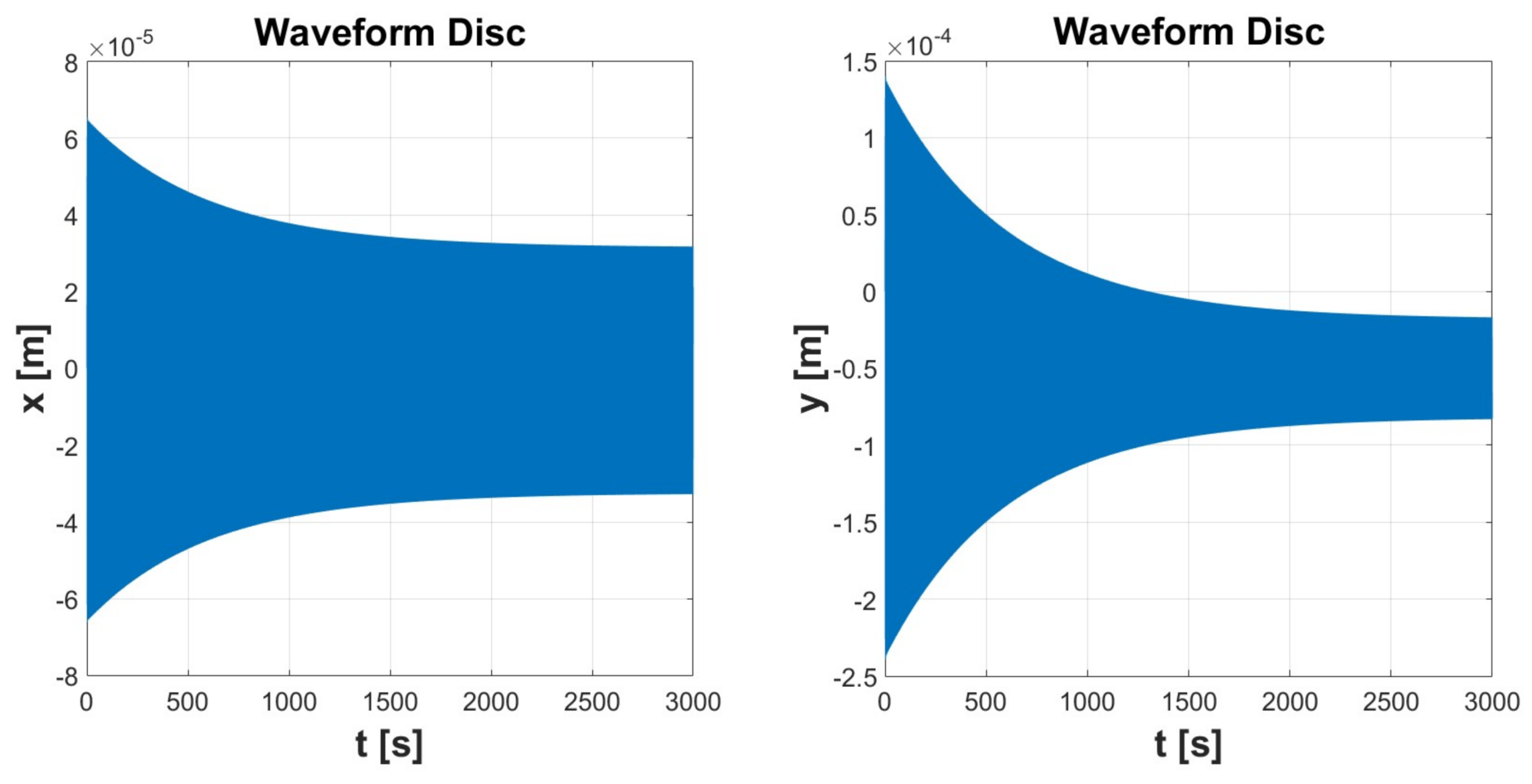
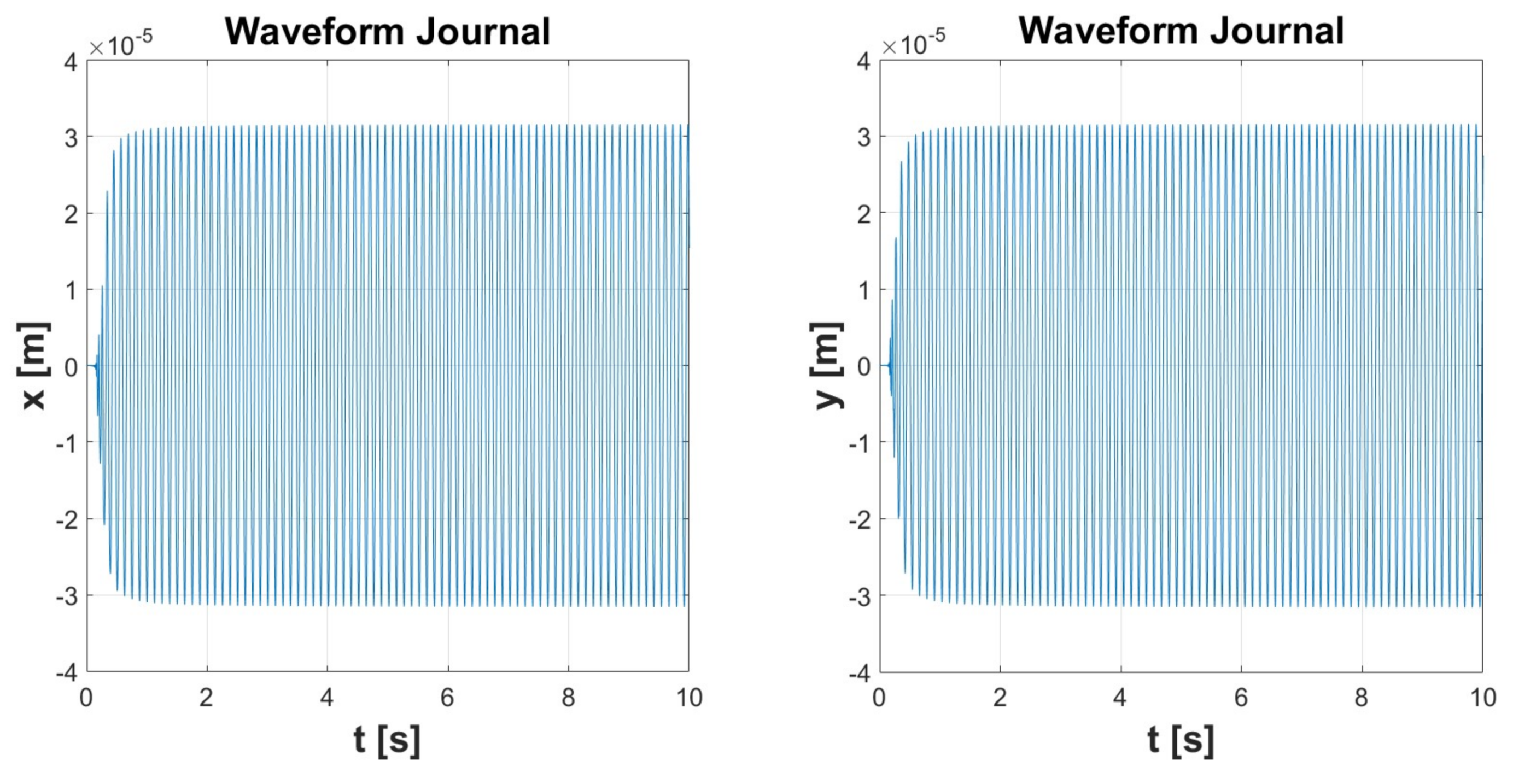
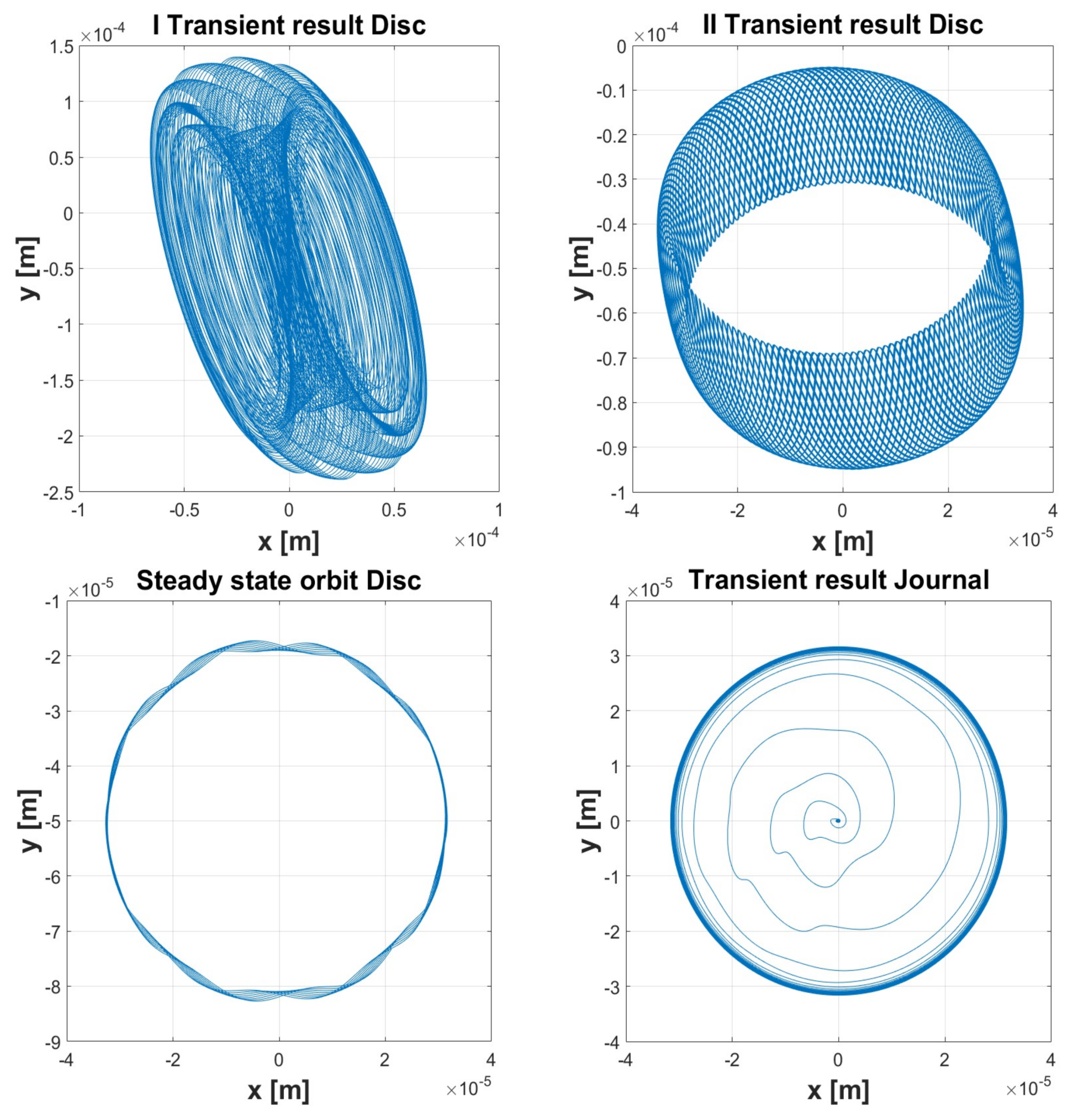
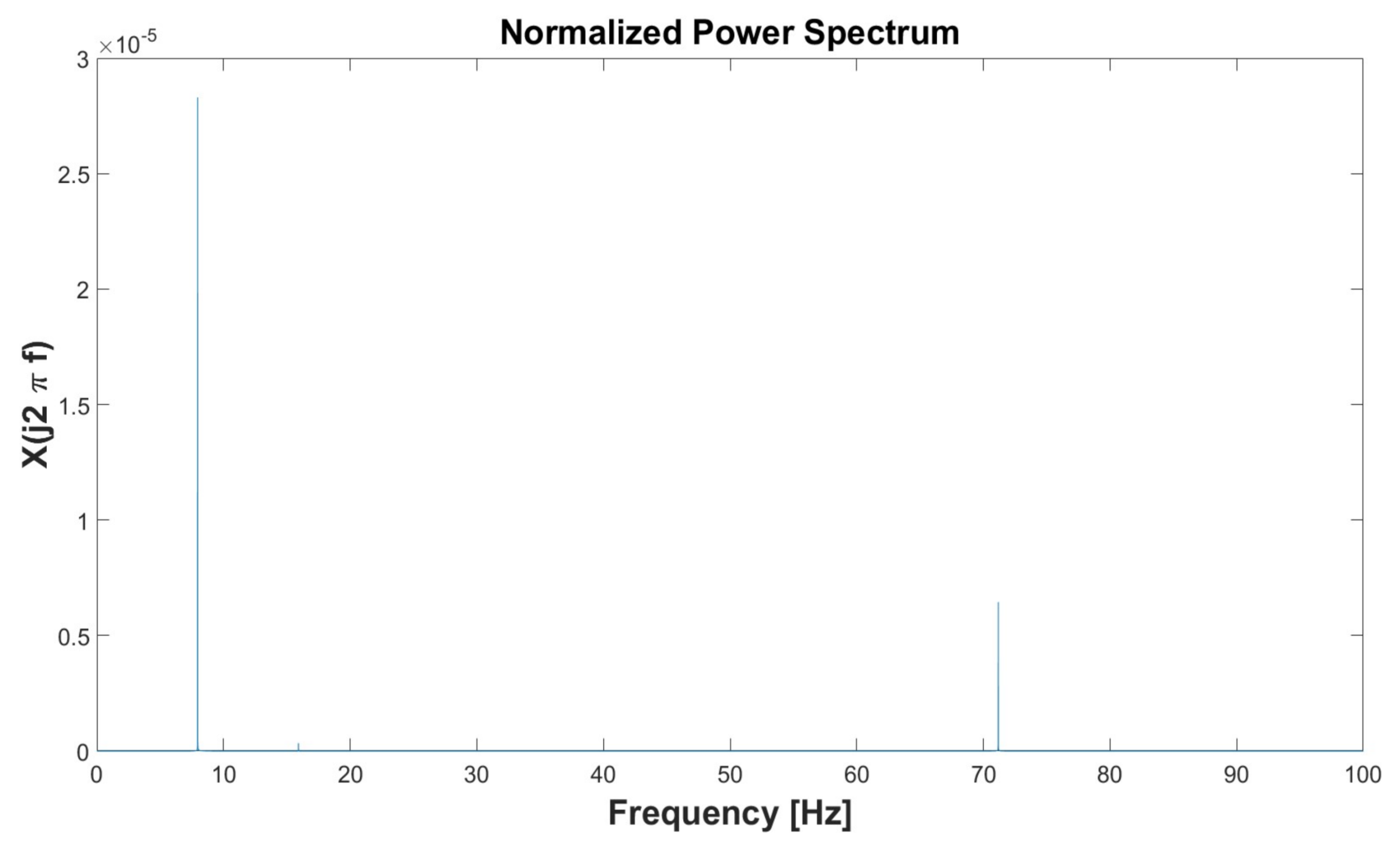
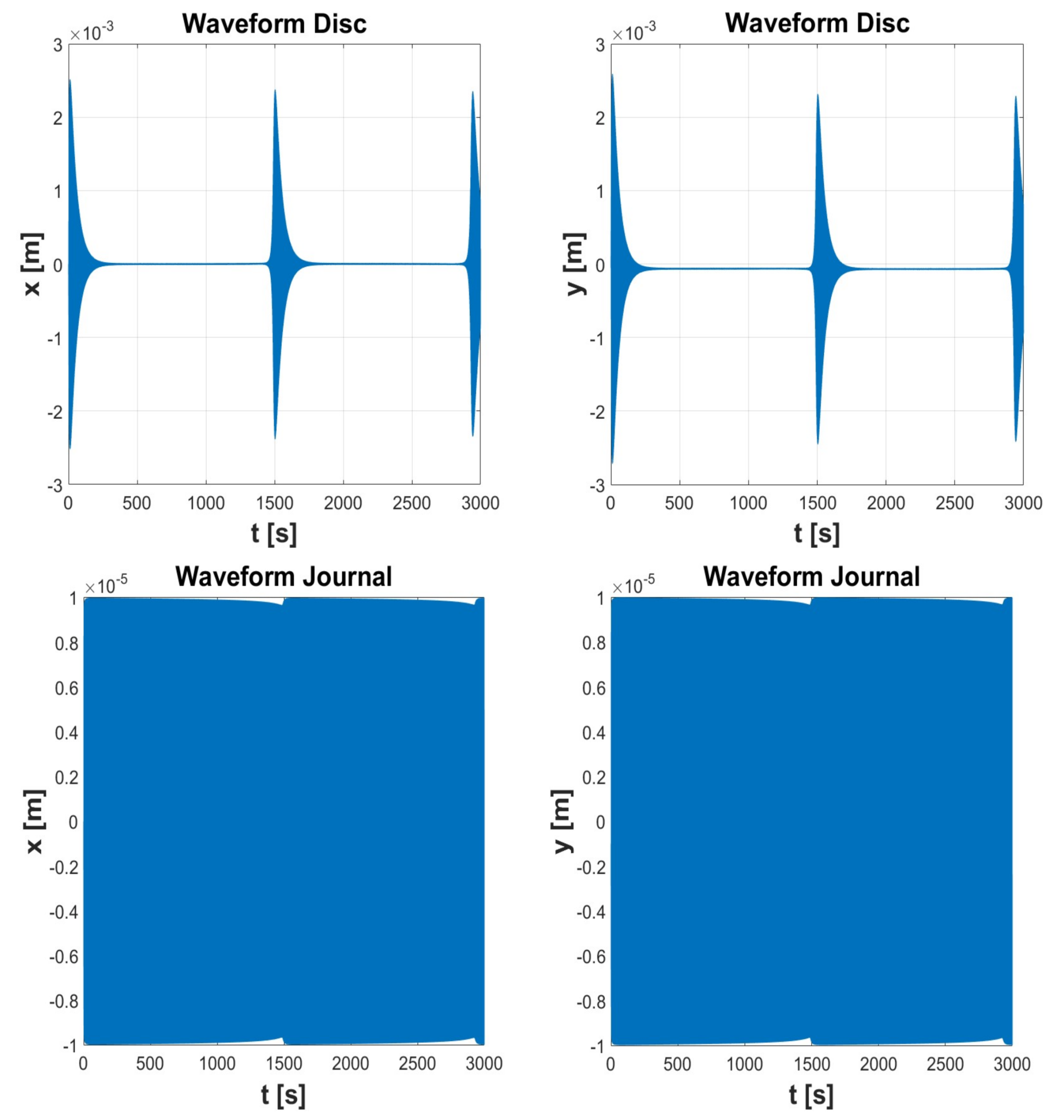
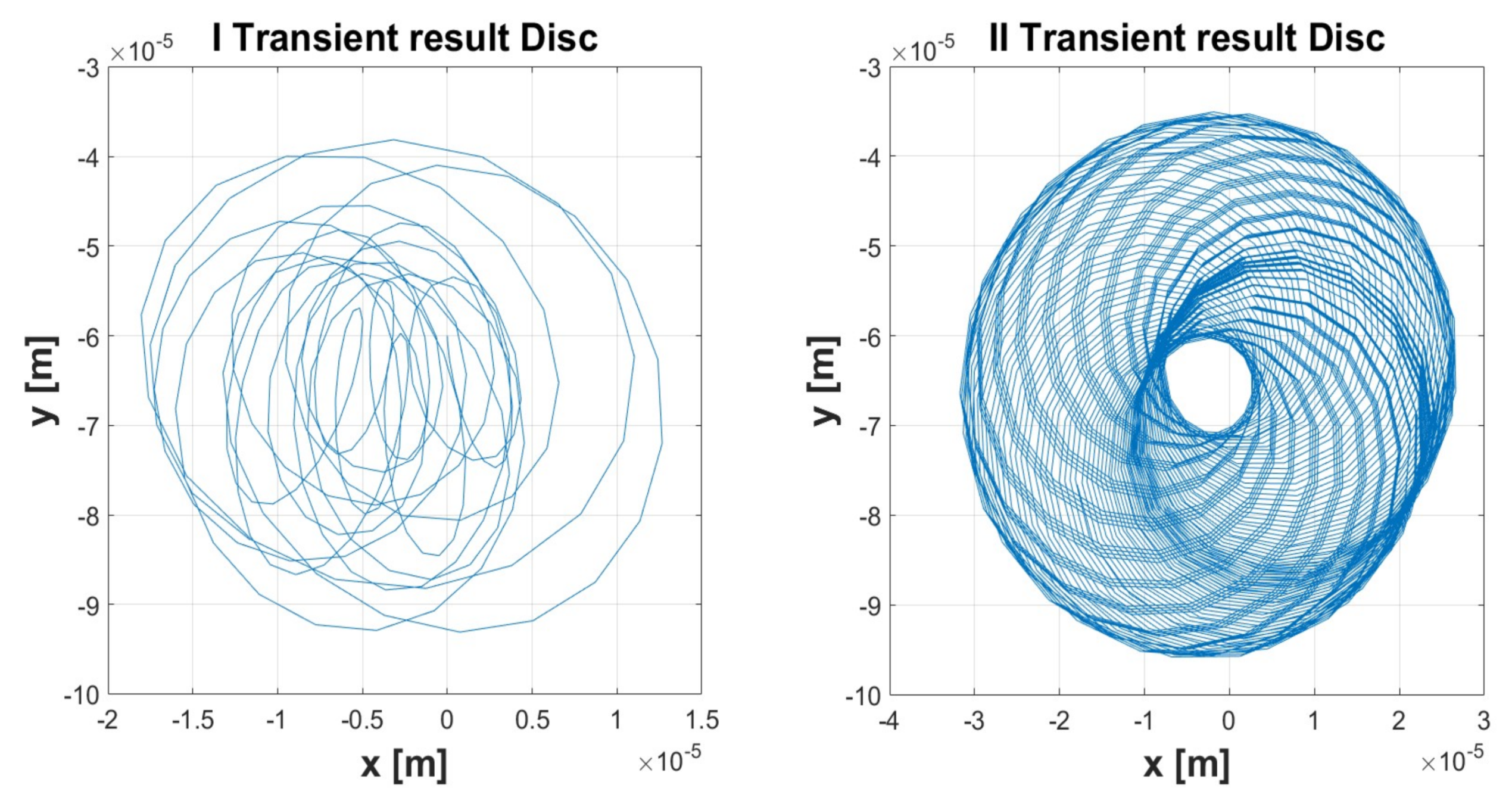
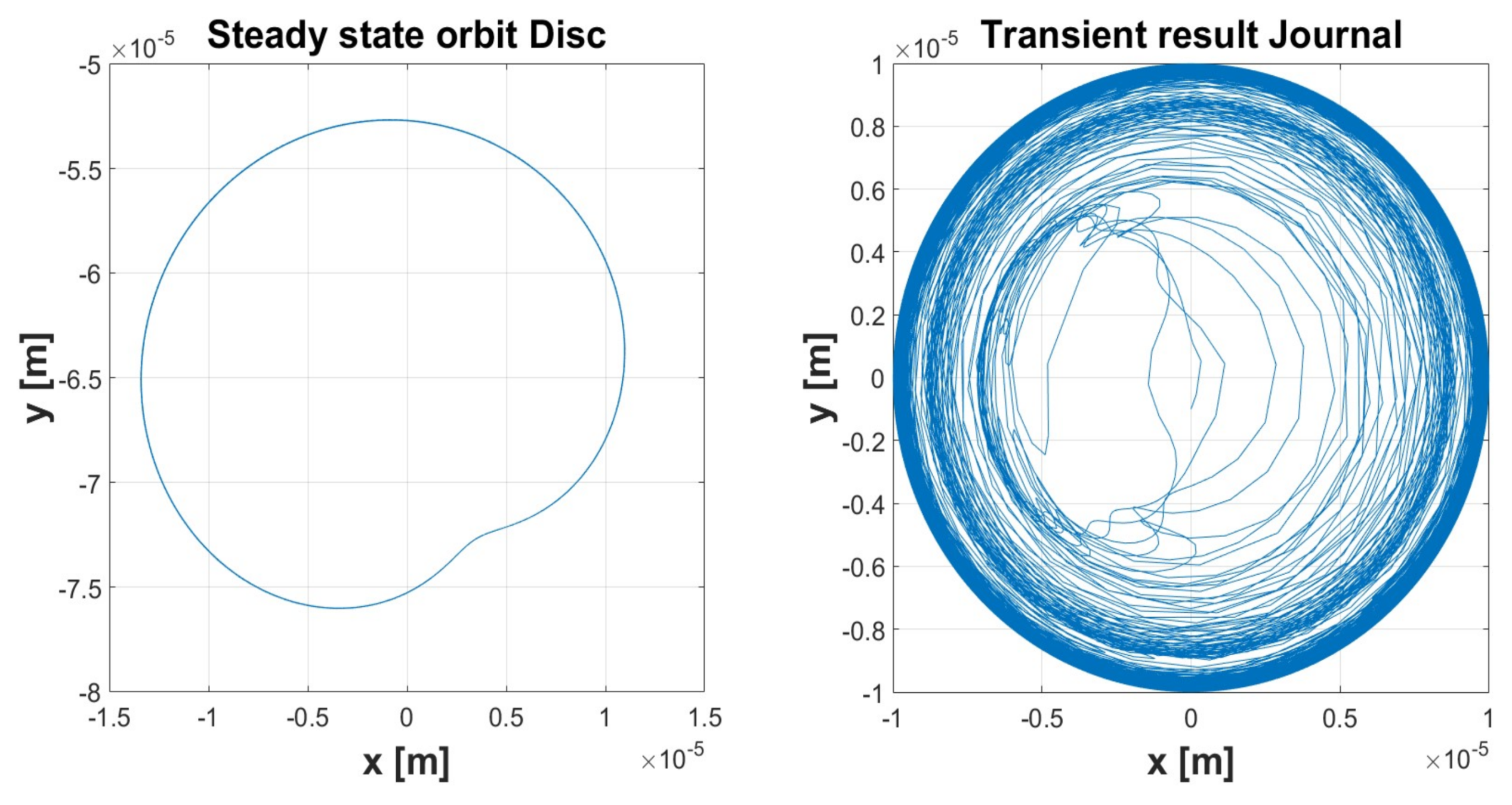
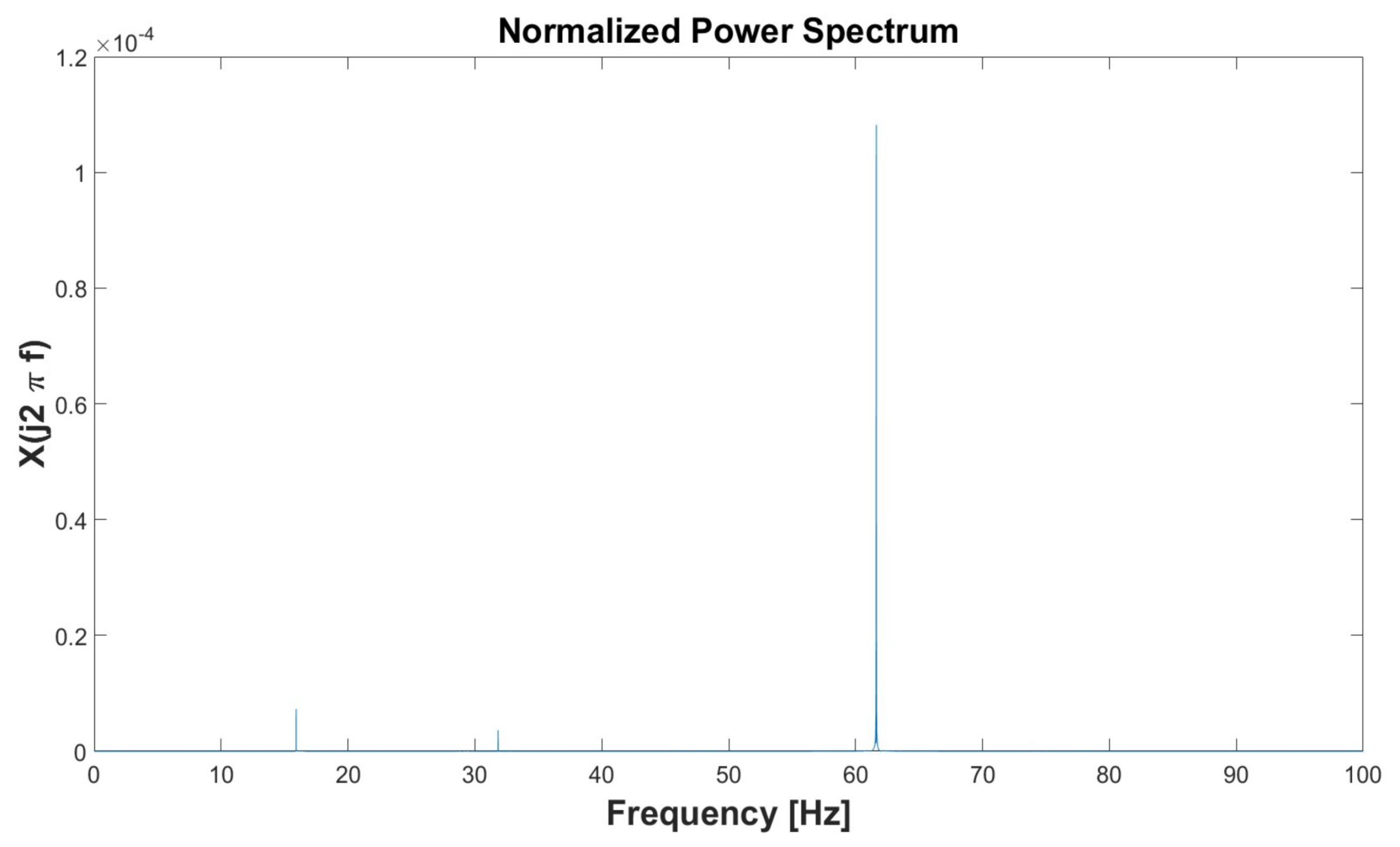
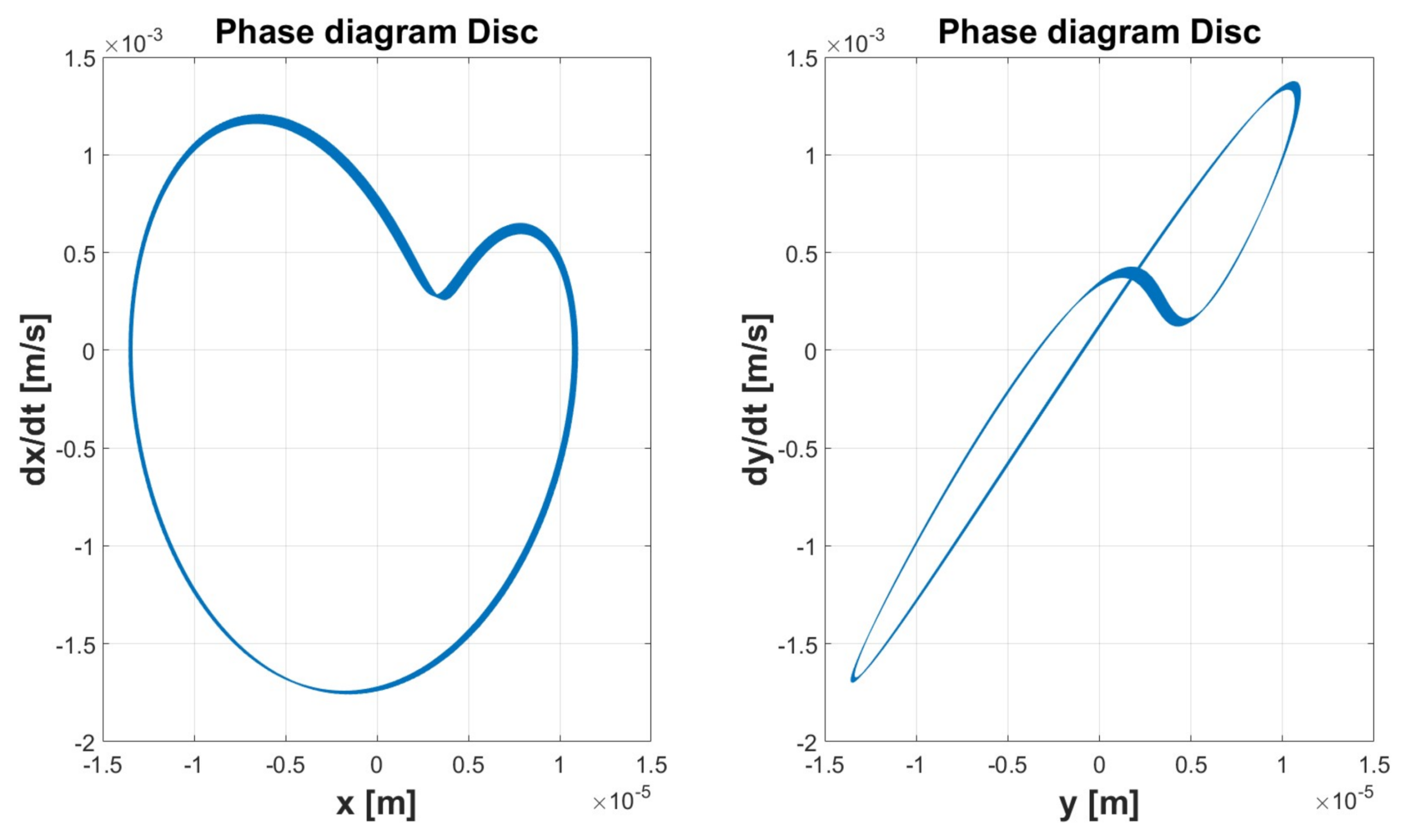
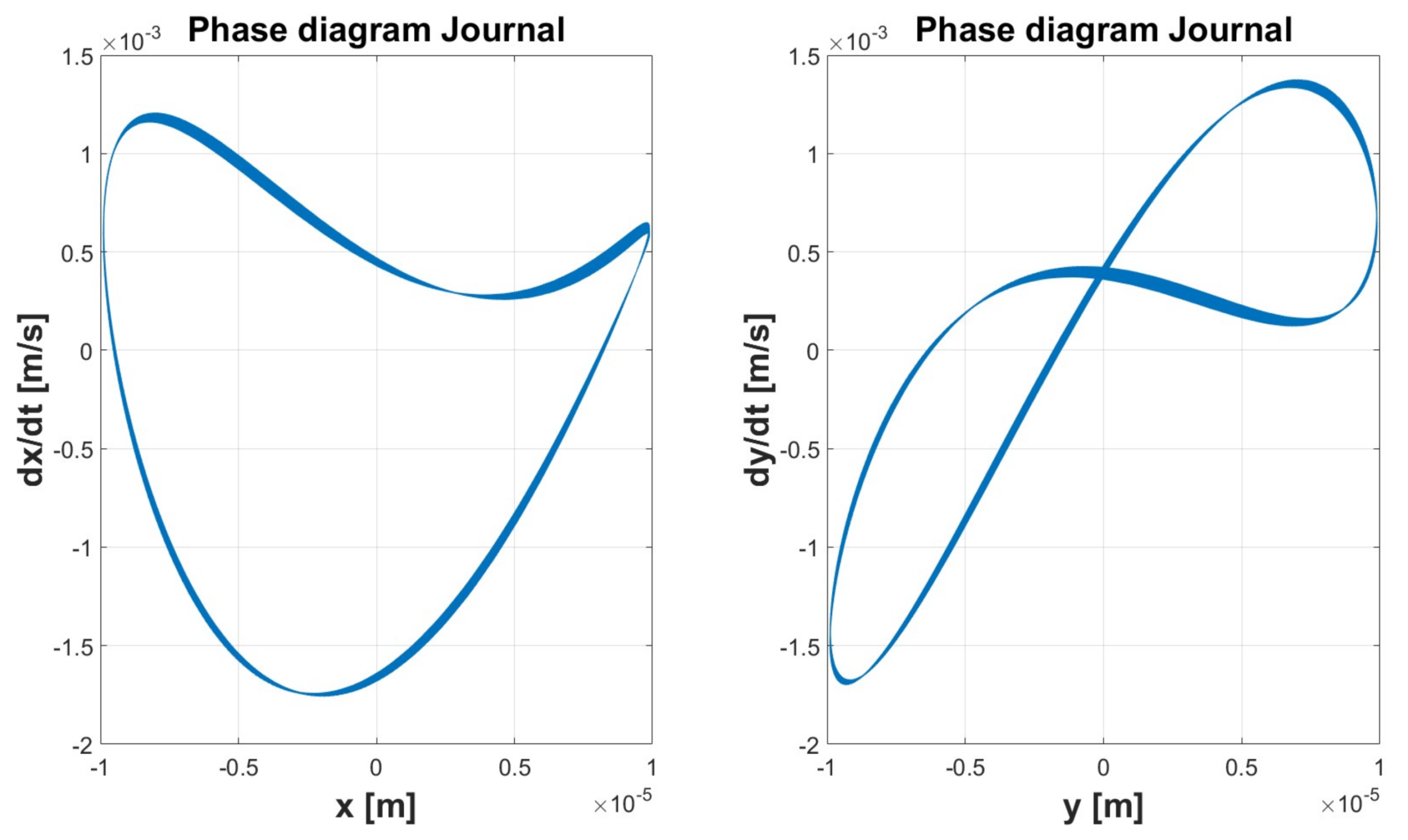
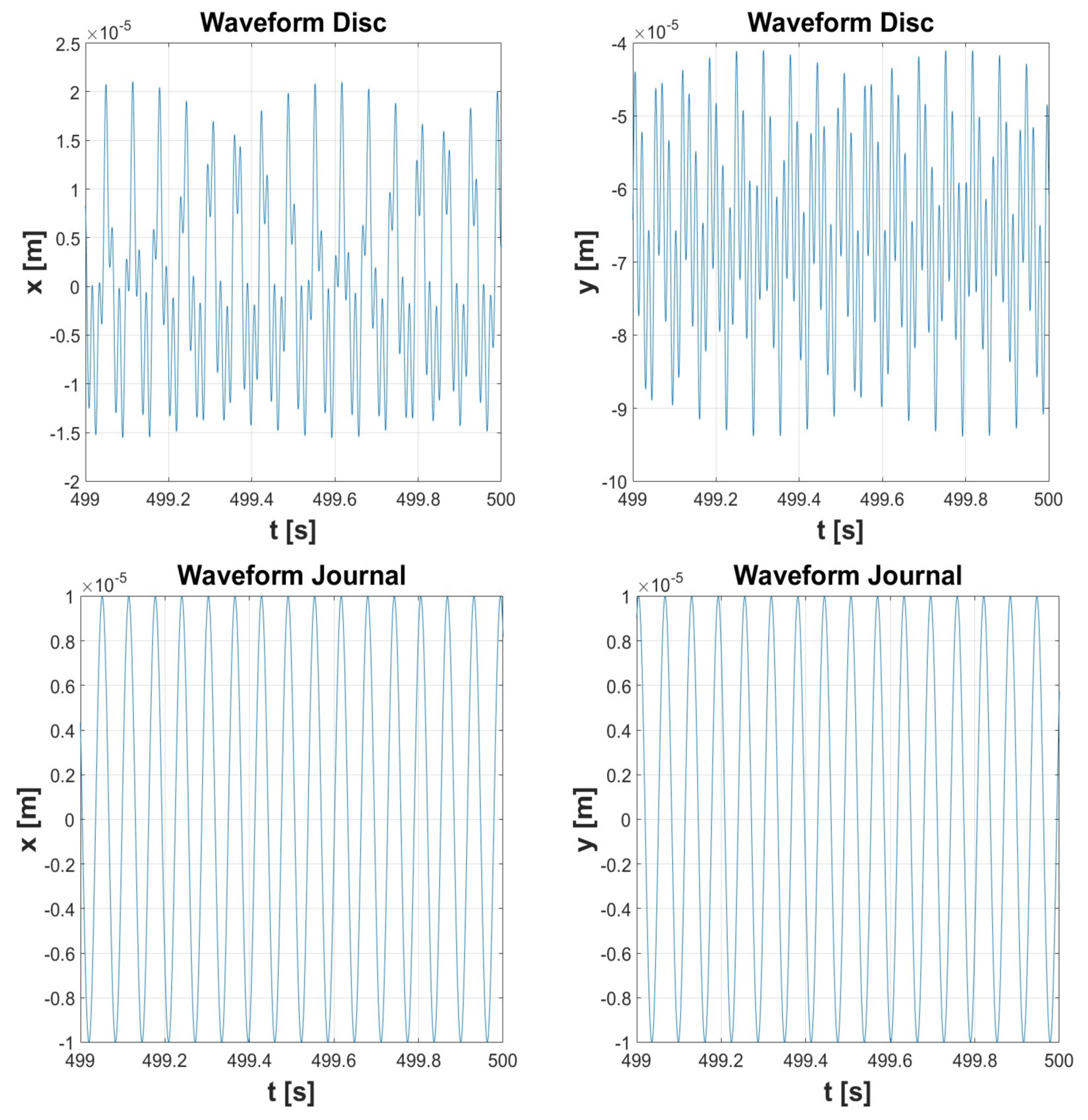
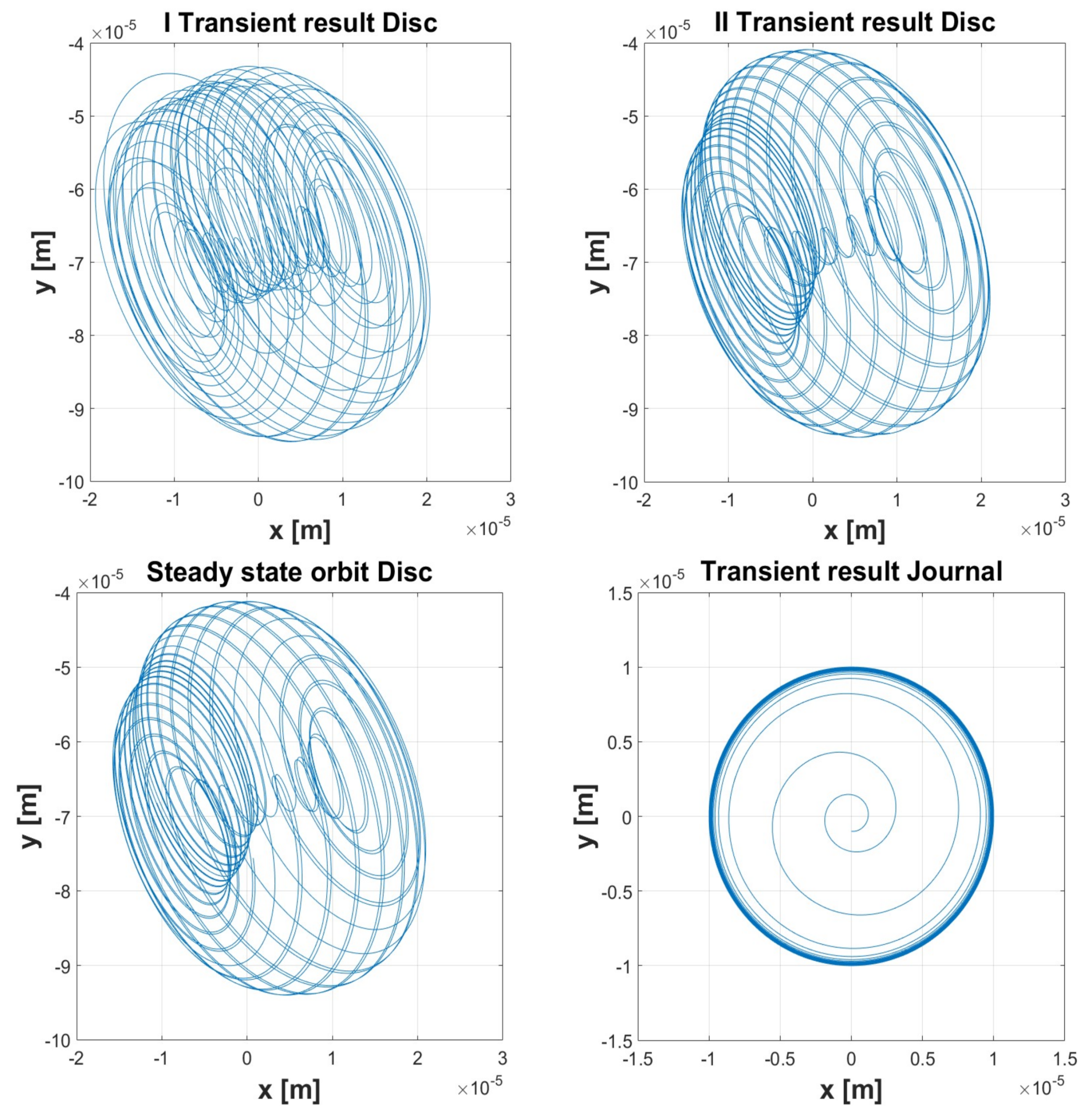
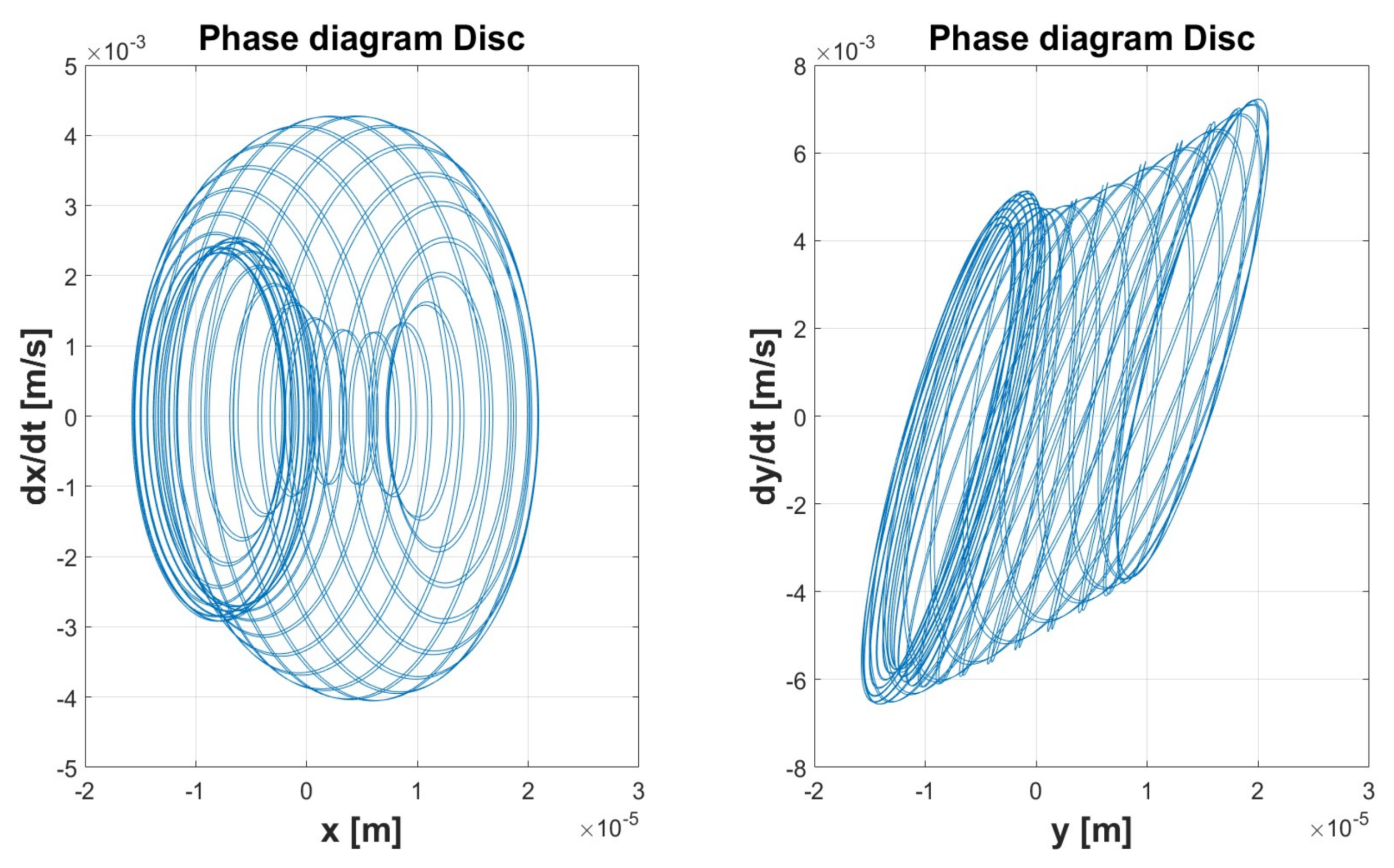
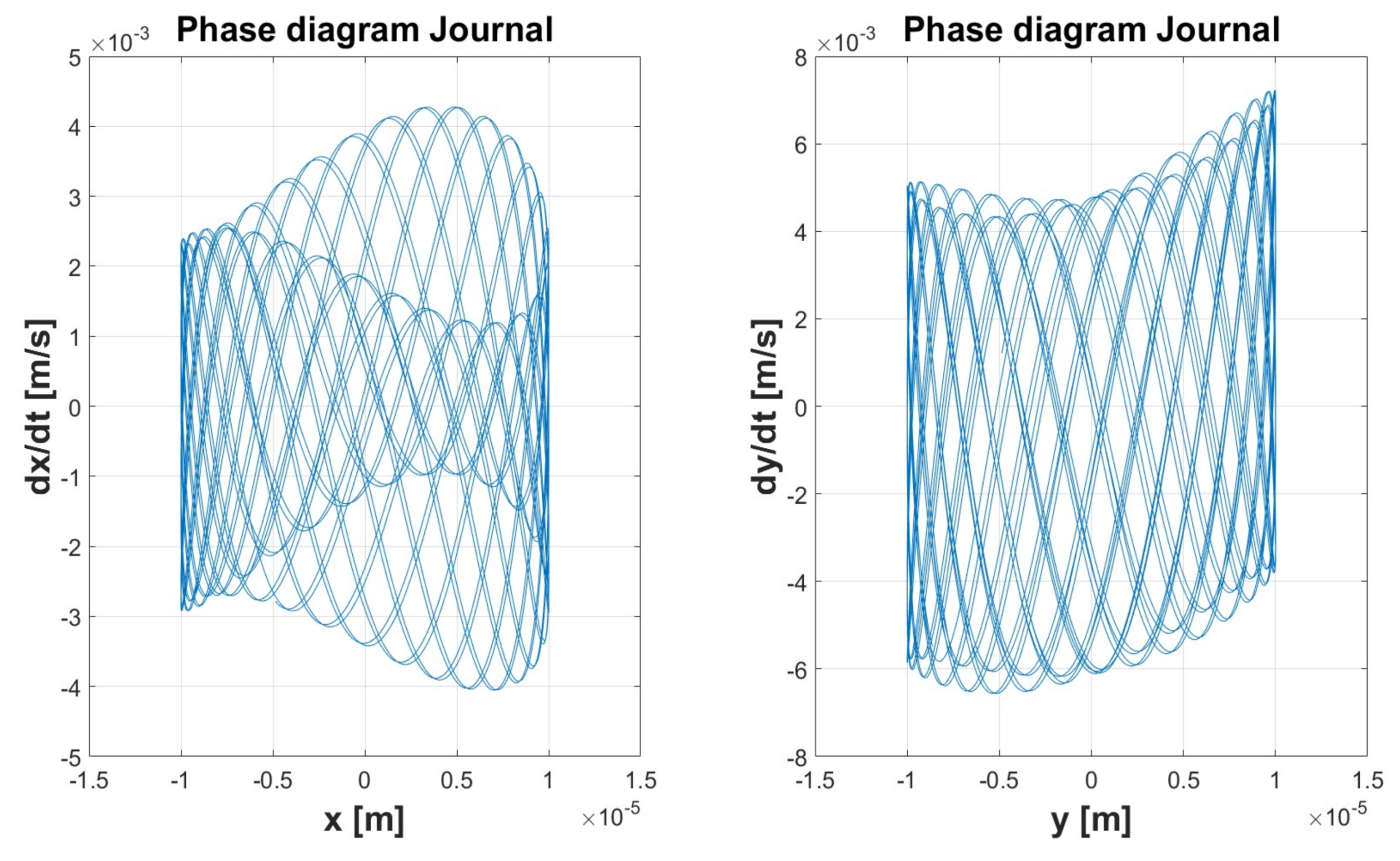
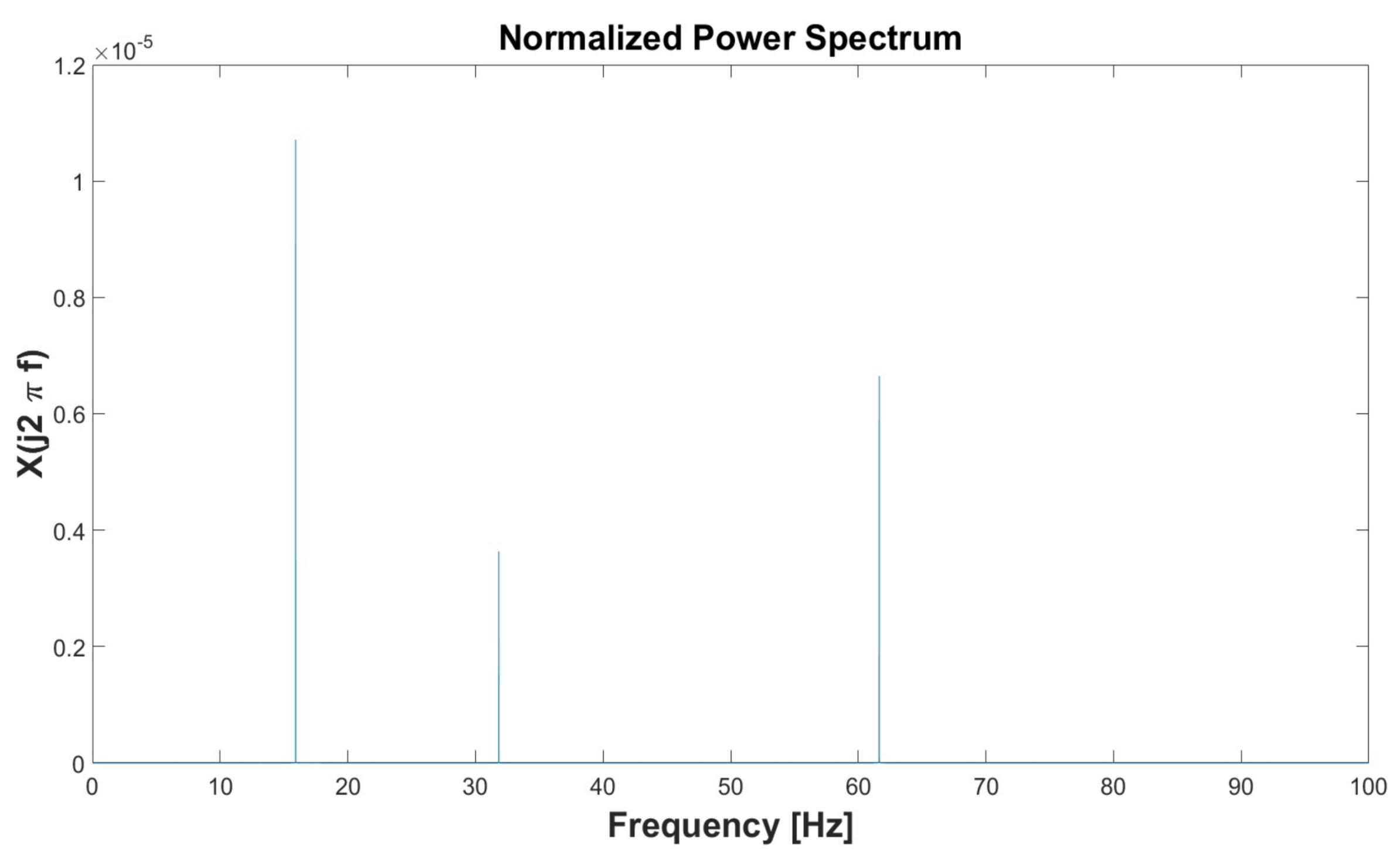
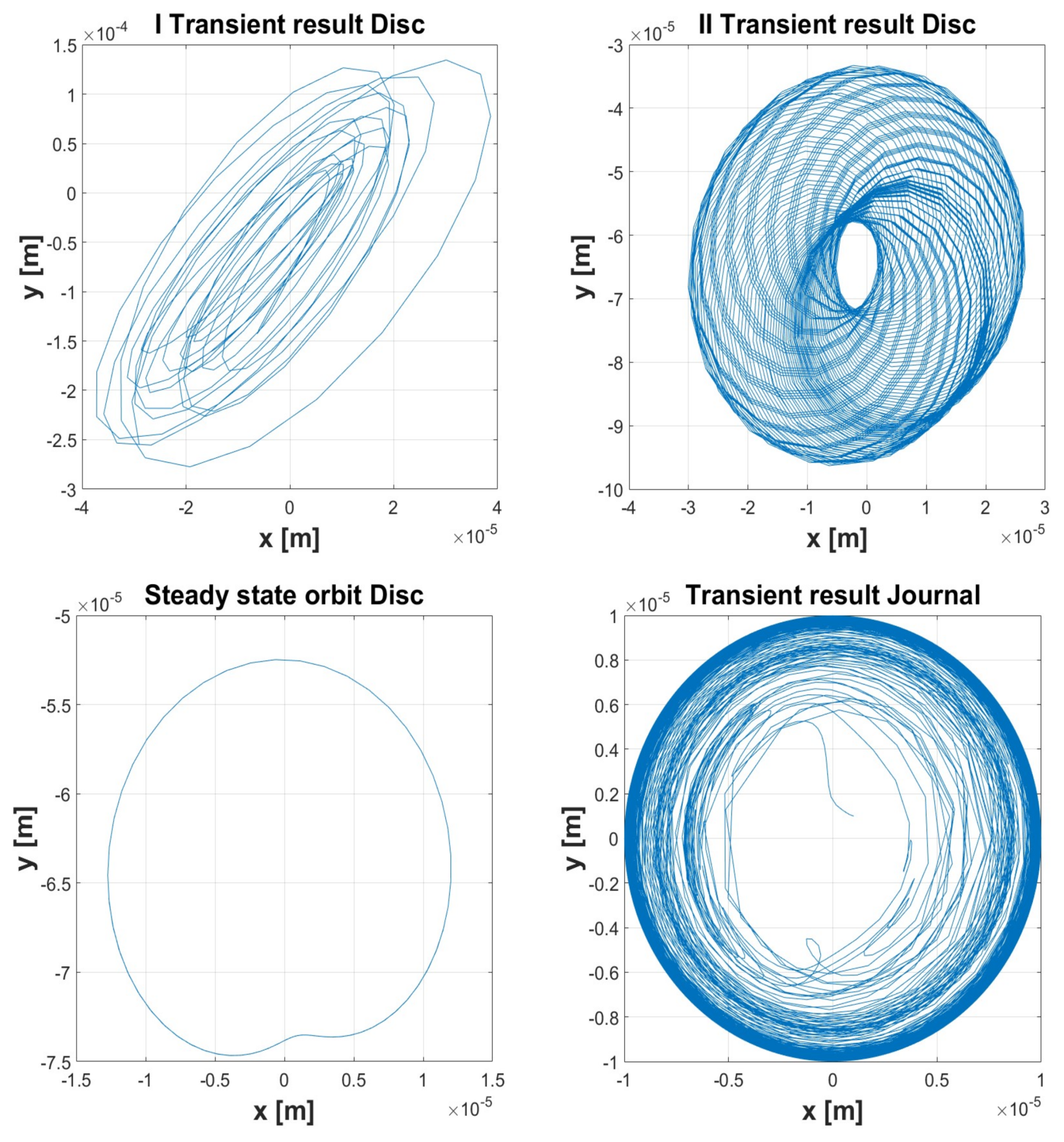
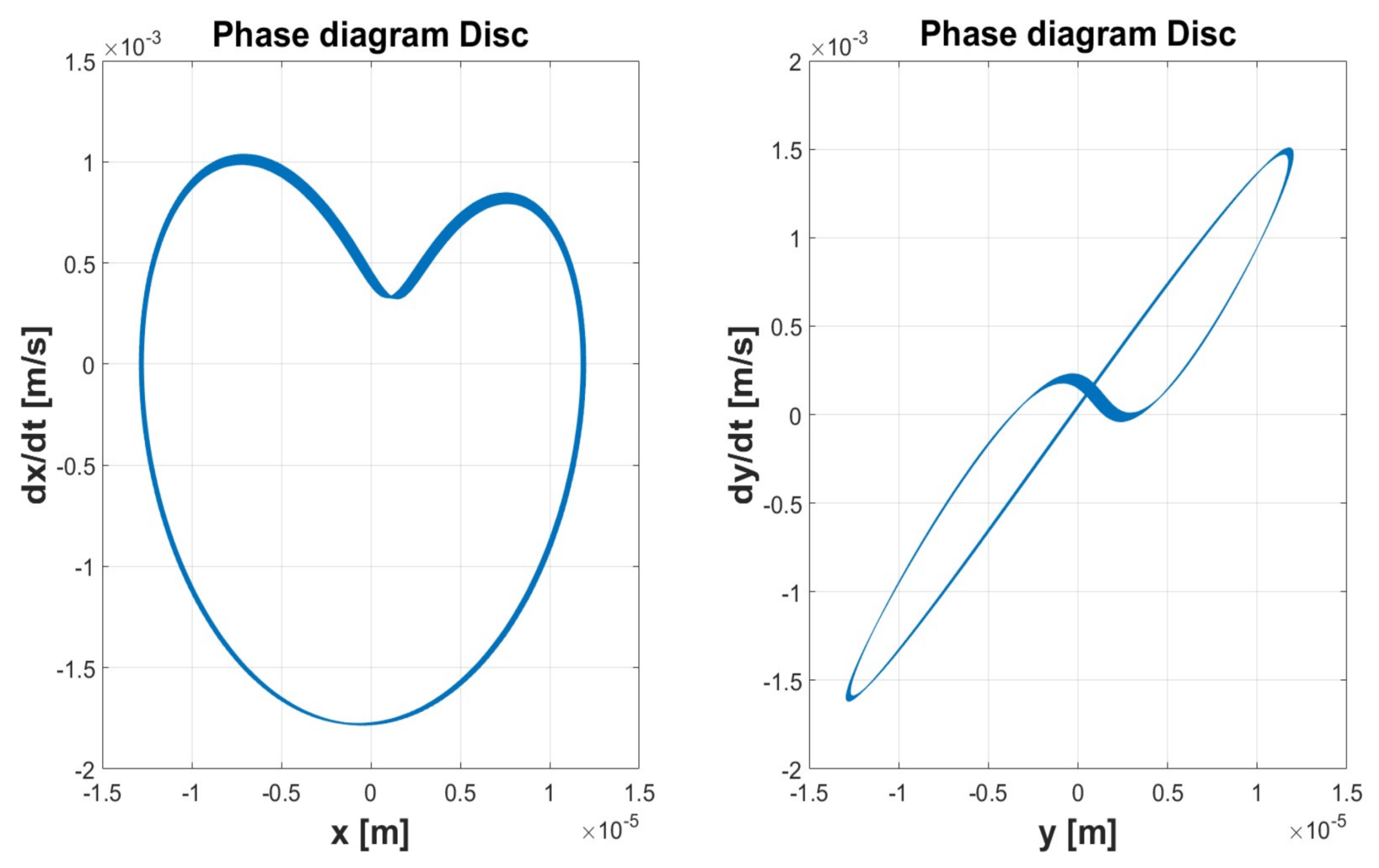

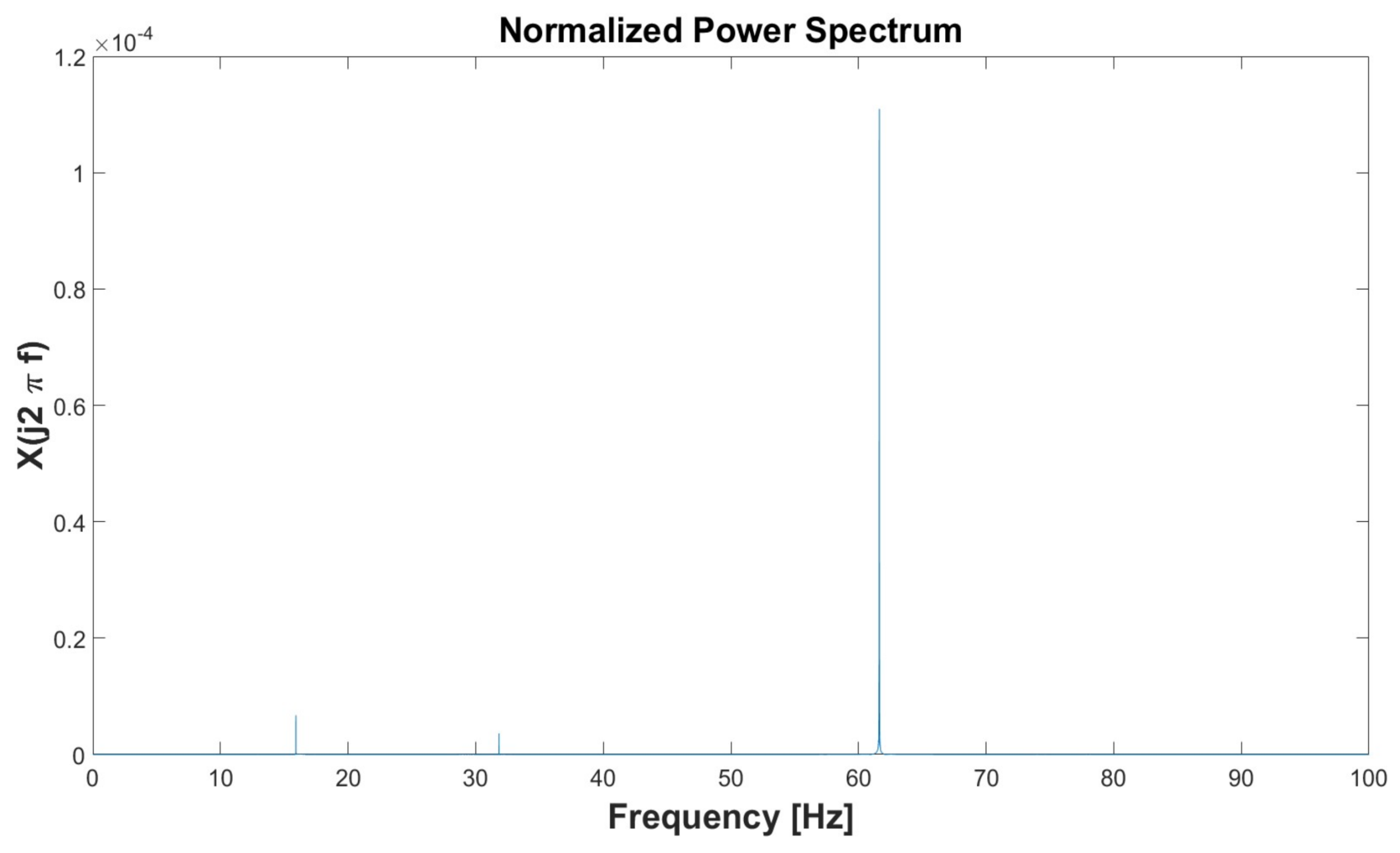
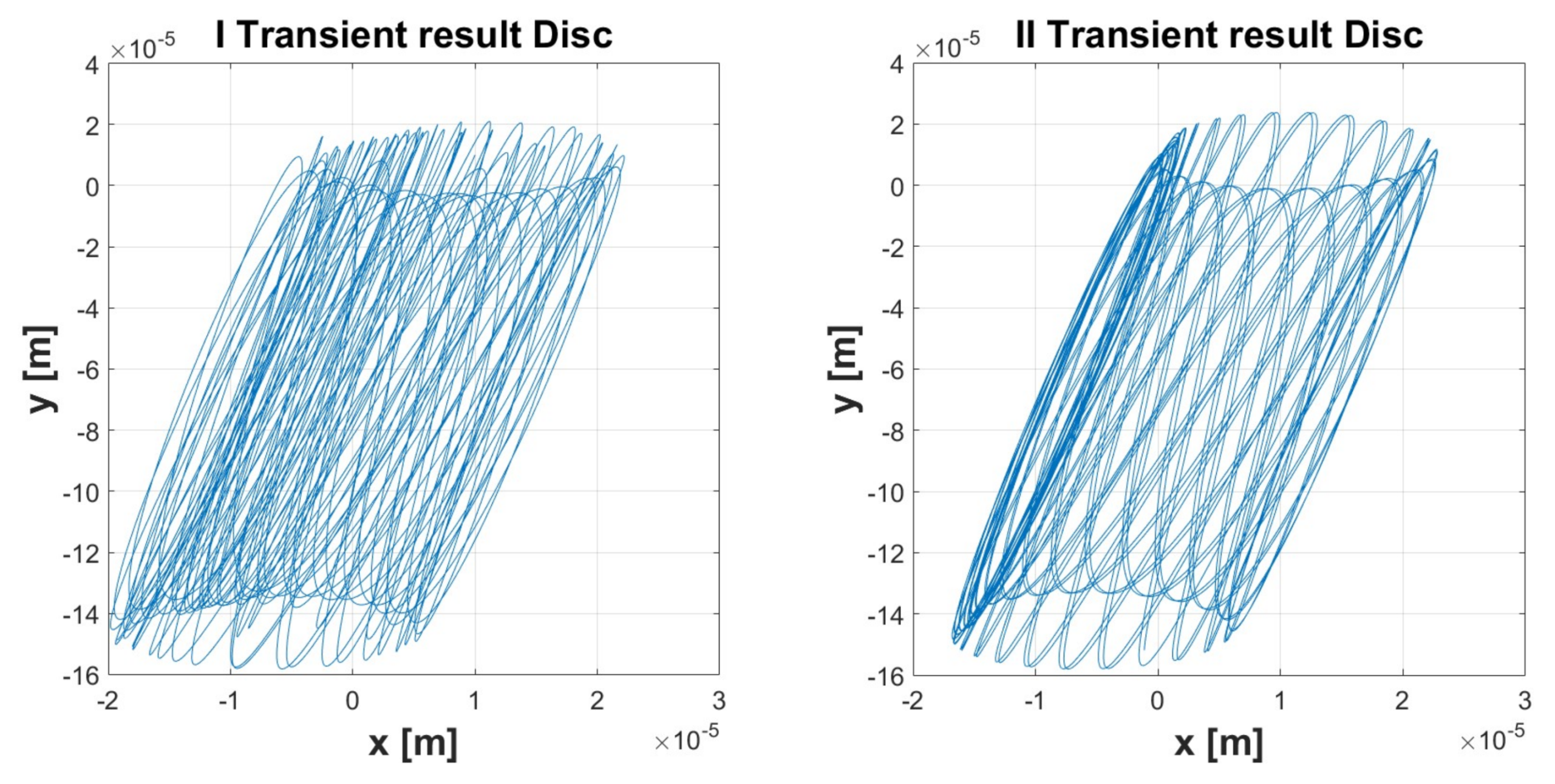
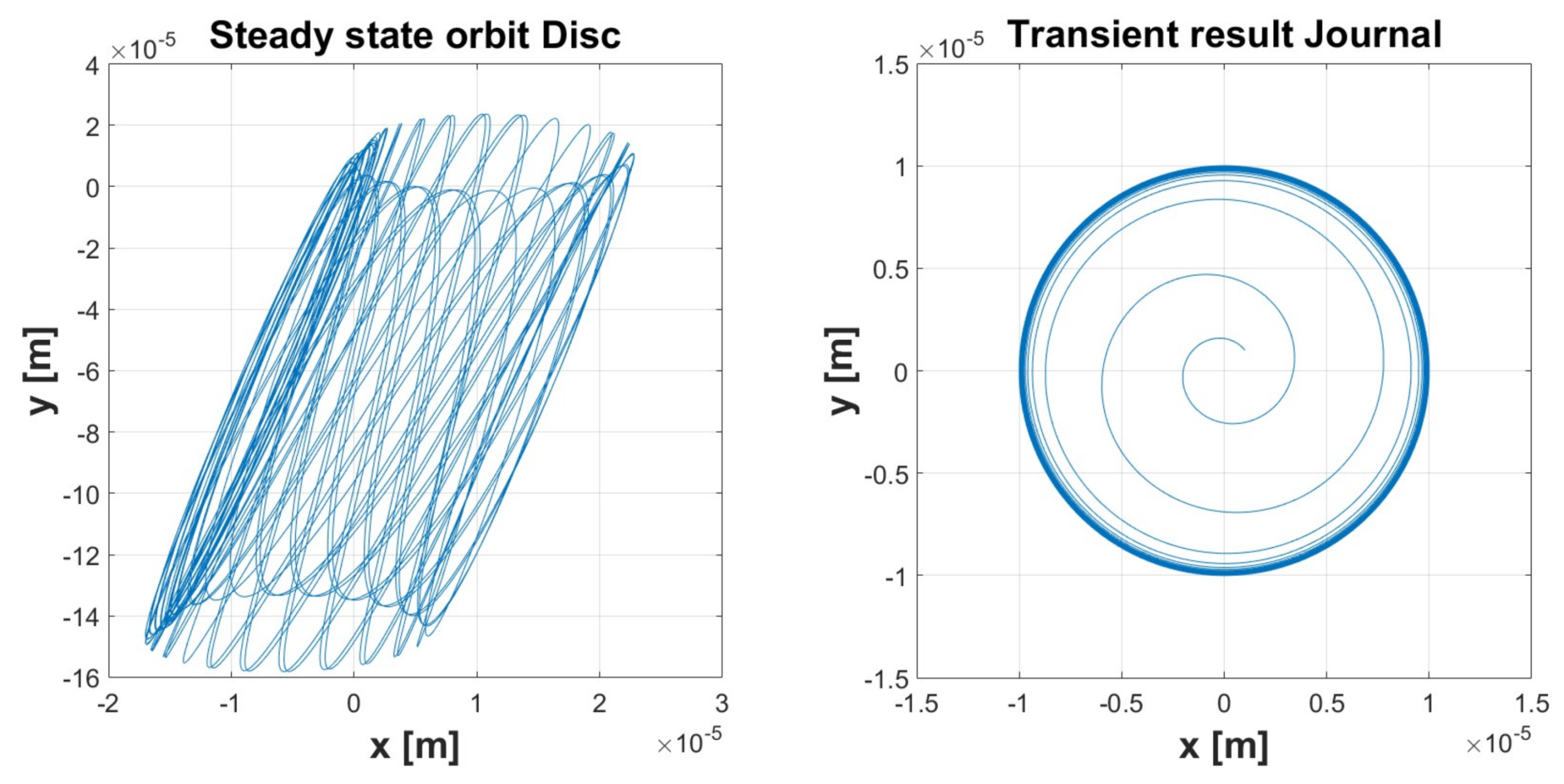
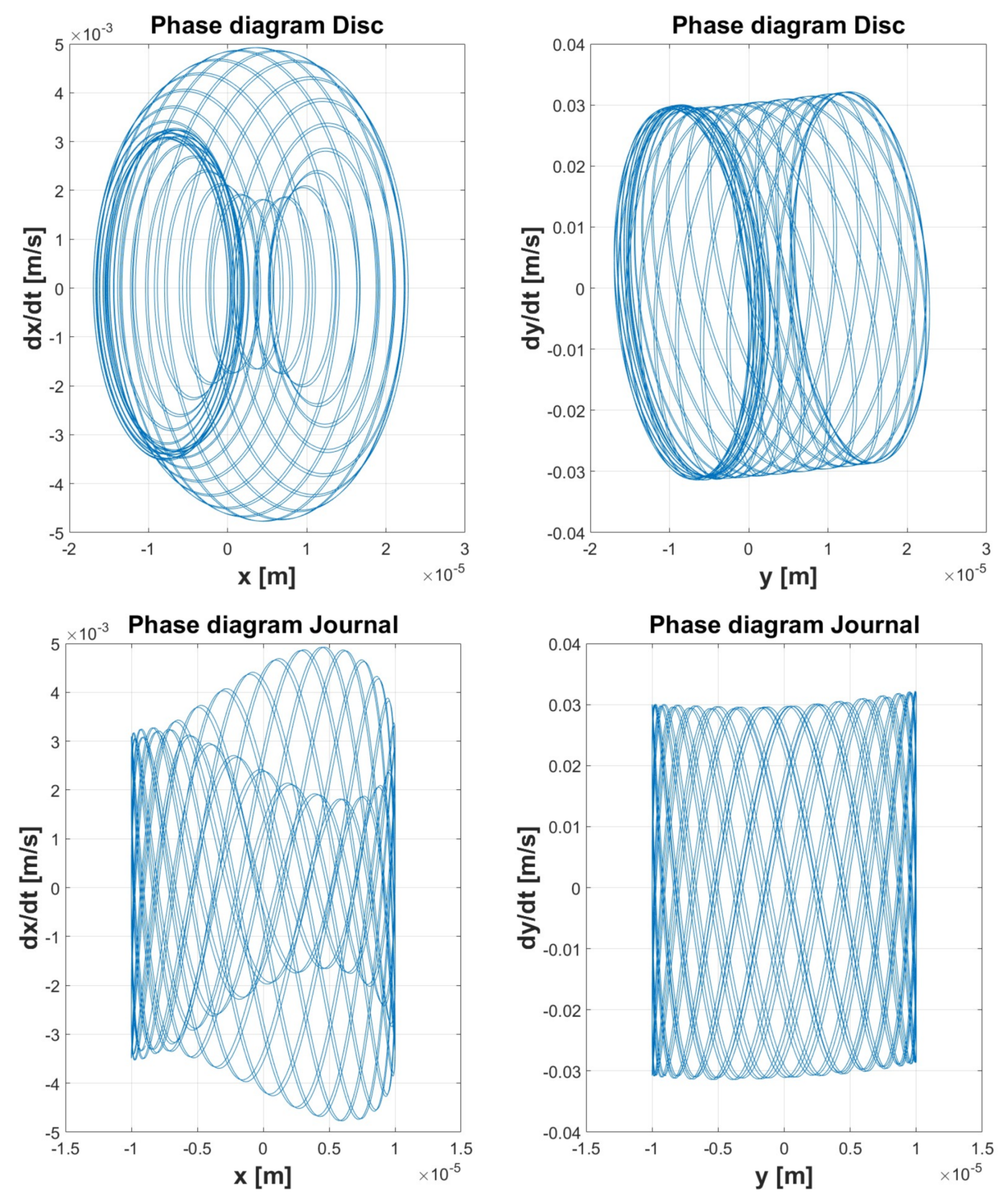
| Simulation 1 | Simulation 2 | Simulation 3 | Simulation 4 | Simulation 5 | ||
|---|---|---|---|---|---|---|
| m (kg) | 10 | 1.5 | 5 × 101 | 2 | 2 | |
| K (N/m) | 106 | 4 × 106 | 107 | 3 × 105 | 3 × 105 | |
| u (m) | 10−4 | 10−3 | 10−5 | 10−5 | 10−5 | |
| R (m) | 5 × 10−2 | 1.6 × 10−2 | 2 × 10−2 | 5 × 10−3 | 5 × 10−3 | |
| L (m) | 5 × 10−2 | 1.6 × 10−2 | 2 × 10−2 | 5 × 10−3 | 5 × 10−3 | |
| μ (kg/s) | 2 × 10−2 | 3.4 × 10−2 | 2.5 × 10−2 | 2 × 10−2 | 2 × 10−2 | |
| ω (Hz) | 50 | 100 | 15.92 | 31.83 | 31.83 | |
| c (m) | 10−4 | 3.16 × 10−5 | 3.16 × 10−5 | 10−5 | 10−5 | |
| p0 (bar) | 2 | 2 | 2 | 2 | 2 | |
| 0 | 0 | 0 | 0 | 10−5 | ||
| 0 | 0 | 0 | 0 | 0 | ||
| −10−5 | −10−5 | −5 × 10−6 | −6 × 10−5 | 10−5 | ||
| 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 10−6 | ||
| −10−5 | −10−6 | −10−6 | −10−6 | 10−6 | ||
| Time | Uncavitated | 103 | 103 | 103 | 3 × 103 | 3 × 103 |
| Cavitated (π−Film) | 5 × 102 | 3 × 103 | 3 × 103 | 2 × 103 | 2 × 103 | |
| Solver | Ode4 | |||||
| Fixed-step size [s] | Uncavitated | 10−4 | 10−4 | 10−3 | 10−3 | 10−3 |
| Cavitated (π−Film) | 10−4 | 10−3 | 10−4 | 10−4 | 10−4 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruggiero, A.; D’Amato, R.; Magliano, E.; Kozak, D. Dynamical Simulations of a Flexible Rotor in Cylindrical Uncavitated and Cavitated Lubricated Journal Bearings. Lubricants 2018, 6, 40. https://doi.org/10.3390/lubricants6020040
Ruggiero A, D’Amato R, Magliano E, Kozak D. Dynamical Simulations of a Flexible Rotor in Cylindrical Uncavitated and Cavitated Lubricated Journal Bearings. Lubricants. 2018; 6(2):40. https://doi.org/10.3390/lubricants6020040
Chicago/Turabian StyleRuggiero, Alessandro, Roberto D’Amato, Emanuele Magliano, and Drazan Kozak. 2018. "Dynamical Simulations of a Flexible Rotor in Cylindrical Uncavitated and Cavitated Lubricated Journal Bearings" Lubricants 6, no. 2: 40. https://doi.org/10.3390/lubricants6020040
APA StyleRuggiero, A., D’Amato, R., Magliano, E., & Kozak, D. (2018). Dynamical Simulations of a Flexible Rotor in Cylindrical Uncavitated and Cavitated Lubricated Journal Bearings. Lubricants, 6(2), 40. https://doi.org/10.3390/lubricants6020040