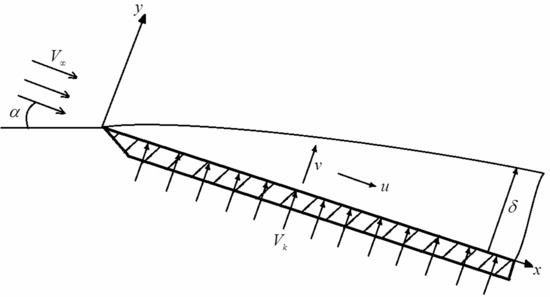
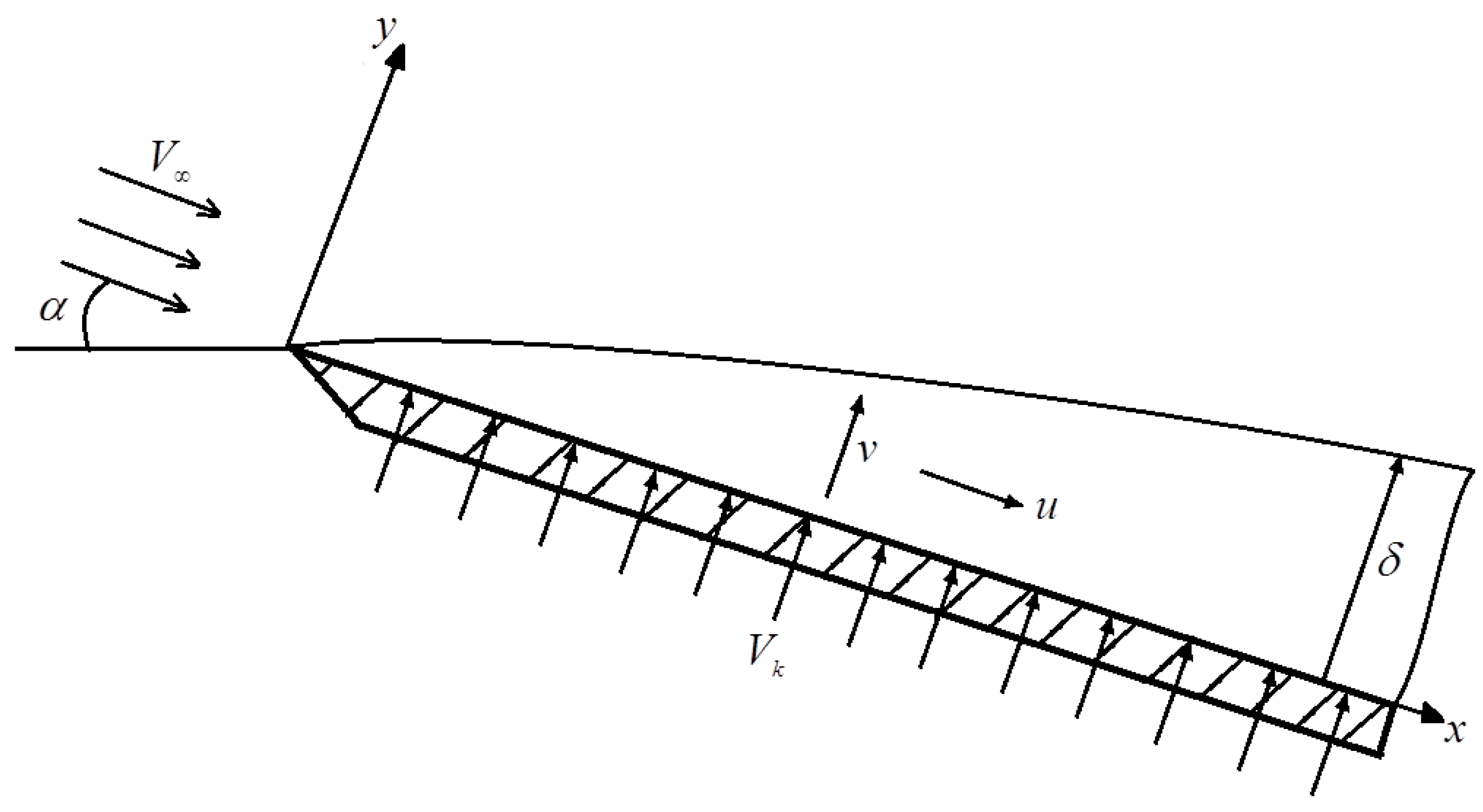
Reducing Friction with a Liquid Film on the Body Surface
Abstract
:1. Introduction
2. Materials and Methods
3. Methods of Solution
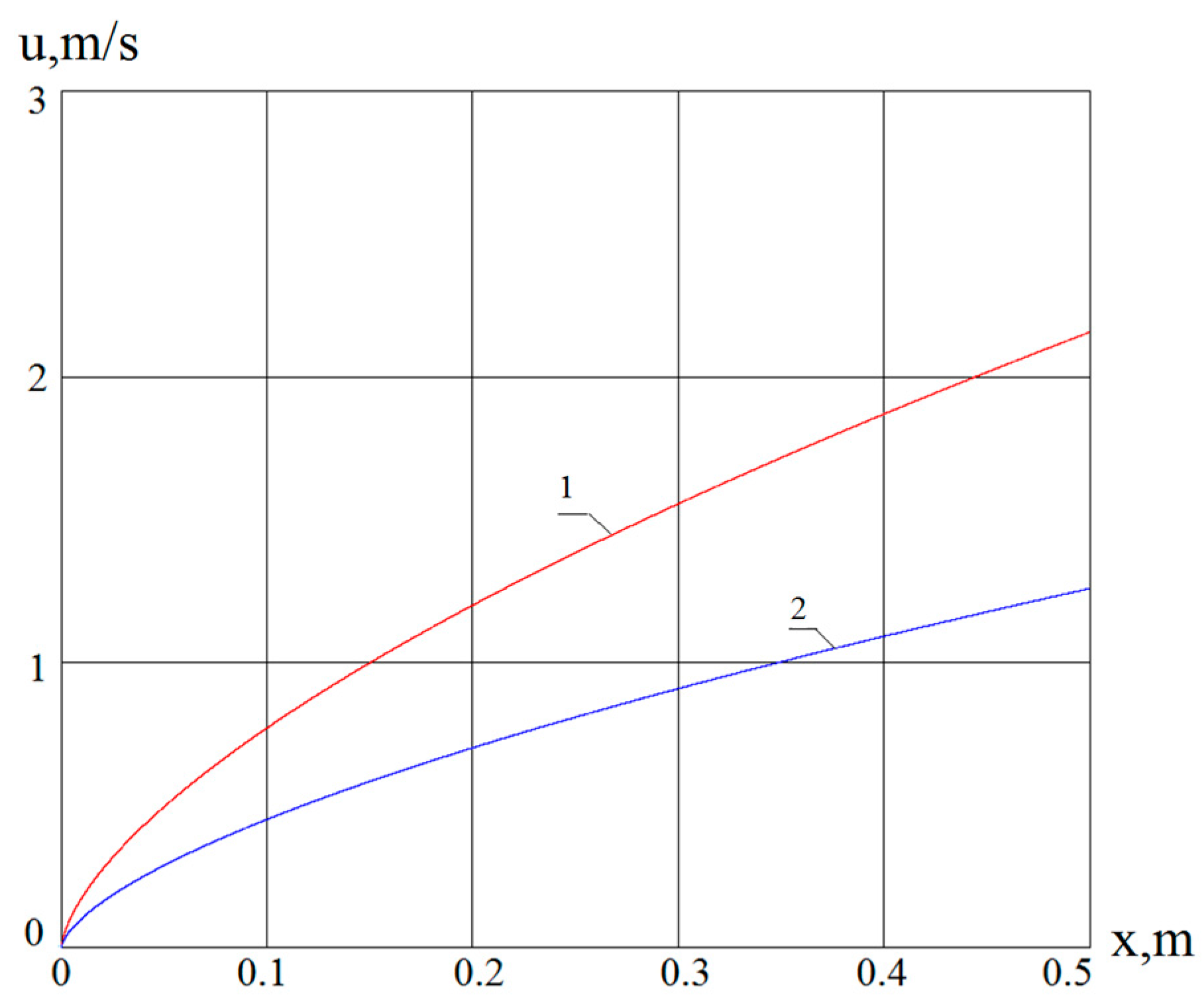
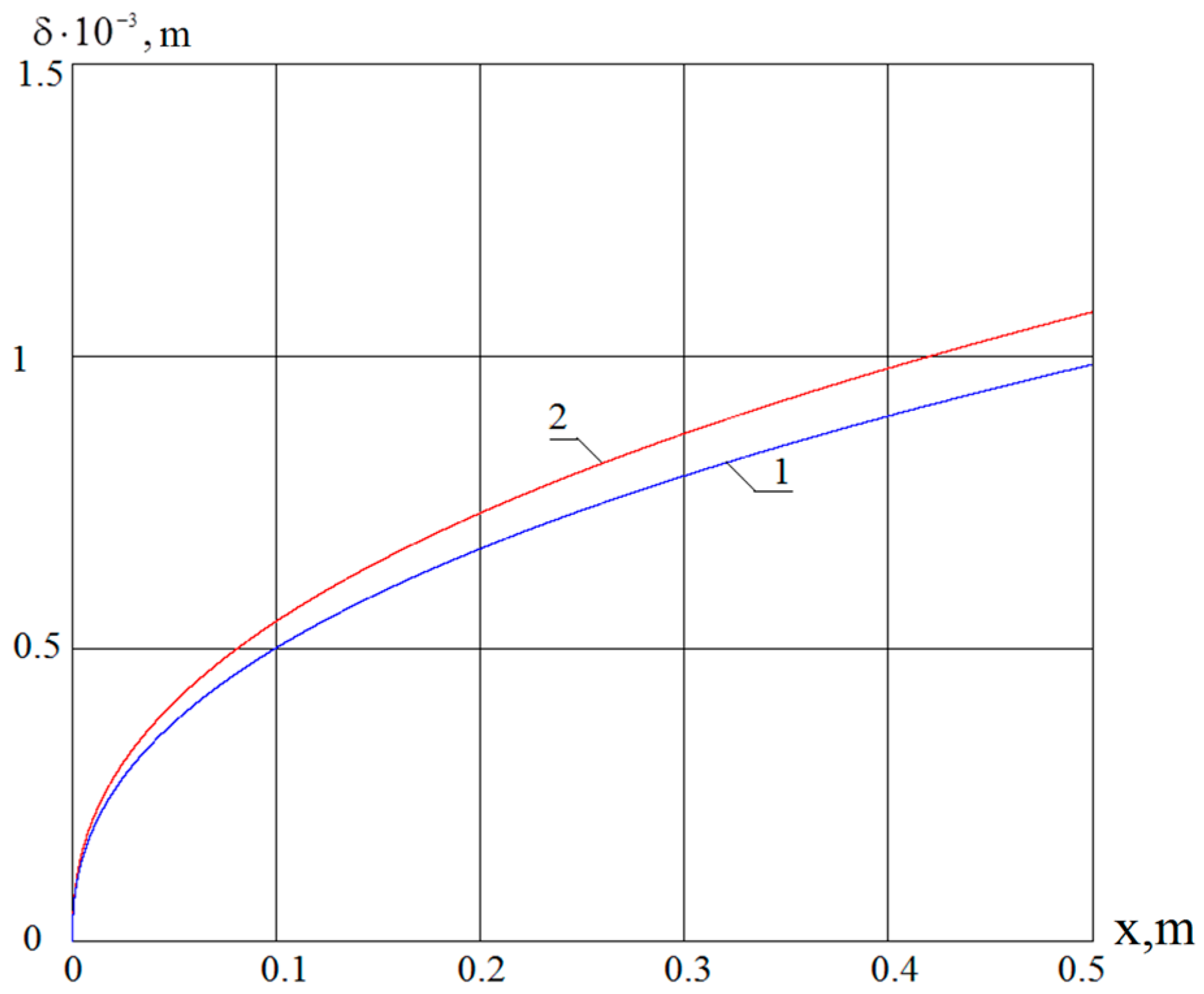
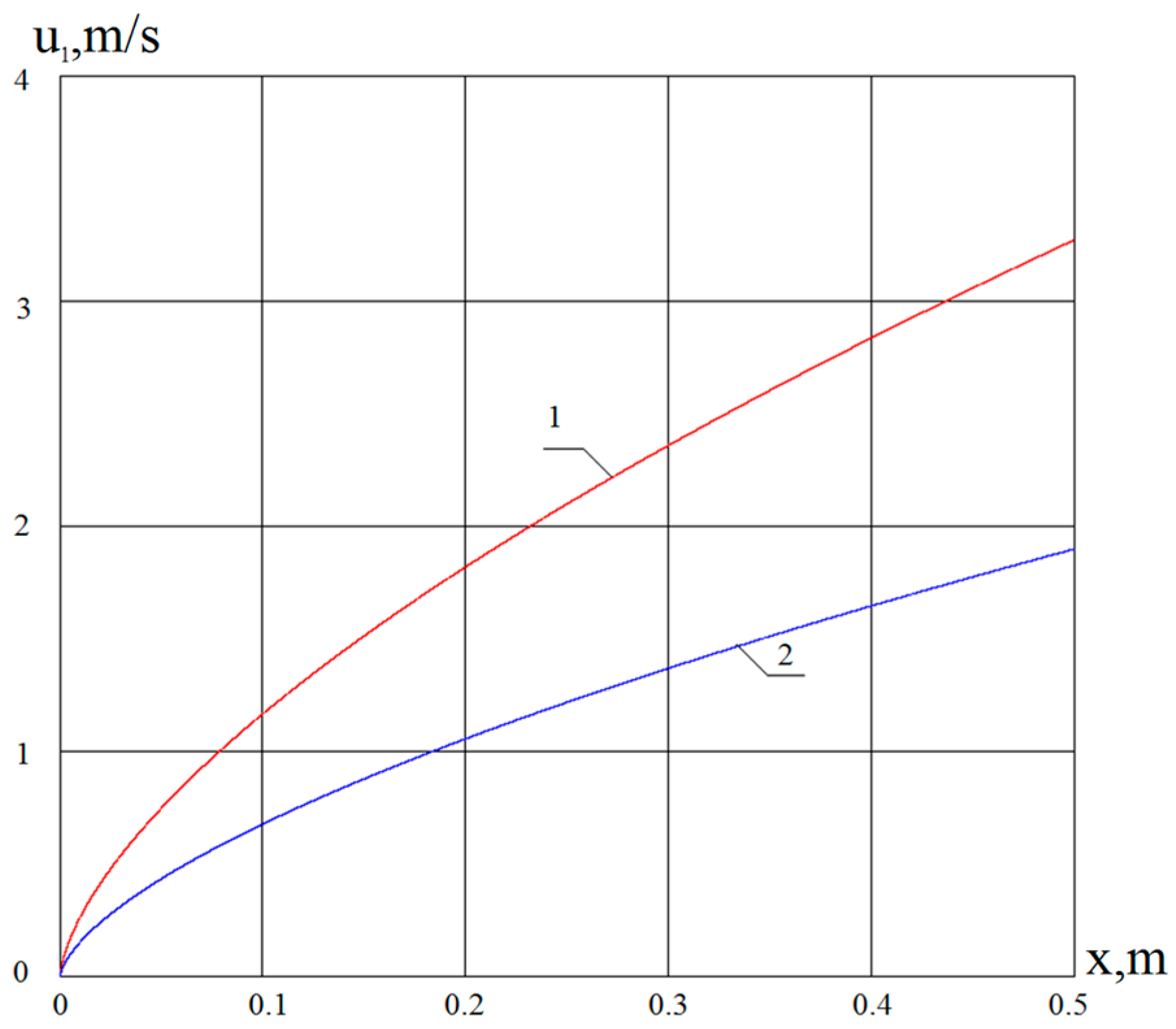
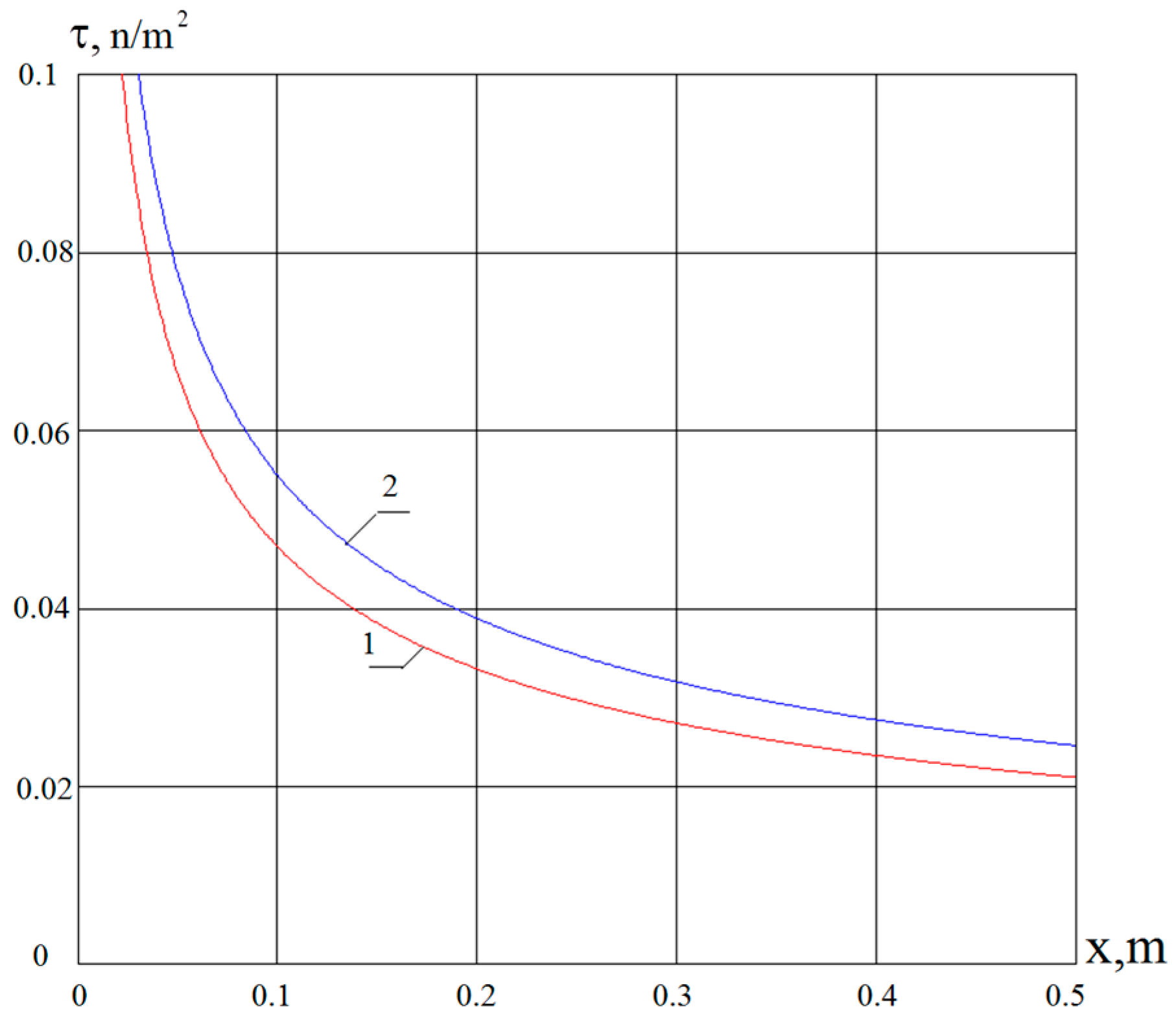
4. Results and Discussions
5. Conclusions
Author Contributions
Conflicts of Interest
References
- López, J.; Pineda, H.; Bello, D.; Ratkovich, N. Study of liquid-gas two-phase flow in horizontal pipes using high speed filming and computational fluid dynamics. Exp. Therm. Fluid Sci. 2016, 76, 126–134. [Google Scholar] [CrossRef]
- Lu, H.; Lu, L.; Luo, Y.; Qi, R. Investigation on the dynamic characteristics of the counter-current flow for liquid desiccant dehumidification. Energy 2016, 101, 229–238. [Google Scholar] [CrossRef]
- Li, M.; Lu, Y.; Zhang, S.; Xiao, Y. A numerical study of effects of counter-current gas flow rate on local hydrodynamic characteristics of falling films over horizontal tubes. Desalination 2016, 383, 68–80. [Google Scholar] [CrossRef]
- Klyuev, N.I.; Gimadiev, A.G.; Kryukov, Y.A. Two-media boundary layer on a flat plate. Int. J. Eng. Technol. 2014, 6, 2368–2374. [Google Scholar]
- Klyuev, N.I.; Kryukov, Y.A. Influence of fluid film on friction of a flat plate. Russ. Aeronaut. (Iz. VUZ) 2014, 57, 372–377. [Google Scholar] [CrossRef]
- Camassa, R.; Ogrosky, H.R. On viscous film flows coating the interior of a tube: Thin-film and long-wave models. J. Fluid Mech. 2015, 772, 569–599. [Google Scholar] [CrossRef]
- Muramatsu, K.; Youn, Y.; Han, Y.; Hasegawa, Y.; Shikazono, N. Numerical study on the effect of initial flow velocity on liquid film thickness of accelerated slug flow in a micro. Int. J. Heat Fluid Flow 2015, 54, 77–86. [Google Scholar] [CrossRef]
- Han, Y.; Kanno, H.; Ahn, Y.-J.; Shikazono, N. Measurement of liquid film thickness in micro tube annular flow. Int. J. Multiph. Flow 2015, 73, 264–274. [Google Scholar] [CrossRef]
- Youn, Y.J.; Muramatsu, K.; Han, Y.; Shikazono, N. The effect of initial flow velocity on the liquid film thickness in micro tube accelerated slug flow. Int. J. Multiph. Flow 2015, 73, 108–117. [Google Scholar] [CrossRef]
- Ju, P.; Brooks, C.S.; Ishii, M.; Liu, Y.; Hibiki, T. Film thickness of vertical upward cocurrent adiabatic flow in pipes. Int. J. Heat Mass Transf. 2015, 89, 985–995. [Google Scholar] [CrossRef]
- Richard, G.L.; Ruyer-Quil, C.; Vila, J.P. A three-equation model for thin films down an inclined plane. J. Fluid Mech. 2016, 804, 162–200. [Google Scholar] [CrossRef]
- Akkuş, Y.; Dursunkaya, Z. A new approach to thin film evaporation modeling. Int. J. Heat Mass Transf. 2016, 101, 742–748. [Google Scholar] [CrossRef]
- Liu, C.L.; Liu, J.L.; Zhu, H.R.; Wu, A.S.; He, Y.H.; Zhou, Z.X. Film cooling sensitivity of laidback fanshape holes to variations in exit configuration and mainstream turbulence intensity. Int. J. Heat Mass Transf. 2015, 89, 1141–1154. [Google Scholar] [CrossRef]
- Degan, G.; Sanya, A.; Akowanou, C. Laminar film condensation along a vertical plate embedded in an anisotropic porous medium with oblique principal axes. Heat Mass Transf. 2016, 52, 2119–2128. [Google Scholar] [CrossRef]
- Kim, S.; Lee, Y.G.; Jerng, D.W. Laminar film condensation of saturated vapor on an isothermal vertical cylinder. Int. J. Heat Mass Transf. 2015, 83, 545–551. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klyuev, N.; Polyakov, K.; Krutovertseva, A. Reducing Friction with a Liquid Film on the Body Surface. Lubricants 2018, 6, 25. https://doi.org/10.3390/lubricants6010025
Klyuev N, Polyakov K, Krutovertseva A. Reducing Friction with a Liquid Film on the Body Surface. Lubricants. 2018; 6(1):25. https://doi.org/10.3390/lubricants6010025
Chicago/Turabian StyleKlyuev, Nikolay, Konstantin Polyakov, and Alyona Krutovertseva. 2018. "Reducing Friction with a Liquid Film on the Body Surface" Lubricants 6, no. 1: 25. https://doi.org/10.3390/lubricants6010025
APA StyleKlyuev, N., Polyakov, K., & Krutovertseva, A. (2018). Reducing Friction with a Liquid Film on the Body Surface. Lubricants, 6(1), 25. https://doi.org/10.3390/lubricants6010025