Low Friction and High Solid-Solid Contact Ratio—A Contradiction for Laser-Patterned Surfaces?
Abstract
:1. Introduction
2. Materials and Methods
2.1. Samples
2.2. Direct Laser Interference Patterning (DLIP)
2.3. Wight Light Interferometry (WLI)
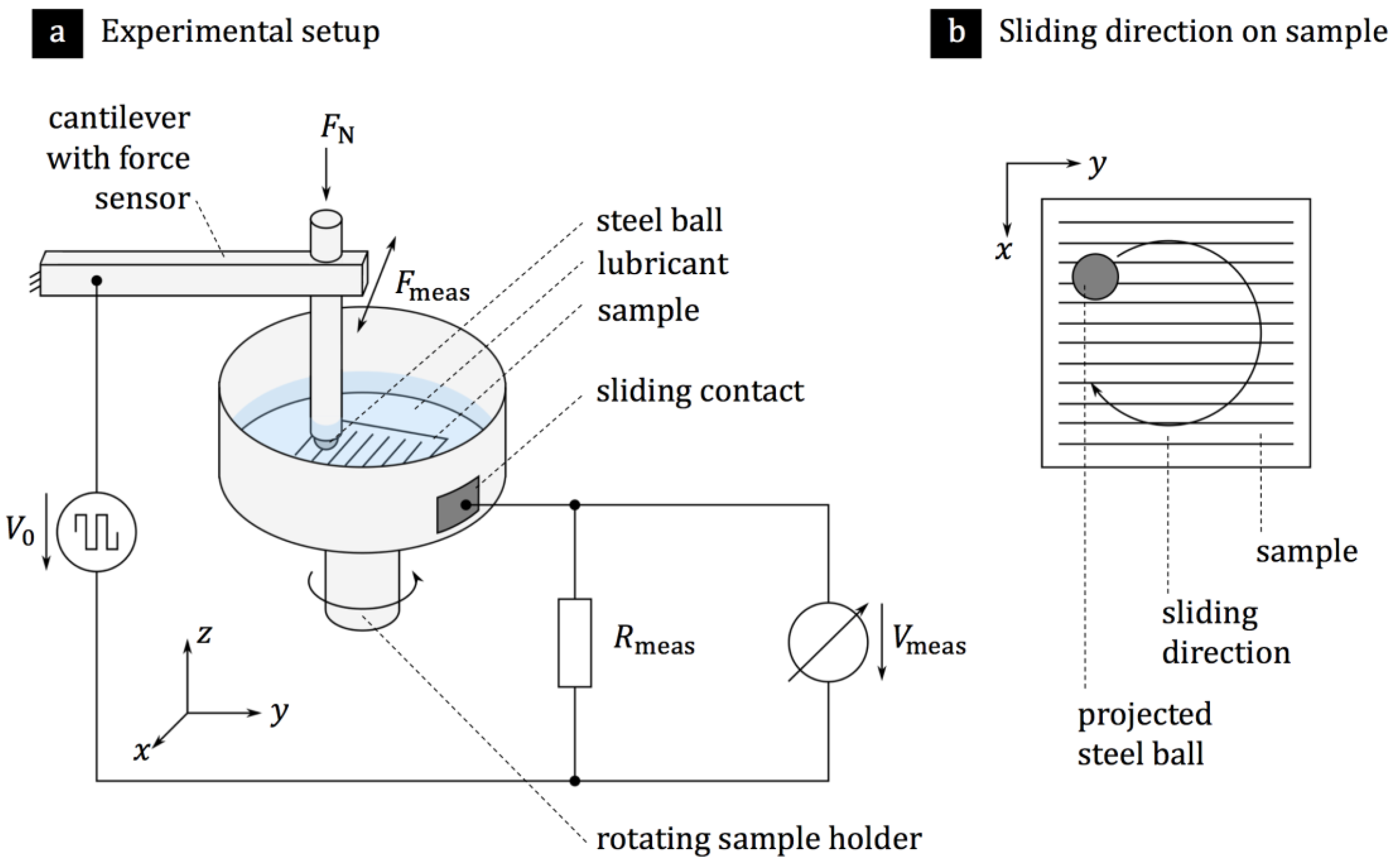
2.4. Ball-On-Disk Tribometer
2.5. Electrical Resistivity Circuit
3. Results
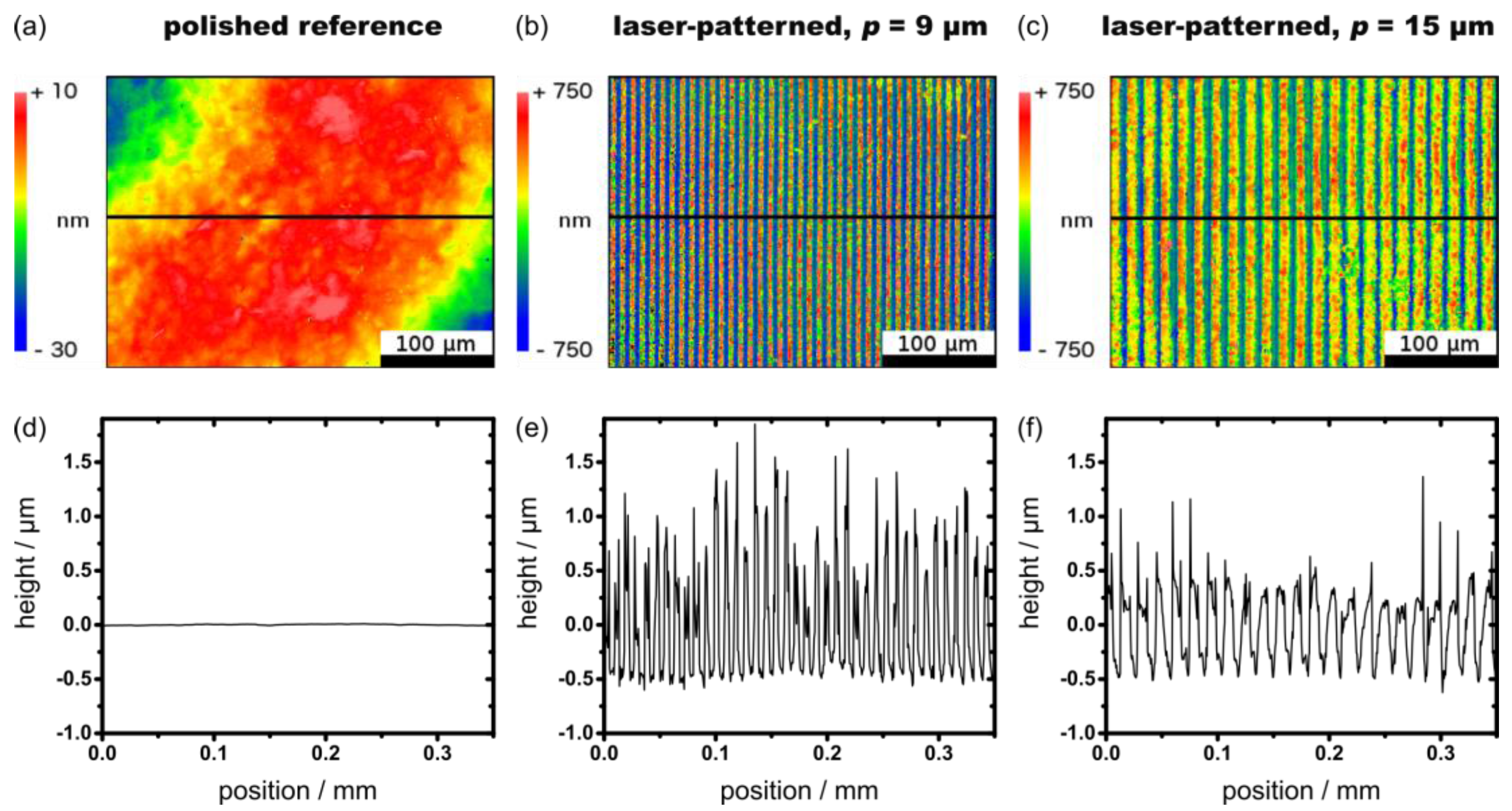
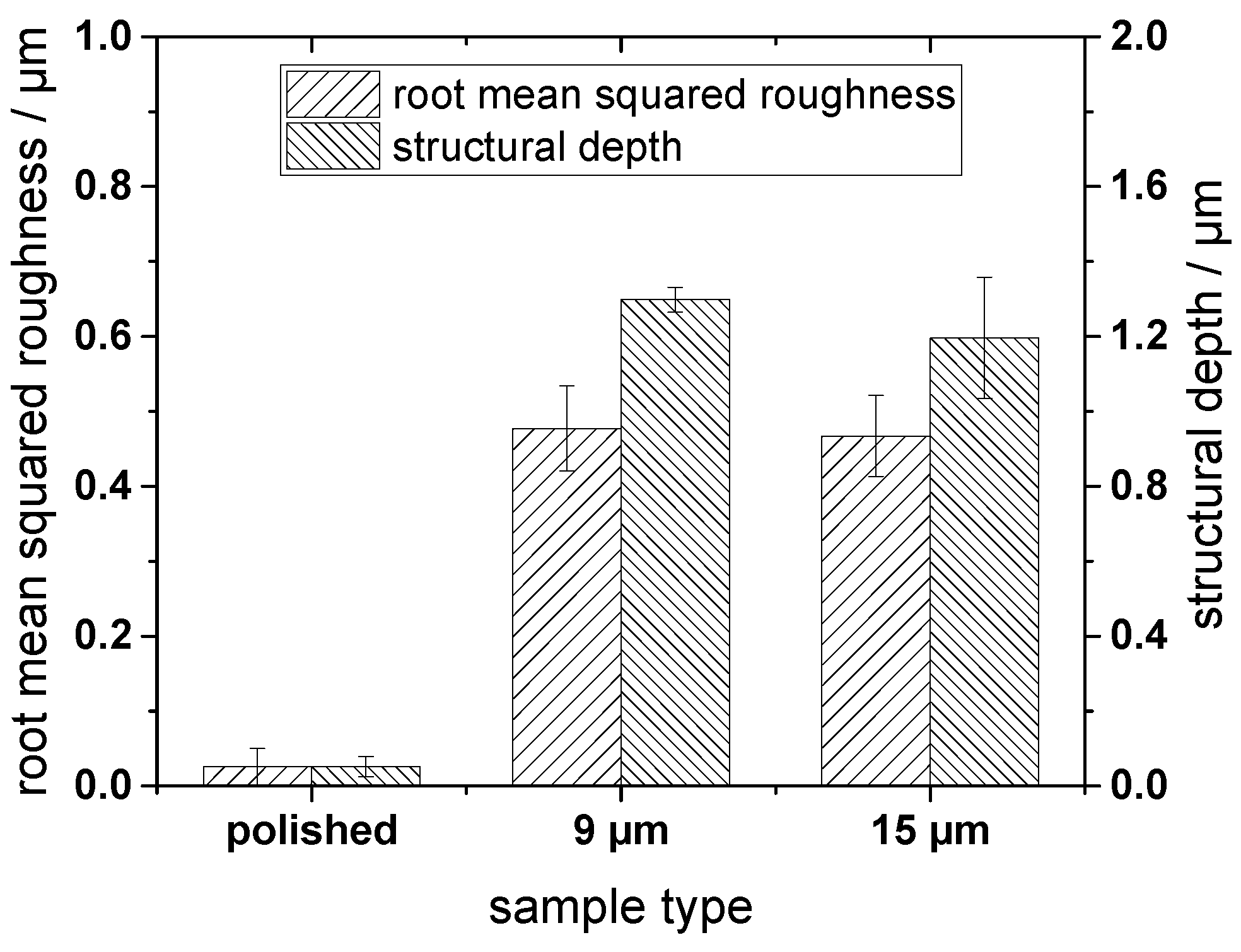
3.1. Topographical Analysis
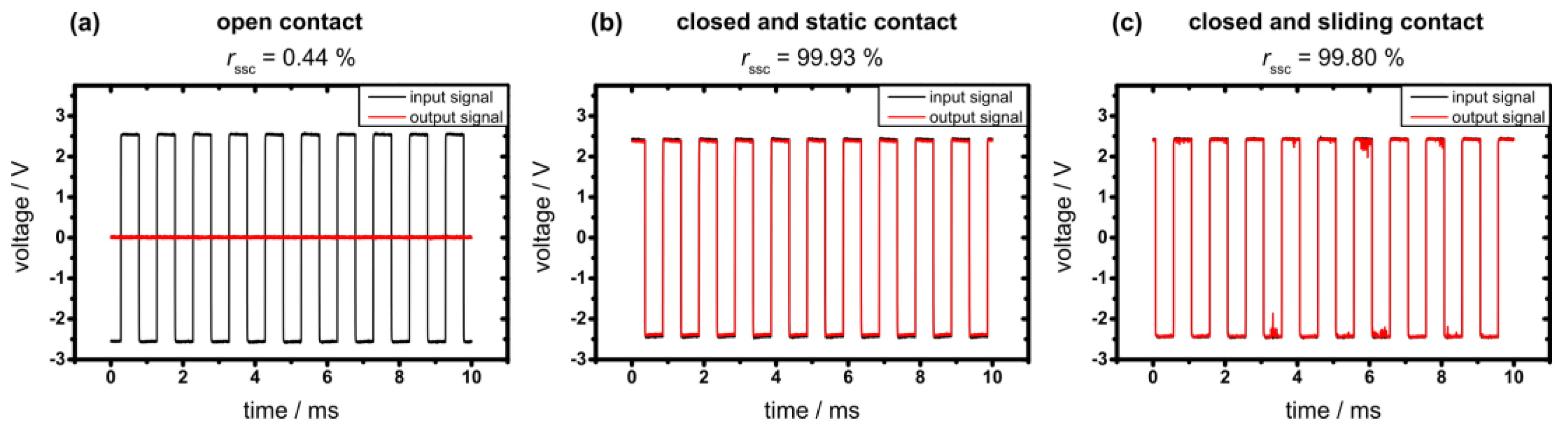
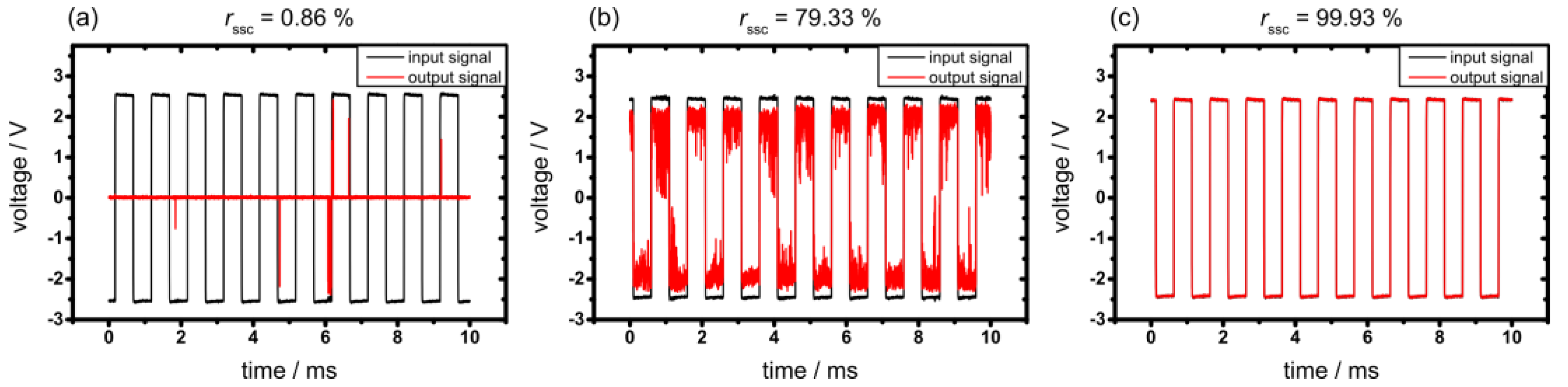
3.2. Calibration of the Electrical Resistivity Circuit
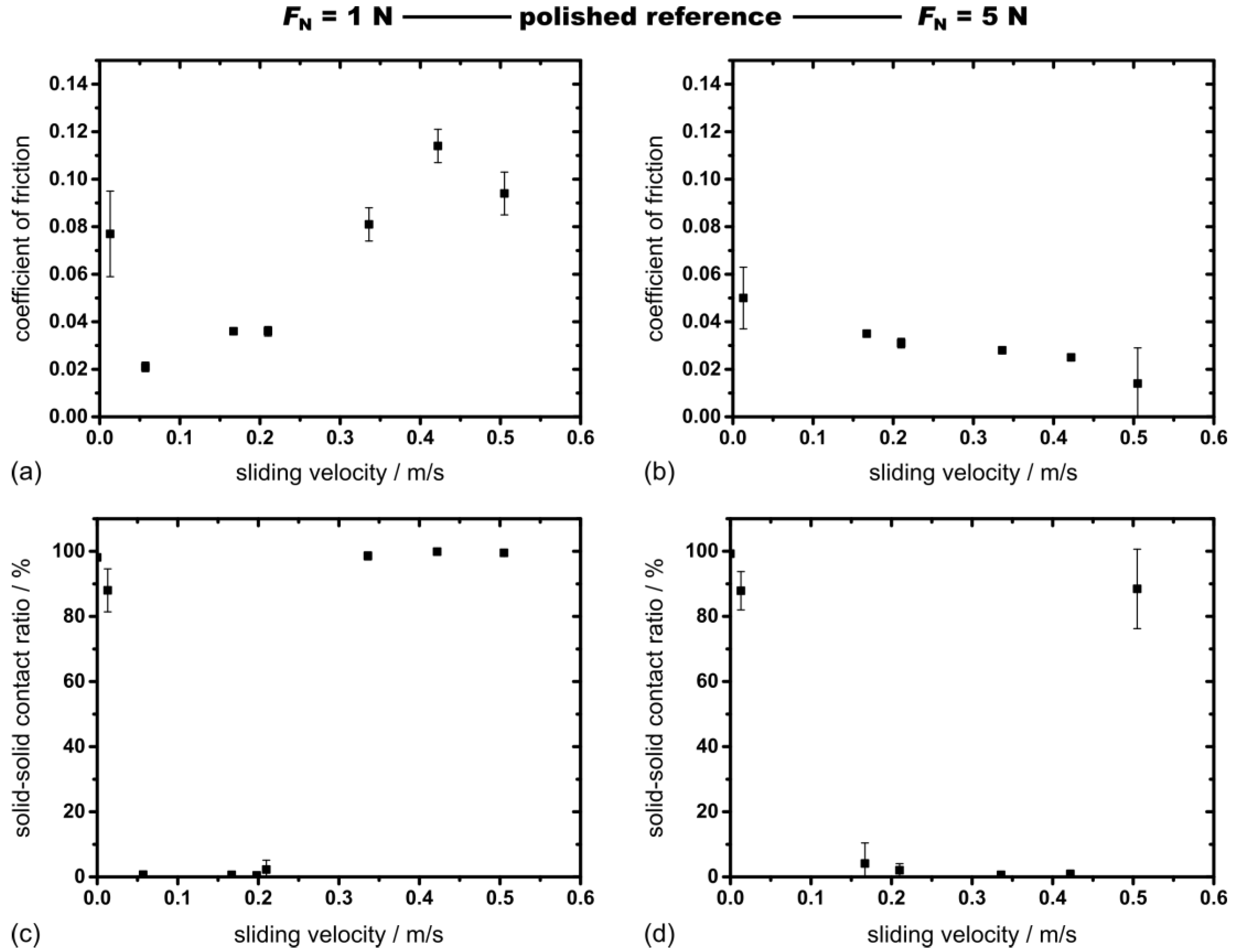
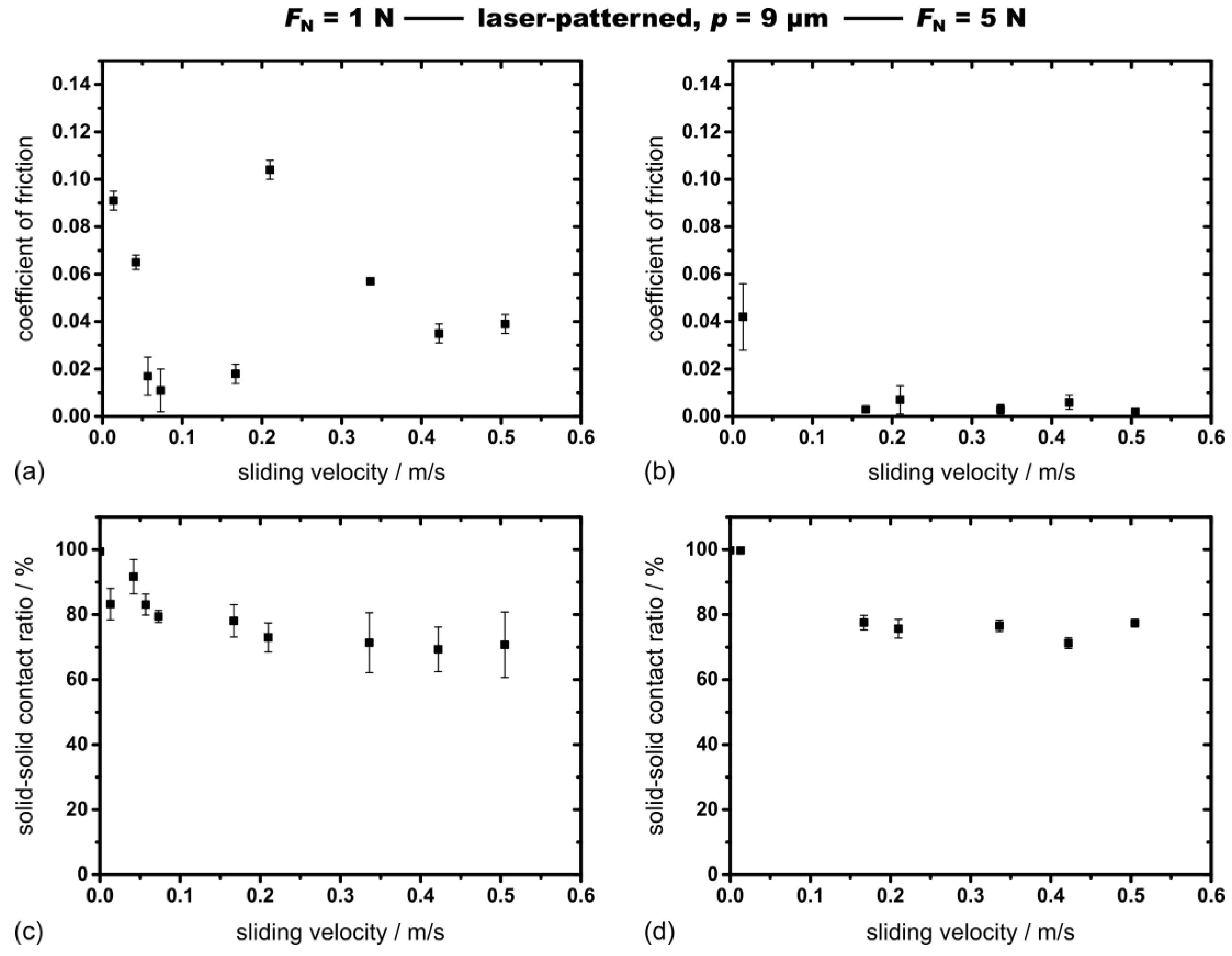
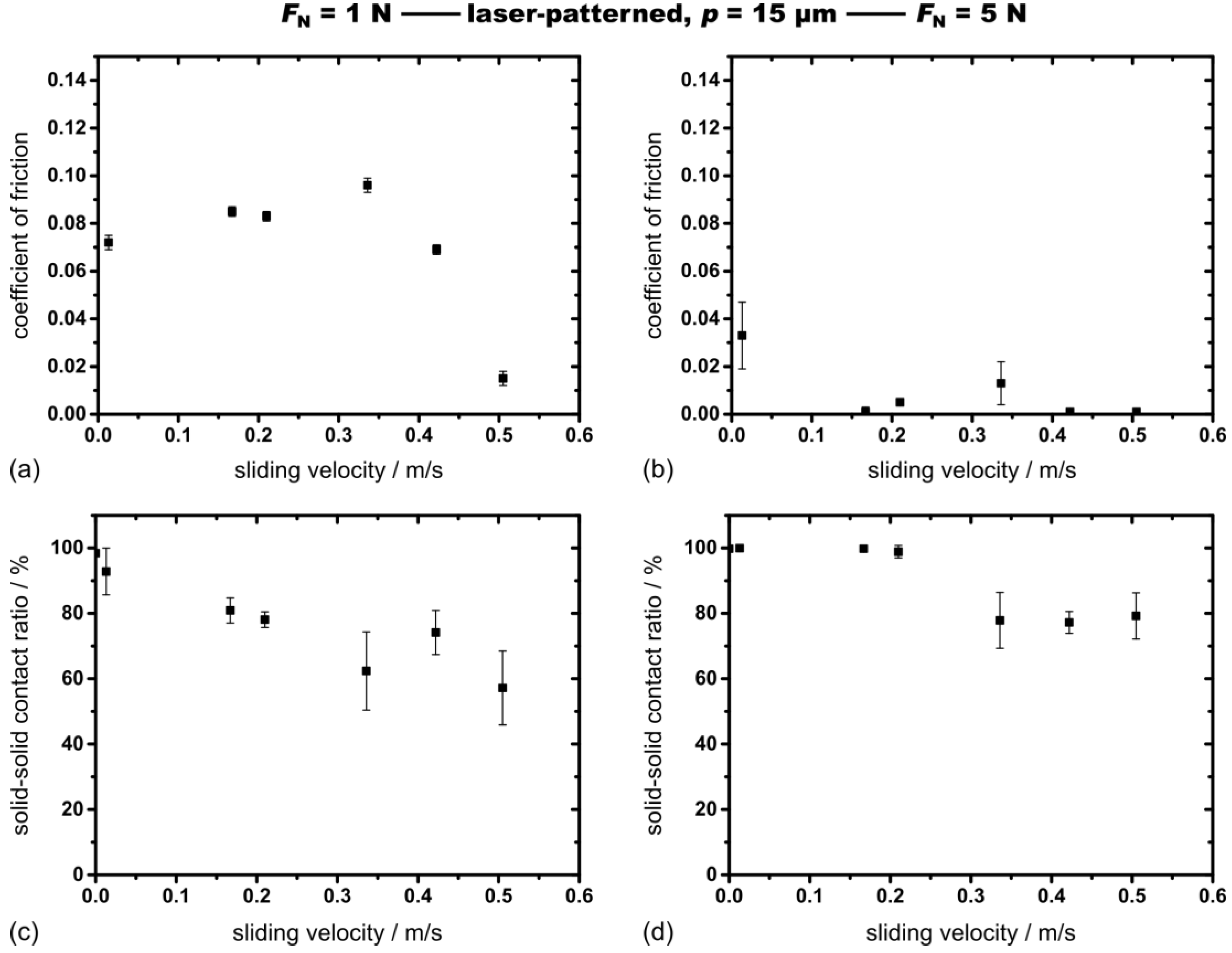
3.3. Tribological Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Carpick, R.W.; Jackson, A.; Sawyer, W.G.; Argibay, N.; Lee, P.; Pachon, A.; Gresham, R.M. The tribology opportunities study: Can tribology save a quad? Tribol. Lubr. Technol. 2016, 72, 44–45. [Google Scholar]
- Greco, A.; Sheng, S.; Keller, J.; Erdemir, A. Material wear and fatigue in wind turbine systems. Wear 2013, 302, 1583–1591. [Google Scholar] [CrossRef]
- Wong, V.W.; Tung, S.C. Overview of automotive engine friction and reduction trends–Effects of surface, material, and lubricant-additive technologies. Friction 2016, 4, 1–28. [Google Scholar] [CrossRef]
- Holmberg, K.; Andersson, P.; Erdemir, A. Global energy consumption due to friction in passenger cars. Tribol. Int. 2012, 47, 221–234. [Google Scholar] [CrossRef]
- Holmberg, K.; Kivikytö-Reponen, P.; Härkisaari, P.; Valtonen, K.; Erdemir, A. Global energy consumption due to friction and wear in the mining industry. Tribol. Int. 2017, 115, 116–139. [Google Scholar] [CrossRef]
- Etsion, I. State of the art in laser surface texturing. J. Tribol. 2005, 127, 248–253. [Google Scholar] [CrossRef]
- Gachot, C.; Rosenkranz, A.; Hsu, S.M.; Costa, H.L. A critical assessment of surface texturing for friction and wear improvement. Wear 2017, 372, 21–41. [Google Scholar] [CrossRef]
- Gropper, D.; Wang, L.; Harvey, T.J. Hydrodynamic lubrication of textured surfaces: A review of modeling techniques and key findings. Tribol. Int. 2016, 94, 509–529. [Google Scholar] [CrossRef]
- Szurdak, A.; Hirt, G. Development and Experimental Verification of a New Roller-Coining Setup to Texture Flat and Curved Surfaces. Appl. Mech. Mater. 2015, 794, 128–135. [Google Scholar] [CrossRef]
- Wei, X.; Li, W.; Liang, B.; Li, B.; Zhang, J.; Zhang, L.; Wang, Z. Surface modification of Co–Cr–Mo implant alloy by laser interference lithography. Tribol. Int. 2016, 97, 212–217. [Google Scholar] [CrossRef]
- Zhang, B.; Huang, W.; Wang, J.; Wang, X. Comparison of the effects of surface texture on the surfaces of steel and UHMWPE. Tribol. Int. 2013, 65, 138–145. [Google Scholar] [CrossRef]
- Gachot, C.; Rosenkranz, A.; Reinert, L.; Ramos-Moore, E.; Souza, N.; Müser, M.H.; Mücklich, F. Dry friction between laser-patterned surfaces: Role of alignment, structural wavelength and surface chemistry. Tribol. Lett. 2013, 49, 193–202. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Reinert, L.; Gachot, C.; Mücklich, F. Alignment and wear debris effects between laser-patterned steel surfaces under dry sliding conditions. Wear 2014, 318, 49–61. [Google Scholar] [CrossRef]
- Prodanov, N.; Gachot, C.; Rosenkranz, A.; Mücklich, F.; Müser, M.H. Contact mechanics of laser-textured surfaces. Tribol. Lett. 2013, 50, 41–48. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Hans, M.; Gachot, C.; Thome, A.; Bonk, S.; Mücklich, F. Direct laser interference patterning: Tailoring of contact area for frictional and antibacterial properties. Lubricants 2016, 4, 2. [Google Scholar] [CrossRef]
- Trinh, K.E.; Tsipenyuk, A.; Varenberg, M.; Rosenkranz, A.; Souza, N.; Mücklich, F. Wear debris and electrical resistance in textured Sn-coated Cu contacts subjected to fretting. Wear 2015, 344, 86–98. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Pangraz, J.C.; Gachot, C.; Mücklich, F. Load-dependent run-in and wear behaviour of line-like surface patterns produced by direct laser interference patterning. Wear 2016, 368, 350–357. [Google Scholar] [CrossRef]
- Xing, Y.; Deng, J.; Feng, X.; Yu, S. Effect of laser surface texturing on Si3N4/TiC ceramic sliding against steel under dry friction. Mater. Des. 2013, 52, 234–245. [Google Scholar] [CrossRef]
- He, D.; Zheng, S.; Pu, J.; Zhang, G.; Hu, L. Improving tribological properties of titanium alloys by combining laser surface texturing and diamond-like carbon film. Tribol. Int. 2015, 82, 20–27. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Heib, T.; Gachot, C.; Mücklich, F. Oil film lifetime and wear particle analysis of laser-patterned stainless steel surfaces. Wear 2015, 334, 1–12. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Szurdak, A.; Gachot, C.; Hirt, G.; Mücklich, F. Friction reduction under mixed and full film EHL induced by hot micro-coined surface patterns. Tribol. Int. 2016, 95, 290–297. [Google Scholar] [CrossRef]
- Braun, D.; Greiner, C.; Schneider, J.; Gumbsch, P. Efficiency of laser surface texturing in the reduction of friction under mixed lubrication. Tribol. Int. 2014, 77, 142–147. [Google Scholar] [CrossRef]
- Ramesh, A.; Akram, W.; Mishra, S.P.; Cannon, A.H.; Polycarpou, A.A.; King, W.P. Friction characteristics of microtextured surfaces under mixed and hydrodynamic lubrication. Tribol. Int. 2013, 57, 170–176. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, D.Y.; Hua, M.; Dong, G.N.; Chin, K.S. A study on the tribological behavior of surface texturing on babbitt alloy under mixed or starved lubrication. Tribol. Lett. 2014, 56, 305–315. [Google Scholar] [CrossRef]
- Costa, H.L.; Hutchings, I.M. Hydrodynamic lubrication of textured steel surfaces under reciprocating sliding conditions. Tribol. Int. 2007, 40, 1227–1238. [Google Scholar] [CrossRef]
- Fowell, M.T.; Medina, S.; Olver, A.V.; Spikes, H.A.; Pegg, I.G. Parametric study of texturing in convergent bearings. Tribol. Int. 2012, 52, 7–16. [Google Scholar] [CrossRef]
- Kovalchenko, A.; Ajayi, O.; Erdemir, A.; Fenske, G.; Etsion, I. The effect of laser surface texturing on transitions in lubrication regimes during unidirectional sliding contact. Tribol. Int. 2005, 38, 219–225. [Google Scholar] [CrossRef]
- Kovalchenko, A.; Ajayi, O.; Erdemir, A.; Fenske, G.; Etsion, I. The effect of laser texturing of steel surfaces and speed-load parameters on the transition of lubrication regime from boundary to hydrodynamic. Tribol. Trans. 2004, 47, 299–307. [Google Scholar] [CrossRef]
- Nakatsuji, T.; Mori, A. The tribological effect of mechanically produced micro-dents by a micro diamond pyramid on medium carbon steel surfaces in rolling-sliding contact. Meccanica 2001, 36, 663–674. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Martin, B.; Bettscheider, S.; Gachot, C.; Kliem, H.; Mücklich, F. Correlation between solid-solid contact ratios and lubrication regimes measured by a refined electrical resistivity circuit. Wear 2014, 320, 51–61. [Google Scholar] [CrossRef]
- Grützmacher, P.G.; Rosenkranz, A.; Rammacher, S.; Gachot, C.; Mücklich, F. The influence of centrifugal forces on friction and wear in rotational sliding. Tribol. Int. 2017, 116, 256–263. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Fleischmann, S.; Gachot, C.; Mücklich, F. Anisotropic Spreading Behavior of PAO Oil on Laser-Patterned Stainless Steel Surfaces. Adv. Eng. Mater. 2015, 17, 1645–1651. [Google Scholar] [CrossRef]
- Mücklich, F.; Lasagni, A.F.; Daniel, C. Laser interference metallurgy—Using interference as a tool for micro/nano structuring. Int. J. Mater. Res. 2006, 97, 1337–1344. [Google Scholar] [CrossRef]
- Lasagni, A.F.; Holzapfel, C.; Weirich, T.; Mücklich, F. Laser interference metallurgy: A new method for periodic surface microstructure design on multilayered metallic thin films. Appl. Surf. Sci. 2007, 253, 8070–8074. [Google Scholar] [CrossRef]
- Lasagni, A.F.; D’Alessandria, M.; Giovanelli, R.; Mücklich, F. Advanced design of periodical architectures in bulk metals by means of Laser Interference Metallurgy. Appl. Surf. Sci. 2007, 254, 930–936. [Google Scholar] [CrossRef]
- Bettscheider, S.; Gachot, C.; Rosenkranz, A. How to measure the real contact area? A simple marker and relocation foot-printing approach. Tribol. Int. 2016, 103, 167–175. [Google Scholar] [CrossRef]
| Used Steel Specimens | Fe | Cr | Ni | Mn | Si | C |
|---|---|---|---|---|---|---|
| Substrate (AISI 304) | 68.9 | 18 | 10 | 2 | 1 | 0.1 |
| Ball (AISI 52100) | 96.7 | 1.5 | / | 0.4 | 0.3 | 1 |
| Parameter | Unit | Values |
|---|---|---|
| Periodicity of laser-patterned samples | µm | 9 and 15 |
| Sliding velocities | m/s | 0 to 0.505 |
| Normal loads | N | 1 and 5 |
| Kinematic oil viscosity at 100 °C | cSt | 39.6 |
| Oil volume | mL | 7 |
| Temperature | °C | 25 ± 1 |
| Relative humidity | % | 45 ± 1 |
| Sample | /µm | /µm | /µm |
|---|---|---|---|
| Steel ball | 0.020 ± 0.003 | – | – |
| Polished reference | 0.040 ± 0.005 | 0.03 ± 0.003 | – |
| Laser-patterned, 9 µm | 0.477 ± 0.057 | 1.298 ± 0.033 | 9.5 ± 0.507 |
| Laser-patterned, 15 µm | 0.467 ± 0.054 | 1.196 ± 0.162 | 15.5 ± 0.532 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bettscheider, S.; Grützmacher, P.G.; Rosenkranz, A. Low Friction and High Solid-Solid Contact Ratio—A Contradiction for Laser-Patterned Surfaces? Lubricants 2017, 5, 35. https://doi.org/10.3390/lubricants5030035
Bettscheider S, Grützmacher PG, Rosenkranz A. Low Friction and High Solid-Solid Contact Ratio—A Contradiction for Laser-Patterned Surfaces? Lubricants. 2017; 5(3):35. https://doi.org/10.3390/lubricants5030035
Chicago/Turabian StyleBettscheider, Simon, Philipp G. Grützmacher, and Andreas Rosenkranz. 2017. "Low Friction and High Solid-Solid Contact Ratio—A Contradiction for Laser-Patterned Surfaces?" Lubricants 5, no. 3: 35. https://doi.org/10.3390/lubricants5030035
APA StyleBettscheider, S., Grützmacher, P. G., & Rosenkranz, A. (2017). Low Friction and High Solid-Solid Contact Ratio—A Contradiction for Laser-Patterned Surfaces? Lubricants, 5(3), 35. https://doi.org/10.3390/lubricants5030035






