Simulation Analysis and Structural Improvements of Oil Return in Main Bearing Chamber of Aero-Engine
Abstract
1. Introduction
2. The Rear Bearing Chamber Structure System
2.1. Structural Characteristic
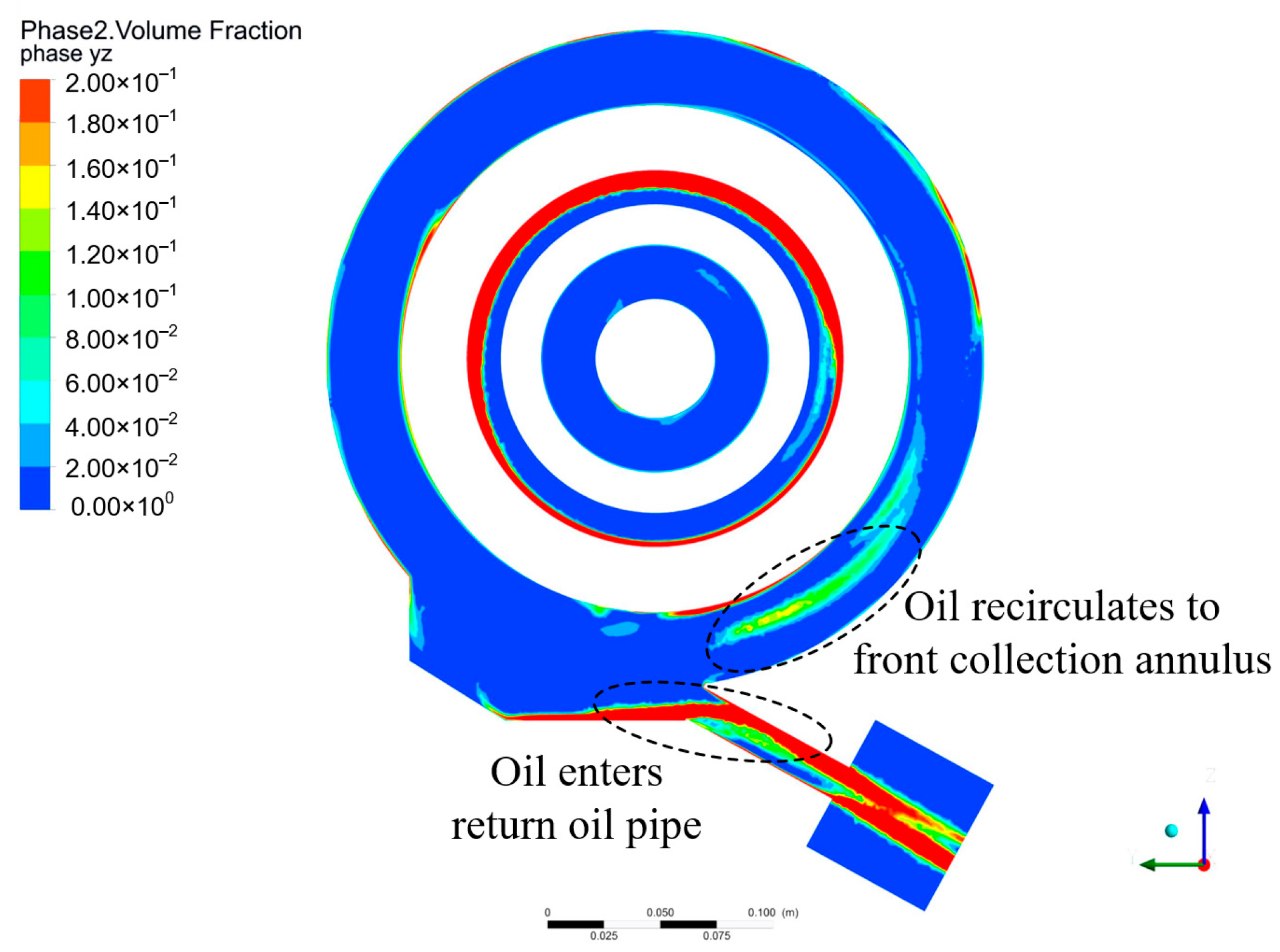
2.2. Oil Flow Process
3. Simulation Model of Oil Return Process
3.1. Geometric Model
3.2. Mesh Division
3.3. Boundary Conditions
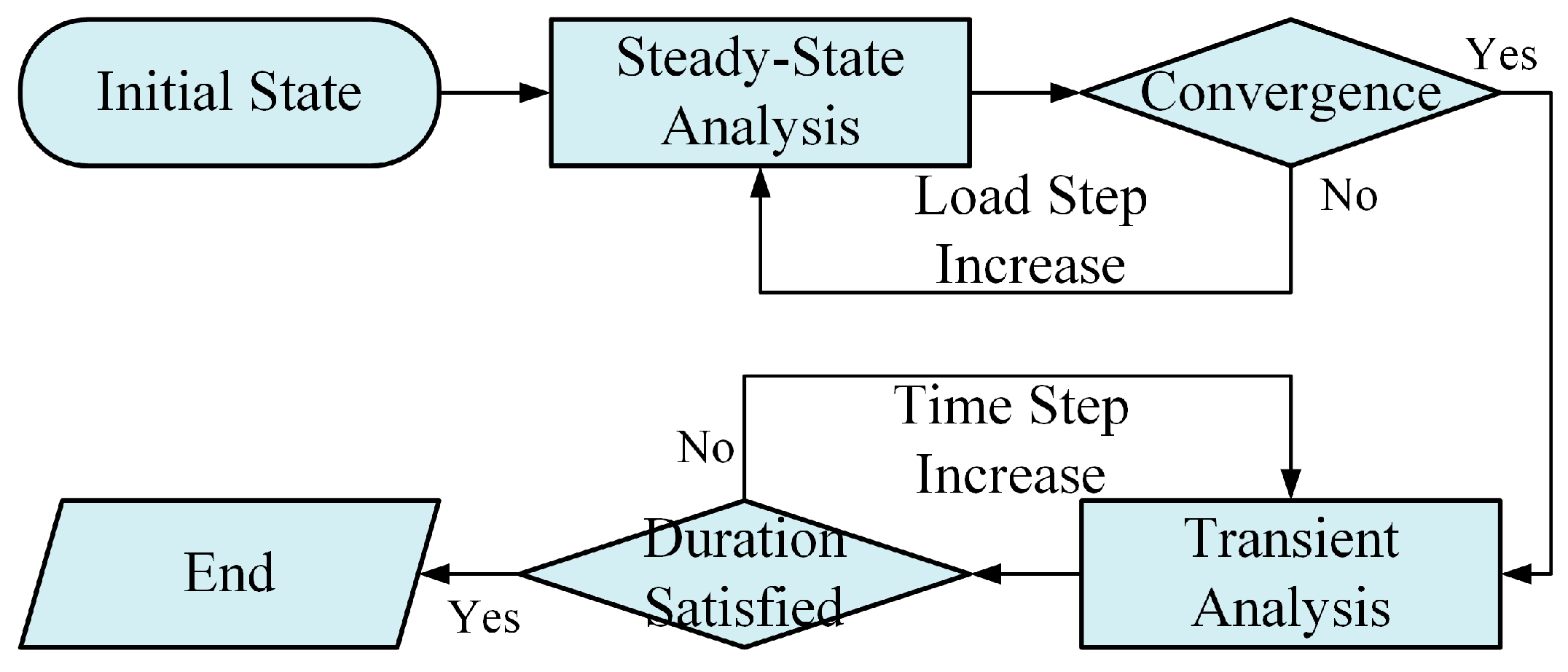
3.4. Oil Flow Characteristics Simulation Process
4. Analysis of Oil Flow Characteristics and Oil Return Process
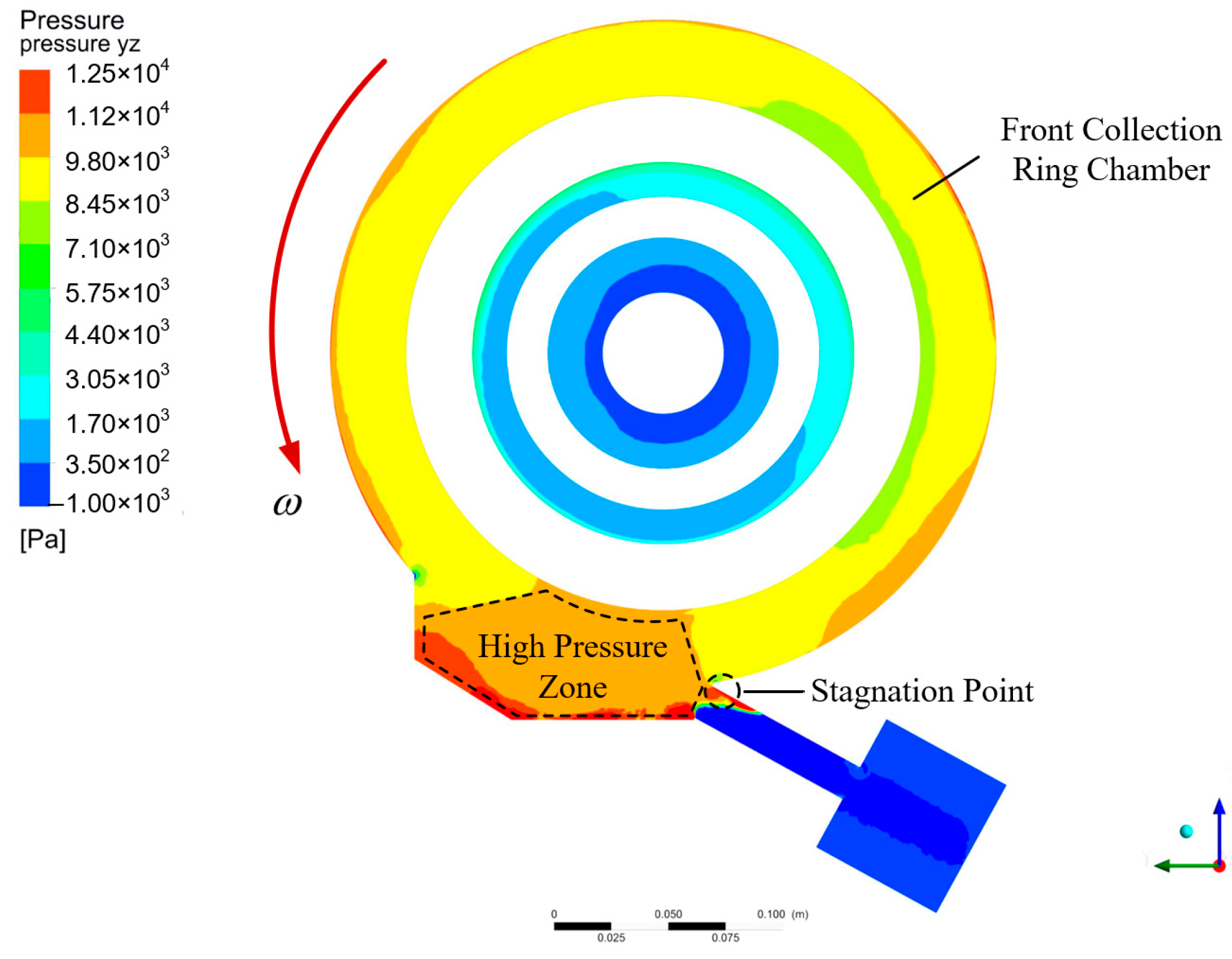
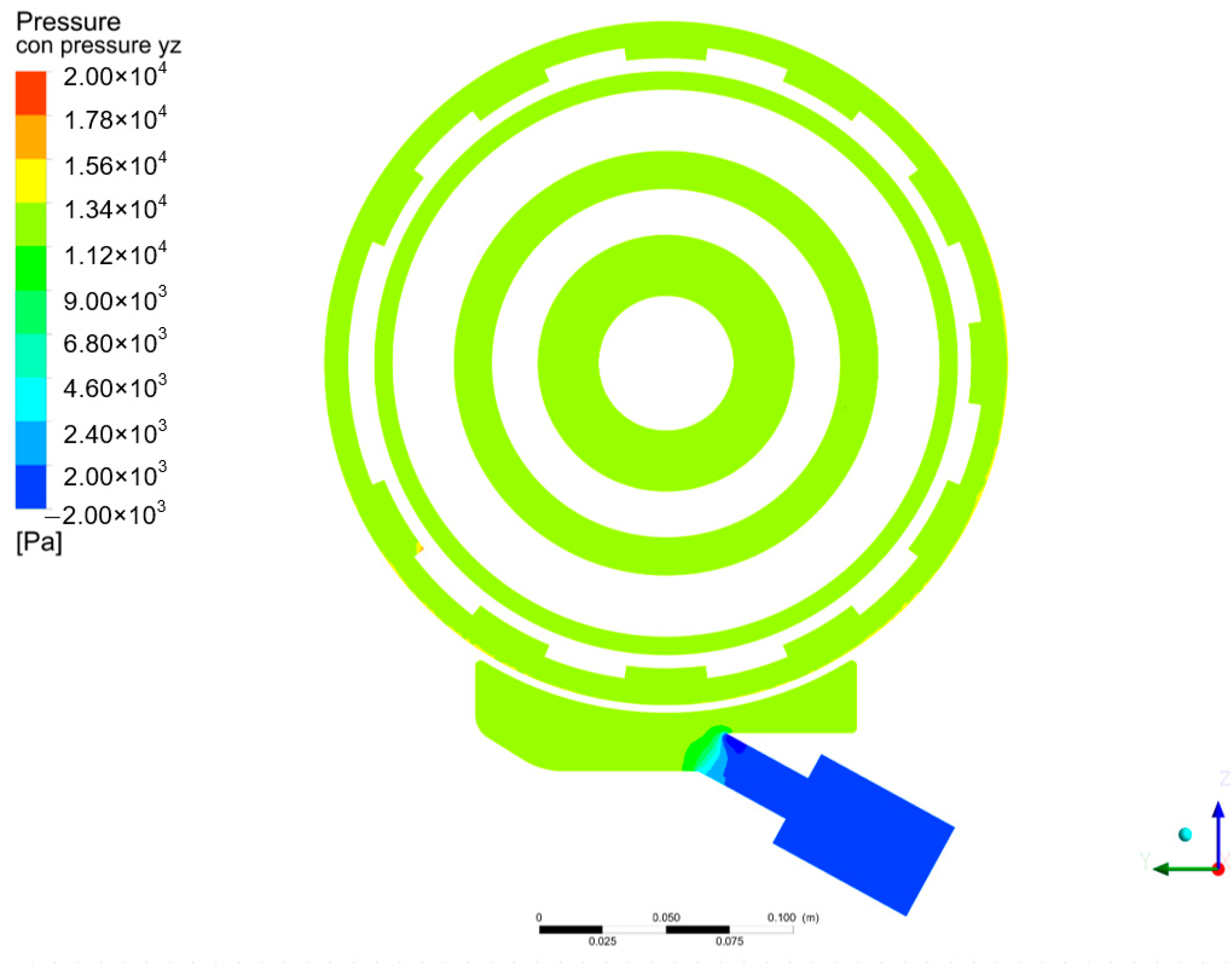
4.1. Pressure Distribution of Bearing Chamber
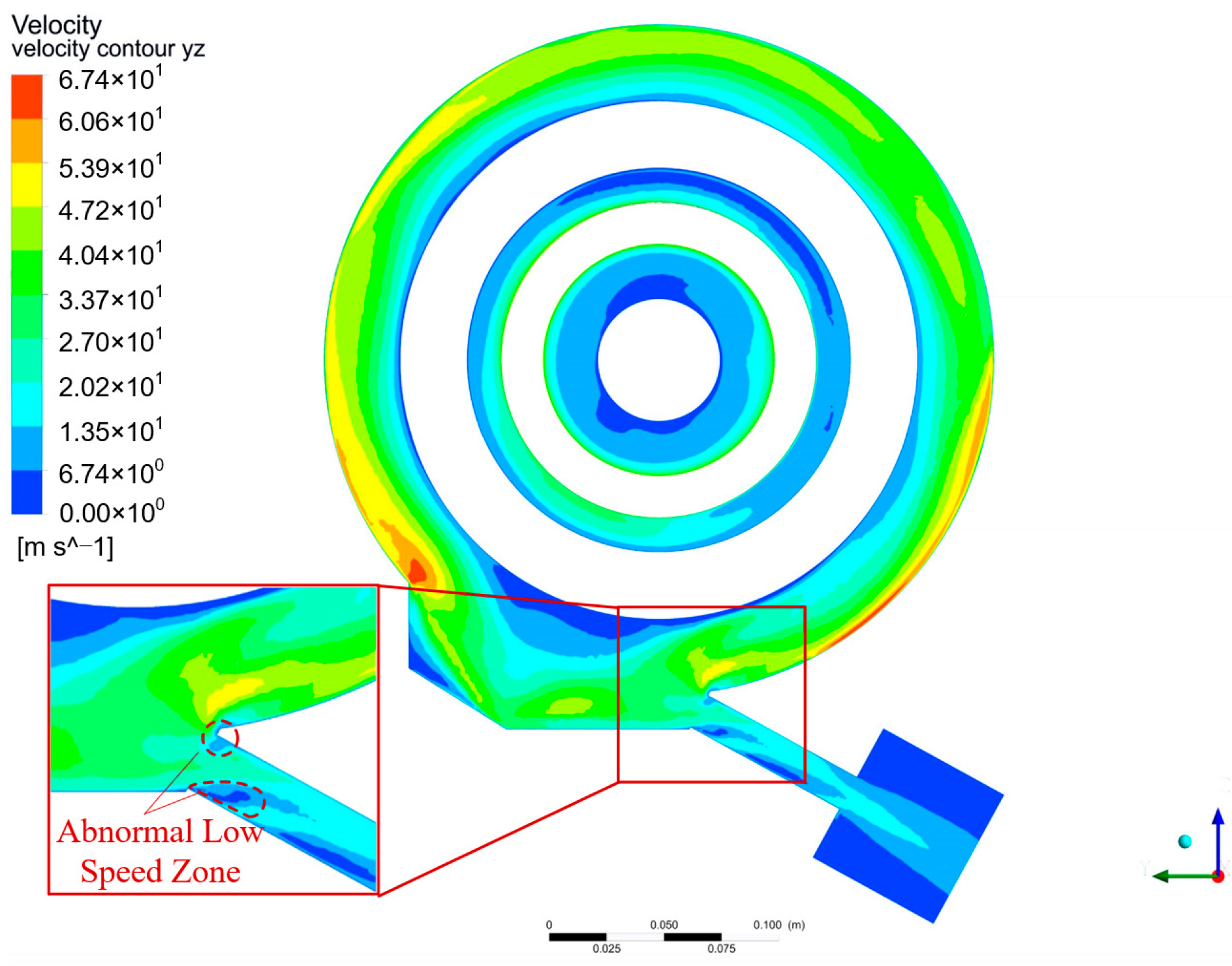
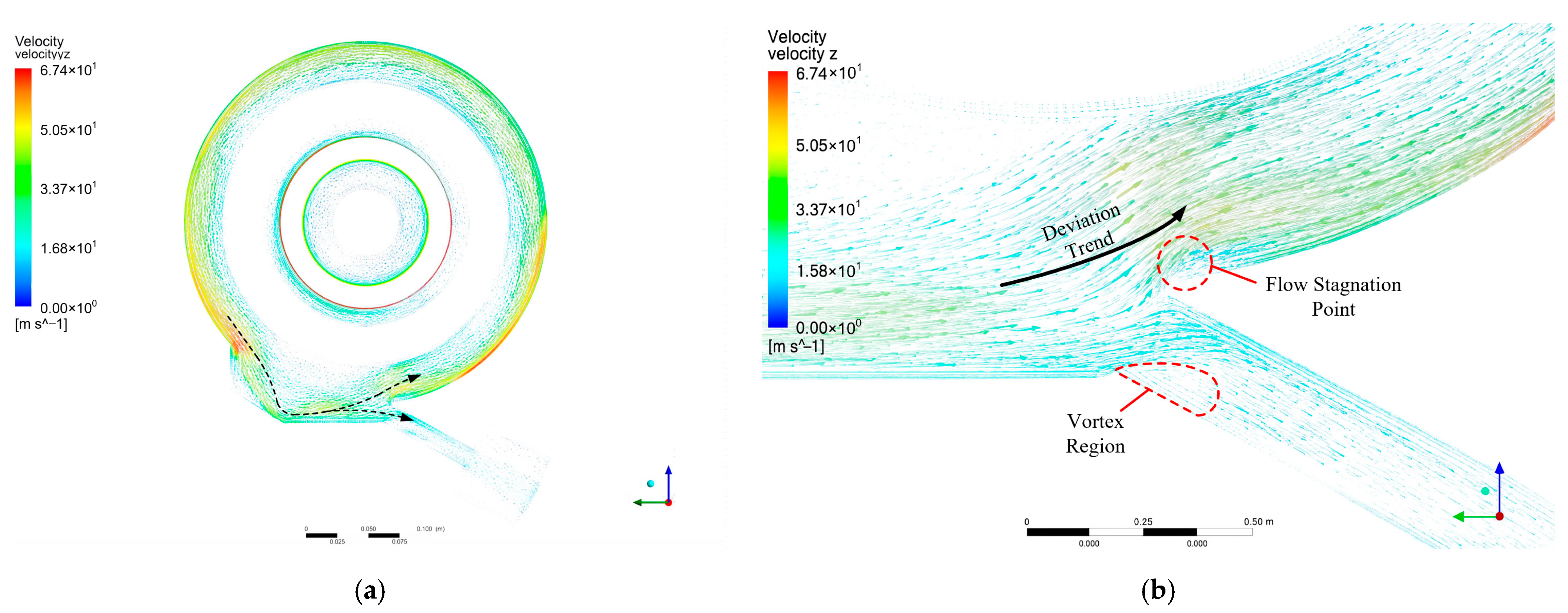
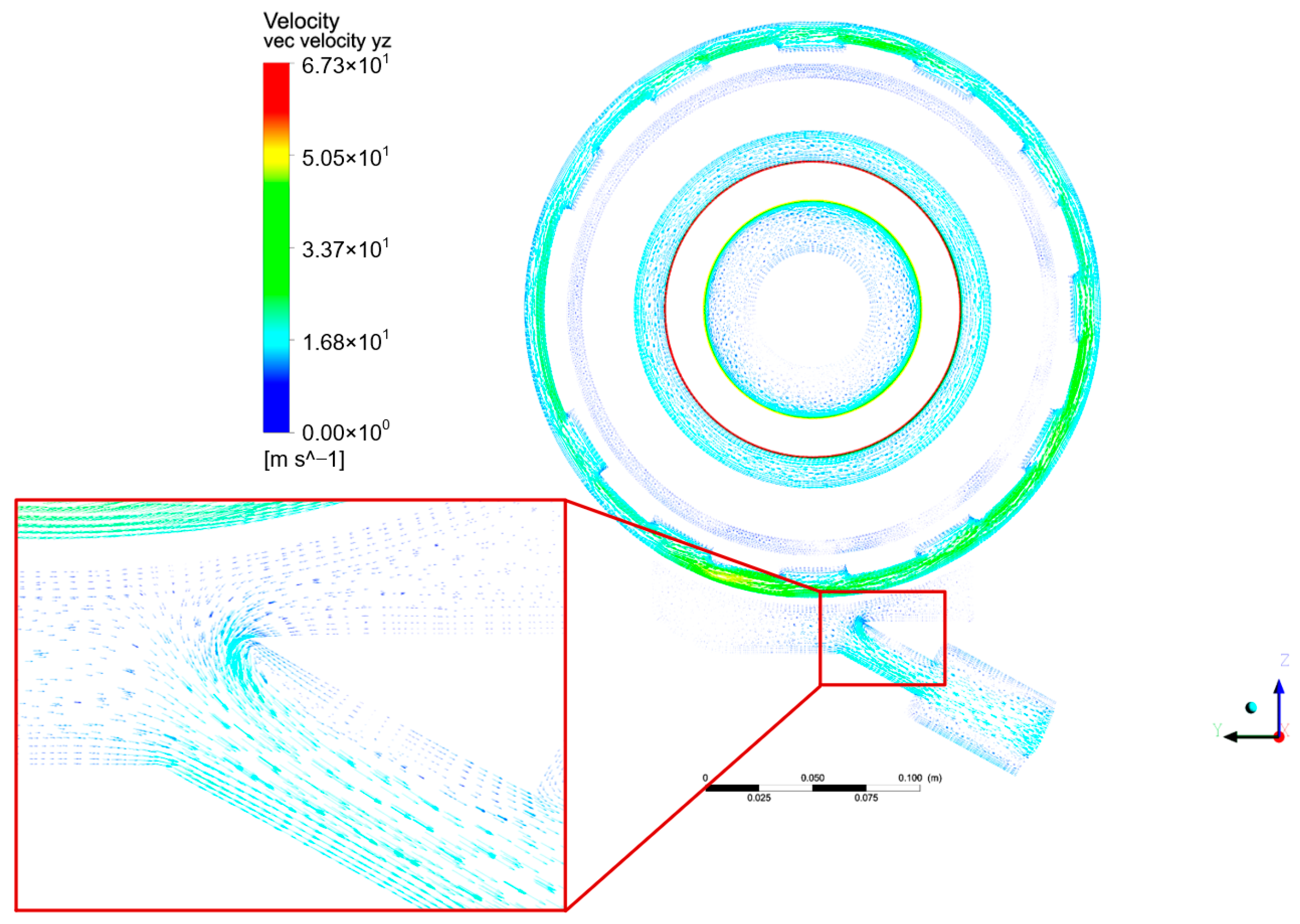
4.2. Velocity Distribution of Bearing Chamber
5. Evaluation of Scavenge Flow Characteristic
6. Optimization Measures of Scavenging Performance
7. Results
- (1)
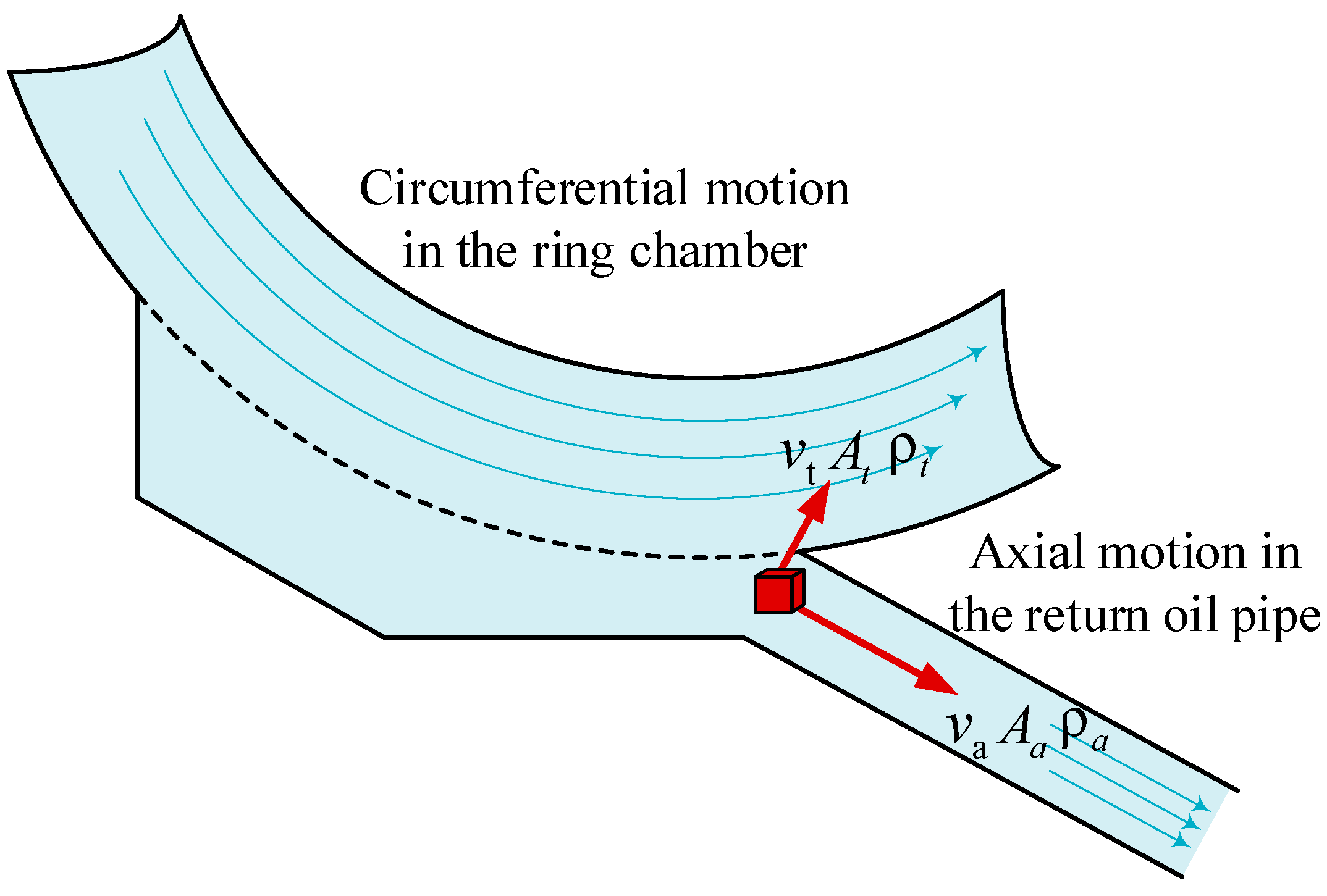
- A normalized momentum–flux ratio evaluation parameter is proposed: In this study, an evaluation parameter is formulated based on the ratio of the momentum flux of the axial inflow into the scavenge pipe to that of the tangential crossflow in the annulus. By incorporating the cross-sectional RMS velocity and normalizing the result to the range [0, 1], this parameter physically reflects the competition between “entering the scavenge pipe” and “recirculating into the annulus,” while providing a quantifiable basis for comparing scavenging performance under different structural configurations. This method demonstrates strong applicability and interpretability for complex, realistic flow fields.
- (2)
- Simulation analysis of the oil flow characteristics for the baseline configuration: In the original structure, the evaluation parameter indicates a moderate tendency for the oil flow to enter the scavenge pipe, with a considerable proportion of the mixture recirculating into the front oil collection annulus. The root cause lies in the direct connection between the oil sump and the front oil collection annulus, which introduces a high tangential velocity flow field and an adverse pressure gradient, thereby reducing the effective flow area at the inlet.
- (3)
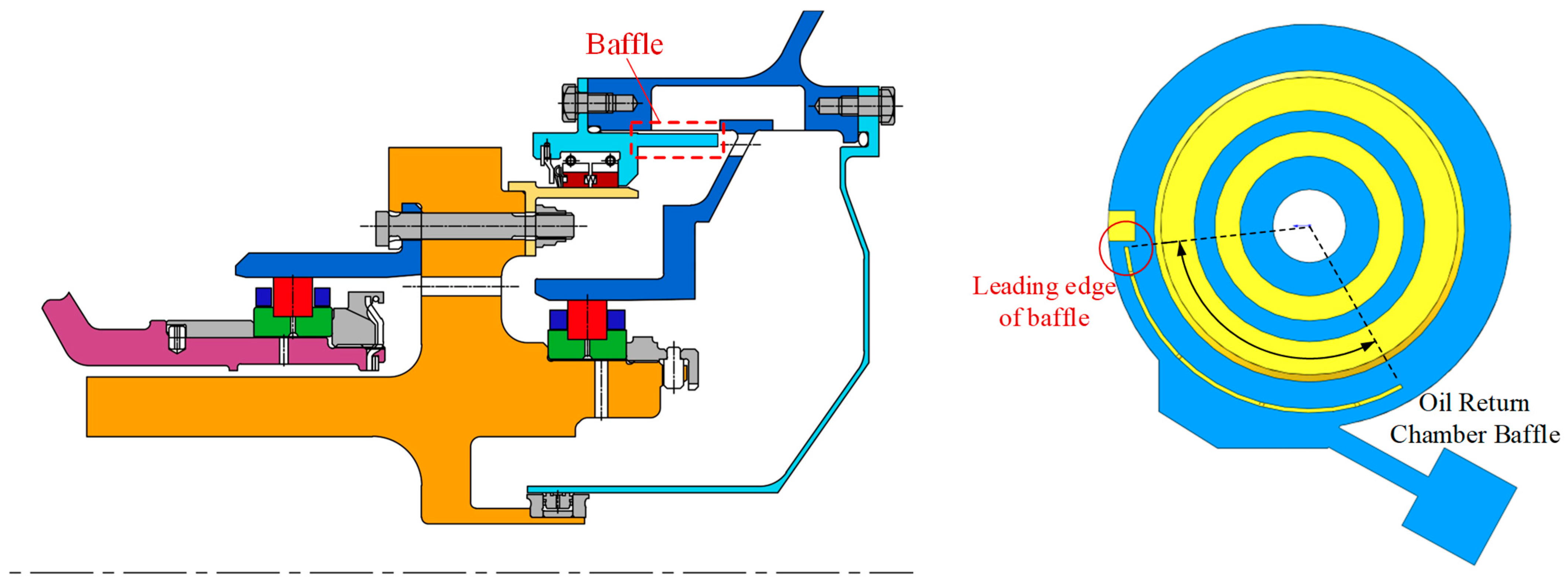
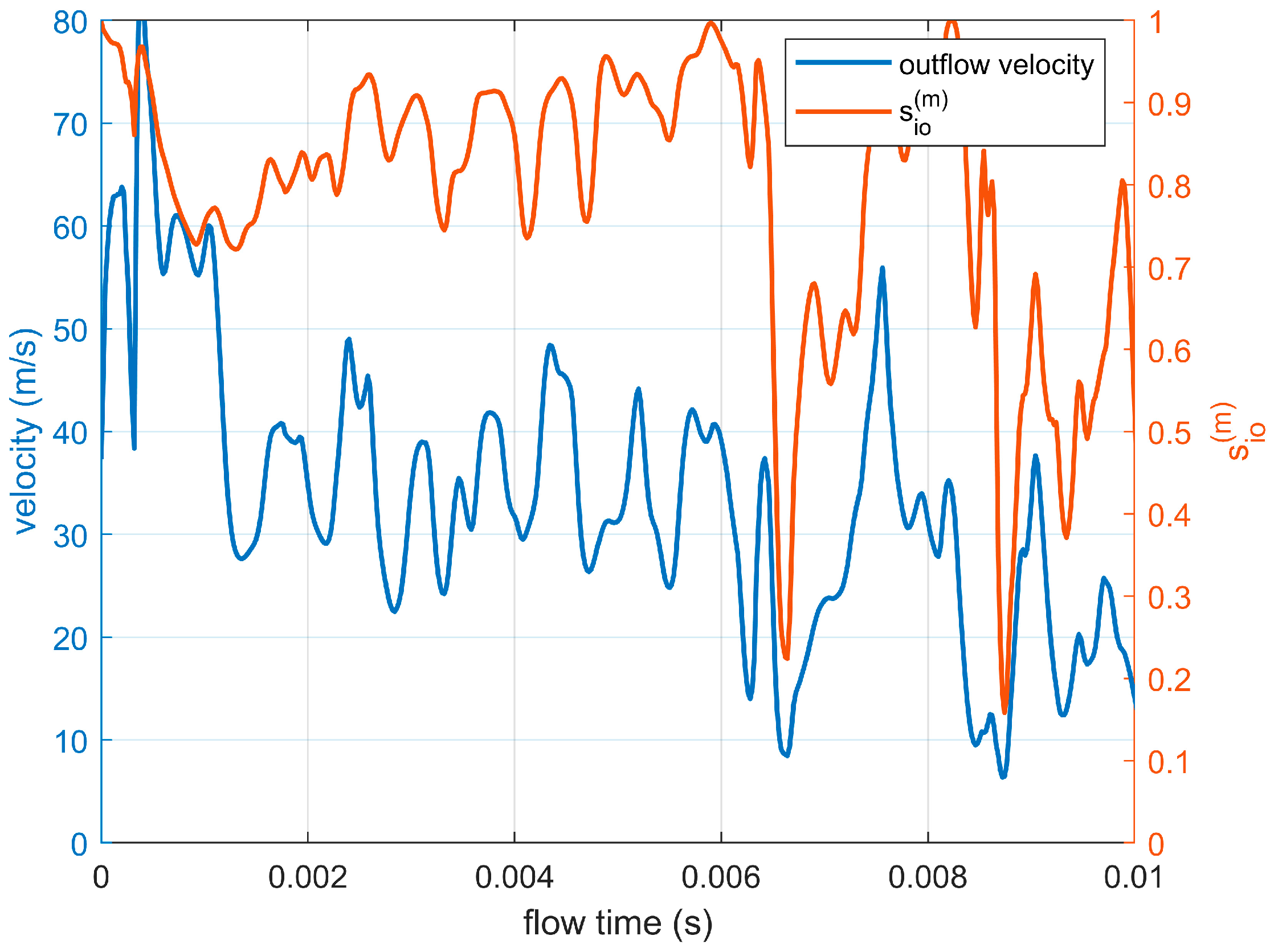
- Effect of the baffle modification (Improved Structure I): After installing a baffle between the oil sump and the front oil collection annulus, the average value of increases to 0.83, representing an improvement of 2.5% compared with the baseline. The internal pressure distribution becomes more uniform, and the flow direction is more favorable for the lubricating oil to enter the scavenge pipe. However, under high-speed flow conditions, significant fluctuations occur in both the inlet velocity and , which may locally reduce the scavenging performance, indicating that further optimization is needed to enhance flow stability.
- (4)
- Effect of full isolation and inlet position optimization (Improved Structure II): By completely isolating the oil sump from the front oil collection annulus and relocating the scavenge pipe inlet to the middle section, stabilizes at approximately 0.95, representing a 17.3% improvement over the baseline and 14.5% improvement over the baffle configuration. This structural arrangement effectively eliminates the interference from high-speed tangential flows, resulting in a stable flow direction with minimal fluctuations, thereby significantly enhancing scavenging performance.
- (5)
- The evaluation parameter proposed in this study provides a quantitative measure for assessing the scavenge flow characteristics of bearing chambers and can be applied directly to compare and select alternative structural configurations. The two improvement schemes demonstrate that geometrically isolating regions of high circumferential flow and optimizing the scavenge-inlet location markedly increase the proportion of momentum flux and enhance flow stability, thereby improving scavenge efficiency, reducing oil residence time and lowering leakage risk. The proposed methodology and design principles offer practical guidance for optimizing lubrication systems in high DN bearing chambers and promote improvements in aero-engine bearing chamber reliability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hong, J.; Ma, Y.H.; Zhang, D.Y. Overall Structure Design and Dynamic Analysis of Aero Gas Turbine; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 2014; pp. 230–276. ISBN 978-7-5124-1360-3. [Google Scholar]
- Wang, W.; Wang, Y.M.; Wang, Z.S.; Wang, H.W.; Zhu, Z.J.; Yang, J.G.; Shen, X.M.; Wu, N.X.; Wu, L.F.; Lu, J.W.; et al. Aero-Engine Design Manual, 12th ed.; Aviation Industry Press: Beijing, China, 2001; pp. 429–432. ISBN 7-80134-943-1. [Google Scholar]
- Chandra, B.W.; Collicott, S.H.; Munson, J.H. Experimental Optimization of Rolls-Royce AE3007 Sump Design. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Computational. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Chang, Y.C.; Hou, T.Y.; Merriman, B.; Osher, S. A Level Set Formulation of Eulerian Interface Capturing Methods for Incompressible Fluid Flows. Computational. Phys. 1996, 124, 449–464. [Google Scholar] [CrossRef]
- Reynolds, O. On the Theory of Lubrication and Its Application to Mr. Beauchamp Tower’s Experiments, Including an Experimental Determination of the Viscosity of Olive Oil. Philos. Trans. R. Soc. Lond. 1886, 177, 157–234. [Google Scholar] [CrossRef]
- Farrall, M.; Simmons, K.; Hibberd, S.; Gorse, P. A Numerical Model for Oil Film Flow in an Aero-Engine Bearing Chamber and Comparison with Experimental Data. J. Eng. Gas Turbines Power 2006, 128, 111–117. [Google Scholar] [CrossRef]
- Wang, C.; Morvan, H.P.; Hibberd, S.; Cliffe, K.A. Thin Film Modelling for Aero-Engine Bearing Chambers. In Proceedings of the ASME Turbo Expo 2011: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 12 October 2010; pp. 277–286. [Google Scholar] [CrossRef]
- Singh, K.; Sharabi, M.; Jefferson-Loveday, R.; Ambrose, S.; Eastwick, C.; Cao, J.; Jacobs, A. Modeling of Partially Wetting Liquid Film Using an Enhanced Thin Film Model for Aero-Engine Bearing Chamber Applications. J. Eng. Gas Turbines Power 2021, 143, 041001. [Google Scholar] [CrossRef]
- Simmons, K.; Hibberd, S.; Wang, Y.; Care, L. Numerical Study of the Two-Phase Air/Oil Flow Within an Aero-Engine Bearing Chamber Model Using a Coupled Lagrangian Droplet Tracking Method. In Proceedings of the ASME 2002 Pressure Vessels and Piping Conference, Vancouver, BC, Canada, 5–9 August 2002; pp. 325–331. [Google Scholar] [CrossRef]
- Kakimpa, B.; Morvan, H.P.; Hibberd, S. The Numerical Simulation of Multi-Scale Oil Films Using Coupled VOF and Eulerian Thin-Film Models. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Republic of Korea, 13–17 June 2016. [Google Scholar] [CrossRef]
- Ren, G.Z. Investigation on Flow and Heat Transfer Characteristics in Aero-Engine Bearing Chambers under Oil-Gas Two-Phase Flow Conditions and Optimization Design of Scavenge Structures. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, December 2016. [Google Scholar]
- Li, W. Numerical Study on Flow Characteristics of Oil-Air Two-Phase Flow in Bearing Chambers. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, December 2016. [Google Scholar]
- Lee, C.W.; Palma, P.C.; Simmons, K.; Pickering, S.J. Comparison of CFD and PIV Data for the Airflow in an Aero-Engine Bearing Chamber. In Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004; pp. 97–105. [Google Scholar] [CrossRef]
- Chen, B.; Chen, G.D.; Zhang, Y.H. Numerical Simulation of Gas-Phase Velocity Field in Aero-engine Bearing Chambers. Mech. Sci. Technol. Aerosp. Eng. 2012, 8, 1241–1246. [Google Scholar] [CrossRef]
- Lü, Y.G.; Zhang, M.H.; Liu, Z.X.; Hu, J.P. Numerical study and validation for two-phase flow of oil and gas in Aero-Engine bearing chambers. J. Aerosp. Power 2014, 29, 2751–2757. [Google Scholar] [CrossRef]
- Wang, T.; Chen, G.D.; Chen, B. Theoretical and Experimental Study on Flow Field of Gas-Phase Medium in Aero-Engine Bearing Chambers. J. Aerosp. Power 2014, 11, 2767–2773. [Google Scholar] [CrossRef]
- Yang, P.J.; Lu, P.; Fang, L.L.; Wang, X.Y. Effect of structural parameters of oil return groove on oil-air two-phase flow in bearing chambers. J. Jiangsu Univ. (Nat. Sci. Ed.) 2019, 40, 643–648. [Google Scholar]
- Crouchez-Pillot, A.; Morvan, H.P. CFD Simulation of an Aero-engine Bearing Chamber Using an Enhanced Volume of Fluid (VOF) Method: An Evaluation Using Adaptive Meshing. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar] [CrossRef]
- Chandra, B.; Collicott, S.H.; Munson, J.H. Scavenge Flow in a Bearing Chamber with Tangential Sump Off-Take. J. Eng. Gas Turbines Power 2013, 135, 032503. [Google Scholar] [CrossRef]
- Chandra, B.; Simmons, K.; Pickering, S.; Tittel, M. Factors Affecting Oil Removal From an Aero-Engine Bearing Chamber. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010; pp. 219–228. [Google Scholar] [CrossRef]
- Collicott, S.H.; Wiedemann, N. Study of Gas/Liquid Behavior Within an Aero-engine Bearing Chamber. J. Eng. Gas Turb. Power 2013, 135, 051201. [Google Scholar] [CrossRef]
- Chandra, B.; Simmons, K. Transient Two-Phase Effects in an Aero-engine Bearing Chamber Scavenge Test Rig. In Proceedings of the ASME 2014 International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014. [Google Scholar] [CrossRef]
- Simmons, K.; Chandra, B. Experimental Investigation Into the Performance of Shallow Aero-engine Off-Takes. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar] [CrossRef]
- Kurz, W.; Dullenkopf, K.; Bauer, H.J. Capacitive Film Thickness Measurements in a Ventless Aero-Engine Bearing Chamber—Influence of Operating Conditions and Offtake Design. J. Eng. Gas Turbines Power 2013, 135, 112504. [Google Scholar] [CrossRef]
- Kurz, W.; Dullenkopf, K.; Bauer, H.J. Influences on the Oil Split Between the Offtakes of an Aero-Engine Bearing Chamber. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; pp. 2251–2259. [Google Scholar] [CrossRef]


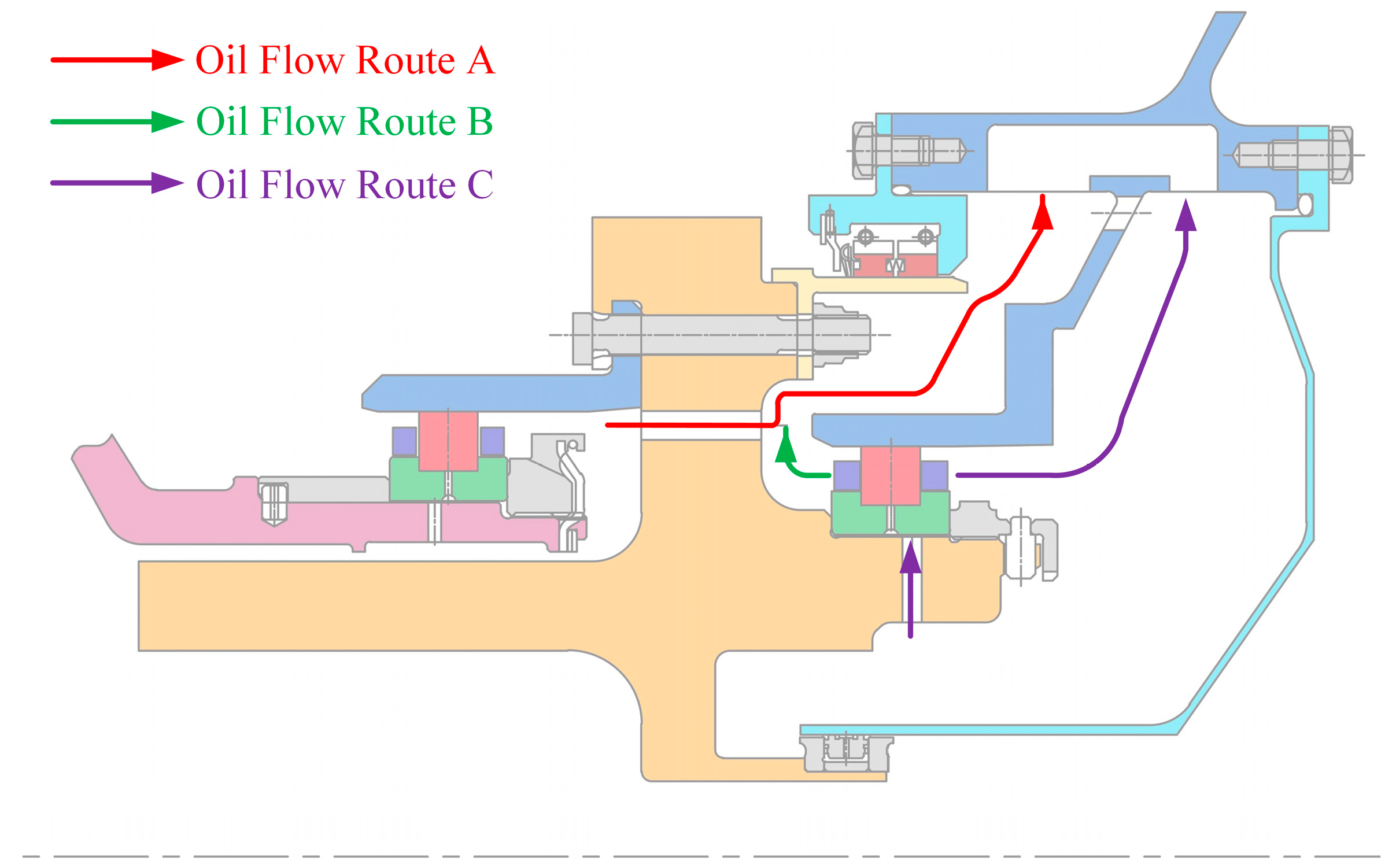

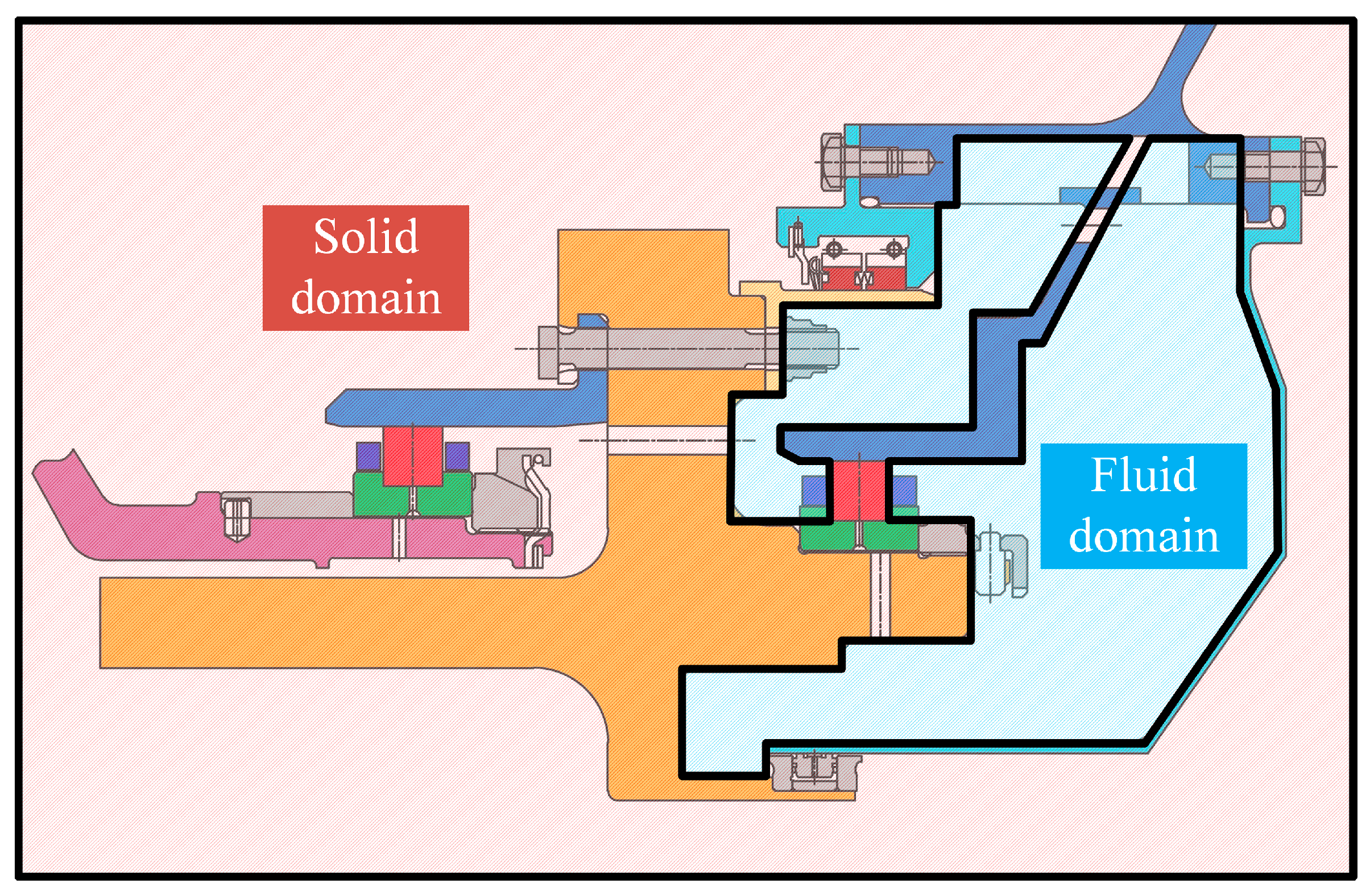
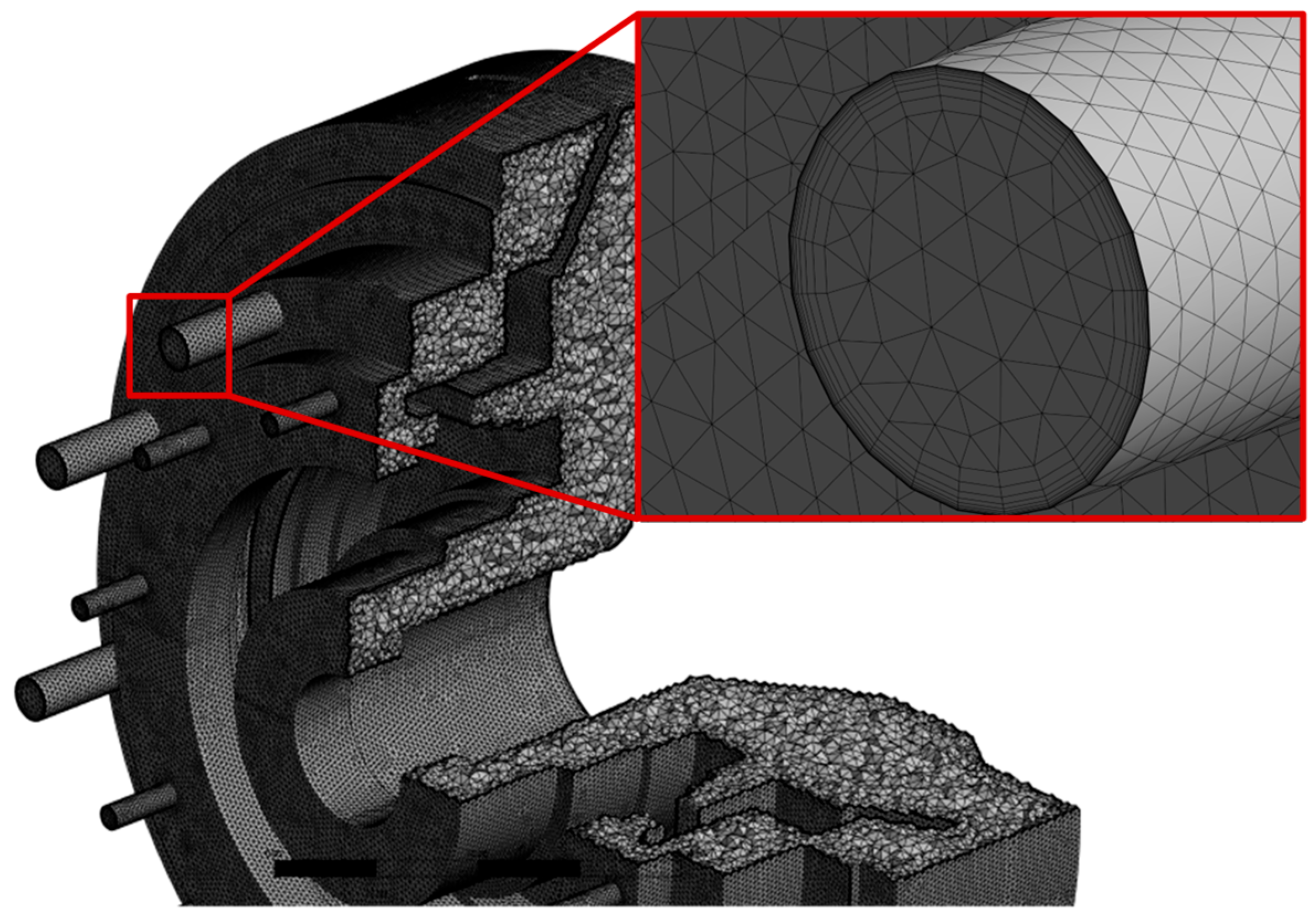

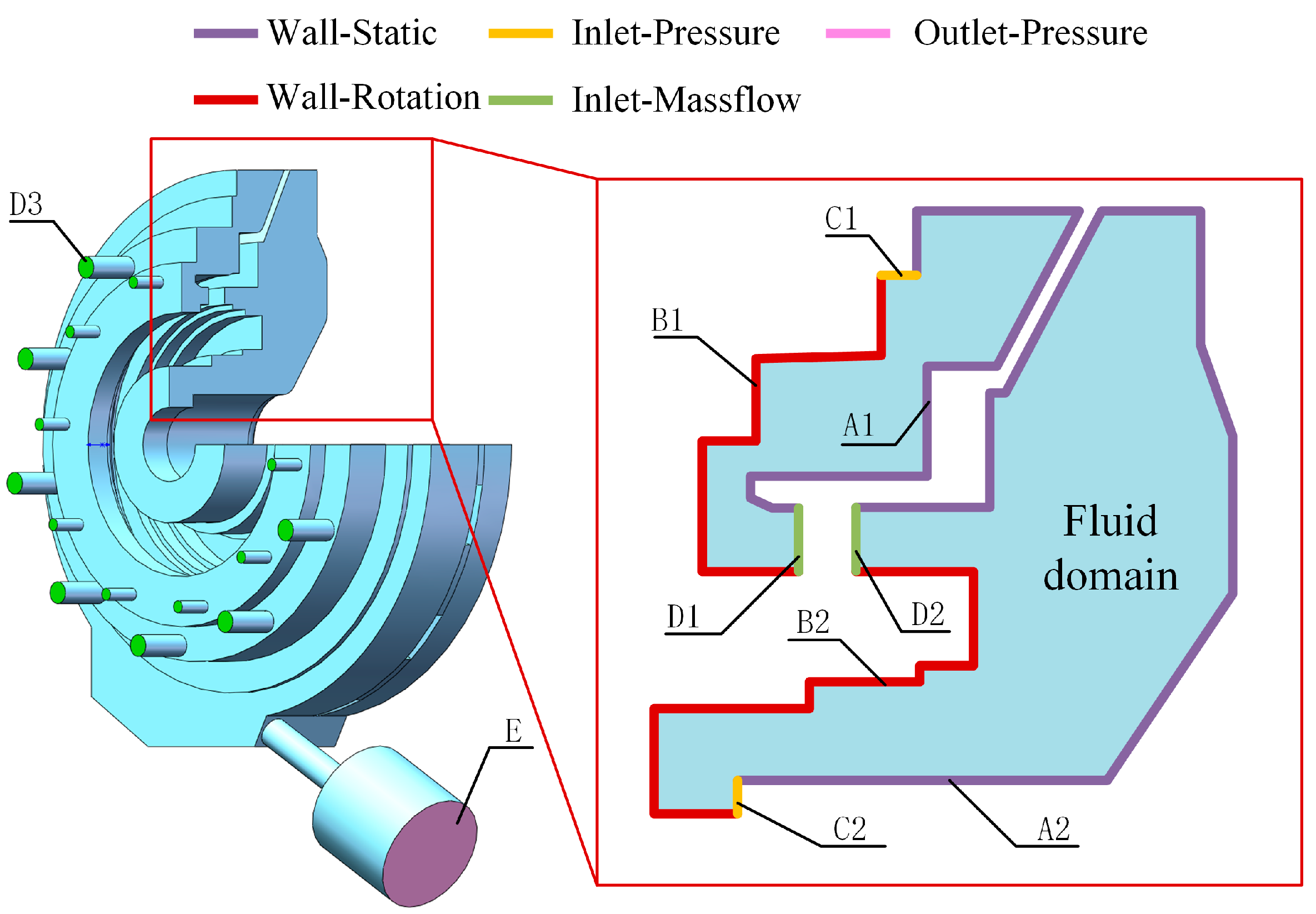






| Geometry | Dimension |
|---|---|
| Bearing chamber diameter | 300 mm |
| Oil sump depth | 15 mm |
| Vent pipe length | 70 mm |
| Vent pipe diameter | 16 mm |
| Scavenge pipe length | 70 mm |
| Scavenge pipe diameter | 16 mm |
| Scavenge pipe inclination angle | 30° |
| Oil sump width | 120 mm |
| Numbering | Type | Density (kg/m3) | Viscosity (kg/(m·s)) | Tension Coefficient (N/m) |
|---|---|---|---|---|
| Phase 1 | Air | 1.227 | 1.790 × 10−5 | 0.04 |
| Phase 2 | Oil 2380 | 974.900 | 4.845 × 10−3 |
| Number | Boundary Type | Effect | Corresponding Parameter |
|---|---|---|---|
| A1 | Wall–Static | Simulation of constraint effect of the stationary wall | - |
| A2 | |||
| B1 | Wall–Moving | Simulation of the rotating wall, driving oil/air circumferential motion | Low-pressure rotor working speed 12,000 rpm |
| B2 | |||
| C1 | Inlet–Pressure | Simulate graphite sealing structure, controlling static pressure in the chamber | Measured static pressure of the chamber 59 kPa |
| C2 | |||
| D1 | Inlet–Mass flow | Simulating No. 5 bearing oil supply | 60 g/s |
| D2 | |||
| D3 | Simulating No. 4 bearing oil supply | 169 g/s | |
| E | Outlet–Pressure | Simulation of scavenge pump for oil suction | 1 kPa lower than the chamber |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Zheng, W.; Chen, X.; Leng, Z.; Hong, J. Simulation Analysis and Structural Improvements of Oil Return in Main Bearing Chamber of Aero-Engine. Lubricants 2025, 13, 381. https://doi.org/10.3390/lubricants13090381
Ma Y, Zheng W, Chen X, Leng Z, Hong J. Simulation Analysis and Structural Improvements of Oil Return in Main Bearing Chamber of Aero-Engine. Lubricants. 2025; 13(9):381. https://doi.org/10.3390/lubricants13090381
Chicago/Turabian StyleMa, Yanhong, Wanfei Zheng, Xueqi Chen, Zihao Leng, and Jie Hong. 2025. "Simulation Analysis and Structural Improvements of Oil Return in Main Bearing Chamber of Aero-Engine" Lubricants 13, no. 9: 381. https://doi.org/10.3390/lubricants13090381
APA StyleMa, Y., Zheng, W., Chen, X., Leng, Z., & Hong, J. (2025). Simulation Analysis and Structural Improvements of Oil Return in Main Bearing Chamber of Aero-Engine. Lubricants, 13(9), 381. https://doi.org/10.3390/lubricants13090381




