Toward Coarse and Fine Bimodal Structures for Improving the Plasma Resistance of Al2O3
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Optimum Recipe for Dense and Less Porous Al2O3 Ceramic
3.2. Plasma Resistance and Local Etching
3.3. Weight Loss Analysis
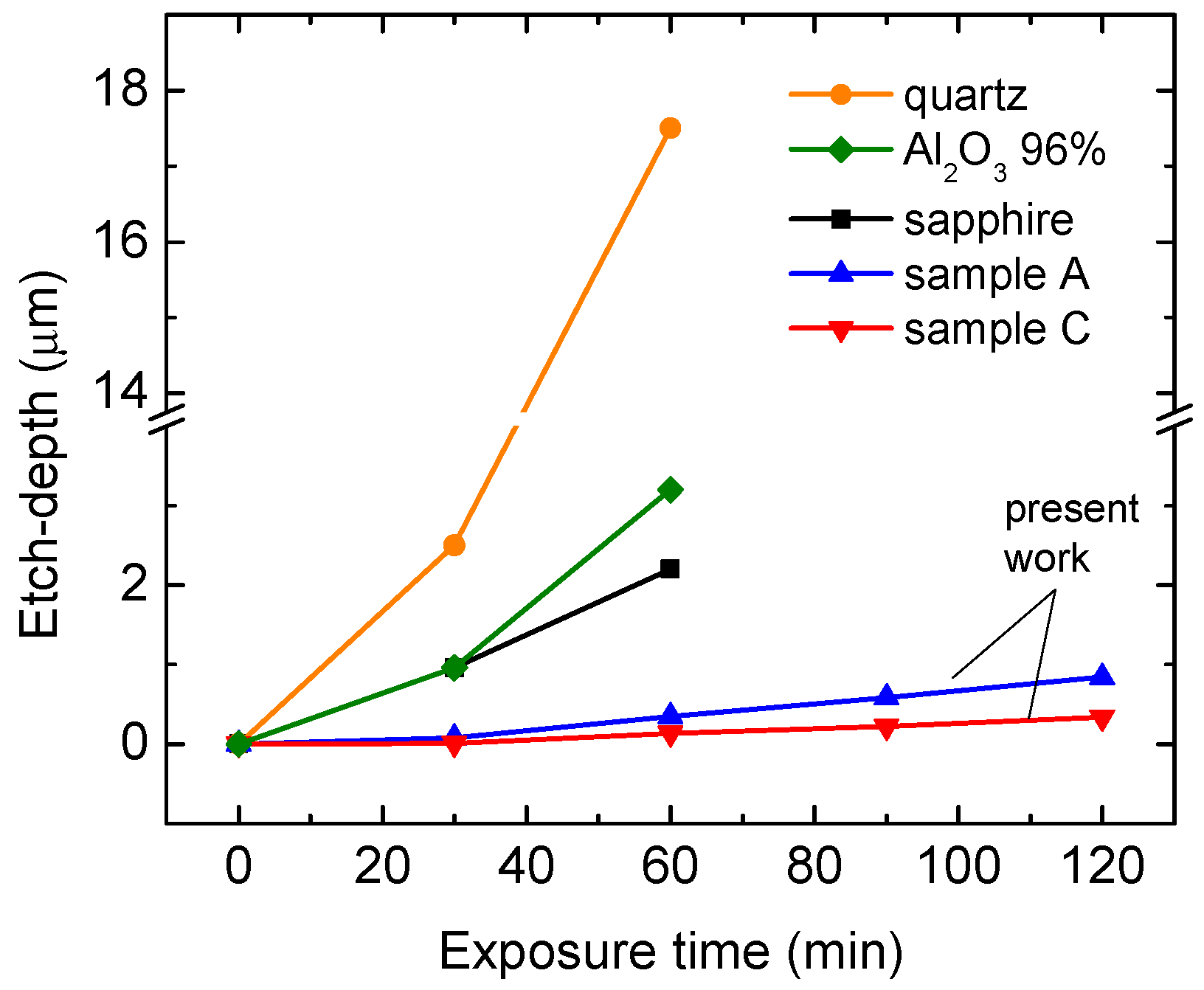
3.4. Etch-Depth Analysis
3.5. Flexural Strength Analysis
4. Discussion
4.1. Sintering of Al2O3 Ceramic
4.2. Densification of Al2O3 Ceramic
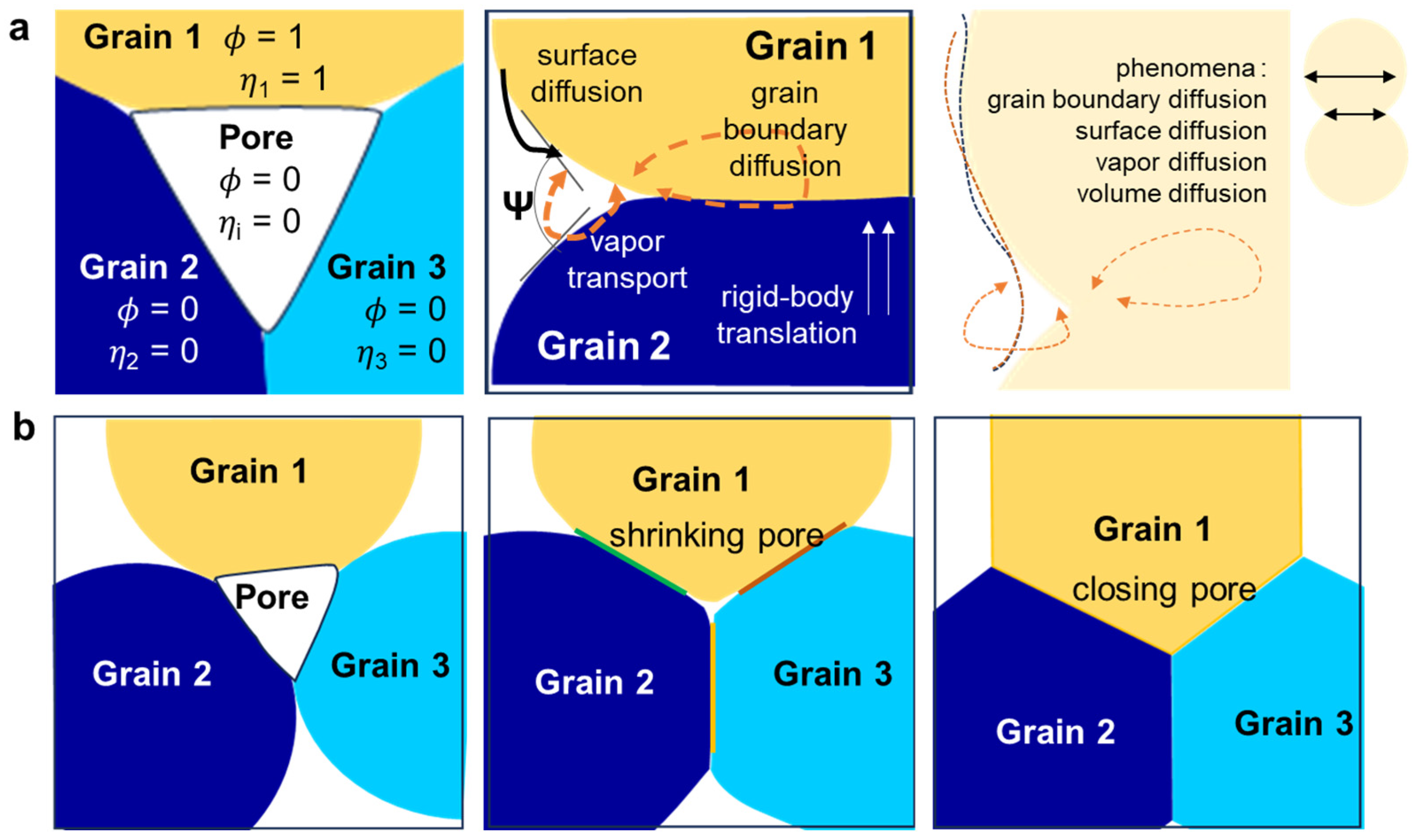
4.3. Plasma Etching Mechanism
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shanu, A.; Sharma, P.; Dixit, P. Micromachining of Alumina Ceramic for Microsystems Applications: A systematic review, challenges and future opportunities. Mater. Manuf. Process. 2023, 39, 892–924. [Google Scholar] [CrossRef]
- Fu, L.; Huang, A.; Gu, H.; Ni, H. Properties and Microstructures of Lightweight Alumina Containing Different Types of Nano-Alumina. Ceram. Int. 2018, 44, 17885–17894. [Google Scholar] [CrossRef]
- Lee, K.M.; Ko, Y.G.; Shin, D.H. Incorporation of Carbon Nanotubes into Micro-Coatings Film Formed on Aluminum Alloy via Plasma Electrolytic Oxidation. Mater. Lett. 2011, 65, 2269–2273. [Google Scholar] [CrossRef]
- Coble, R.L. Transparent Alumina and Method of Preparation. U.S. Patent 3026210A, 20 March 1962. [Google Scholar]
- Hsu, Y.-F.; Wang, S.-F.; Cheng, T.-W. Effects of Additives on the Densification and Microstructural Evolution of Fine θ-Al2O3 Powder. Mater. Sci. Eng. A 2003, 362, 300–308. [Google Scholar] [CrossRef]
- Bae, S.I.; Baik, S. Sintering and Grain Growth of Ultrapure Alumina. J. Mater. Sci. 1993, 28, 4197–4204. [Google Scholar] [CrossRef]
- Bae, S.I.; Baik, S. Determination of Critical Concentrations. J. Am. Ceram. Soc. 1993, 76, 1065–1067. [Google Scholar] [CrossRef]
- Louet, N.; Reveron, H.; Fantozzi, G. Sintering Behaviour and Microstructural Evolution of Ultrapure α-Alumina Containing Low Amounts of SiO2. J. Eur. Ceram. Soc. 2008, 28, 205–215. [Google Scholar] [CrossRef]
- Li, L.; Yang, H.; Sun, X.; Kang, Y.; Zhang, F.; Zhao, Y.; Li, J.; Zhao, L.; Li, J. Influence of SiO2 Addition on the Sintering Behavior and Kinetics of Fine-Sized α-Al2O3 Nanoparticles. Ceramics 2023, 49, 22187–22196. [Google Scholar] [CrossRef]
- Baud, S.; Thévenot, F.; Pisch, A.; Chatillon, C. High Temperature Sintering of SiC with Oxide Additives: I. Analysis in the SiC-Al2O3 and SiC-Al2O3-Y2O3 Systems. J. Eur. Ceram. Soc. 2003, 23, 1–8. [Google Scholar] [CrossRef]
- Wu, T.; Zhou, J.; Wu, B.; Xiong, Y. Effect of Y2O3 Additives on the Wet Abrasion Resistance of an Alumina-Based Grinding Medium. Wear 2016, 356–357, 9–16. [Google Scholar] [CrossRef]
- Koyama, C.; Ishikawa, T.; Watanabe, Y. Density Measurements of Molten Y3Al5O12 and Y2O3-Al2O3 Compounds Using an Electrostatic Levitation Technique. J. Am. Ceram. Soc. 2023, 106, 5648–5653. [Google Scholar] [CrossRef]
- Sifat, R.; Akter, M.; Rashid, A.K.M.B. Properties of Micro-Nano Particle Size Admixtures of Alumina at Different Sintering Condition. AIP Conf. Proc. 2016, 1754, 030005. [Google Scholar] [CrossRef]
- Koli, D.K.; Agnihotri, G.; Purohit, R. A Review on Properties, Behaviour and Processing Methods for Al- Nano Al2O3 Composites. Procedia Mater. Sci. 2014, 6, 567–589. [Google Scholar] [CrossRef]
- Teng, X.; Liu, H.; Huang, C. Effect of Al2O3 Particle Size on the Mechanical Properties of Alumina-Based Ceramics. Mater. Sci. Eng. A 2007, 452–453, 545–551. [Google Scholar] [CrossRef]
- Sadeghi, B.; Shamanian, M.; Ashrafizadeh, F.; Cavaliere, P.; Sanayei, M.; Szpunar, J.A. Microstructural Behaviour of Spark Plasma Sintered Composites Containing Bimodal Micro- and Nano-Sized Al2O3 Particles. Powder Metall. 2018, 61, 50–63. [Google Scholar] [CrossRef]
- Fellah, M.; Hezil, N.; Bouras, D.; Montagne, A.; Obrosov, A.; Jamshed, W.; Ibrahim, R.W.; Iqbal, A.; El Din, S.M.; Abd El-Wahed Khalifa, H. Investigating the Effect of Milling Time on Structural, Mechanical and Tribological Properties of a Nanostructured Hiped Alpha Alumina for Biomaterial Applications. Arab. J. Chem. 2023, 16, 105112. [Google Scholar] [CrossRef]
- Toozandehjani, M.; Matori, K.A.; Ostovan, F.; Aziz, S.A.; Mamat, M.S. Effect of Milling Time on the Microstructure, Physical and Mechanical Properties of Al- Al2O3 Nanocomposite Synthesized by Ball Milling and Powder Metallurgy. Materials 2017, 10, 1232. [Google Scholar] [CrossRef]
- Panigrahi, N.; Chaini, R.; Nayak, A.; Chandra Mishra, P. Impact of Milling Time and Method on Particle Size and Surface Morphology during Nano Particle Synthesis from α-Al2O3. Mater. Today Proc. 2018, 5, 20727–20735. [Google Scholar] [CrossRef]
- Kang, S.-J.L. What We Should Consider for Full Densification When Sintering. Materials 2020, 13, 3578. [Google Scholar] [CrossRef]
- Nivot, C.; Valdivieso, F. Microstructure Refinement of Alumina: Optimisation by Gas Pressure Sintering Process. Ceram. Int. 2008, 34, 1595–1602. [Google Scholar] [CrossRef]
- Pan, Y.; Li, H.; Liu, Y.; Liu, Y.; Hu, K.; Wang, N.; Lu, Z.; Liang, J.; He, S. Effect of Holding Time During Sintering on Microstructure and Properties of 3D Printed Alumina Ceramics. Front. Mater. 2020, 7, 54. [Google Scholar] [CrossRef]
- Coble, R.L. Sintering Alumina: Effect of Atmospheres. J. Am. Ceram. Soc. 1962, 45, 123–127. [Google Scholar] [CrossRef]
- Kingery, W.D.; Bowen, H.K.; Uhlmann, D.R.; Frieser, R. Introduction to Ceramics. J. Electrochem. Soc. 1977, 124, 152C. [Google Scholar] [CrossRef]
- Mortensen, A. Kinetics of Densification by Solution-Reprecipitation. Acta Mater. 1997, 45, 749–758. [Google Scholar] [CrossRef]
- Wang, Y.U. Computer Modeling and Simulation of Solid-State Sintering: A Phase Field Approach. Acta Mater. 2006, 54, 953–961. [Google Scholar] [CrossRef]
- Allen, S.M.; Cahn, J.W. A Microscopic Theory for Antiphase Boundary Motion and Its Application to Antiphase Domain Coarsening. Acta Metall. 1979, 27, 1085–1095. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free Energy of a Nonuniform System. I. Interfacial Free Energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Abdeljawad, F.; Bolintineanu, D.S.; Cook, A.; Brown-Shaklee, H.; DiAntonio, C.; Kammler, D.; Roach, A. Sintering Processes in Direct Ink Write Additive Manufacturing: A Mesoscopic Modeling Approach. Acta Mater. 2019, 169, 60–75. [Google Scholar] [CrossRef]
- Ofori-Opoku, N.; Provatas, N. A Quantitative Multi-Phase Field Model of Polycrystalline Alloy Solidification. Acta Mater. 2010, 58, 2155–2164. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, Y.; Shi, Z.; Li, W.; Ye, X. Effect of Plasma Etching Depth on Subsurface Defects in Quartz Crystal Elements. Crystals 2023, 13, 1477. [Google Scholar] [CrossRef]
- Tezani, L.L.; Pessoa, R.S.; Maciel, H.S.; Petraconi, G. Chemistry Studies of SF6/CF4, SF6/O2 and CF4/O2 Gas Phase during Hollow Cathode Reactive Ion Etching Plasma. Vacuum 2014, 106, 64–68. [Google Scholar] [CrossRef]
- Kim, J.-W.; Kim, Y.-C.; Lee, W.-J. Reactive Ion Etching Mechanism of Plasma Enhanced Chemically Vapor Deposited Aluminum Oxide Film in CF4/O2 Plasma. J. Appl. Phys. 1995, 78, 2045–2049. [Google Scholar] [CrossRef]
- Kimura, T.; Noto, M. Experimental Study and Global Model of Inductively Coupled CF4/O2 Discharges. J. Appl. Phys. 2006, 100, 063303. [Google Scholar] [CrossRef]
- Plumb, I.C.; Ryan, K.R. A Model of the Chemical Processes Occurring in CF4/O2 Discharges Used in Plasma Etching. Plasma Chem. Plasma Process. 1986, 6, 205–230. [Google Scholar] [CrossRef]
- Schoenborn, P.; Patrick, R.; Baltes, H.P. Numerical Simulation of a CF4/O2 Plasma and Correlation with Spectroscopic and Etch Rate Data. J. Electrochem. Soc. 1989, 136, 199–205. [Google Scholar] [CrossRef]
- Venkatesan, S.P.; Trachtenberg, I.; Edgar, T.F. Modeling of Silicon Etching in CF4/O2 and CF4/H2 Plasmas. J. Electrochem. Soc. 1990, 137, 2280–2290. [Google Scholar] [CrossRef]
- Chun, I.; Efremov, A.; Yeom, G.Y.; Kwon, K.-H. A Comparative Study of CF4/O2/Ar and C4F8/O2/Ar Plasmas for Dry Etching Applications. Thin Solid Films 2015, 579, 136–143. [Google Scholar] [CrossRef]
- Racka-Szmidt, K.; Stonio, B.; Żelazko, J.; Filipiak, M.; Sochacki, M. A Review: Inductively Coupled Plasma Reactive Ion Etching of Silicon Carbide. Materials 2022, 15, 123. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.-M.; Kim, K.-B.; Yoon, S.-Y.; Oh, Y.-S.; Kim, H.-T.; Lee, S.-M. Effects of Artificial Pores and Purity on the Erosion Behaviors of Polycrystalline Al2O3 Ceramics under Fluorine Plasma. J. Ceram. Soc. Jpn. 2009, 117, 863–867. [Google Scholar] [CrossRef]
- Duan, X.; Jia, D.; Zhou, Y.; Yang, Z.; Wang, Y.; Ren, F.; Yu, D.; Ding, Y. Mechanical Properties and Plasma Erosion Resistance of BNp/Al2O3-SiO2 composite ceramics. J. Cent. South Univ. 2013, 20, 1462–1468. [Google Scholar] [CrossRef]
- Yıldız, B.K.; Tür, Y.K. An Investigation of Equibiaxial Flexural Strength and Hardness Properties of Al2O3–Ni Nanocomposites Based Microstructures with ZrO2 and Cr2O3 Additives. Mater. Sci. Eng. A 2019, 758, 103–111. [Google Scholar] [CrossRef]
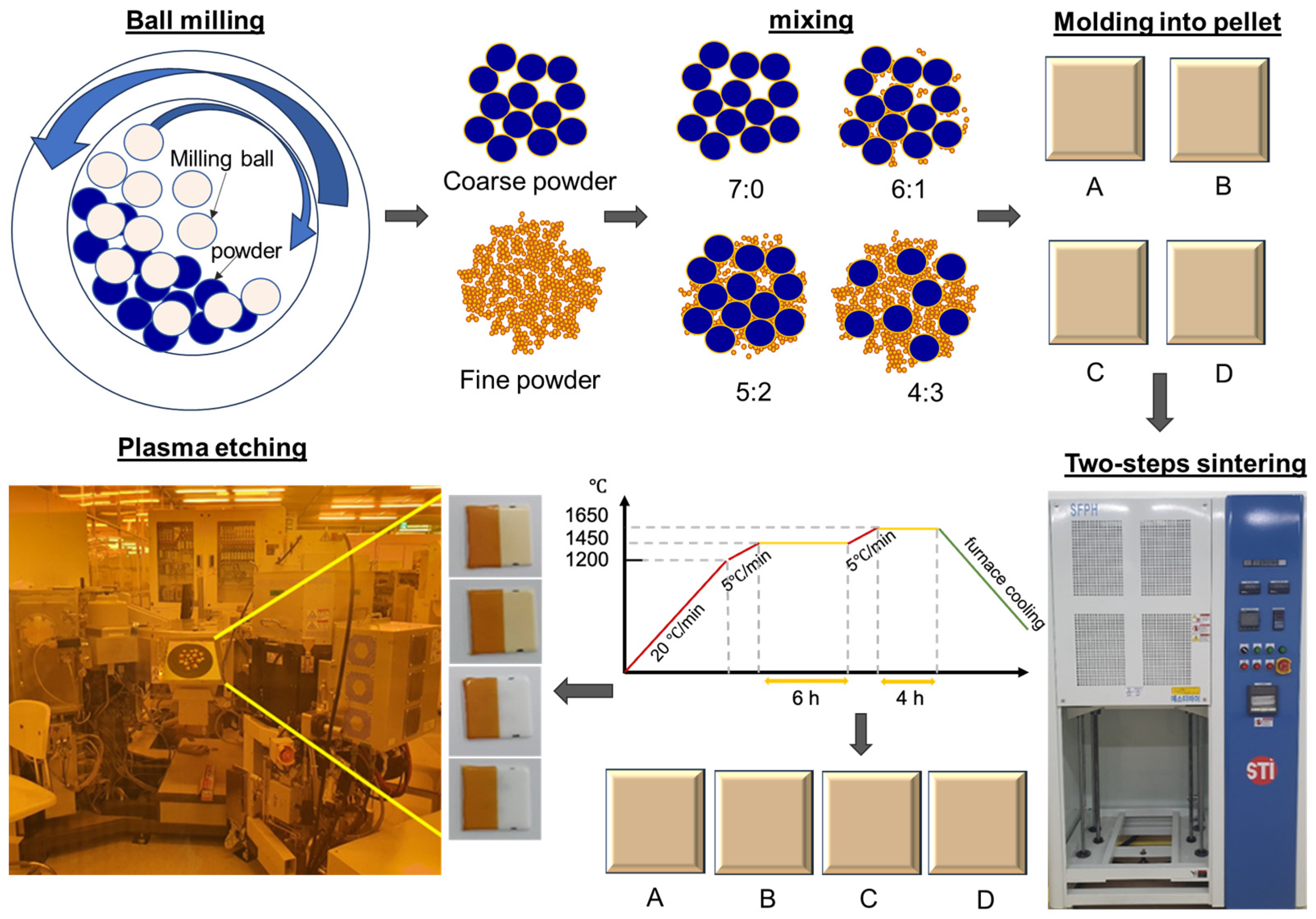





| Composition | Sample A 7:0 | Sample B 6:1 | Sample C 5:2 | Sample D 4:3 |
|---|---|---|---|---|
| micro-scale Al2O3 (35 ± 17 μm) | 7 g | 6 g | 5 g | 4 g |
| sub-micron Al2O3 (611 ± 95 nm) | 0 g | 1 g | 2 g | 3 g |
| Specimen | Purity | Raw Materials | Sintering Temperature |
|---|---|---|---|
| sample A | 99.99% Al2O3 | micron Al2O3 | 20 °C/min to 1200 °C, then 5 °C/min to 1450 °C (hold 6 h), and 5 °C/min to 1650 °C (hold 4 h) |
| sample C | 99.99% Al2O3 | micron & submicron Al2O3 |
| Specimen | Mass (g) | Volume (mm3) | Density (g/mm3) | Density (g/cm3) | Average (g/cm3) |
|---|---|---|---|---|---|
| sample A_1 | 3.9091 | 994.011992 | 0.003932649 | 3.932649 | 3.91915 ± 0.00961 |
| sample A_2 | 3.9200 | 995.006997 | 0.003939671 | 3.939671 | |
| sample A_3 | 3.9082 | 994.011992 | 0.003931743 | 3.931743 | |
| sample A_4 | 3.8952 | 1000 | 0.003895200 | 3.895200 | |
| sample A_5 | 3.8965 | 999.999 | 0.003896504 | 3.896504 | |
| sample C_1 | 3.9681 | 1007.006985 | 0.003940489 | 3.940489 | 3.95192 ± 0.00347 |
| sample C_2 | 3.9682 | 1001.998998 | 0.003960283 | 3.960283 | |
| sample C_3 | 3.9655 | 1002.998997 | 0.003953643 | 3.953643 | |
| sample C_4 | 3.9687 | 1002.998997 | 0.003948359 | 3.948359 | |
| sample C_5 | 3.9687 | 1002.998997 | 0.003956833 | 3.956833 |
| Porosity (%) | ||||
|---|---|---|---|---|
| Before Etching | After Etching | Difference | Average | |
| Sample A_1 | 10.87 | 22.35 | 11.48 | 12.03 ± 0.386 |
| Sample A_2 | 11.54 | 23.07 | 11.53 | |
| Sample A_3 | 11.13 | 23.10 | 11.97 | |
| Sample A_4 | 11.15 | 24.29 | 13.14 | |
| Sample C_1 | 8.50 | 13.90 | 5.40 | 5.98 ± 0.221 |
| Sample C_2 | 7.98 | 13.94 | 5.96 | |
| Sample C_3 | 7.45 | 13.57 | 6.12 | |
| Sample C_4 | 7.32 | 13.78 | 6.46 | |
| Time (min) | Weight (g) Before Etching | Weight (g) After Etching | Weight Loss (g) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Tape (X) | Tape (O) | Tape (X) | Tape (O) | Tape (X) | Average (X) | Tape (O) | Average (O) | ||
| Sample A | 30 | 1.42469 | 1.38748 | 1.42297 | 1.38747 | 0.00172 | 0.004225 ± 1.084 × 10−3 | 0.00001 | 0.0002525 ± 1.200 × 10−4 |
| 60 | 1.41934 | 1.38077 | 1.41581 | 1.38067 | 0.00353 | 0.00010 | |||
| 90 | 1.42319 | 1.38623 | 1.41842 | 1.38586 | 0.00477 | 0.00037 | |||
| 120 | 1.41228 | 1.37472 | 1.40540 | 1.37419 | 0.00688 | 0.00053 | |||
| Sample C | 30 | 1.36368 | 1.33688 | 1.36235 | 1.33677 | 0.00133 | 0.002535 ± 5.788 × 10−4 | 0.00011 | 0.000233 ± 6.909 × 10−5 |
| 60 | 1.34957 | 1.32286 | 1.34748 | 1.32265 | 0.00209 | 0.00021 | |||
| 90 | 1.37055 | 1.34283 | 1.36790 | 1.34265 | 0.00265 | 0.00018 | |||
| 120 | 1.2547 | 1.22821 | 1.25064 | 1.22778 | 0.00407 | 0.00043 | |||
| 30 min | 60 min | 90 min | 120 min | Average | |
|---|---|---|---|---|---|
| Sample A | 79 nm | 345 nm | 588 nm | 843 nm | 463.75 ± 81.83 nm |
| Sample C | 6 nm | 132 nm | 218 nm | 337 nm | 173.25 ± 34.91 nm |
| Width (nm) | Thickness (mm) | Peak Load (kN) | Strength (MPa) | Strength (MPa) | |
|---|---|---|---|---|---|
| Sample A_1 | 4.00 | 3.02 | 0.279 | 344.3 | 337.5 ± 3.733 |
| Sample A_2 | 4.00 | 3.02 | 0.267 | 329.2 | |
| Sample A_3 | 4.00 | 3.02 | 0.278 | 343.3 | |
| Sample A_4 | 4.00 | 3.02 | 0.270 | 333.2 | |
| Sample C_1 | 4.02 | 3.00 | 0.50 | 615.1 | 636.3 ± 23.495 |
| Sample C_2 | 4.02 | 3.00 | 0.56 | 699.9 | |
| Sample C_3 | 4.02 | 3.05 | 0.53 | 640.0 | |
| Sample C_4 | 4.02 | 3.05 | 0.49 | 590.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, J.H.; Widiantara, I.P.; Fatimah, S.; Bahanan, W.; Kang, J.-H.; Ko, Y.G. Toward Coarse and Fine Bimodal Structures for Improving the Plasma Resistance of Al2O3. Lubricants 2025, 13, 374. https://doi.org/10.3390/lubricants13090374
Kwon JH, Widiantara IP, Fatimah S, Bahanan W, Kang J-H, Ko YG. Toward Coarse and Fine Bimodal Structures for Improving the Plasma Resistance of Al2O3. Lubricants. 2025; 13(9):374. https://doi.org/10.3390/lubricants13090374
Chicago/Turabian StyleKwon, Jeong Hyeon, I Putu Widiantara, Siti Fatimah, Warda Bahanan, Jee-Hyun Kang, and Young Gun Ko. 2025. "Toward Coarse and Fine Bimodal Structures for Improving the Plasma Resistance of Al2O3" Lubricants 13, no. 9: 374. https://doi.org/10.3390/lubricants13090374
APA StyleKwon, J. H., Widiantara, I. P., Fatimah, S., Bahanan, W., Kang, J.-H., & Ko, Y. G. (2025). Toward Coarse and Fine Bimodal Structures for Improving the Plasma Resistance of Al2O3. Lubricants, 13(9), 374. https://doi.org/10.3390/lubricants13090374







