Research on the Load Characteristics of Aerostatic Spindle Considering Straightness Errors
Abstract
1. Introduction
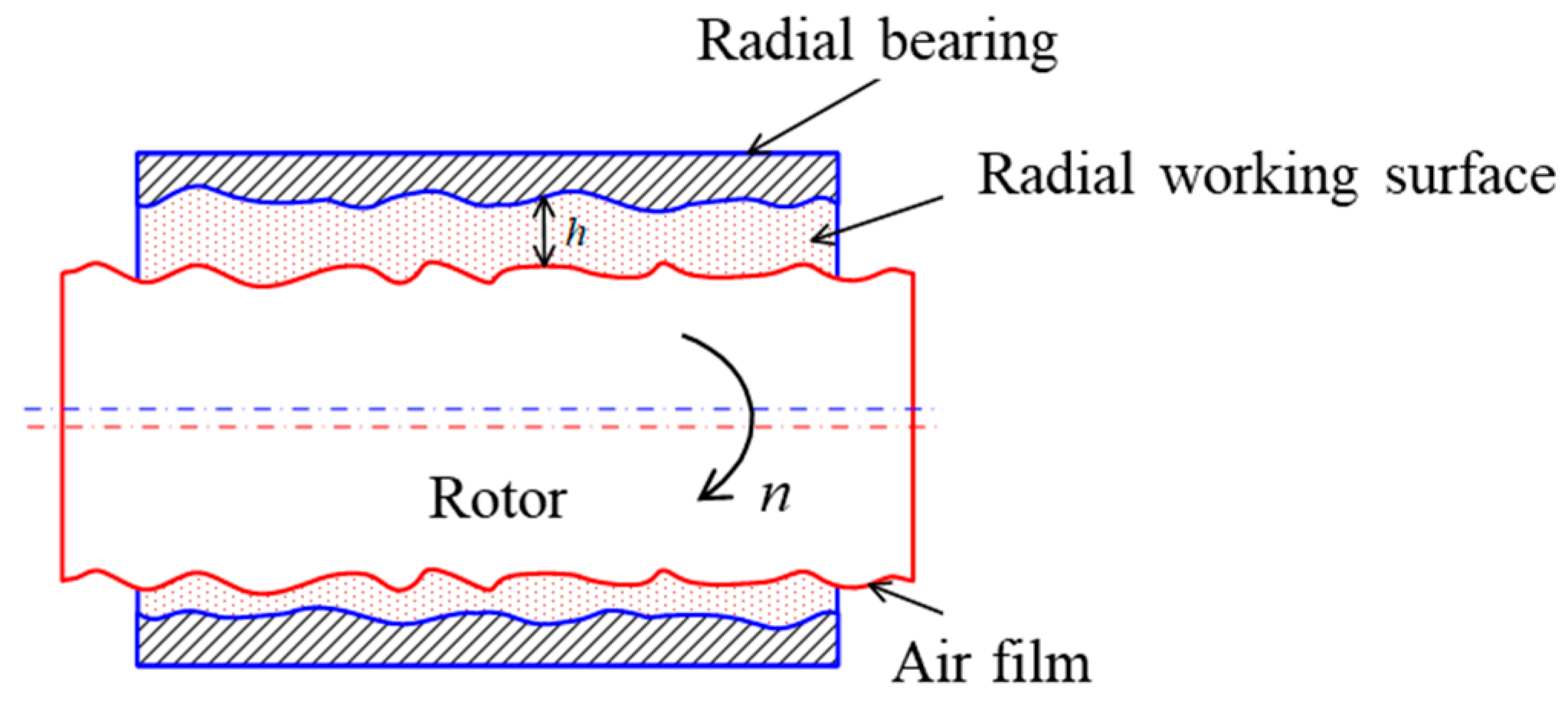
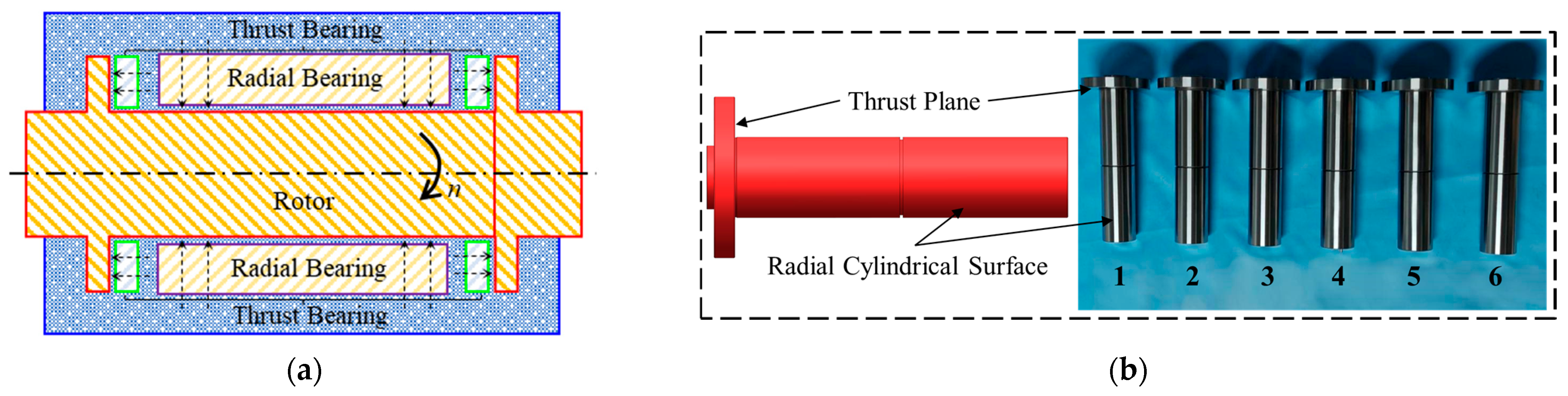
2. Establishment of the Force Model for an Aerostatic Spindle Considering Straightness Errors
2.1. Formulation of the Steady-State Reynolds Equation
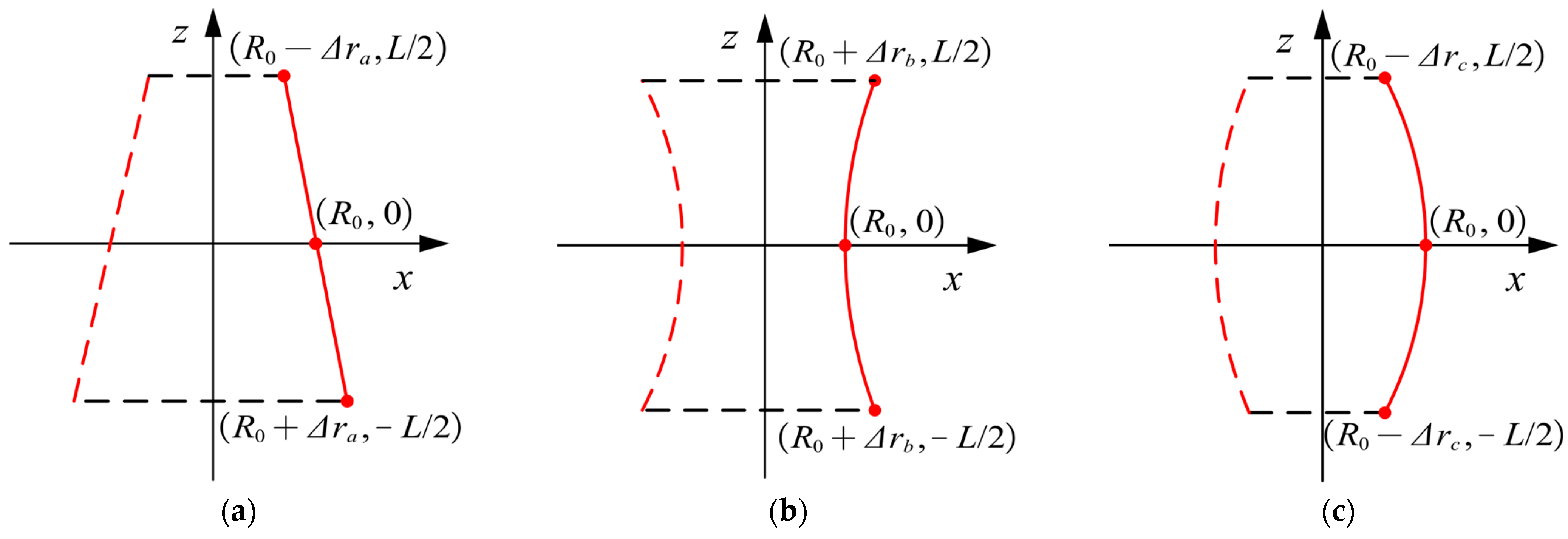
2.2. Fluid Mechanics Modeling of the Radial Surface Considering Straightness Errors
2.3. Fluid Mechanics Modeling of the Thrust Surface Considering Straightness Error
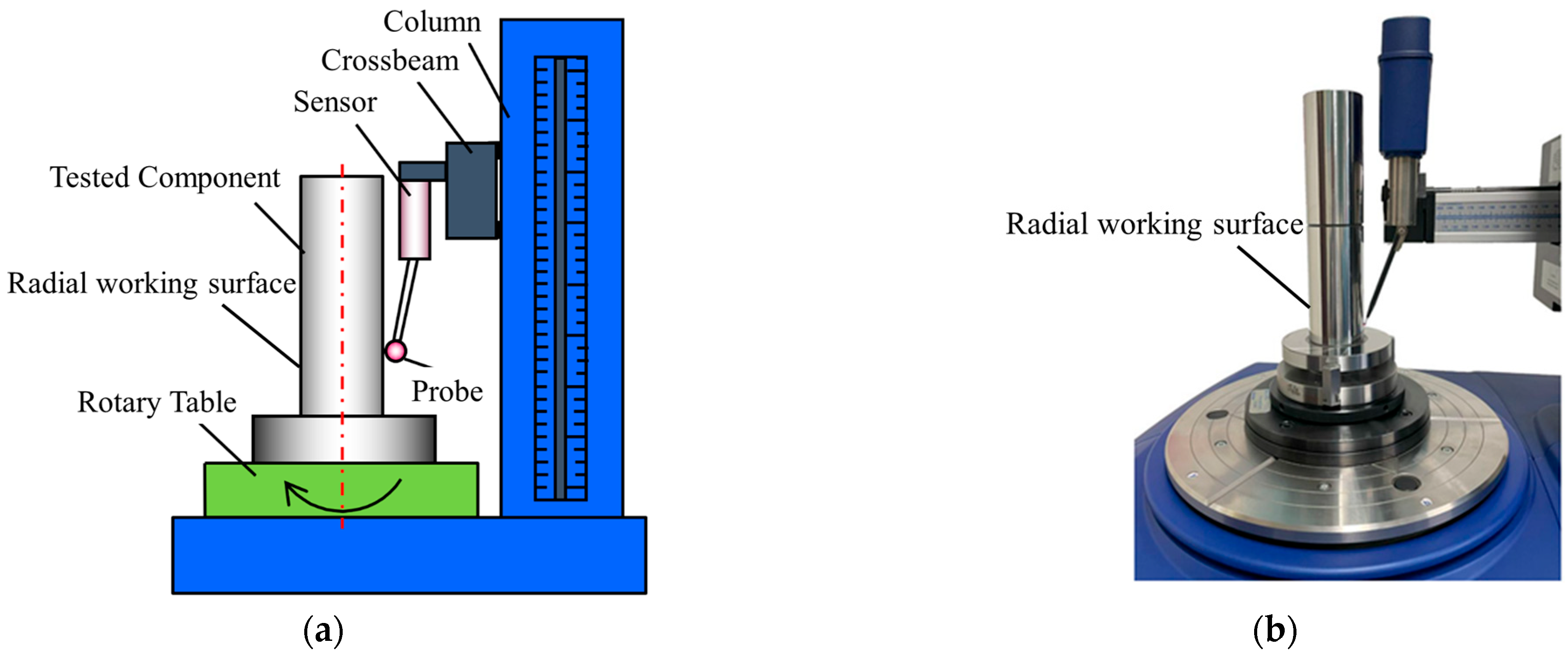
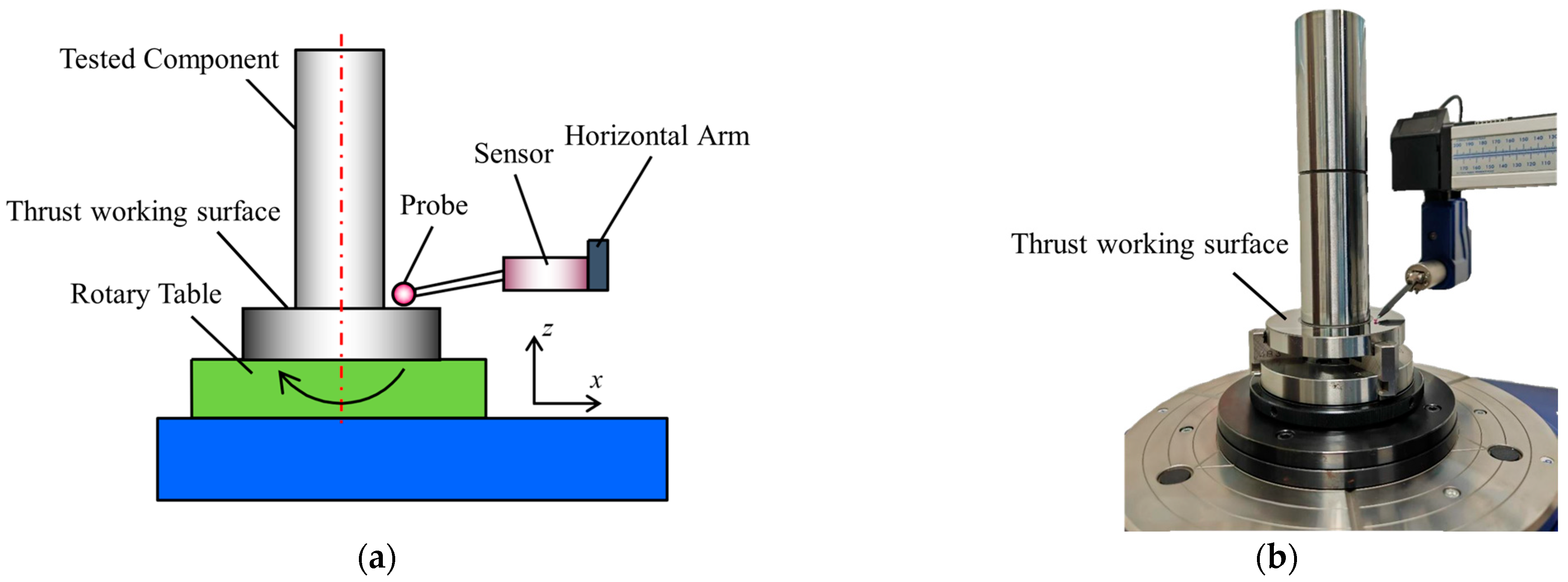
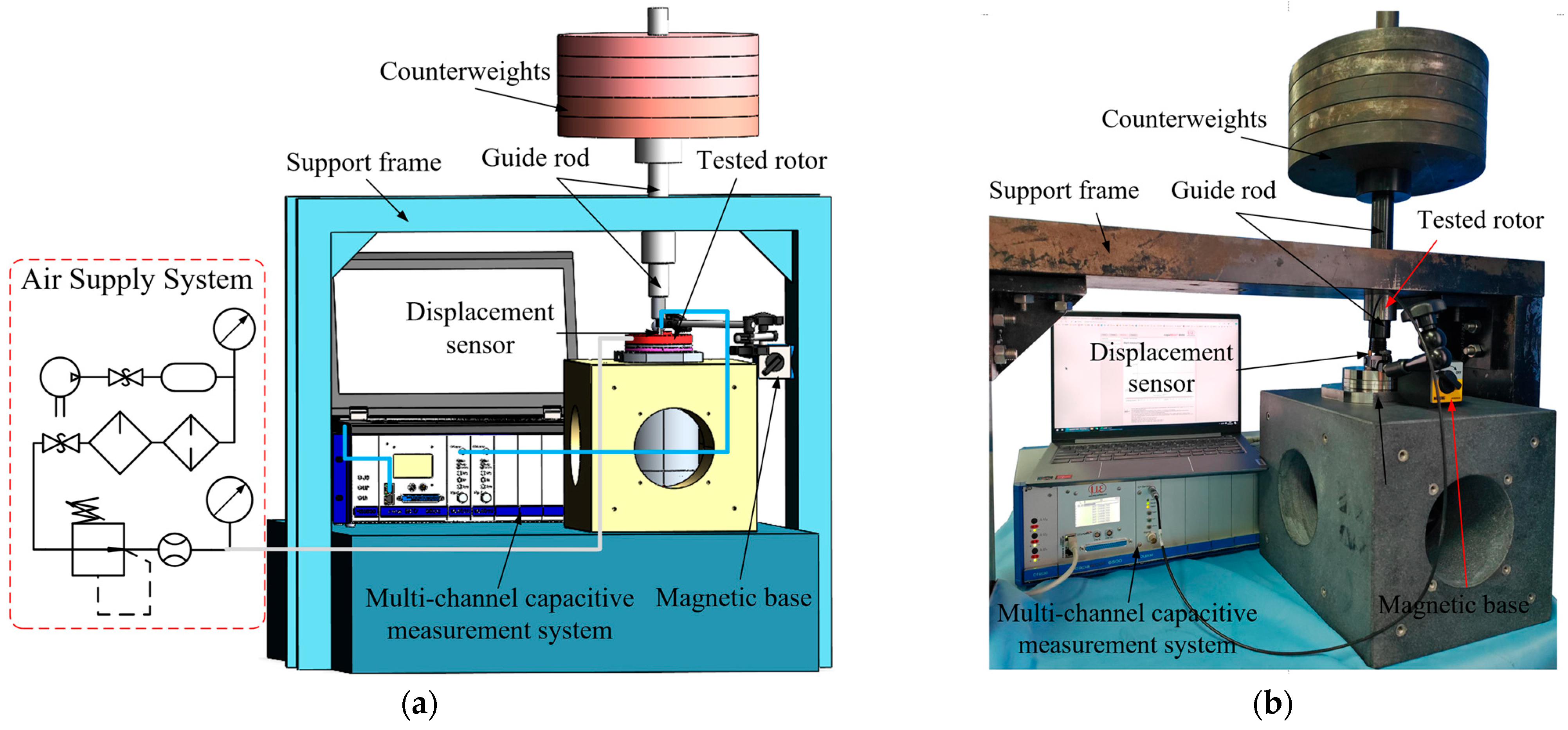
3. Measurement and Testing Equipment
3.1. Measurement Equipment
3.2. Experiment Equipment
4. Effect of Straightness Errors on the Static Characteristics of the Aerostatic Spindle
4.1. Simulation Analysis of the Effect of Straightness Errors on Load Capacity
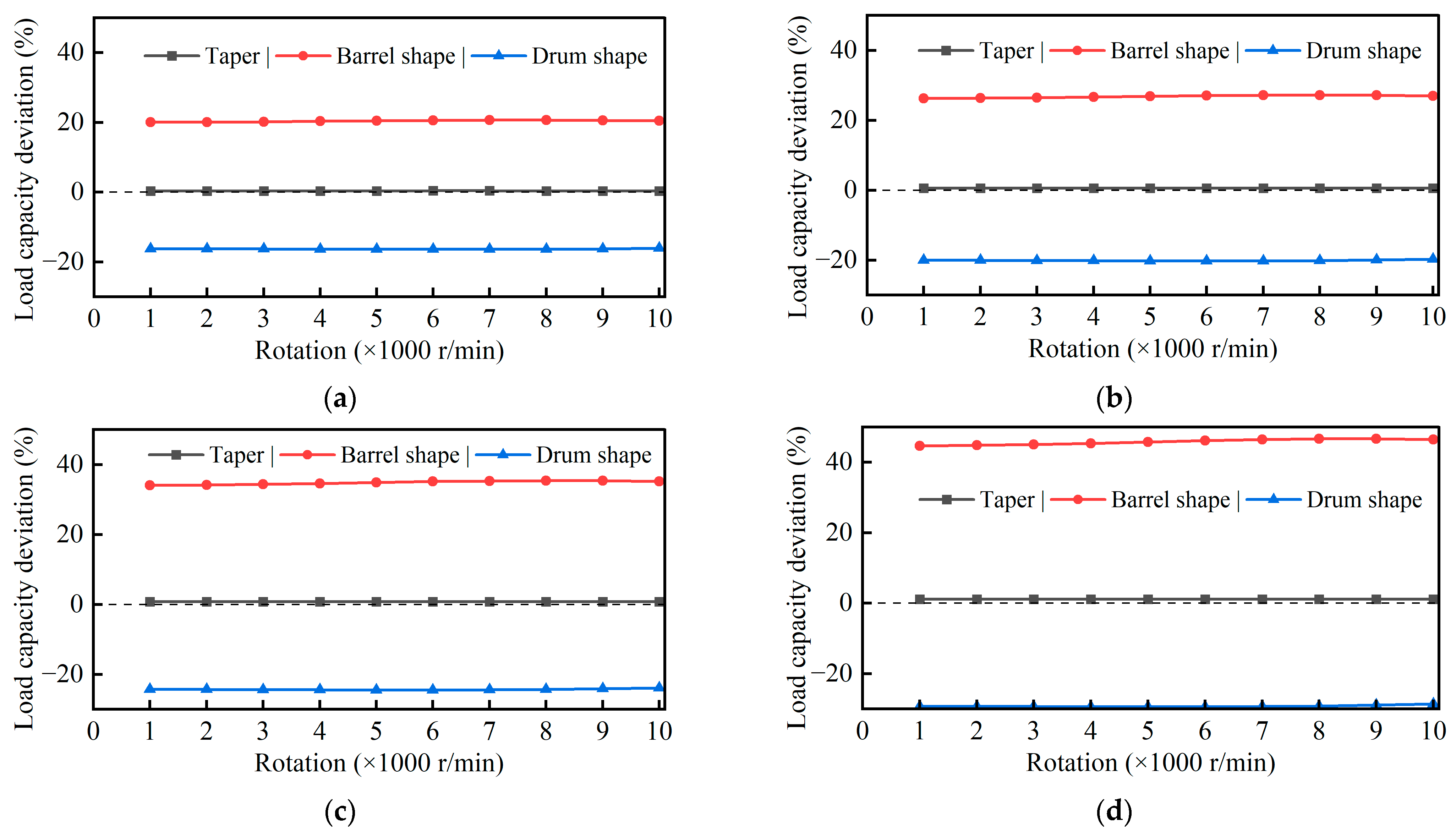
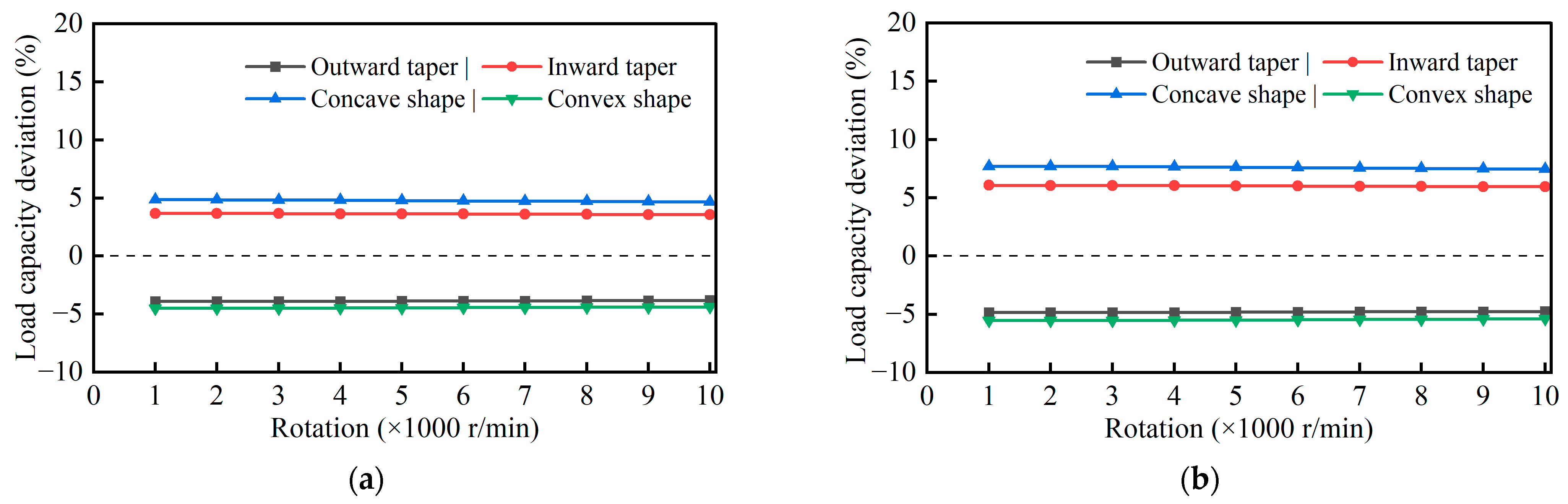
4.1.1. Effect of Straightness Errors on Radial Surface Load Capacity
4.1.2. Effect of Straightness Error on Thrust Surface Load Capacity
4.2. Comparison and Analysis of Experiment and Simulation Results
4.2.1. Comparison of Radial Load Capacity
4.2.2. Comparison of Axial Load Capacity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zang, L.; Hou, W.; Liu, L.; Hu, H.; Wang, X.; Jia, Y.; Hao, Y.; Li, Y.; Zhao, B. The Application and Development of Static Pressure Air Floating in the Field of Micro-Low-Gravity Simulation Experiments for Spacecraft. Lubricants 2025, 13, 258. [Google Scholar] [CrossRef]
- Wen, Z.; Gu, H.; Shi, Z. Key Technologies and Design Methods of Ultra-Precision Aerostatic Bearings. Lubricants 2023, 11, 315. [Google Scholar] [CrossRef]
- Wang, L.; Han, J.; Tang, Z.; Zhang, Y.; Wang, D.; Li, X. Geometric Accuracy Design of High Performance CNC Machine Tools: Modeling, Analysis, and Optimization. Chin. J. Mech. Eng. 2025, 38, 87. [Google Scholar] [CrossRef]
- Zha, C.; Li, T.; Zhao, Y.; Chen, D. Influence of microscale effect on the radial rotation error of aerostatic spindle. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 234, 1131–1142. [Google Scholar] [CrossRef]
- Li, B.; Zhou, D.; Xu, W.; Zhang, Y. Effect of Surface Waviness on Stability of Hydrodynamic Journal Bearing Systems. J. Mech. Eng. 2019, 55, 51–59. [Google Scholar]
- Bangotra, A.; Sharma, S. Effect of partial surface waviness on the dynamic and stability performance of journal bearing. Lubr. Sci. 2024, 36, 197–215. [Google Scholar] [CrossRef]
- Chu, J.; Wu, S.; Wang, J.; Wang, Y.; Wang, S.; Xu, F. Analysis of gas foil thrust bearing considering manufacturing errors: Modeling and experiments. Mech. Syst. Signal Process. 2025, 232, 112698. [Google Scholar] [CrossRef]
- Zhang, G.; Zheng, J.; Yu, H.; Zhao, R.; Shi, W.; Wang, J. Rotation accuracy analysis of aerostatic spindle considering shaft’s roundness and cylindricity. Appl. Sci. 2021, 11, 7912. [Google Scholar] [CrossRef]
- Cappa, S.; Reynaerts, D.; Al-Bender, F. Reducing the Radial Error Motion of an Aerostatic Journal Bearing to a Nanometre Level: Theoretical Modelling. Tribol. Lett. 2014, 53, 27–41. [Google Scholar] [CrossRef]
- Zhuang, H.; Ding, J.; Chen, P.; Chang, Y.; Zeng, X.; Yang, H.; Liu, X.; Wei, W. Effect of surface waviness on the performances of an aerostatic thrust bearing with orifice-type restrictor. Int. J. Precis. Eng. Manuf. 2021, 22, 1735–1759. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, L.; Huang, M.; Yue, X.; Xu, Q. Numerical investigation of journal misalignment on the static and dynamic characteristics of aerostatic journal bearings. Measurement 2018, 128, 314–324. [Google Scholar] [CrossRef]
- Chen, P.; Ding, J.; Zhuang, H.; Chang, Y. A novel method for studying fluid-solid interaction problems of the rotor system in air bearings with manufacturing errors. Mech. Syst. Signal Process. 2023, 202, 110709. [Google Scholar] [CrossRef]
- Li, R.; Li, Y.; Wang, P.; Ye, Y.; Li, X.; Chen, Y. Influence of Manufacturing Errors on Static and Dynamic Performances of Aerostatic Spindle. Mech. Sci. Technol. Aerosp. Eng. 2024, 43, 650–659. [Google Scholar]
- Lin, J. Surface roughness effect on the dynamic stiffness and damping characteristics of compensated hydrostatic thrusts bearings. Int. J. Mach. Tools Manuf. Des. Res. Appl. 2000, 40, 1671–1689. [Google Scholar] [CrossRef]
- Kumar, R.; Azam, M.S.; Ghosh, S.K. Influence of stochastic roughness on performance of a Rayleigh step bearing operating under Thermo-elastohydrodynamic lubrication considering shear flow factor. Tribol. Int. 2019, 134, 264–280. [Google Scholar] [CrossRef]
- Zhang, P. Accuracy prediction model of an orifice-compensated aerostatic bearing. Precis. Eng. 2021, 72, 837–846. [Google Scholar] [CrossRef]
- Chen, P.; Ding, J.; Zhuang, H.; Chang, Y.; Liu, X. Influence of manufacturing errors and misalignment on the performances of air journal bearings considering inertia effects based on SUPG finite element method. Measurement 2022, 189, 110443. [Google Scholar] [CrossRef]
- Ji Hua Laboratory. A Dual-Axis Air-Bearing Platform with Dynamic Tilt Compensation, Control Method and Exposure Machine. CN202411522424.4, 17 December 2024. [Google Scholar]
- Cui, H.; Wang, Y.; Yue, X.; Huang, M.; Wang, W.; Jiang, Z. Numerical analysis and experimental investigation into the effects of manufacturing errors on the running accuracy of the aerostatic porous spindle. Tribol. Int. 2018, 118, 20–36. [Google Scholar] [CrossRef]
- Sharma, S.C.; Phalle, V.M.; Jain, S.C. Combined Influence of Wear and Misalignment of Journal on the Performance Analysis of Three-Lobe Three-Pocket Hybrid Journal Bearing Compensated with Capillary Restrictor. J. Tribol. 2012, 134, 011703-1–011703-11. [Google Scholar] [CrossRef]
- COIMS. LTD High Precision Air Bearing Stage with Capability of Parasitic Error Compensation. US202217668425, 10 October 2023. [Google Scholar]
- Michalec, M.; Polnický, V.; Foltýn, J.; Svoboda, P.; Šperka, P.; Hurník, J. The prediction of large-scale hydrostatic bearing pad misalignment error and its compensation using compliant support. Precis. Eng. 2022, 75, 67–79. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, H.; Zou, D.; Ta, N.; Rao, Z. Comparison study of misalignment effect along two perpendicular directions on the stability of rigid rotor-aerostatic journal bearing system. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 234, 1618–1634. [Google Scholar] [CrossRef]
- Ning, Y.; Li, Y.; Zhang, D. The effect of manufacturing errors on the performance of a gas-dynamic bearing gyroscope. Machines 2022, 10, 1010. [Google Scholar] [CrossRef]
- An, C.H.; Zhang, Y.; Xu, Q.; Zhang, F.H.; Zhang, J.F.; Zhang, L.J.; Wang, J.H. Modeling of dynamic characteristic of the aerostatic bearing spindle in an ultra-precision fly cutting machine. Int. J. Mach. Tools Manuf. 2010, 50, 374–385. [Google Scholar] [CrossRef]
- Mallya, R.; Shenoy, S.B.; Pai, R. Static characteristics of misaligned multiple axial groove water-lubricated bearing in the turbulent regime. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 231, 385–398. [Google Scholar] [CrossRef]
- Sanying Precision (Tianjin) Instrument Equipment Co., Ltd. A High-Precision Air-Bearing Motion Platform and Method for Wafer Inspection. CN202111374217.5, 14 June 2024. [Google Scholar]
- Sun, Y.; Hong, J.; Liu, Z.; Guo, J. A Calculating Method for the Geometric Rotation Accuracy of Precision Spindles Considering the Manufacturing Errors of Component Parts. J. Mech. Eng. 2017, 53, 173–182. [Google Scholar] [CrossRef]
- Zhang, G.; Zheng, J.; Yu, H.; Chen, T.; Shan, S.; Peng, C. Influence of shape errors and inertia effects on the error motion of the aerostatic spindle. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2024, 238, 260–271. [Google Scholar] [CrossRef]
- Xiao, H.; Li, W.; Zhou, Z.; Huang, X.; Ren, Y. Performance analysis of aerostatic journal micro-bearing and its application to high-speed precision micro-spindles. Tribol. Int. 2018, 120, 476–490. [Google Scholar] [CrossRef]
- Banerjee, M.B.; Shandil, R.G.; Katyal, S.P.; Dube, G.S.; Pal, T.S.; Banerjee, K. A nonlinear theory of hydrodynamic lubrication. J. Math. Anal. Appl. 1986, 117, 48–56. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Schmid, S.R.; Jacobson, B.O. Fundamentals of Fluid Film Lubrication; Taylor and Francis: Milton Park, UK; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Pinkus, O.; Lund, J.W. Centrifugal Effects in Thrust Bearings and Seals Under Laminar Conditions. J. Lubr. Technol. 1981, 103, 126–136. [Google Scholar] [CrossRef]
- Zhang, G. Manufacturing Errors Modeling and Dynamic, Static Characteristics Research of High-Precision Aerostatic Spindle. Ph.D. Thesis, Xi’an University of Technology, Xi’an, China, 2024. [Google Scholar]






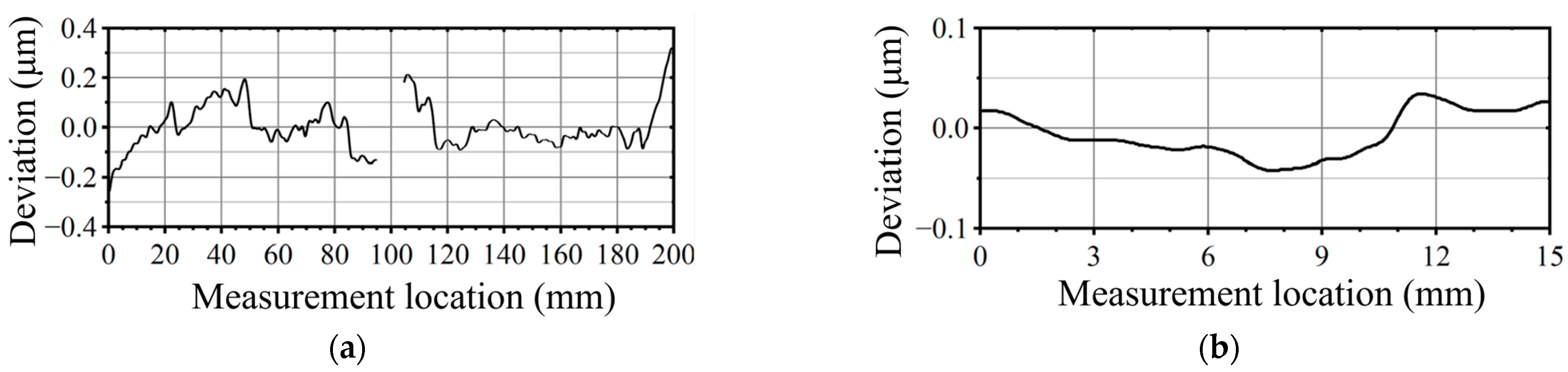
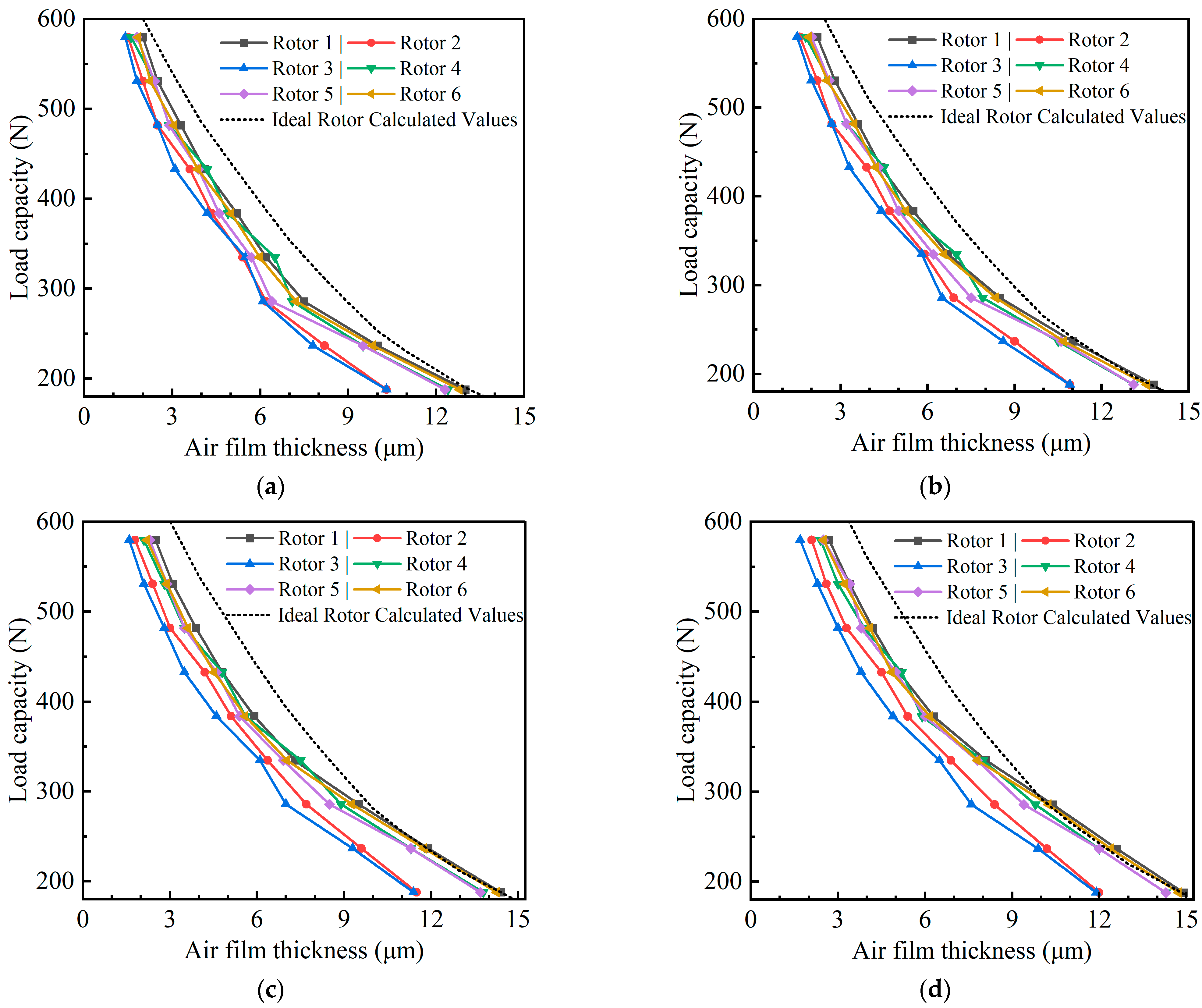
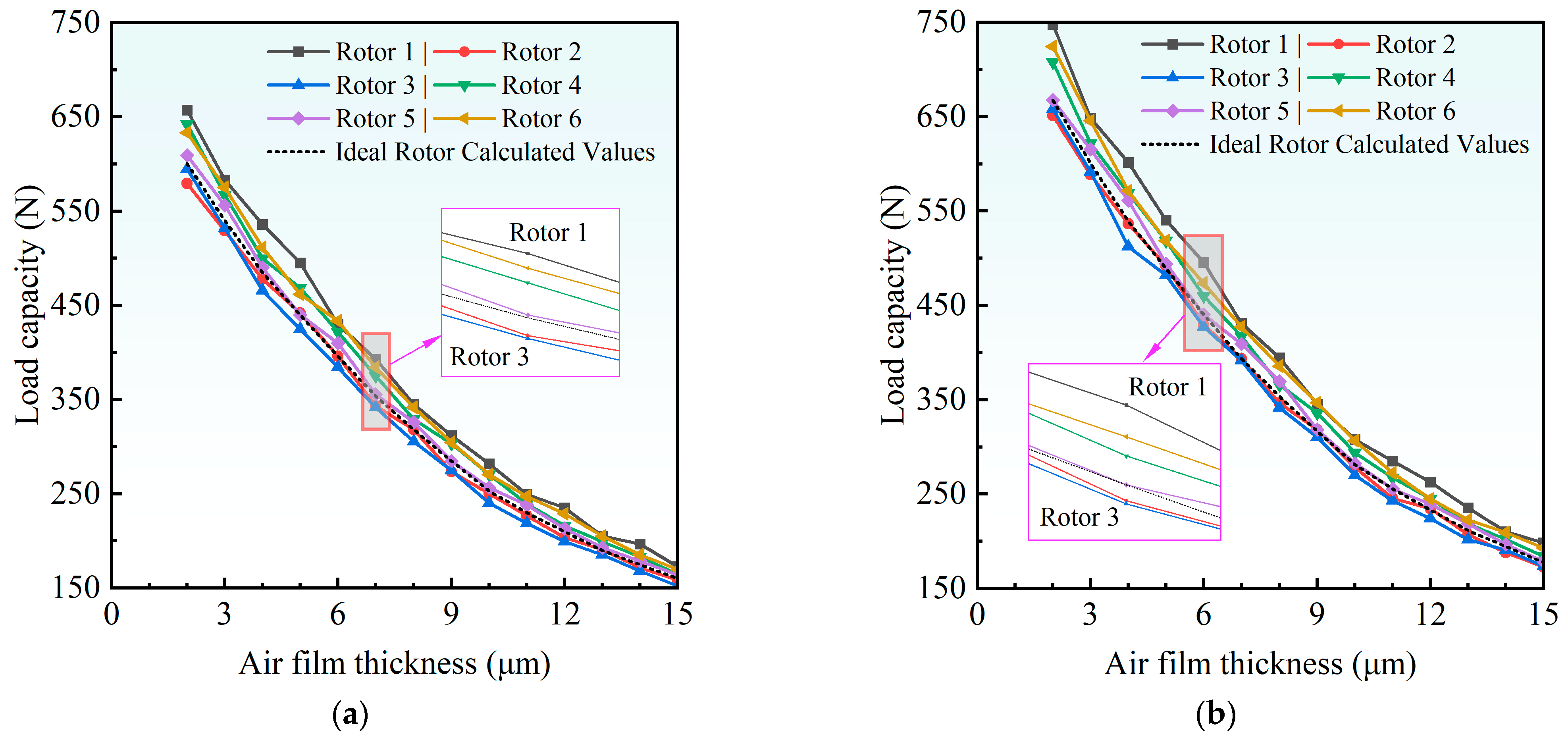
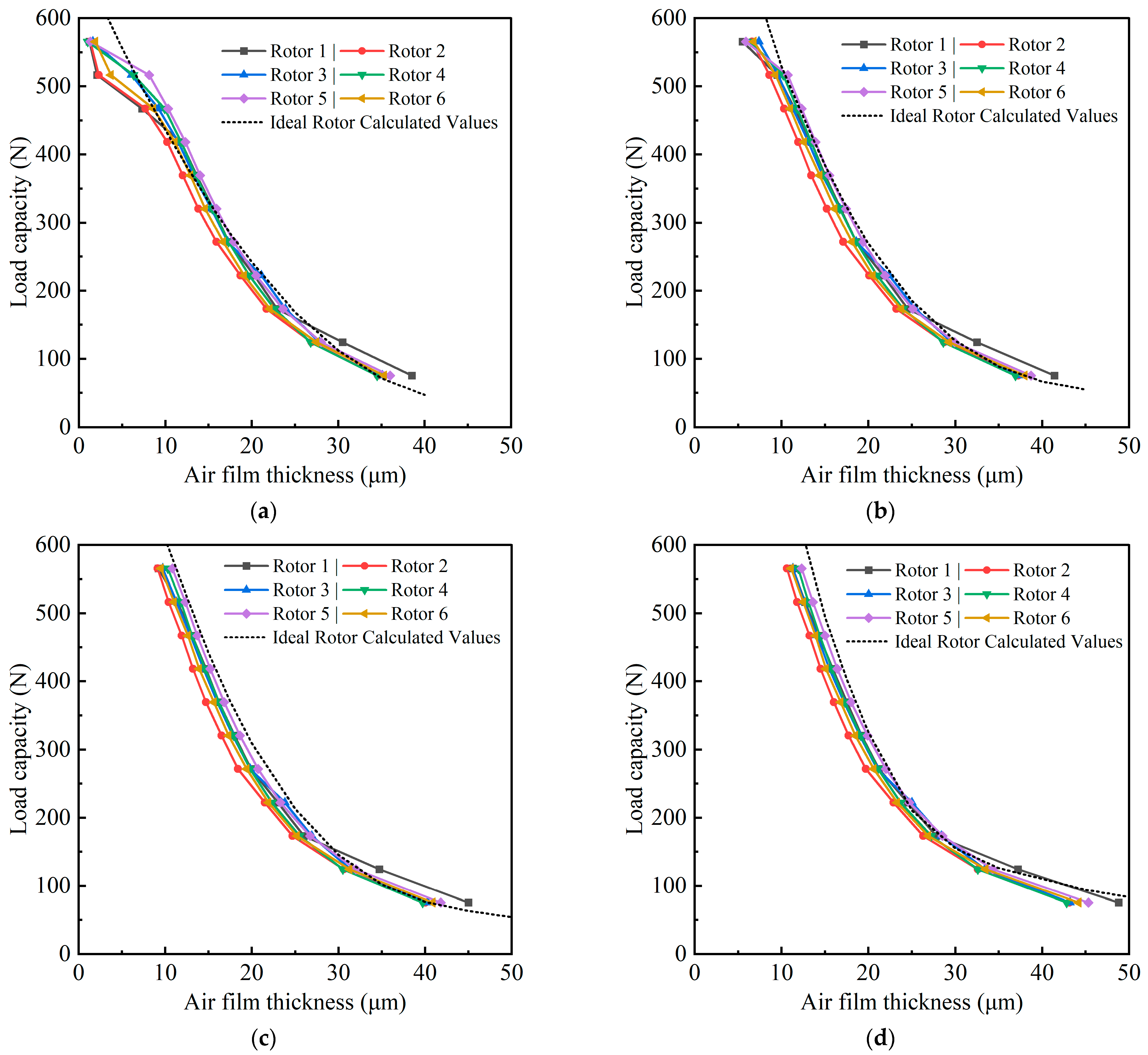

| Parameter | Error Value | Units |
|---|---|---|
| radial/axial motion error of the rotary table | <0.05 | μm |
| straightness error of the column | <0.07/490 | μm/mm |
| parallelism error between column and spindle axis | <0.24/490 | μm/mm |
| Equipment | Measurement Range | Resolution |
|---|---|---|
| tension-compression force sensor (Tianmu Instrument Co., Ltd., Shanghai, China) | 0–100 kg | 0.02 kg |
| CS05 capacitive sensor (Micro-Epsilon, Ortenburg, Germany) | 0–500 μm | 0.01 μm |
| AW30 pressure regulator (SMC, Tokyo, Japan) | 0–0.80 MPa | stepless adjustment |
| PFM711S-C8L flow meter (SMC, Tokyo, Japan) | 2–100 L/min | 0.1 L/min |
| Rotor | Axial Straightness Error/μm | Average Air Film Thickness/μm |
|---|---|---|
| rotor 1 | 0.58 | 12.5 |
| rotor 2 | 0.44 | 10.0 |
| rotor 3 | 0.45 | 11.5 |
| rotor 4 | 0.75 | 9.5 |
| rotor 5 | 0.73 | 11.0 |
| rotor 6 | 0.80 | 10.5 |
| Rotor | Radial Straightness Error/μm | Average Air Film Thickness/μm |
|---|---|---|
| rotor 1 | 0.080 | 19.8 |
| rotor 2 | 0.060 | 21.3 |
| rotor 3 | 0.120 | 18.6 |
| rotor 4 | 0.090 | 19.2 |
| rotor 5 | 0.140 | 21.7 |
| rotor 6 | 0.006 | 22.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Guo, Y.; Wang, G.; Wang, W.; Li, Y.; Yu, H.; Zhang, S. Research on the Load Characteristics of Aerostatic Spindle Considering Straightness Errors. Lubricants 2025, 13, 326. https://doi.org/10.3390/lubricants13080326
Zhang G, Guo Y, Wang G, Wang W, Li Y, Yu H, Zhang S. Research on the Load Characteristics of Aerostatic Spindle Considering Straightness Errors. Lubricants. 2025; 13(8):326. https://doi.org/10.3390/lubricants13080326
Chicago/Turabian StyleZhang, Guoqing, Yu Guo, Guangzhou Wang, Wenbo Wang, Youhua Li, Hechun Yu, and Suxiang Zhang. 2025. "Research on the Load Characteristics of Aerostatic Spindle Considering Straightness Errors" Lubricants 13, no. 8: 326. https://doi.org/10.3390/lubricants13080326
APA StyleZhang, G., Guo, Y., Wang, G., Wang, W., Li, Y., Yu, H., & Zhang, S. (2025). Research on the Load Characteristics of Aerostatic Spindle Considering Straightness Errors. Lubricants, 13(8), 326. https://doi.org/10.3390/lubricants13080326




